Statistical Difference Representation-Based Transformer for Heterogeneous Change Detection
Abstract
1. Introduction
- (1)
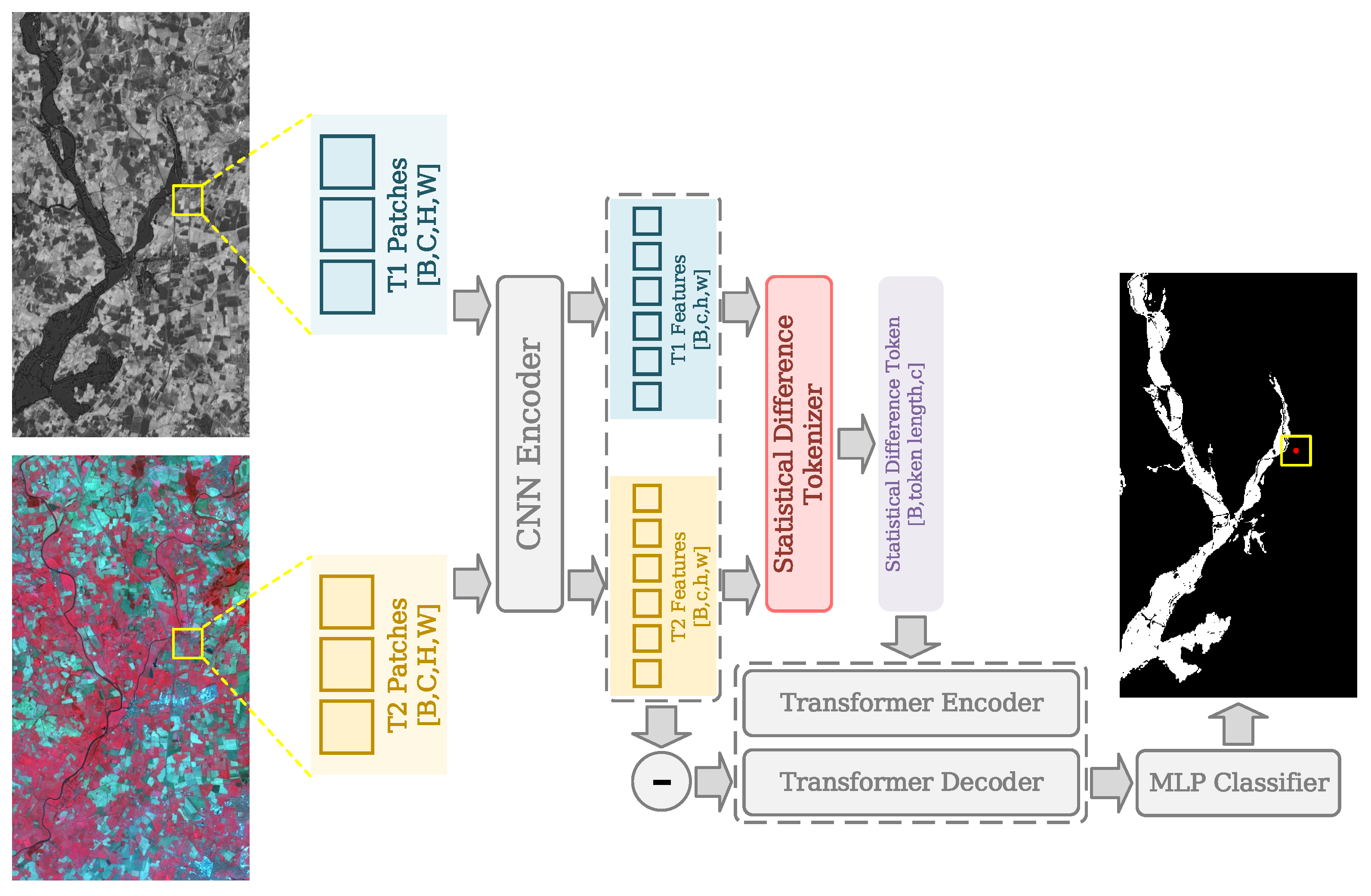
- The Statistical Difference representation Transformer (SDFormer) is proposed to reduce modal differences and enhance the ability of change information extraction through feature-level statistical analysis.
- (2)
- A weakly supervised framework combined with structural similarity-guided sample generation strategy () is designed to iteratively generate reliable pseudo-labels to expand the training set and improve the model performance.
- (3)
- A statistical difference tokenization scheme within the Transformer architecture is developed to explicitly mitigate modality discrepancies while leveraging global contextual awareness, enhancing accuracy and robustness in complex HCD scenarios.
2. Related Works
3. Methodology
3.1. Overview
3.2. Initialization
3.3. Iteration
Structure Similarity-Guided Sample Generating
3.4. Statistical Difference Representation Transformer
4. Experiments and Results
4.1. Data Set Descriptions
4.2. Comparative Approaches and Evaluation Indicators
4.2.1. Comparative Approaches
4.2.2. Evaluation Indicators
4.3. Implementation Details
4.4. Comparison of DIs with Different Methods
4.4.1. Comparison Based on ROC
4.4.2. Comparison Based on PR
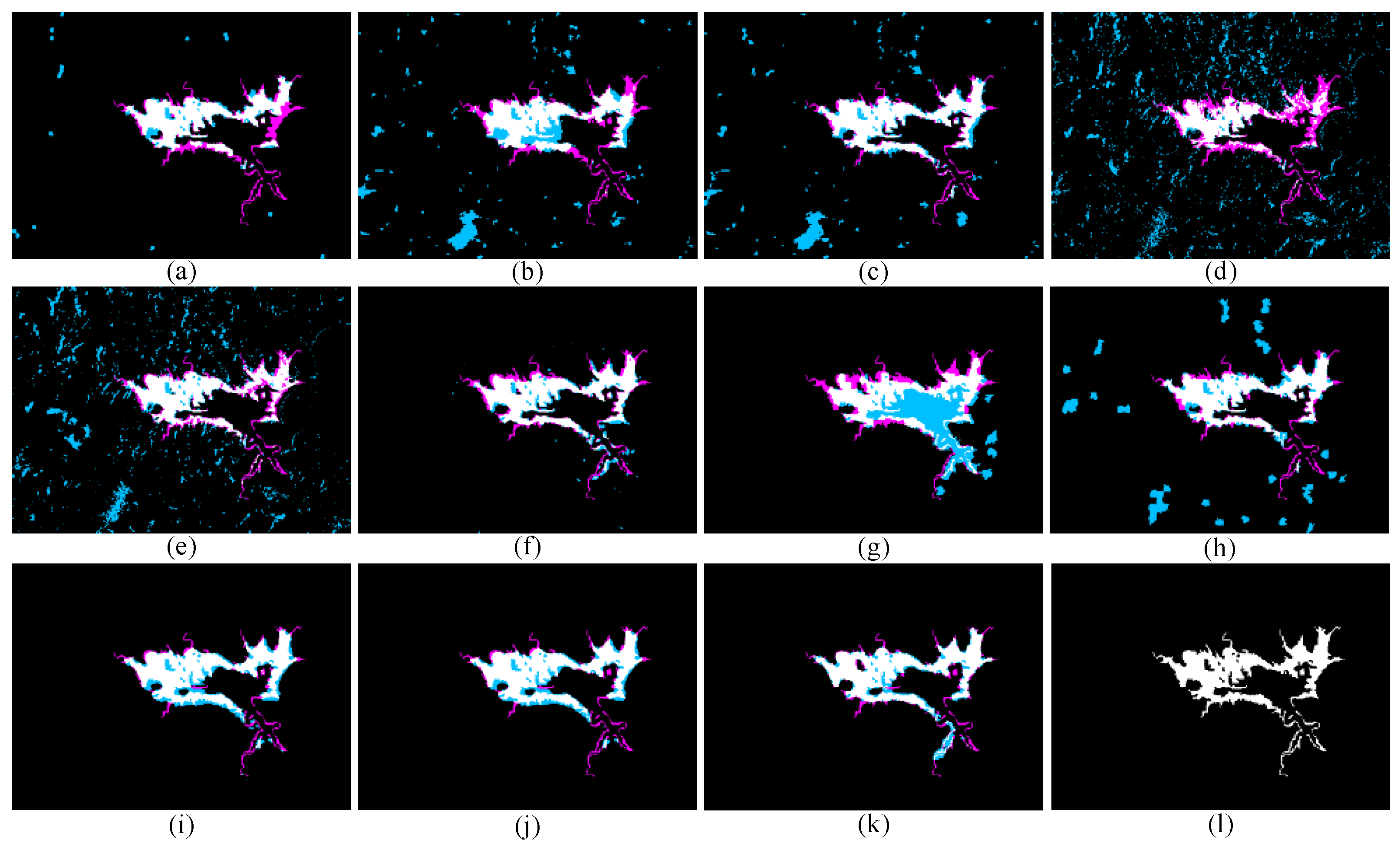
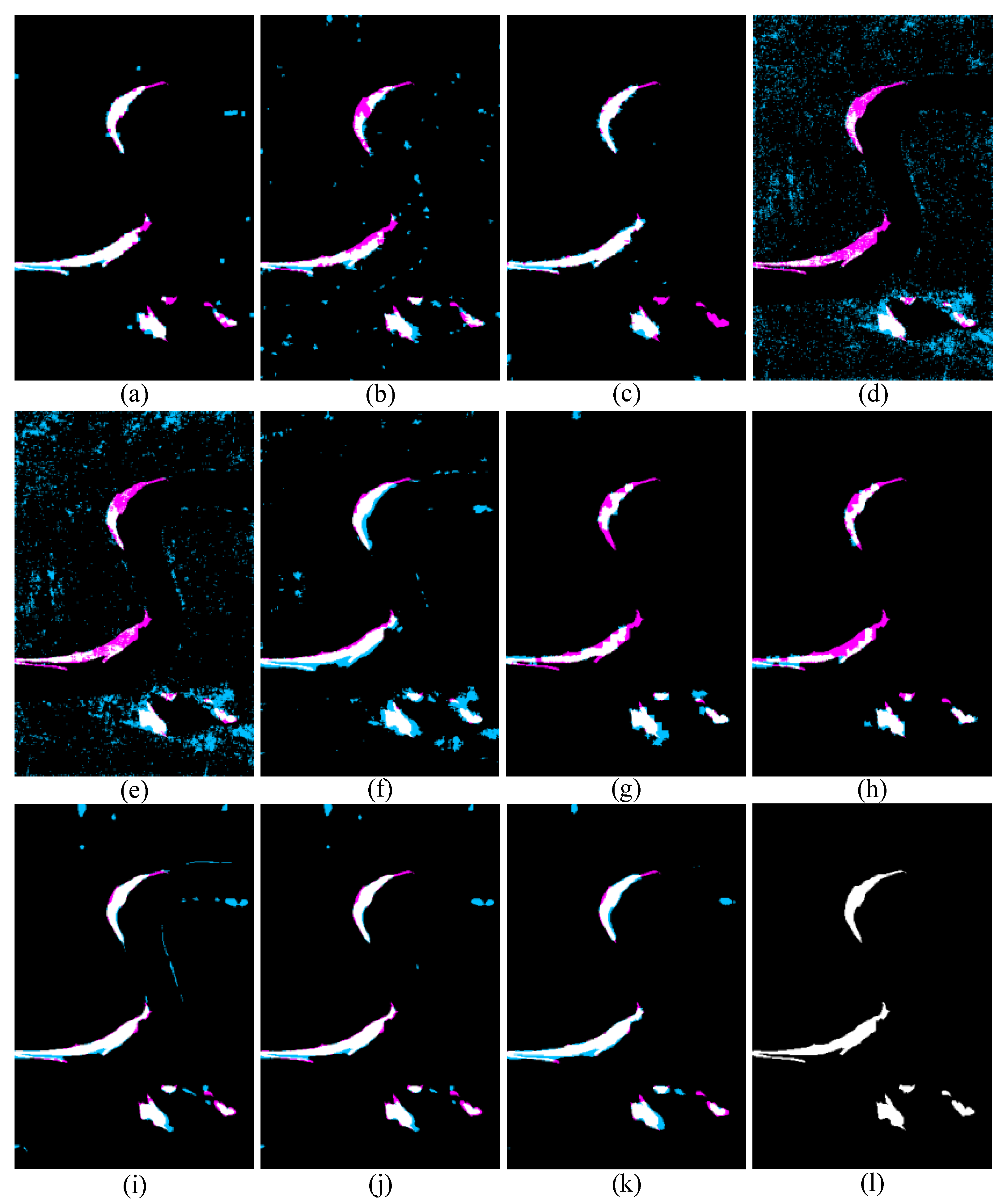
4.5. Comparison of BCIs with Different Methods
4.5.1. Results on Data Set #1
4.5.2. Results on Data Set #2
4.5.3. Results on Data Set #3
5. Discussion
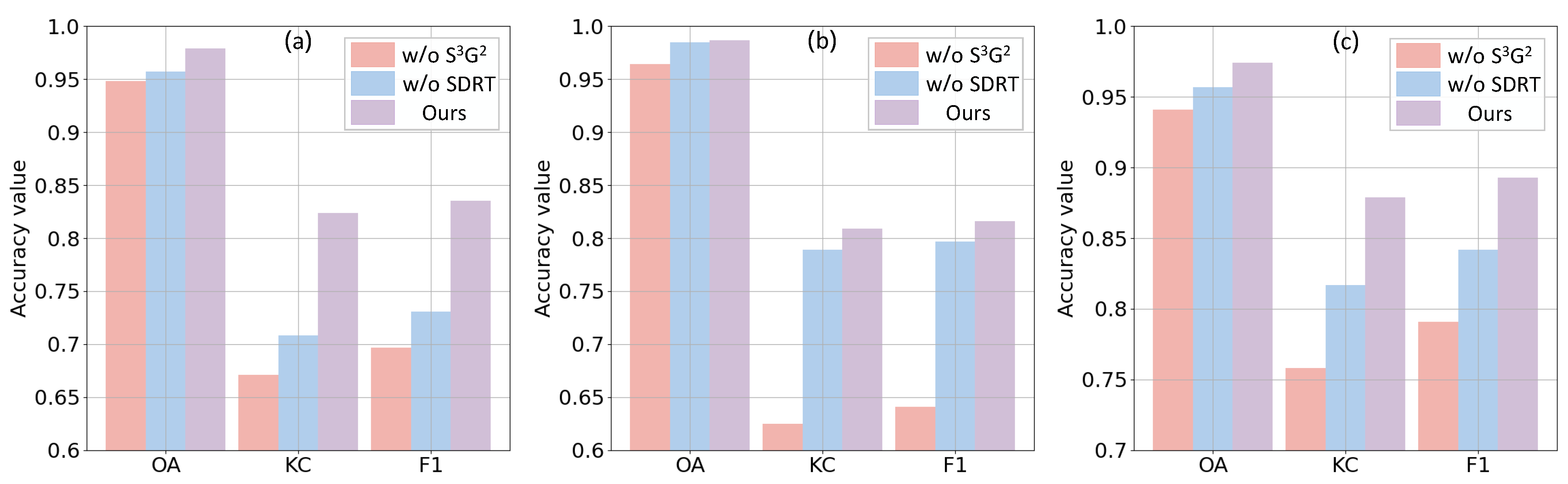
5.1. Ablation Study for Different Components
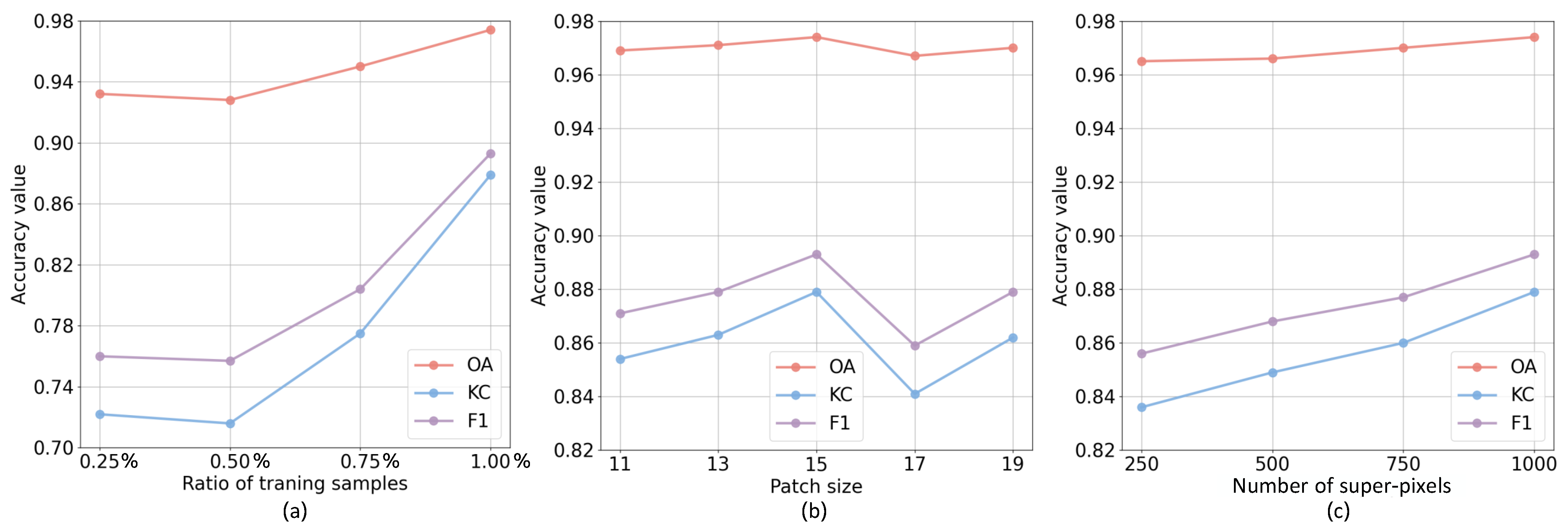
5.2. Sensitivity Analysis of Parameters
5.2.1. Sensitivity Analysis of Ratio of Training Samples
5.2.2. Sensitivity Analysis of Patch Size
5.2.3. Sensitivity Analysis of Number of Super-Pixels
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xu, X.; Zhou, Y.; Lu, X.; Chen, Z. FERA-net: A building change detection method for high-resolution remote sensing imagery based on residual attention and high-frequency features. Remote Sens. 2023, 15, 395. [Google Scholar] [CrossRef]
- Lv, Z.; Liu, T.; Benediktsson, J.A.; Falco, N. Land cover change detection techniques: Very-high-resolution optical images: A review. IEEE Geosci. Remote Sens. Mag. 2021, 10, 44–63. [Google Scholar] [CrossRef]
- Zheng, H.; Gong, M.; Liu, T.; Jiang, F.; Zhan, T.; Lu, D.; Zhang, M. HFA-Net: High frequency attention siamese network for building change detection in VHR remote sensing images. Pattern Recognit. 2022, 129, 108717. [Google Scholar] [CrossRef]
- Chen, Z.; Zhou, Y.; Wang, B.; Xu, X.; He, N.; Jin, S.; Jin, S. EGDE-Net: A building change detection method for high-resolution remote sensing imagery based on edge guidance and differential enhancement. ISPRS J. Photogramm. Remote Sens. 2022, 191, 203–222. [Google Scholar] [CrossRef]
- Li, J.; Gong, M.; Liu, H.; Zhang, Y.; Zhang, M.; Wu, Y. Multiform ensemble self-supervised learning for few-shot remote sensing scene classification. IEEE Trans. Geosci. Remote Sens. 2023, 61, 4500416. [Google Scholar] [CrossRef]
- Huang, X.; Cao, Y.; Li, J. An automatic change detection method for monitoring newly constructed building areas using time-series multi-view high-resolution optical satellite images. Remote Sens. Environ. 2020, 244, 111802. [Google Scholar] [CrossRef]
- Liu, T.; Gong, M.; Jiang, F.; Zhang, Y.; Li, H. Landslide inventory mapping method based on adaptive histogram-mean distance with bitemporal VHR aerial images. IEEE Geosci. Remote Sens. Lett. 2021, 19, 3003005. [Google Scholar] [CrossRef]
- Saha, S.; Bovolo, F.; Bruzzone, L. Building change detection in VHR SAR images via unsupervised deep transcoding. IEEE Trans. Geosci. Remote Sens. 2020, 59, 1917–1929. [Google Scholar] [CrossRef]
- Lu, D.; Mausel, P.; Brondizio, E.; Moran, E. Change detection techniques. Int. J. Remote Sens. 2004, 25, 2365–2401. [Google Scholar] [CrossRef]
- Shi, W.; Zhang, M.; Zhang, R.; Chen, S.; Zhan, Z. Change detection based on artificial intelligence: State-of-the-art and challenges. Remote Sens. 2020, 12, 1688. [Google Scholar] [CrossRef]
- Walter, V. Object-based classification of remote sensing data for change detection. ISPRS J. Photogramm. Remote Sens. 2004, 58, 225–238. [Google Scholar] [CrossRef]
- Daudt, R.C.; Le Saux, B.; Boulch, A. Fully convolutional siamese networks for change detection. In Proceedings of the 2018 25th IEEE International Conference on Image Processing (ICIP), Athens, Greece, 7–10 October 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 4063–4067. [Google Scholar]
- Li, J.; Li, H.; Liu, Y.; Gong, M. Multi-fidelity evolutionary multitasking optimization for hyperspectral endmember extraction. Appl. Soft Comput. 2021, 111, 107713. [Google Scholar] [CrossRef]
- Liu, T.; Gong, M.; Lu, D.; Zhang, Q.; Zheng, H.; Jiang, F.; Zhang, M. Building change detection for VHR remote sensing images via local–global pyramid network and cross-task transfer learning strategy. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4704817. [Google Scholar] [CrossRef]
- Chen, H.; Qi, Z.; Shi, Z. Remote sensing image change detection with transformers. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4704817. [Google Scholar] [CrossRef]
- Shafique, A.; Cao, G.; Khan, Z.; Asad, M.; Aslam, M. Deep learning-based change detection in remote sensing images: A review. Remote Sens. 2022, 14, 871. [Google Scholar] [CrossRef]
- Ghaderpour, E.; Pagiatakis, S.D.; Hassan, Q.K. A survey on change detection and time series analysis with applications. Appl. Sci. 2021, 11, 6141. [Google Scholar] [CrossRef]
- Li, J.; Gong, M.; Wei, J.; Zhang, Y.; Zhao, Y.; Wang, S.; Jiang, X. Evolutionary multitasking cooperative transfer for multiobjective hyperspectral sparse unmixing. Knowl.-Based Syst. 2024, 285, 111306. [Google Scholar] [CrossRef]
- Li, J.; Gong, M.; Li, W.; Zhang, M.; Zhang, Y.; Wang, S.; Wu, Y. MSANet: Multiscale Self-Attention Aggregation Network for Few-Shot Aerial Imagery Segmentation. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4500216. [Google Scholar] [CrossRef]
- Saidi, S.; Idbraim, S.; Karmoude, Y.; Masse, A.; Arbelo, M. Deep-Learning for Change Detection Using Multi-Modal Fusion of Remote Sensing Images: A Review. Remote Sens. 2024, 16, 3852. [Google Scholar] [CrossRef]
- Chen, H.; Yokoya, N.; Wu, C.; Du, B. Unsupervised multimodal change detection based on structural relationship graph representation learning. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5635318. [Google Scholar] [CrossRef]
- Li, J.; Gong, M.; Liu, Z.; Wang, S.; Zhang, Y.; Zhou, Y.; Gao, Y. Towards Multi-Party Personalized Collaborative Learning in Remote Sensing. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4503616. [Google Scholar]
- Liu, T.; Xu, J.; Lei, T.; Wang, Y.; Du, X.; Zhang, W.; Lv, Z.; Gong, M. AEKAN: Exploring Superpixel-based AutoEncoder Kolmogorov-Arnold Network for Unsupervised Multimodal Change Detection. IEEE Trans. Geosci. Remote Sens. 2025, 63, 5601114. [Google Scholar] [CrossRef]
- Liu, T.; Zhang, M.; Gong, M.; Zhang, Q.; Jiang, F.; Zheng, H.; Lu, D. Commonality Feature Representation Learning for Unsupervised Multimodal Change Detection. IEEE Trans. Image Process. 2025, 34, 1219–1233. [Google Scholar] [CrossRef] [PubMed]
- Pu, Y.; Gong, M.; Liu, T.; Zhang, M.; Gao, T.; Jiang, F.; Hu, X. Adversarial feature equilibrium network for multimodal change detection in heterogeneous remote sensing images. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4512617. [Google Scholar] [CrossRef]
- Gong, M.; Liu, T.; Zhang, M.; Zhang, Q.; Lu, D.; Zheng, H.; Jiang, F. Context–content collaborative network for building extraction from high-resolution imagery. Knowl.-Based Syst. 2023, 263, 110283. [Google Scholar] [CrossRef]
- Lv, Z.Y.; Liu, T.F.; Zhang, P.; Benediktsson, J.A.; Lei, T.; Zhang, X. Novel adaptive histogram trend similarity approach for land cover change detection by using bitemporal very-high-resolution remote sensing images. IEEE Trans. Geosci. Remote Sens. 2019, 57, 9554–9574. [Google Scholar] [CrossRef]
- Liu, M.; Lin, S.; Zhong, Y.; Shi, Q.; Li, J. A Memory Guided Network and A Novel Dataset for Cropland Semantic Change Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4410013. [Google Scholar] [CrossRef]
- Lang, C.; Cheng, G.; Wu, J.; Li, Z.; Xie, X.; Li, J.; Han, J. Toward Open-World Remote Sensing Imagery Interpretation: Past, present, and future. IEEE Geosci. Remote Sens. Mag. 2024, 2–38. [Google Scholar] [CrossRef]
- Liu, T.; Pu, Y.; Lei, T.; Xu, J.; Gong, M.; He, L.; Nandi, A.K. Hierarchical Feature Alignment-based Progressive Addition Network for Multimodal Change Detection. Pattern Recognit. 2025, 162, 111355. [Google Scholar] [CrossRef]
- Chen, H.; Yokoya, N.; Chini, M. Fourier domain structural relationship analysis for unsupervised multimodal change detection. ISPRS J. Photogramm. Remote Sens. 2023, 198, 99–114. [Google Scholar] [CrossRef]
- Hu, M.; Wu, C.; Du, B.; Zhang, L. Binary change guided hyperspectral multiclass change detection. IEEE Trans. Image Process. 2023, 32, 791–806. [Google Scholar] [CrossRef] [PubMed]
- Hu, M.; Wu, C.; Zhang, L. HyperNet: Self-supervised hyperspectral spatial–spectral feature understanding network for hyperspectral change detection. IEEE Trans. Geosci. Remote Sens. 2022, 60, 5543017. [Google Scholar] [CrossRef]
- Radke, R.J.; Andra, S.; Al-Kofahi, O.; Roysam, B. Image change detection algorithms: A systematic survey. IEEE Trans. Image Process. 2005, 14, 294–307. [Google Scholar] [CrossRef] [PubMed]
- Lei, T.; Wang, J.; Ning, H.; Wang, X.; Xue, D.; Wang, Q.; Nandi, A.K. Difference enhancement and spatial–spectral nonlocal network for change detection in VHR remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4507013. [Google Scholar] [CrossRef]
- Chen, X.; Vierling, L.; Deering, D. A simple and effective radiometric correction method to improve landscape change detection across sensors and across time. Remote Sens. Environ. 2005, 98, 63–79. [Google Scholar] [CrossRef]
- Wang, L.; Zhang, J.; Bruzzone, L. MixCDNet: A Lightweight Change Detection Network Mixing Features across CNN and Transformer. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4411915. [Google Scholar] [CrossRef]
- Bruzzone, L.; Bovolo, F. A novel framework for the design of change-detection systems for very-high-resolution remote sensing images. Proc. IEEE 2012, 101, 609–630. [Google Scholar] [CrossRef]
- Wang, X.; Du, J.; Tan, K.; Ding, J.; Liu, Z.; Pan, C.; Han, B. A high-resolution feature difference attention network for the application of building change detection. Int. J. Appl. Earth Obs. Geoinf. 2022, 112, 102950. [Google Scholar] [CrossRef]
- Gong, M.; Li, J.; Zhang, Y.; Wu, Y.; Zhang, M. Two-path aggregation attention network with quad-patch data augmentation for few-shot scene classification. IEEE Trans. Geosci. Remote Sens. 2022, 60, 4511616. [Google Scholar] [CrossRef]
- Marin, C.; Bovolo, F.; Bruzzone, L. Building change detection in multitemporal very high resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2014, 53, 2664–2682. [Google Scholar] [CrossRef]
- Wang, S.; Li, J.; Liu, Z.; Gong, M.; Zhang, Y.; Zhao, Y.; Deng, B.; Zhou, Y. Personalized Multi-Party Few-Shot Learning for Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4506115. [Google Scholar]
- Shuai, W.; Jiang, F.; Zheng, H.; Li, J. MSGATN: A superpixel-based multi-scale Siamese graph attention network for change detection in remote sensing images. Appl. Sci. 2022, 12, 5158. [Google Scholar] [CrossRef]
- Liu, Y.; Li, J.; Gong, M.; Liu, H.; Sheng, K.; Zhang, Y.; Tang, Z.; Zhou, Y. Collaborative Self-Supervised Evolution for Few-Shot Remote Sensing Scene Classification. IEEE Trans. Geosci. Remote Sens. 2024, 62, 4509215. [Google Scholar] [CrossRef]
- Ding, Q.; Shao, Z.; Huang, X.; Altan, O. DSA-Net: A novel deeply supervised attention-guided network for building change detection in high-resolution remote sensing images. Int. J. Appl. Earth Obs. Geoinf. 2021, 105, 102591. [Google Scholar] [CrossRef]
- Yu, S.; Tao, C.; Zhang, G.; Xuan, Y.; Wang, X. Remote Sensing Image Change Detection Based on Deep Learning: Multi-Level Feature Cross-Fusion with 3D-Convolutional Neural Networks. Appl. Sci. 2024, 14, 6269. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Li, X.; Tan, X.; Kuang, G. Structure consistency-based graph for unsupervised change detection with homogeneous and heterogeneous remote sensing images. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4700221. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Guan, D.; Kuang, G. Iterative robust graph for unsupervised change detection of heterogeneous remote sensing images. IEEE Trans. Image Process. 2021, 30, 6277–6291. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Guan, D.; Li, M.; Kuang, G. Sparse-constrained adaptive structure consistency-based unsupervised image regression for heterogeneous remote-sensing change detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4405814. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Tan, X.; Guan, D.; Wu, J.; Kuang, G. Structured graph based image regression for unsupervised multimodal change detection. ISPRS J. Photogramm. Remote Sens. 2022, 185, 16–31. [Google Scholar] [CrossRef]
- Sun, Y.; Lei, L.; Guan, D.; Kuang, G.; Li, Z.; Liu, L. Locality preservation for unsupervised multimodal change detection in remote sensing imagery. IEEE Trans. Neural Netw. Learn. Syst. 2025, 36, 6955–6969. [Google Scholar] [CrossRef]
- Han, T.; Tang, Y.; Yang, X.; Lin, Z.; Zou, B.; Feng, H. Change detection for heterogeneous remote sensing images with improved training of hierarchical extreme learning machine (HELM). Remote Sens. 2021, 13, 4918. [Google Scholar] [CrossRef]
- Liu, J.; Gong, M.; Qin, K.; Zhang, P. A deep convolutional coupling network for change detection based on heterogeneous optical and radar images. IEEE Trans. Neural Netw. Learn. Syst. 2016, 29, 545–559. [Google Scholar] [CrossRef] [PubMed]
- Luppino, L.T.; Kampffmeyer, M.; Bianchi, F.M.; Moser, G.; Serpico, S.B.; Jenssen, R.; Anfinsen, S.N. Deep image translation with an affinity-based change prior for unsupervised multimodal change detection. IEEE Trans. Geosci. Remote Sens. 2021, 60, 4700422. [Google Scholar] [CrossRef]
- Wu, Y.; Li, J.; Yuan, Y.; Qin, A.K.; Miao, Q.G.; Gong, M.G. Commonality autoencoder: Learning common features for change detection from heterogeneous images. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 4257–4270. [Google Scholar] [CrossRef]
- Cheng, M.; He, W.; Li, Z.; Yang, G.; Zhang, H. Harmony in diversity: Content cleansing change detection framework for very-high-resolution remote-sensing images. ISPRS J. Photogramm. Remote Sens. 2024, 218, 1–19. [Google Scholar] [CrossRef]
- Han, T.; Tang, Y.; Chen, Y.; Yang, X.; Guo, Y.; Jiang, S. SDC-GAE: Structural Difference Compensation Graph Autoencoder for Unsupervised Multimodal Change Detection. IEEE Trans. Geosci. Remote Sens. 2024, 62, 5622416. [Google Scholar] [CrossRef]
- Liu, B.; Chen, H.; Li, K.; Yang, M.Y. Transformer-based multimodal change detection with multitask consistency constraints. Inf. Fusion 2024, 108, 102358. [Google Scholar] [CrossRef]
- Zou, C.; Liang, W.; Liu, L.; Zou, C. Hyperspectral image change detection based on an improved multi-scale and spectral-wise transformer. Int. J. Remote Sens. 2024, 45, 1904–1925. [Google Scholar] [CrossRef]
- Roy, S.K.; Jamali, A.; Chanussot, J.; Ghamisi, P.; Ghaderpour, E.; Shahabi, H. SimPoolFormer: A two-stream vision transformer for hyperspectral image classification. Remote Sens. Appl. Soc. Environ. 2025, 37, 101478. [Google Scholar] [CrossRef]
- Zhu, X.X.; Tuia, D.; Mou, L.; Xia, G.S.; Zhang, L.; Xu, F.; Fraundorfer, F. Deep learning in remote sensing: A comprehensive review and list of resources. IEEE Geosci. Remote Sens. Mag. 2017, 5, 8–36. [Google Scholar] [CrossRef]
- Cheng, G.; Huang, Y.; Li, X.; Lyu, S.; Xu, Z.; Zhao, H.; Zhao, Q.; Xiang, S. Change detection methods for remote sensing in the last decade: A comprehensive review. Remote Sens. 2024, 16, 2355. [Google Scholar] [CrossRef]
- Lv, Z.; Huang, H.; Li, X.; Zhao, M.; Benediktsson, J.A.; Sun, W.; Falco, N. Land cover change detection with heterogeneous remote sensing images: Review, progress, and perspective. Proc. IEEE 2022, 110, 1976–1991. [Google Scholar] [CrossRef]





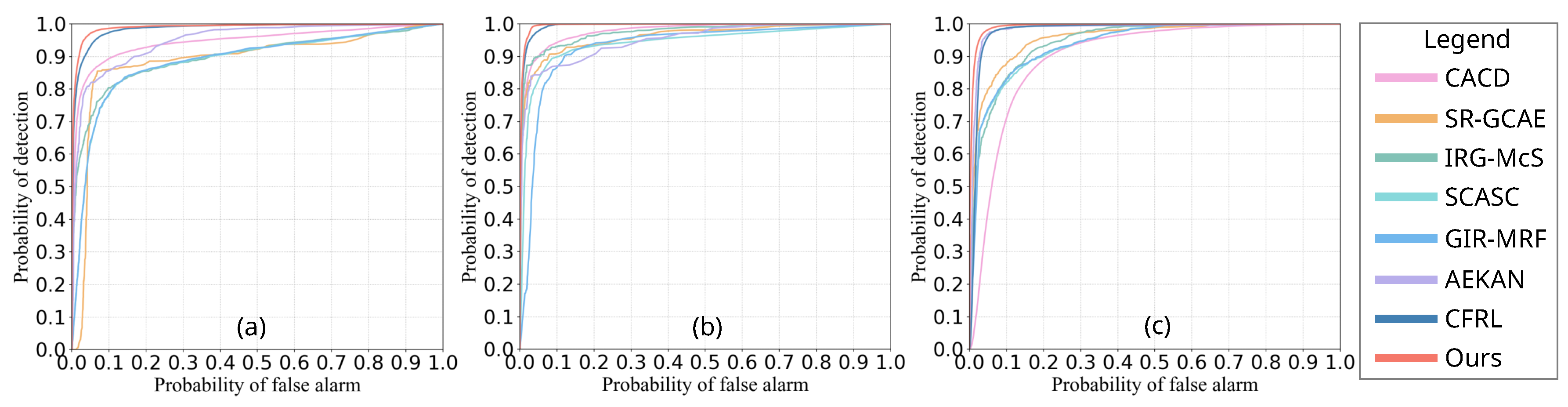
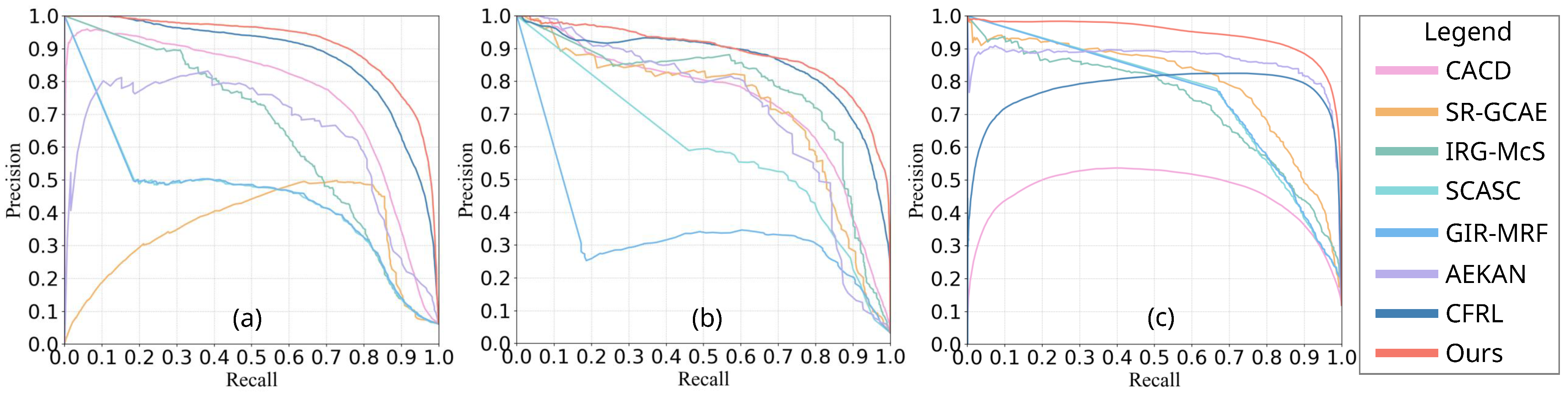

| Methods | Data Set #1 | Data Set #2 | Data Set #3 | Average | ||||
|---|---|---|---|---|---|---|---|---|
| AUR | AUP | AUR | AUP | AUR | AUP | AUR | AUP | |
| CACD [55] | 0.947 | 0.763 | 0.978 | 0.742 | 0.902 | 0.459 | 0.942 | 0.655 |
| SR-GCAE [21] | 0.888 | 0.339 | 0.961 | 0.719 | 0.957 | 0.795 | 0.935 | 0.618 |
| IRG-McS [48] | 0.899 | 0.643 | 0.973 | 0.773 | 0.946 | 0.735 | 0.939 | 0.717 |
| SCASC [49] | 0.886 | 0.456 | 0.942 | 0.594 | 0.938 | 0.758 | 0.922 | 0.603 |
| GIR-MRF [50] | 0.888 | 0.457 | 0.932 | 0.348 | 0.939 | 0.759 | 0.920 | 0.521 |
| AEKAN [23] | 0.950 | 0.646 | 0.951 | 0.712 | 0.984 | 0.865 | 0.962 | 0.741 |
| CFRL [24] | 0.985 | 0.876 | 0.994 | 0.859 | 0.980 | 0.773 | 0.986 | 0.836 |
| Proposed SDFormer | 0.990 | 0.915 | 0.996 | 0.886 | 0.993 | 0.945 | 0.993 | 0.915 |
| Methods | OA | KC | F1 |
|---|---|---|---|
| IRG-McS [48] | 0.971 | 0.739 | 0.754 |
| SCASC [49] | 0.947 | 0.593 | 0.621 |
| GIR-MRF [50] | 0.957 | 0.674 | 0.697 |
| X-Net [54] | 0.918 | 0.340 | 0.443 |
| ACE-Net [54] | 0.935 | 0.549 | 0.582 |
| CACD [55] | 0.975 | 0.776 | 0.790 |
| SR-GCAE [21] | 0.937 | 0.546 | 0.579 |
| AEKAN [23] | 0.955 | 0.660 | 0.684 |
| CFRL+Otsu [24] | 0.973 | 0.780 | 0.795 |
| CFRL+FLICM [24] | 0.974 | 0.785 | 0.799 |
| Ours | 0.979 | 0.824 | 0.835 |
| Methods | OA | KC | F1 |
|---|---|---|---|
| IRG-McS [48] | 0.986 | 0.788 | 0.795 |
| SCASC [49] | 0.976 | 0.623 | 0.636 |
| GIR-MRF [50] | 0.986 | 0.788 | 0.795 |
| X-Net [54] | 0.918 | 0.232 | 0.268 |
| ACE-Net [54] | 0.928 | 0.297 | 0.329 |
| CACD [55] | 0.967 | 0.614 | 0.630 |
| SR-GCAE [21] | 0.981 | 0.694 | 0.704 |
| AEKAN [23] | 0.982 | 0.682 | 0.691 |
| CFRL+Otsu [24] | 0.985 | 0.787 | 0.795 |
| CFRL+FLICM [24] | 0.987 | 0.809 | 0.815 |
| Ours | 0.987 | 0.809 | 0.816 |
| Methods | OA | KC | F1 |
|---|---|---|---|
| IRG-McS [48] | 0.936 | 0.704 | 0.740 |
| SCASC [49] | 0.950 | 0.776 | 0.804 |
| GIR-MRF [50] | 0.937 | 0.734 | 0.770 |
| X-Net [54] | 0.909 | 0.637 | 0.688 |
| ACE-Net [54] | 0.928 | 0.659 | 0.701 |
| CACD [55] | 0.798 | 0.417 | 0.516 |
| SR-GCAE [21] | 0.885 | 0.586 | 0.649 |
| AEKAN [23] | 0.964 | 0.837 | 0.858 |
| CFRL+Otsu [24] | 0.960 | 0.822 | 0.845 |
| CFRL+FLICM [24] | 0.963 | 0.835 | 0.856 |
| Ours | 0.974 | 0.879 | 0.893 |
| Methods | Data Set #1 | Data Set #2 | Data Set #3 | Average | ||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| OA | KC | F1 | OA | KC | F1 | OA | KC | F1 | OA | KC | F1 | |
| w/o | 0.948 | 0.671 | 0.697 | 0.964 | 0.625 | 0.641 | 0.941 | 0.758 | 0.791 | 0.951 | 0.685 | 0.710 |
| w/o SDFormer | 0.957 | 0.708 | 0.731 | 0.985 | 0.789 | 0.797 | 0.957 | 0.817 | 0.842 | 0.966 | 0.771 | 0.790 |
| Ours | 0.979 | 0.824 | 0.835 | 0.987 | 0.809 | 0.816 | 0.974 | 0.879 | 0.893 | 0.980 | 0.837 | 0.848 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cao, X.; Dong, M.; Liu, X.; Gong, J.; Zheng, H. Statistical Difference Representation-Based Transformer for Heterogeneous Change Detection. Sensors 2025, 25, 3740. https://doi.org/10.3390/s25123740
Cao X, Dong M, Liu X, Gong J, Zheng H. Statistical Difference Representation-Based Transformer for Heterogeneous Change Detection. Sensors. 2025; 25(12):3740. https://doi.org/10.3390/s25123740
Chicago/Turabian StyleCao, Xinhui, Minggang Dong, Xingping Liu, Jiaming Gong, and Hanhong Zheng. 2025. "Statistical Difference Representation-Based Transformer for Heterogeneous Change Detection" Sensors 25, no. 12: 3740. https://doi.org/10.3390/s25123740
APA StyleCao, X., Dong, M., Liu, X., Gong, J., & Zheng, H. (2025). Statistical Difference Representation-Based Transformer for Heterogeneous Change Detection. Sensors, 25(12), 3740. https://doi.org/10.3390/s25123740






