All-Ceramic Fiber Fabry–Perot Cavity High-Temperature Pulsating Pressure Sensor Based on HTCC
Abstract
1. Introduction
2. Sensor Principle and Design
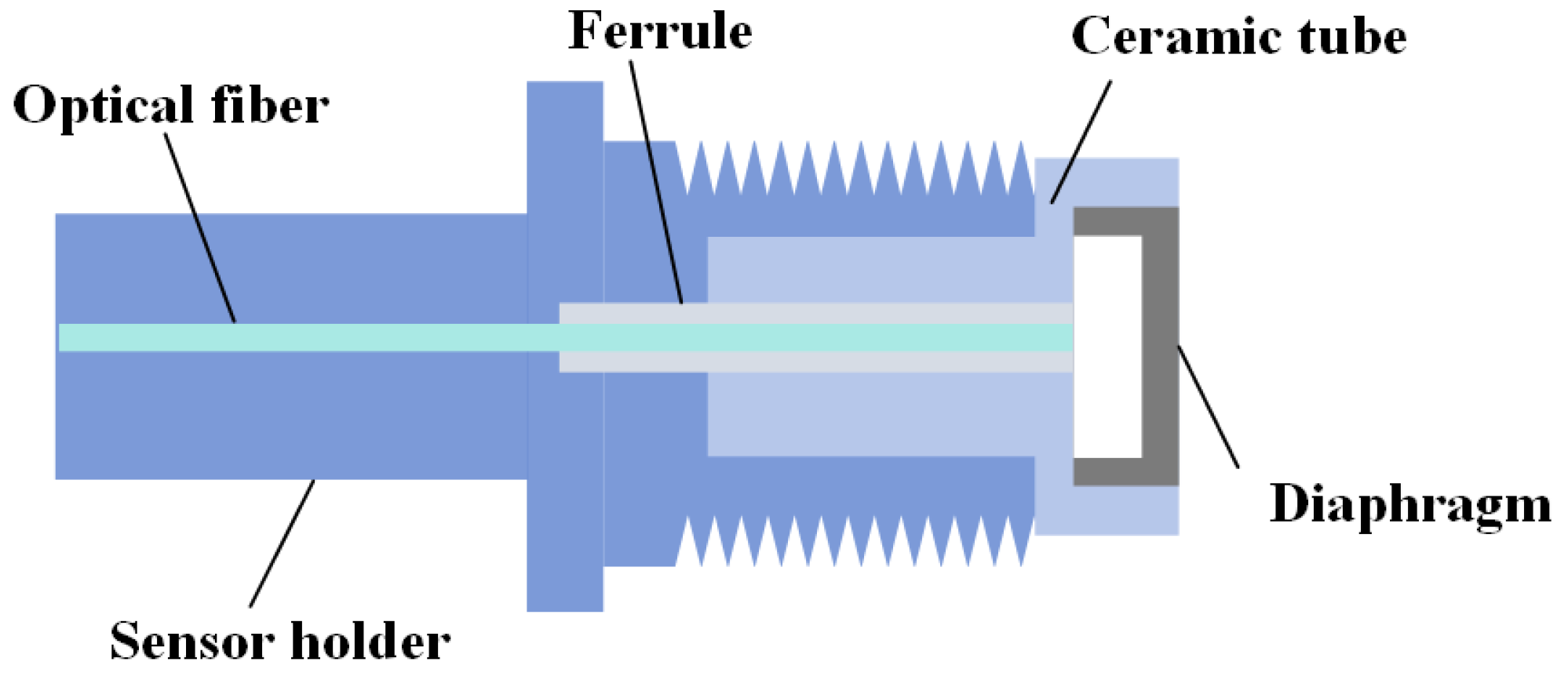
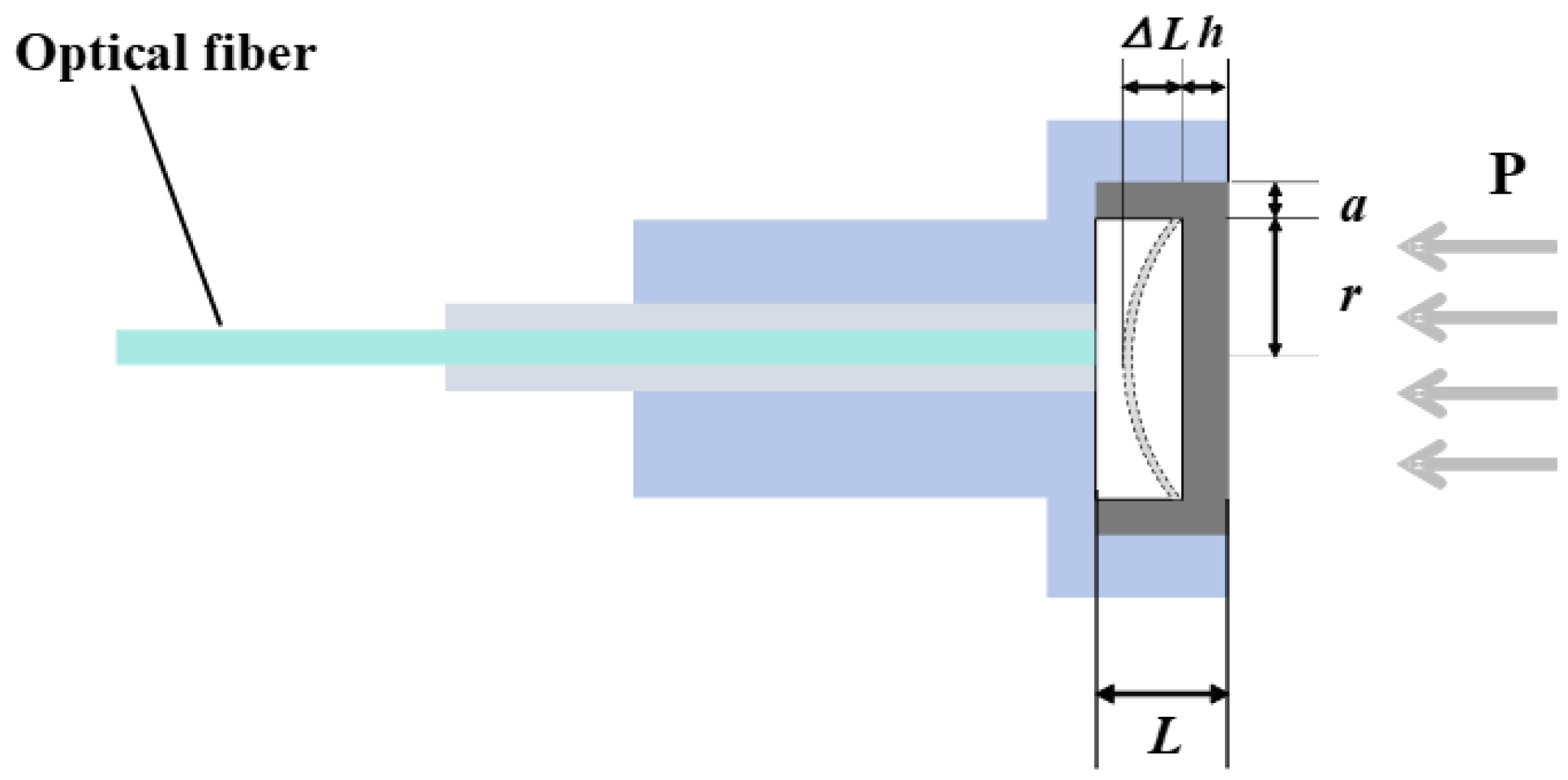
2.1. Structural Design
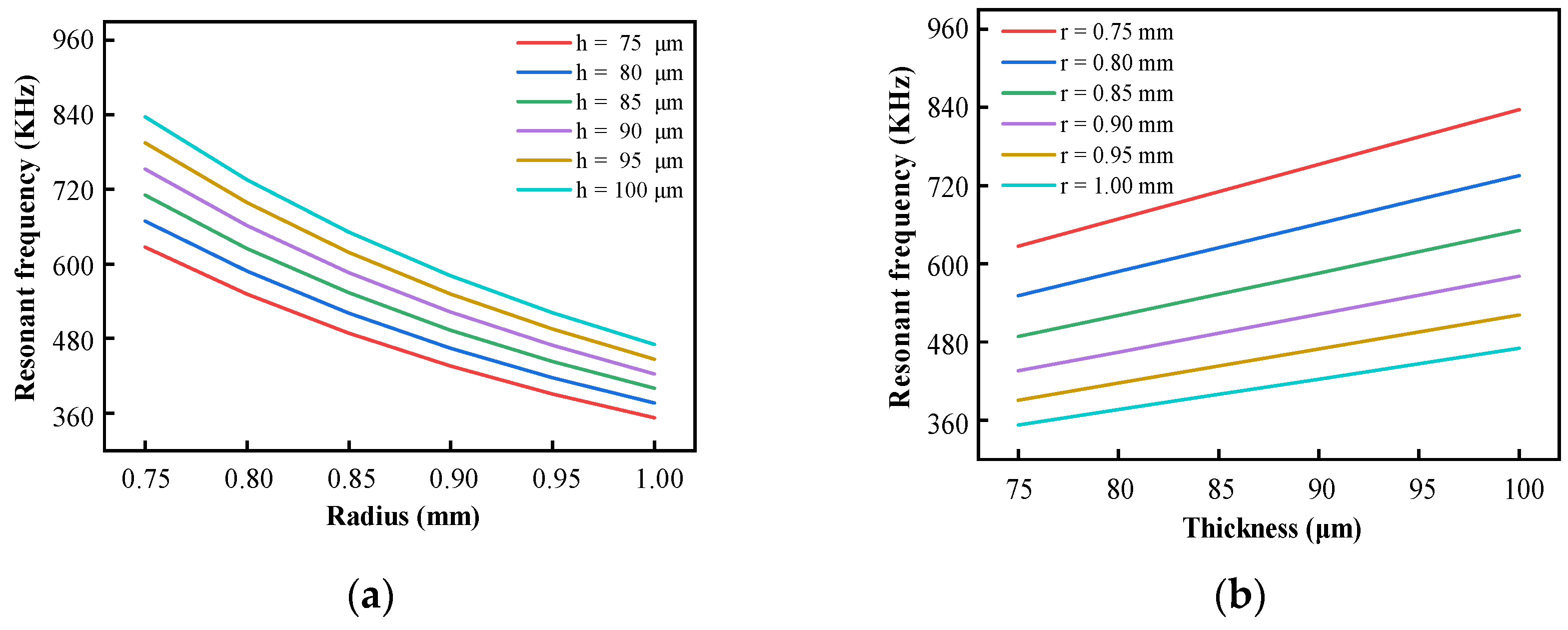
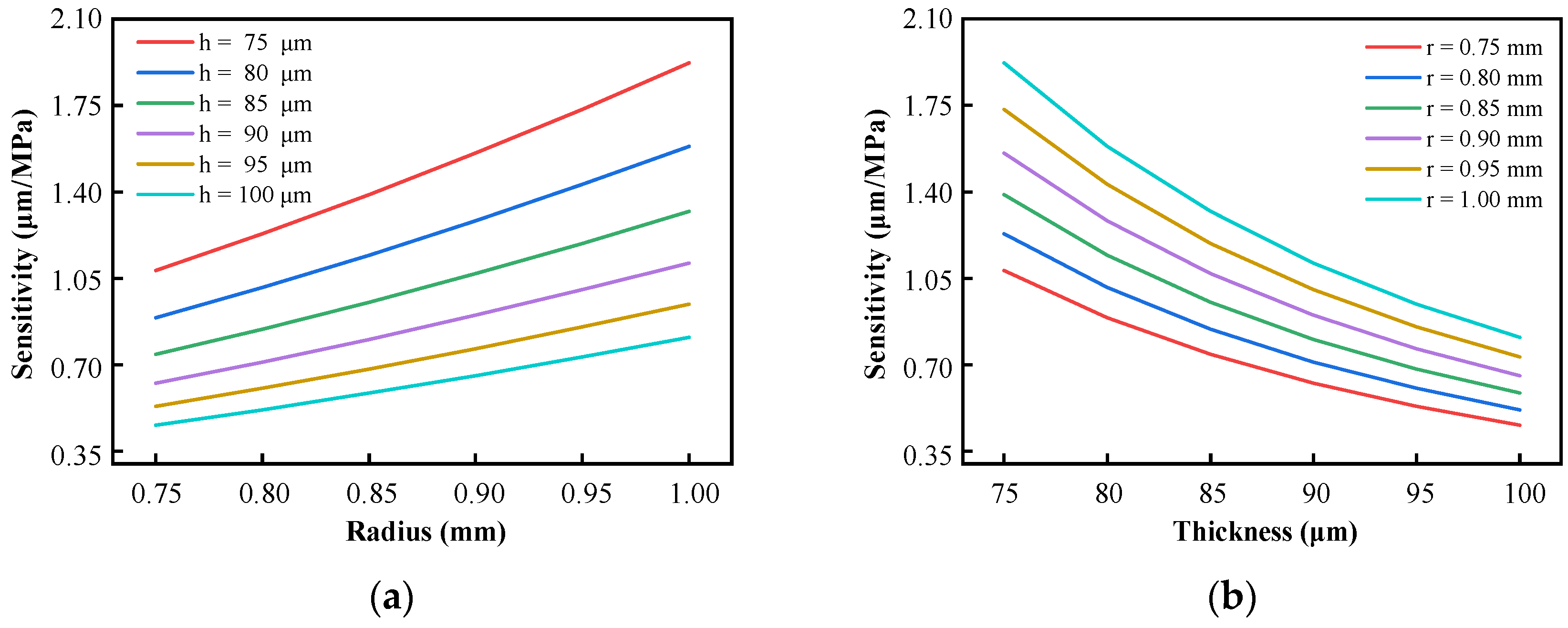
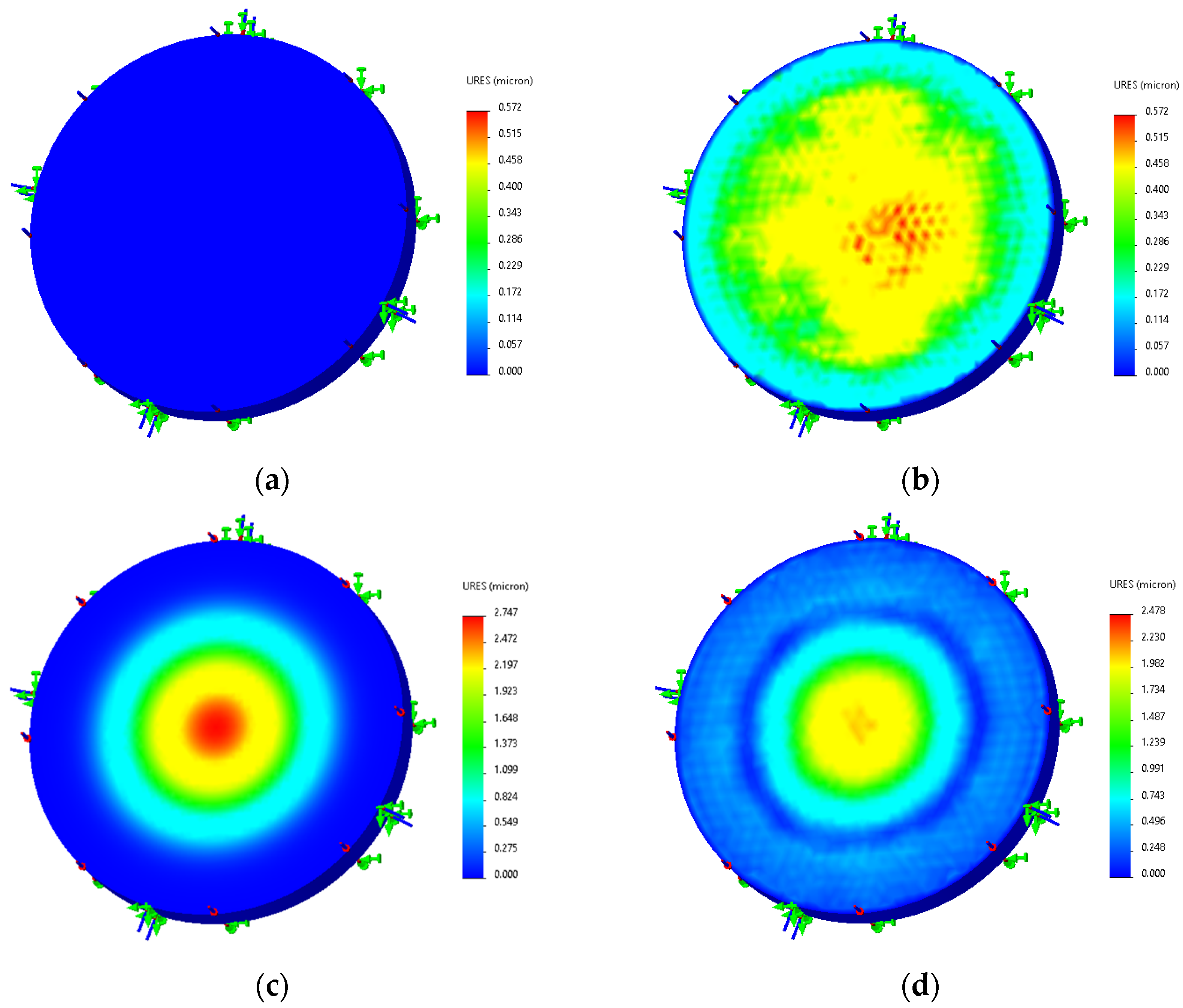
2.2. Sensor Characteristic Analysis
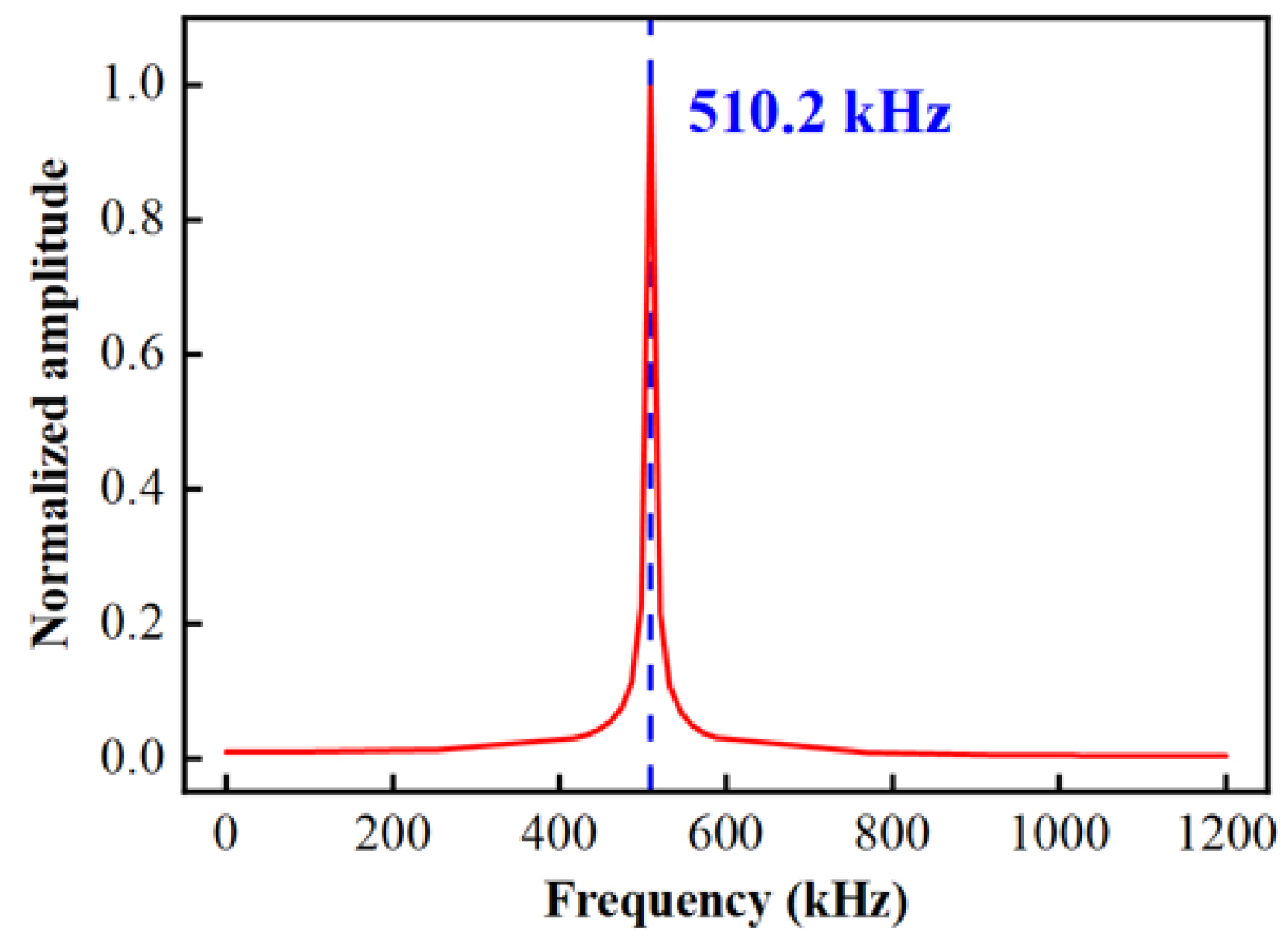
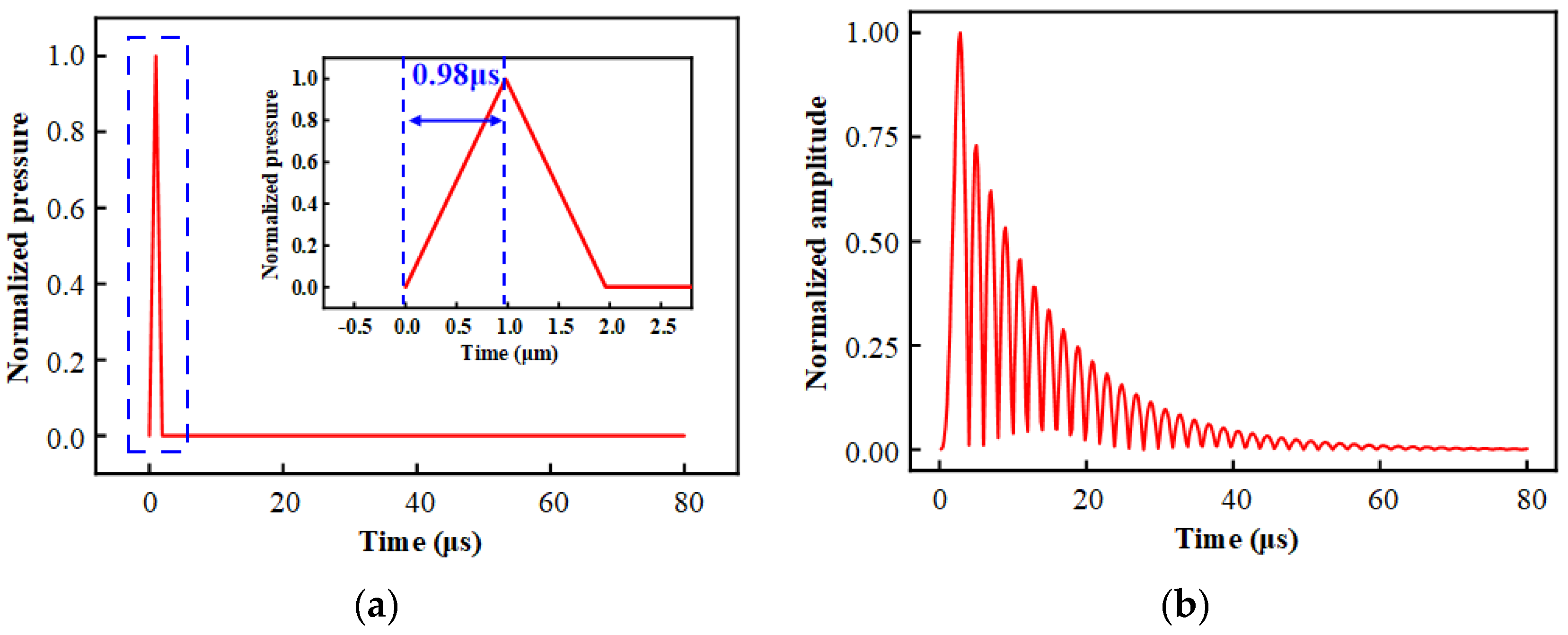
2.2.1. Transient Response Analysis
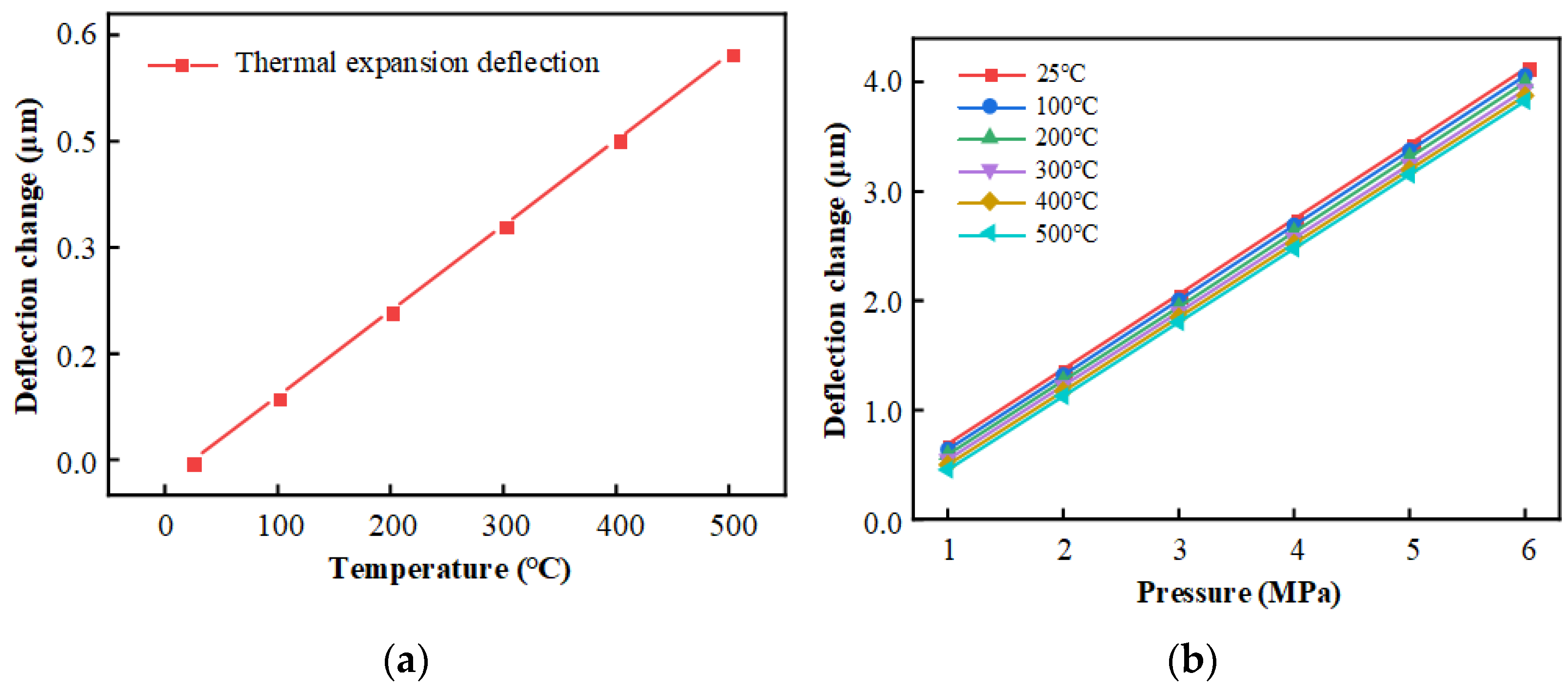
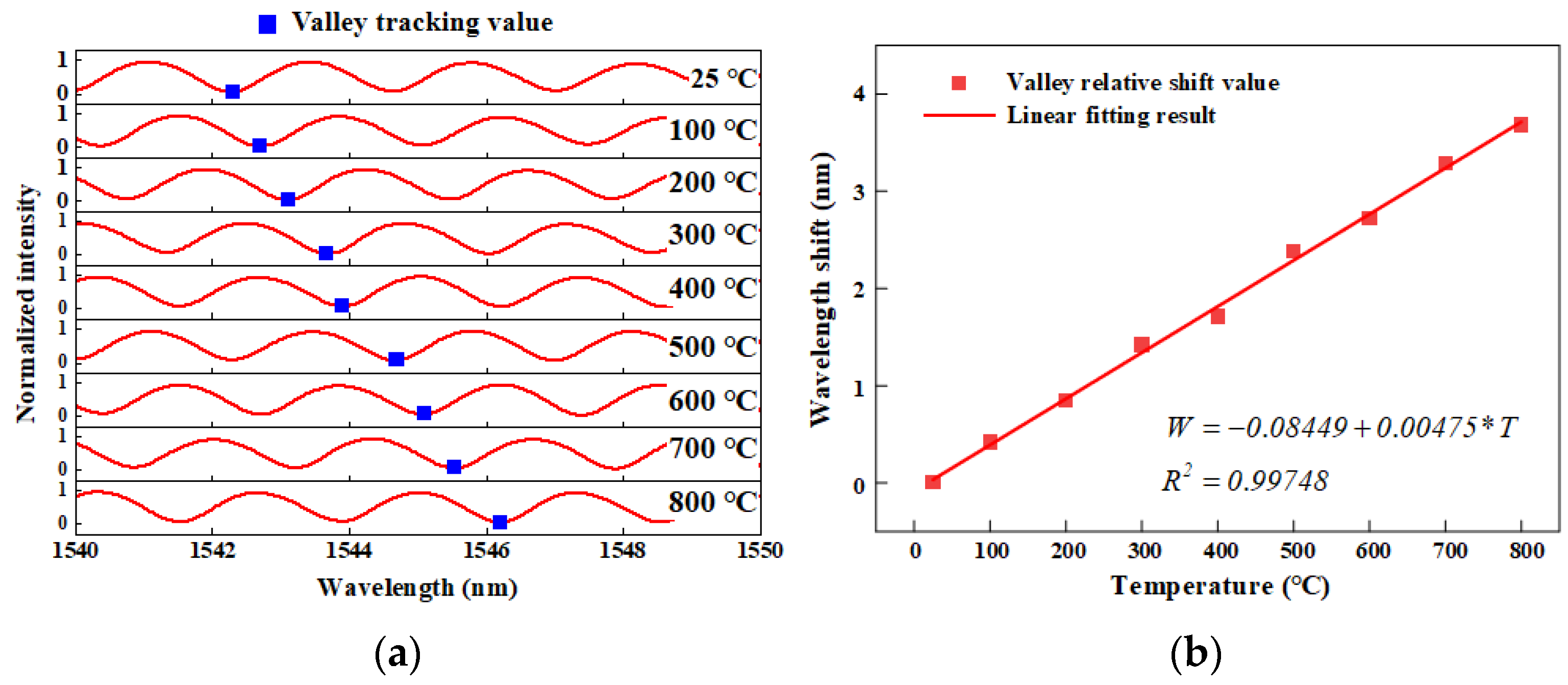
2.2.2. High-Temperature Performance Analysis
3. Processing and Packaging
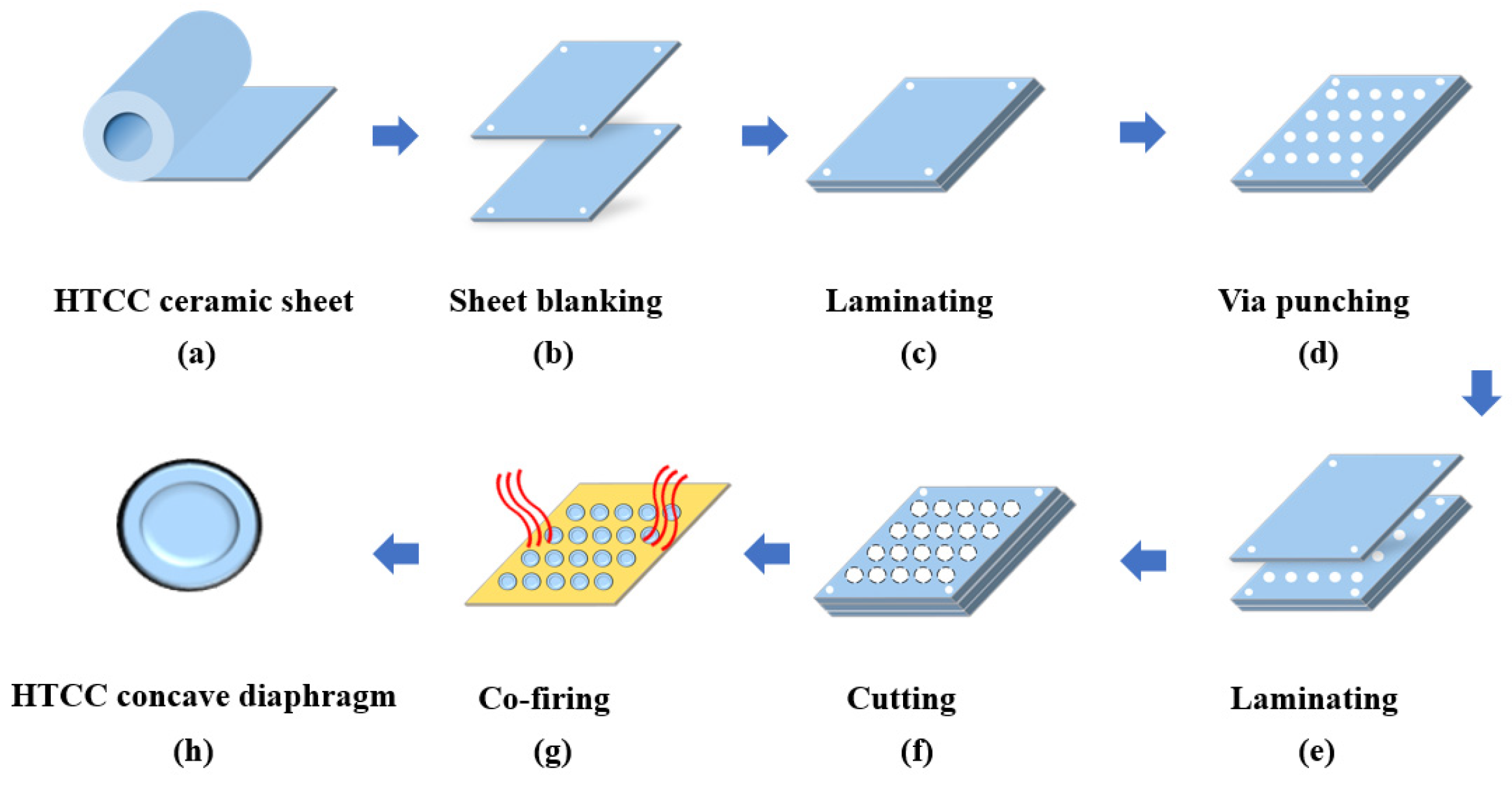
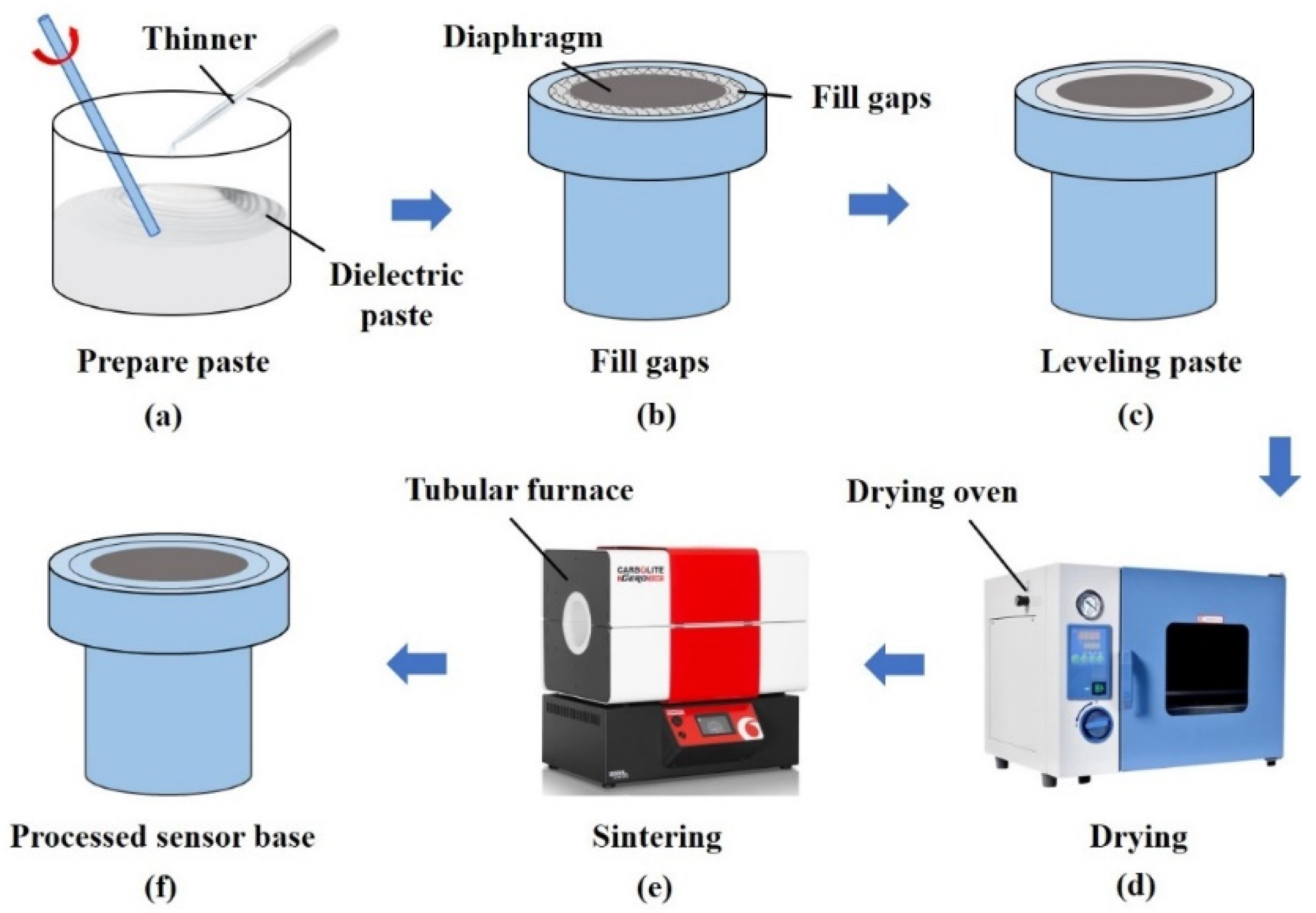
3.1. Pressure-Sensitive Diaphragm Preparation
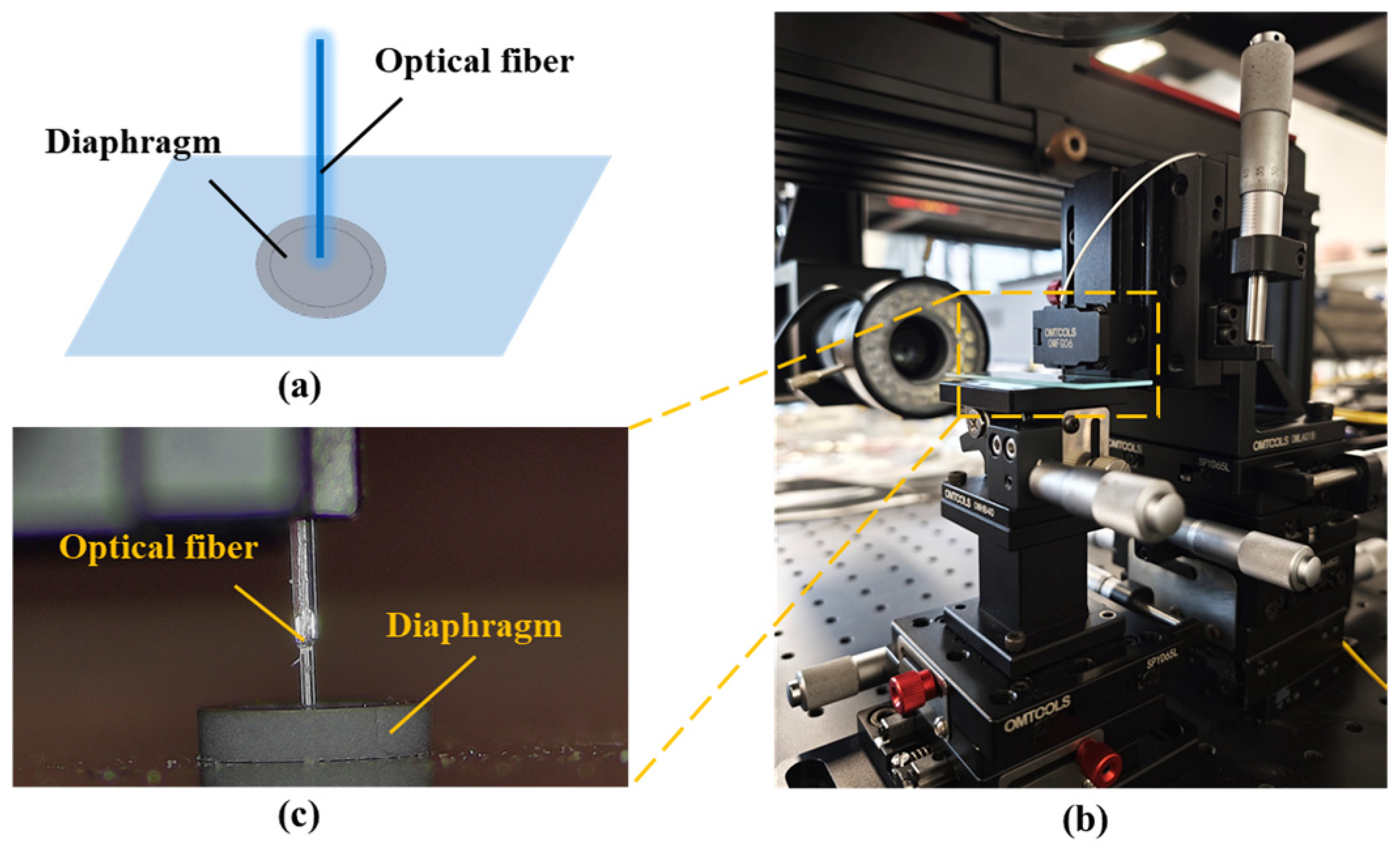
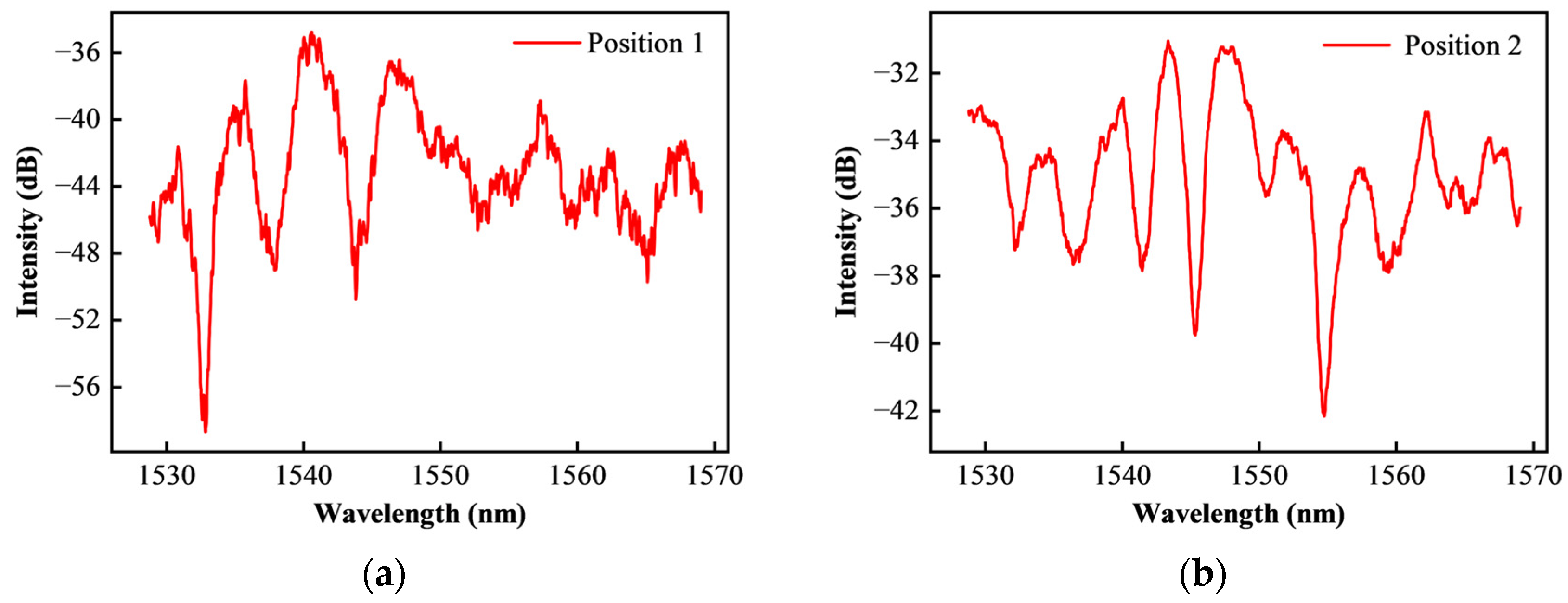
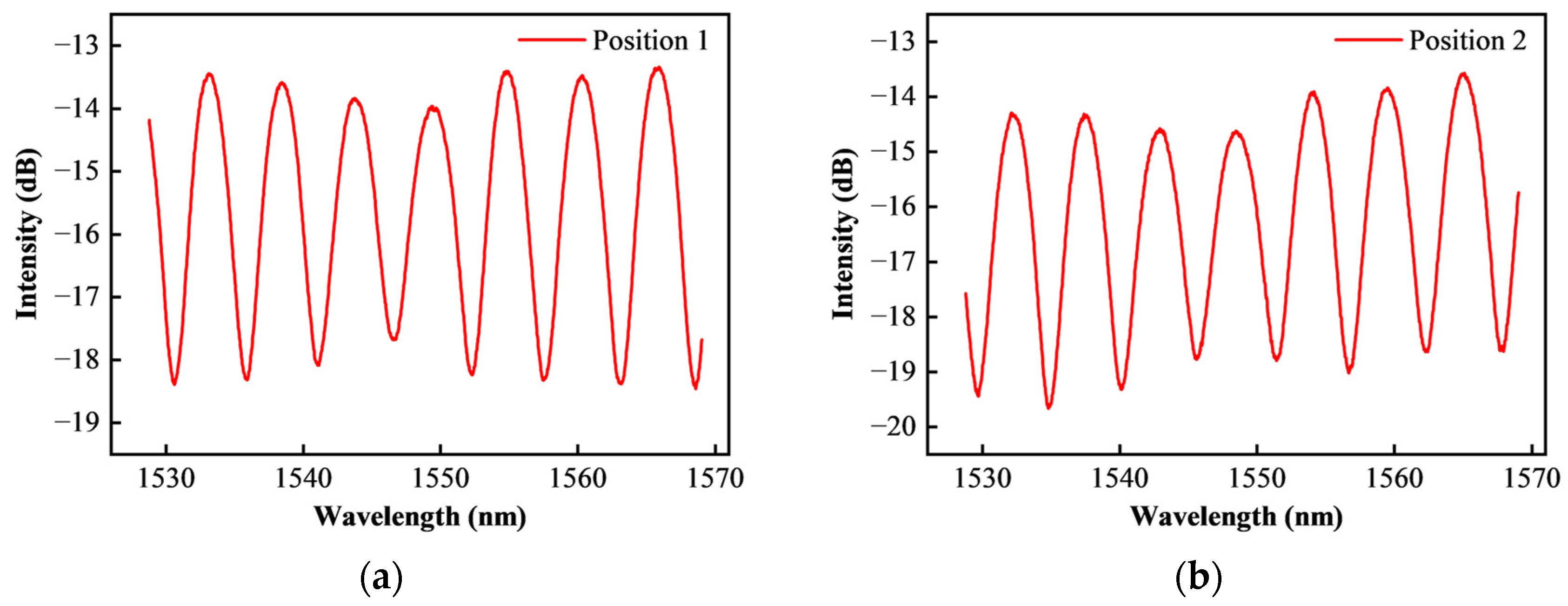
3.2. Optical Performance Test and Optimization of Pressure-Sensitive Diaphragm
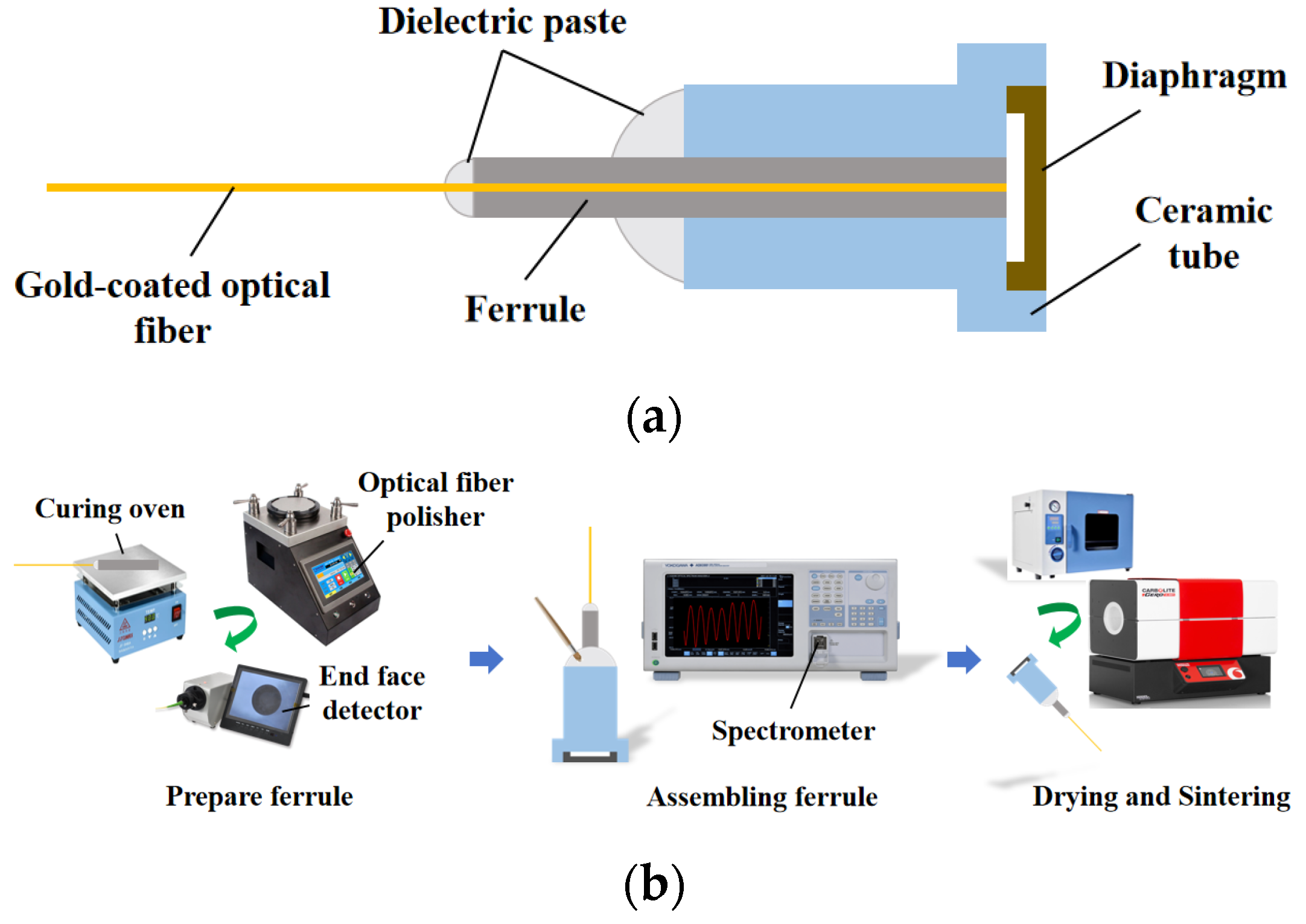
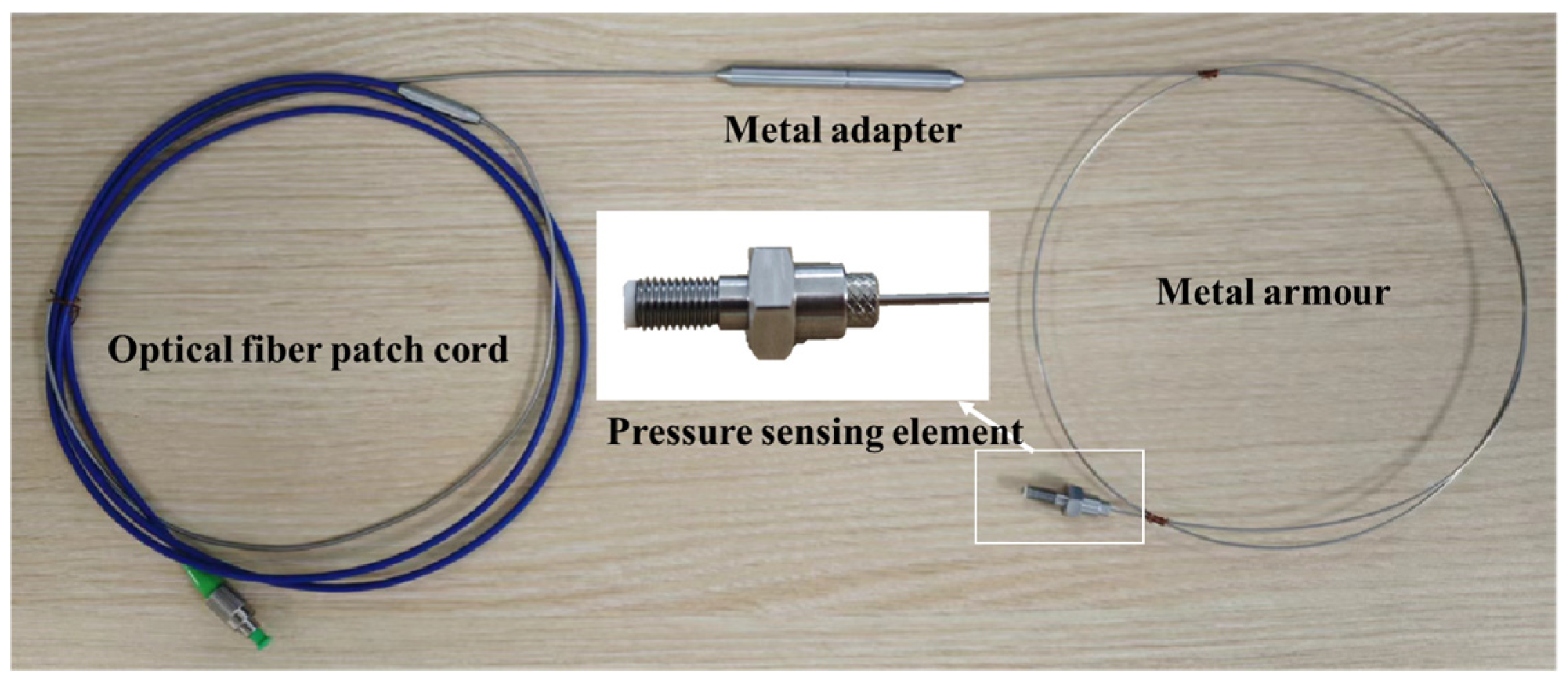
3.3. Integration and Packaging
4. Results and Discussion
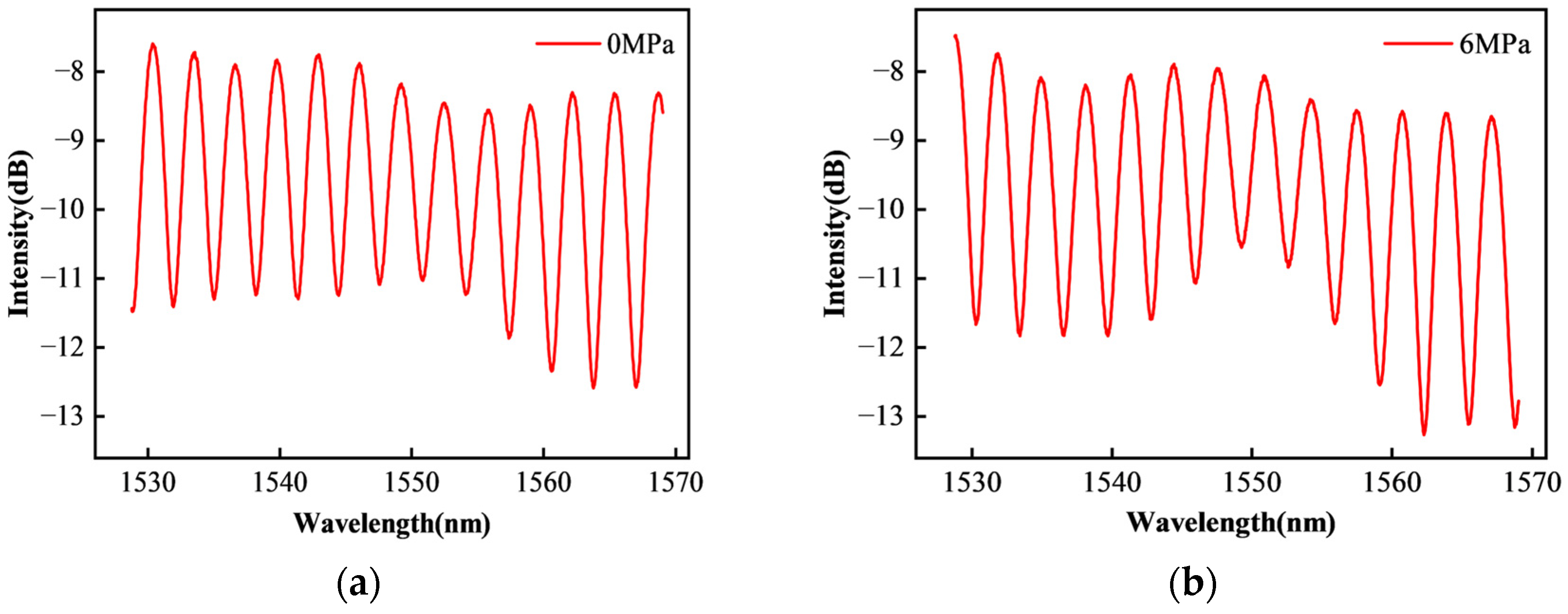
4.1. Static Experiment
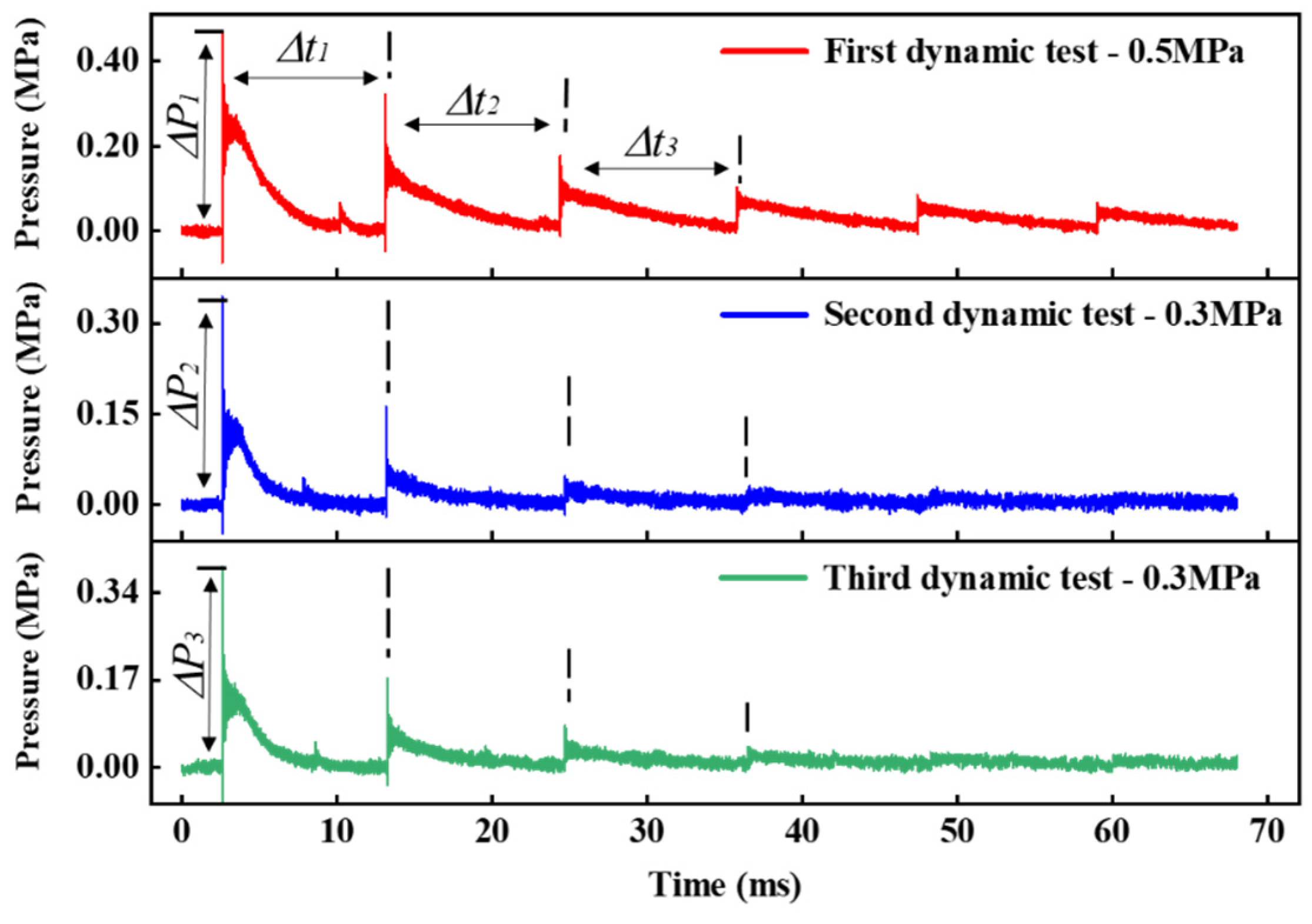
4.2. Dynamic Experiment
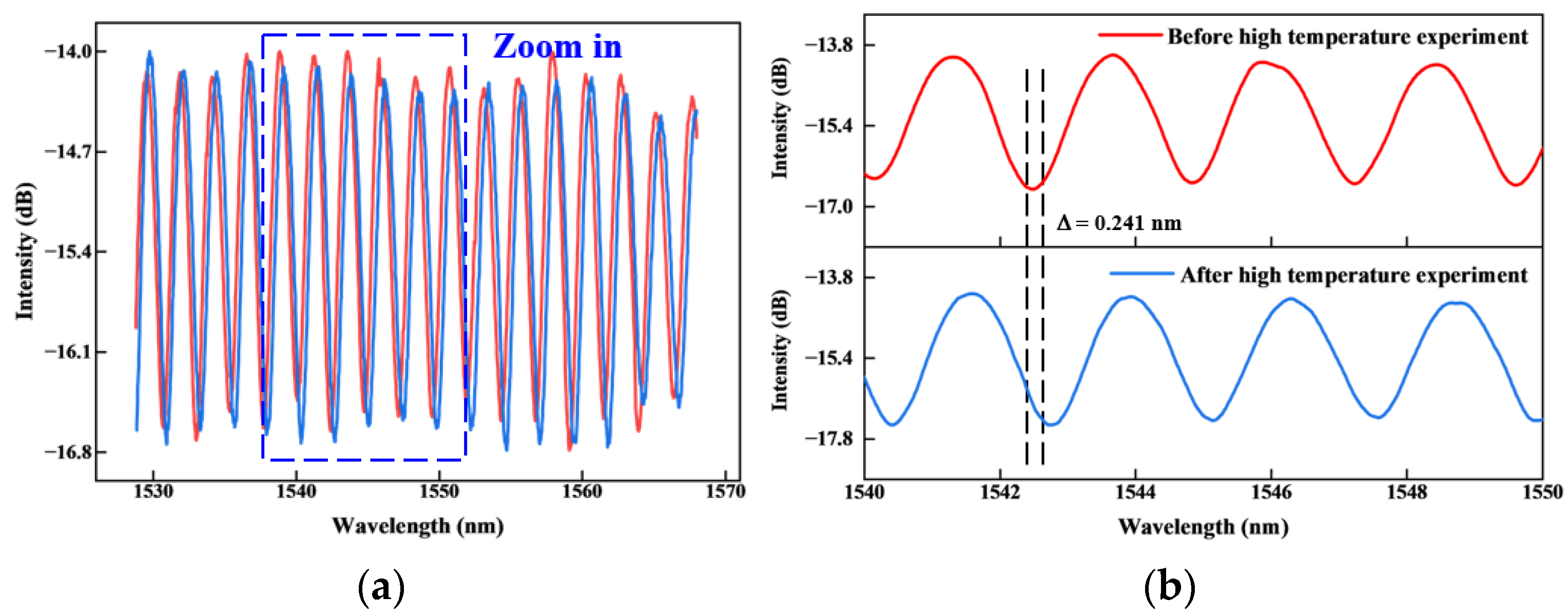
4.3. High-Temperature Experiment
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, Z.; Sun, D.; Dong, X.; Sun, X. A review on aero-engine inlet-compressor integration and inlet flow distortion in axial com-pressors. Fundam. Res. 2024. [Google Scholar] [CrossRef]
- Li, X.; Liu, Q.; Pang, S.; Xu, K.; Tang, H.; Sun, C. High-Temperature Piezoresistive Pressure Sensor Based On Implantation of Oxygen into Silicon Wafer. Sens. Actuators A Phys. 2012, 179, 277–282. [Google Scholar] [CrossRef]
- Han, G.; Hu, J.; Liu, X.; Lei, X.; Zhang, P. Fiber Bragg Grating Total Temperature Probes for High-Speed Airflow with High Recovery Factor. IEEE Sens. J. 2023, 23, 27406–27415. [Google Scholar] [CrossRef]
- Cui, Y.; Qiu, K.; Gao, S.; Chen, L.; Jiang, J.; Niu, Y.; Wang, C. Advances in the application of non-contact temperature measurement technology for aero-engine blade. Rev. Sci. Instrum. 2024, 95, 081502. [Google Scholar] [CrossRef]
- Pulliam, W.J.; Russler, P.M.; Fielder, R.S. High-temperature High-bandwidth Fiber Optic MEMS Pressure-sensor Technology for Turbine-engine Component Testing. Fiber Opt. Sens. Technol. Appl. 2001, 2002, 229–238. [Google Scholar]
- García, I.; Zubia, J.; Durana, G.; Aldabaldetreku, G.; Illarramendi, M.A.; Villatoro, J. Optical Fiber Sensors for Aircraft Structural Health Monitoring. Sensors 2015, 15, 15494–15519. [Google Scholar] [CrossRef]
- Liu, H.; Shao, B.; Chen, W.; Zhang, W.; Xiong, B.; Zhang, P. Study on Suppressing Doppler Effect and Non-linearity Simultaneously in Dynamic Clearance Measurement of Frequency Swept Interferometry. In Optical Metrology and Inspection for Industrial Applications VIII; SPIE: Bellingham, WA, USA, 2021; pp. 81–86. [Google Scholar]
- Udd, E.; Spillman, W.B., Jr. Fiber Optic Sensors: An Introduction for Engineers and Scientists; John Wiley & Sons: Hoboken, NJ, USA, 2024. [Google Scholar]
- Wang, J.; Wang, M.; Xu, J.; Peng, L.; Yang, M.; Xia, M.; Jiang, D. Underwater Blast Wave Pressure Sensor Based on Polymer Film Fiber Fabry–Perot Cavity. Appl. Opt. 2014, 53, 6494–6502. [Google Scholar] [CrossRef]
- Cranch, G.A.; Grün, J.; Weaver, J.; Gran, J.K.; Groethe, M.A.; Compton, S.; Fournier, K.; Dunlop, B. High Power Laser and Explosive Driven Shock Wave Characterization in Solids Using Fiber Optic Probes. In Proceedings of the 24th International Conference on Optical Fibre Sensors, Curitiba, Brazil, 28 September–2 October 2015; pp. 189–192. [Google Scholar]
- Ortigoza-Diaz, J.; Scholten, K.; Larson, C.; Cobo, A.; Hudson, T.; Yoo, J.; Baldwin, A.; Weltman Hirschberg, A.; Meng, E. Techniques and Considerations in the Microfabrication of Parylene C Microelectromechanical Systems. Micromachines 2018, 9, 422. [Google Scholar] [CrossRef]
- Sweeney, D.C.; Schrell, A.M.; Liu, Y.; Petrie, C.M. Metal-Embedded Fiber Optic Sensor Packaging and Signal Demodulation Scheme Towards High-Frequency Dynamic Measurements in Harsh Environments. Sens. Actuators A Phys. 2020, 312, 112075. [Google Scholar] [CrossRef]
- He, X.; Ran, Z.; Ding, Z.; Shao, T.; Gan, L.; Wang, N.; Xiao, Y.; Yu, M.; Yang, T.; He, Z.; et al. Fast-Response Sensitivity-Enhanced All-fiber Fabry–Perot High-Pressure Sensor for Internal Combustion Engines. J. Light. Technol. 2021, 40, 299–307. [Google Scholar] [CrossRef]
- Tuv, A.L.; Akatov, M.S.; Opekunova, A.A.; Starostenko, V.I. Overview of Fiber Optic Sensor Applications. In Proceedings of the 2024 Conference of Young Researchers in Electrical and Electronic Engineering (ElCon), Saint Petersburg, Russian, 29–30 January 2024; pp. 91–94. [Google Scholar]
- Ghildiyal, S.; Balasubramaniam, R.; John, J. Diamond Turned Micro Machined Metal Diaphragm Based Fabry Perot Pressure Sensor. Opt. Laser Technol. 2020, 128, 106243. [Google Scholar] [CrossRef]
- Qin, C.; Guo, X.; Zhou, J.; Wang, C.; Rong, J.; Zhang, Q.; Li, G.; Zhang, P.; Zhang, T. Optical characterization of a fiber Fabry-Perot cavity: Precision measurement of intra-cavity loss, transmittance, and re-flectance. Opt. Express 2024, 32, 14780–14788. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Y.; Jiang, Y.; Yang, S.; Zhang, D. All-sapphire fiber-optic sensor for the simultaneous measurement of ultra-high temperature and high pressure. Opt. Express 2024, 32, 14826–14836. [Google Scholar] [CrossRef]
- Huang, M.; Han, X.; Zhao, L.; Fan, S.; Xia, Y.; Qiao, Z.; Li, W.; Gao, Y.; Yang, P.; Chen, S.; et al. Design and Fabrication of a MEMS Temperature and Pressure Integrated Sensor with Back-Inlet Package Structure. IEEE Sens. J. 2024, 24, 25476–25485. [Google Scholar] [CrossRef]
- Chen, Y.; Lu, D.; Xing, H.; Ding, H.; Luo, J.; Liu, H.; Kong, X.; Xu, F. Recent Progress in MEMS Fiber-Optic Fabry–Perot Pressure Sensors. Sensors 2024, 24, 1079. [Google Scholar] [CrossRef]
- Salvatori, S.; Pettinato, S.; Piccardi, A.; Sedov, V.; Voronin, A.; Ralchenko, V. Thin Diamond Film on Silicon Substrates for Pressure Sensor Fabrication. Materials 2020, 13, 3697. [Google Scholar] [CrossRef]
- Li, H.; Liu, J.; Sheng, T.; Li, J.; Zhang, D.; Jiang, Y. All-SiC fiber-optic sensor for pressure and temperature dual-mode sensing in harsh environments. Sens. Actuators A Phys. 2024, 373, 115388. [Google Scholar] [CrossRef]
- Nikiforov, A.Y.; Skorobogatov, P.K. SiC pressure sensors radiation hardness investigations. In Proceedings of the Eighth Workshop on Electronics for LHC Experiments, Colmar, France, 9–13 September 2002; CERN: Geneva, Switzerland, 2002; pp. 1–4. [Google Scholar] [CrossRef]
- Salvatori, S.; Ponticelli, G.S.; Pettinato, S.; Genna, S.; Guarino, S. High-Pressure Sensors Based on Laser-Manufactured Sintered Silicon Carbide. Appl. Sci. 2020, 10, 7095. [Google Scholar] [CrossRef]
- Sebastian, M.T.; Jantunen, H. High Temperature Cofired Ceramic (HTCC), Low Temperature Cofired Ceramic (LTCC), and Ultralow Temperature Cofired Ceramic (ULTCC) Materials. In Microwave Materials and Applications 2V Set; Wiley Online Library: Hoboken, NJ, USA, 2017; pp. 355–425. [Google Scholar]
- Chen, Y.; Xu, Q.; Zhang, X.; Kuang, M. Materials and Sensing Mechanisms for High-Temperature Pressure Sensors: A Review. IEEE Sens. J. 2023, 23, 26910–26924. [Google Scholar] [CrossRef]
- Ma, M.; Wang, Y.; Liu, F.; Zhang, F.; Liu, Z.; Li, Y. Passive Wireless LC Proximity Sensor Based on LTCC Technology. Sensors 2019, 19, 1110. [Google Scholar] [CrossRef]
- Sun, F.; Xu, X.; Tang, H.; Xiao, Y.; Sun, L.; Zhang, P.; Lei, X.; Liu, X. A fiber-optic Fabry-Perot pressure sensor based on HTCC. In Proceedings of the 4th International Conference on Laser, Optics and Optoelectronic Technology (LOPET 2024), Chongqing, China, 17–19 May 2024; SPIE: Bellingham, WA, USA, 2024; Volume 13231, pp. 65–309. [Google Scholar]
- Ni, W.; Lu, P.; Fu, X.; Zhang, W.; Shum, P.P.; Sun, H.; Yang, C.; Liu, D.; Zhang, J. Ultrathin graphene diaphragm-based extrinsic Fabry-Perot interferometer for ultra-wideband fiber optic acoustic sensing. Opt. Express 2018, 26, 20758–20767. [Google Scholar] [CrossRef] [PubMed]
- Li, B.; Huang, N.; Yang, J.; Qin, H.; Yin, X.; Zhang, Z. Effects of medium and static pressure on dynamic characteristics of piezoresistive absolute pressure sensor calibrated by shock tube. Explos. Shock. Waves 2020, 40, 054101. [Google Scholar]
- Li, J.Y.; Chen, J.H.; Zhao, H.L.; Wang, S.Y.; Jia, X.H. Theoretical analysis of diaphragm fracture in diaphragm compressor. Eng. Mech. 2015, 32, 192–197. [Google Scholar]
- Diao, K.; Yao, Z.; Wang, Z.; Liu, X.; Wang, C.; Shang, Z. Investigation of Vibration Effect on Dynamic Calibration of Pressure Sensors Based On Shock Tube System. Measurement 2020, 149, 107015. [Google Scholar] [CrossRef]
- Zelan, M.; Arrhén, F.; Jarlemark, P.; Mollmyr, O.; Johansson, H. Characterization of a Fiber-Optic Pressure Sensor in a Shock Tube System for Dynamic Calibrations. Metrologia 2014, 52, 48–53. [Google Scholar] [CrossRef]
- Nowak, D.; Dziedzic, A. LTCC Package for High Temperature Applications. Microelectron. Reliab. 2011, 51, 1241–1244. [Google Scholar] [CrossRef]
- Liang, X.; Li, Y.; Liu, J.; Sang, S.; Chen, Y.; Li, B.; Aneziris, C.G. Improvement of the Mechanical Properties of SiC Reticulated Porous Ceramics with Optimized Three-Layered Struts for Porous Media Combustion. Ceram. Int. 2017, 43, 3741–3747. [Google Scholar] [CrossRef]
- Zhang, H.Q.; Bai, H.L.; Jia, Q.; Guo, W.; Liu, L.; Zou, G.S. High Electrical and Thermal Conductivity of Nano-Ag Paste for Power Electronic Applica-tions. Acta Metall. Sin. (Engl. Lett.) 2020, 33, 1543–1555. [Google Scholar] [CrossRef]
- Kashif, T.A.; Subburaj, J.; Khan, Z.A.; Farooq, A. Insights into shock velocity variation in double-diaphragm shock tubes. Phys. Fluids 2024, 36, 056124. [Google Scholar] [CrossRef]
- Zou, X.; Wu, N.; Tian, Y.; Zhang, Y.; Fitek, J.; Maffeo, M.; Niezrecki, C.; Chen, J.; Wang, X. Ultrafast Fabry–Perot Fiber-Optic Pressure Sensors for Multimedia Blast Event Measurements. Appl. Opt. 2013, 52, 1248–1254. [Google Scholar] [CrossRef]



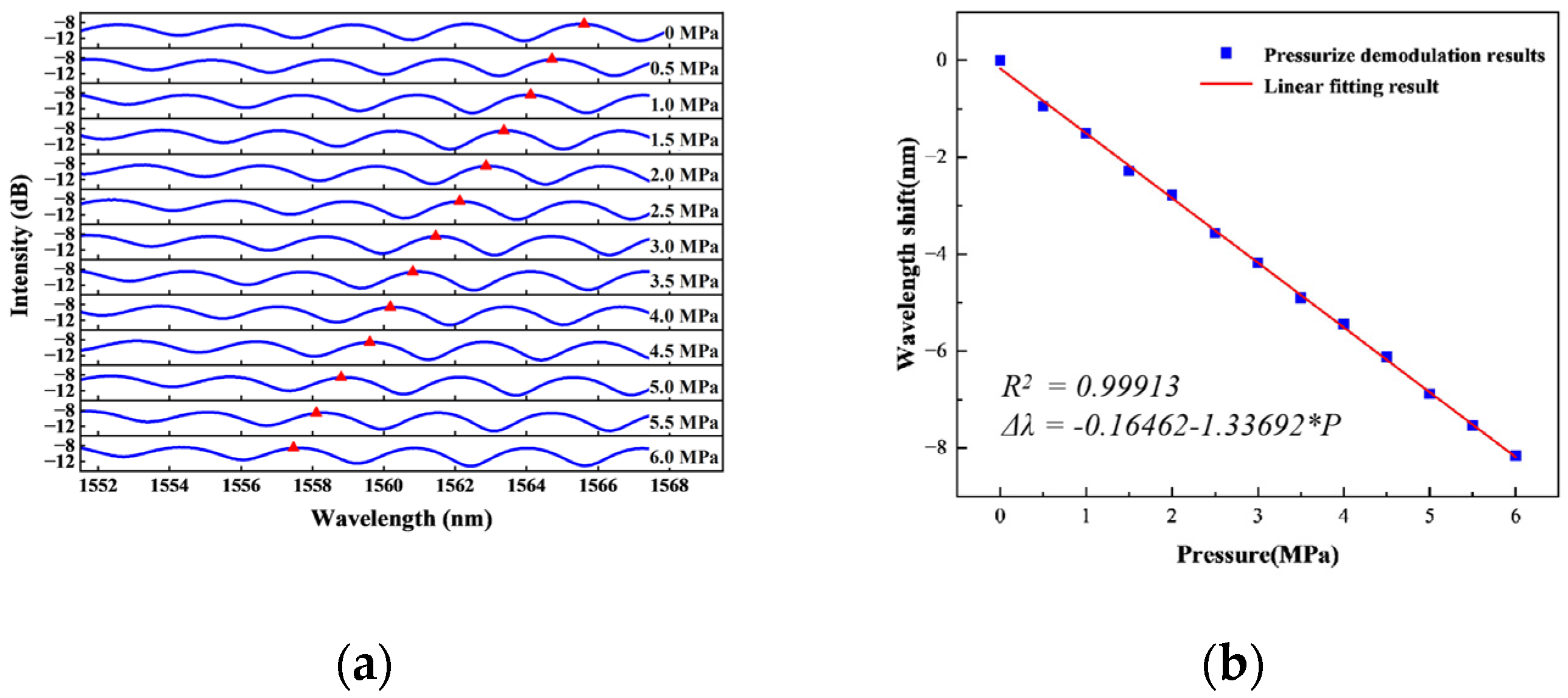
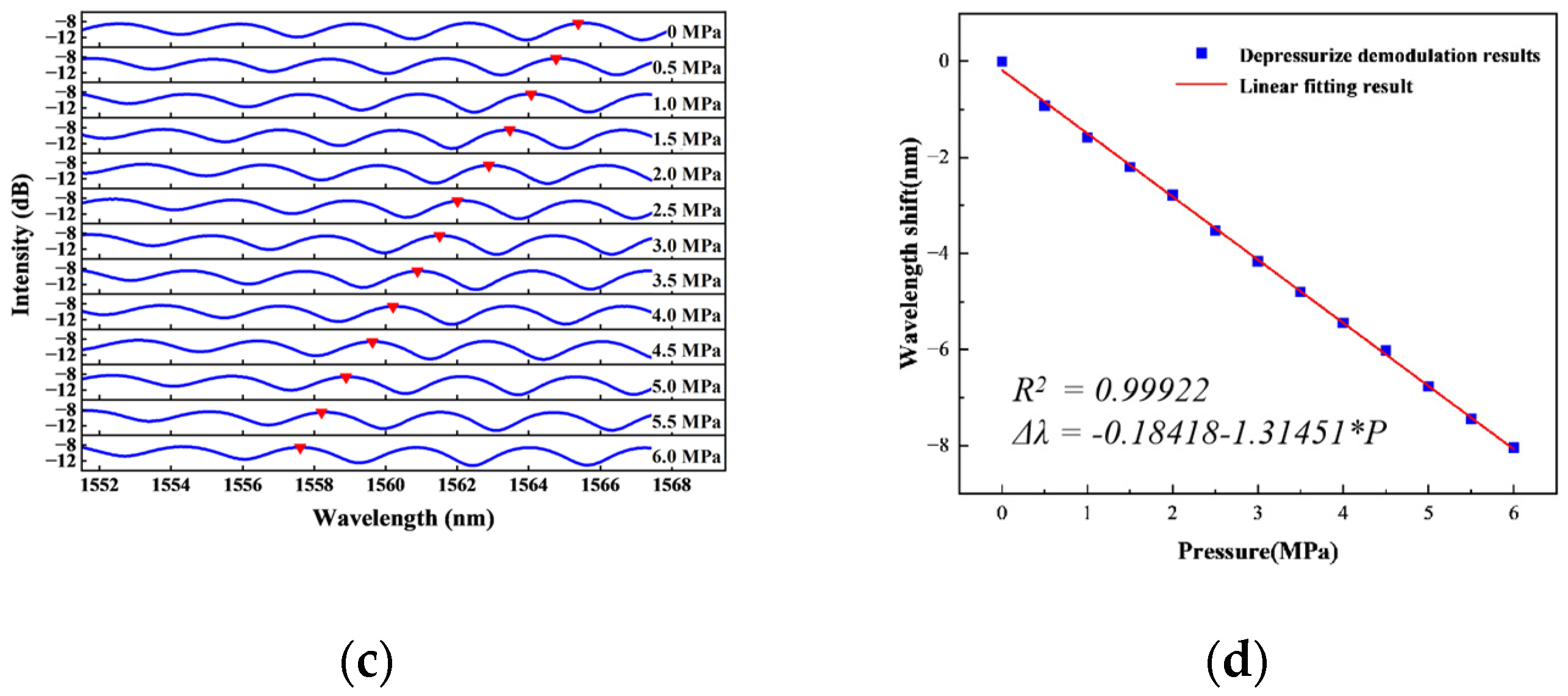
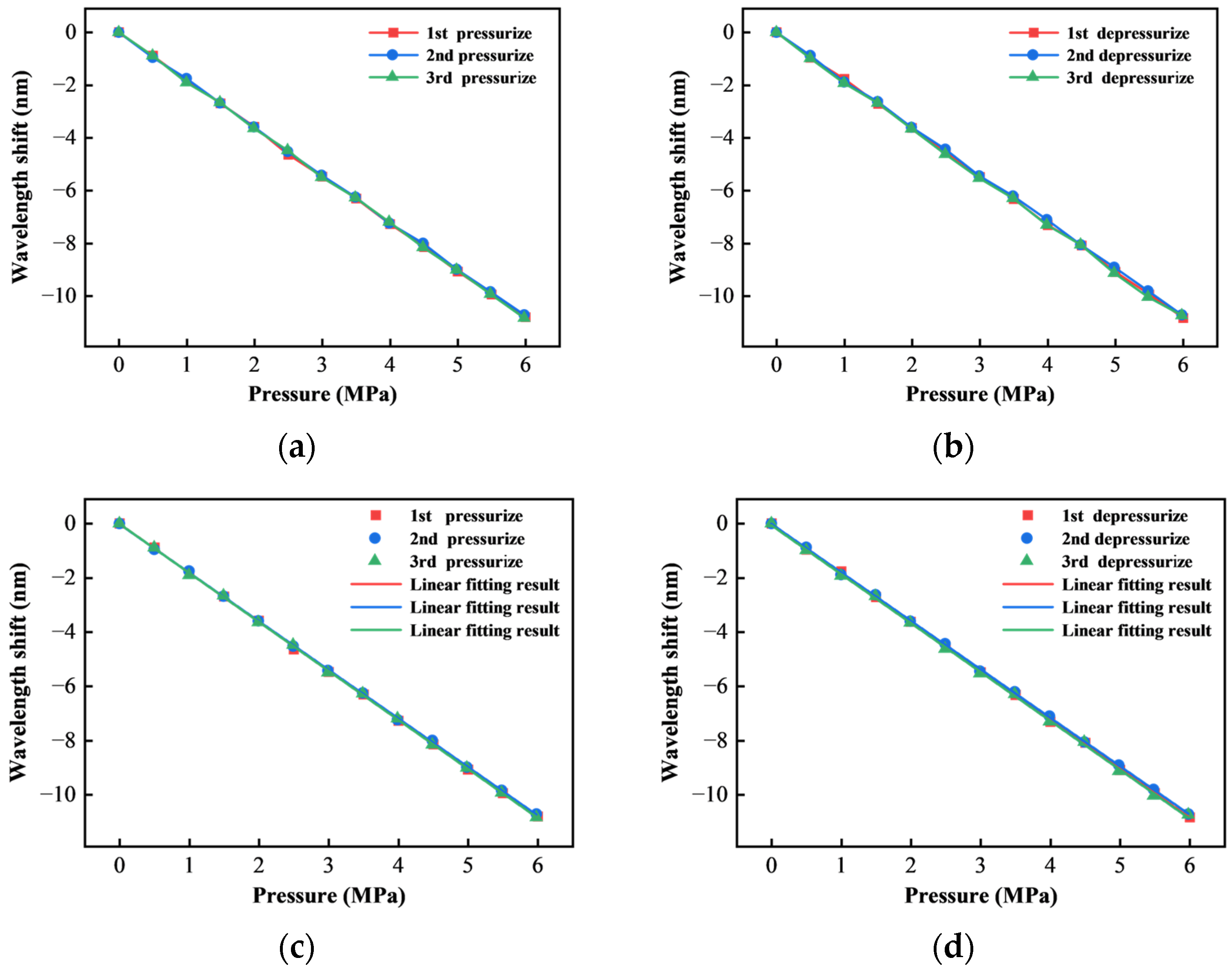



| Pressure Experiments | First Pressurization | First Depressurization | Second Pressurization | Second Depressurization | Third Pressurization | Third Depressurization |
|---|---|---|---|---|---|---|
| Slope | 1.807 | 1.792 | 1.809 | 1.806 | 1.788 | 1.804 |
| R2 | 0.99984 | 0.99976 | 0.99982 | 0.99987 | 0.99982 | 0.99956 |
| RSS | 0.02312 | 0.01828 | 0.02743 | 0.01979 | 0.02680 | 0.06500 |
| Standard Pressure (MPa) | Measure Pressure (MPa) | Test Error (F.S.) | Standard Pressure (MPa) | Measure Pressure (MPa) | Test Error (F.S.) |
|---|---|---|---|---|---|
| 0 | 0.019 | 0.3% | 3.5 | 3.514 | 0.2% |
| 0.5 | 0.480 | −0.3% | 4 | 3.996 | −0.1% |
| 1 | 0.962 | −0.6% | 4.5 | 4.481 | −0.3% |
| 1.5 | 1.473 | −0.4% | 5 | 4.977 | −0.4% |
| 2 | 1.994 | −0.1% | 5.5 | 5.532 | 0.5% |
| 2.5 | 2.522 | 0.4% | 6 | 5.959 | −0.7% |
| 3 | 3.037 | 0.6% | - | - | - |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, X.; Wang, F.; Han, G.; Tang, H.; Zhou, W.; Lei, X.; Liu, X. All-Ceramic Fiber Fabry–Perot Cavity High-Temperature Pulsating Pressure Sensor Based on HTCC. Sensors 2025, 25, 3678. https://doi.org/10.3390/s25123678
Xu X, Wang F, Han G, Tang H, Zhou W, Lei X, Liu X. All-Ceramic Fiber Fabry–Perot Cavity High-Temperature Pulsating Pressure Sensor Based on HTCC. Sensors. 2025; 25(12):3678. https://doi.org/10.3390/s25123678
Chicago/Turabian StyleXu, Xiangcong, Fei Wang, Guoqing Han, Huiyi Tang, Wanfeng Zhou, Xiaohua Lei, and Xianming Liu. 2025. "All-Ceramic Fiber Fabry–Perot Cavity High-Temperature Pulsating Pressure Sensor Based on HTCC" Sensors 25, no. 12: 3678. https://doi.org/10.3390/s25123678
APA StyleXu, X., Wang, F., Han, G., Tang, H., Zhou, W., Lei, X., & Liu, X. (2025). All-Ceramic Fiber Fabry–Perot Cavity High-Temperature Pulsating Pressure Sensor Based on HTCC. Sensors, 25(12), 3678. https://doi.org/10.3390/s25123678








