Simple and Cost-Effective Design of a THz-Metamaterial-Based Hybrid Sensor on a Single Substrate
Abstract
1. Introduction
2. Materials and Methods
3. Results and Discussions
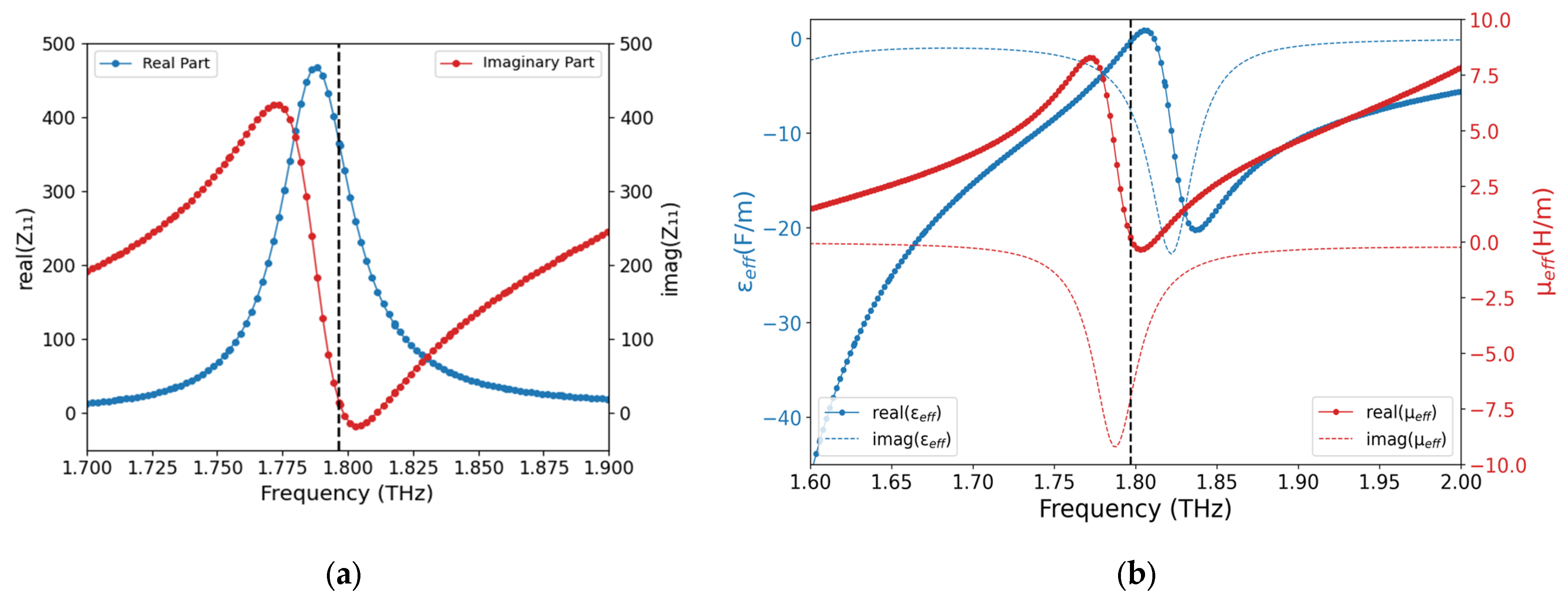
3.1. Absorption Theory and Analysis
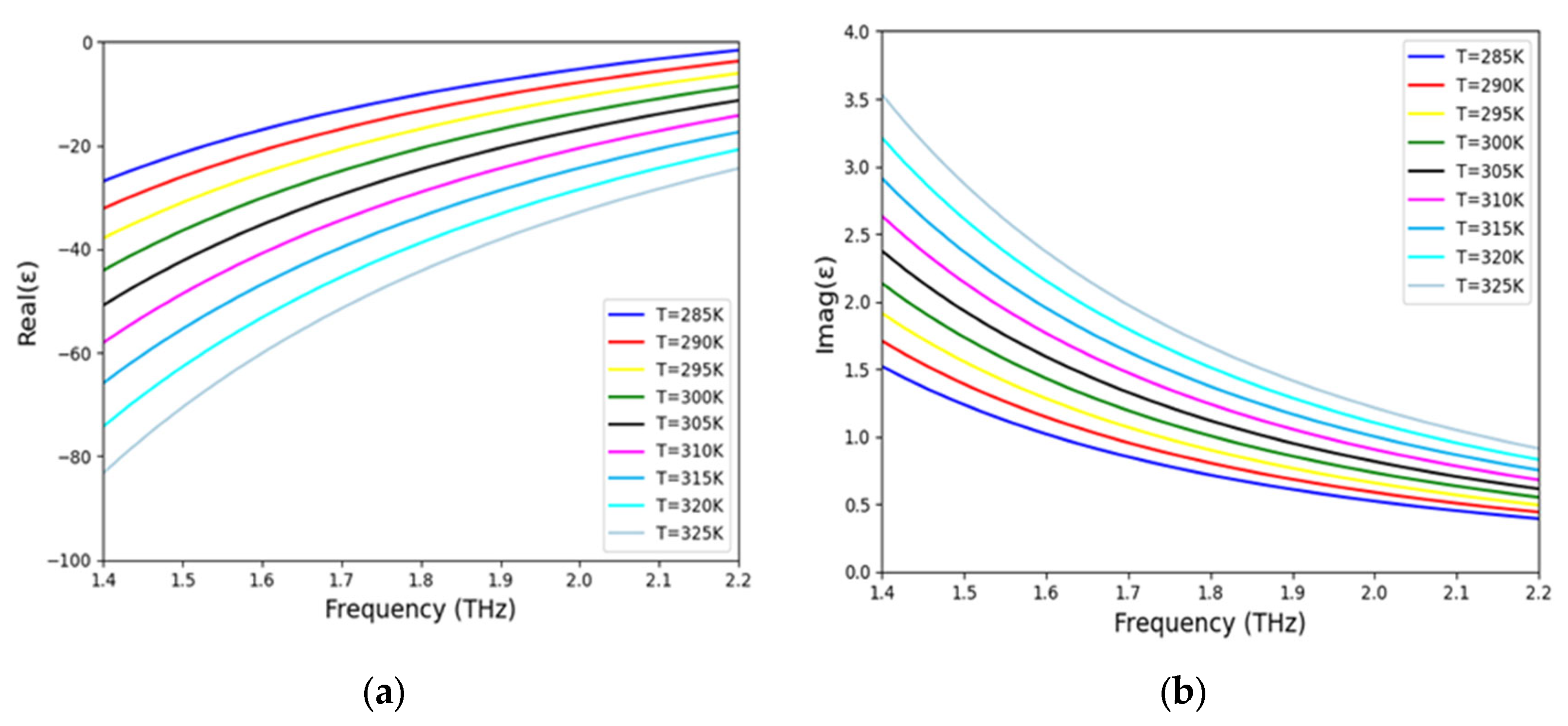
3.2. Effect of the Material and Structure Characteristics on Perfect Absorption
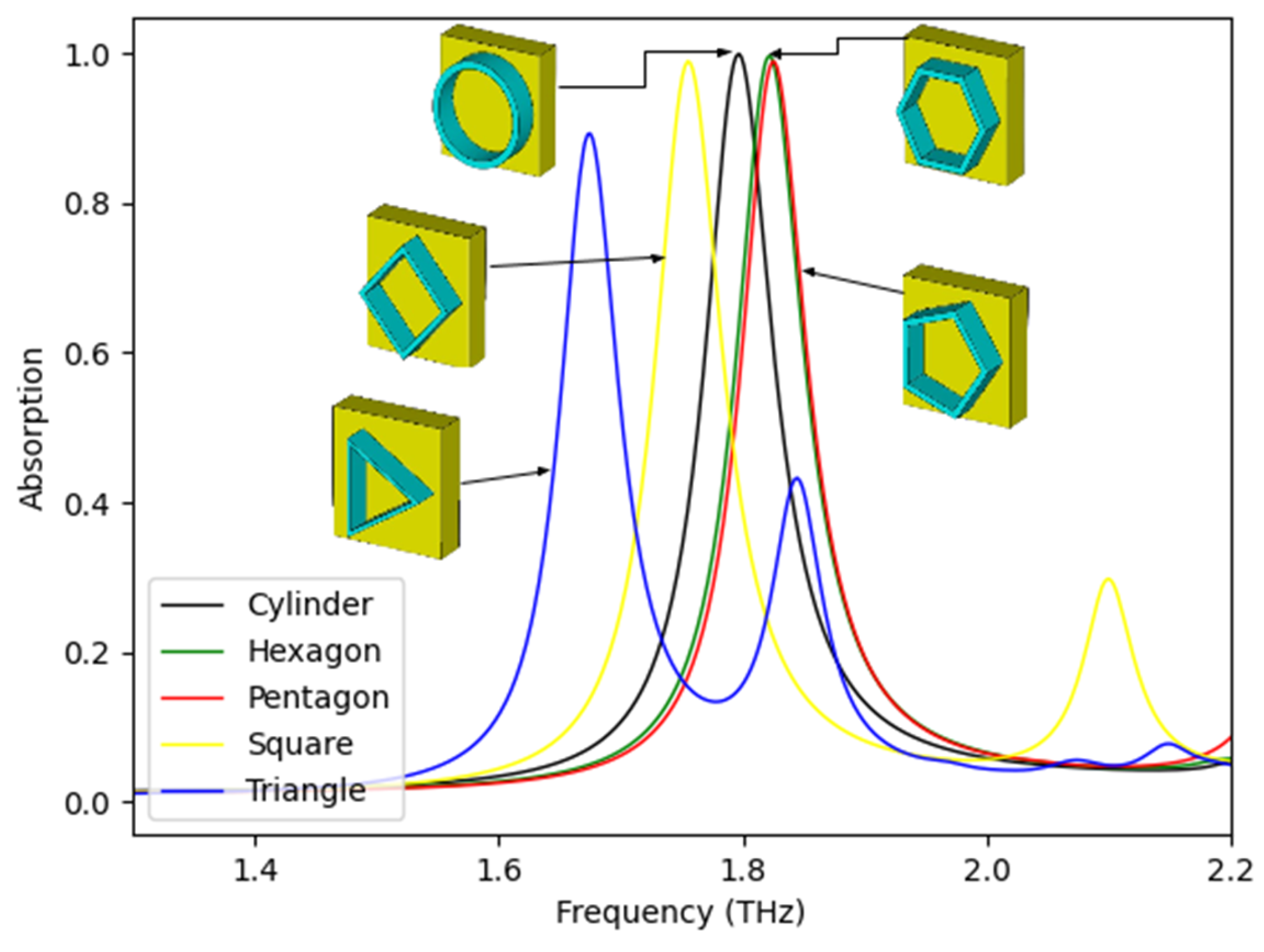
3.3. Parametric Analysis
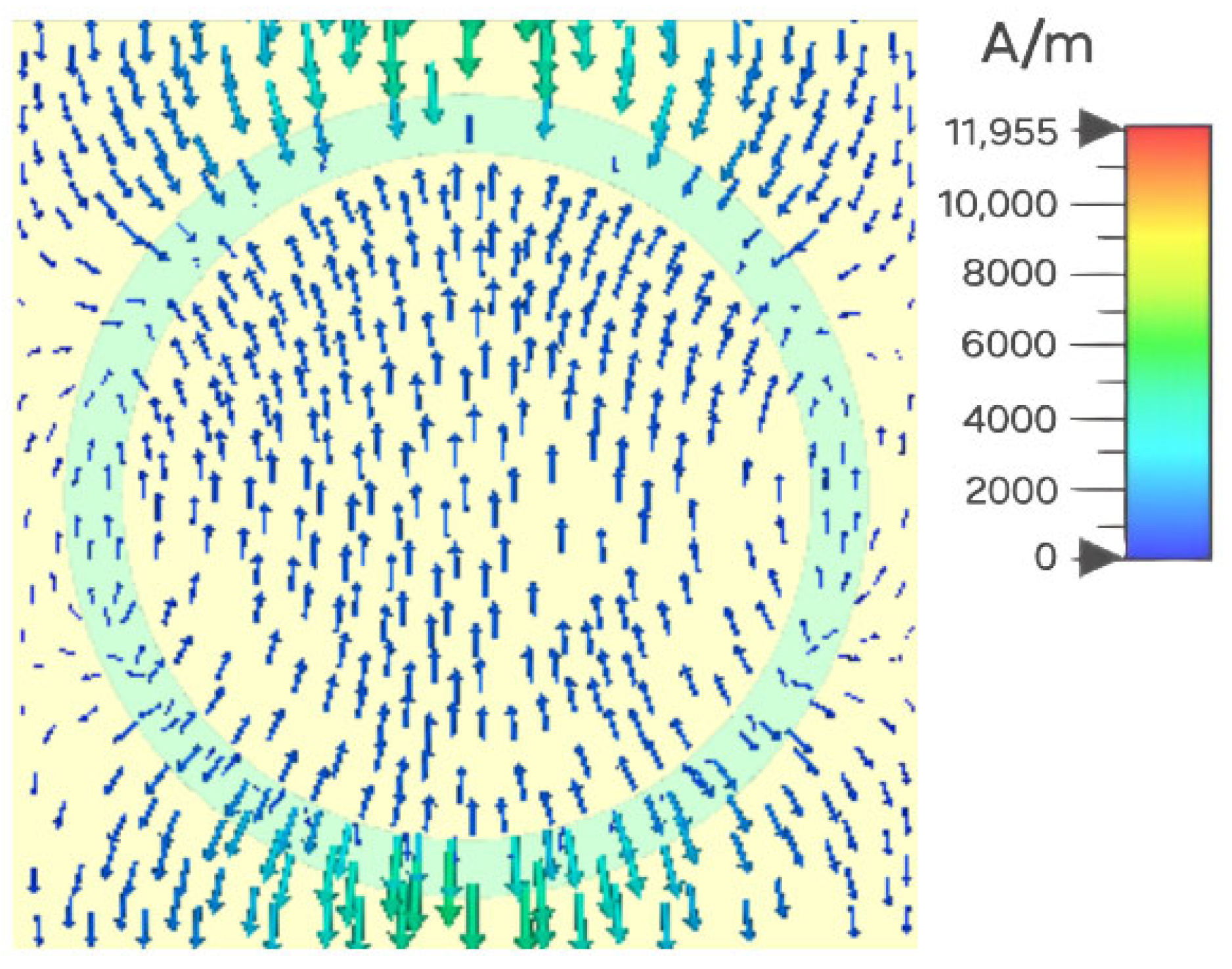
3.4. Surface Current
3.5. Sensitivity
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Abbreviations
| MMA | Metamaterial Absorber |
| TMA | Terahertz Metamaterial Absorber |
| HMA | Hybrid Metamaterial Absorber |
| MSA | Metasurface Absorber |
| SRR | Square Ring Resonator |
| FWHM | Full Width Half Maximum |
| RIU | Refractive Index Unit |
| InSb | Indium Antimonide |
| Q-factor | Quality Factor |
| SIS | Semiconductor-Insulator-Semiconductor |
| IATAI | InSb1-Analyte1-(TiO2-Si)7-Analyte2-InSb2 |
References
- Lee, Y.S. Principles of Terahertz Science and Technology; Springer: Boston, MA, USA, 2009; ISBN 978-0-387-09539-4. [Google Scholar]
- Puc, U.; Abina, A.; Rutar, M.; Zidanšek, A.; Jeglič, A.; Valušis, G. Terahertz Spectroscopic Identification of Explosive and Drug Simulants Concealed by Various Hiding Techniques. Appl. Opt. 2015, 54, 4495. [Google Scholar] [CrossRef] [PubMed]
- Siegel, P.H. Terahertz Technology. IEEE Trans. Microw. Theory Technol. 2002, 50, 910–928. [Google Scholar] [CrossRef]
- Tonouchi, M. Cutting-Edge Terahertz Technology. Nat. Photonics 2007, 1, 97–105. [Google Scholar] [CrossRef]
- Citroni, R.; Di Paolo, F.; Di Carlo, A. Replacing Noble Metals with Alternative Metals in MID-IR Frequency: A Theoretical Approach. In Proceedings of the Nanoinnovation 2017, Rome, Italy, 26–29 September 2017; p. 020004. [Google Scholar]
- Bakır, M.; Karaaslan, M.; Unal, E.; Akgol, O.; Sabah, C. Microwave Metamaterial Absorber for Sensing Applications. Opto-Electron. Rev. 2017, 25, 318–325. [Google Scholar] [CrossRef]
- Binda, P.; Singh, R.K.; Mitharwal, R. A Highly Sensitive Terahertz Temperature Sensor Based on Polarization Insensitive Perfect Metamaterial Absorber with Tunable Characteristics. Opt. Mater. 2024, 148, 114940. [Google Scholar] [CrossRef]
- Li, W.; Kuang, D.; Fan, F.; Chang, S.; Lin, L. Subwavelength B-Shaped Metallic Hole Array Terahertz Filter with InSb Bar as Thermally Tunable Structure. Appl. Opt. 2012, 51, 7098. [Google Scholar] [CrossRef]
- Zou, H.; Cheng, Y. A Thermally Tunable Terahertz Three-Dimensional Perfect Metamaterial Absorber for Temperature Sensing Application. Mod. Phys. Lett. B 2020, 34, 2050207. [Google Scholar] [CrossRef]
- Singh, R.K.; Gupta, A. A Wrenched-Square Shaped Polarization Independent and Wide Angle Stable Ultra-Thin Metamaterial Absorber for S-Band, X-Band and Ku-Band Applications. AEU Int. J. Electron. Commun. 2021, 132, 153648. [Google Scholar] [CrossRef]
- Banerjee, S.; Dutta, P.; Jha, A.V.; Appasani, B.; Khan, M.S. A Biomedical Sensor for Detection of Cancer Cells Based on Terahertz Metamaterial Absorber. IEEE Sens. Lett. 2022, 6, 6002004. [Google Scholar] [CrossRef]
- Banerjee, S.; Nath, U.; Dutta, P.; Jha, A.V.; Appasani, B.; Bizon, N. A Theoretical Terahertz Metamaterial Absorber Structure with a High Quality Factor Using Two Circular Ring Resonators for Biomedical Sensing. Inventions 2021, 6, 78. [Google Scholar] [CrossRef]
- Banerjee, S.; Nath, U.; Shruti; Jha, A.V.; Pahadsingh, S.; Appasani, B.; Bizon, N.; Srinivasulu, A. A Terahertz Metamaterial Absorber Based Refractive Index Sensor with High Quality Factor. In Proceedings of the 2021 13th International Conference on Electronics, Computers and Artificial Intelligence (ECAI), Pitesti, Romania, 1–3 July 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–4. [Google Scholar]
- Chen, F.; Cheng, Y.; Luo, H. Temperature Tunable Narrow-Band Terahertz Metasurface Absorber Based on InSb Micro-Cylinder Arrays for Enhanced Sensing Application. IEEE Access 2020, 8, 82981–82988. [Google Scholar] [CrossRef]
- Agarwal, P.; Kishor, K.; Sinha, R.K. Ultrasensitive Dual-Band Terahertz Metasurface Sensor Based on All InSb Resonator. Opt. Commun. 2022, 522, 128667. [Google Scholar] [CrossRef]
- Cheng, Y.; Li, Z.; Cheng, Z. Terahertz Perfect Absorber Based on InSb Metasurface for Both Temperature and Refractive Index Sensing. Opt. Mater. 2021, 117, 111129. [Google Scholar] [CrossRef]
- Luo, H.; Cheng, Y. Thermally Tunable Terahertz Metasurface Absorber Based on All Dielectric Indium Antimonide Resonator Structure. Opt. Mater. 2020, 102, 109801. [Google Scholar] [CrossRef]
- Appasani, B. Temperature Tunable Seven Band Terahertz Metamaterial Absorber Using Slotted Flower–Shaped Resonator on an InSb Substrate. Plasmonics 2021, 16, 833–839. [Google Scholar] [CrossRef]
- Jing, H.; Wei, Y.; Duan, J.; Hao, J.; Zhao, W.; Qu, Z.; Wang, J.; Zhang, B. Thermally and Magnetically Controlled Dual-Band Terahertz Metamaterial Absorber Based on InSb. Opt. Mater. 2022, 129, 112311. [Google Scholar] [CrossRef]
- Shen, F.; Qin, J.; Han, Z. Planar Antenna Array as a Highly Sensitive Terahertz Sensor. Appl. Opt. 2019, 58, 540. [Google Scholar] [CrossRef]
- Li, Y.; Chen, X.; Hu, F.; Li, D.; Teng, H.; Rong, Q.; Zhang, W.; Han, J.; Liang, H. Four Resonators Based High Sensitive Terahertz Metamaterial Biosensor Used for Measuring Concentration of Protein. J. Phys. D Appl. Phys. 2019, 52, 095105. [Google Scholar] [CrossRef]
- Banerjee, S.; Ghosh, I.; Santini, C.; Mangini, F.; Citroni, R.; Frezza, F. All-Metal Metamaterial-Based Sensor with Novel Geometry and Enhanced Sensing Capability at Terahertz Frequency. Sensors 2025, 25, 507. [Google Scholar] [CrossRef]
- Faist, J.; Capasso, F.; Sivco, D.L.; Sirtori, C.; Hutchinson, A.L.; Cho, A.Y. Quantum Cascade Laser. Science 1994, 264, 553–556. [Google Scholar] [CrossRef]
- Vitiello, M.S.; De Natale, P. Terahertz Quantum Cascade Lasers as Enabling Quantum Technology. Adv. Quantum Technol. 2022, 5, 2100082. [Google Scholar] [CrossRef]
- Kumar, S. Recent Progress in Terahertz Quantum Cascade Lasers. IEEE J. Select. Top. Quantum Electron. 2011, 17, 38–47. [Google Scholar] [CrossRef]
- Rösch, M.; Scalari, G.; Beck, M.; Faist, J. Octave-Spanning Semiconductor Laser. Nat. Photonics 2015, 9, 42–47. [Google Scholar] [CrossRef]
- Silvestri, C.; Qi, X.; Taimre, T.; Rakić, A.D. Frequency Combs Induced by Optical Feedback and Harmonic Order Tunability in Quantum Cascade Lasers. APL Photonics 2023, 8, 116102. [Google Scholar] [CrossRef]
- Rakić, A.D.; Taimre, T.; Bertling, K.; Lim, Y.L.; Dean, P.; Valavanis, A.; Indjin, D. Sensing and Imaging Using Laser Feedback Interferometry with Quantum Cascade Lasers. Appl. Phys. Rev. 2019, 6, 021320. [Google Scholar] [CrossRef]
- Banerjee, S.; Dutta, P.; Basu, S.; Mishra, S.K.; Appasani, B.; Nanda, S.; Abdulkarim, Y.I.; Muhammadsharif, F.F.; Dong, J.; Jha, A.V.; et al. A New Design of a Terahertz Metamaterial Absorber for Gas Sensing Applications. Symmetry 2022, 15, 24. [Google Scholar] [CrossRef]
- Zhan, Y.; Yin, H.; Wang, J.; Yao, H.; Fan, C. Tunable Multiple Band THz Perfect Absorber with InSb Metamaterial for Enhanced Sensing Application. Results Opt. 2022, 8, 100255. [Google Scholar] [CrossRef]
- Zhang, Y.; Wu, P.; Zhou, Z.; Chen, X.; Yi, Z.; Zhu, J.; Zhang, T.; Jile, H. Study on Temperature Adjustable Terahertz Metamaterial Absorber Based on Vanadium Dioxide. IEEE Access 2020, 8, 85154–85161. [Google Scholar] [CrossRef]
- Saadatmand, S.B.; Ahmadi, V.; Hamidi, S.M. Quasi-BIC Based All-Dielectric Metasurfaces for Ultra-Sensitive Refractive Index and Temperature Sensing. Sci. Rep. 2023, 13, 20625. [Google Scholar] [CrossRef]
- Gao, W.; Chen, F.; Yang, W. Temperature and Refractive Index Sensor Based on Perfect Absorber in InSb Double Rectangular Ring Resonator Metamaterials. Mater. Today Commun. 2024, 40, 109461. [Google Scholar] [CrossRef]
- Li, Z.; Cheng, Y.; Luo, H.; Chen, F.; Li, X. Dual-Band Tunable Terahertz Perfect Absorber Based on All-Dielectric InSb Resonator Structure for Sensing Application. J. Alloys Compd. 2022, 925, 166617. [Google Scholar] [CrossRef]
- Zamani Noughabi, S.; Nooramin, A.S.; Soleimani, M. Proposing a THz Refractive Index Sensor Based on the Excitation of SPPs with InSb Cylinder. AUT J. Electr. Eng. 2023, 55, 133–144. [Google Scholar] [CrossRef]
- Xiong, S.; Tang, X.; Chen, F. Enhanced Temperature and Refractive Index Sensor Based on InSb Plasmonic Waveguide Resonator Structure with a Disk Defect. Plasmonics 2025. [Google Scholar] [CrossRef]
- Lu, M.; Deng, X.-H.; Hu, P. Dual-Band InSb Metamaterial Absorber Based on Temperature and Magnetic Field Control. MRS Adv. 2024, 9, 1121–1127. [Google Scholar] [CrossRef]
- Wan, B.-F.; Ye, H.-N.; Zhang, H.-F. Double-Layer InSb Photonic Crystal Structure for Enhanced Nonreciprocal OTS and Its Potential in Extending the Measurement Range of Bivariate Sensors. IEEE Sens. J. 2024, 24, 4236–4245. [Google Scholar] [CrossRef]






| Design Parameter | Magnitude (µm) | Definitions of the Parameters |
|---|---|---|
| u | 80 | Unit cell’s periodicity |
| h | 23 | Height of the metal film |
| d | 20 | Height of the InSb cylindrical structure |
| r1 | 30 | Inner radius of the InSb cylindrical structure |
| r2 | 35 | Outer radius of the InSb cylindrical structure |
| Temperature (K) | Resonance Frequency (THz) | FWHM Bandwidth (THz) | Absorptivity | Q-Factor |
|---|---|---|---|---|
| 285 | 1.589 | 0.048 | 85.70% | 33.10 |
| 290 | 1.648 | 0.056 | 93.18% | 29.43 |
| 295 | 1.723 | 0.063 | 98.04% | 27.35 |
| 300 | 1.797 | 0.068 | 99.94% | 26.43 |
| 305 | 1.854 | 0.072 | 99.02% | 25.75 |
| 310 | 1.917 | 0.075 | 95.80% | 25.56 |
| 315 | 1.996 | 0.076 | 91.23% | 26.26 |
| 320 | 2.055 | 0.075 | 85.18% | 27.40 |
| 325 | 2.097 | 0.073 | 79.97% | 28.73 |
| Refractive Index | Resonance Frequency (THz) | FWHM Bandwidth (THz) | Absorptivity | Q-Factor |
|---|---|---|---|---|
| 1.00 | 1.797 | 0.068 | 99.94% | 26.43 |
| 1.01 | 1.788 | 0.068 | 99.95% | 26.29 |
| 1.02 | 1.767 | 0.068 | 99.96% | 25.99 |
| 1.03 | 1.751 | 0.069 | 99.98% | 25.38 |
| 1.04 | 1.755 | 0.068 | 99.99% | 25.81 |
| 1.05 | 1.740 | 0.068 | 99.97% | 25.59 |
| References | Temperature Sensor | Refractive Index Sensor | Thickness (µm), Periodicity (µm) | Material Configurations | Absorptivity (%) | Temperature Sensitivity (GHz/K) | Refractive Index Sensitivity (GHz/RIU) | Polarization Sensitive | Incident Angle Stability |
|---|---|---|---|---|---|---|---|---|---|
| [7] | Yes | No | 42, 100 | InSb–Au | 99.94 | 16.1 | N/A | Yes | N/A |
| [11] | No | Yes | 8.4, 102 | Au-GaAs-Au | 99.0 | N/A | 1447.0 | Yes | N/A |
| [12] | No | Yes | 8.4, 100 | Al-GaAs-Al | 99.5 | N/A | 1500.0 | No | N/A |
| [13] | No | Yes | 8.7, 80 | Al-GaAs-Al | 99.8 | N/A | 187.0 | N/A | N/A |
| [14] | Yes | Yes | 139, 150 | InSb–Au–Glass | 99.9 | 2.13 | 960.0 | Yes | N/A |
| [15] | Yes | Yes | 160, 150 | InSb | 98.0, 91.0 | 5.5, 7.5 | 1900.0, 1800.0 | N/A | N/A |
| [16] | Yes | Yes | 160, 150 | InSb | 99.9 | 4.2 | 920.0 | Yes | N/A |
| [17] | Yes | No | 46, 150 | InSb–Au | 99.9 | 9.6 | N/A | Yes | N/A |
| [19] | Yes | No | 90.4, 80 | InSb-Teflon-Copper | 94.0, 94.0 | 4.64, 8.36 | N/A | Yes | 0–45° |
| [33] | Yes | Yes | 41.5, 150 | InSb-Au-SiO2 | 98.95, 99.45 | 8.6, 12.8 | 1065.0, 499.0 | Yes | 0–60° |
| [34] | Yes | Yes | 240, 120 | InSb-InSb | 99.9, 99.8 | 5.9, 6.4 | 1300.0, 1000.0 | Yes | 0–30° |
| [30] | Yes | Yes | 15.8, 35 | InSb-SiO2-Au | 100 | 22 | 287 | N/A | N/A |
| [35] | No | Yes | 78, 150 | InSb-Au | 99.9 | N/A | 672.0 | Yes | N/A |
| [36] | Yes | Yes | 120, 400 | SIS | N/A | 0.46, 0.59 | 736.5, 661.3 | N/A | N/A |
| [37] | Yes | No | 195, 150 | InSb | 98.0, 92.0 | 10.12, 5.62 | N/A | Yes | N/A |
| [38] | No | Yes | 56.4, N/A | IATAI | 94.20, 91.80 | N/A | 520.0, 810.0 | N/A | N/A |
| This Work | Yes | Yes | 43, 80 | InSb–Copper | 99.94 | 13.07 | 1146.0 | Yes | 0–45° |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nath, U.; Banerjee, S.; Santini, C.; Citroni, R.; Mangini, F.; Frezza, F. Simple and Cost-Effective Design of a THz-Metamaterial-Based Hybrid Sensor on a Single Substrate. Sensors 2025, 25, 3660. https://doi.org/10.3390/s25123660
Nath U, Banerjee S, Santini C, Citroni R, Mangini F, Frezza F. Simple and Cost-Effective Design of a THz-Metamaterial-Based Hybrid Sensor on a Single Substrate. Sensors. 2025; 25(12):3660. https://doi.org/10.3390/s25123660
Chicago/Turabian StyleNath, Uddipan, Sagnik Banerjee, Carlo Santini, Rocco Citroni, Fabio Mangini, and Fabrizio Frezza. 2025. "Simple and Cost-Effective Design of a THz-Metamaterial-Based Hybrid Sensor on a Single Substrate" Sensors 25, no. 12: 3660. https://doi.org/10.3390/s25123660
APA StyleNath, U., Banerjee, S., Santini, C., Citroni, R., Mangini, F., & Frezza, F. (2025). Simple and Cost-Effective Design of a THz-Metamaterial-Based Hybrid Sensor on a Single Substrate. Sensors, 25(12), 3660. https://doi.org/10.3390/s25123660







