Robust Estimation of Unsteady Beat-to-Beat Systolic Blood Pressure Trends Using Photoplethysmography Contextual Cycles
Abstract
1. Introduction
- We develop a new approach for SBP trend estimation to transform the task into sequence prediction. Our method prioritizes beat-to-beat SBP variability for assisting in health applications, particularly for heterogeneous populations with frequent and dramatic fluctuations in SBP.
- We present a hybrid architecture based on the contextual cycles. ResU blocks extract hemodynamic information and enhance semantic representation. The patch-based structure provides temporal order and context for intra-cycle feature vectors, enabling a Transformer with RPE (Trans-RPE) that considers the relative temporal distance to explore inter-cycle interaction and more reliable temporal dependencies for complex SBP fluctuation patterns.
- We conduct studies with adequate variations in SBP, and the results demonstrate that our model excels in estimating the trend of beat-to-beat SBP with MAE and VE of 3.186 and 1.199 mmHg, especially in unsteady states. The classification accuracy for abnormal variations reaches 80.36%. Furthermore, our model meets the AAMI and BHS grade A standards.
2. Materials and Methods
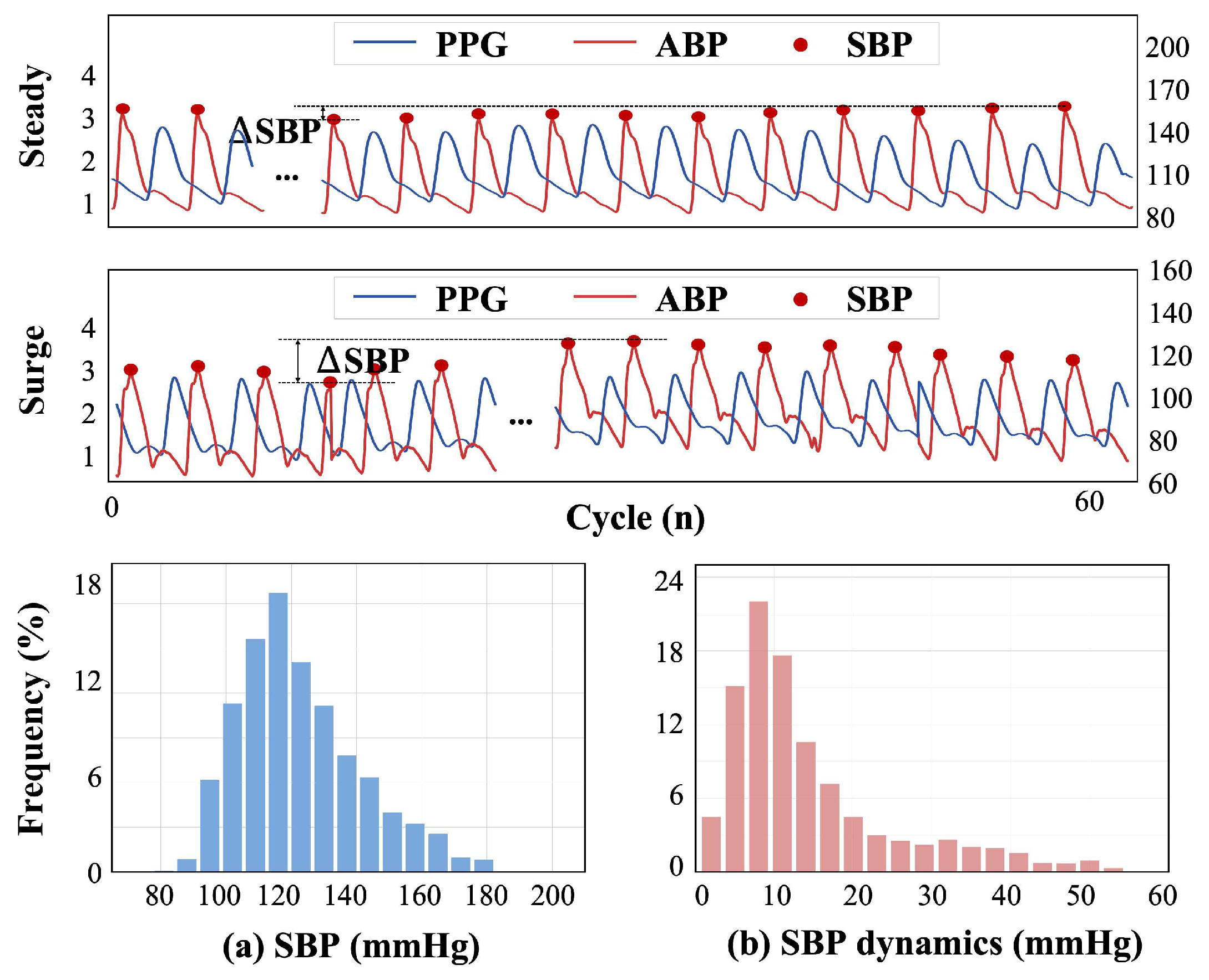
2.1. Database and Data Pre-Processing
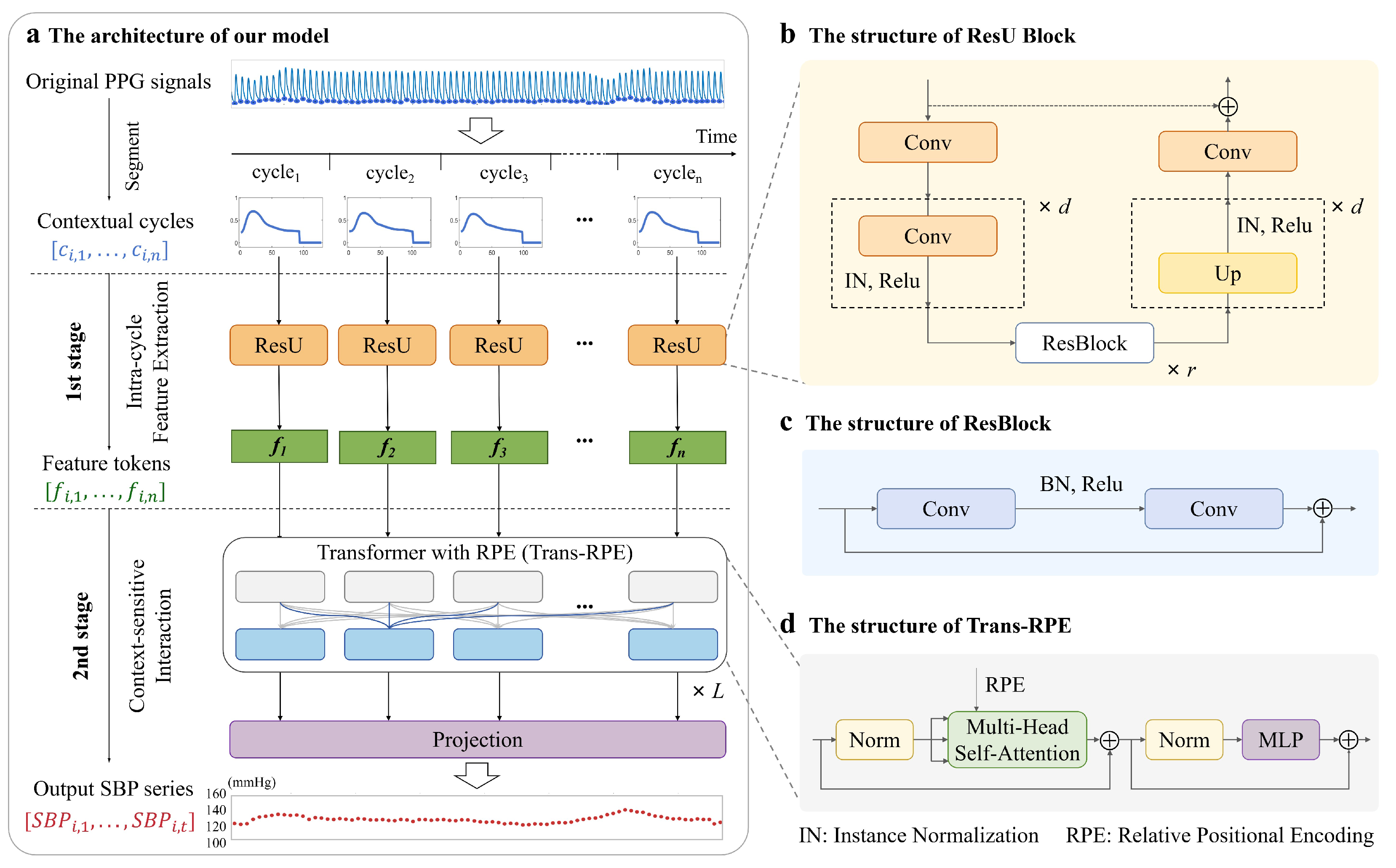
2.2. Network Architecture
2.2.1. Intra-Cycle Feature Extraction
2.2.2. Context-Sensitive Interaction
| Algorithm 1 The architecture of our proposed model |
Input: mini-batch size B, training dataset , where denotes contextual cycles containing n cycle slices of length , and denotes the sequence containing n SBP values Output: the optimal parameters of model Initialization: ResU block, Trans-RPE layers, number of Trans-RPE layers L
|
2.3. Experimental Settings
2.4. Performance Evaluation Metrics
3. Results
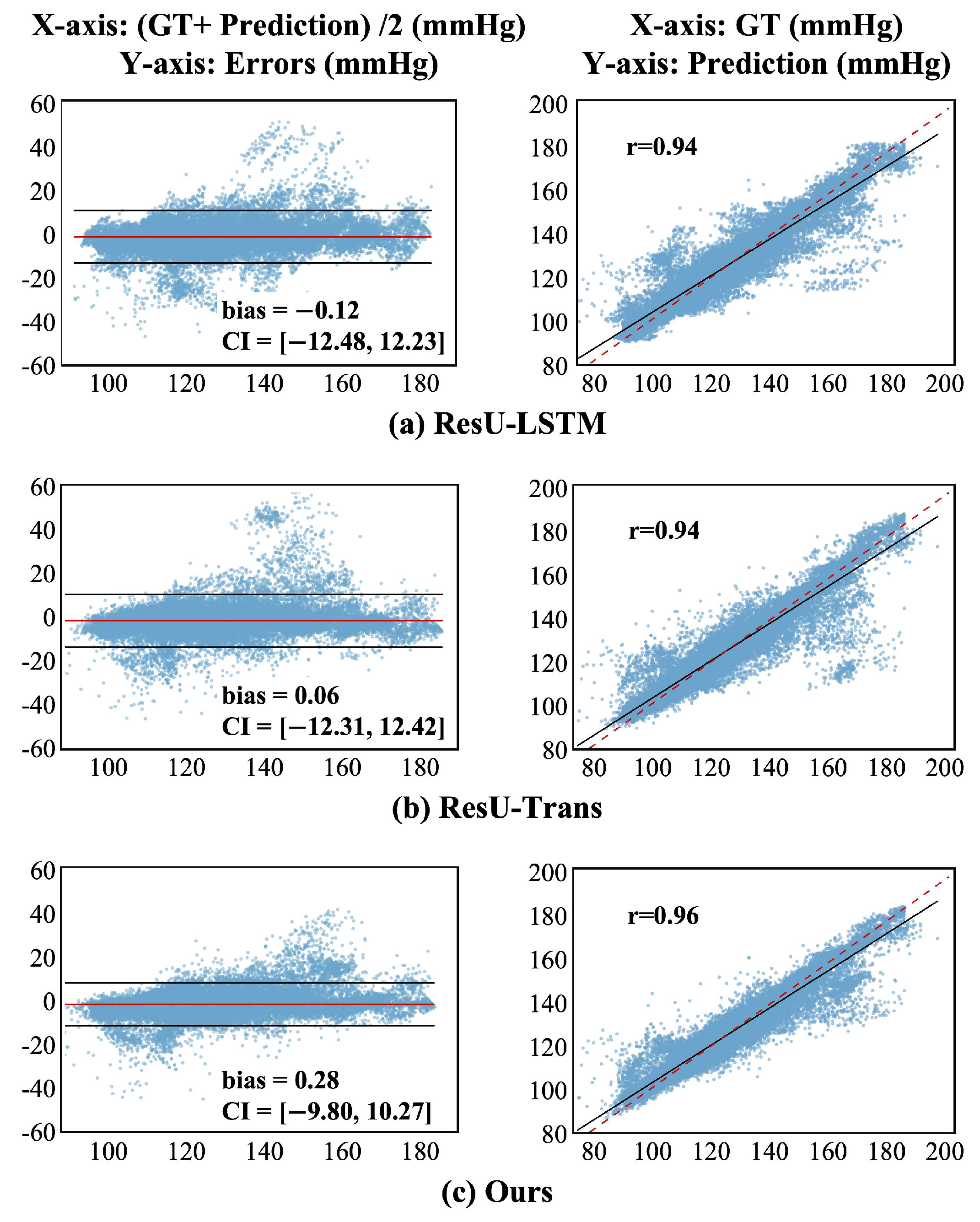
3.1. SBP Trend Estimation
3.1.1. Quantitative Evaluation
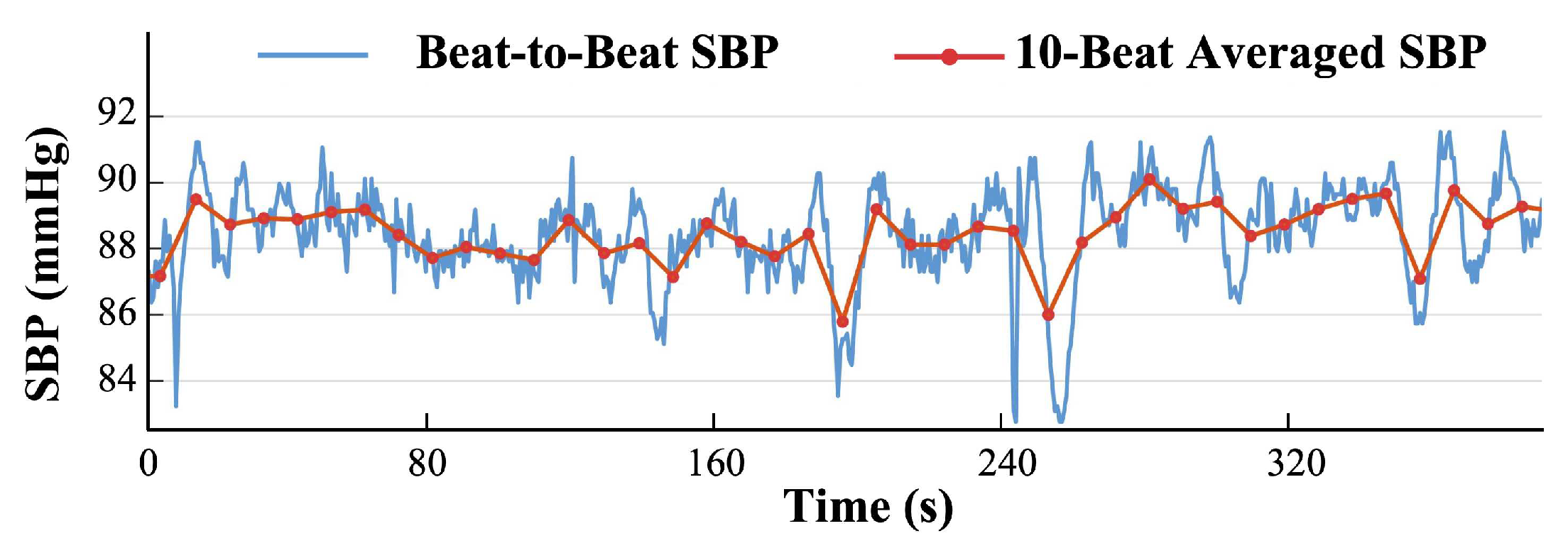
3.1.2. Qualitative Evaluation
3.2. SBP Value Prediction
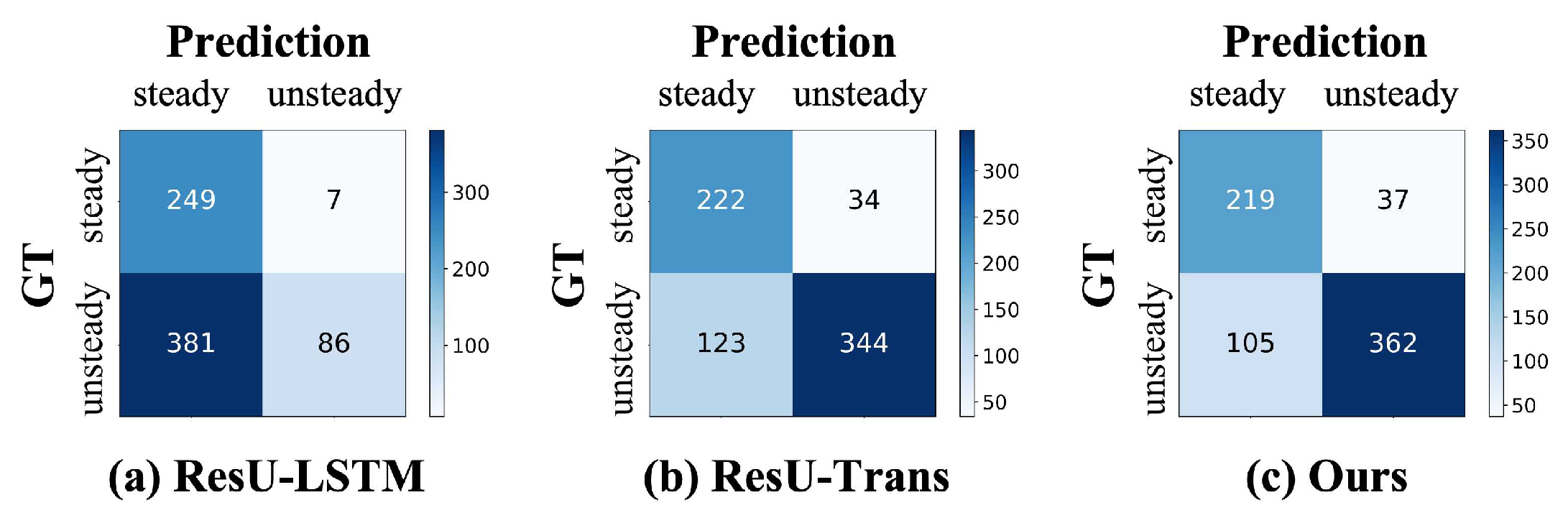
3.3. Comparisons
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Vaduganathan, M.; Mensah, G.A.; Turco, J.V.; Fuster, V.; Roth, G.A. The global burden of cardiovascular diseases and risk: A compass for future health. J. Am. Coll. Cardiol. 2022, 80, 2361–2371. [Google Scholar] [CrossRef] [PubMed]
- Rothwell, P.M.; Howard, S.C.; Dolan, E.; O’Brien, E.; Dobson, J.E.; Dahlöf, B.; Sever, P.S.; Poulter, N.R. Prognostic significance of visit-to-visit variability, maximum systolic blood pressure, and episodic hypertension. Lancet 2010, 375, 895–905. [Google Scholar] [CrossRef] [PubMed]
- Berry, M.; Lairez, O.; Fourcade, J.; Roncalli, J.; Carrié, D.; Pathak, A.; Chamontin, B.; Galinier, M. Prognostic value of systolic short-term blood pressure variability in systolic heart failure. Clin. Hypertens. 2016, 22, 16. [Google Scholar] [CrossRef] [PubMed]
- Messerli, F.H.; Hofstetter, L.; Rimoldi, S.F.; Rexhaj, E.; Bangalore, S. Risk factor variability and cardiovascular outcome: JACC review topic of the week. J. Am. Coll. Cardiol. 2019, 73, 2596–2603. [Google Scholar] [CrossRef]
- Zhou, T.L.; Kroon, A.A.; van Sloten, T.T.; van Boxtel, M.P.; Verhey, F.R.; Schram, M.T.; Köhler, S.; Stehouwer, C.D.; Henry, R.M. Greater blood pressure variability is associated with lower cognitive performance: The Maastricht study. Hypertension 2019, 73, 803–811. [Google Scholar] [CrossRef]
- Webb, A.J.; Mazzucco, S.; Li, L.; Rothwell, P.M. Prognostic significance of blood pressure variability on beat-to-beat monitoring after transient ischemic attack and stroke. Stroke 2018, 49, 62–67. [Google Scholar] [CrossRef]
- Talle, M.A.; Ngarande, E.; Doubell, A.F.; Herbst, P.G. Cardiac complications of hypertensive emergency: Classification, diagnosis and management challenges. J. Cardiovasc. Dev. Dis. 2022, 9, 276. [Google Scholar] [CrossRef]
- Kario, K. Obstructive sleep apnea syndrome and hypertension: Ambulatory blood pressure. Hypertens. Res. 2009, 32, 428–432. [Google Scholar] [CrossRef]
- Lim, S.S.; Vos, T.; Flaxman, A.D.; Danaei, G.; Shibuya, K.; Adair-Rohani, H.; AlMazroa, M.A.; Amann, M.; Anderson, H.R.; Andrews, K.G.; et al. A comparative risk assessment of burden of disease and injury attributable to 67 risk factors and risk factor clusters in 21 regions, 1990–2010: A systematic analysis for the Global Burden of Disease Study 2010. Lancet 2012, 380, 2224–2260. [Google Scholar] [CrossRef]
- Schutte, A.E.; Kollias, A.; Stergiou, G.S. Blood pressure and its variability: Classic and novel measurement techniques. Nat. Rev. Cardiol. 2022, 19, 643–654. [Google Scholar] [CrossRef]
- Jhee, J.H.; Oh, D.; Seo, J.; Lee, C.J.; Chung, M.Y.; Park, J.T.; Han, S.H.; Kang, S.W.; Park, S.; Yoo, T.H. Short-term blood pressure variability and incident CKD in patients with hypertension: Findings From the cardiovascular and metabolic disease etiology research center–high risk (CMERC-HI) study. Am. J. Kidney Dis. 2023, 81, 384–393. [Google Scholar] [CrossRef] [PubMed]
- Allen, J. Photoplethysmography and its application in clinical physiological measurement. Physiol. Meas. 2007, 28, R1. [Google Scholar] [CrossRef] [PubMed]
- Charlton, P.H.; Paliakaitė, B.; Pilt, K.; Bachler, M.; Zanelli, S.; Kulin, D.; Allen, J.; Hallab, M.; Bianchini, E.; Mayer, C.C.; et al. Assessing hemodynamics from the photoplethysmogram to gain insights into vascular age: A review from VascAgeNet. Am. J. Physiol.-Heart Circ. Physiol. 2022, 322, H493–H522. [Google Scholar] [CrossRef] [PubMed]
- Parati, G.; Saul, J.P.; Di Rienzo, M.; Mancia, G. Spectral analysis of blood pressure and heart rate variability in evaluating cardiovascular regulation: A critical appraisal. Hypertension 1995, 25, 1276–1286. [Google Scholar] [CrossRef]
- Lo, F.P.W.; Li, C.X.T.; Wang, J.; Cheng, J.; Meng, M.Q.H. Continuous systolic and diastolic blood pressure estimation utilizing long short-term memory network. In Proceedings of the 2017 39th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Jeju, Republic of Korea, 11–15 July 2017; pp. 1853–1856. [Google Scholar]
- Mohammed, H.; Wang, K.; Wu, H.; Wang, G. Subject-wise model generalization through pooling and patching for regression: Application on non-invasive systolic blood pressure estimation. Comput. Biol. Med. 2022, 151, 106299. [Google Scholar] [CrossRef]
- Kario, K. Evidence and perspectives on the 24-hour management of hypertension: Hemodynamic biomarker-initiated ‘anticipation medicine’for zero cardiovascular event. Prog. Cardiovasc. Dis. 2016, 59, 262–281. [Google Scholar] [CrossRef]
- Khalid, S.G.; Zhang, J.; Chen, F.; Zheng, D. Blood pressure estimation using photoplethysmography only: Comparison between different machine learning approaches. J. Healthc. Eng. 2018, 2018, 1548647. [Google Scholar] [CrossRef]
- Fleischhauer, V.; Feldheiser, A.; Zaunseder, S. Beat-to-beat blood pressure estimation by photoplethysmography and its interpretation. Sensors 2022, 22, 7037. [Google Scholar] [CrossRef]
- Gupta, S.; Singh, A.; Sharma, A.; Tripathy, R.K. Higher order derivative-based integrated model for cuff-less blood pressure estimation and stratification using PPG signals. IEEE Sens. J. 2022, 22, 22030–22039. [Google Scholar] [CrossRef]
- Liu, L.; Zhang, Y.T.; Wang, W.; Chen, Y.; Ding, X. Causal inference based cuffless blood pressure estimation: A pilot study. Comput. Biol. Med. 2023, 159, 106900. [Google Scholar] [CrossRef]
- He, R.; Huang, Z.P.; Ji, L.Y.; Wu, J.K.; Li, H.; Zhang, Z.Q. Beat-to-beat ambulatory blood pressure estimation based on random forest. In Proceedings of the 2016 IEEE 13th International Conference on Wearable and Implantable Body Sensor Networks (BSN), San Francisco, CA, USA, 14–17 June 2016; pp. 194–198. [Google Scholar]
- Yu, M.; Huang, Z.; Zhu, Y.; Zhou, P.; Zhu, J. Attention-based residual improved U-Net model for continuous blood pressure monitoring by using photoplethysmography signal. Biomed. Signal Process. Control 2022, 75, 103581. [Google Scholar] [CrossRef]
- Huang, B.; Chen, W.; Lin, C.L.; Juang, C.F.; Wang, J. MLP-BP: A novel framework for cuffless blood pressure measurement with PPG and ECG signals based on MLP-Mixer neural networks. Biomed. Signal Process. Control 2022, 73, 103404. [Google Scholar] [CrossRef]
- Miao, F.; Wen, B.; Hu, Z.; Fortino, G.; Wang, X.P.; Liu, Z.D.; Tang, M.; Li, Y. Continuous blood pressure measurement from one-channel electrocardiogram signal using deep-learning techniques. Artif. Intell. Med. 2020, 108, 101919. [Google Scholar] [CrossRef]
- Wang, W.; Mohseni, P.; Kilgore, K.L.; Najafizadeh, L. Demographic Information Fusion Using Attentive Pooling In CNN-GRU Model For Systolic Blood Pressure Estimation. In Proceedings of the 2023 45th Annual International Conference of the IEEE Engineering in Medicine & Biology Society (EMBC), Sydney, Australia, 24–27 July 2023; pp. 1–4. [Google Scholar]
- Liu, Z.; Zhang, Y.; Zhou, C. BiGRU-attention for Continuous blood pressure trends estimation through single channel PPG. Comput. Biol. Med. 2024, 168, 107795. [Google Scholar] [CrossRef]
- Ma, K.; Zou, L.; Yang, F.; Chang’an, A.Z.; Gong, Y.; Huang, D. Continuous non-invasive arterial blood pressure monitoring with photoplethysmography via SE-MSResUNet network. Biomed. Signal Process. Control 2024, 90, 105862. [Google Scholar] [CrossRef]
- Masum, S.; Chiverton, J.P.; Liu, Y.; Vuksanovic, B. Investigation of machine learning techniques in forecasting of blood pressure time series data. In Proceedings of the Artificial Intelligence XXXVI: 39th SGAI International Conference on Artificial Intelligence, AI 2019, Cambridge, UK, 17–19 December 2019; Proceedings 39. Springer: Berlin/Heidelberg, Germany, 2019; pp. 269–282. [Google Scholar]
- Chen, J.; Song, P.; Zhao, C. Multi-scale self-supervised representation learning with temporal alignment for multi-rate time series modeling. Pattern Recognit. 2024, 145, 109943. [Google Scholar] [CrossRef]
- Jiang, X.; Cai, Y.; Wu, X.; Huang, B.; Chen, Y.; Zhong, L.; Gao, X.; Guo, Y.; Zhou, J. The multiscale dynamics of beat-to-beat blood pressure fluctuation links to functions in older adults. Front. Cardiovasc. Med. 2022, 9, 833125. [Google Scholar] [CrossRef]
- Bakkar, N.M.Z.; El-Yazbi, A.F.; Zouein, F.A.; Fares, S.A. Beat-to-beat blood pressure variability: An early predictor of disease and cardiovascular risk. J. Hypertens. 2021, 39, 830–845. [Google Scholar] [CrossRef]
- He, S.; Dajani, H.R.; Meade, R.D.; Kenny, G.P.; Bolic, M. Continuous tracking of changes in systolic blood pressure using BCG and ECG. In Proceedings of the 2019 41st Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Berlin, Germany, 23–27 July 2019; pp. 6826–6829. [Google Scholar]
- Liu, Z.D.; Li, Y.; Zhang, Y.T.; Zeng, J.; Chen, Z.X.; Cui, Z.W.; Liu, J.K.; Miao, F. Cuffless blood pressure measurement using smartwatches: A large-scale validation study. IEEE J. Biomed. Health Inform. 2023, 27, 4216–4227. [Google Scholar] [CrossRef]
- Qin, K.; Huang, W.; Zhang, T.; Tang, S. Machine learning and deep learning for blood pressure prediction: A methodological review from multiple perspectives. Artif. Intell. Rev. 2023, 56, 8095–8196. [Google Scholar] [CrossRef]
- Cheung, M.Y.; Sabharwal, A.; Cot, G.L.; Veeraraghavan, A. Wearable Blood Pressure Monitoring Devices: Understanding Heterogeneity in Design and Evaluation. IEEE Trans. Biomed. Eng. 2024, 71, 3569–3592. [Google Scholar] [CrossRef] [PubMed]
- Wu, H.; Hu, T.; Liu, Y.; Zhou, H.; Wang, J.; Long, M. Timesnet: Temporal 2d-variation modeling for general time series analysis. In Proceedings of the Eleventh International Conference on Learning Representations, Online, 25–29 April 2022. [Google Scholar]
- Gong, Z.; Tang, Y.; Liang, J. Patchmixer: A patch-mixing architecture for long-term time series forecasting. arXiv 2023, arXiv:2310.00655. [Google Scholar]
- Nie, Y.; Nguyen, N.H.; Sinthong, P.; Kalagnanam, J. A time series is worth 64 words: Long-term forecasting with transformers. arXiv 2022, arXiv:2211.14730. [Google Scholar]
- Kachuee, M.; Kiani, M.M.; Mohammadzade, H.; Shabany, M. Cuffless blood pressure estimation algorithms for continuous health-care monitoring. IEEE Trans. Biomed. Eng. 2016, 64, 859–869. [Google Scholar] [CrossRef] [PubMed]
- Liang, Y.; Elgendi, M.; Chen, Z.; Ward, R. An optimal filter for short photoplethysmogram signals. Sci. Data 2018, 5, 1–12. [Google Scholar] [CrossRef]
- Zong, W.; Heldt, T.; Moody, G.; Mark, R. An open-source algorithm to detect onset of arterial blood pressure pulses. In Proceedings of the Computers in Cardiology, Thessaloniki, Greece, 21–24 September 2003; pp. 259–262. [Google Scholar]
- Vaswani, A. Attention is all you need. arXiv 2017, arXiv:1706.03762. [Google Scholar]
- Zhang, Y.; Ma, L.; Pal, S.; Zhang, Y.; Coates, M. Multi-resolution Time-Series Transformer for Long-term Forecasting. In Proceedings of the International Conference on Artificial Intelligence and Statistics, PMLR, Valencia, Spain, 2–4 May 2024; pp. 4222–4230. [Google Scholar]
- Xiong, Q.; Tang, K.; Ma, M.; Xu, J.; Li, T. TDT Loss Takes It All: Integrating Temporal Dependencies among Targets into Non-Autoregressive Time Series Forecasting. arXiv 2024, arXiv:2406.04777. [Google Scholar]
- Kokubo, A.; Kuwabara, M.; Nakajima, H.; Tomitani, N.; Yamashita, S.; Shiga, T.; Kario, K. Automatic detection algorithm for establishing standard to identify “surge blood pressure”. Med. Biol. Eng. Comput. 2020, 58, 1393–1404. [Google Scholar] [CrossRef]
- Vardhan, K.R.; Vedanth, S.; Poojah, G.; Abhishek, K.; Kumar, M.N.; Vijayaraghavan, V. BP-Net: Efficient deep learning for continuous arterial blood pressure estimation using photoplethysmogram. In Proceedings of the 2021 20th IEEE International Conference on Machine Learning and Applications (ICMLA), Virtual, 13–16 December 2021; pp. 1495–1500. [Google Scholar]
- Esmaelpoor, J.; Moradi, M.H.; Kadkhodamohammadi, A. A multistage deep neural network model for blood pressure estimation using photoplethysmogram signals. Comput. Biol. Med. 2020, 120, 103719. [Google Scholar] [CrossRef]



| Model | Metrics (mmHg) | ||
|---|---|---|---|
| MAE | VE | ||
| Trans | 5.578 | 0.520 | 1.800 |
| Trans-RPE | 4.304 | 0.671 | 1.318 |
| ResU-LSTM | 4.015 | 0.356 | 2.500 |
| ResU-Trans | 3.595 | 0.681 | 1.510 |
| ResU-Trans-RPE (L=1) | 3.463 | 0.683 | 1.464 |
| ResU-Trans-RPE (L=2) | 3.348 | 0.706 | 1.321 |
| Ours | 3.186 | 0.743 | 1.199 |
| ME | SD | Subject | |
|---|---|---|---|
| Error standard | ≤5 mmHg | ≤8 mmHg | 85 |
| Ours | −0.238 | 5.120 | 238 |
| Cumulative Absolute Error Percentage | Grade | |||
|---|---|---|---|---|
| ≤5 mmHg | ≤10 mmHg | ≤15 mmHg | ||
| Our method | 82.88% | 94.39% | 97.43% | A |
| Grade A | 60% | 85% | 95% | |
| Grade B | 50% | 75% | 90% | |
| Grade C | 40% | 65% | 85% | |
| Model | Database (No. of Samples) | Input | Beat-to-Beat SBP | Beat-Averaged SBP | ||||
|---|---|---|---|---|---|---|---|---|
| MAE | ME | SD | MAE | ME | SD | |||
| Regression tree [18] | Queensland(32 subjects) | 3 features | - | −1.1 | 5.7 | - | - | - |
| Xgboost [19] | CPT, PPG-BP, and Queensland (327, 840 beats) | 15 features | 6.37 | 2.89 | 12.02 | - | - | - |
| U-Net [47] | MIMIC-II(949 subjects) | 10 s PPG segment | 5.16 | - | - | - | - | - |
| CNN-LSTM [48] | MIMIC-II(200 subjects) | 256-sample PPG segment(contains one complete cardiac cycle) | - | 1.91 | 5.55 | - | - | - |
| Attention-basedresidual improved U-Net [23] | MIMIC-III(100 subjects) | 600 samples (PPG, VPG, and APG)(contains 5 consecutive cycles) | - | - | - | 4.75 | - | 6.72 |
| MLPlstm-BP [24] | MIMIC-II (3000 segments) | 10 s ECG and PPG segments | - | - | - | 3.52 | - | 5.10 |
| CNN-GRU [26] | MIMIC-III(1293 segments) | 10 s ECG and PPG segments | - | - | - | 4.90 | 0.12 | 7.00 |
| SE-MSResUNet [28] | MIMIC-II(111,097 segments) | 10 s PPG segment | - | - | - | 3.88 | - | 6.17 |
| Ours | MIMIC-II(238 subjects) | contextual cycles(contains 60 complete cardiac cycles) | 3.186 | −0.238 | 5.120 | 3.053 | −0.238 | 4.723 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, X.; Zhang, X.; Millham, R.; Xu, L.; Wu, W. Robust Estimation of Unsteady Beat-to-Beat Systolic Blood Pressure Trends Using Photoplethysmography Contextual Cycles. Sensors 2025, 25, 3625. https://doi.org/10.3390/s25123625
Huang X, Zhang X, Millham R, Xu L, Wu W. Robust Estimation of Unsteady Beat-to-Beat Systolic Blood Pressure Trends Using Photoplethysmography Contextual Cycles. Sensors. 2025; 25(12):3625. https://doi.org/10.3390/s25123625
Chicago/Turabian StyleHuang, Xinyi, Xianbin Zhang, Richard Millham, Lin Xu, and Wanqing Wu. 2025. "Robust Estimation of Unsteady Beat-to-Beat Systolic Blood Pressure Trends Using Photoplethysmography Contextual Cycles" Sensors 25, no. 12: 3625. https://doi.org/10.3390/s25123625
APA StyleHuang, X., Zhang, X., Millham, R., Xu, L., & Wu, W. (2025). Robust Estimation of Unsteady Beat-to-Beat Systolic Blood Pressure Trends Using Photoplethysmography Contextual Cycles. Sensors, 25(12), 3625. https://doi.org/10.3390/s25123625








