Microwire vs. Micro-Ribbon Magnetoelastic Sensors for Vibration-Based Structural Health Monitoring of Rectangular Concrete Beams
Abstract
1. Introduction
2. Materials and Methods
2.1. Sensing Elements
2.2. Sample Preparation
3. Experimental Methods
3.1. Experimental Setup for Exciting the Beams
3.2. Sensor Signal Comparison
3.3. Magnetic Characterization of Sensors
3.4. Thermal Treatment of Sensors
4. Results and Discussion
4.1. Comparison of the Two Sensors for Crack Detection Experiments
4.2. Crack Detection by Sensors
5. Comparison to Accelerometry Measurements
6. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Wu, T.; Liu, G.; Fu, S.; Xing, F. Recent progress of fiber-optic sensors for the structural health monitoring of civil infrastructure. Sensors 2020, 20, 4517. [Google Scholar] [CrossRef]
- Ono, K. Review on structural health evaluation with acoustic emission. Appl. Sci. 2018, 8, 958. [Google Scholar] [CrossRef]
- Varanis, M.; Silva, A.; Mereles, A.; Pederiva, R. MEMS accelerometers for mechanical vibrations analysis: A comprehensive review with applications. J. Braz. Soc. Mech. Sci. Eng. 2018, 40, 527. [Google Scholar] [CrossRef]
- Ceylan, H.; Gopalakrishnan, K.; Kim, S.; Taylor, P.C.; Prokudin, M.; Buss, A.F. Highway infrastructure health monitoring using micro-electromechanical sensors and systems (MEMS). J. Civ. Eng. Manag. 2013, 19, S188–S201. [Google Scholar] [CrossRef]
- Han, H.S.; Duong, T.A.; Ahn, C.W.; Kim, B.W.; Lee, J.S. A brief review on piezoelectrics-based paint sensors. J. Korean Inst. Electr. Electron. Mater. Eng. 2023, 36, 433–441. [Google Scholar]
- Khan, Y.; Thielens, A.; Muin, S.; Ting, J.; Baumbauer, C.; Arias, A.C. A new frontier of printed electronics: Flexible hybrid electronics. Adv. Mater. 2020, 32, 1905279. [Google Scholar] [CrossRef] [PubMed]
- Abbas, M.; Shafiee, M. Structural health monitoring (SHM) and determination of surface defects in large metallic structures using ultrasonic guided waves. Sensors 2018, 18, 3958. [Google Scholar] [CrossRef]
- Flah, M.; Nunez, I.; Ben Chaabene, W.; Nehdi, M.L. Machine learning algorithms in civil structural health monitoring: A systematic review. Arch. Comput. Methods Eng. 2021, 28, 2621–2643. [Google Scholar] [CrossRef]
- Avci, O.; Abdeljaber, O.; Kiranyaz, S.; Hussein, M.; Gabbouj, M.; Inman, D.J. A review of vibration-based damage detection in civil structures: From traditional methods to Machine Learning and Deep Learning applications. Mech. Syst. Signal Process. 2021, 147, 107077. [Google Scholar] [CrossRef]
- Cao, H.; Liang, N.; Gu, F. Vibration Structural Damage Diagnosis Based on Modal Parameters. In Proceedings of the UNIfied Conference of DAMAS, IncoME and TEPEN Conferences (UNIfied 2023), Huddersfield, UK, 29 August–1 September 2023; Springer: Cham, Switzerland, 2023; pp. 475–485. [Google Scholar]
- Shi, Z.Y.; Law, S.S.; Zhang, L.M. Structural damage detection from modal strain energy change. J. Eng. Mech. 2000, 126(12), 1216–1223. [Google Scholar]
- Hussein, H.A.; Rahim, S.B.A.; Mustapha, F.B.; Krishnan, P.S.; Jalil, N.A.B.A. Data-driven multi-fault detection in pipelines utilizing frequency response function and artificial neural networks. J. Pipeline Sci. Eng. 2025, 5, 100223. [Google Scholar] [CrossRef]
- Aranizadeh, A.; Shad, H.; Vahidi, B.; Khorsandi, A. A novel small-scale wind-turbine blade failure detection according to monitored-data. Results Eng. 2025, 25, 103809. [Google Scholar] [CrossRef]
- Hamza, M.; Akhtar, K.; Khan, M.A. Modal and dynamic analysis of damaged steel column-beam frame structure subjected to seismic vibrations using experimental and finite element analysis approach. J. Braz. Soc. Mech. Sci. Eng. 2024, 46, 94. [Google Scholar] [CrossRef]
- Ramakrishna, S.; Sathish, J.; Raj Kumar, V.; Raghu Vamsi, S. Experimental investigation on crack localization in steel and composite structures by intersection of first three normalized mode shape curves. J. Fail. Anal. Prev. 2022, 22, 1970–1981. [Google Scholar] [CrossRef]
- Rao, R.K.; Sasmal, S. Smart nano-engineered cementitious composite sensors for vibration-based health monitoring of large structures. Sens. Actuators A Phys. 2020, 311, 112088. [Google Scholar] [CrossRef]
- Modesti, M.; Gentilini, C.; Palermo, A.; Reynders, E.; Lombaert, G. A two-step procedure for damage detection in beam structures with incomplete mode shapes. J. Civ. Struct. Health Monit. 2024, 15, 287–306. [Google Scholar] [CrossRef]
- Modzelewski, C.; Savage, H.; Kabacoff, L.; Clark, A. Magnetomechanical coupling and permeability in transversely annealed Metglas 2605 alloys. IEEE Trans. Magn. 1981, 17, 2837–2839. [Google Scholar] [CrossRef]
- Savage, H.; Spano, M. Theory and application of highly magnetoelastic Metglas 2605SC. J. Appl. Phys. 1982, 53, 8092–8097. [Google Scholar] [CrossRef]
- Song, H.; Jang, Y.; Lee, J.P.; Choe, J.K.; Yun, M.; Baek, Y.K.; Kim, J. Highly compressible 3D-printed soft magnetoelastic sensors for human–machine interfaces. ACS Appl. Mater. Interfaces 2023, 15, 59776–59786. [Google Scholar] [CrossRef]
- Shekhar, S.; Karipott, S.S.; Guldberg, R.E.; Ong, K.G. Magnetoelastic sensors for real-time tracking of cell growth. Biotechnol. Bioeng. 2021, 118, 2380–2385. [Google Scholar] [CrossRef]
- Samourgkanidis, G.; Kouzoudis, D. Characterization of magnetoelastic ribbons as vibration sensors based on the measured natural frequencies of a cantilever beam. Sens. Actuators A Phys. 2020, 301, 111711. [Google Scholar] [CrossRef]
- Vázquez, M. Advanced magnetic microwires. In Handbook of Magnetism and Advanced Magnetic Materials; Willey: Hoboken, NJ, USA, 2007. [Google Scholar]
- Zhukov, A.; Ipatov, M.; Corte-León, P.; Gonzalez-Legarreta, L.; Blanco, J.; Zhukova, V. Soft magnetic microwires for sensor applications. J. Magn. Magn. Mater. 2020, 498, 166180. [Google Scholar] [CrossRef]
- Panina, L.; Makhnovskiy, D.; Morchenko, A.; Kostishin, V. Tunable permeability of magnetic wires at microwaves. J. Magn. Magn. Mater. 2015, 383, 120–125. [Google Scholar] [CrossRef]
- Salaheldeen, M.; Garcia-Gomez, A.; Corte-León, P.; Gonzalez, A.; Ipatov, M.; Zhukova, V.; Gonzalez, J.; Antón, R.L.; Zhukov, A. Manipulation of magnetic and structure properties of Ni2FeSi glass-coated microwires by annealing. J. Alloys Compd. 2023, 942, 169026. [Google Scholar] [CrossRef]
- Tapeinos, C.I.; Kamitsou, M.D.; Dassios, K.G.; Kouzoudis, D.; Christogerou, A.; Samourgkanidis, G. Contactless and Vibration-Based Damage Detection in Rectangular Cement Beams Using Magnetoelastic Ribbon Sensors. Sensors 2023, 23, 5453. [Google Scholar] [CrossRef]
- EN 196-1:2005; Methods of Testing Cement–Part 1: Determination of Strength. European Committee for Standardization: Brussels, Belgium, 2005.
- Xiao, F.; Mao, Y.; Tian, G.; Chen, G.S. Partial-Model-Based Damage Identification of Long-Span Steel Truss Bridge Based on Stiffness Separation Method. Struct. Control. Health Monit. 2024, 2024, 5530300. [Google Scholar] [CrossRef]





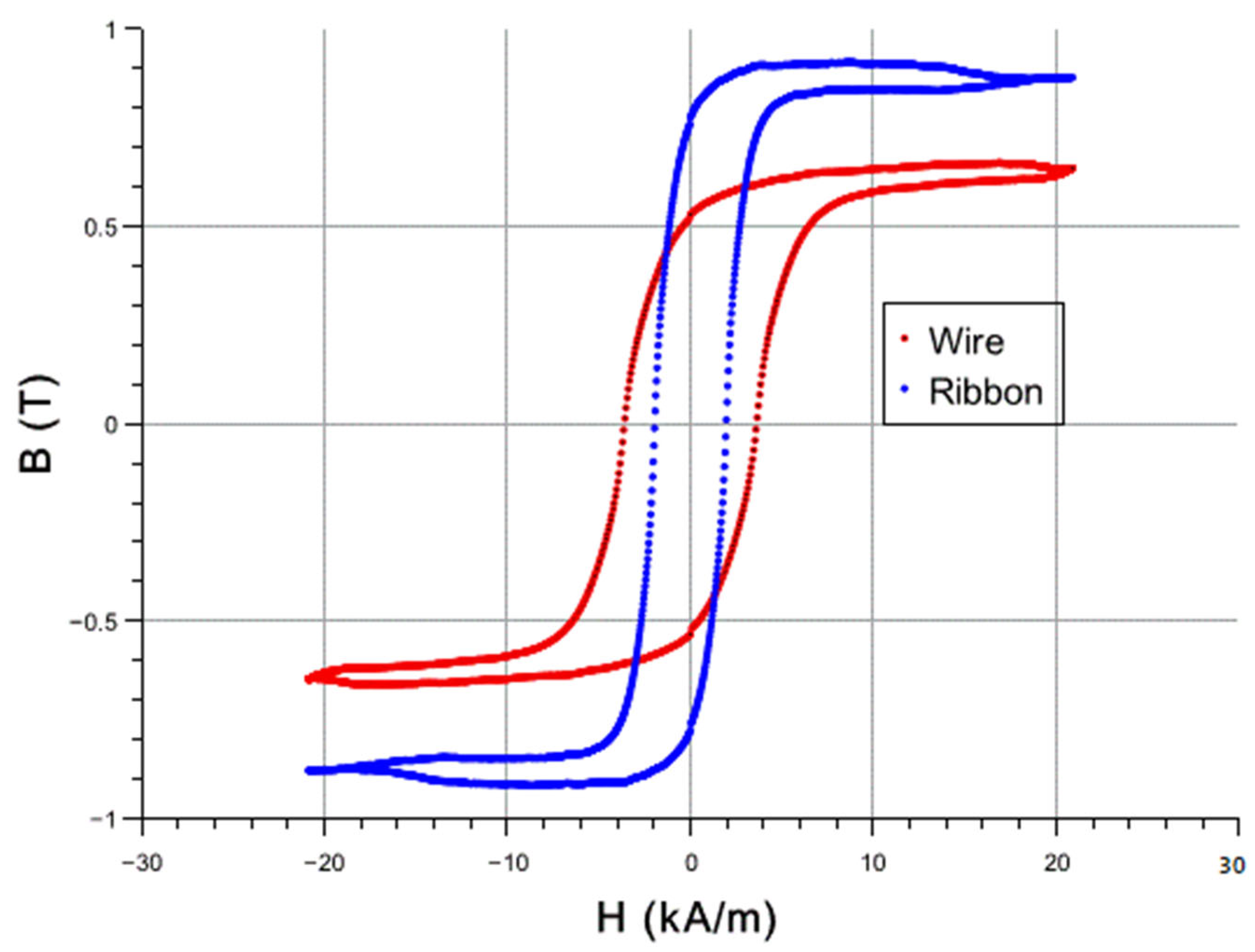

| Saturation Magnetization Ms (T) | Saturation Magnetization Ms Literature (T) | Mangetostriction λ (ppm) | Magnetic Susceptibility χ | |
|---|---|---|---|---|
| Ribbon sensor | 0.9 | 0.9 | 12 | 57 × 104 |
| Microwire sensor | 0.65 (at the maximum applied ) | 1.6 | 32 | 4.4 × 104 |
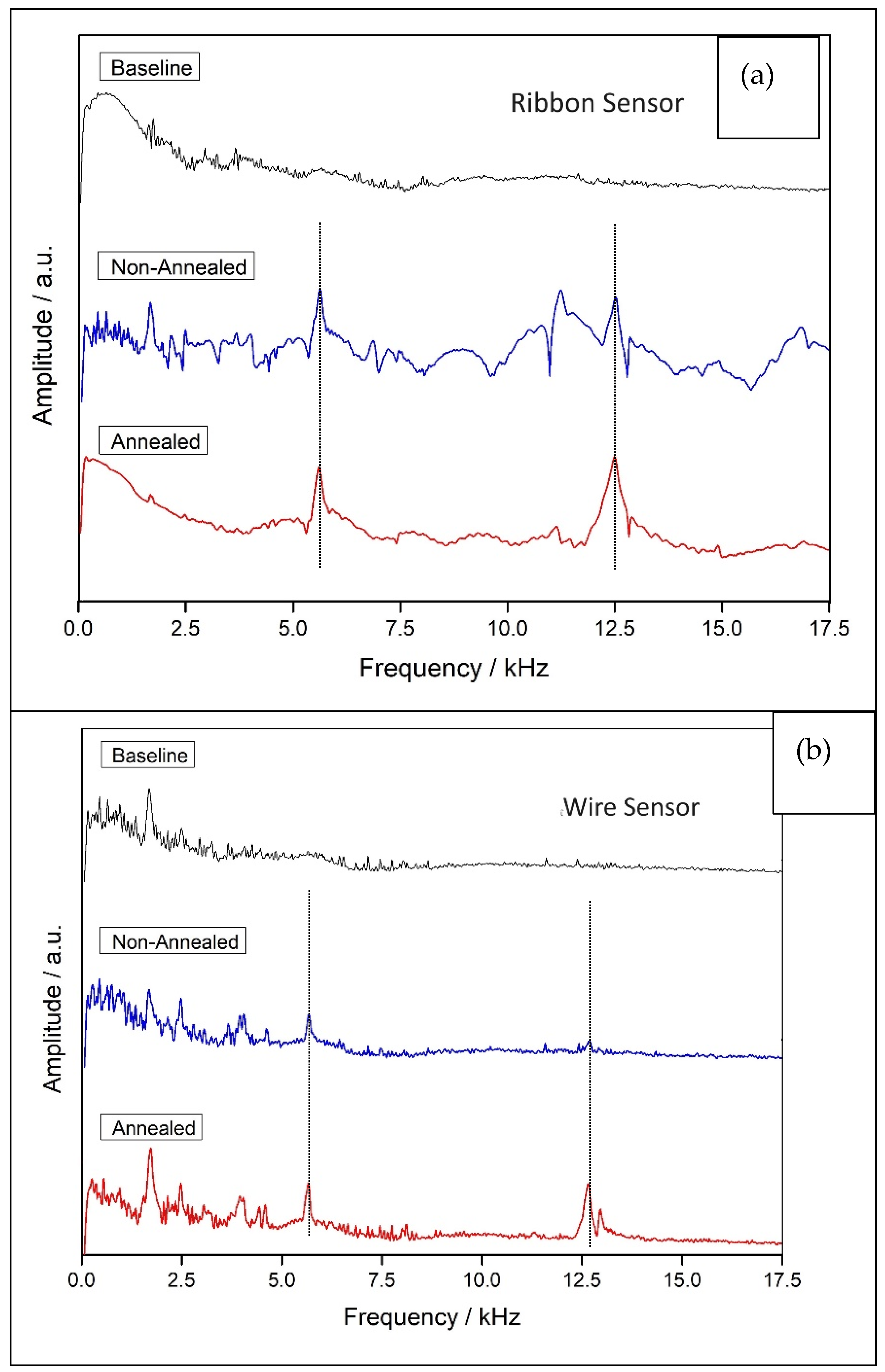
| Ribbon Sensor | Annealed Ribbon | Difference % | Wire Sensor | Annealed Wire | Difference % | |
|---|---|---|---|---|---|---|
| Peak 1 Amplitude (a.u.) | −5.73 × 104 | −4.97 × 104 | 15 | −7.86 × 104 | −7.17 × 104 | 9 |
| Peak 1 Frequency (kHz) | 5.59 | 5.59 | 0 | 5.67 | 5.65 | 0.3 |
| Peak 2 Amplitude (a.u.) | −6.08 × 104 | −4.59 × 104 | 32 | −8.92 × 104 | −7.18 × 104 | 24 |
| Peak 2 Frequency (kHz) | 12.5 | 12.5 | 0.25 | 12.7 | 12.6 | 0.14 |
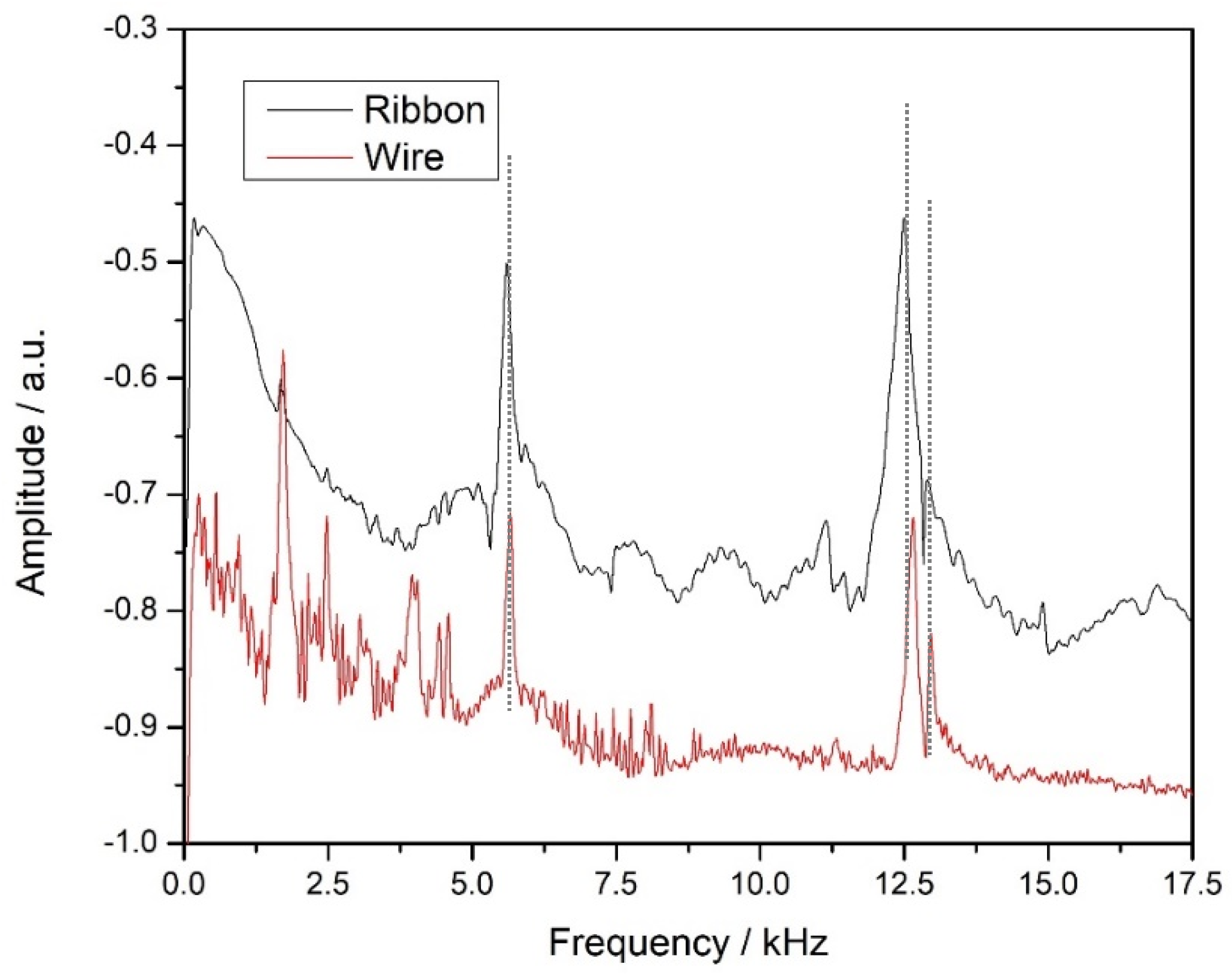
| Frequency (kHz) | Wire | Ribbon | Difference % |
|---|---|---|---|
| Peak 1 | 5.66 | 5.58 | 1.4 |
| Peak 2 | 12.67 | 12.63 | 0.3 |
| Peak 3 | 13.00 | 12.91 | 0.6 |
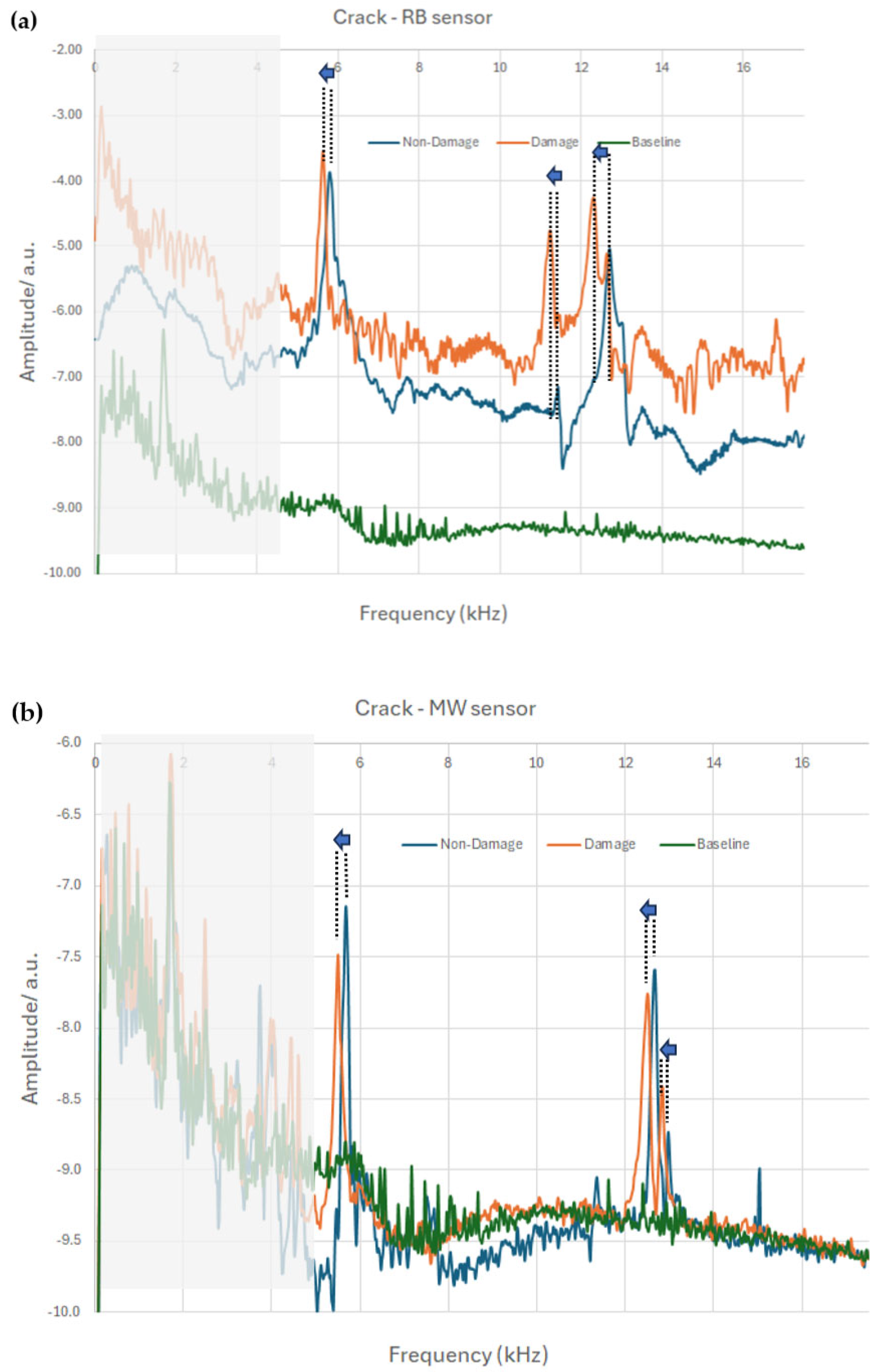
| Frequency (kHz) | Ribbon | Wire | |
|---|---|---|---|
| Peak 1 | no-crack | 5.79 | 5.64 |
| crack | 5.61 | 5.49 | |
| −0.18 | −0.15 | ||
| −0.03 | −0.03 | ||
| Peak 2 | no-crack | 11.44 | 12.66 |
| crack | 11.22 | 12.44 | |
| −0.22 | −0.22 | ||
| −0.02 | −0.02 | ||
| Peak 3 | no-crack | 12.69 | 12.96 |
| crack | 12.3 | 12.83 | |
| −0.39 | −0.13 | ||
| −0.03 | −0.01 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tapeinos, C.I.; Kouzoudis, D.; Varvatsoulis, K.; Vázquez, M.; Samourgkanidis, G. Microwire vs. Micro-Ribbon Magnetoelastic Sensors for Vibration-Based Structural Health Monitoring of Rectangular Concrete Beams. Sensors 2025, 25, 3590. https://doi.org/10.3390/s25123590
Tapeinos CI, Kouzoudis D, Varvatsoulis K, Vázquez M, Samourgkanidis G. Microwire vs. Micro-Ribbon Magnetoelastic Sensors for Vibration-Based Structural Health Monitoring of Rectangular Concrete Beams. Sensors. 2025; 25(12):3590. https://doi.org/10.3390/s25123590
Chicago/Turabian StyleTapeinos, Christos I., Dimitris Kouzoudis, Kostantis Varvatsoulis, Manuel Vázquez, and Georgios Samourgkanidis. 2025. "Microwire vs. Micro-Ribbon Magnetoelastic Sensors for Vibration-Based Structural Health Monitoring of Rectangular Concrete Beams" Sensors 25, no. 12: 3590. https://doi.org/10.3390/s25123590
APA StyleTapeinos, C. I., Kouzoudis, D., Varvatsoulis, K., Vázquez, M., & Samourgkanidis, G. (2025). Microwire vs. Micro-Ribbon Magnetoelastic Sensors for Vibration-Based Structural Health Monitoring of Rectangular Concrete Beams. Sensors, 25(12), 3590. https://doi.org/10.3390/s25123590








