A Robust Rotation-Equivariant Feature Extraction Framework for Ground Texture-Based Visual Localization
Abstract
1. Introduction
- Active localization (UWB, Radar, RFID, etc.): Employs nanosecond-level wireless pulses or radio frequency signals to achieve centimeter-level accuracy suitable for complex environments; however, these methods entail high hardware costs, elevated energy consumption, and susceptibility to multipath effects and obstacle interference [12,13,14,15].
- Inertial/Visual/LiDAR-based localization: Utilizes inertial measurement units (IMUs), visual sensors, or LiDAR for environment perception without pre-installed infrastructure; nevertheless, these methods face challenges such as sensitivity to lighting conditions, sparse textures, cumulative drift errors, and issues in map storage and cross-environment adaptation [22,23,24,25,26].
- Rotation-equivariant convolutional backbone: GT-REKD embeds cyclic-group convolutions into the feature extractor, yielding intrinsic invariance to arbitrary in-plane rotations across multiple spatial scales while preserving computational efficiency.
- End-to-end learnable orientation head: GT-REKD decouples orientation encoding from descriptor learning, ensuring consistent keypoint direction labels and robust matching.
- Extensive multi-scenario evaluation with leading performance: Extensive multi-scenario evaluation, including pure rotation matching, incremental localization, and absolute relocalization across diverse ground materials (brick, asphalt, concrete, and gravel), demonstrates GT-REKD’s leading performance, achieving 96.14% matching accuracy in pure rotation, 94.08% in incremental localization, and average relocalization errors of 5.55°/4.41 px, consistently outperforming baseline methods, such as ORB, SIFT, SuperPoint, etc.
2. Preliminaries
2.1. Pose Estimation on Ground Texture
2.2. Group-Equivariant Convolutions
3. Methodology
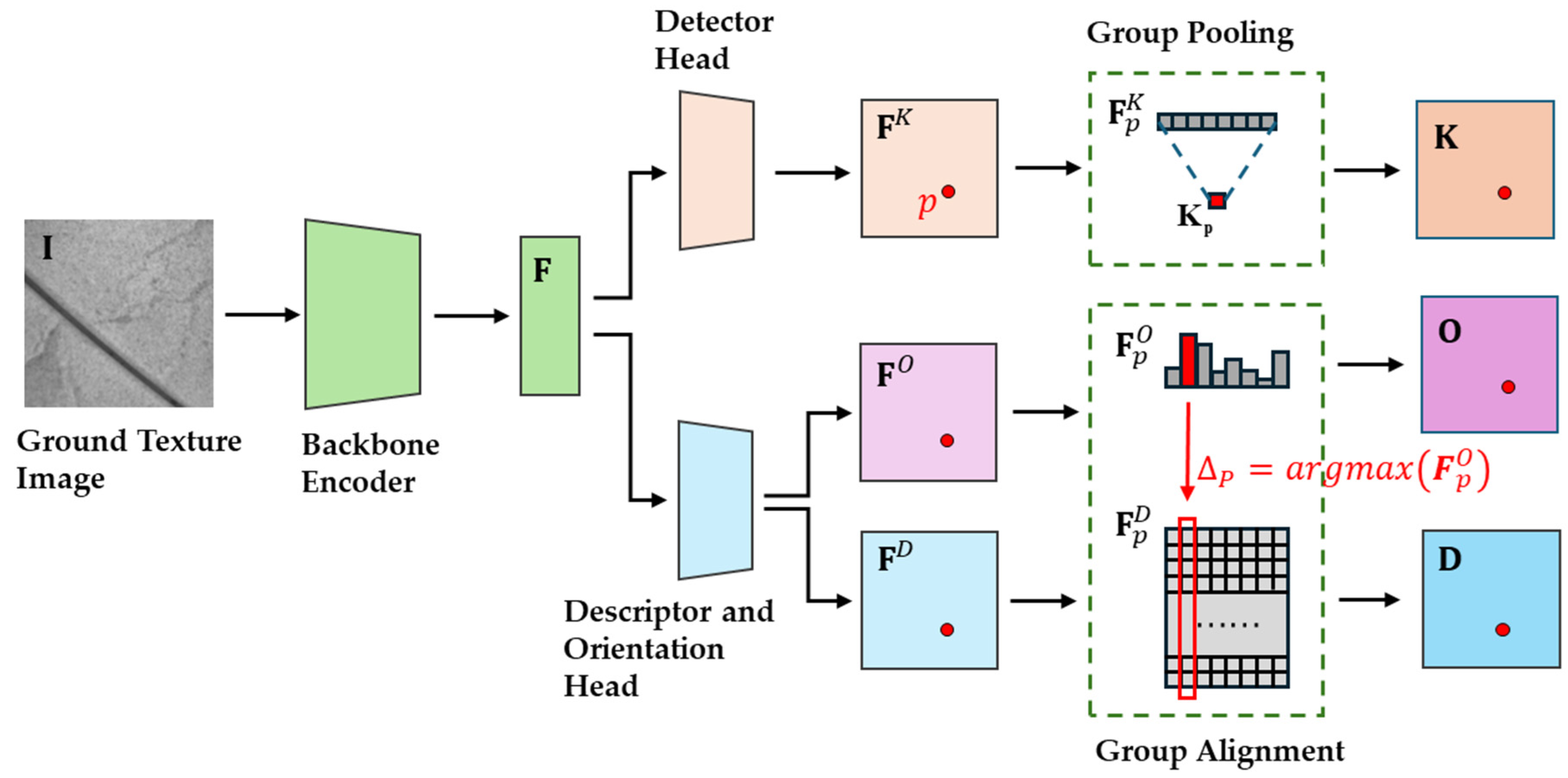
3.1. Network Architecture
- (a)
- Group-equivariant encoder backbone
- (b)
- Detector head—()
- (c)
- Orientation head—()
- (d)
- Descriptor head—()
3.2. Feature Extraction Based on Rotational Equivariance
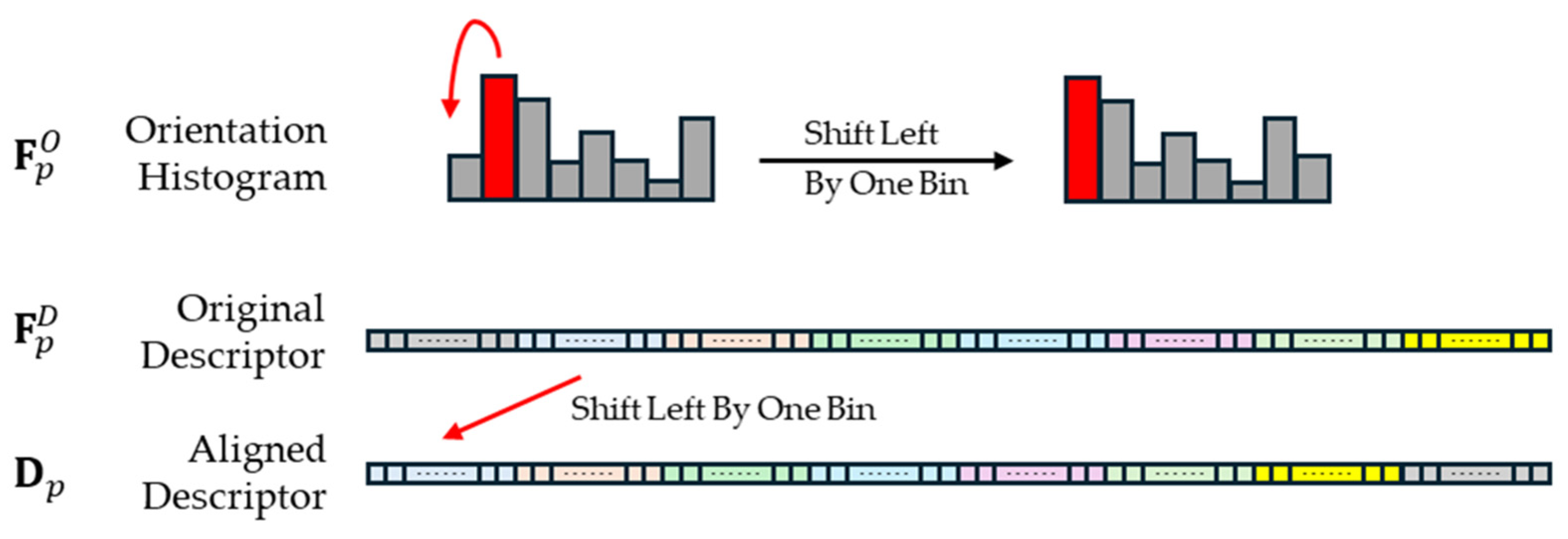
3.3. Descriptor and Keypoint Extraction Based on Rotational Equivariance
3.4. Loss Function
4. Experiment
4.1. Implementation Details
4.2. Datasets
- (a)
- Micro-GPS Dataset:
- (b)
- HD Ground Dataset:
- (c)
- GeoTracking Dataset:
4.3. Hyperparameter Settings
4.4. Evaluation Protocol
5. Results
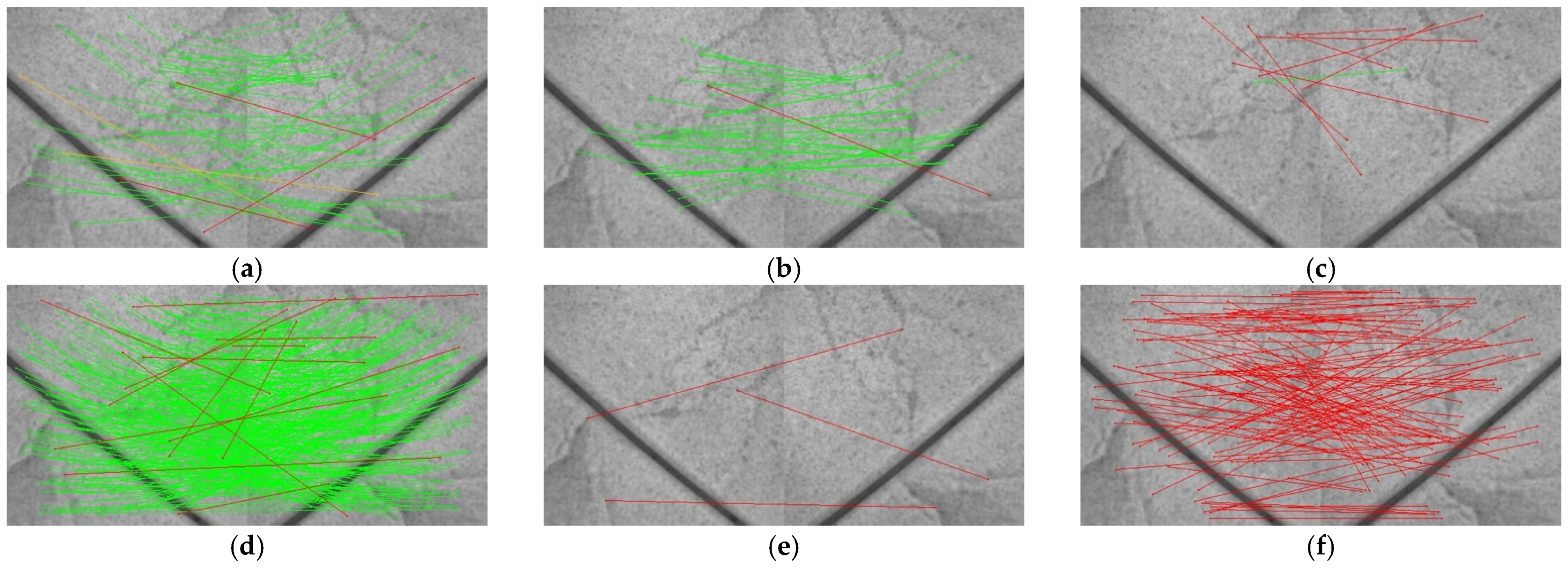
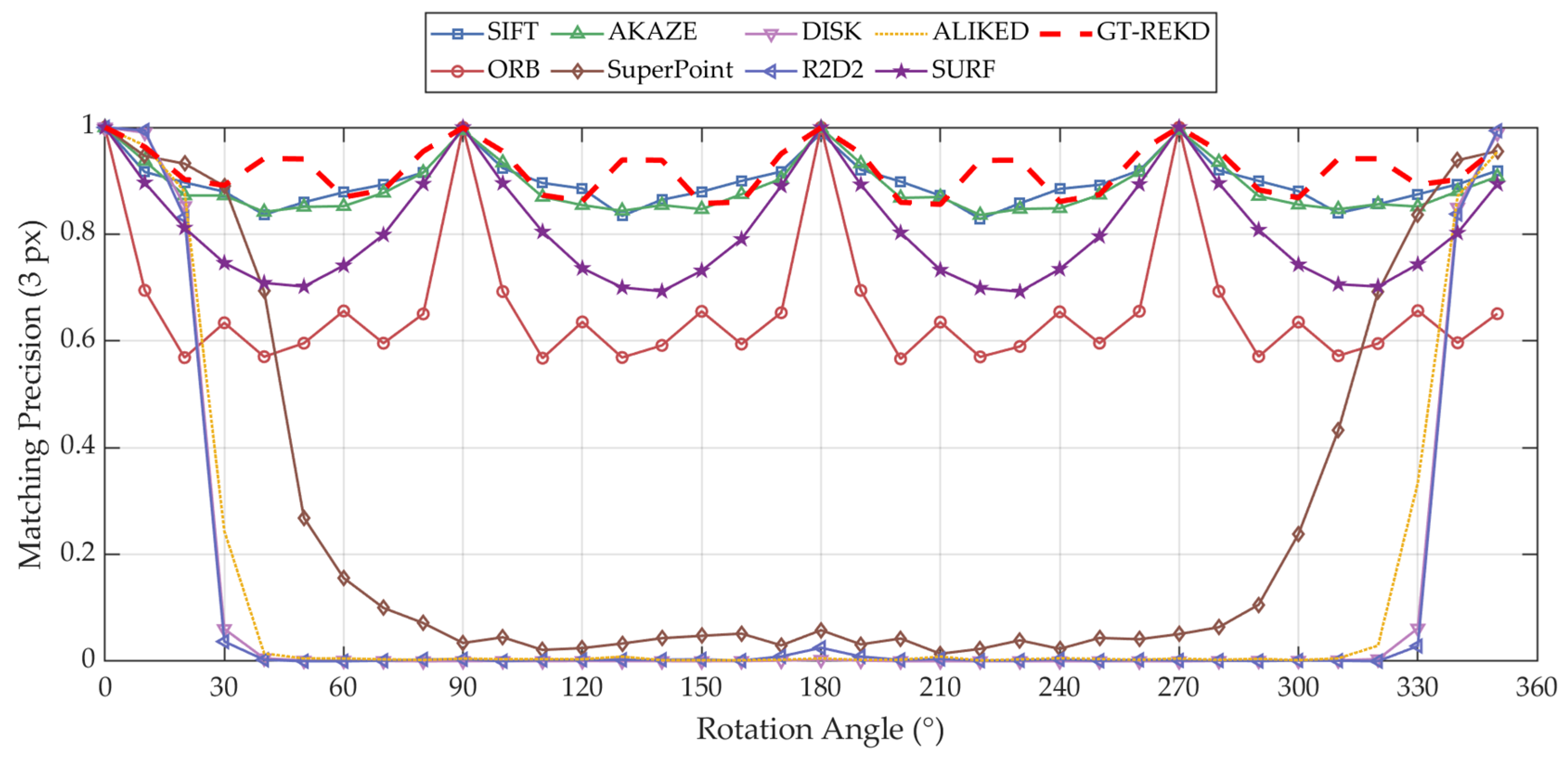
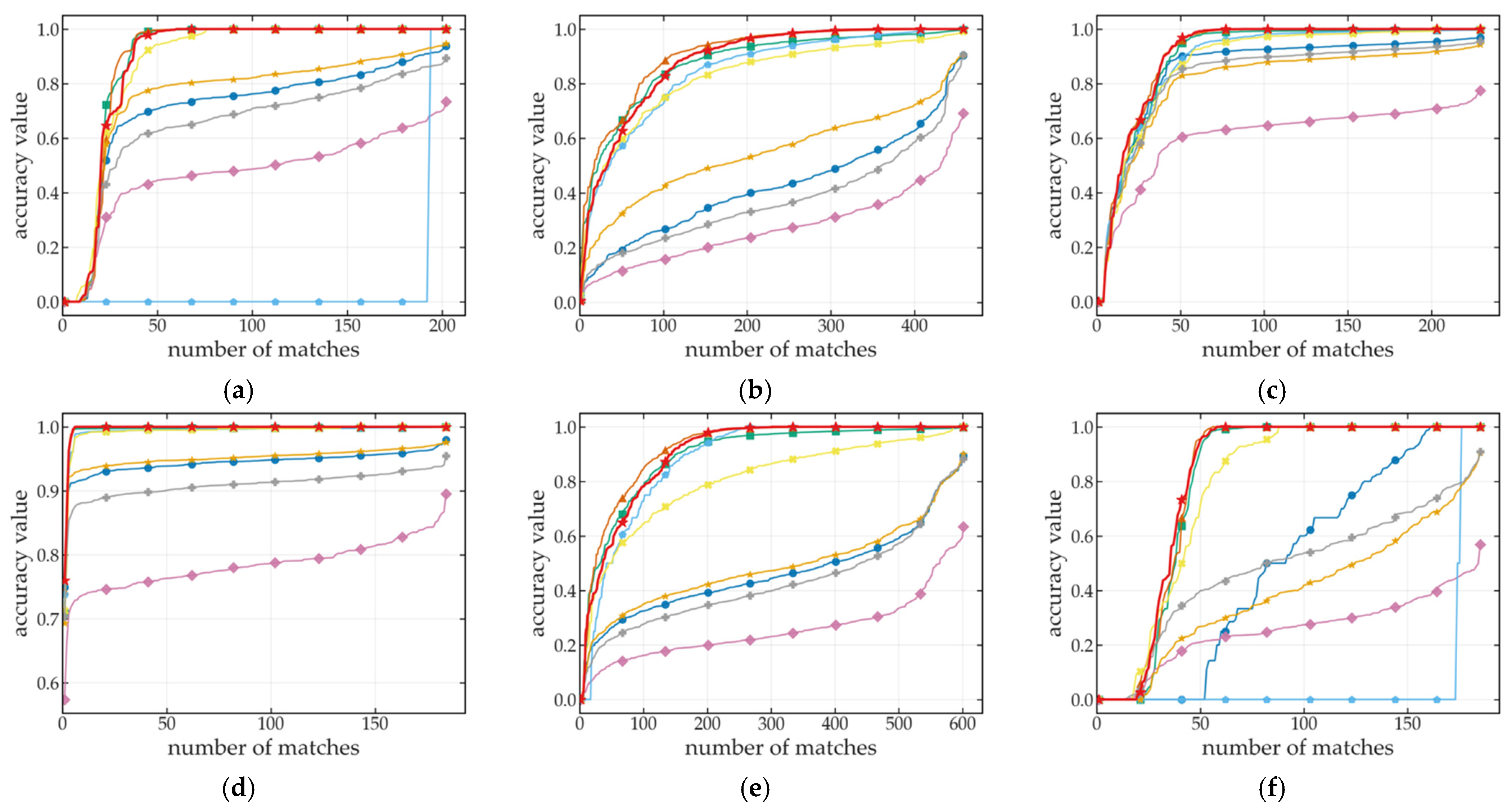
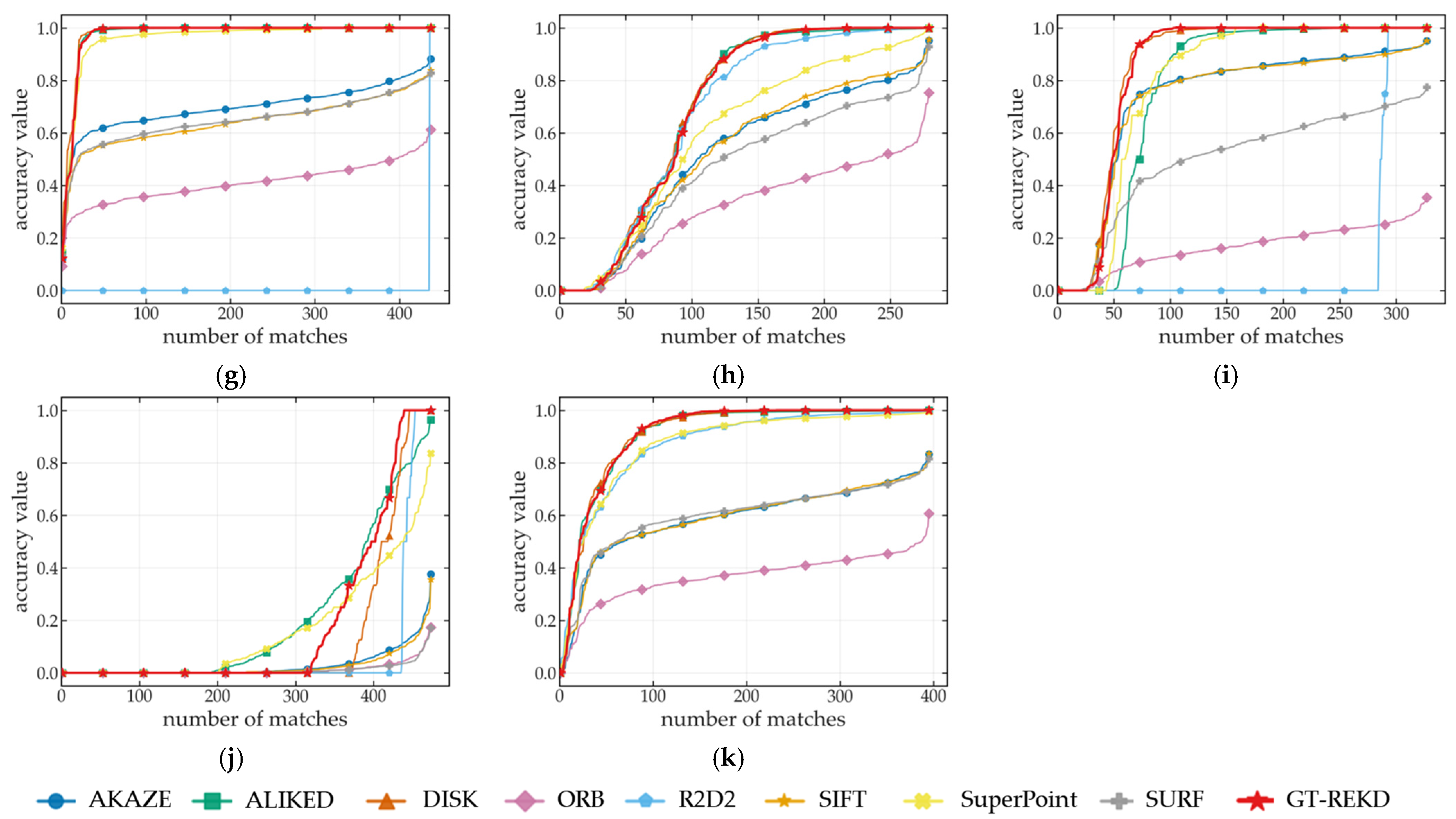
5.1. Rotation Localization Accuracy Analysis
5.2. Accuracy of Incremental Localization
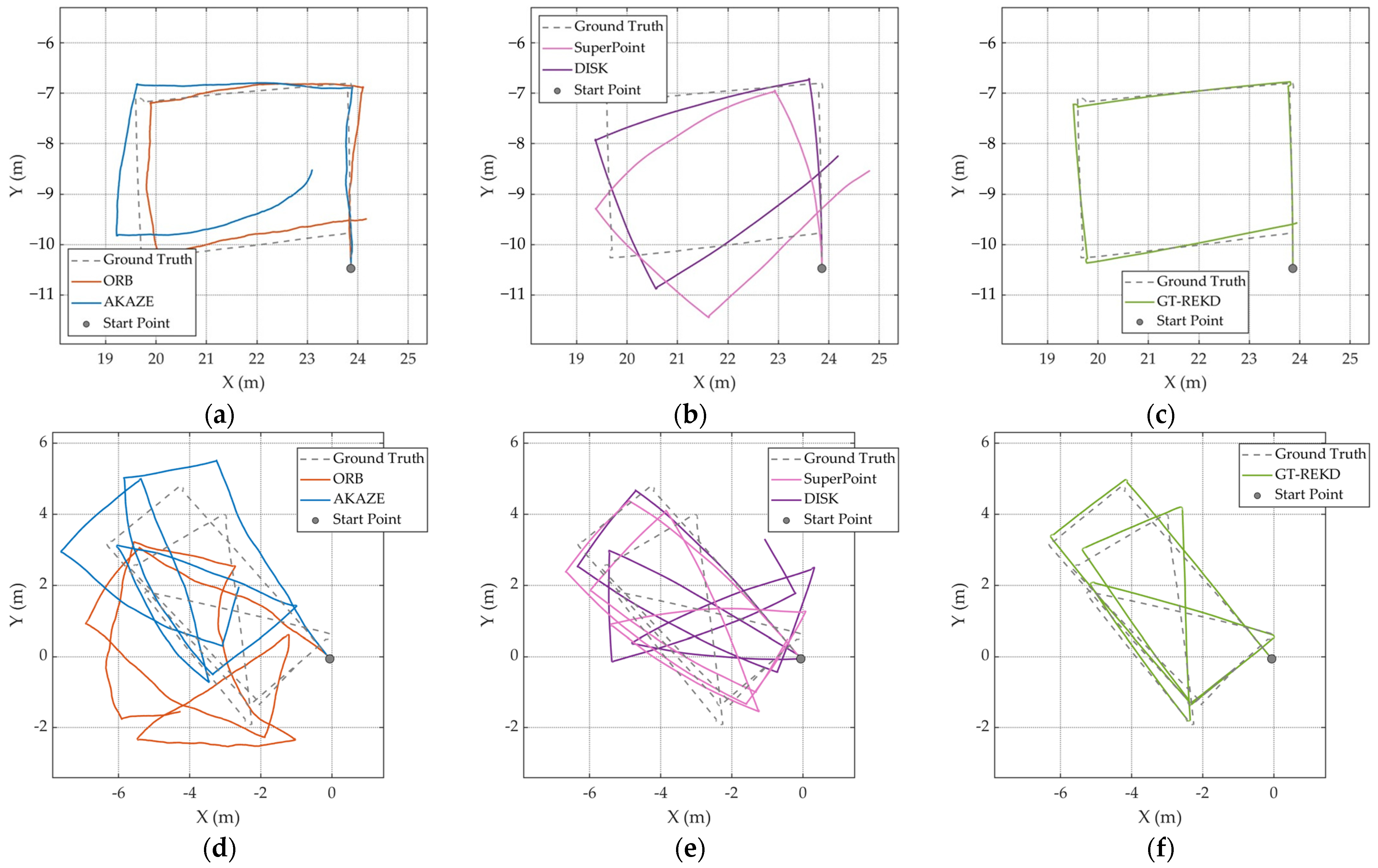
5.3. Absolute Localization Accuracy Analysis
6. Discussion
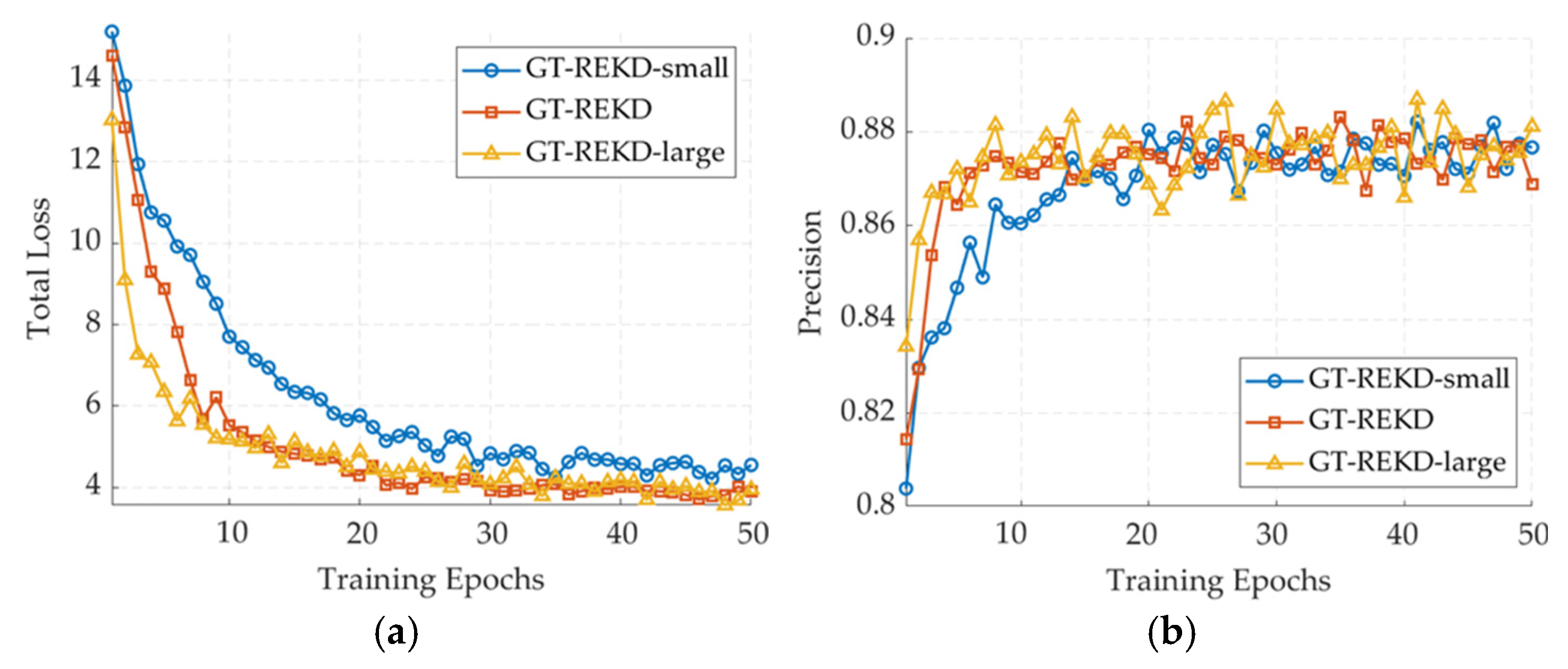
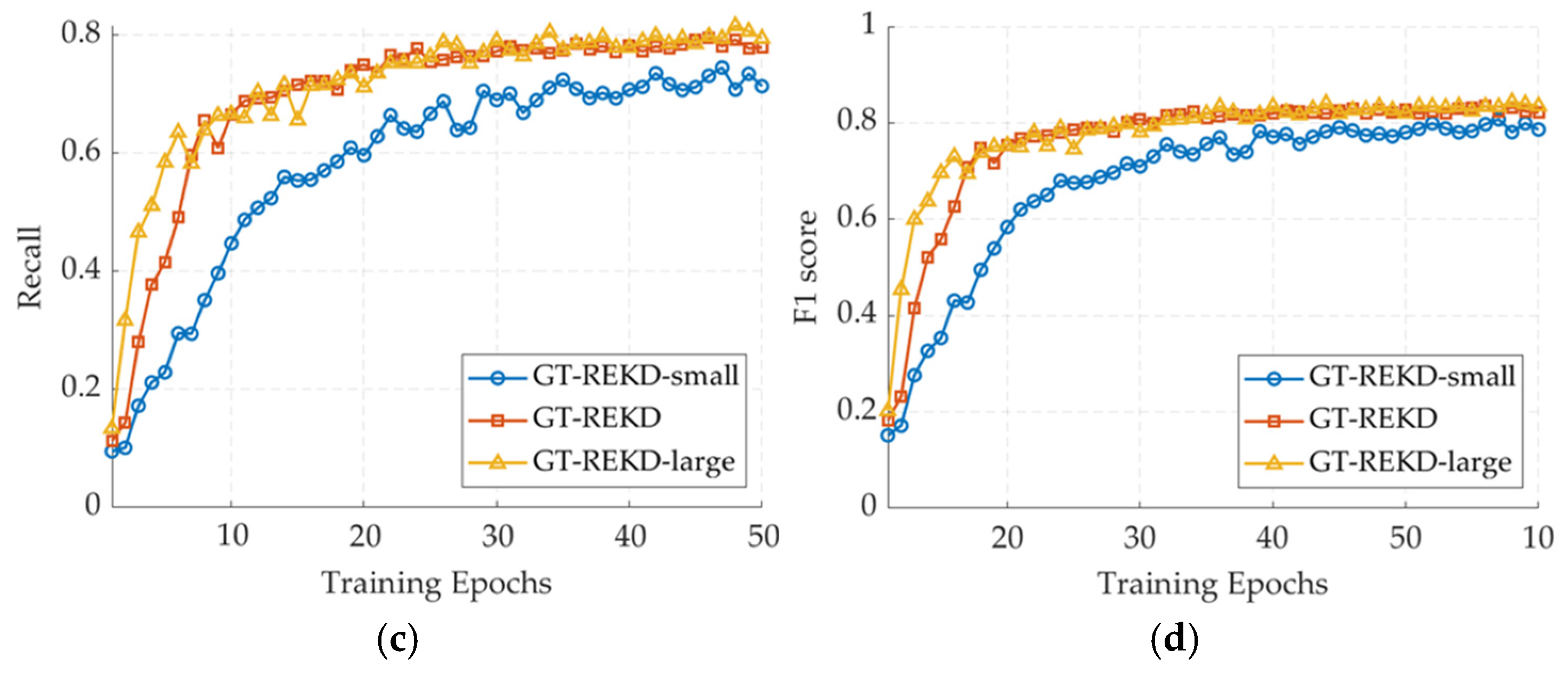
6.1. Ablation Study on Feature Dimensionality and Group Number
6.2. Cumulative Drift on Incremental Localization
6.3. Inference Performance and Real-Time Feasibility
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Jiang, W.; Cao, Z.; Cai, B.; Li, B.; Wang, J. Indoor and Outdoor Seamless Positioning Method Using UWB Enhanced Multi-Sensor Tightly-Coupled Integration. IEEE Trans. Veh. Technol. 2021, 70, 10633–10645. [Google Scholar] [CrossRef]
- El-Sheimy, N.; Li, Y. Indoor Navigation: State of the Art and Future Trends. Satell. Navig. 2021, 2, 7. [Google Scholar] [CrossRef]
- Mallik, M.; Panja, A.K.; Chowdhury, C. Paving the Way with Machine Learning for Seamless Indoor–Outdoor Positioning: A Survey. Inf. Fusion 2023, 94, 126–151. [Google Scholar] [CrossRef]
- Pettorru, G.; Pilloni, V.; Martalò, M. Trustworthy Localization in IoT Networks: A Survey of Localization Techniques, Threats, and Mitigation. Sensors 2024, 24, 2214. [Google Scholar] [CrossRef] [PubMed]
- Li, P.; Wu, W.; Zhao, Z.; Huang, G.Q. Indoor Positioning Systems in Industry 4.0 Applications: Current Status, Opportunities, and Future Trends. Digit. Eng. 2024, 3, 100020. [Google Scholar] [CrossRef]
- Huang, J.; Junginger, S.; Liu, H.; Thurow, K. Indoor Positioning Systems of Mobile Robots: A Review. Robotics 2023, 12, 47. [Google Scholar] [CrossRef]
- Zhao, C.; Song, A.; Zhu, Y.; Jiang, S.; Liao, F.; Du, Y. Data-Driven Indoor Positioning Correction for Infrastructure-Enabled Autonomous Driving Systems: A Lifelong Framework. IEEE Trans. Intell. Transp. Syst. 2023, 24, 3908–3921. [Google Scholar] [CrossRef]
- Lu, Y.; Ma, H.; Smart, E.; Yu, H. Real-Time Performance-Focused Localization Techniques for Autonomous Vehicle: A Review. IEEE Trans. Intell. Transp. Syst. 2021, 23, 6082–6100. [Google Scholar] [CrossRef]
- Adin, I.; Mendizabal, J.; de Miguel, G.; Goya, J.; Zamora, L.; Arrizabalaga, S. Complementary Positioning System in GNSS-Denied Areas. Transp. Res. Procedia 2016, 14, 4562–4571. [Google Scholar] [CrossRef]
- Iyer, K.; Dey, A.; Xu, B.; Sharma, N.; Hsu, L.-T. Enhancing Positioning in GNSS-Denied Environments Based on an Extended Kalman Filter Using Past GNSS Measurements and IMU. IEEE Trans. Veh. Technol. 2024, 73, 7908–7924. [Google Scholar] [CrossRef]
- Jarraya, I.; Al-Batati, A.; Kadri, M.B.; Abdelkader, M.; Ammar, A.; Boulila, W.; Koubaa, A. GNSS-Denied Unmanned Aerial Vehicle Navigation: Analyzing Computational Complexity, Sensor Fusion, and Localization Methodologies. Satell. Navig. 2025, 6, 9. [Google Scholar] [CrossRef]
- Barbieri, L.; Brambilla, M.; Trabattoni, A.; Boulila, W.; Koubaa, A. UWB Localization in a Smart Factory: Augmentation Methods and Experimental Assessment. IEEE Trans. Instrum. Meas. 2021, 70, 2508218. [Google Scholar] [CrossRef]
- Jang, B.-J. Principles and Trends of UWB Positioning Technology. J. Korean Inst. Electromagn. Eng. Sci. 2022, 33, 1–11. [Google Scholar] [CrossRef]
- Li, W.; Chen, R.; Wu, Y.; Zhou, H. Indoor Positioning System Using a Single-Chip Millimeter Wave Radar. IEEE Sens. J. 2023, 23, 5232–5242. [Google Scholar] [CrossRef]
- Xu, J.; Li, Z.; Zhang, K.; Yang, J.; Gao, N.; Zhang, Z.; Meng, Z. The Principle, Methods and Recent Progress in RFID Positioning Techniques: A Review. IEEE J. Radio Freq. Identif. 2023, 7, 50–63. [Google Scholar] [CrossRef]
- Wang, K.; Liu, Y.; Hong, Z. RSS-Based Visible Light Positioning Based on Channel State Information. Opt. Express 2022, 30, 5683–5699. [Google Scholar] [CrossRef]
- Shang, S.; Wang, L. Overview of WiFi Fingerprinting-Based Indoor Positioning. IET Commun. 2022, 16, 725–733. [Google Scholar] [CrossRef]
- Feng, X.; Nguyen, K.A.; Luo, Z. A Review of Open Access WiFi Fingerprinting Datasets for Indoor Positioning. IEEE Access 2024, 12, 3496561. [Google Scholar] [CrossRef]
- Ouyang, G.; Abed-Meraim, K. A Survey of Magnetic-Field-Based Indoor Localization. Electronics 2022, 11, 864. [Google Scholar] [CrossRef]
- Morselli, F.; Razavi, S.M.; Win, M.Z.; Conti, A. Soft Information-Based Localization for 5G Networks and Beyond. IEEE Trans. Wirel. Commun. 2023, 22, 9923–9938. [Google Scholar] [CrossRef]
- Szyc, K.; Nikodem, M.; Zdunek, M. Bluetooth Low Energy Indoor Localization for Large Industrial Areas and Limited Infrastructure. Ad Hoc Netw. 2023, 139, 103024. [Google Scholar] [CrossRef]
- Mumuni, F.; Mumuni, A. Adaptive Kalman Filter for MEMS IMU Data Fusion Using Enhanced Covariance Scaling. Control Theory Technol. 2021, 19, 365–374. [Google Scholar] [CrossRef]
- Abaspur Kazerouni, I.; Fitzgerald, L.; Dooly, G.; Toal, D. A Survey of State-of-the-Art on Visual SLAM. Expert Syst. Appl. 2022, 205, 117734. [Google Scholar] [CrossRef]
- Pan, C.; Li, Z.; Zhang, Q.; Soja, B.; Gao, J. Smartphone-Based Vision/MEMS-IMU/GNSS Tightly Coupled Seamless Positioning Using Factor Graph Optimization. Measurement 2024, 229, 114420. [Google Scholar] [CrossRef]
- Matsuki, H.; Murai, R.; Kelly, P.H.; Davison, A.J. Gaussian Splatting SLAM. In Proceedings of the 2024 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Seattle, WA, USA, 20–25 June 2024; pp. 18039–18048. [Google Scholar]
- Chou, C.-C.; Chou, C.-F. Efficient and Accurate Tightly-Coupled Visual-Lidar SLAM. IEEE Trans. Intell. Transp. Syst. 2021, 23, 14509–14523. [Google Scholar] [CrossRef]
- Schmid, J.F.; Simon, S.F.; Mester, R. Features for Ground Texture Based Localization—A Survey. arXiv 2020, arXiv:2002.11948. [Google Scholar]
- Kozak, K.; Alban, M. Ranger: A Ground-Facing Camera-Based Localization System for Ground Vehicles. In Proceedings of the 2016 IEEE/ION Position, Location and Navigation Symposium (PLANS), Savannah, GA, USA, 11–14 April 2016; pp. 170–178. [Google Scholar]
- Chen, X.; Vempati, A.S.; Beardsley, P. StreetMap—Mapping and Localization on Ground Planes Using a Downward-Facing Camera. In Proceedings of the 2018 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Madrid, Spain, 1–5 October 2018; pp. 1672–1679. [Google Scholar]
- Zhang, L.; Finkelstein, A.; Rusinkiewicz, S. High-Precision Localization Using Ground Texture. In Proceedings of the 2019 IEEE International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2019; pp. 6381–6387. [Google Scholar]
- Wilhelm, A.; Napp, N. Lightweight Ground Texture Localization. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–18 May 2024; pp. 10223–10229. [Google Scholar]
- Wang, Q.; Pan, Z.; Hou, J.; Yu, L. High-Precision Offline Mapping and Localization System Based on Ground Texture with Binary Descriptors. Expert Syst. Appl. 2024, 240, 122650. [Google Scholar] [CrossRef]
- Sheng, C.; Pan, Z.; Ye, C.; Yu, L. Camera Pose Estimation and Relocalization Algorithm Based on Ground Texture. IEEE Trans. Instrum. Meas. 2024, 73, 1–11. [Google Scholar] [CrossRef]
- Hart, K.M.; Englot, B.; O’Shea, R.P.; Kelly, J.D.; Martinez, D. Monocular Simultaneous Localization and Mapping Using Ground Textures. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 2032–2038. [Google Scholar]
- Xu, K.; Yang, Z.; Xie, L.; Wang, C. GroundSLAM: A Robust Visual SLAM System for Warehouse Robots Using Ground Textures. arXiv 2025, arXiv:1710.05502v4. [Google Scholar]
- Schmid, J.F.; Simon, S.F.; Mester, R. Ground Texture Based Localization: Do We Need to Detect Keypoints? In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 25–29 October 2020; pp. 4575–4580. [Google Scholar]
- Weiler, M.; Cesa, G. General E(2)-Equivariant Steerable CNNs. arXiv 2019, arXiv:1911.08251. [Google Scholar]
- Revaud, J.; Weinzaepfel, P.; de Souza, C.R.; Pion, N.; Csurka, G.; Cabon, Y.; Humenberger, M. R2D2: Reliable and Repeatable Detector and Descriptor. In Proceedings of the 33rd Conference on Neural Information Processing Systems (NeurIPS 2019), Vancouver, BC, Canada, 8–14 December 2019; pp. 12414–12424. [Google Scholar]
- Dusmanu, M.; Rocco, I.; Pajdla, T.; Pollefeys, M.; Sivic, J.; Torii, A.; Sattler, T. D2-Net: A Trainable CNN for Joint Description and Detection of Local Features. In Proceedings of the 2019 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Long Beach, CA, USA, 15–20 June 2019; pp. 8092–8101. [Google Scholar]
- DeTone, D.; Malisiewicz, T.; Rabinovich, A. SuperPoint: Self-Supervised Interest Point Detection and Description. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), Salt Lake City, UT, USA, 18–22 June 2018; pp. 224–236. [Google Scholar]
- Gleize, P.; Wang, W.; Feiszli, M. SiLK: Simple Learned Keypoints. In Proceedings of the 2023 IEEE/CVF International Conference on Computer Vision (ICCV), Paris, France, 2–6 October 2023; pp. 22442–22451. [Google Scholar]
- Lee, J.; Kim, B.; Kim, S.; Cho, M. Learning Rotation-Equivariant Features for Visual Correspondence. In Proceedings of the 2023 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Vancouver, BC, Canada, 19–24 June 2023; pp. 21887–21897. [Google Scholar]
- Karaoglu, M.A.; Markova, V.; Navab, N.; Busam, B.; Ladikos, A. RIDE: Self-Supervised Learning of Rotation-Equivariant Keypoint Detection and Invariant Description for Endoscopy. In Proceedings of the 2024 IEEE International Conference on Robotics and Automation (ICRA), Yokohama, Japan, 13–17 May 2024; pp. 10764–10771. [Google Scholar]
- Simonyan, K.; Zisserman, A. Very Deep Convolutional Networks for Large-Scale Image Recognition. arXiv 2014, arXiv:1409.1556. [Google Scholar]
- Han, J.; Ding, J.; Xue, N.; Xia, G.-S. ReDet: A Rotation-Equivariant Detector for Aerial Object Detection. In Proceedings of the 2021 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), Nashville, TN, USA, 20–25 June 2021; pp. 2786–2795. [Google Scholar]
- Schmid, J.F.; Simon, S.F.; Radhakrishnan, R.; Frintrop, S.; Mester, R. HD Ground—A Database for Ground Texture Based Localization. In Proceedings of the 2022 IEEE International Conference on Robotics and Automation (ICRA), Philadelphia, PA, USA, 23–27 May 2022; pp. 7628–7634. [Google Scholar]
- Hu, W.; Tong, M. TRR360D: A Dataset for 360 Degree Rotated Rectangular Box Table Detection. arXiv 2023, arXiv:2303.01894. [Google Scholar]





| Micro-GPS | HD Ground | GeoTracking | |
|---|---|---|---|
| Image resolution | 1288 × 964 px/1280 × 720 px | 1600 × 1200 px | 640 × 480 px |
| Pixel size (mm/px) | 0.16/0.21 | 0.10 | 0.12 |
| Camera height (mm) | 260 | 234 | 99.8 |
| Number of texture types | 4 outdoor/3 indoor | 5 outdoor/6 indoor | 6 outdoor/4 indoor |
| Number of frames | 26,012 | 128,605 | 125,422 |
| Feature Extraction Method | 3 px | 5 px | 10 px |
|---|---|---|---|
| SIFT | 95.33% | 95.38% | 95.41% |
| SURF | 91.23% | 91.26% | 91.27% |
| ORB | 66.29% | 66.48% | 66.53% |
| AKAZE | 94.92% | 95.06% | 95.18% |
| SuperPoint | 27.82% | 29.11% | 29.77% |
| DISK | 13.68% | 14.44% | 15.35% |
| R2D2 | 13.37% | 13.50% | 13.88% |
| ALIKED | 15.00% | 15.31% | 15.91% |
| GT-REKD | 96.14% | 96.15% | 96.16% |
| Methods | Number of Detected Keypoints | Number of Matched Keypoints | Keypoint Redundancy Rate (%) | Matching Accuracy @ 3 px (%) | Matching Accuracy @ 5 px (%) | Matching Accuracy @ 10 px (%) |
|---|---|---|---|---|---|---|
| SIFT | 925.14 | 448.83 | 54.40% | 58.54% | 63.03% | 64.95% |
| SURF | 989.80 | 464.06 | 58.34% | 53.51% | 57.63% | 59.31% |
| ORB | 500.00 | 216.99 | 29.89% | 35.47% | 38.29% | 29.40% |
| AKAZE | 758.59 | 409.09 | 61.06% | 58.56% | 62.99% | 64.96% |
| SuperPoint | 348.08 | 137.07 | 53.32% | 77.52% | 86.88% | 91.91% |
| DISK | 7192.20 | 1887.16 | 70.02% | 81.82% | 89.02% | 92.34% |
| R2D2 | 9981.35 | 201.78 | 81.13% | 49.63% | 56.03% | 58.48% |
| ALIKED | 4895.40 | 2067.06 | 73.35% | 80.96% | 88.96% | 93.57% |
| GT-REKD | 10,000.98 | 1025.07 | 69.92% | 81.81% | 89.65% | 94.08% |
| Trajectory | Length (m) | RMSE (m) | |||||
|---|---|---|---|---|---|---|---|
| ORB | AKAZE | SuperPoint | DISK | GT-REKD | |||
| Indoor | Carpet1_seq2 | 38.37 | 4.966 | 3.267 | 3.441 | 2.617 | 2.220 |
| Carpet2_seq1 | 41.47 | 6.224 | 2.843 | 1.929 | 1.222 | 1.168 | |
| Carpet3_seq1 | 16.64 | 5.304 | 2.280 | 0.751 | 0.633 | 0.378 | |
| Carpet3_seq3 | 45.04 | 6.581 | 5.321 | 7.704 | 6.212 | 1.563 | |
| Granite_tiles_seq1 | 27.16 | 5.020 | 2.996 | 2.942 | 0.862 | 0.937 | |
| Granite_tiles_seq2 | 40.66 | 7.559 | 4.998 | 2.126 | 1.448 | 1.473 | |
| Outdoor | Brick_seq1 | 14.06 | 5.036 | 1.707 | 0.728 | 0.330 | 0.204 |
| Coarse_asphalt_seq1 | 15.55 | 0.471 | 0.382 | 1.649 | 0.797 | 0.357 | |
| Concrete_seq2 | 23.53 | - | 2.471 | 1.133 | 0.990 | 0.536 | |
| Fine_asphalt_seq1 | 22.18 | 1.451 | 0.724 | 0.438 | 0.361 | 0.287 | |
| Gravel_road1_seq1 | 17.52 | 1.838 | 1.113 | 0.665 | 0.357 | 0.137 | |
| Gravel_road2_seq1 | 46.11 | 1.591 | 1.020 | 1.017 | 0.730 | 0.408 | |
| Methods | Relocalization Success Rate (%) | Rotation Error (°) | Translation Error (px) | ||
|---|---|---|---|---|---|
| Mean | Standard Deviation | Mean | Standard Deviation | ||
| SIFT | 93.45% | 7.82 | 2.60 | 7.78 | 2.82 |
| SURF | 92.36% | 7.07 | 2.63 | 7.51 | 3.24 |
| ORB | 88.18% | 6.52 | 2.61 | 5.11 | 4.18 |
| AKAZE | 86.09% | 7.38 | 2.46 | 6.88 | 2.89 |
| SuperPoint | 22.09% | 9.32 | 3.18 | 11.59 | 3.35 |
| DISK | 15.91% | 9.12 | 2.71 | 11.60 | 4.02 |
| R2D2 | 5.45% | 6.94 | 1.99 | 5.68 | 2.44 |
| ALIKED | 22.18% | 9.78 | 2.27 | 11.84 | 2.15 |
| GT-REKD | 57.09% | 5.55 | 2.53 | 4.42 | 2.41 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cai, Y.; Xia, L.; Chan, T.O.; Li, J.; Li, Q. A Robust Rotation-Equivariant Feature Extraction Framework for Ground Texture-Based Visual Localization. Sensors 2025, 25, 3585. https://doi.org/10.3390/s25123585
Cai Y, Xia L, Chan TO, Li J, Li Q. A Robust Rotation-Equivariant Feature Extraction Framework for Ground Texture-Based Visual Localization. Sensors. 2025; 25(12):3585. https://doi.org/10.3390/s25123585
Chicago/Turabian StyleCai, Yuezhen, Linyuan Xia, Ting On Chan, Junxia Li, and Qianxia Li. 2025. "A Robust Rotation-Equivariant Feature Extraction Framework for Ground Texture-Based Visual Localization" Sensors 25, no. 12: 3585. https://doi.org/10.3390/s25123585
APA StyleCai, Y., Xia, L., Chan, T. O., Li, J., & Li, Q. (2025). A Robust Rotation-Equivariant Feature Extraction Framework for Ground Texture-Based Visual Localization. Sensors, 25(12), 3585. https://doi.org/10.3390/s25123585








