Design and Validation of a New Tilting Rotor VTOL Drone: Structural Optimization, Flight Dynamics, and PID Control
Abstract
1. Introduction
- Firstly, to meet the requirements of the flight characteristics of a tilt-rotor vertical take-off and landing UAV, a tilt-rotor aircraft with a quad-rotor fuselage layout is introduced and dynamically modeled, and, based on the conclusions of the dynamic modeling, the structure of the experimental aircraft without a skin is reasonably designed.
- In addition, to meet the landing characteristics and lightweight requirements of vertical take-off and landing UAV, the mechanical characteristics of the fuselage and landing gear are analyzed, and it is proposed to optimize the landing gear structure by adopting the unified objective method and to optimize the main motor seat and the wing ribs of the UAV by using the topology optimization module in workbench.
- The vibration characteristics of the test aircraft body are analyzed, and a harmonic response analysis method is proposed to be introduced, which, compared with the traditional vibration analysis method, can directly verify and derive the frequency that will produce danger in the actual system, and thus determine the dangerous excitation frequency point for the final tilt-rotor vertical take-off and landing UAV flight.
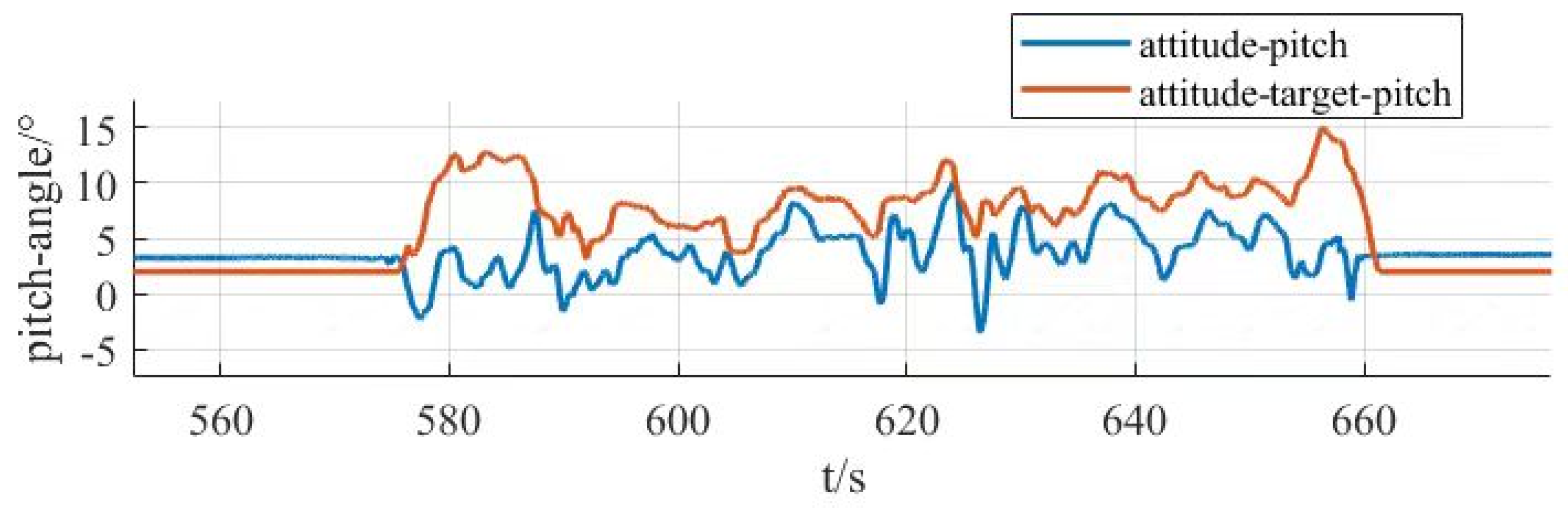
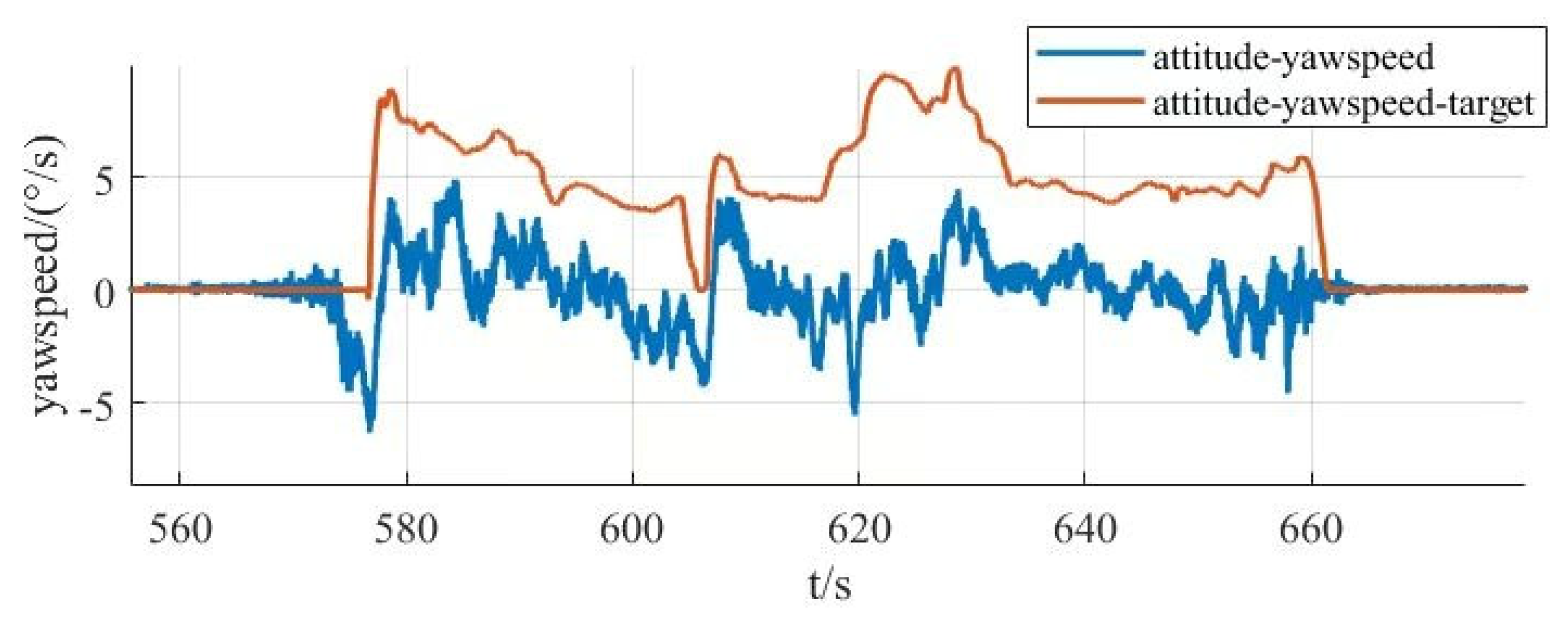
- Finally, for the large tilt-rotor vertical take-off and landing UAV, which is subject to many disturbances, long control response time, and complex control algorithms in the working process, this study pioneered the application of dual-serial PID control method to the large tilt-rotor vertical take-off and landing UAV. The control parameters are optimized through simulation, then the simulation and experimental data of the prototype’s flight attitudes, such as roll, pitch, and yaw, are collected, and conclusions are drawn. It provides reference and guidance for the research of tilt-rotor vertical take-off and landing UAVs.
2. Complete UAV Design
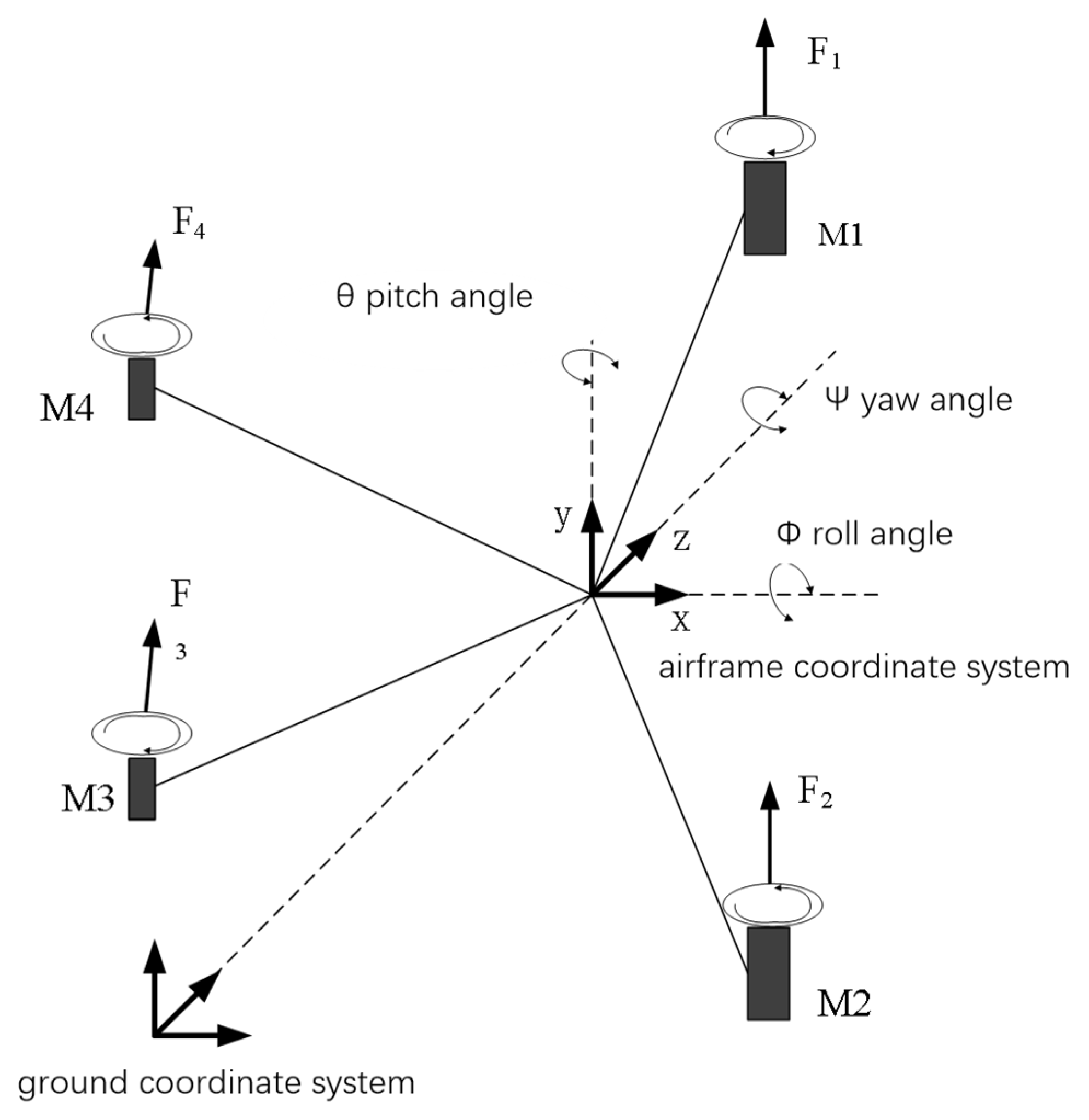
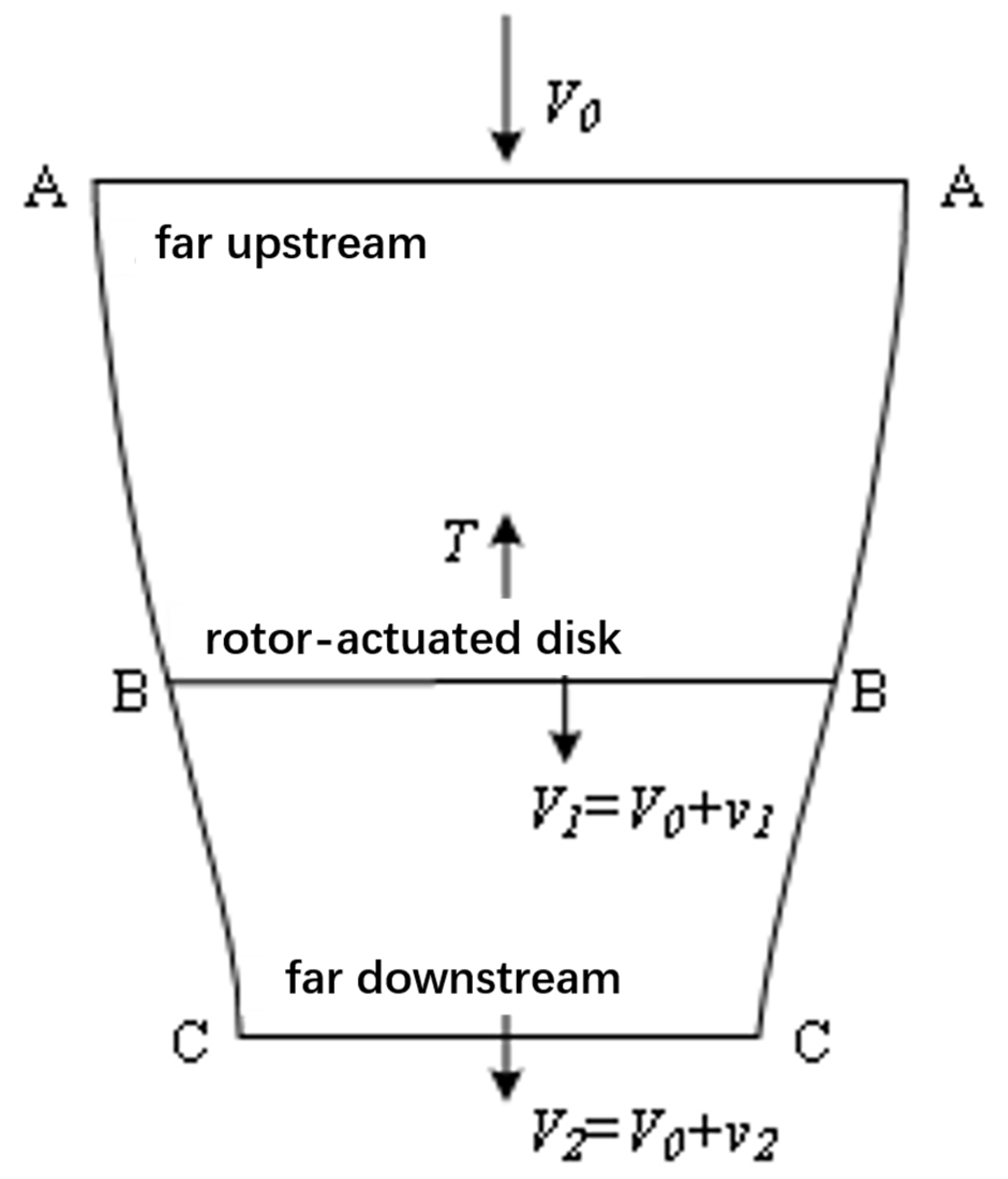
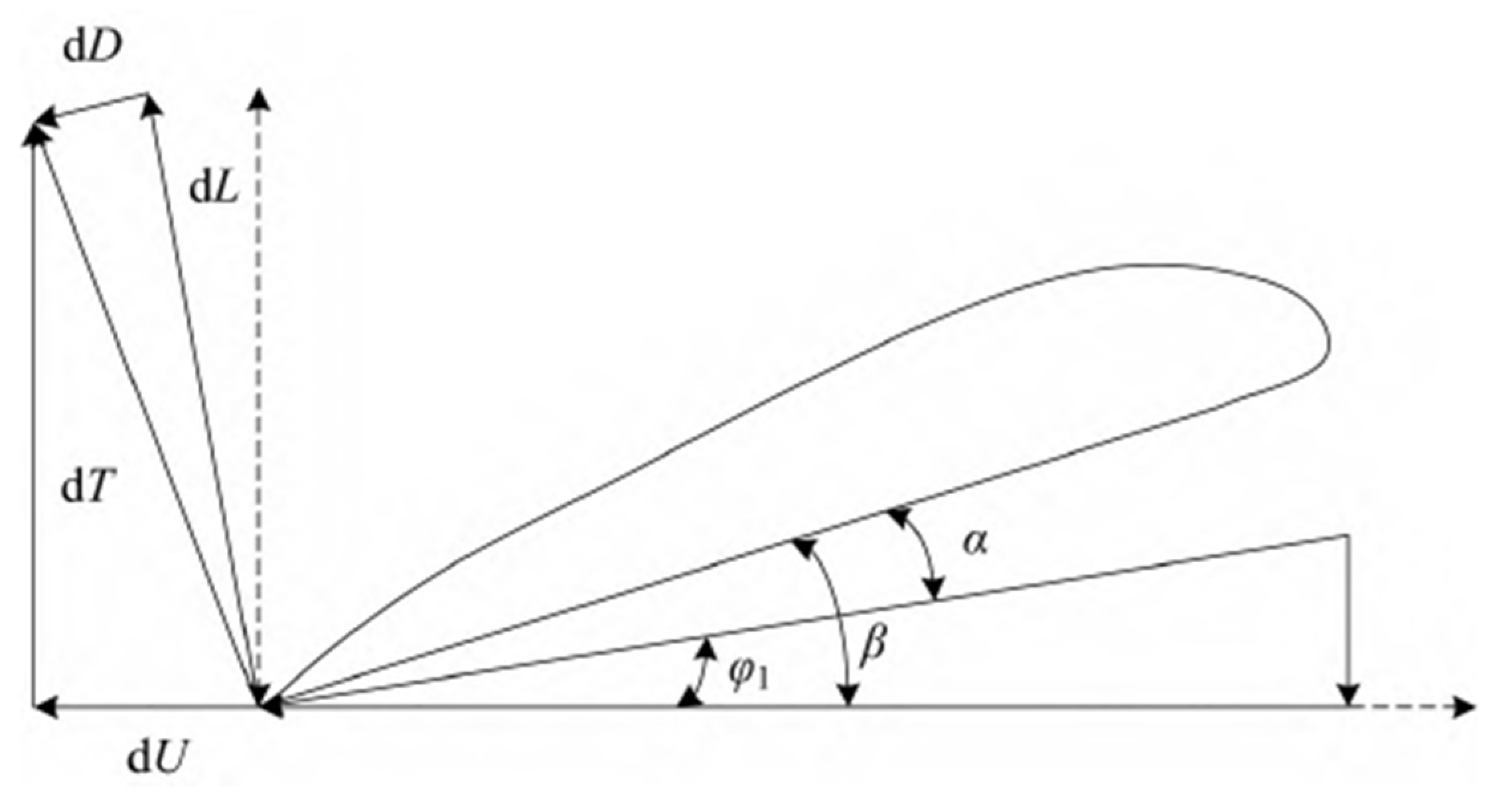
2.1. Dynamic Modeling
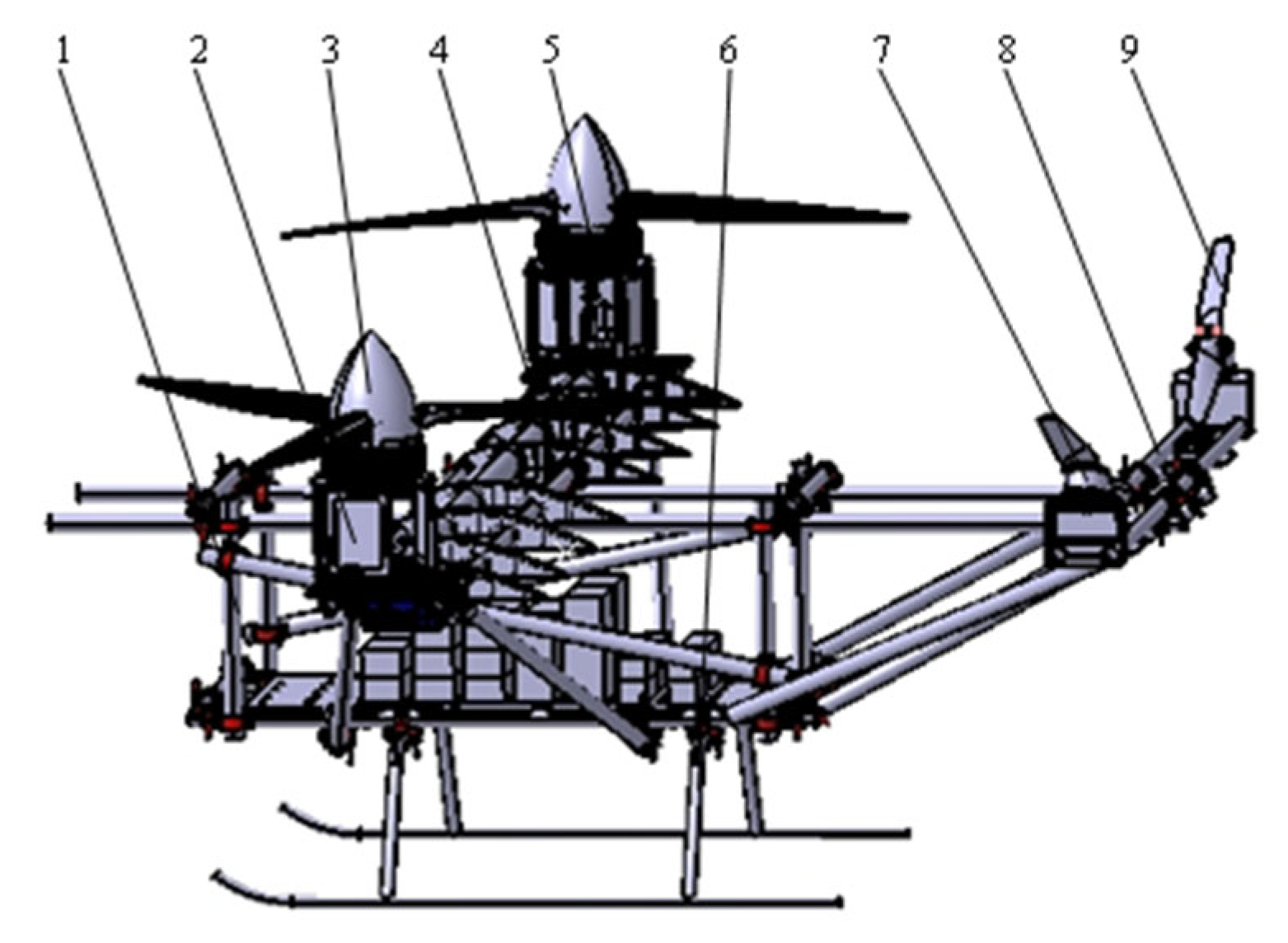
2.2. Fuselage Design
3. Mechanical Characterization and Structural Optimization of Prototype
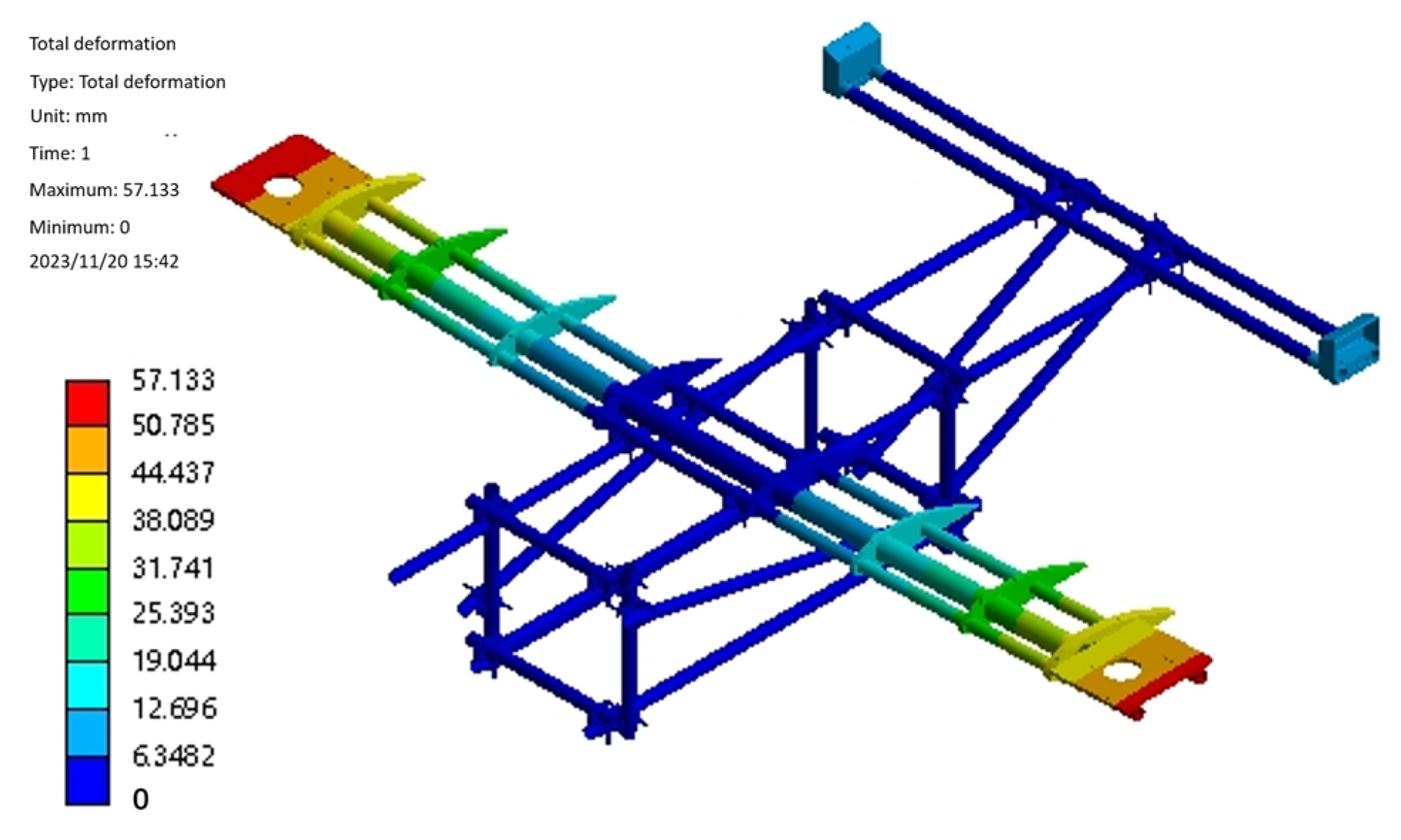
3.1. Static Analysis
3.2. Mechanical Properties Analysis of Landing Gear
3.2.1. Landing Gear Static Analysis
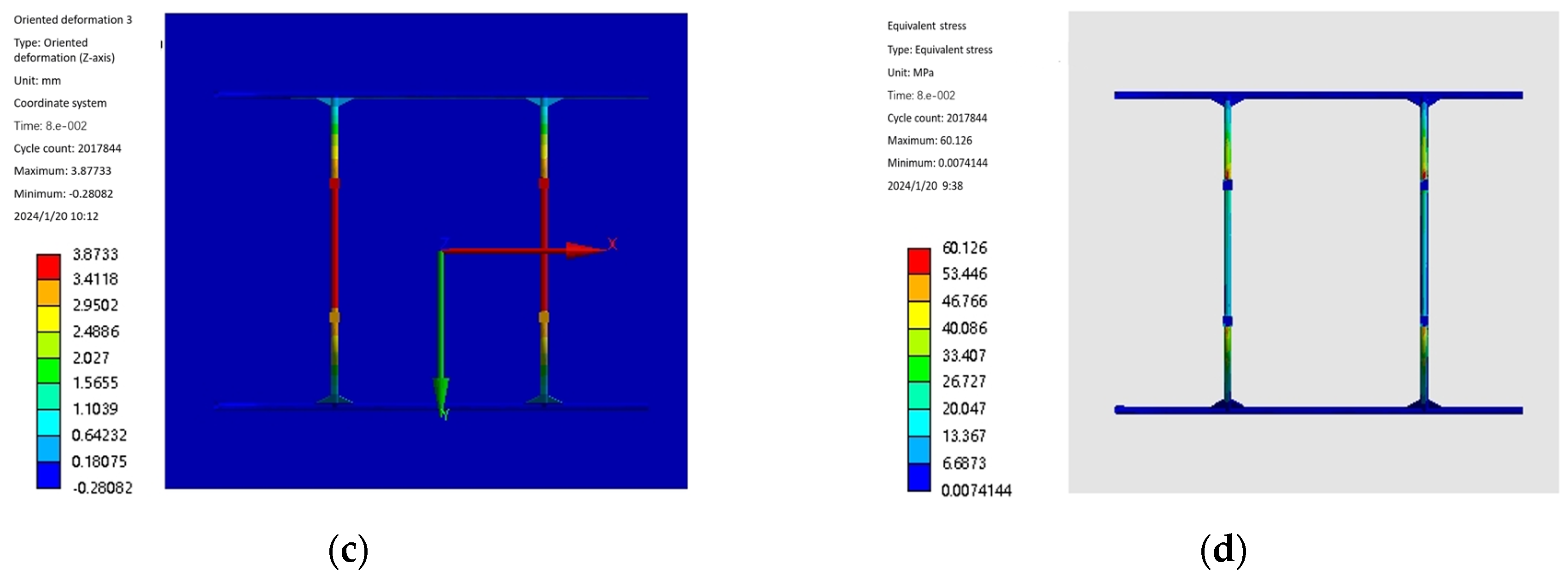
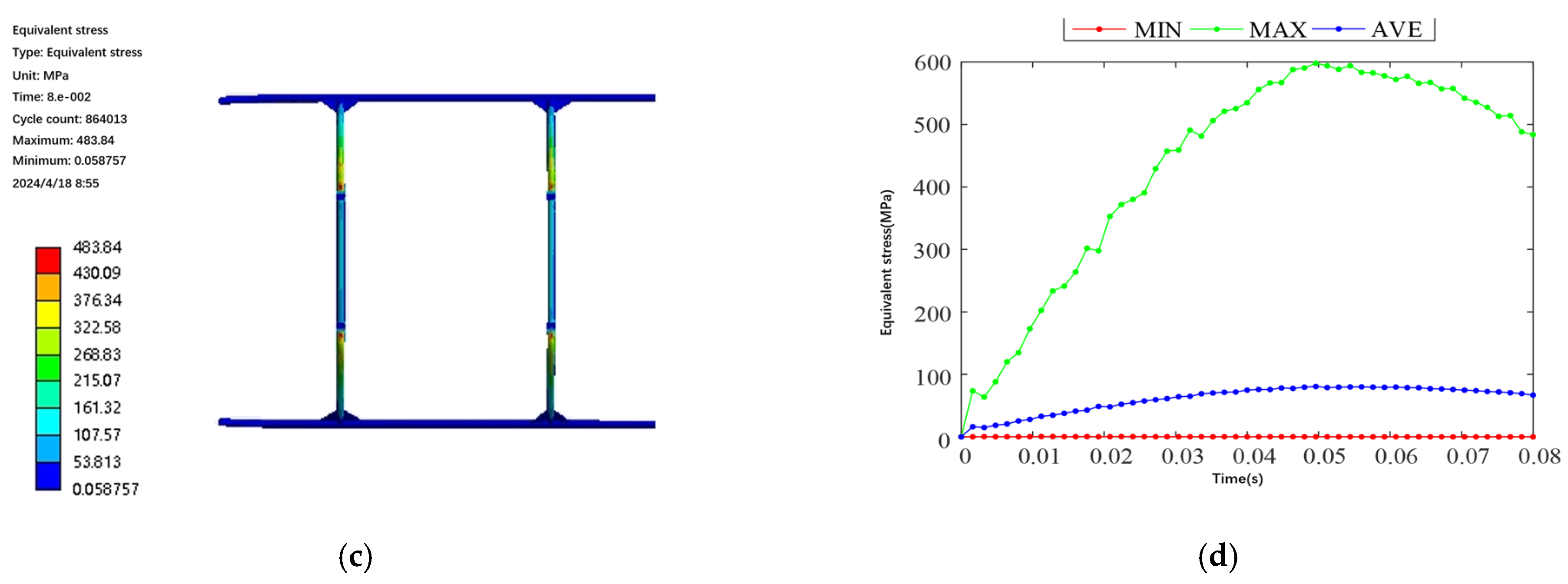
3.2.2. Simulation Analysis of Landing Gear Impact
3.3. Optimization of Tester Body Structure
3.3.1. Landing Gear Structure Optimization
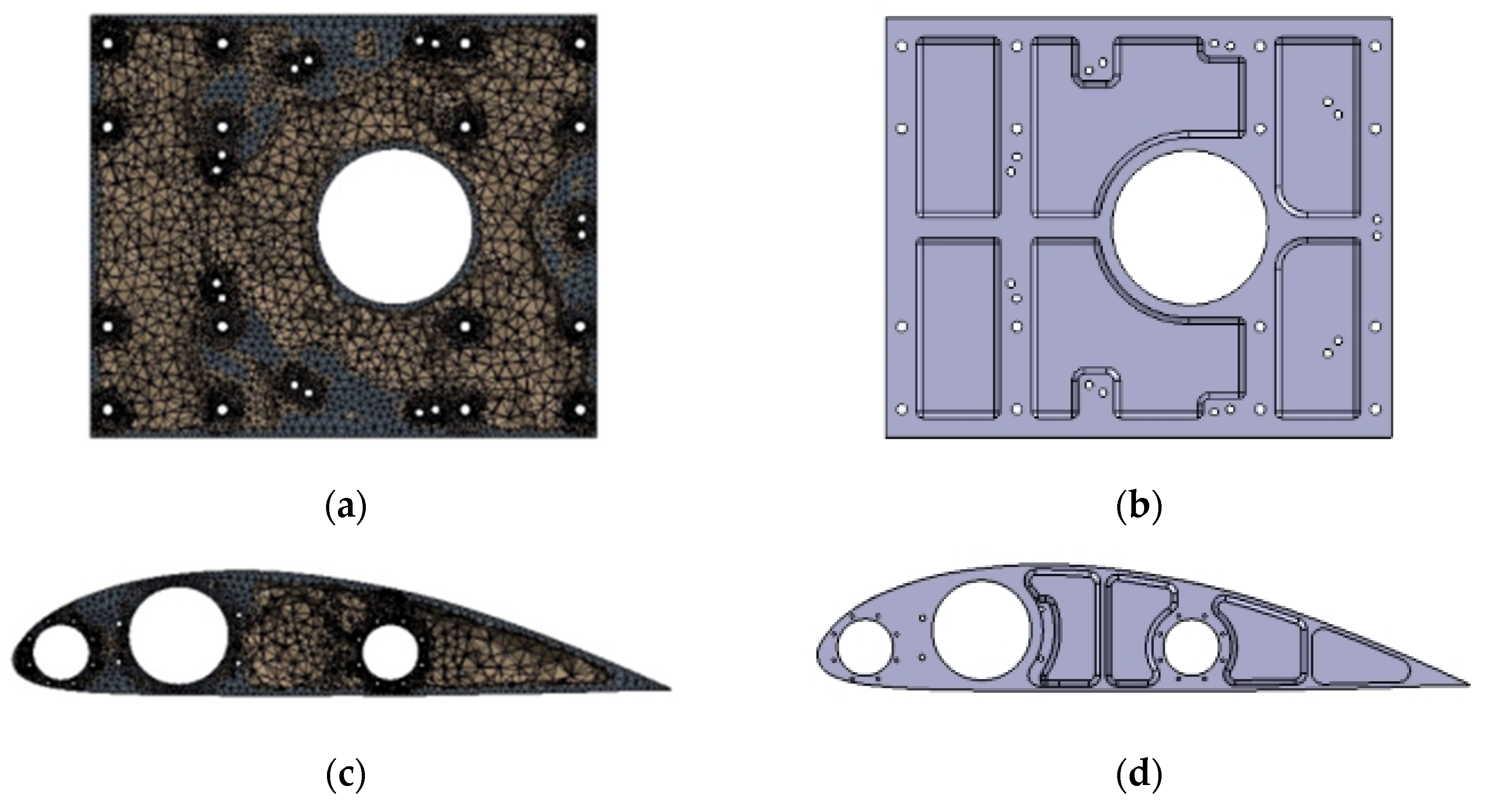
3.3.2. Wing Ribs and Main Motor Mount Optimization
4. Vibration Characterization of the Prototype
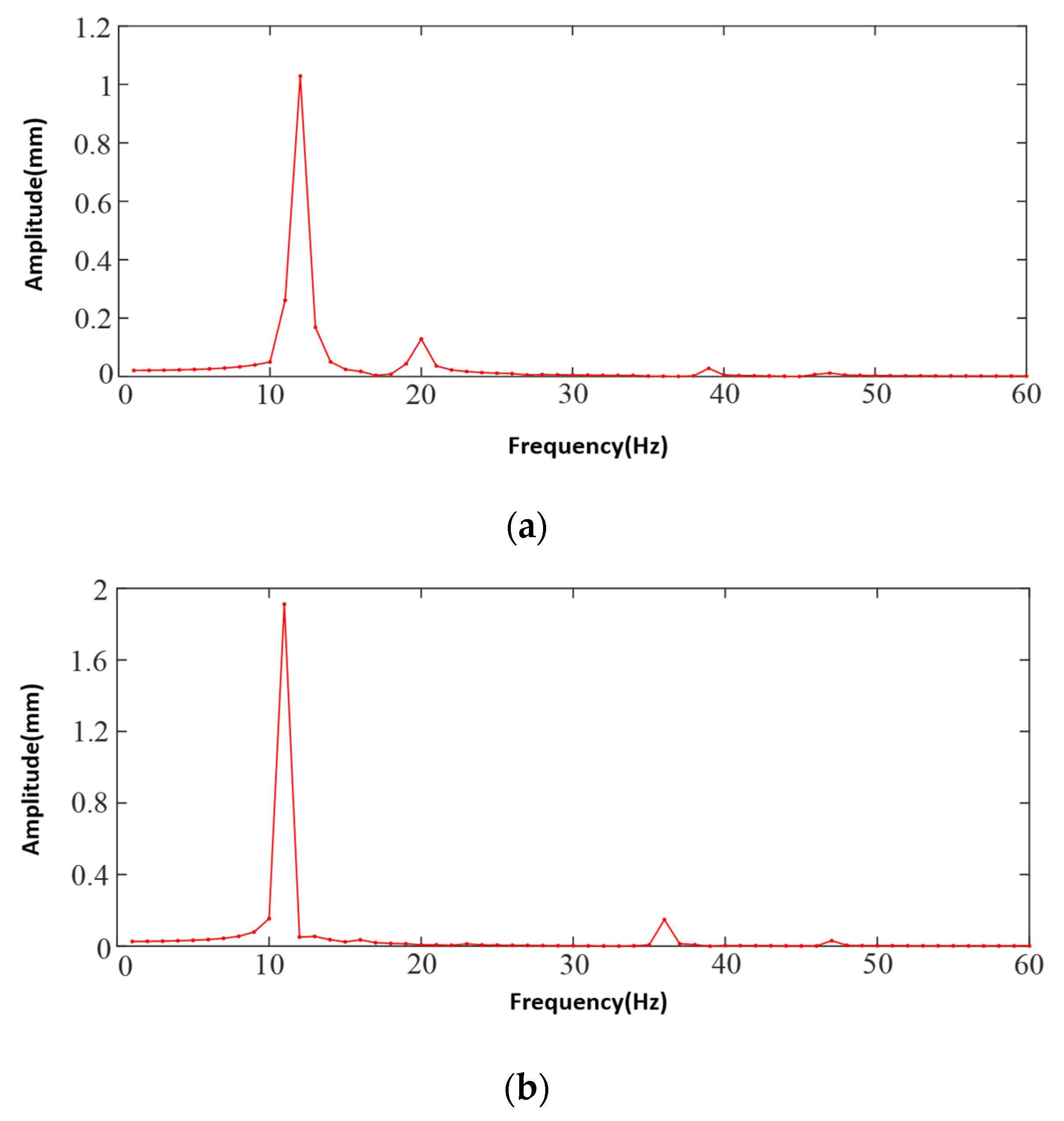
4.1. Modal Analysis of Prototype
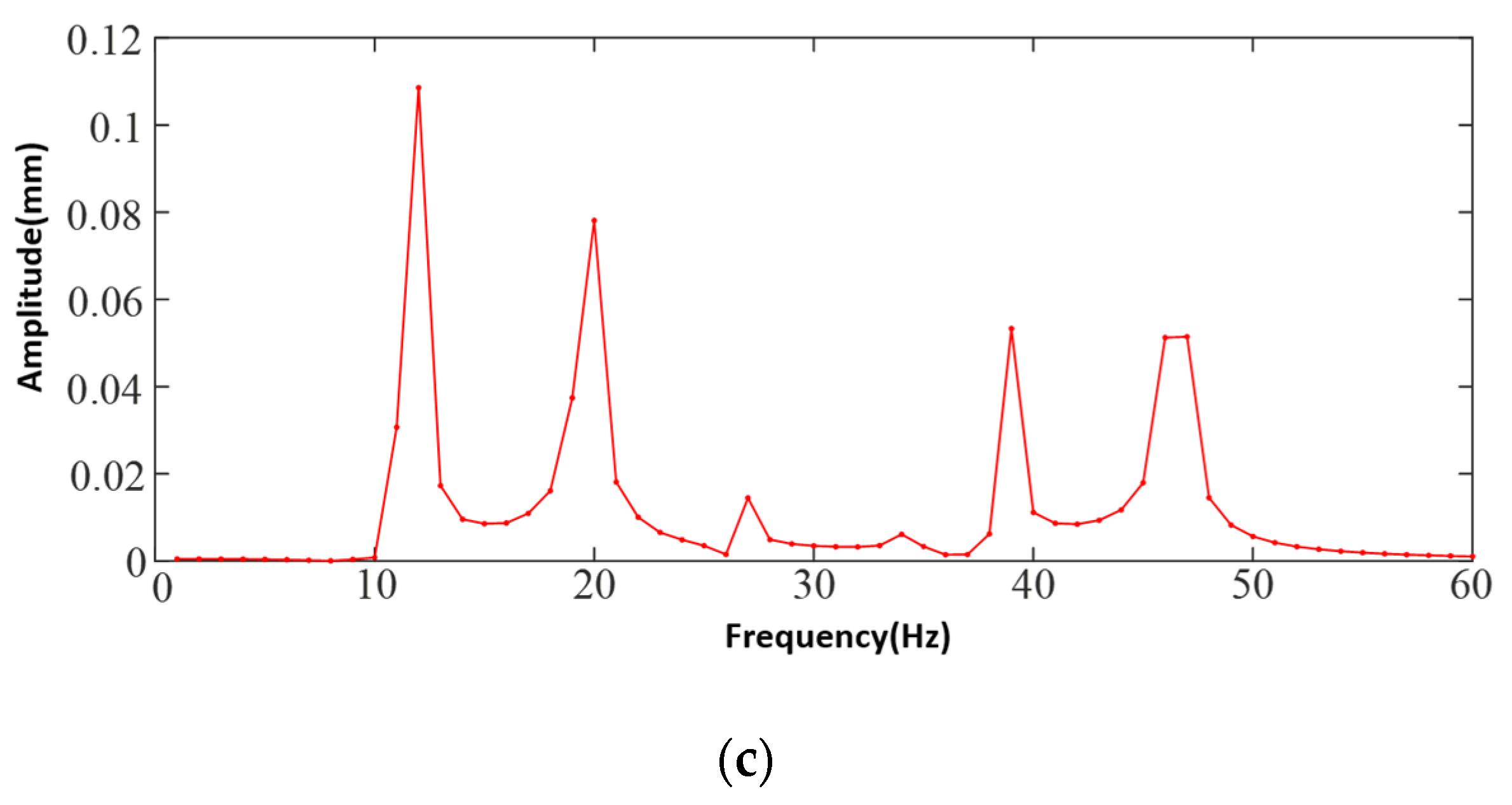
4.2. Tester Body Harmonic Response Analysis
5. Prototype System Integration and Control Scheme Optimization
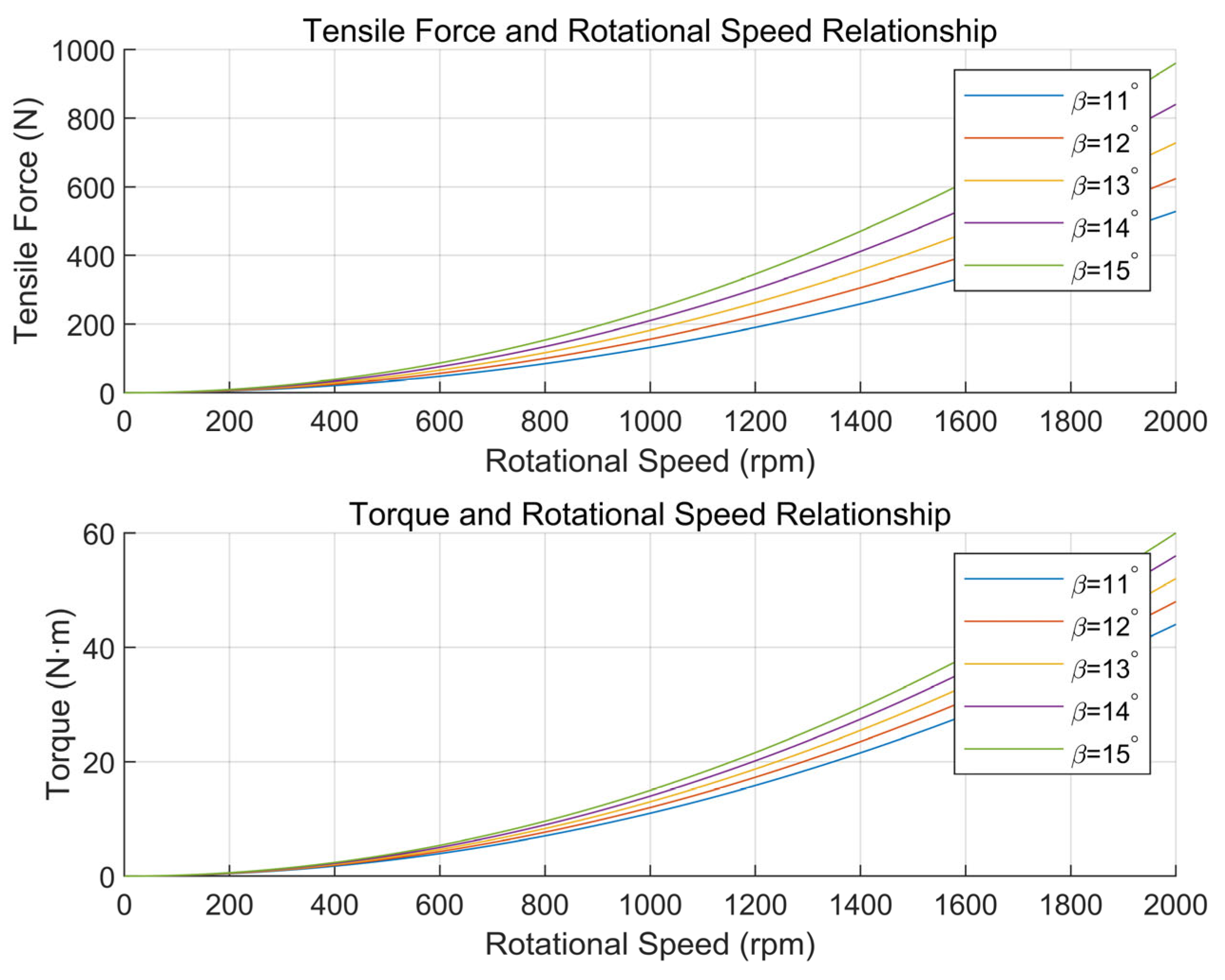
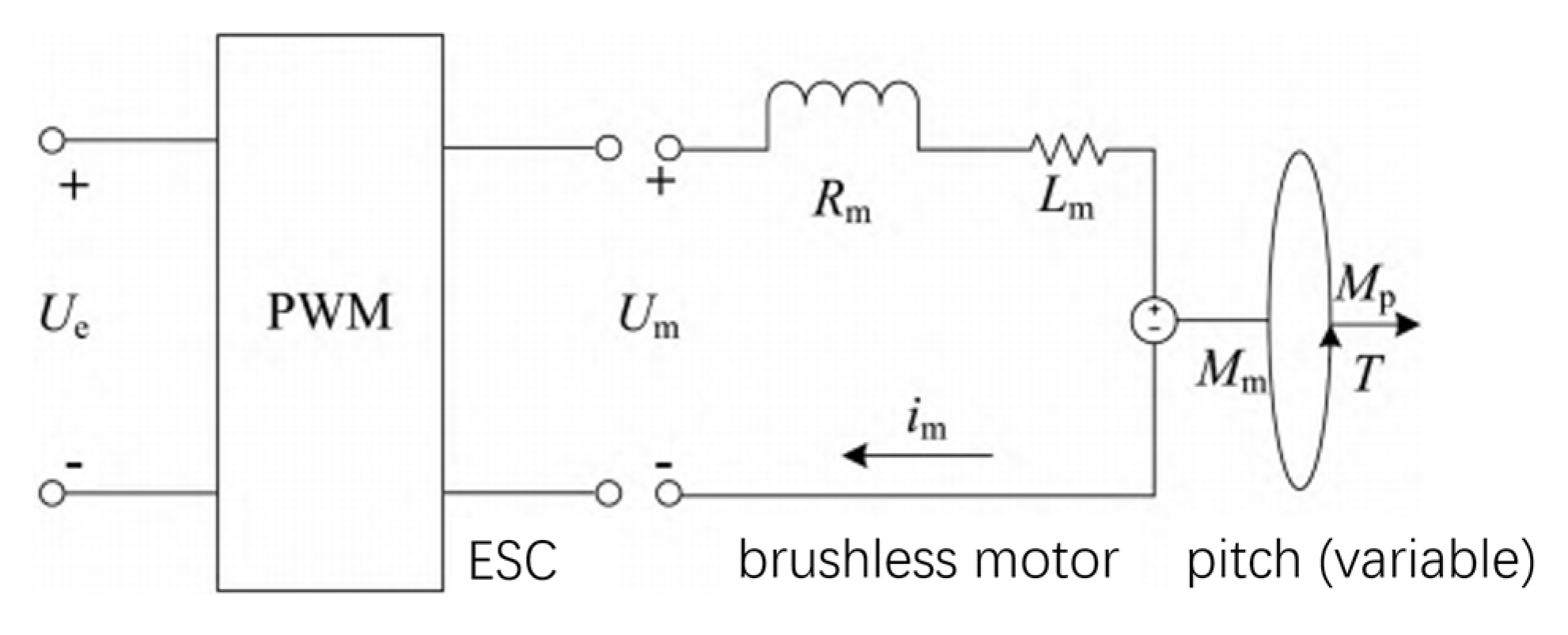
5.1. Power System Design
5.2. Control System Design
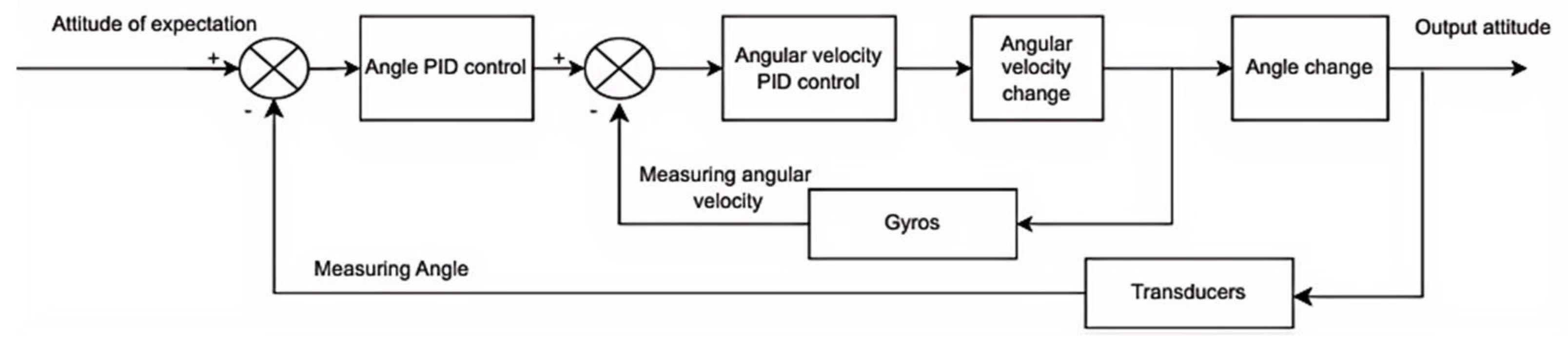
5.2.1. Control Object Modeling
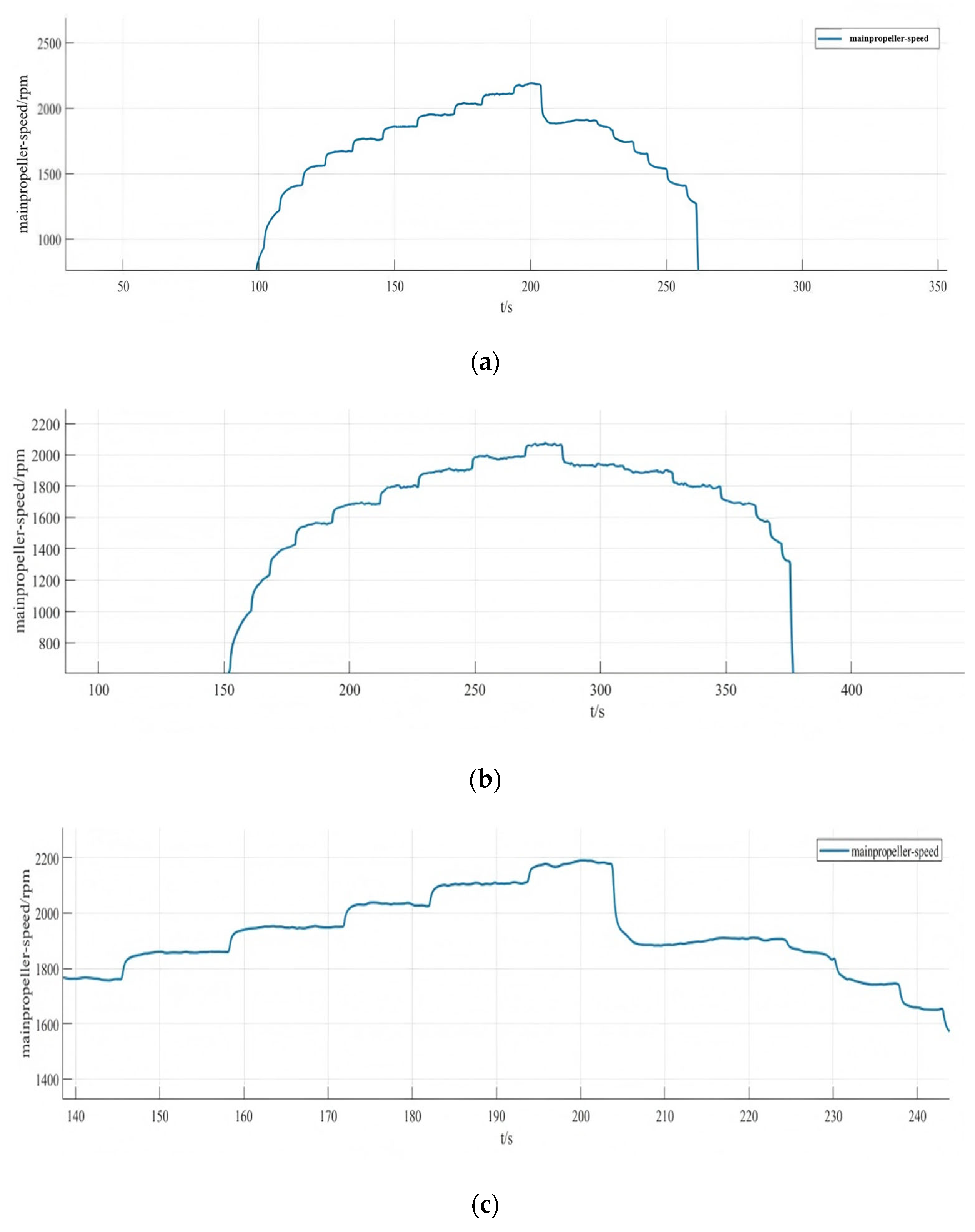
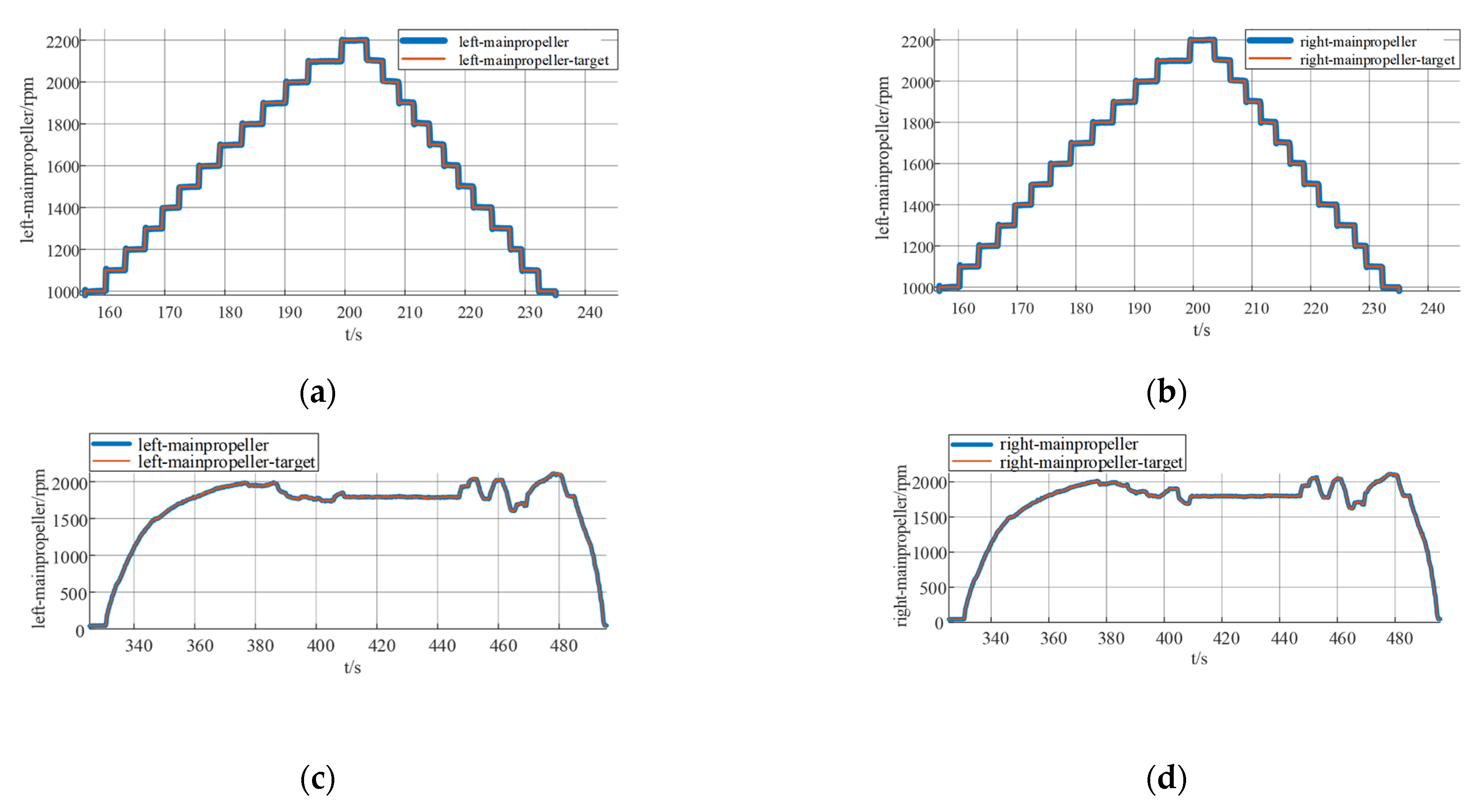
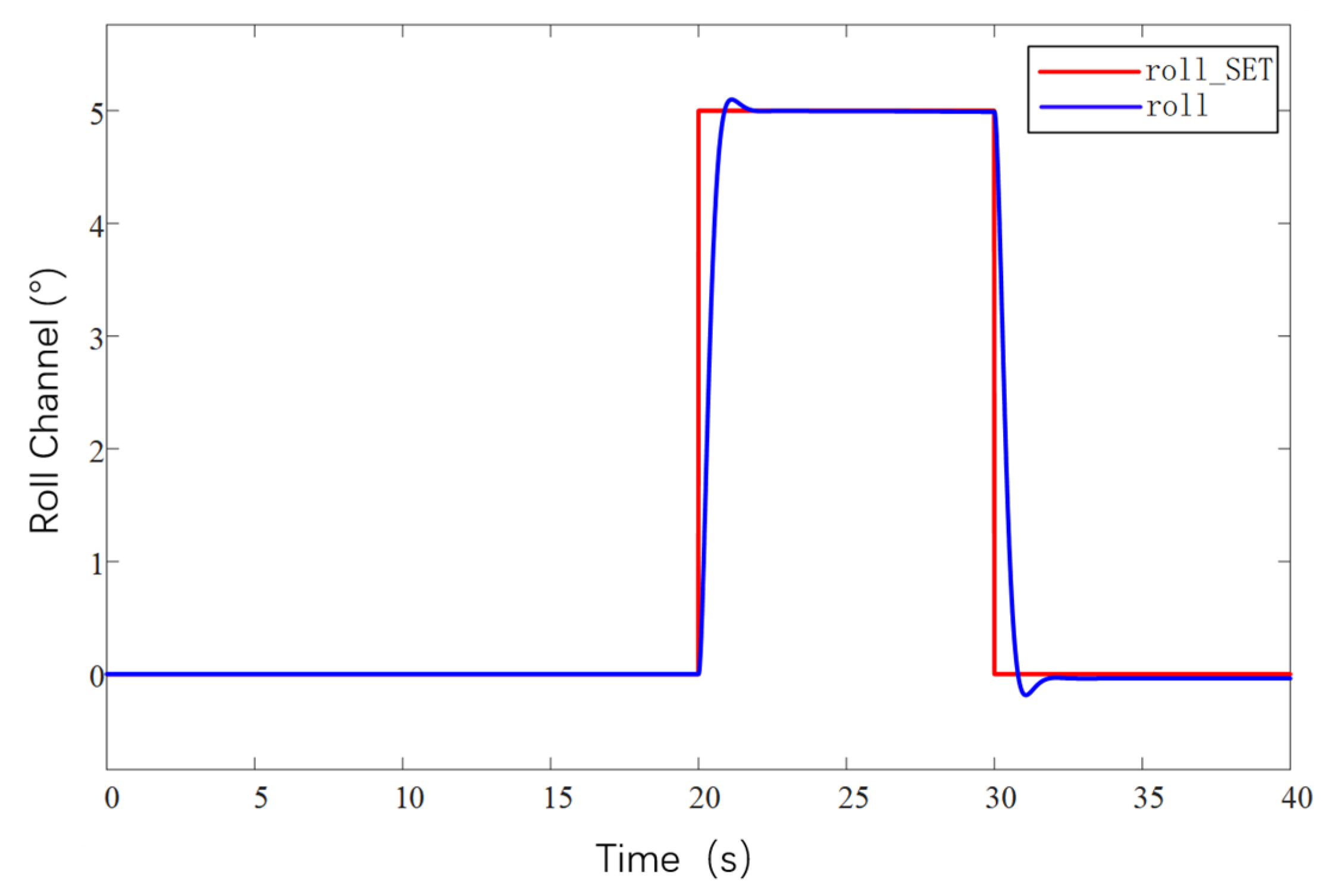
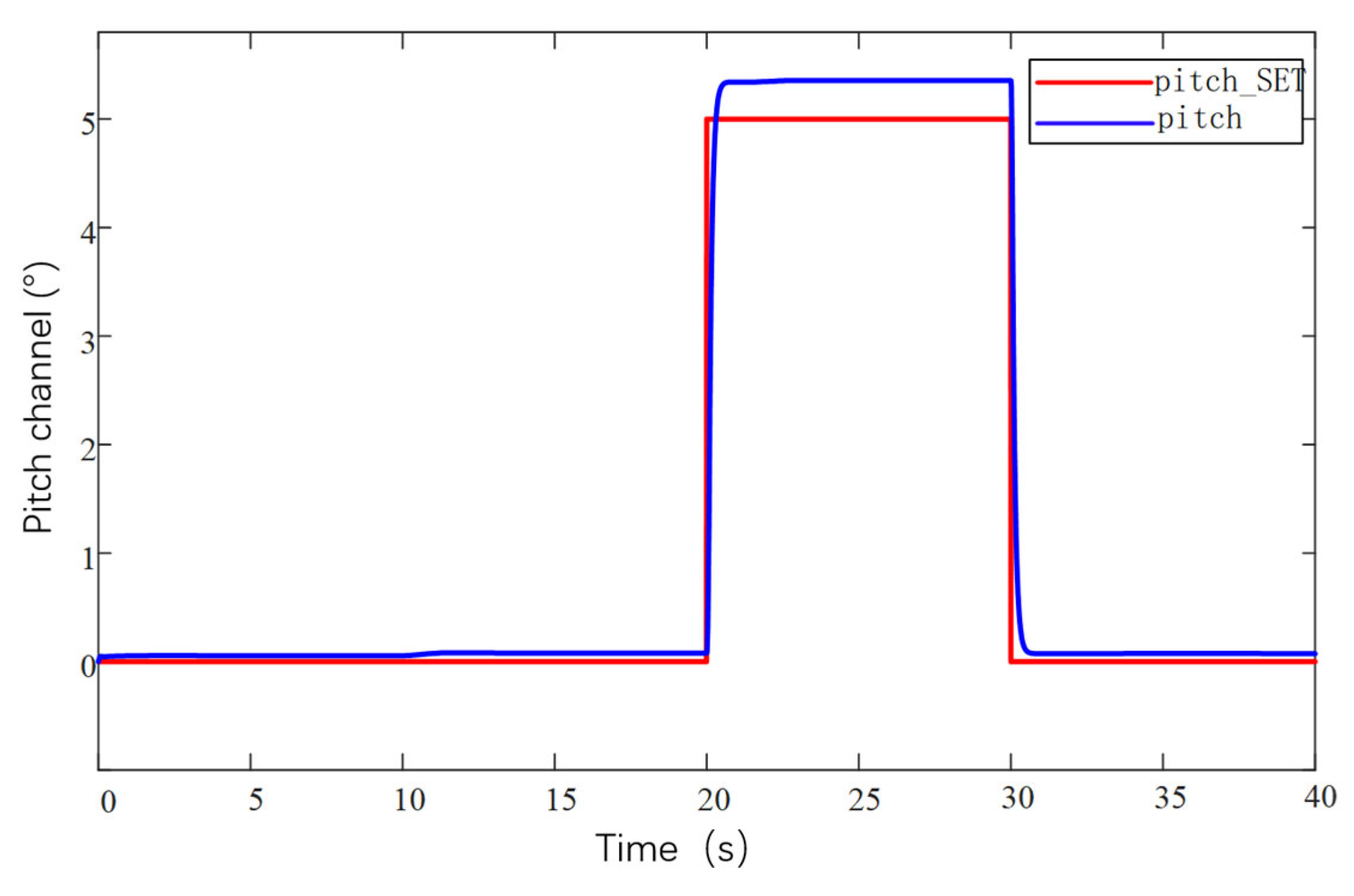
5.2.2. Control System Design and Parameter Tuning
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, K.; Liu, C.; Li, C.; Chen, R. Flight Dynamics Modeling and Dynamic Stability Analysis of Tilt-Rotor Aircraft. Int. J. Aerosp. Eng. 2019, 2019, 5737212. [Google Scholar] [CrossRef]
- Kang, Y.; Park, B.J.; Cho, A.; Yoo, C.S.; Koo, S.O.; Tahk, M.J. Development of Flight Control System and Troubleshooting on Flight Test of a Tilt-Rotor Unmanned Aerial Vehicle. Int. J. Aeronaut. Space 2016, 17, 120–131. [Google Scholar] [CrossRef]
- Qiao, Z.; Wang, D.; Xu, J.; Pei, X.; Su, W.; Wang, D.; Bai, Y. A Comprehensive Design and Experiment of a Biplane Quadrotor Tail-Sitter UAV. Drones 2023, 7, 292. [Google Scholar] [CrossRef]
- Zhang, Q.; Zhang, J.J.; Wang, X.Y.; Xu, Y.F.; Yu, Z.L. Wind Field Disturbance Analysis and Flight Control System Design for a Novel Tilt-Rotor UAV. IEEE Access 2020, 8, 211401–211410. [Google Scholar] [CrossRef]
- Ducard, G.J.J.; Allenspach, M. Review of designs and flight control techniques of hybrid and convertible VTOL UAVs. Aerosp. Sci. Technol. 2021, 118, 107035. [Google Scholar] [CrossRef]
- Su, J.; Su, C.; Xu, S.; Yang, X. A Multibody Model of Tilt-Rotor Aircraft Based on Kane’s Method. Int. J. Aerosp. Eng. 2019, 2019, 9396352. [Google Scholar] [CrossRef]
- Zhao, H.; Wang, B.; Shen, Y.; Zhang, Y.; Li, N.; Gao, Z. Development of Multimode Flight Transition Strategy for Tilt-Rotor VTOL UAVs. Drones 2023, 7, 580. [Google Scholar] [CrossRef]
- Mimouni, M.Z.; Araar, O.; Oudda, A.; Haddad, M. A new control scheme for an aerodynamic-surface-free tilt-rotor convertible UAV. Aeronaut. J. 2023, 128, 1119–1144. [Google Scholar] [CrossRef]
- Chen, Z.; Jia, H. Design of Flight Control System for a Novel Tilt-Rotor UAV. Complexity 2020, 2020, 4757381. [Google Scholar] [CrossRef]
- Ta, D.A.; Fantoni, I.; Lozano, R. Modeling and Control of a Tilt Tri-Rotor Airplane. In Proceedings of the 2012 American Control Conference (ACC), Fairmont Queen Elizabeth, Montréal, QC, Canada, 27–29 June 2012. [Google Scholar]
- Su, W.; Qu, S.; Zhu, G.; Swei, S.S.-M.; Hashimoto, M.; Zeng, T. Modeling and control of a class of urban air mobility tiltrotor aircraft. Aerosp. Sci. Technol. 2022, 124, 107561. [Google Scholar] [CrossRef]
- Chowdhury, A.B.; Kulhare, A.; Raina, G. Back-stepping control strategy for stabilization of a Tilt-Rotor UAV. In Proceedings of the 2012 24th Chinese Control and Decision Conference (CCDC), Taiyuan, China, 23–25 May 2012. [Google Scholar]
- Cardoso, D.N.; Esteban, S.; Raffo, G. A new robust adaptive mixing control for trajectory tracking with improved forward flight of a tilt-rotor UAV. ISA Trans. 2021, 110, 86–104. [Google Scholar] [CrossRef] [PubMed]
- Kumar, R.; Agarwal, S.R.; Kumar, M. Modeling and Control of a Tethered Tilt-Rotor Quadcopter with Atmospheric Wind Model. IFAC PapersOnLine 2021, 54, 463–468. [Google Scholar] [CrossRef]
- Al-Radaideh, A.; Sun, L. Self-Localization of a Tethered Quadcopter Using Inertial Sensors in a GPS-Denied Environment. In Proceedings of the 2017 International Conference on Unmanned Aircraft Systems (ICUAS), Miami, FL, USA, 13–16 June 2017. [Google Scholar]
- Panza, S.; Lovera, M.; Sato, M.; Muraoka, K. Structured μ-Synthesis of Robust Attitude Control Laws for Quad-Tilt-Wing Unmanned Aerial Vehicle. J. Guid. Control Dynam. 2020, 43, 2258–2274. [Google Scholar] [CrossRef]
- Borase, R.P.; Maghade, D.K.; Sondkar, S.Y.; Pawar, S.N. A review of PID control, tuning methods and applications. Int. J. Dyn. Control. 2020, 9, 818–827. [Google Scholar] [CrossRef]
- Song, Y.; Scaramuzza, D. Policy Search for Model Predictive Control with Application to Agile Drone Flight. IEEE Trans. Robot. 2022, 38, 2114–2130. [Google Scholar] [CrossRef]
- Xie, M.; Xu, S.; Su, C.Y.; Feng, Z.Y.; Chen, Y.; Shi, Z.; Lian, J. An adaptive recursive sliding mode attitude control for tiltrotor UAV in flight mode transition based on super-twisting extended state observer. arXiv 2021, arXiv:2111.02046. [Google Scholar]
- Liu, N.J.; Cai, Z.H.; Zhao, J.; Wang, Y.X. Predictor-based model reference adaptive roll and yaw control of a quad-tiltrotor UAV. Chin. J. Aeronaut. 2020, 33, 282–295. [Google Scholar] [CrossRef]
- Irmawan, E.; Harjoko, A.; Dharmawan, A. Model, Control, and Realistic Visual 3D Simulation of VTOL Fixed-Wing Transition Flight Considering Ground Effect. Drones 2023, 7, 330. [Google Scholar] [CrossRef]
- Wei, Q.L.; Yang, Z.S.; Su, H.Z.; Wang, L.J. Online Adaptive Dynamic Programming for Optimal Self-Learning Control of VTOL Aircraft Systems with Disturbances. IEEE Trans. Autom. Sci. Eng. 2024, 2, 343–352. [Google Scholar] [CrossRef]
- El-Dalatony, A.M.; Attia, T.; Ragheb, H.; Sharaf, A.M. Cascaded PID Trajectory Tracking Control for Quadruped Robotic Leg. Int. J. Mech. Eng. Robot. 2023, 12, 40–47. [Google Scholar] [CrossRef]
- Zhu, C.; Jun, L.; Huang, B.; Su, Y.; Zheng, Y. Trajectory tracking control for autonomous underwater vehicle based on rotation matrix attitude representation. Ocean. Eng. 2022, 252, 111206. [Google Scholar] [CrossRef]
- Zheng, E.H.; Xiong, J.J.; Luo, J.L. Second order sliding mode control for a quadrotor UAV. ISA Trans. 2014, 53, 1350–1356. [Google Scholar] [CrossRef] [PubMed]
- Kazemzadeh Azad, S.; Aminbakhsh, S. ε-constraint guided stochastic search with successive seeding for multi-objective optimization of large-scale steel double-layer grids. J. Build. Eng. 2022, 46, 103767. [Google Scholar] [CrossRef]


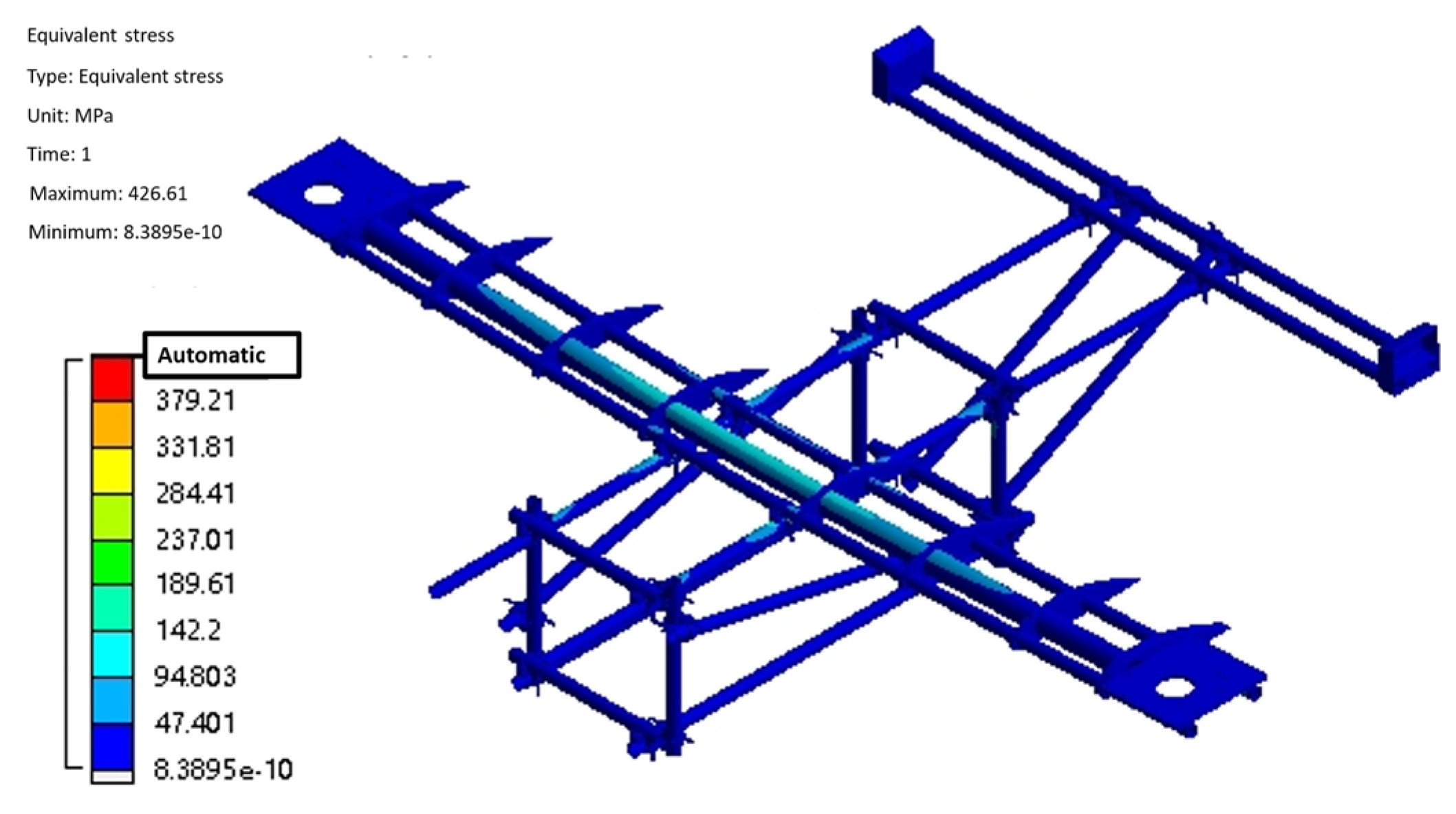
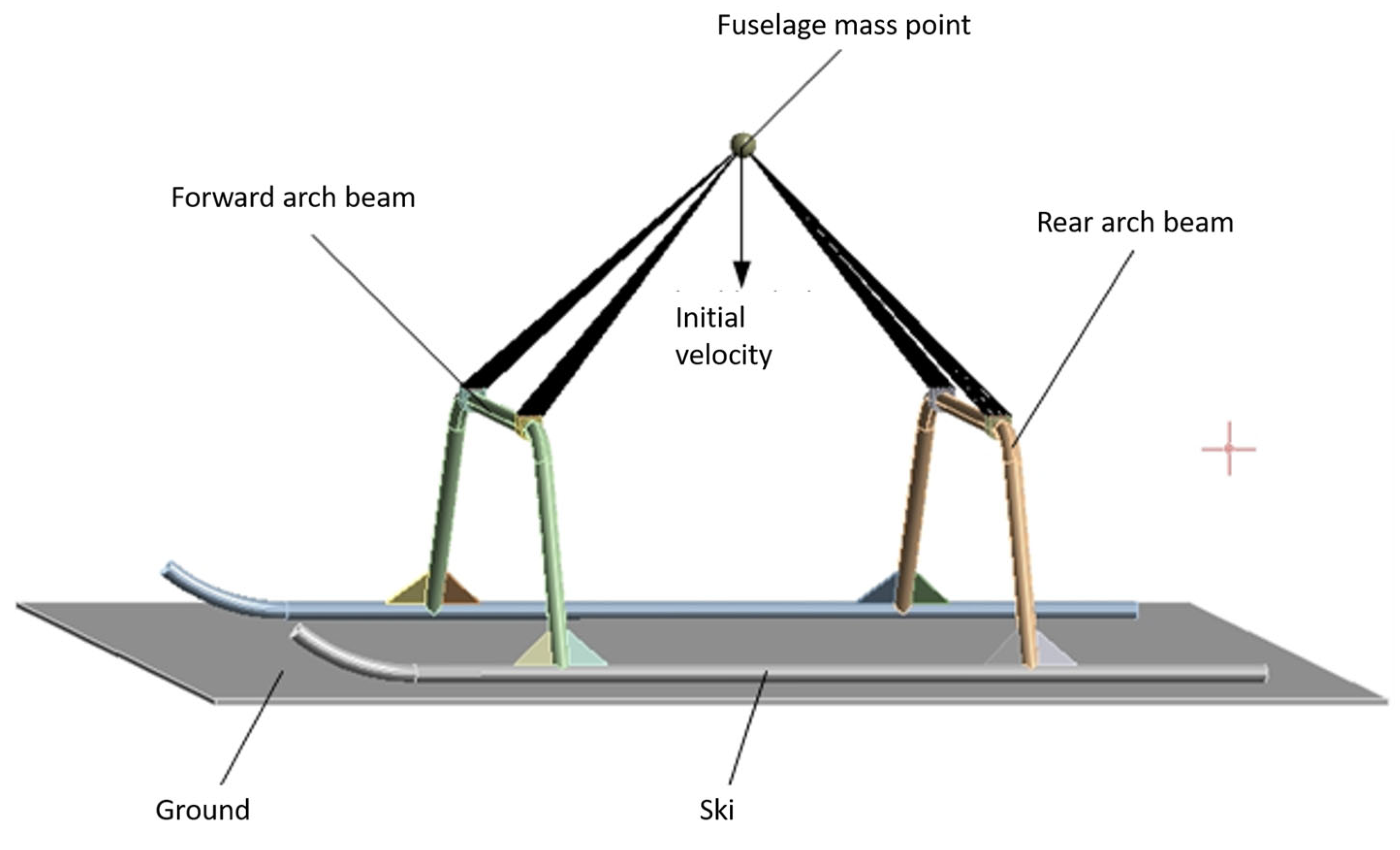
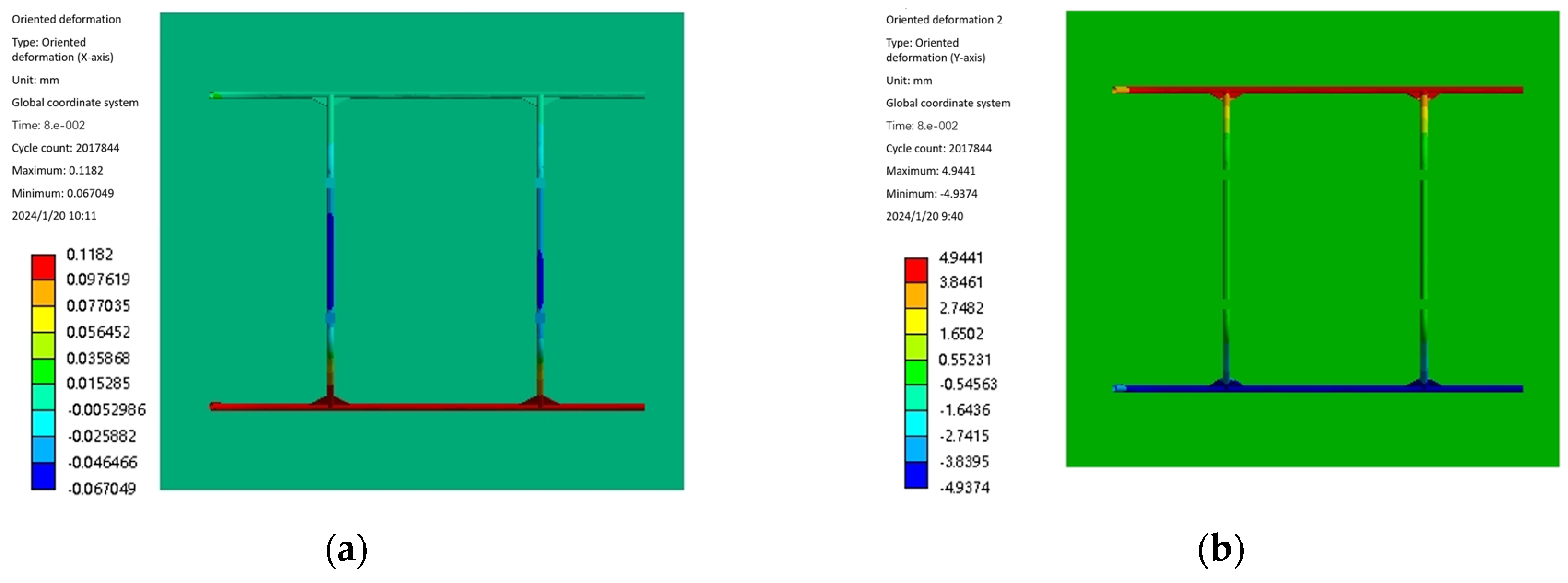














| Parameters | Numerical Value | Parameters | Numerical Value |
|---|---|---|---|
| fuselage length | 3000 mm | Tail rotor wheelbase | 2190 mm |
| fuselage width | 548 mm | Main tail rotor X-direction wheelbase | 1763.7 mm |
| fuselage height | 645 mm | Maximum weight of the drone | 350 kg |
| wingspan | 4045 mm | Maximum main rotor power | 160 kW |
| tail spread | 2260 mm | Tail rotor power | 18 kW |
| main rotor wheelbase | 3695.4 mm | Thrust ratio | 1.3 |
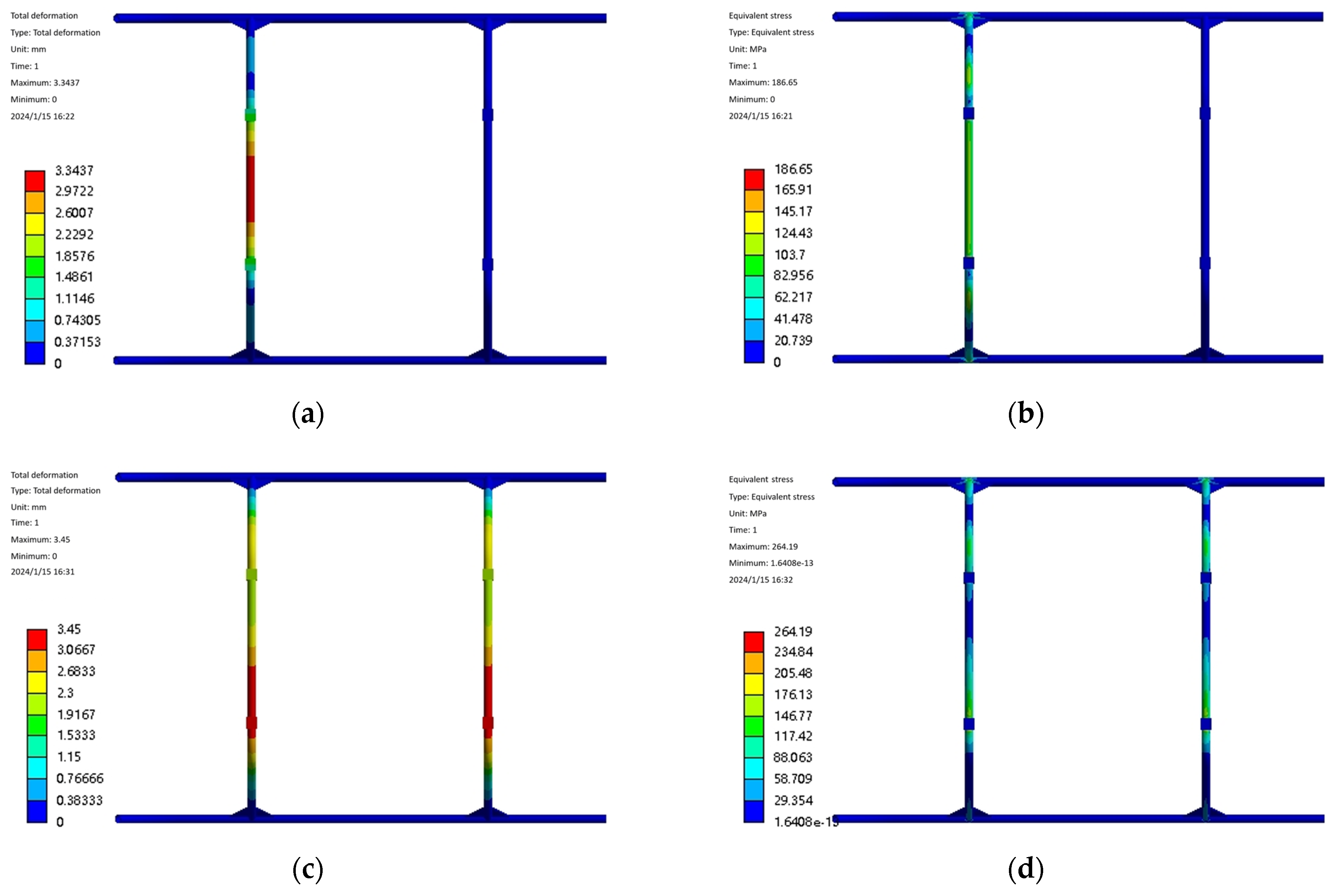
| Working Condition | Maximum Deformation (mm) | Maximum Equivalent Force (Mpa) |
|---|---|---|
| working condition 1 | 3.34 | 186.65 |
| working condition 2 | 3.45 | 264.19 |
| Optimization Variables | Bow-Beam Pole Length L (mm) | Bow-Beam Angle α (°) | Mass m (kg) | Maximum Equivalent Force (Physics) σ (Mpa) |
|---|---|---|---|---|
| pre-optimization | 600 | 120 | 5.795 | 616.54 |
| post-optimization | 579.15 | 123.9 | 5.758 | 412.46 |
| Name | Quality Before Optimization (kg) | Quality After Optimization (kg) | Optimization Percentage |
|---|---|---|---|
| Electric motor base | 5.071 | 2.234 | 55.94% |
| Reinforced wing ribs | 3.485 | 1.693 | 51.42% |
| Ordinary wing ribs | 1.706 | 0.845 | 50.46% |
| Order (Number of Step) | Intrinsic Frequency (Hz) | Vibration Pattern |
|---|---|---|
| 1 | 0 | / |
| 2 | 0 | / |
| 3 | 0 | / |
| 4 | 6.70 | Rotational deformation of the fuselage around the z-axis of the fuselage coordinates |
| 5 | 8.52 | Rotational deformation of the fuselage around the x-axis of the fuselage coordinates |
| 6 | 9.40 | Rotational deformation of the fuselage around the y-axis of the fuselage coordinates |
| 7 | 14.68 | Torsional deformation of the tail section of the fuselage around the x-axis |
| 8 | 21.13 | Wing and tail twist in opposite directions around the z-axis, tail ends twist up and down irregularly |
| 9 | 24.07 | Fuselage twisted from side to side, wing ends swinging up and down in deformation |
| 10 | 27.13 | Fuselage twisting from side to side, tail swinging up and down in deformation |
| 11 | 36.25 | Fuselage twisted and deformed fore and aft, tail wing swung up and down. |
| 12 | 36.81 | Fuselage twisted and deformed left and right, tail wing swung up and down and deformed |
| Order (Number of Step) | Intrinsic Frequency (Hz) | Vibration Pattern |
|---|---|---|
| 1 | 10.93 | The fuselage rotates and deforms around the landing gear. |
| 2 | 12.09 | The fuselage rotates around the landing gear and deforms forward and backward. |
| 3 | 12.67 | Wing and tail swing up and down. |
| 4 | 15.79 | Wing twisting forward and backward, tail swinging up and down, and deformation. |
| 5 | 19.69 | The fuselage moves forward and backward, and the tail swings up and down. |
| 6 | 22.71 | The fuselage is twisted and deformed from side to side, and the tail is swinging up and down irregularly. |
| 7 | 26.82 | The fuselage swings up and down at the wing and up and down in the opposite direction at the tail. |
| 8 | 34.52 | Fuselage and tail swing up and down. |
| 9 | 36.07 | Fuselage twisted from side to side, wings and tail swinging up and down, and deformed. |
| 10 | 38.84 | Fuselage twisted forward and backward, wing reverse-twisted forward and backward, tail swinging up and down. |
| 11 | 46.48 | Fuselage twisted up and down, wings twisted back and forth, up and down. |
| 12 | 46.92 | Combined left-right and up-down twisting and deformation of the fuselage. |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Gong, H.; He, W.; Hou, S.; Chen, M.; Yang, Z.; Si, Q.; Zhao, D. Design and Validation of a New Tilting Rotor VTOL Drone: Structural Optimization, Flight Dynamics, and PID Control. Sensors 2025, 25, 3537. https://doi.org/10.3390/s25113537
Gong H, He W, Hou S, Chen M, Yang Z, Si Q, Zhao D. Design and Validation of a New Tilting Rotor VTOL Drone: Structural Optimization, Flight Dynamics, and PID Control. Sensors. 2025; 25(11):3537. https://doi.org/10.3390/s25113537
Chicago/Turabian StyleGong, Haixia, Wei He, Shuping Hou, Ming Chen, Ziang Yang, Qin Si, and Deming Zhao. 2025. "Design and Validation of a New Tilting Rotor VTOL Drone: Structural Optimization, Flight Dynamics, and PID Control" Sensors 25, no. 11: 3537. https://doi.org/10.3390/s25113537
APA StyleGong, H., He, W., Hou, S., Chen, M., Yang, Z., Si, Q., & Zhao, D. (2025). Design and Validation of a New Tilting Rotor VTOL Drone: Structural Optimization, Flight Dynamics, and PID Control. Sensors, 25(11), 3537. https://doi.org/10.3390/s25113537








