An Integrated Spatial-Spectral Denoising Framework for Robust Electrically Evoked Compound Action Potential Enhancement and Auditory Parameter Estimation
Abstract
1. Introduction
- This study proposes a novel two-stage framework that combines spatial and spectral filtering for noise reduction in ECAP matrix signals.
- A reordering technique is introduced to estimate the noise in the ECAP matrix, based on the physiological ECAP measurements obtained using the forward-masking technique [10].
- A three-convolutional-layer neural network is proposed for denoising mask estimation. This network serves as one of the baselines, and is used to validate the noise estimation effect achieved by the proposed reordering technique.
- The reordering ECAP vector is treated as a speech-like signal and further denoised in the second stage using LSA Wiener filtering.
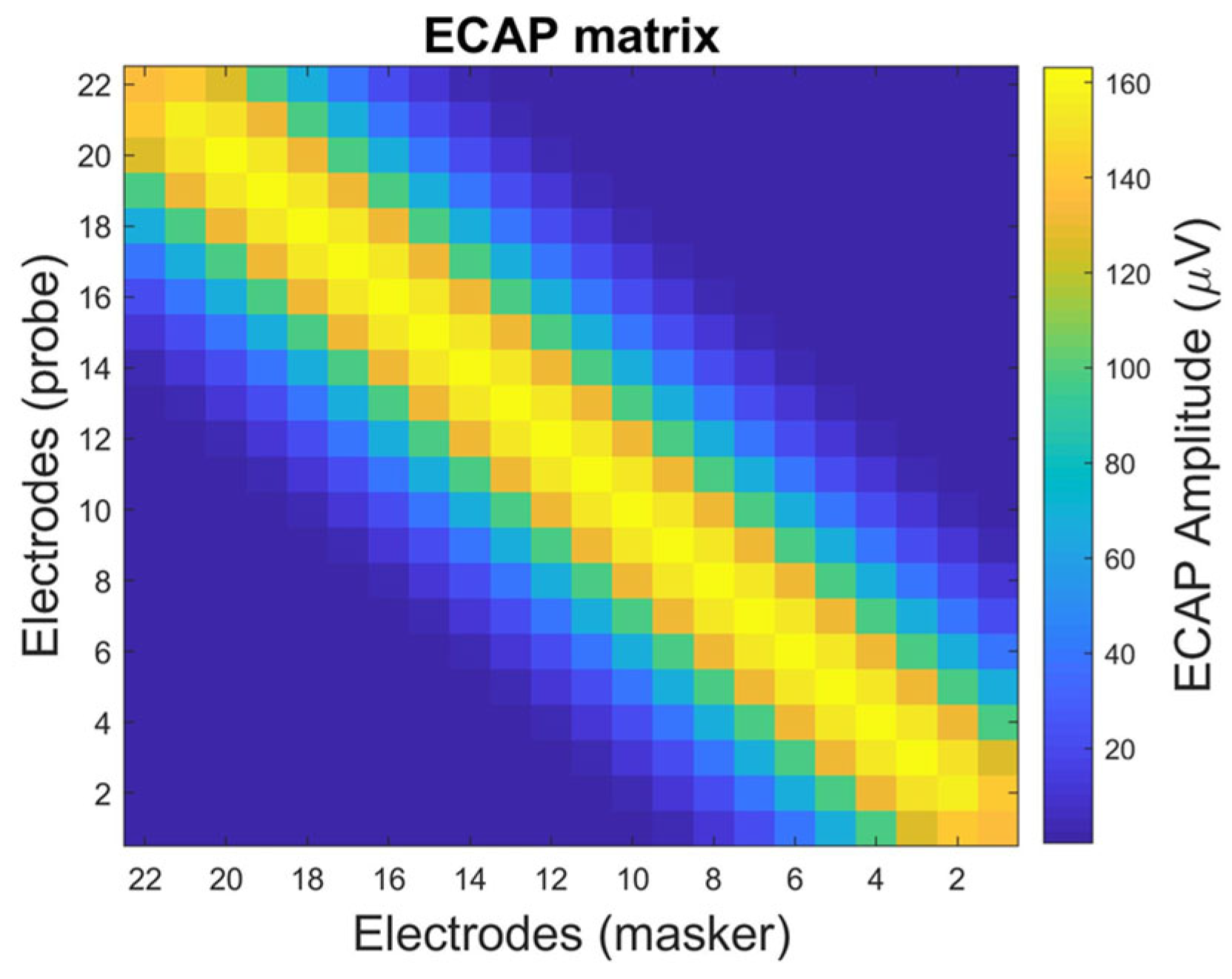
2. Panoramic ECAP Method
3. Proposed Method
3.1. First Stage of Noise Reduction Processing
- Calculate the absolute value of index minus indexwhere is an index matrix that records the absolute value of the position difference between and
- Record for each element in and concatenate each row into a long vector.where is the -th entry of .
- Order in descending order and record the descending order index.where represents the descending order operation, is a vector based on the descending order of the results of , and is the index vector corresponding to .
- The desired vector can then be obtained using the following equation:where is a row vector containing both noise components and noisy ECAP signal components. The noise, where the ECAP signal is weak, is placed in the first part of the vector, while the target signal, where the ECAP signal is stronger, is placed in the last part of the vector. The reordering process is part of the second stage of TSPD, which employs LSA Wiener filtering for improved noise reduction, as stated below.
3.2. Second Stage of Noise Reduction Processing
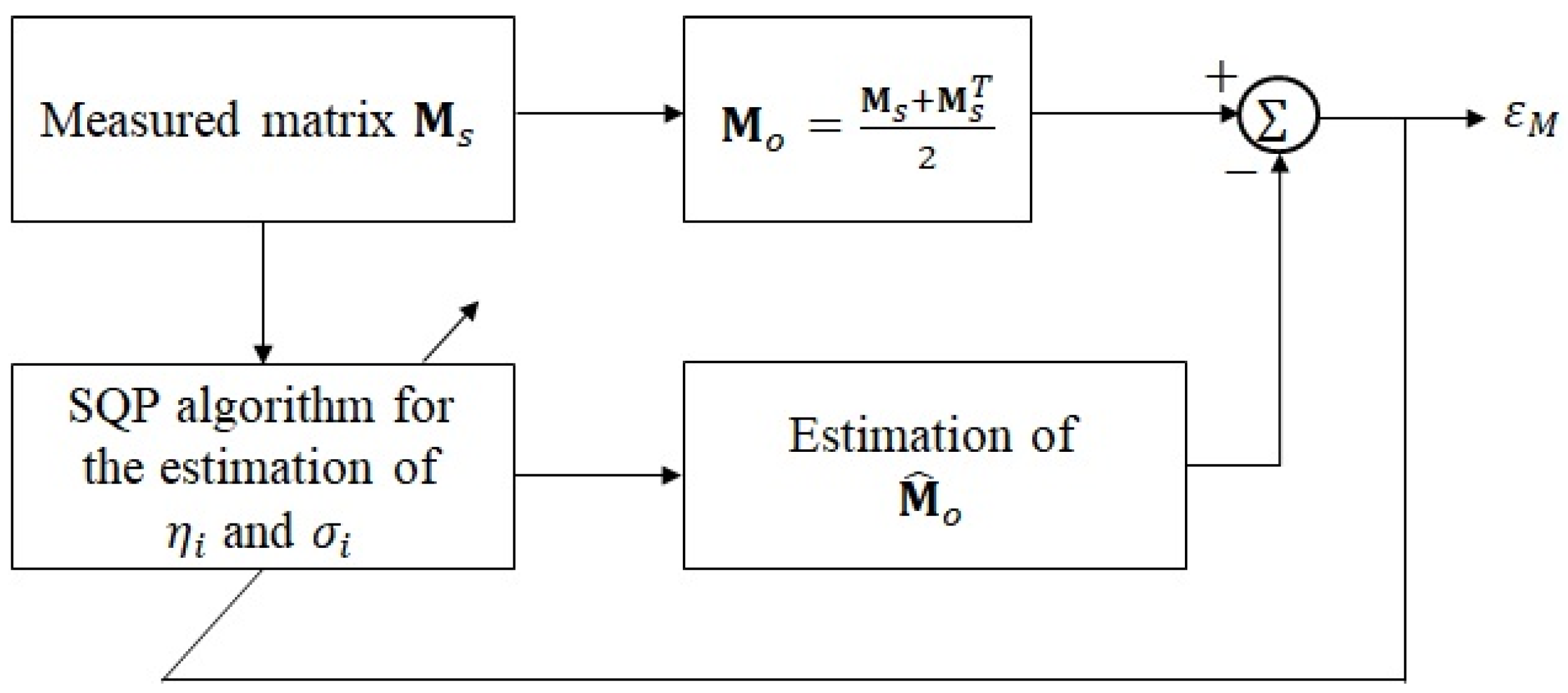
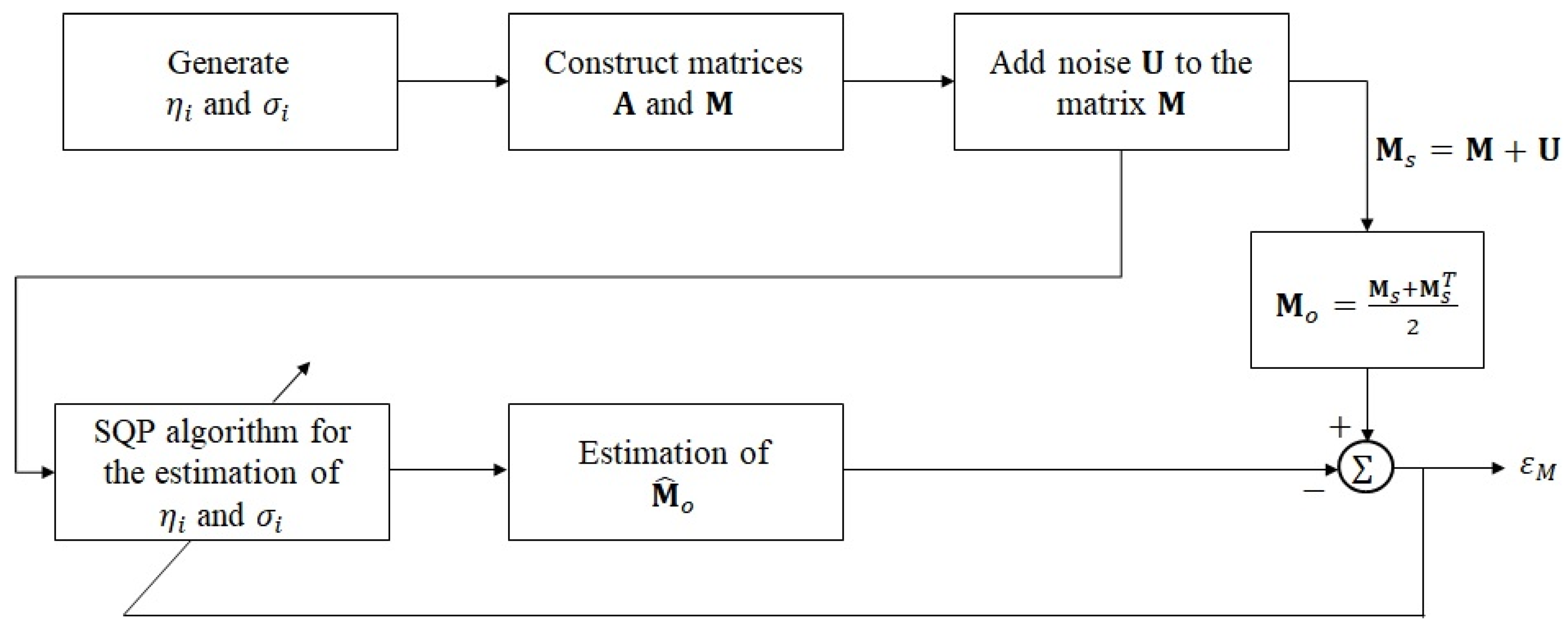
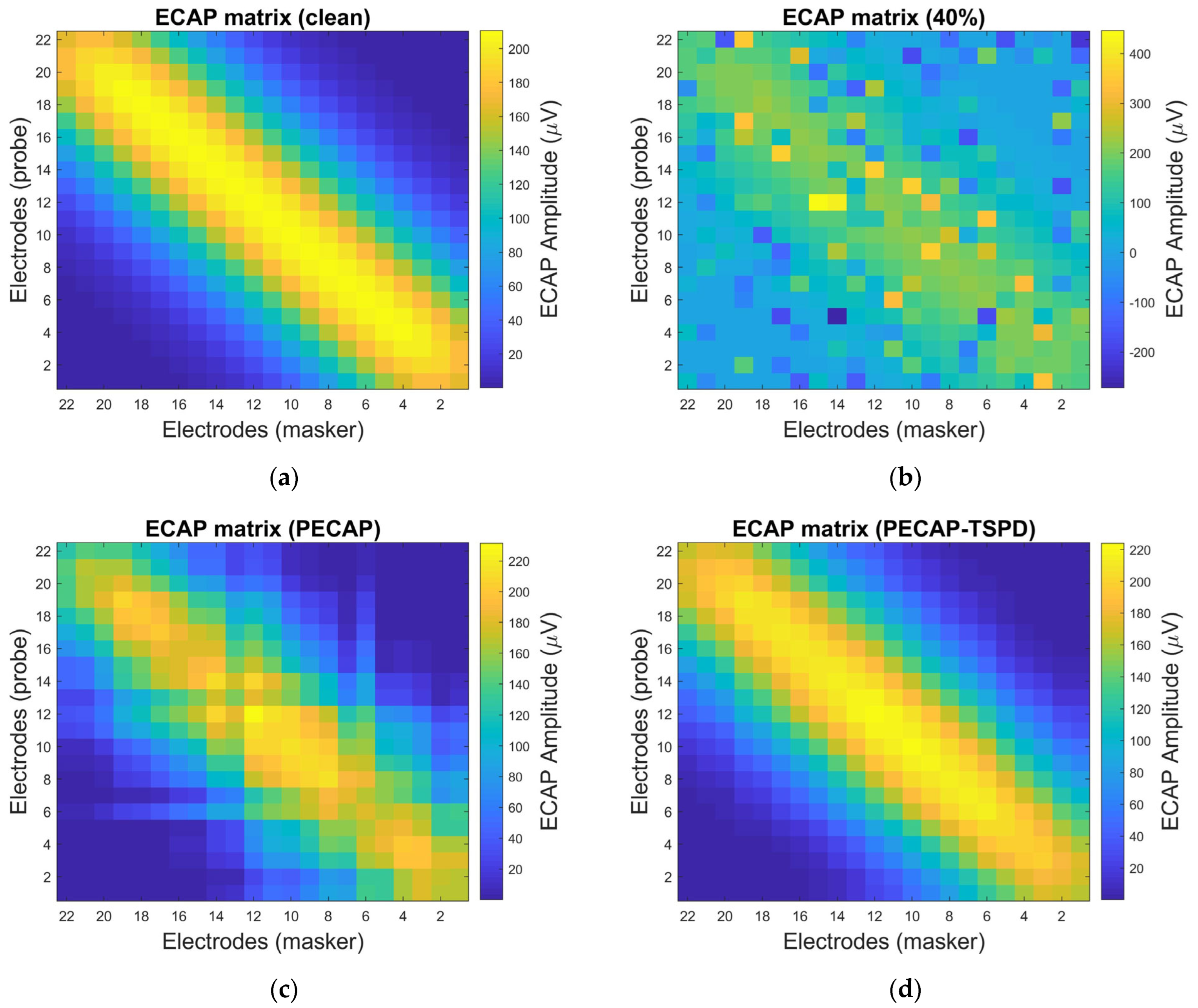
4. Settings and Results
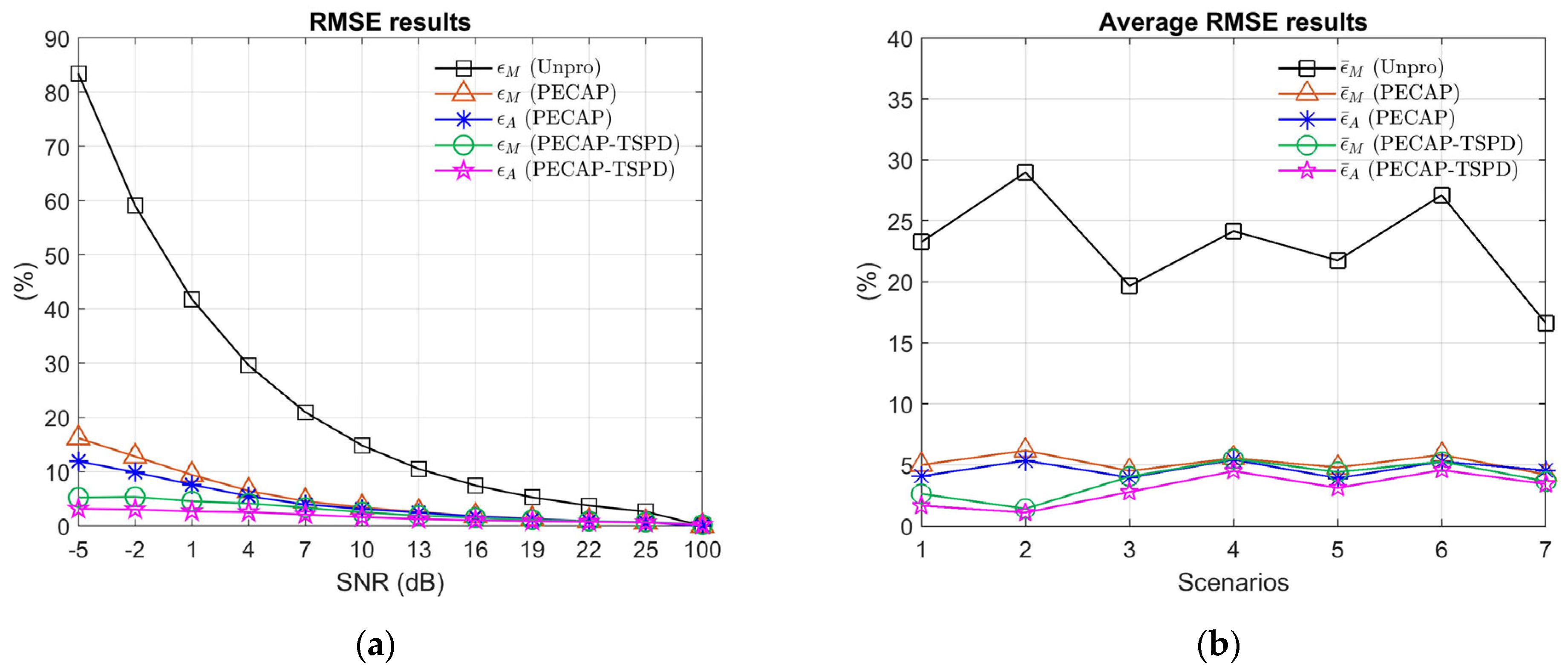
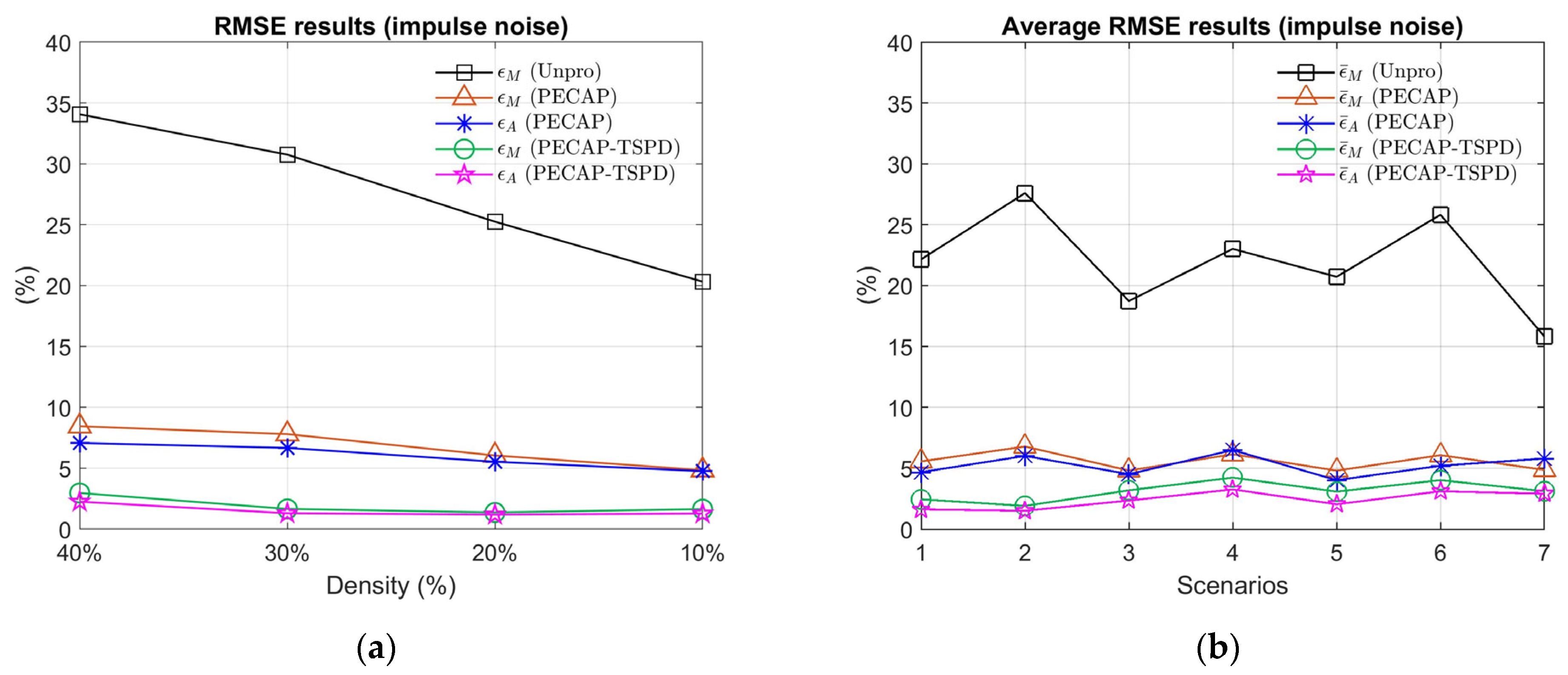
4.1. Simulation Arrangement and Results
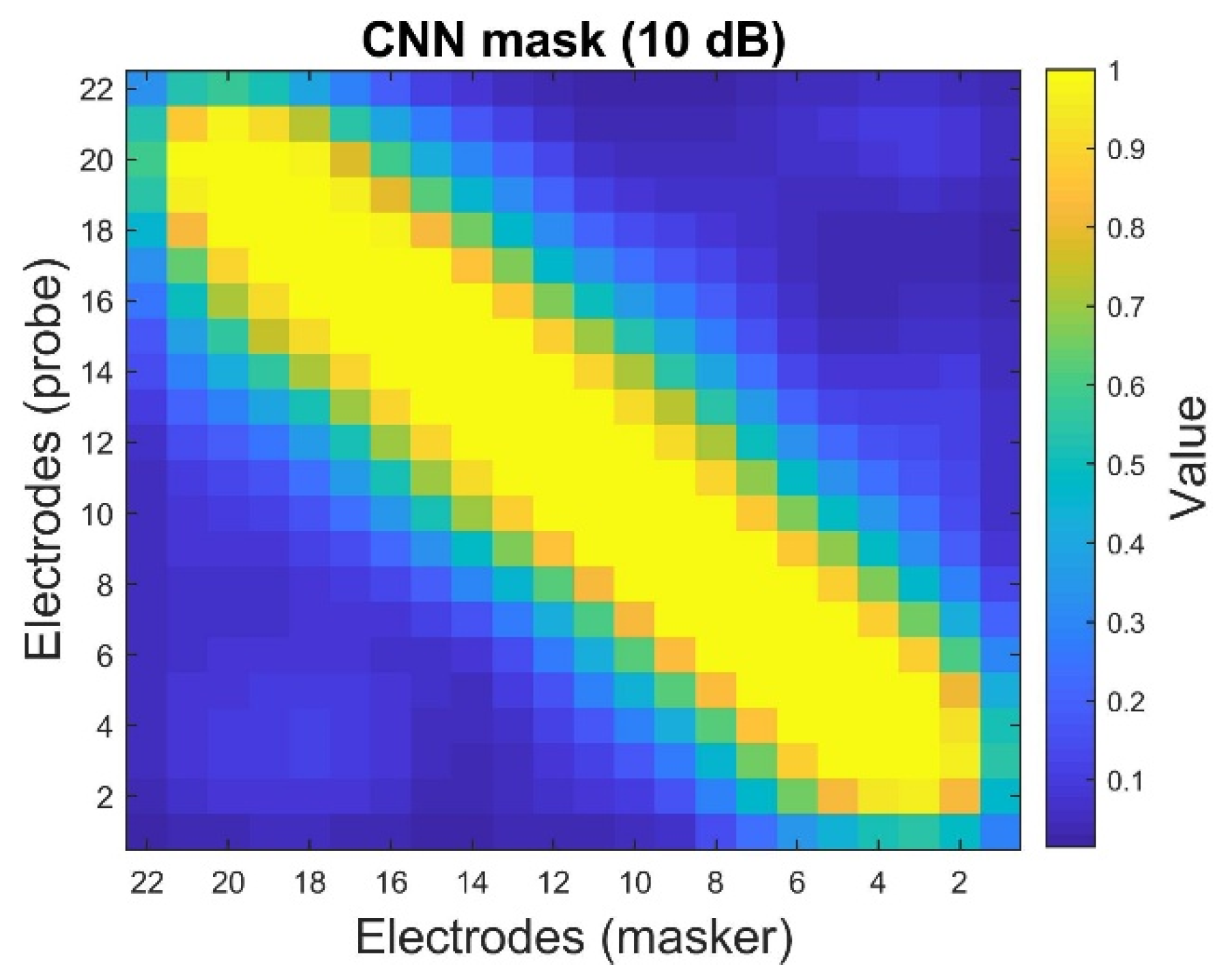
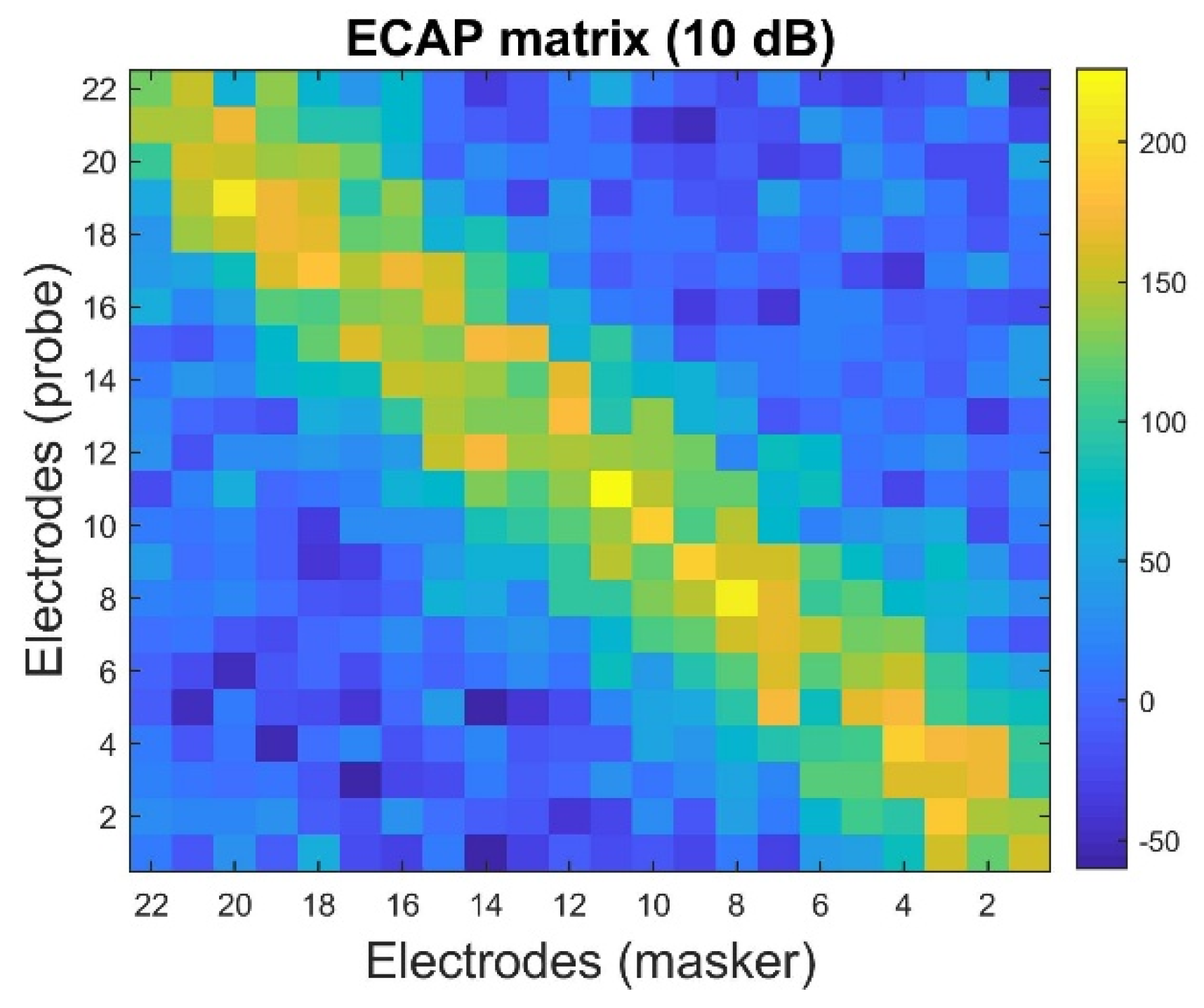
4.2. CNN-Based Denoising Mask Estimation
4.3. LSA Wiener Filtering Improvements After I-Median Filtering
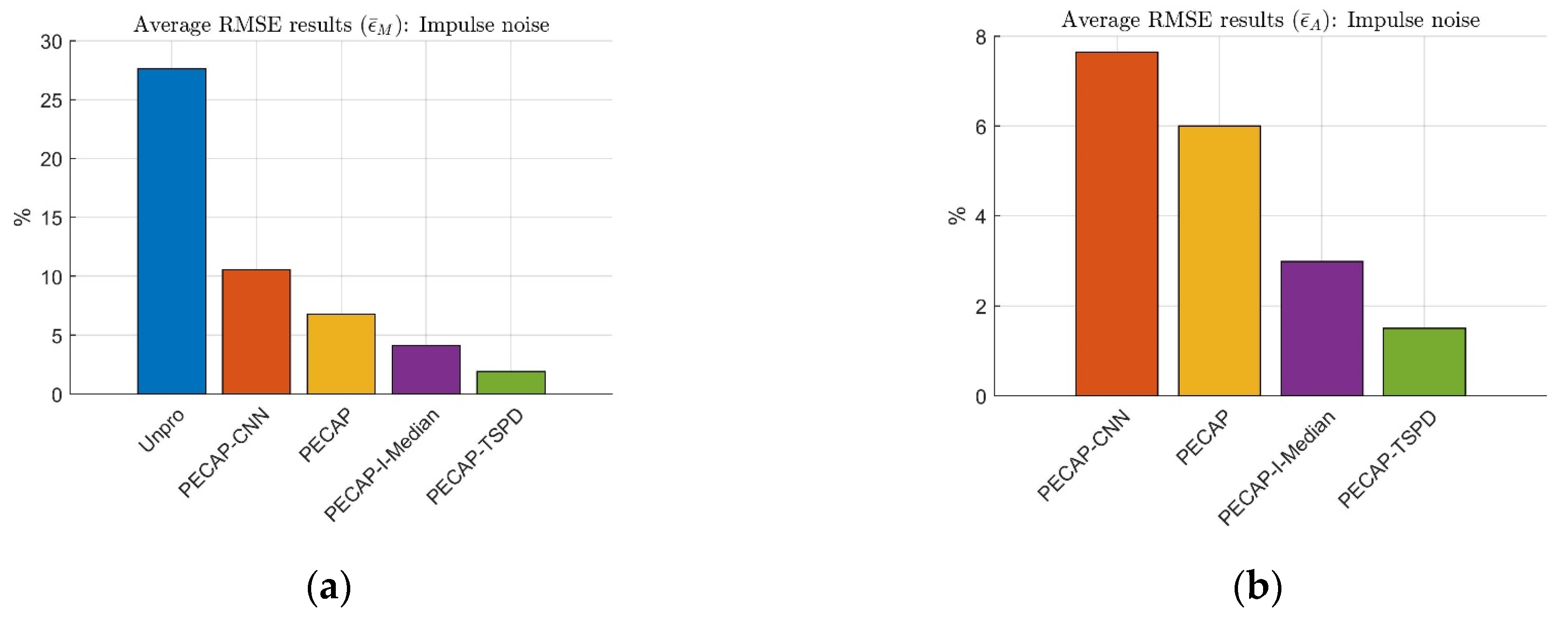
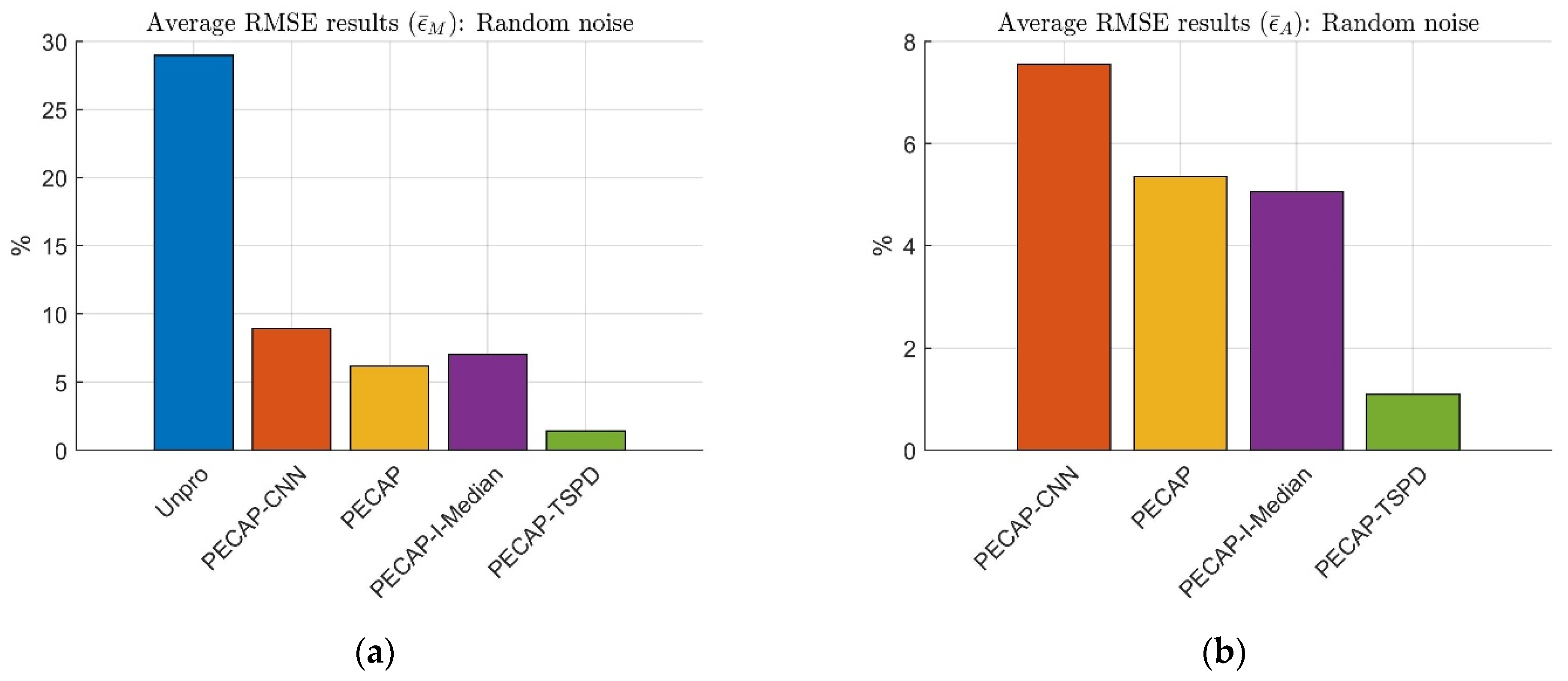
4.4. Experimental Results
5. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ECAP | Electrically evoked compound action potential |
| PECAP | Panoramic ECAP |
| CI | Cochlear implant |
| SNR | Signal-to-noise ratio |
| TSPD | Two-stage preprocessing denoising algorithm |
| LSA | Log-spectral amplitude |
| RMSE | Root mean square error |
| Unpro | Unprocessed data |
| I-Median | Improved median filtering |
| CNN | Convolutional neural network |
| TDCC | Two-dimensional correlation coefficient |
| SSIM | Structural similarity index |
References
- Liebscher, T.; Hornung, J.; Hoppe, U. Electrically evoked compound action potentials in cochlear implant users with preoperative residual hearing. Front. Hum. Neurosci. 2023, 17, 1125747. [Google Scholar] [CrossRef] [PubMed]
- He, S.; Teagle, H.F.B.; Bunchman, C.A. The electrically evoked compound action potential: From laboratory to clinic. Front. Neurosci. 2017, 11, 339. [Google Scholar] [CrossRef] [PubMed]
- Hughes, M.L. Fundamentals of Clinical ECAP Measures in Cochlear Implants: Part 1: Use of the ECAP in Speech Processor Programming (2nd ed.). Available online: https://www.audiologyonline.com/articles/fundamentals-clinical-ecap-measures-in-846 (accessed on 13 February 2025).
- DeVries, L.; Scheperle, R.; Bierer, J.A. Assessing the electrode-neuron interface with the electrically evoked compound action potential, electrode position, and behavioral thresholds. J. Assoc. Res. Otolaryngol. 2016, 22, 237–252. [Google Scholar] [CrossRef]
- Choi, C.T.M.; Wu, D.L. Electrically evoked compound action potential studies based on finite element and neuron models. IEEE Trans. Magn. 2022, 58, 7501404. [Google Scholar] [CrossRef]
- Garcia, C. The Panoramic ECAP Method: Estimating Patient-Specific Patterns of Current Spread and Neural Health in Cochlear-Implant Users. Ph.D. Dissertation, University of Cambridge, Cambridge, UK, 2022. [Google Scholar]
- Dong, Y.; Briaire, J.J.; Stronks, H.C.; Frijns, H.M. Speech perception performance in cochlear implant recipients correlates to the number and synchrony of excited auditory nerve fibers derived from electrically evoked compound action potentials. Ear Hear. 2023, 44, 276–286. [Google Scholar] [CrossRef]
- Takanen, M.; Strahl, S.; Schwarz, K. Insights into electrophysiological metrics of cochlear health in cochlear implant users using a computational model. J. Assoc. Res. Otolaryngol. 2024, 25, 63–78. [Google Scholar] [CrossRef] [PubMed]
- Takanen, M.; Seeber, B.U. A phenomenological model reproducing temporal response characteristics of an electrically stimulated auditory nerve fiber. Trends Hear. 2022, 26, 23312165221117079. [Google Scholar] [CrossRef]
- Garcia, C.; Deeks, J.M.; Goehring, T.; Borsetto, D.; Bance, M.; Carlyon, R.P. SpeedCAP: An efficient method for estimating neural activation patterns using electrically evoked compound action-potentials in cochlear implant users. Ear Hear. 2023, 44, 627–640. [Google Scholar] [CrossRef]
- Cosentino, S.; Gaudrain, E.; Deeks, J.M.; Carlyon, R.P. Multistage nonlinear optimization to recover neural activation patterns from evoked compound action potentials of cochlear implant users. IEEE Trans. Biomed. Eng. 2015, 63, 833–840. [Google Scholar] [CrossRef]
- Garcia, C.; Goehring, T.; Cosentino, S.; Turner, R.E.; Deeks, J.M.; Brochier, T.; Rughooputh, T.; Bance, M.; Carlyon, R.P. The panoramic ECAP method: Estimating patient-specific patterns of current spread and neural health in cochlear implant users. J. Assoc. Res. Otolaryngol. 2021, 22, 567–589. [Google Scholar] [CrossRef]
- Isnanto, R.R.; Windarto, Y.E.; Mangkuratmaja, M.V. Assessment on image quality changes as a results of implementing median filtering, Wiener filtering, histogram equalization, and hybrid methods on noisy images. In Proceedings of the International Conference on Information Technology, Computer, and Electrical Engineering, Semarang, Indonesia, 24–25 September 2020. [Google Scholar]
- Gupta, G. Algorithm for image processing using improved median filter and comparison of mean, median and improved median filter. Int. J. Soft Comput. Eng. 2011, 1, 304–311. [Google Scholar]
- Sun, M. Comparison of processing results of median filter and mean filter on Gaussian noise. Appl. Comput. Eng. 2023, 5, 779–785. [Google Scholar] [CrossRef]
- Hou, Y.; Li, Q.; Zhang, C.; Lu, G.; Ye, Z.; Chen, Y.; Wang, L.; Cao, D. The state-of-the-art review on applications of intrusive sensing, image processing techniques, and machine learning methods in pavement monitoring and analysis. Engineering 2021, 7, 845–856. [Google Scholar] [CrossRef]
- Zhu, Y.; Huang, C. An improved median filtering algorithm for image noise reduction. Phys. Procedia 2021, 25, 609–616. [Google Scholar] [CrossRef]
- Jiang, D. A study on Adaptive Filtering for Noise and Echo Cancellation. Master’s Thesis, University of Windsor, Windsor, ON, Canada, 2005. [Google Scholar]
- Yazdanpanah, H.; Diniz, P.S.R. Recursive least-squares algorithms for sparse system modeling. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, New Orleans, LA, USA, 5–9 March 2017. [Google Scholar]
- Creighton, J.; Doraiswami, R. Real time implementation of an adaptive filter for speech enhancement. In Proceedings of the Canadian Conference on Electrical and Computer Engineering, Niagara Falls, ON, Canada, 2–5 May 2004. [Google Scholar]
- Wang, P.; Kam, P.-Y. An automatic step-size adjustment algorithm for LMS adaptive filters, and an application to channel estimation. Phys. Commun. 2012, 5, 280–286. [Google Scholar] [CrossRef]
- Loizou, P.C. Speech Enhancement: Theory and Practice, 1st ed.; CRC Press: New York, NY, USA, 2007; pp. 143–208. [Google Scholar]
- Benesty, J.; Chen, J.; Huang, Y. Microphone Array Signal Processing; Springer: Berlin/Heidelberg, Germany, 2008; pp. 8–15. [Google Scholar]
- Ephraim, Y.; Malah, D. Speech enhancement using a minimum mean-square error log-spectral amplitude estimator. IEEE Trans. Acoust. Speech Signal Process. 1985, 33, 443–445. [Google Scholar] [CrossRef]
- Borgström, B.J.; Alwan, A. Log-spectral amplitude estimation with Generalized Gamma distributions for speech enhancement. In Proceedings of the IEEE International Conference on Acoustics, Speech and Signal Processing, Prague, Czech Republic, 22–27 May 2011. [Google Scholar]
- Hirszhorn, A.; Dov, D.; Talmon, R.; Cohen, I. Transient interference suppression in speech signals based on the OM-LSA algorithm. In Proceedings of the International Workshop on Acoustic Echo and Noise Control, Aachen, Germany, 4–6 September 2012. [Google Scholar]
- Hsu, Y.; Bai, M.R. Learning-based robust speaker counting and separation with the aid of spatial coherence. EURASIP J. Audio Speech Music. Process. 2023, 2023, 36. [Google Scholar] [CrossRef]
- Hsu, Y.; Lee, Y.; Bai, M.R. Array configuration-agnostic personalized speech enhancement using long-short-term spatial coherence. J. Acoust. Soc. Am. 2023, 154, 2499–2511. [Google Scholar] [CrossRef] [PubMed]
- Richard, G.; Smaragdis, P.; Gannot, S.; Naylor, P.A.; Makino, S.; Kellermann, W.; Sugiyama, A. Audio signal processing in the 21st century: The important outcomes of the past 25 years. IEEE Signal Process. Mag. 2023, 40, 12–26. [Google Scholar] [CrossRef]
- Gannot, S.; Tan, Z.-H.; Haardt, M.; Chen, N.F.; Wai, H.-T.; Tashev, I.; Kellermann, W.; Dauwels, J. Data science education: The signal processing perspective. IEEE Signal Process. Mag. 2023, 40, 89–93. [Google Scholar] [CrossRef]
- Tan, K.; Wang, D. A convolutional recurrent neural network for real-time speech enhancement. In Proceedings of the Interspeech, Hyderabad, India, 2–6 September 2018. [Google Scholar]
- Bianco, M.J.; Gerstoft, P.; Traer, J.; Ozanich, E.; Roch, M.A.; Gannot, S.; Deledalle, C.-A. Machine learning in acoustics: Theory and applications. J. Acoust. Soc. Am. 2019, 146, 3590–3628. [Google Scholar] [CrossRef] [PubMed]
- Lewis, J.P. Fast Template Matching. In Proceedings of the Vision Interface 95, Canadian Image Processing and Pattern Recognition Society, Quebec City, QC, Canada, 15–19 May 1995. [Google Scholar]
- Wang, Z.; Bovik, A.C.; Sheikh, H.R.; Simoncelli, E.P. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef] [PubMed]
- Brunet, D.; Vass, J.; Vrscay, E.R.; Wang, Z. On the mathematical properties of the structural similarity index. IEEE Trans. Image Process. 2012, 21, 1488–1499. [Google Scholar] [CrossRef] [PubMed]
- Zhang, K.; Zuo, W.; Chen, Y.; Meng, D.; Zhang, L. Beyond a Gaussian denoiser: Residual learning of deep CNN for image denoising. IEEE Trans. Image Process. 2017, 26, 3142–3155. [Google Scholar] [CrossRef]
- Fang, M.Z. Some results on the Hadamard product of tensors. Bull. Iran. Math. Soc. 2019, 45, 1193–1219. [Google Scholar]
- Feng, X.; Huang, Z.; He, J.; Xue, D. Efficient direct position determination using Frobenius norm approximation. Electron. Lett. 2022, 58, 402–404. [Google Scholar] [CrossRef]






| Step 1. Initialization of for each frequency bin For each and : Step 2. Estimation of If , then , else Step 3. Estimation of using Equation (16) If , then Equation (16) can be rewritten as Step 4. check the VAD criterion If , then using Equation (20) for updating Step 5. Calculation of using Equation (15) Step 6. Calculation of using Equation (21) End for |
| Scenario 1: , , , where in this study. Scenario 2: , , . Scenario 3: , . , , , . , . Scenario 4: , . , , , . , . Scenario 5: , . , , , . , . Scenario 6: , . , , , . , . Scenario 7: , . , , , , , , |
| SNR = 16 dB | SNR = 19 dB | SNR = 22 dB | SNR = 25 dB | |
|---|---|---|---|---|
| PECAP | 1.1842% | 1.2858% | 0.9113% | 0.6459% |
| PECAP-TSPD | 1.4958% | 1.1209% | 0.8892% | 0.7239% |
| Layer Name | Input Size | Hyperparameters | Output Size |
|---|---|---|---|
| Reshape | |||
| Conv 1 | |||
| Conv 2 | |||
| Conv 3 | |||
| Reshape |
| TDCC | ||
| Clean ECAP matrix | Noisy ECAP matrix | |
| CNN mask | 0.9553 | 0.8888 |
| SSIM | ||
| Clean ECAP matrix | Noisy ECAP matrix | |
| CNN mask | 0.5764 | 0.3691 |
| PECAP-CNN | PECAP | PECAP-I-Median | PECAP-TSPD | |
| Average TDCC | 0.9733 | 0.9855 | 0.9959 | 0.9988 |
| PECAP-CNN | PECAP | PECAP-I-Median | PECAP-TSPD | |
| Average SSIM | 0.8727 | 0.9166 | 0.9678 | 0.9929 |
| PECAP-CNN | PECAP | PECAP-I-Median | PECAP-TSPD | |
| Average TDCC | 0.9620 | 0.9709 | 0.9805 | 0.9993 |
| PECAP-CNN | PECAP | PECAP-I-Median | PECAP-TSPD | |
| Average SSIM | 0.8566 | 0.8744 | 0.8709 | 0.9952 |
| TDCC | 0.9952 | 0.9989 | 0.9331 |
| SSIM | 0.9520 | 0.9920 | 0.5521 |
| PECAP-CNN | PECAP | PECAP-I-Median | PECAP-TSPD | |
| Average TDCC | 0.9799 | 0.9864 | 0.9940 | 0.9988 |
| PECAP-CNN | PECAP | PECAP-I-Median | PECAP-TSPD | |
| Average SSIM | 0.8938 | 0.8828 | 0.9262 | 0.9934 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Kung, F.-J. An Integrated Spatial-Spectral Denoising Framework for Robust Electrically Evoked Compound Action Potential Enhancement and Auditory Parameter Estimation. Sensors 2025, 25, 3523. https://doi.org/10.3390/s25113523
Kung F-J. An Integrated Spatial-Spectral Denoising Framework for Robust Electrically Evoked Compound Action Potential Enhancement and Auditory Parameter Estimation. Sensors. 2025; 25(11):3523. https://doi.org/10.3390/s25113523
Chicago/Turabian StyleKung, Fan-Jie. 2025. "An Integrated Spatial-Spectral Denoising Framework for Robust Electrically Evoked Compound Action Potential Enhancement and Auditory Parameter Estimation" Sensors 25, no. 11: 3523. https://doi.org/10.3390/s25113523
APA StyleKung, F.-J. (2025). An Integrated Spatial-Spectral Denoising Framework for Robust Electrically Evoked Compound Action Potential Enhancement and Auditory Parameter Estimation. Sensors, 25(11), 3523. https://doi.org/10.3390/s25113523







