Research on Quantitative Evaluation of Defects in Ferromagnetic Materials Based on Electromagnetic Non-Destructive Testing
Abstract
:1. Introduction
2. Theoretical Framework
2.1. Electromagnetic Model
2.2. Electromagnetic Induction Model
3. Simulation Analysis
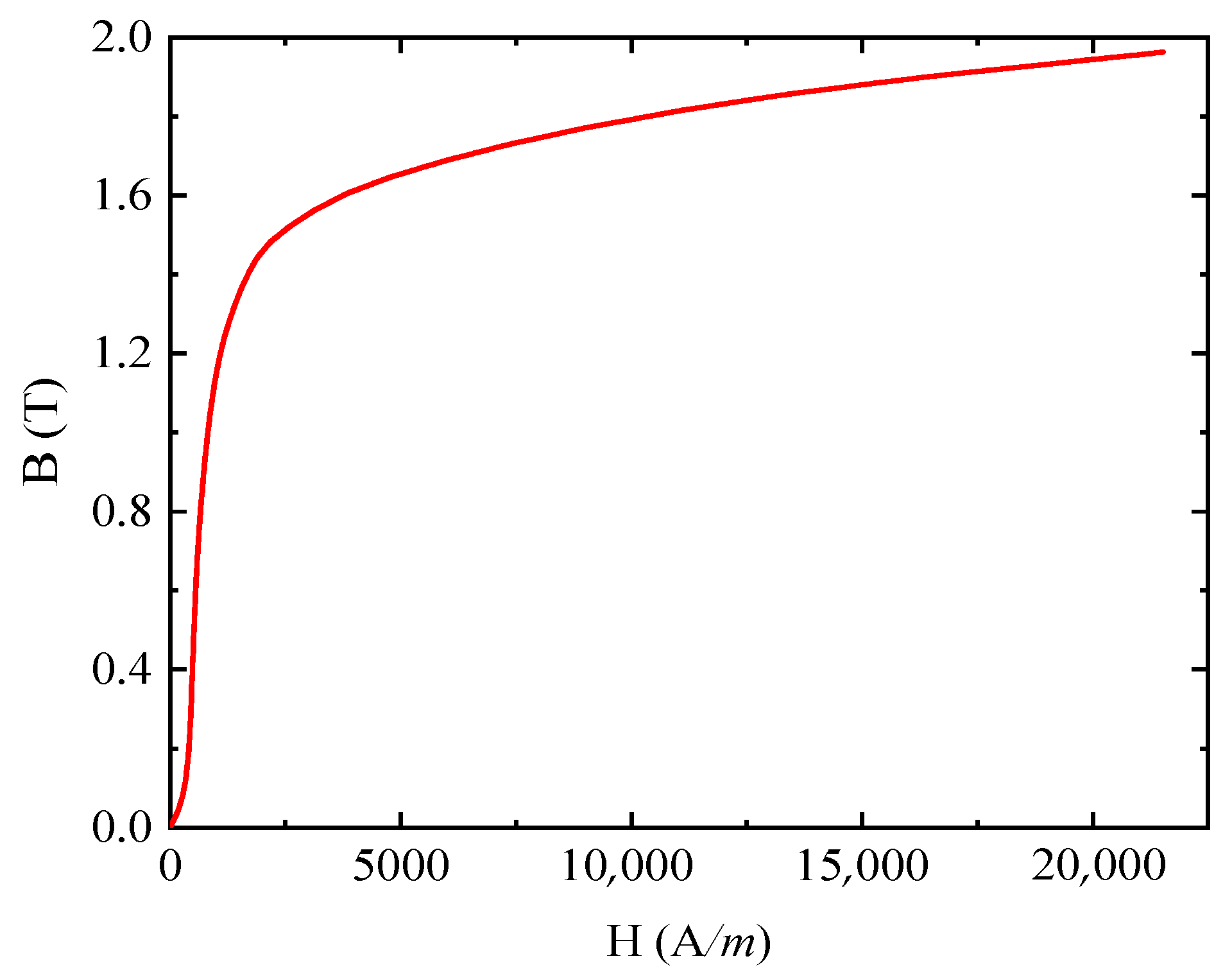
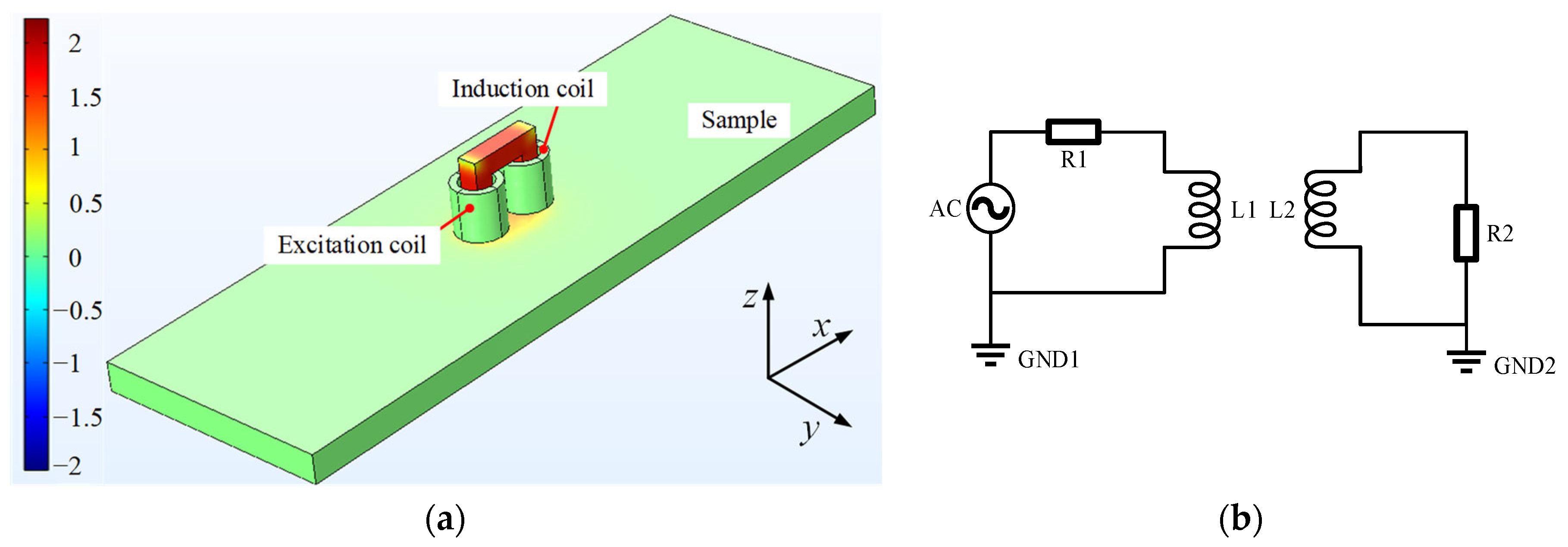
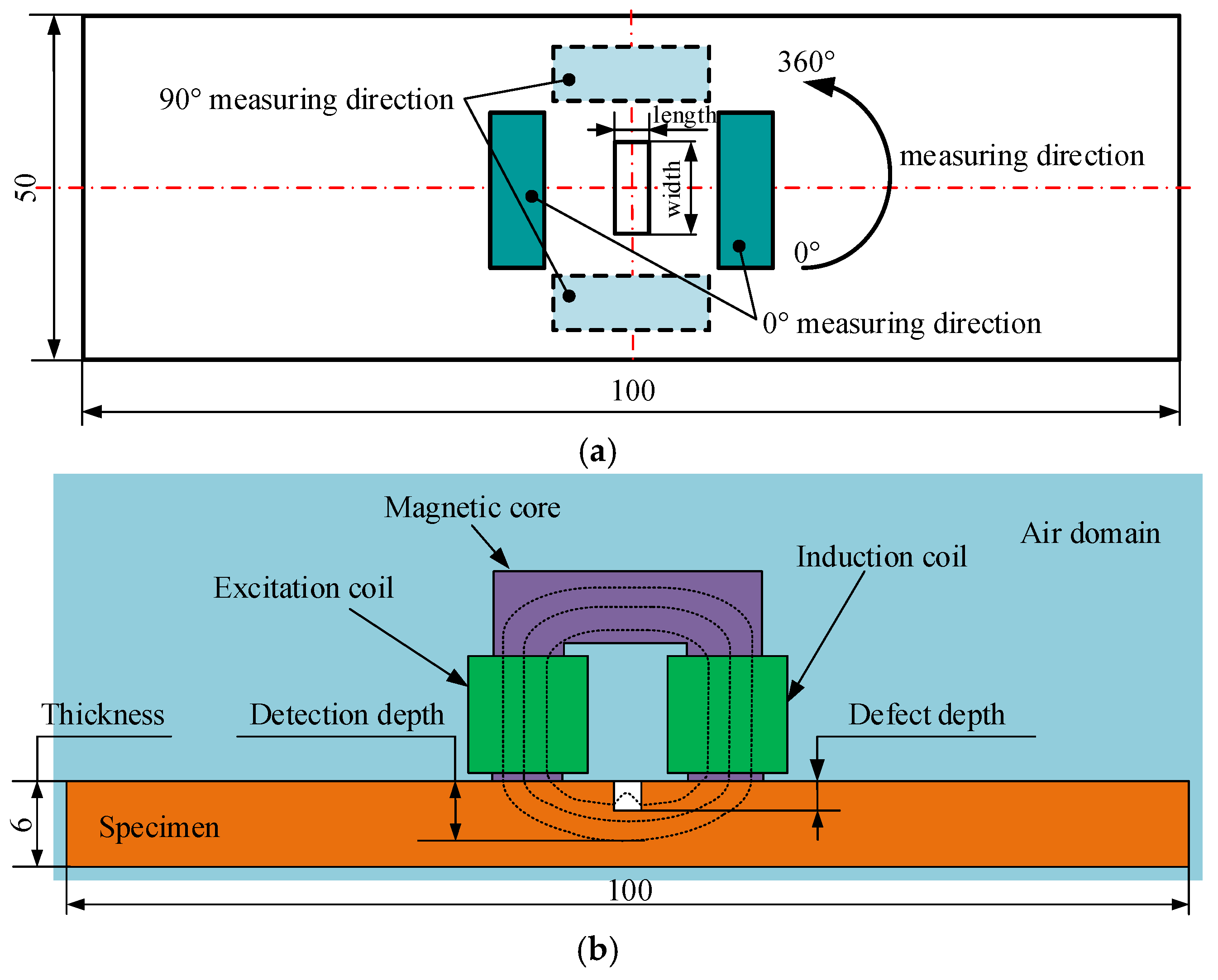
3.1. Simulation Model and Simulation Parameters
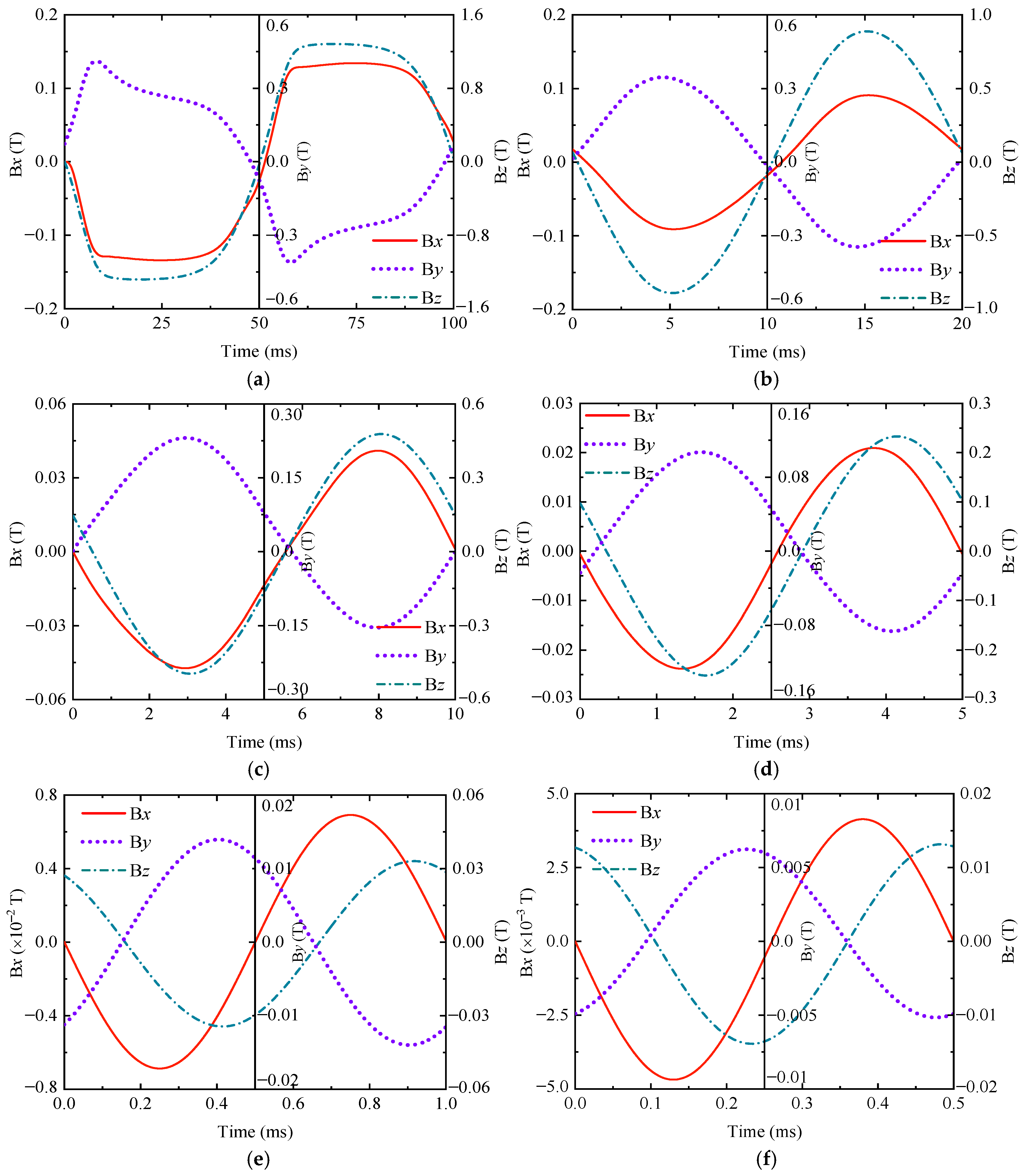
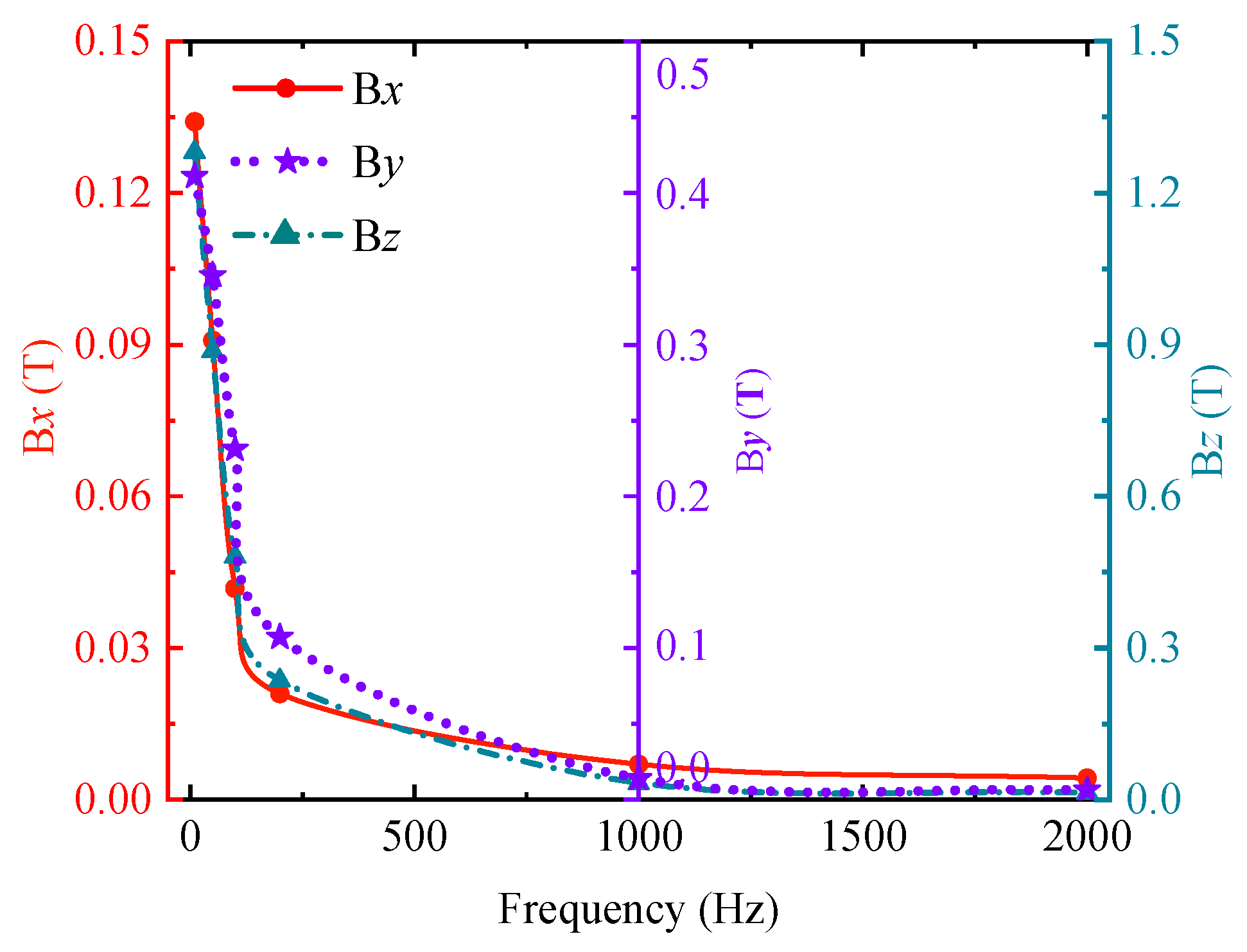
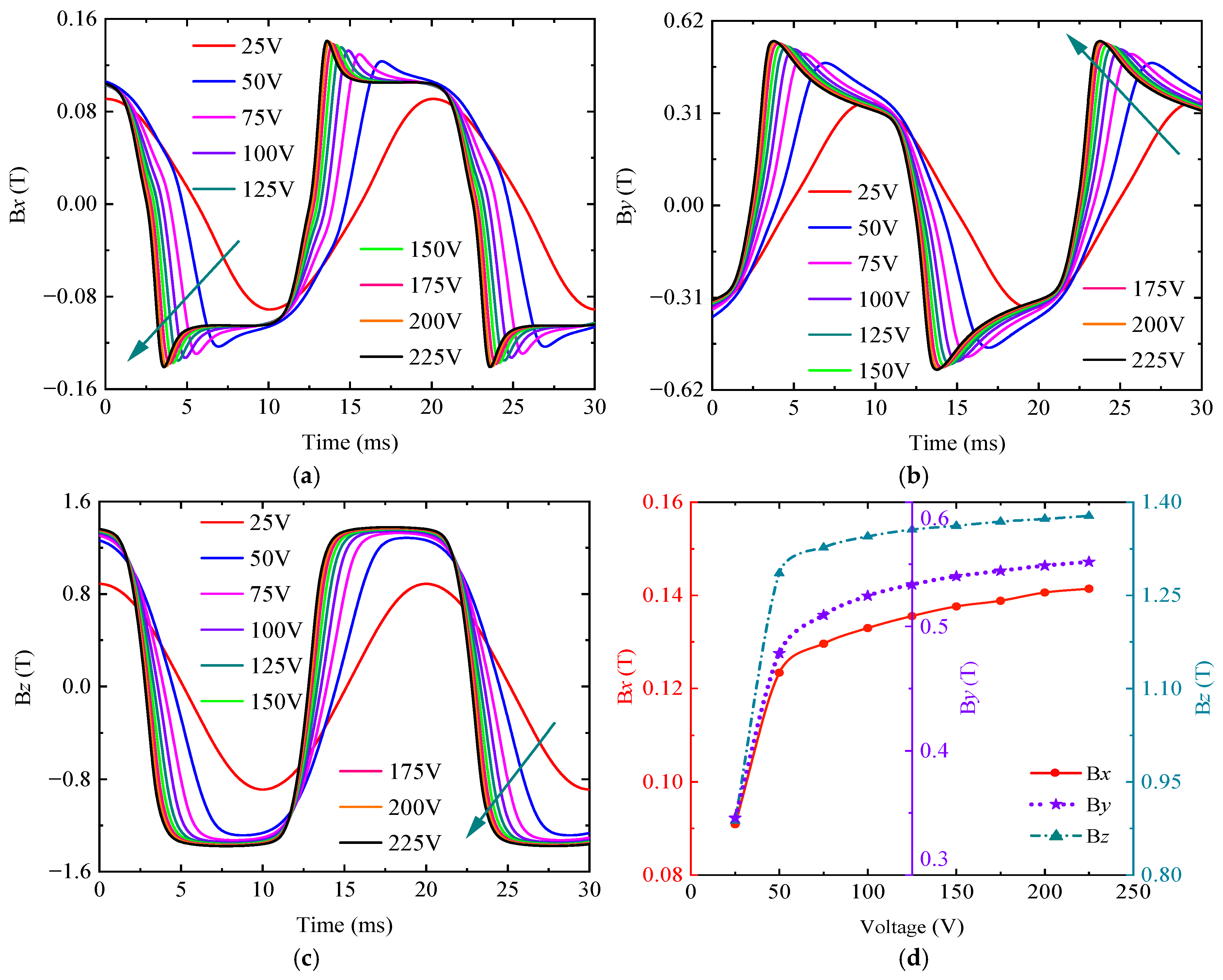
3.2. Determination of Excitation Parameters
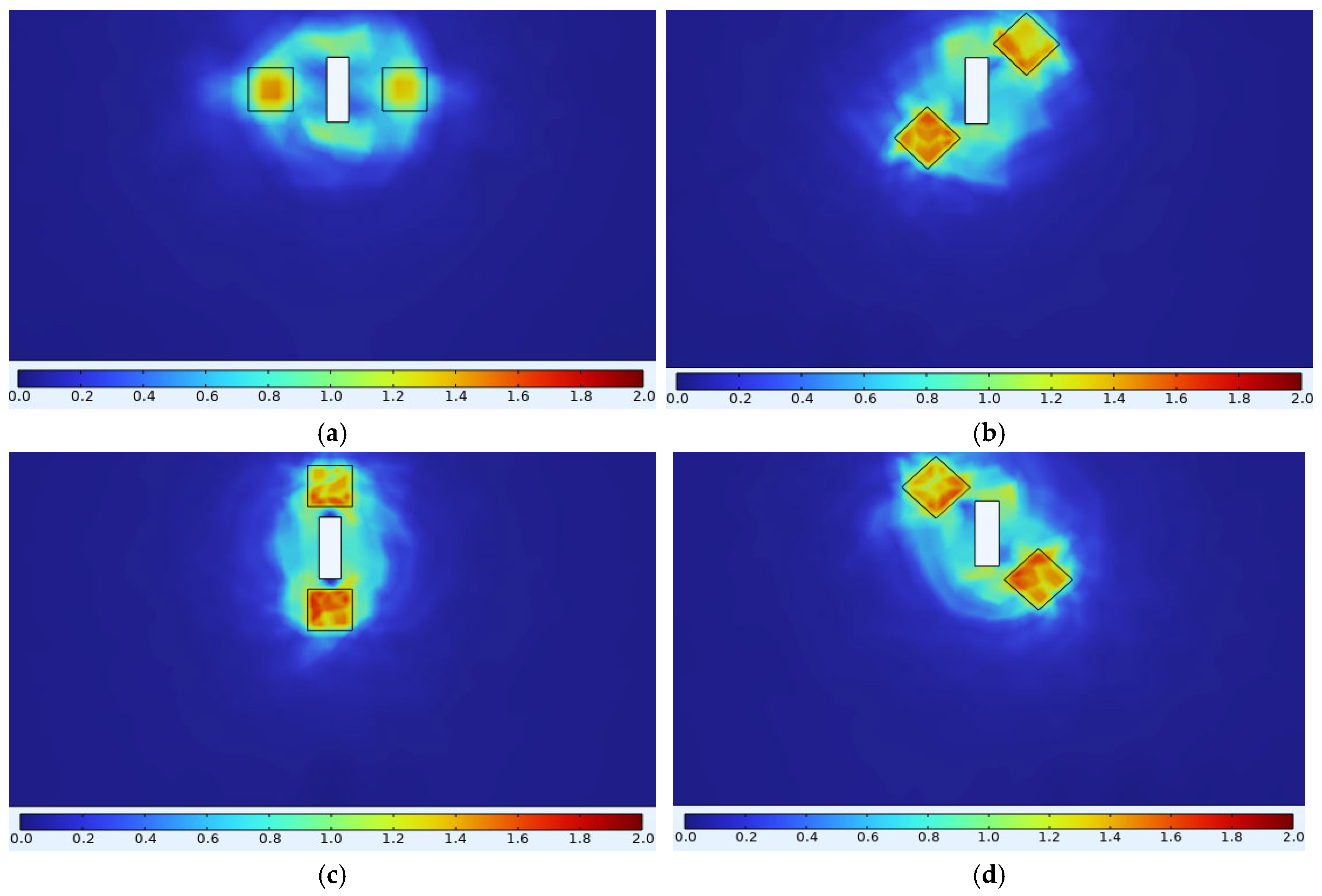
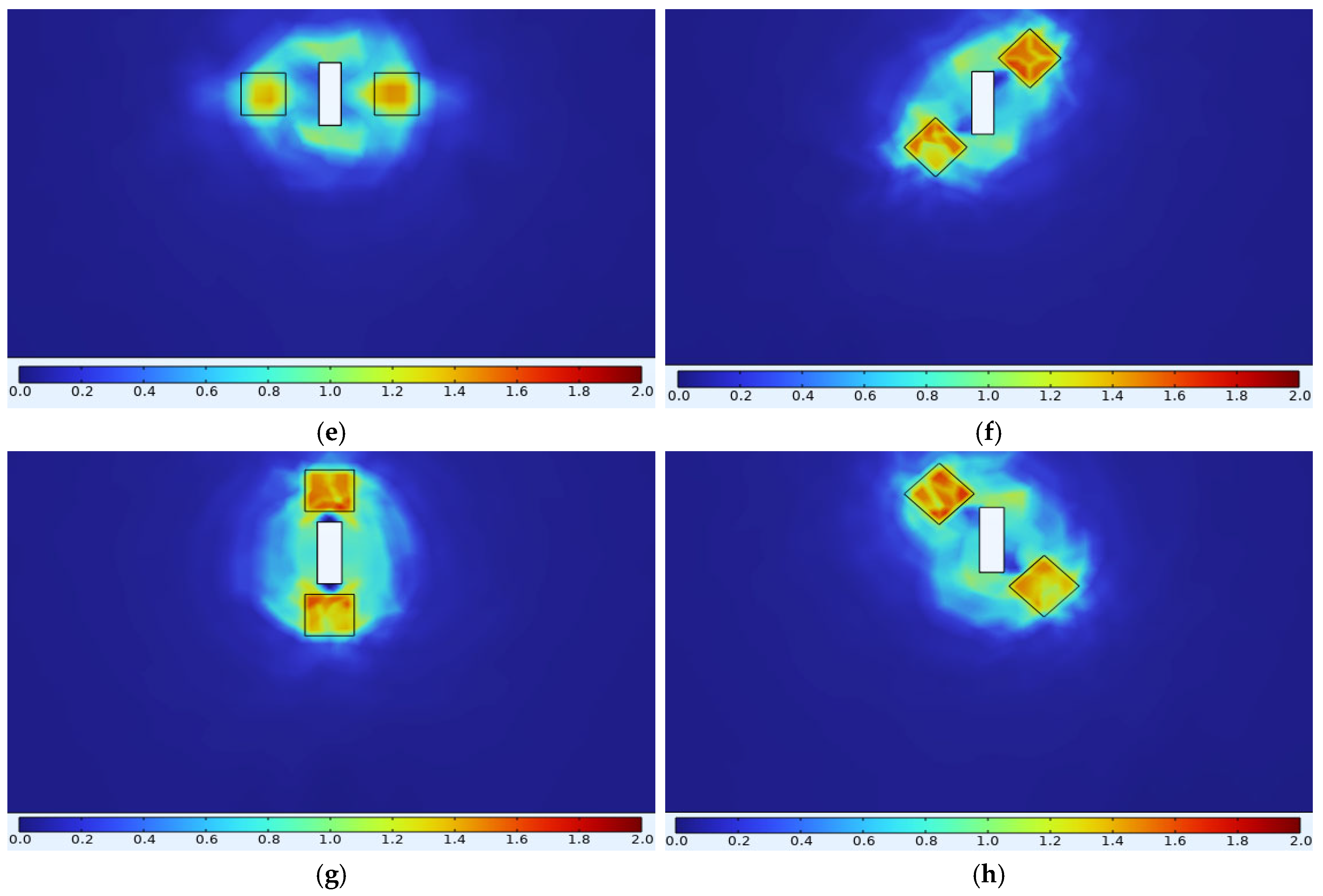
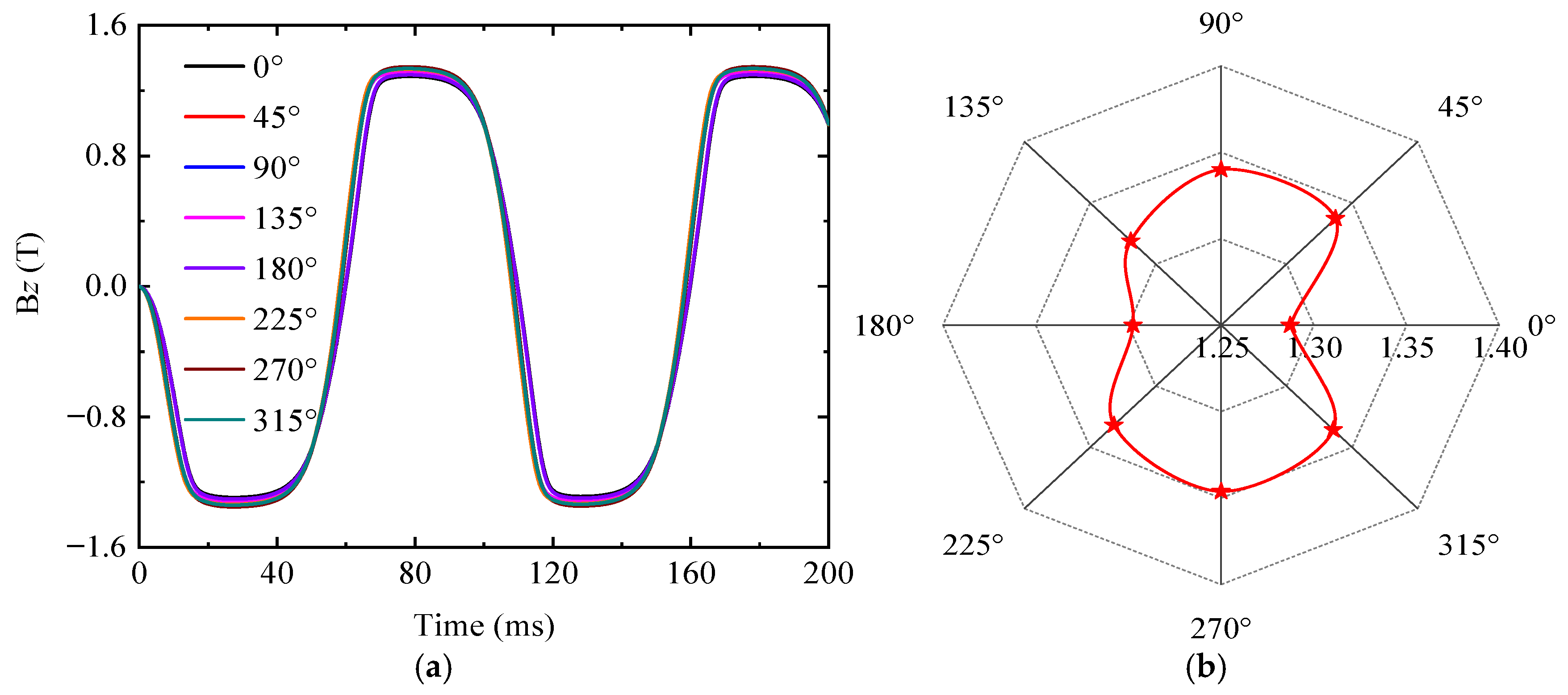
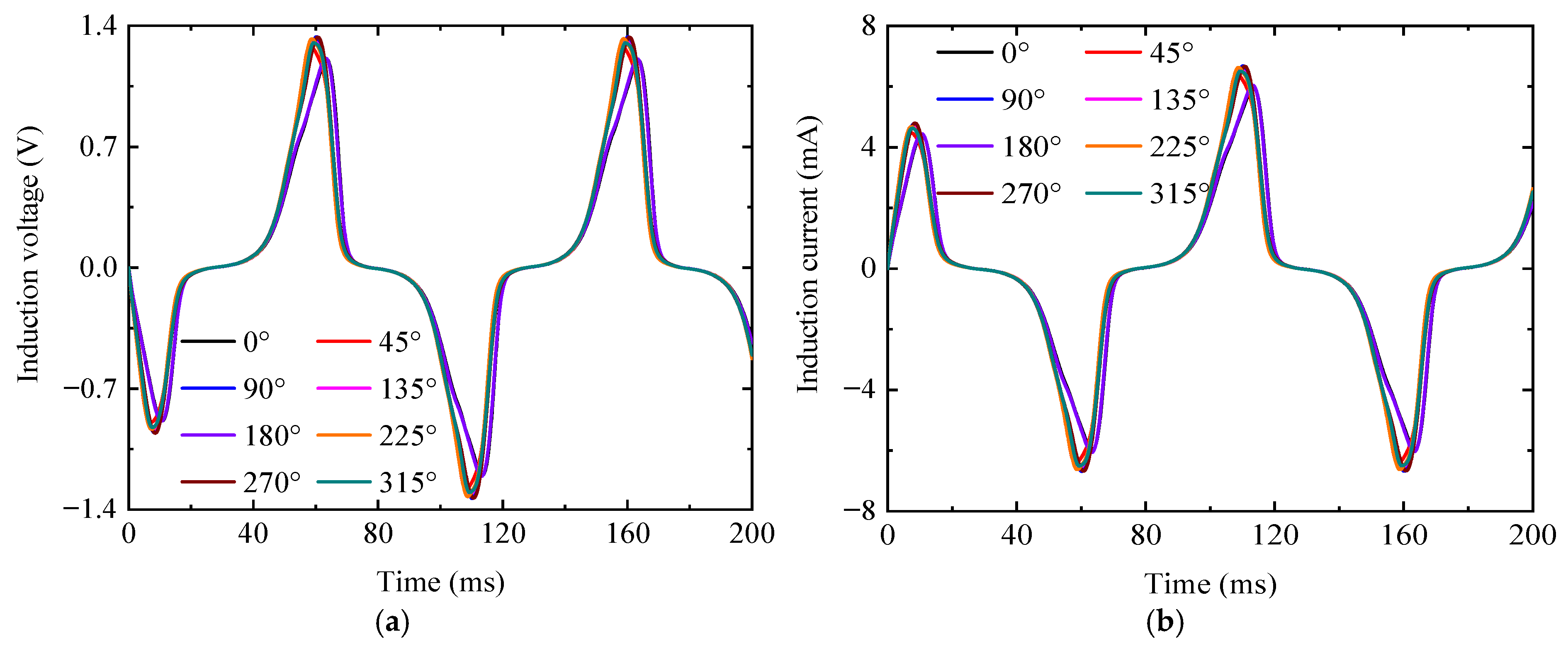
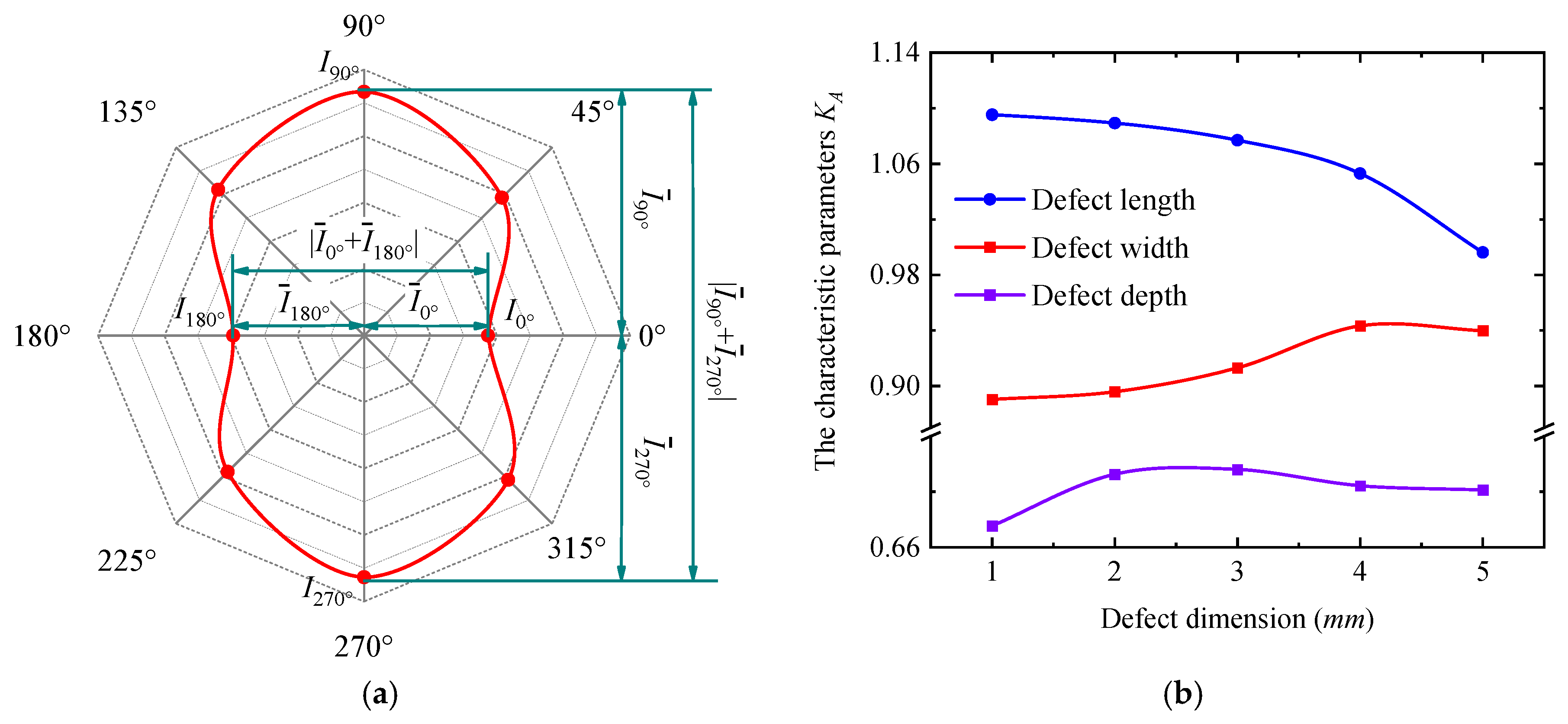
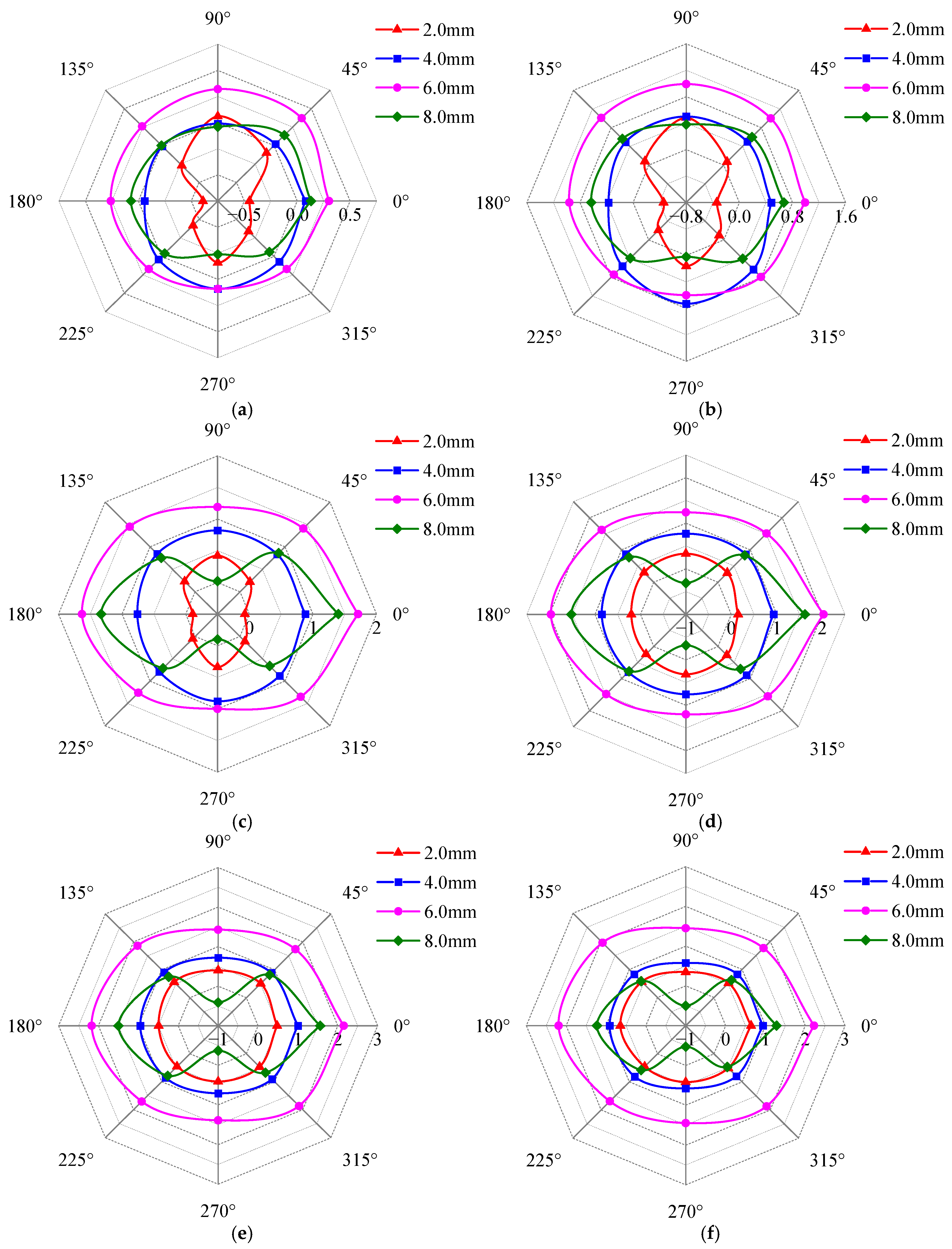
3.3. Variation of Magnetic/Electric Signals with Defects
4. Experimental Results and Discussions
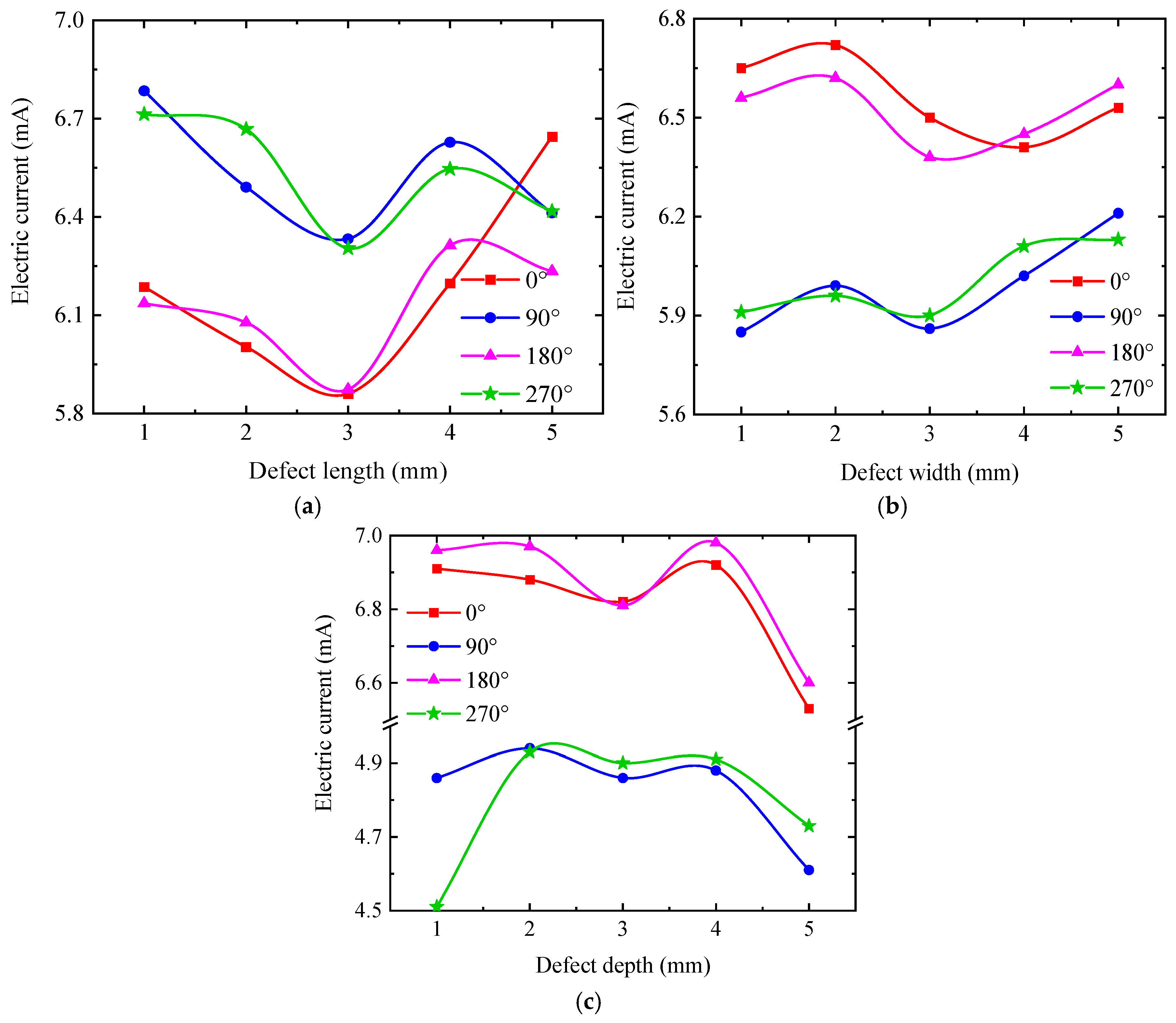
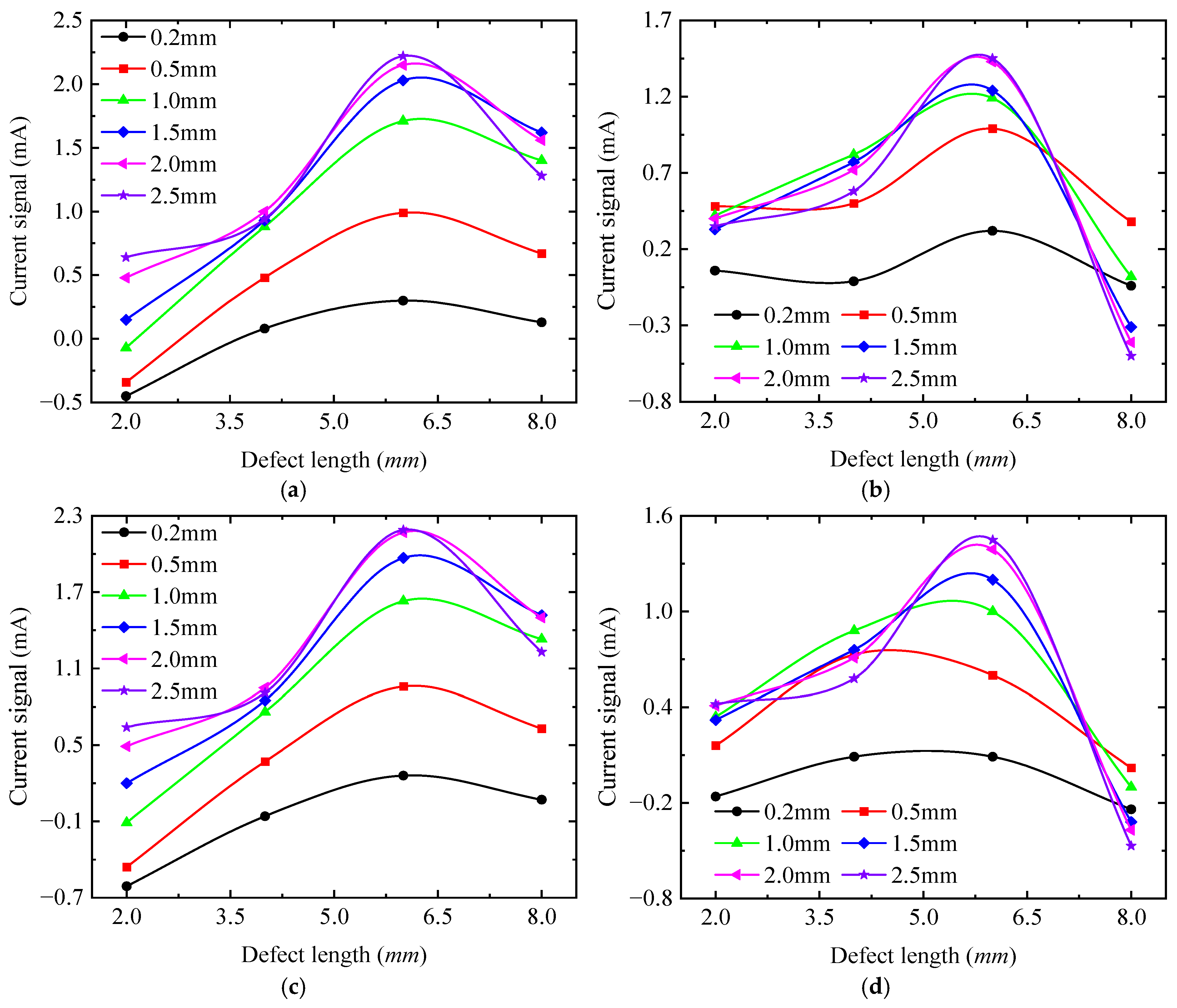
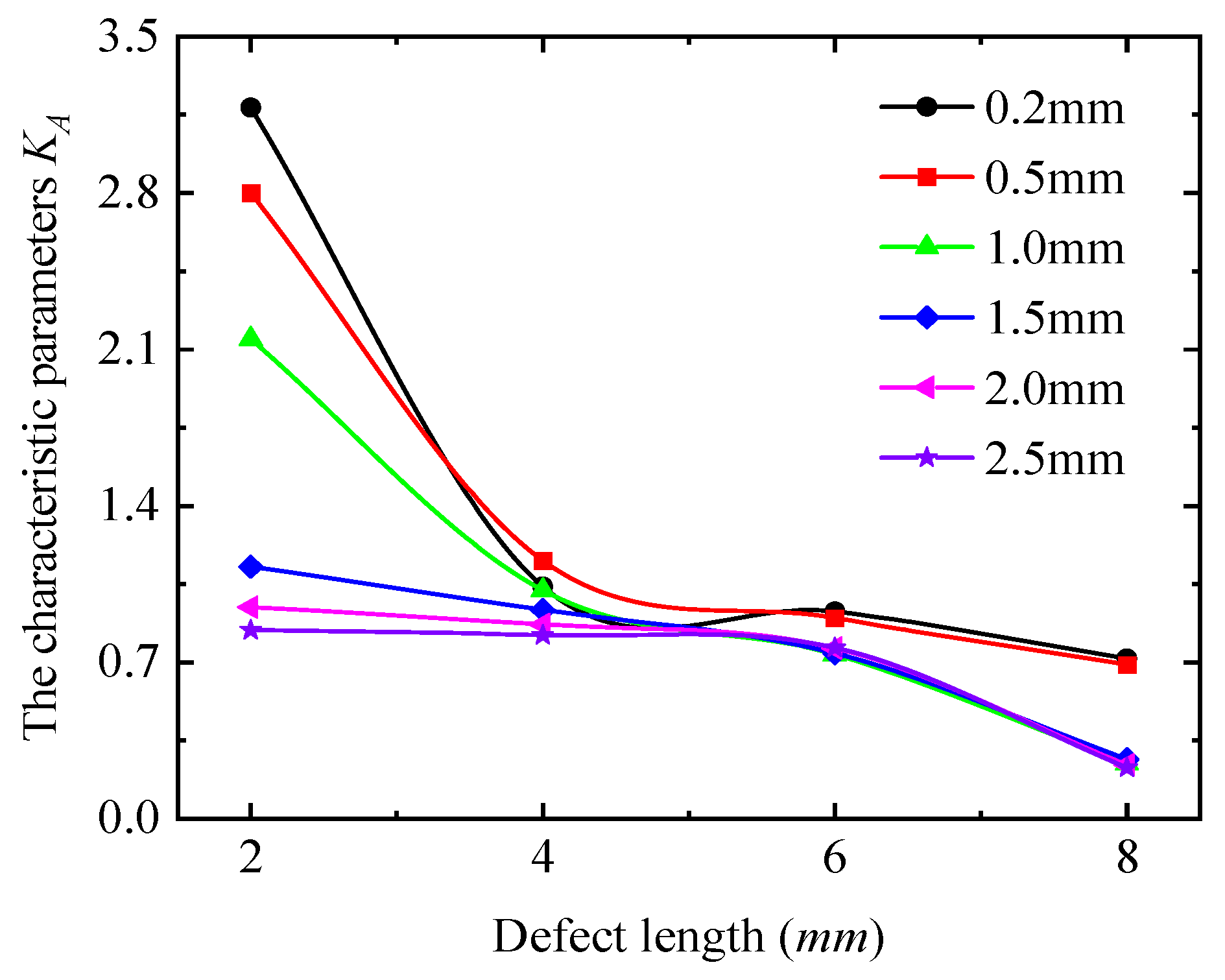
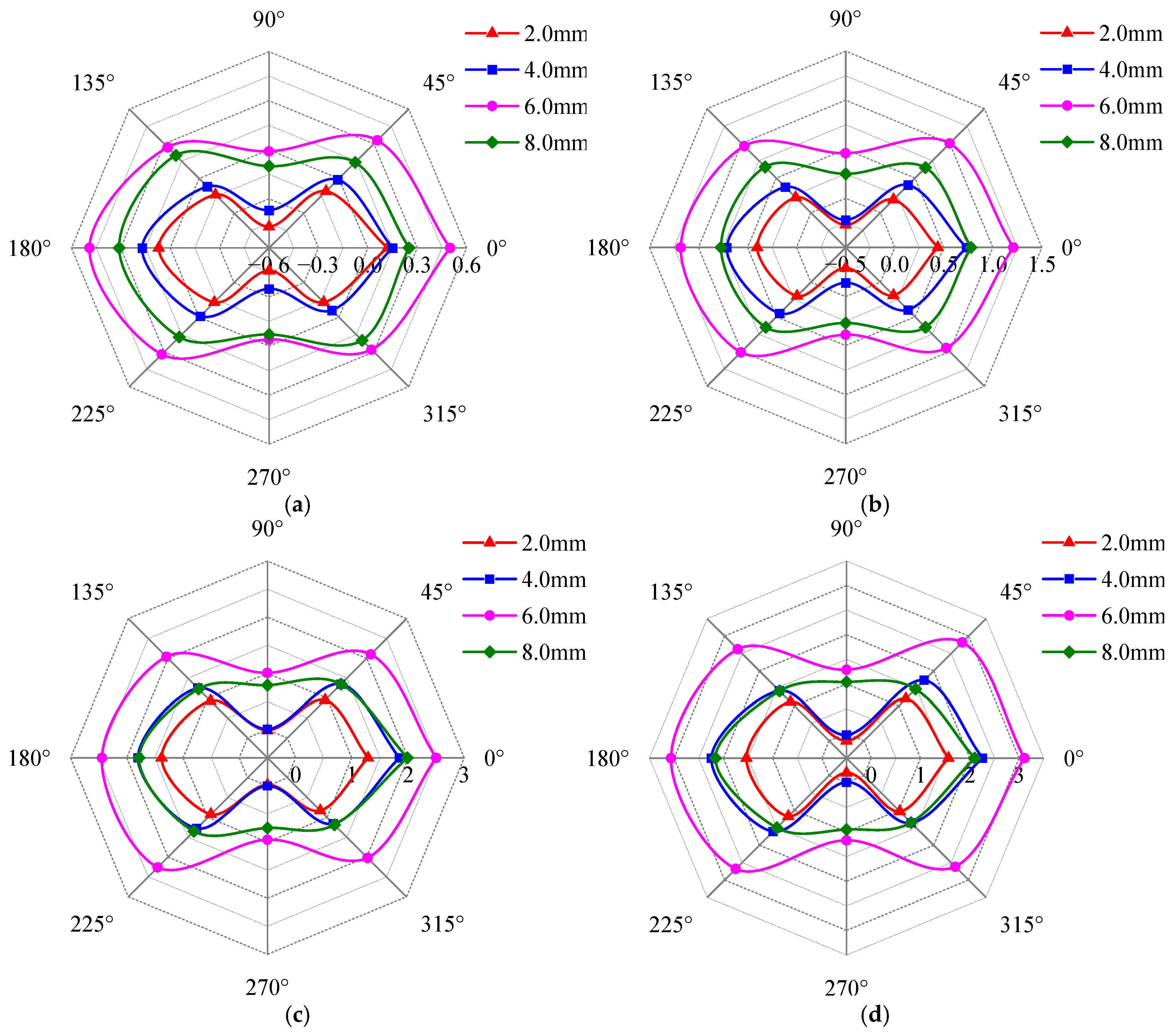
4.1. The Effect of Defect Length on Detection Signal
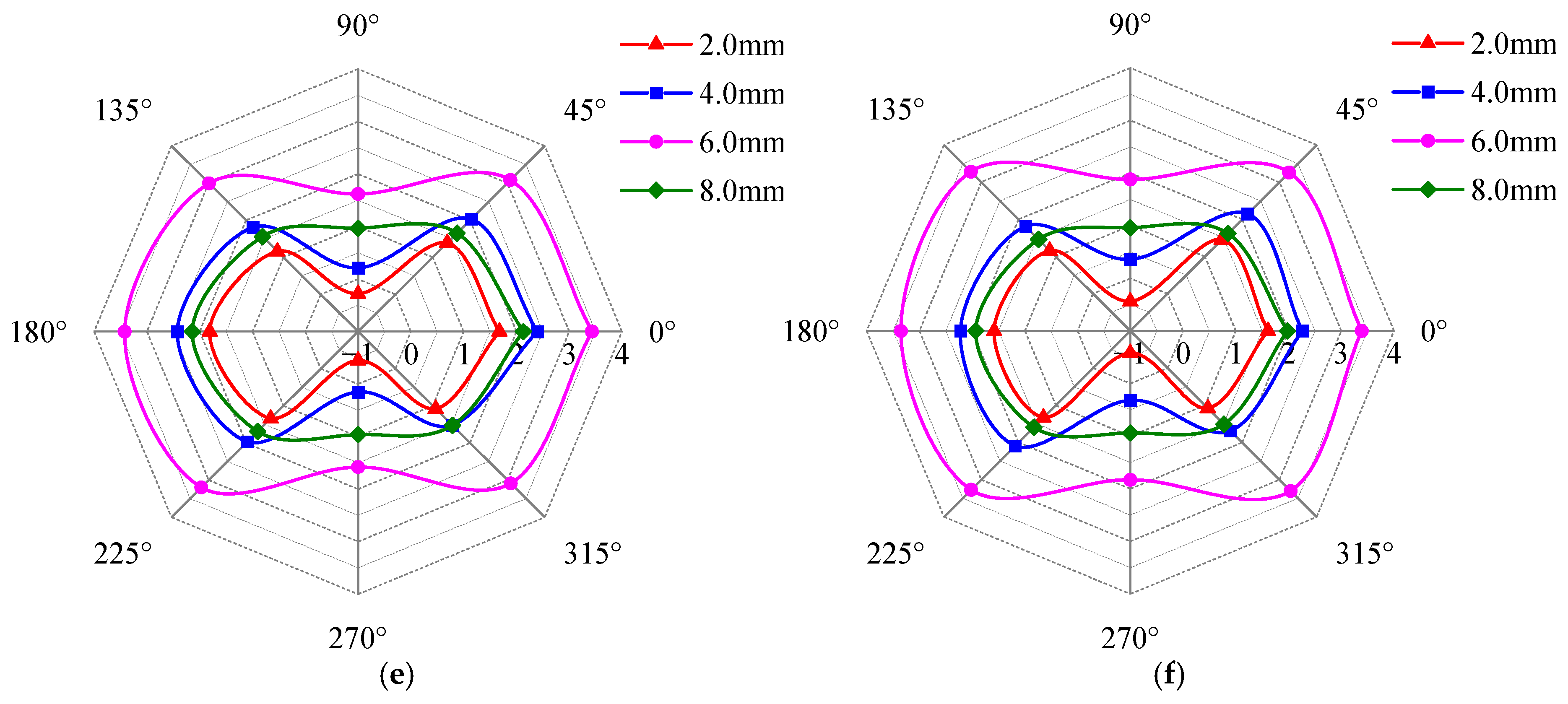
4.2. The Effect of Defect Width on Detection Signal
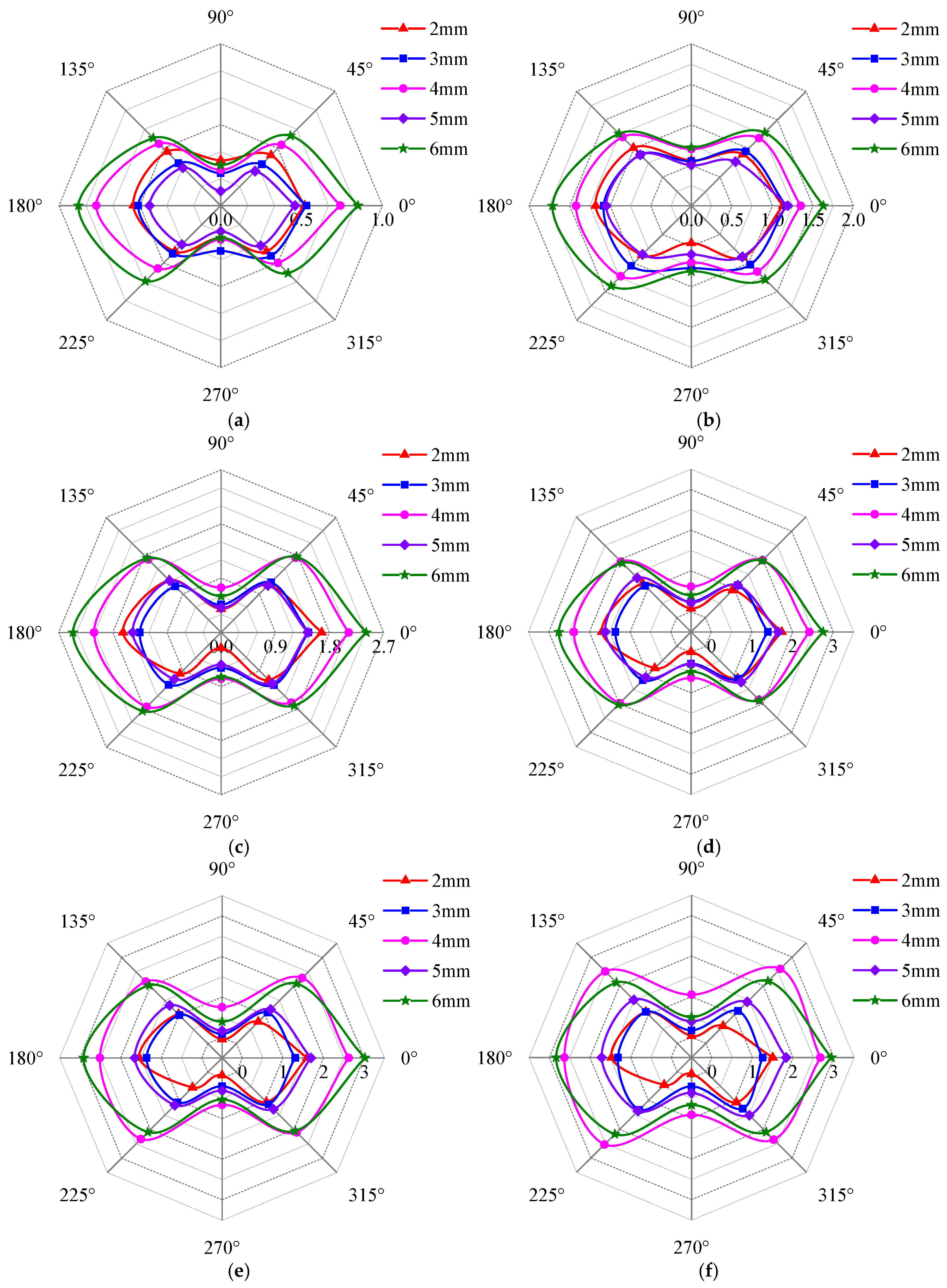
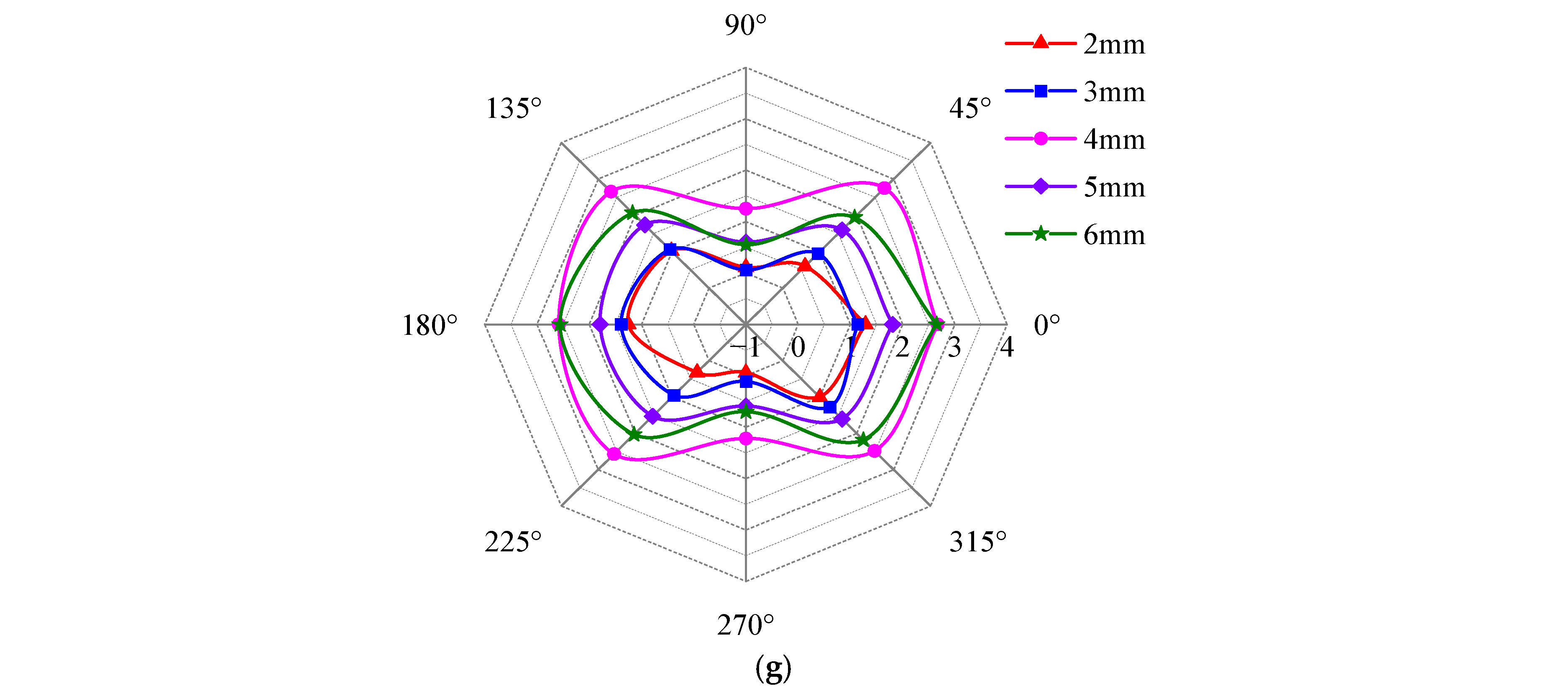
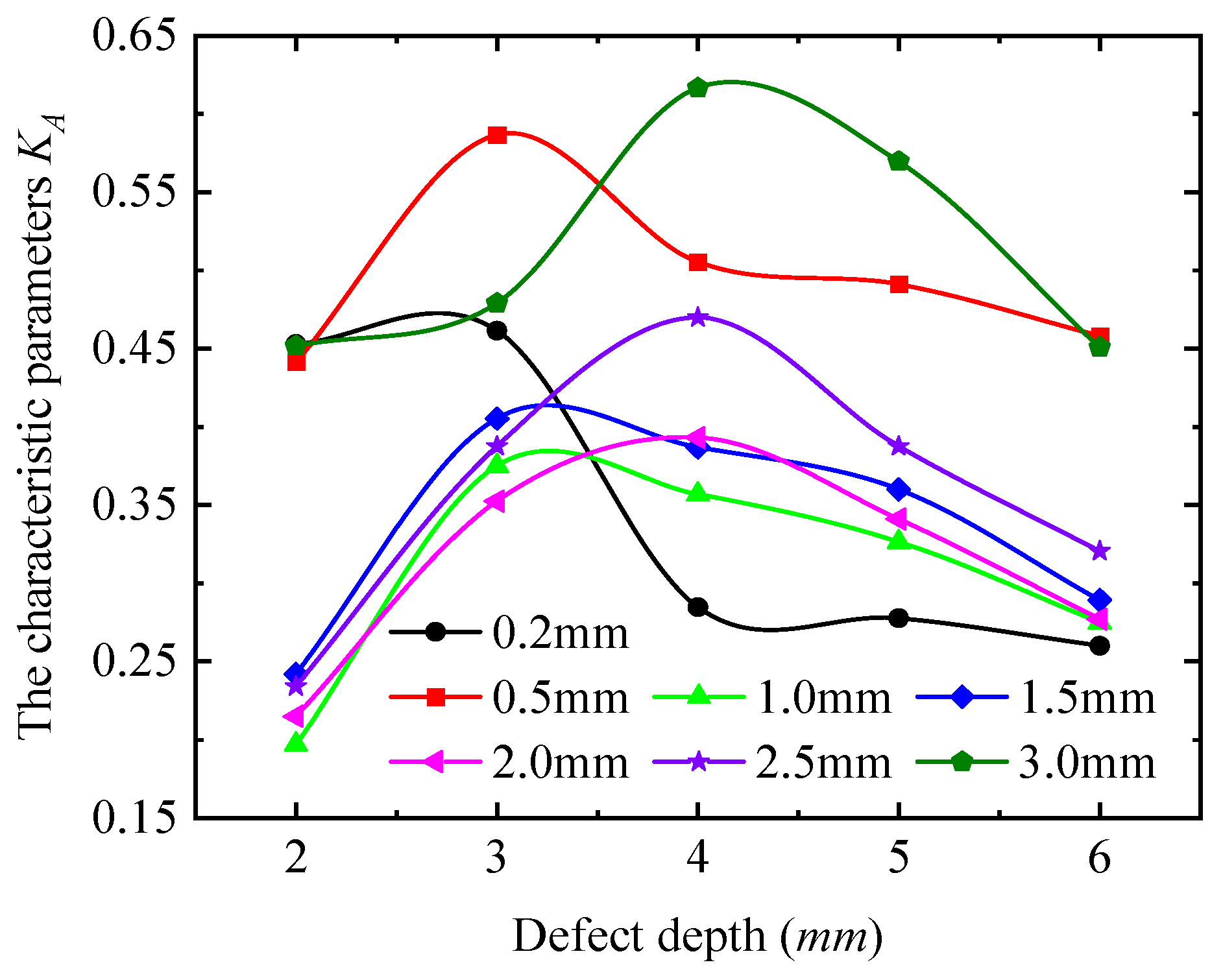
4.3. The Effect of Defect Depth on Detection Signal
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Qiu, X. Structure and electrochemical properties of laser cladding Al2CoCrCuFeNiTix high-entropy alloy coatings. Met. Mater. Int. 2020, 26, 998–1003. [Google Scholar] [CrossRef]
- Zerbst, U.; Klinger, C. Material defects as cause for the fatigue failure of metallic components. Int. J. Fatigue 2019, 127, 312–323. [Google Scholar] [CrossRef]
- Zerbst, U.; Madia, M.; Klinger, C.; Bettge, D.; Murakami, Y. Defects as a root cause of fatigue failure of metallic components. II: Non-metallic inclusions. Eng. Fail. Anal. 2019, 98, 228–239. [Google Scholar] [CrossRef]
- Zhang, W.; Sun, H.; Tao, A.; Li, Y.; Shi, Y. Local defect detection of ferromagnetic metal casing based on pulsed eddy current testing. IEEE Trans. Instrum. Meas. 2022, 71, 6003109. [Google Scholar] [CrossRef]
- Li, E.; Guo, W.; Cao, X.; Zhu, J. A magnetic head-based eddy current array for defect detection in ferromagnetic steels. Sens. Actuators A Phys. 2024, 379, 115862. [Google Scholar] [CrossRef]
- Wu, D.; Liu, Z.; Wang, X.; Su, L. Composite magnetic flux leakage detection method for pipelines using alternating magnetic field excitation. NDTE Int. 2017, 91, 148–155. [Google Scholar] [CrossRef]
- Yuan, X.; Wang, H.; Li, W.; Yin, X.; Zhang, X.; Ding, J. A flexible alternating current field measurement magnetic sensor array for in situ inspection of cracks in underwater structure. IEEE Trans. Instrum. Meas. 2024, 73, 4505610. [Google Scholar] [CrossRef]
- Tang, J.; Wang, R.; Liu, B.; Kang, Y. A novel magnetic flux leakage method based on the ferromagnetic lift-off layer with through groove. Sens. Actuators A Phys. 2021, 332, 113091. [Google Scholar] [CrossRef]
- Ege, Y.; Coramik, M. A new measurement system using magnetic flux leakage method in pipeline inspection. Measurement 2018, 123, 163–174. [Google Scholar] [CrossRef]
- Long, Y.; Zhang, J.; Huang, S.; Peng, L.; Wang, W.; Wang, S. A novel crack quantification method for ultra-high-definition magnetic flux leakage detection in pipeline inspection. IEEE Sens. J. 2022, 22, 16402–16413. [Google Scholar] [CrossRef]
- Wei, H.; Dong, S.; Xu, L.; Chen, F.; Zhang, H.; Li, X. Internal inspection method for crack defects in ferromagnetic pipelines under remanent magnetization. Measurement 2025, 242, 115907. [Google Scholar] [CrossRef]
- Shi, P.; Jin, K.; Zhang, P.; Xie, S.; Chen, Z.; Zheng, X. Quantitative inversion of stress and crack in ferromagnetic materials based on metal magnetic memory method. IEEE Trans. Magn. 2018, 54, 6202011. [Google Scholar] [CrossRef]
- Liu, B.; Feng, G.; He, L.; Luo, N.; Ren, J.; Yang, L. Quantitative study of MMM signal features for internal weld crack detection in long-distance oil and gas pipelines. IEEE Trans. Instrum. Meas. 2021, 70, 6008013. [Google Scholar] [CrossRef]
- Bao, S.; Fu, M.; Lou, H.; Bai, S. Defect identification in ferromagnetic steel based on residual magnetic field measurements. J. Magn. Magn. Mater. 2017, 441, 590–597. [Google Scholar] [CrossRef]
- Hwang, J.H.; Lord, W. Finite element modeling of magnetic field/defect interactions. J. Test. Eval. 1975, 3, 21–25. [Google Scholar] [CrossRef]
- Dutta, S.M.; Ghorbel, F.H.; Stanley, R.K. Simulation and analysis of 3-D magnetic flux leakage. IEEE Trans. Magn. 2008, 45, 1966–1972. [Google Scholar] [CrossRef]
- Xu, P.; Qian, T. High-speed rail defect detection using multi-frequency exciting 3D ACFM. Measurement 2024, 227, 114160. [Google Scholar] [CrossRef]
- Wang, R.; Chen, Y.; Yu, H.; Xu, Z.; Tang, J.; Feng, B.; Kang, Y.; Song, K. Defect classification and quantification method based on AC magnetic flux leakage time domain signal characteristics. NDTE Int. 2025, 149, 103250. [Google Scholar] [CrossRef]
- Yuan, X.; Zhang, X.; Li, W.; Yin, X.; Xie, S.; Peng, L.; Li, X.; Zhao, J.; Zhao, J.; Ding, J.; et al. Bicharacteristic probability of detection of crack under multi-factor influences using alternating current field measurement technique. NDT E Int. 2024, 147, 103173. [Google Scholar] [CrossRef]
- Ru, G.; Gao, B.; Liu, D.; Ma, Q.; Li, H.; Woo, W.L. Structural coupled electromagnetic sensing of defects diagnostic system. IEEE Trans. Ind. Electron. 2023, 70, 951–964. [Google Scholar] [CrossRef]
- Guo, W.; Gao, B.; Tian, G.; Si, D. Physic perspective fusion of electromagnetic acoustic transducer and pulsed eddy current testing in non-destructive testing system. Philos. Trans. R. Soc. A 2020, 378, 32921232. [Google Scholar] [CrossRef] [PubMed]
- Grochowalski, J.M.; Chady, T. Rapid identification of material defects based on pulsed multifrequency eddy current testing and the k-Nearest Neighbor method. Materials 2023, 16, 6650. [Google Scholar] [CrossRef] [PubMed]
- Gong, W.; Muhammad, F.; Ghassan, N.; Nawaf, S.; Zhang, F. A Magnetic Field Concentration Method for Magnetic Flux Leakage Detection of Rail-Top Surface Cracks. IEEE Access 2024, 12, 43245–43254. [Google Scholar] [CrossRef]
- Wu, D.; Su, L.; Wang, X.; Liu, Z. A novel non-destructive testing method by measuring the change rate of magnetic flux leakage. J. Nondestruct. Eval. 2017, 36, 24. [Google Scholar] [CrossRef]
- Richard, L. Measurement of the mechanical stress in mild steel by means of rotation of magnetic field strength—Part 2: Biaxial stress. NDTE Int. 1982, 15, 91–97. [Google Scholar] [CrossRef]
- Eslamlou, A.D.; Ghaderiaram, A.; Schlangen, E.; Fotouhi, M. A review on non-destructive evaluation of construction materials and structures using magnetic sensors. Constr. Build. Mater. 2023, 397, 132460. [Google Scholar] [CrossRef]
- Liu, J.; Shen, X.; Wang, J.; Jiang, L.; Zhang, H. An intelligent defect detection approach based on cascade attention network under complex magnetic flux leakage signals. IEEE Trans. Ind. Electron. 2023, 70, 7417–7427. [Google Scholar] [CrossRef]
- Zhang, H.; Li, H.; Xia, R.; Hu, T.; Qiu, J.; Zhou, J. Corrosion degree detection of ferromagnetic materials using a hybrid machine learning approach and self-magnetic flux leakage technology. Measurement 2025, 240, 115611. [Google Scholar] [CrossRef]
- Sun, H.; Peng, L.; Huang, S.; Li, S.; Long, Y.; Wang, S. Development of a physics-Informed doubly fed cross-residual deep neural network for high-precision magnetic flux leakage defect size estimation. IEEE Trans. Ind. Inform. 2022, 18, 1629–1640. [Google Scholar] [CrossRef]
- Lewis, A.M.; Michael, D.H.; Lugg, M.C.; Collins, R. Thin-skin electromagnetic fields around surface-breaking cracks in metals. Appl. Phys. Lett. 1988, 64, 3777–3784. [Google Scholar] [CrossRef]
- Saguy, H.; Rittel, D. Bridging thin and thick skin solutions for alternating currents in cracked conductors. Appl. Phys. Lett. 2005, 87, 084103. [Google Scholar] [CrossRef]
- Bi, C.; Bi, E.; Wang, H.; Deng, C.; Chen, H.; Wang, Y. Magnetic circuit design for the performance experiment of shear yield stress enhanced by compression of magnetorheological fluids. Sci. Rep. 2024, 14, 741. [Google Scholar] [CrossRef] [PubMed]
- Bastos, J.; Sadowski, N. Magnetic Materials and 3D Finite Element Modeling; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar] [CrossRef]


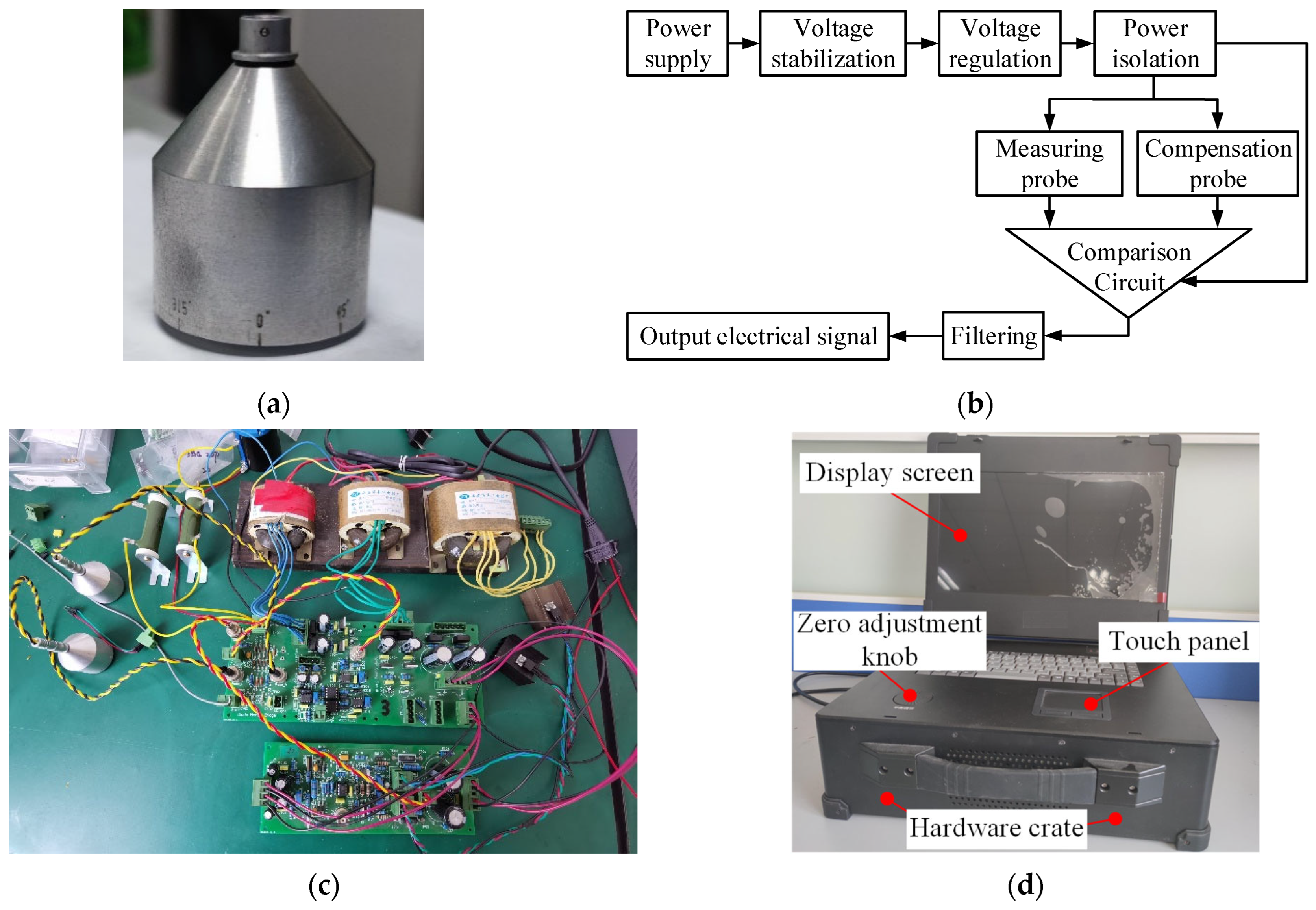
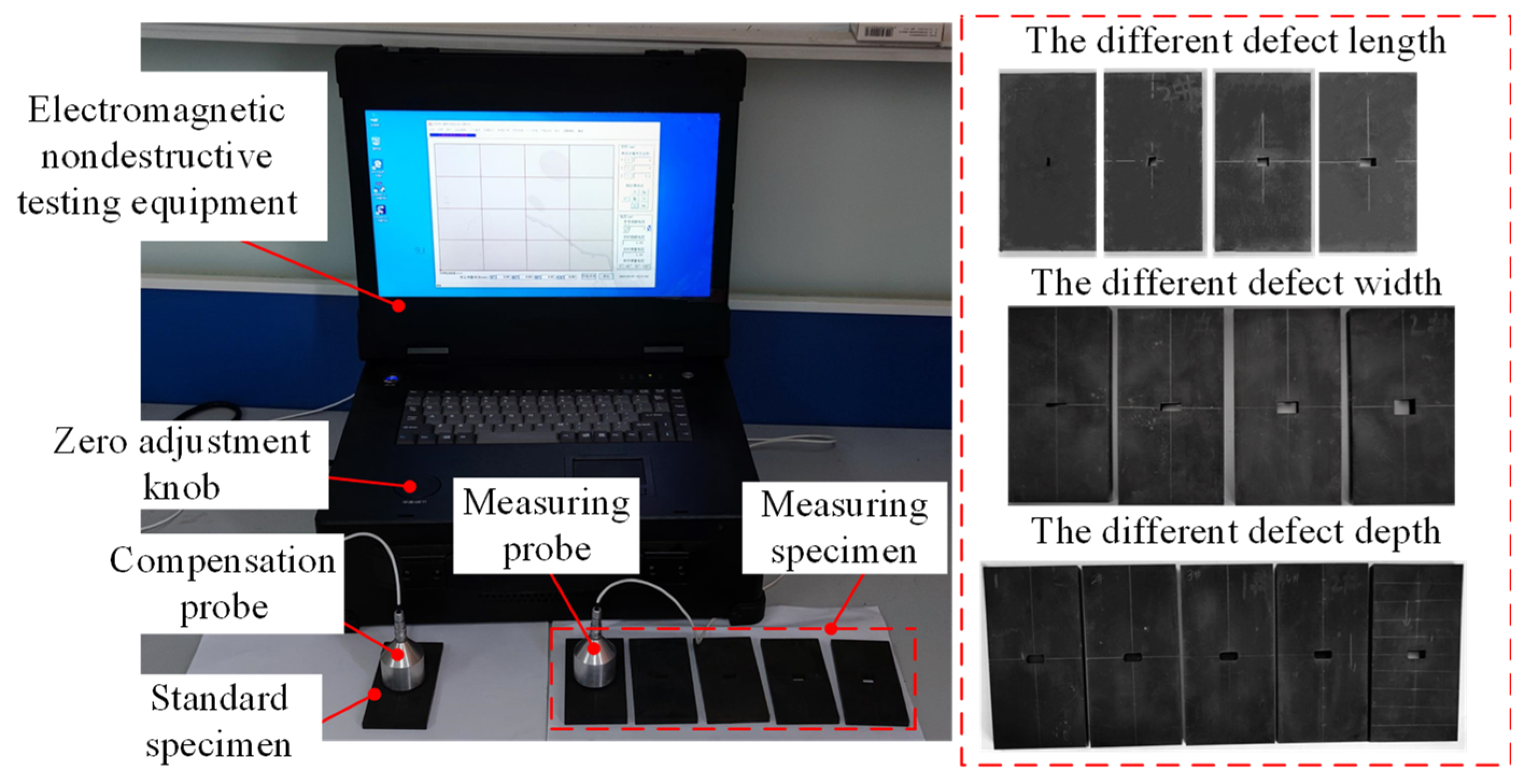

| Elements | C | Si | Mn | P | S | Nb | V | Ti | Cr | Ni | Cu | Mo |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Percentage | 0.17 | 0.42 | 1.5 | 0.014 | 0.009 | 0.002 | 0.002 | 0.001 | 0.043 | 0.008 | 0.01 | 0.008 |
| Turn Number | Cross-Sectional Area of Coil Wire (m2) | Sample Conductivity (S/m) | Coil Conductivity (S/m) | Circuit Resistance R1 (Ω) | Circuit Resistance R2 (Ω) |
|---|---|---|---|---|---|
| 450 | 1 × 10−6 | 1.2 × 107 | 6 × 107 | 200 | 200 |
| Parameter | Saturation Magnetization (A/m) | Domain Wall Density (A/m) | Pinning Loss (A/m) | Magnetization Reversibility | Inter-Domain Coupling |
|---|---|---|---|---|---|
| Values on the diagonal | 1.31 × 106 | 233.78 | 374.96 | 0.74 | 5.62 × 10−4 |
| 1.33 × 106 | 177.86 | 232.65 | 0.65 | 4.17 × 10−4 | |
| 1.31 × 106 | 233.78 | 374.98 | 0.74 | 5.62 × 10−4 |
| Defect Size | Length (mm) | Width (mm) | Depth (mm) |
|---|---|---|---|
| length experiment | 2, 4, 6, 8 | 10 | 6 |
| width experiment | 5 | 2, 4, 6, 8 | 6 |
| depth experiment | 5 | 10 | 2, 3, 4, 5, 6 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Xie, R.; Wang, R.; Wang, J.; Cai, H.; Wang, X.; Li, X.; Guan, Q.; Zhang, J. Research on Quantitative Evaluation of Defects in Ferromagnetic Materials Based on Electromagnetic Non-Destructive Testing. Sensors 2025, 25, 3508. https://doi.org/10.3390/s25113508
Hu X, Xie R, Wang R, Wang J, Cai H, Wang X, Li X, Guan Q, Zhang J. Research on Quantitative Evaluation of Defects in Ferromagnetic Materials Based on Electromagnetic Non-Destructive Testing. Sensors. 2025; 25(11):3508. https://doi.org/10.3390/s25113508
Chicago/Turabian StyleHu, Xiangyi, Ruijie Xie, Ruotian Wang, Jiapeng Wang, Haichao Cai, Xiaoqiang Wang, Xiang Li, Qingzhu Guan, and Jianhua Zhang. 2025. "Research on Quantitative Evaluation of Defects in Ferromagnetic Materials Based on Electromagnetic Non-Destructive Testing" Sensors 25, no. 11: 3508. https://doi.org/10.3390/s25113508
APA StyleHu, X., Xie, R., Wang, R., Wang, J., Cai, H., Wang, X., Li, X., Guan, Q., & Zhang, J. (2025). Research on Quantitative Evaluation of Defects in Ferromagnetic Materials Based on Electromagnetic Non-Destructive Testing. Sensors, 25(11), 3508. https://doi.org/10.3390/s25113508






