Displacement Transmissibility Analysis of Stewart Platform Based SINS’s Bumper Under Base Vibration Excitation
Abstract
1. Introduction
- (1)
- A dynamic model for the bumper is established.
- (2)
- Dynamic equations of the bumper under base vibration excitation are derived.
- (3)
- A calculation flowchart of the vibration isolation performance of the bumper is proposed.
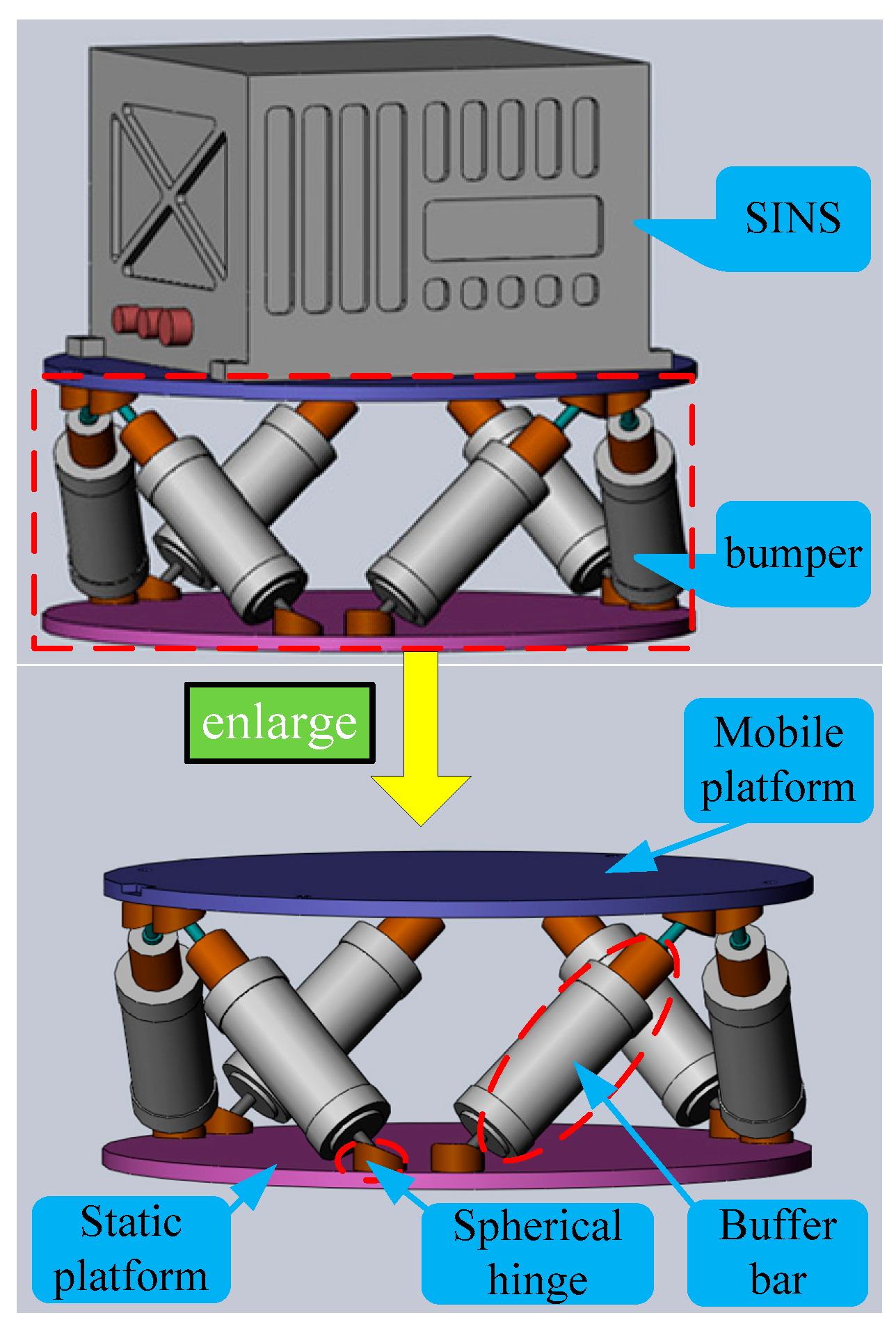
2. Stewart Platform Based SINS’s Bumper
2.1. Mechanical Configuration
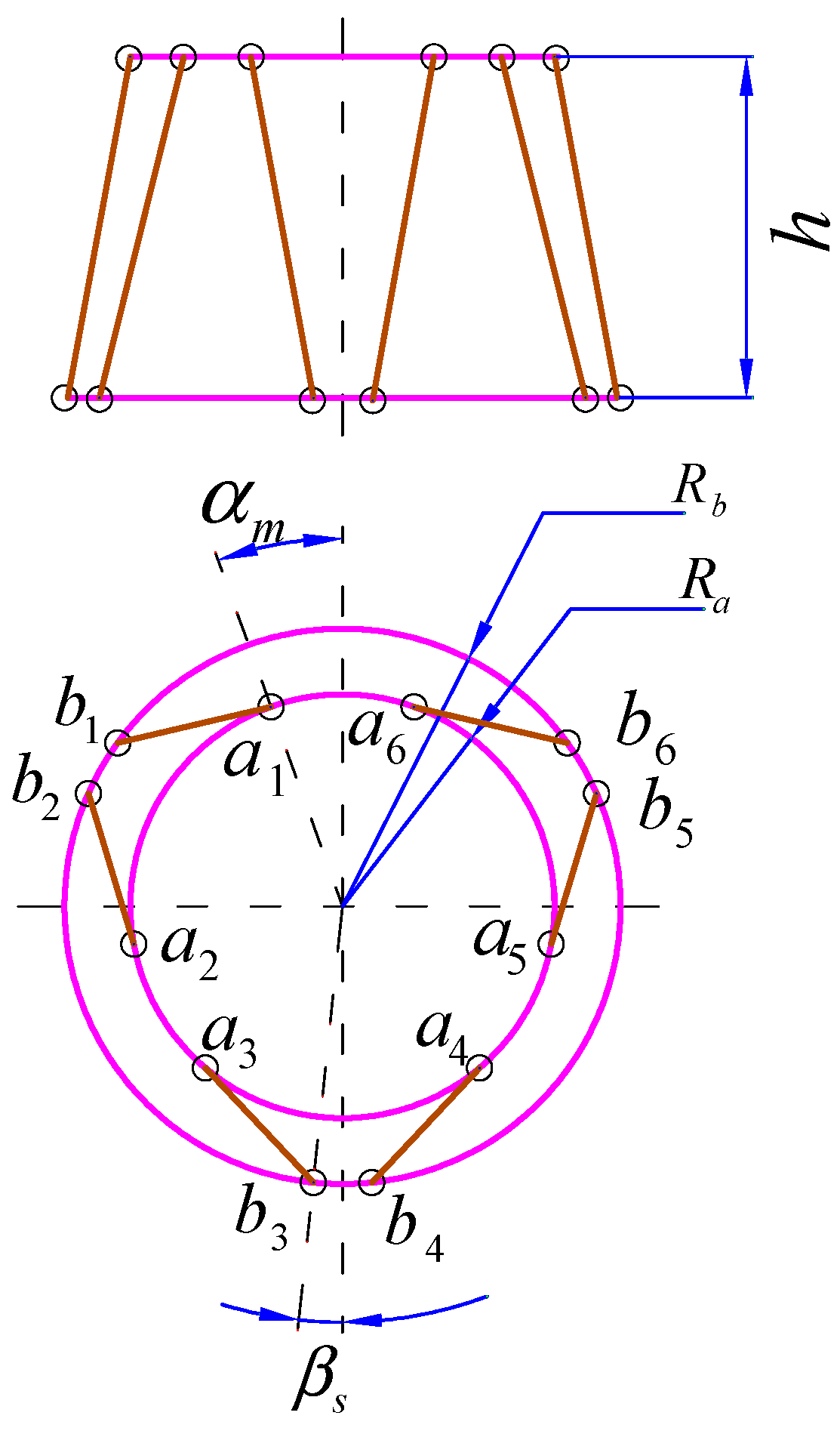
2.2. Geometric Configuration
3. Dynamic Model and Equations
- (1)
- Geometry variation of the bumper during vibration can be neglected because the base vibration excitations are small, so Jacobian matrix is regarded as a constant matrix dependent on the static configuration of the bumper, and dynamic matrices of the bumper are also constant matrices because Jacobian matrix is a constant matrix.
- (2)
- The force on the buffer bars is mainly completed by the spring inside the buffer bars, and the mass of the outer shell of the buffer bar itself is relatively small compared to the load weight, so the kinetic energy of buffer bars is neglected.
- (3)
- All joints are regarded as ideal spherical, so their clearance and stiffness are neglected.
3.1. Coupled Dynamic Equations
3.2. Decoupling Method
3.3. Decoupled Dynamic Equations
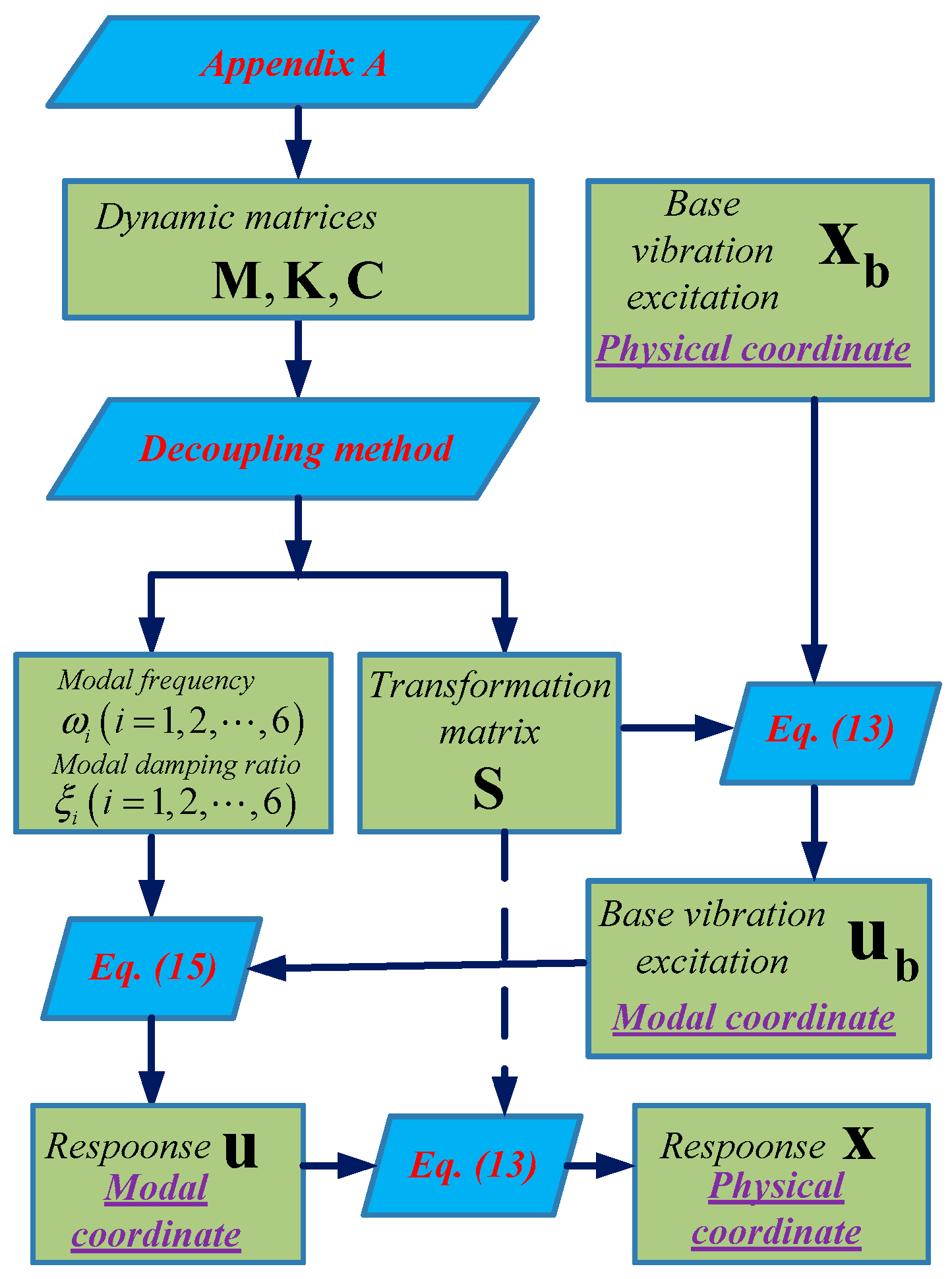
4. Displacement Transmissibility of the Bumper
4.1. Calculation Flowchart for Response of the Load
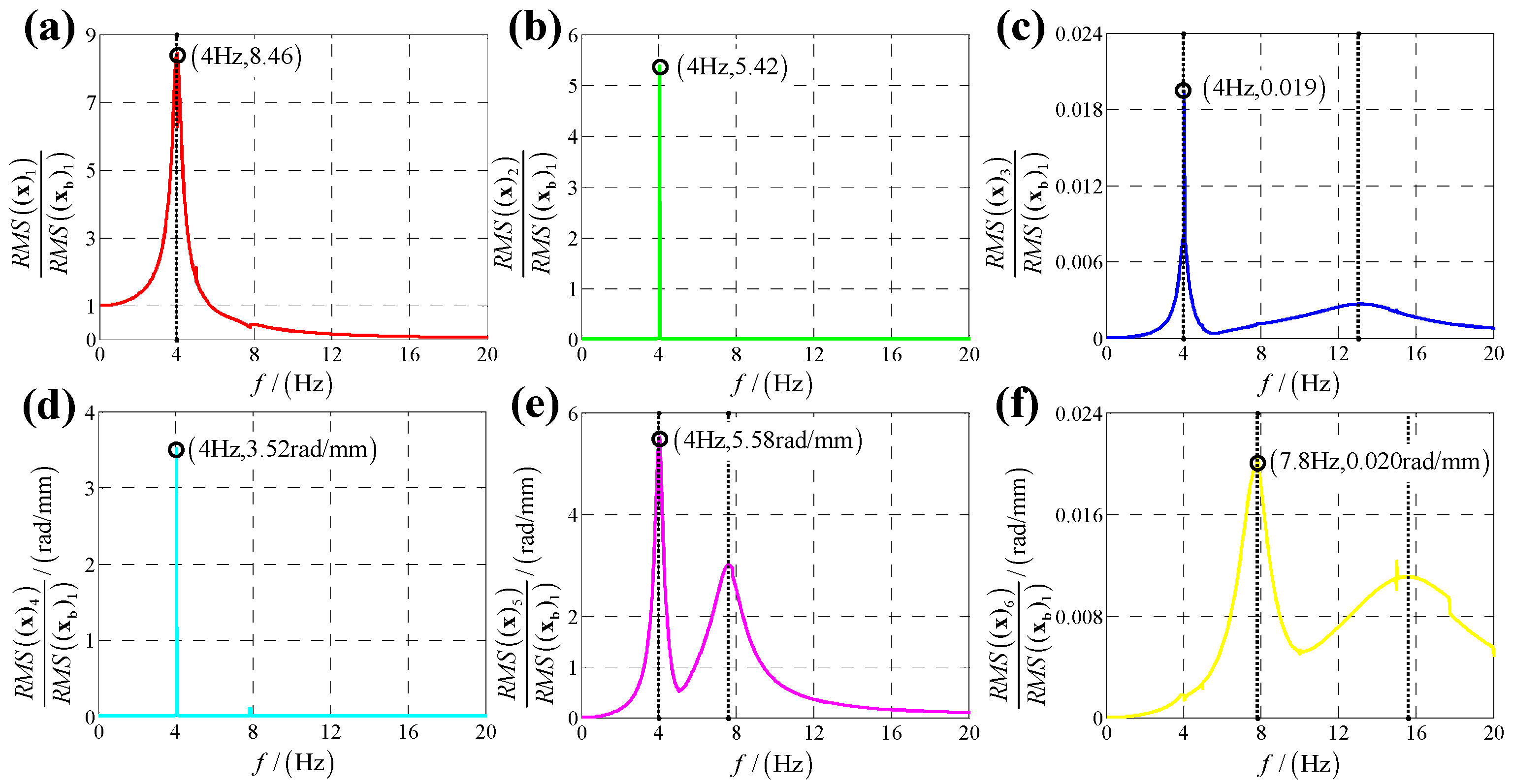
4.2. Theoretical Displacement Transmissibility
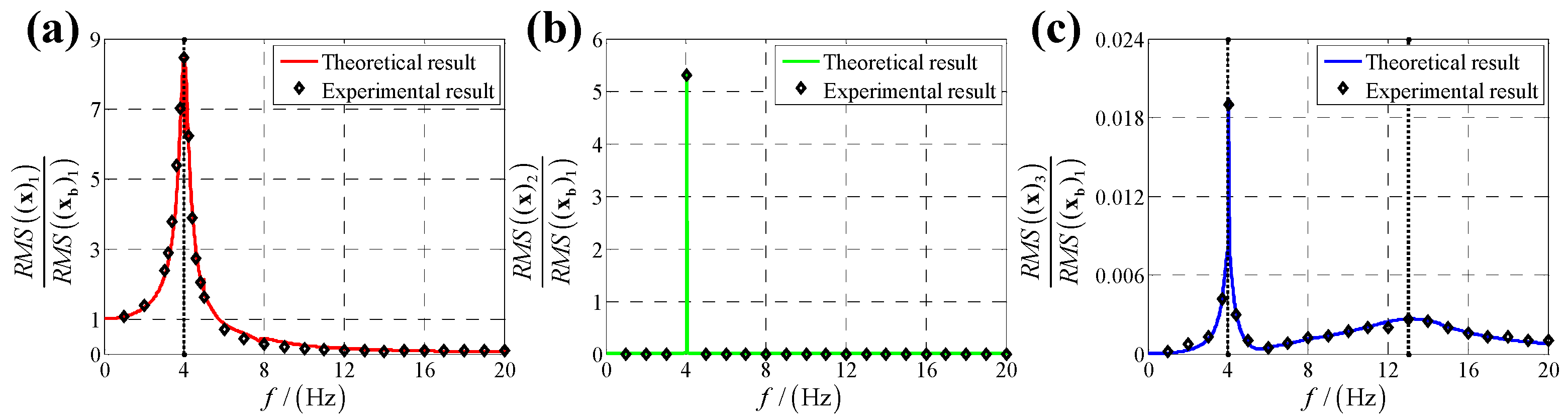
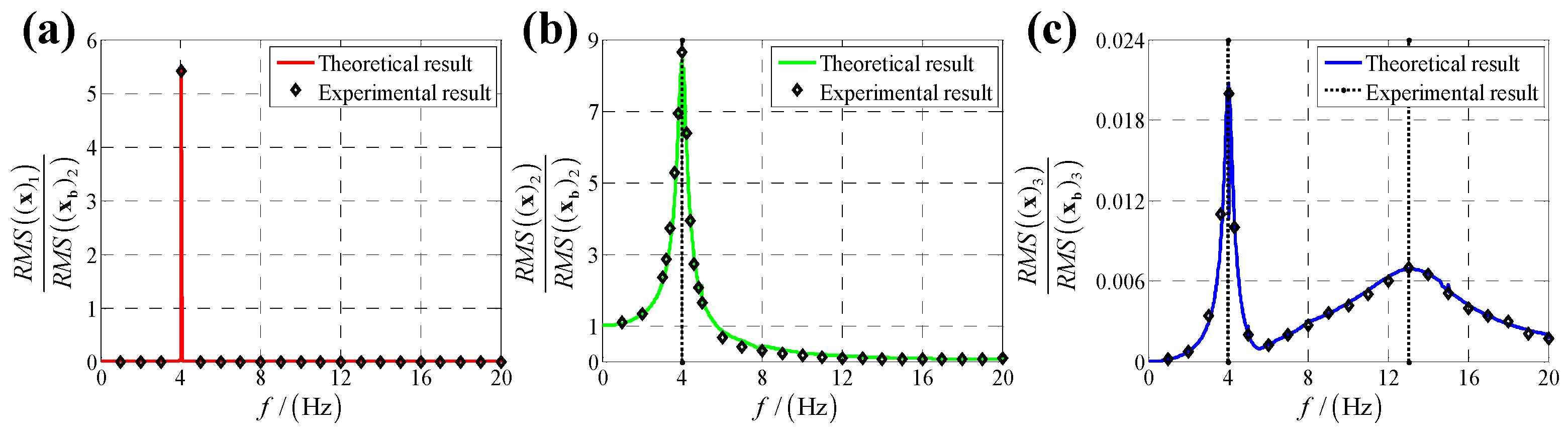
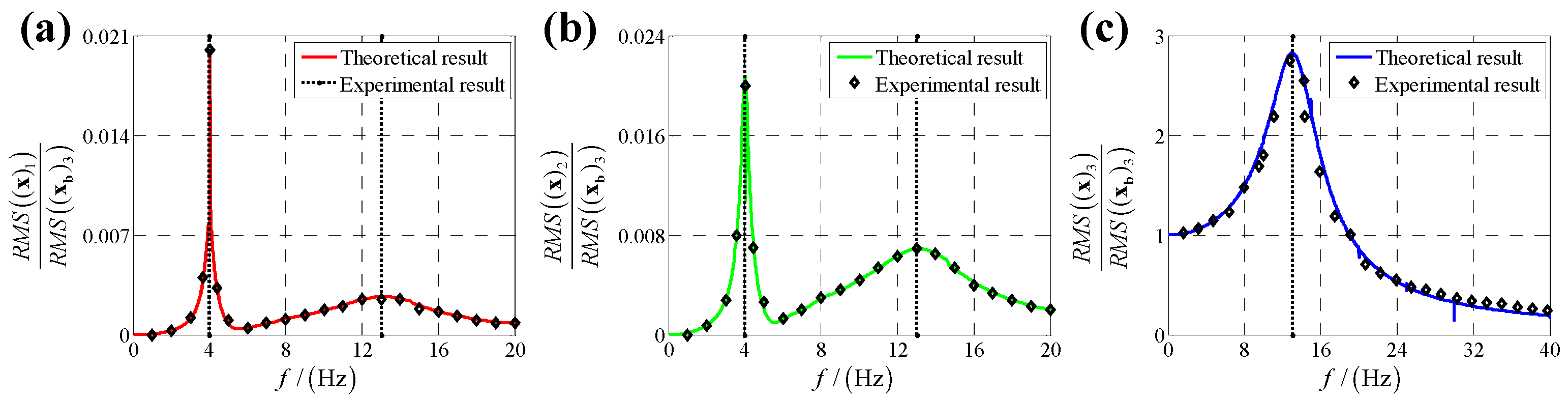
5. Experimental Verification
6. Conclusions
- (1)
- Some simplifications (considering Jacobian matrix as a constant matrix, neglecting kinetic energy of buffer bars, ideal joints assumption) might limit the applicability of the results in more complex real-world scenarios.
- (2)
- This work lacks sensitivity analysis to determine how structural parameter variations affect the displacement transmissibility.
- (3)
- Nonlinear damping or frequency-dependent damping characteristics is not considered.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SINS | Strap-down inertial navigation system |
| DOF | Degrees of freedom |
| Height of bumper | |
| Radius of static platform | |
| Radius of mobile platform | |
| Half flare angle of adjoining spherical hinge on static platform | |
| Half flare angle of adjoining spherical hinge on mobile platform | |
| Center of mass of static platform | |
| Static platform frame | |
| Center of mass of load | |
| Load frame | |
| Euler-angles of mobile platform related to | |
| Generalized coordinate of mobile platform in physical coordinate | |
| Generalized coordinate of static platform in physical coordinate | |
| Mass matrix of bumper | |
| Stiffness matrix of bumper | |
| Damping matrix of bumper | |
| Stiffness of buffer bar | |
| Damping of buffer bar | |
| Ratio of damping to stiffness for buffer bars | |
| Generalized coordinate of mobile platform in modal coordinate | |
| Generalized coordinate of static platform in modal coordinate | |
| Coordinate transformation matrix between physical and modal coordinate | |
| Modal frequency | |
| Modal damping ratio | |
| Vibration amplitude | |
| Vibration frequency | |
| Response amplitude in modal coordinate | |
| Response phase angle in modal coordinate | |
| Displacement transmissibility |
Appendix A
Appendix A.1
| Symbol | Parameter Definition |
|---|---|
| Center of mass of static platform | |
| Static platform frame | |
| Center of mass of load | |
| Load frame | |
| Upper spherical hinges centers | |
| Lower spherical hinges centers | |
| Euler-angles of mobile platform related to | |
| Generalized coordinate of mobile platform | |
| Rotation matrix of platform | |
| Rotation angular velocity of mobile platform | |
| Length scalars of buffer bars | |
| Stiffness of buffer bar | |
| Damping of buffer bar | |
| Mass of load | |
Appendix A.2

Appendix A.3
Appendix A.4
Appendix A.5
Appendix A.6
| Dynamic Parameters | Values |
|---|---|
| mm | |
| N/m | |
| N·s/s | |
| kg | |
| kg·m2 |
References
- Chang, J.; Fan, S.; Zhang, Y.; Li, J.; Shao, J.; Xu, D. A time asynchronous parameters calibration method of high-precision FOG-IMU based on a single-axis continuous rotation scheme. Meas. Sci. Technol. 2023, 34, 055108. [Google Scholar] [CrossRef]
- Hung, H.-H.; Huang, Y.-H.; Ma, C.-C. An investigation on coupling analysis and vibration rectification of vibration isolation system for strap-down inertia measurement unit. J. Mech. 2024, 40, 604–624. [Google Scholar] [CrossRef]
- Sun, J.; Chen, Y.; Cui, B. An Improved Initial Alignment Method Based on SE2(3)/EKF for SINS/GNSS Integrated Navigation System with Large Misalignment Angles. Sensors 2024, 24, 2945. [Google Scholar] [CrossRef]
- Tao, Y.; Rui, X.; Zhang, J.; Yang, F. Simulation of vibration characteristics of IMU with controllable magnetorheological isolation system. Multibody Syst. Dyn. 2023, 59, 293–312. [Google Scholar] [CrossRef]
- Zhang, T.; Gong, X.; Zhang, L.; Wang, Y.; Liu, Y.; Li, L. A Method for Solving the Additional Stiffness Introduced by Flexible Joints in Stewart Platform Based on FEM Modal Analysis. Machines 2023, 11, 457. [Google Scholar] [CrossRef]
- Han, Q.; Gao, S.; Chu, F. Micro-Vibration Analysis, Suppression, and Isolation of Spacecraft Flywheel Rotor Systems: A Review. Vibration 2024, 7, 229–263. [Google Scholar] [CrossRef]
- Sun, K.; Tang, J.; Wu, Z.; Li, Y.; Cao, D. Coupled nonlinear vibration characteristics of quasi-zero-stiffness Gough-Stewart isolation platform. Aerosp. Sci. Technol. 2024, 152, 109352. [Google Scholar] [CrossRef]
- Tu, Y.; Yang, G.; Cai, Q.; Wang, L.; Zhou, X. Optimal design of SINS’s Stewart platform bumper for restoration accuracy based on genetic algorithm. Mech. Mach. Theory 2018, 124, 42–54. [Google Scholar] [CrossRef]
- du Plooy, N.F.; Heyns, P.S.; Brennan, M.J. The development of a tunable vibration absorbing isolator. Int. J. Mech. Sci. 2005, 47, 983–997. [Google Scholar] [CrossRef]
- Lu, Z.; Brennan, M.J.; Yang, T.; Li, X.; Liu, Z. An investigation of a two-stage nonlinear vibration isolation system. J. Sound Vib. 2013, 332, 1456–1464. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Li, F. Vibration isolation using a hybrid lever-type isolation system with an X-shape supporting structure. Int. J. Mech. Sci. 2015, 98, 169–177. [Google Scholar] [CrossRef]
- Xu, J.; Sun, X. A multi-directional vibration isolator based on Quasi-Zero-Stiffness structure and time-delayed active control. Int. J. Mech. Sci. 2015, 100, 126–135. [Google Scholar] [CrossRef]
- Liu, C.; Jing, X.; Chen, Z. Band stop vibration suppression using a passive X-shape structured lever-type isolation system. Mech. Syst. Signal Process. 2016, 68–69, 342–353. [Google Scholar] [CrossRef]
- Li, Y.; Xu, D. Vibration attenuation of high dimensional quasi-zero stiffness floating raft system. Int. J. Mech. Sci. 2017, 126, 186–195. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Kovacic, I.; Waters, T.P. On the force transmissibility of a vibration isolator with quasi-zero-stiffness. J. Sound Vib. 2009, 322, 707–717. [Google Scholar] [CrossRef]
- Carrella, A.; Brennan, M.J.; Waters, T.P.; Lopes, V. Force and displacement transmissibility of a nonlinear isolator with high-static-low-dynamic-stiffness. Int. J. Mech. Sci. 2012, 55, 22–29. [Google Scholar] [CrossRef]
- Mofidian, S.M.M.; Bardaweel, H. Displacement transmissibility evaluation of vibration isolation system employing nonlinear-damping and nonlinear-stiffness elements. J. Vib. Control 2017, 24, 4247–4259. [Google Scholar] [CrossRef]
- Lu, Z.; Brennan, M.J.; Chen, L.-Q. On the transmissibilities of nonlinear vibration isolation system. J. Sound Vib. 2016, 375, 28–37. [Google Scholar] [CrossRef]
- Shi, B.; Yang, J.; Rudd, C. On vibration transmission in oscillating systems incorporating bilinear stiffness and damping elements. Int. J. Mech. Sci. 2019, 150, 458–470. [Google Scholar] [CrossRef]
- Chaudhury, A.N.; Ghosal, A. Optimum design of multi-degree-of-freedom closed-loop mechanisms and parallel manipulators for a prescribed workspace using Monte Carlo method. Mech. Mach. Theory 2017, 118, 115–138. [Google Scholar] [CrossRef]
- Qi, Y.; Song, Y. Coupled kinematic and dynamic analysis of parallel mechanism flying in space. Mech. Mach. Theory 2018, 124, 104–117. [Google Scholar] [CrossRef]
- Chen, G.; Rui, X.; Abbas, L.K.; Wang, G.; Yang, F.; Zhu, W. A novel method for the dynamic modeling of Stewart parallel mechanism. Mech. Mach. Theory 2018, 126, 397–412. [Google Scholar] [CrossRef]
- Ribeiro, E.A.; Lopes, E.M.d.O.; Bavastri, C.A. A numerical and experimental study on optimal design of multi-DOF viscoelastic supports for passive vibration control in rotating machinery. J. Sound Vib. 2017, 411, 346–361. [Google Scholar] [CrossRef]
- Dong, G.; Zhang, X.; Luo, Y.; Zhang, Y.; Xie, S. Analytical study of the low frequency multi-direction isolator with high-static-low-dynamic stiffness struts and spatial pendulum. Mech. Syst. Signal Process. 2018, 110, 521–539. [Google Scholar] [CrossRef]
- Liao, X.; Li, S.; Yang, S.-K.; Wang, J.; Xu, Y. Advanced component transmission path analysis based on transmissibility matrices and blocked displacements. J. Sound Vib. 2018, 437, 242–263. [Google Scholar] [CrossRef]
- Zhou, J.; Wang, K.; Xu, D.; Ouyang, H.; Li, Y. A Six Degrees-of-Freedom Vibration Isolation Platform Supported by a Hexapod of Quasi-Zero-Stiffness Struts. J. Vib. Acoust. 2017, 139, 034502. [Google Scholar] [CrossRef]
- Zheng, Y.; Li, Q.; Yan, B.; Luo, Y.; Zhang, X. A Stewart isolator with high-static-low-dynamic stiffness struts based on negative stiffness magnetic springs. J. Sound Vib. 2018, 422, 390–408. [Google Scholar] [CrossRef]
- Wu, Z.; Jing, X.; Sun, B.; Li, F. A 6DOF passive vibration isolator using X-shape supporting structures. J. Sound Vib. 2016, 380, 90–111. [Google Scholar] [CrossRef]
- Liu, Z.; Tang, X.; Wang, L. Research on the dynamic coupling of the rigid-flexible manipulator. Robot. Comput.—Integr. Manuf. 2015, 32, 72–82. [Google Scholar] [CrossRef]
- Li, C.; Tang, Q.; Xi, C.; Zhong, B.; Wen, B. Coupling vibration behaviors of drum-disk-shaft structures with elastic connection. Int. J. Mech. Sci. 2019, 155, 392–404. [Google Scholar] [CrossRef]
- Synnegård, E.; Gustavsson, R.; Aidanpää, J.-O. Influence of cross-coupling stiffness in tilting pad journal bearings for vertical machines. Int. J. Mech. Sci. 2016, 111–112, 43–54. [Google Scholar] [CrossRef]
- Wu, P.; Xiong, H.; Kong, J. Dynamic analysis of 6-SPS parallel mechanism. Int. J. Mech. Mater. Des. 2012, 8, 121–128. [Google Scholar] [CrossRef]
- Wohlhart, K. Mobile 6-SPS Parallel Manipulators. J. Robot. Syst. 2003, 20, 509–516. [Google Scholar] [CrossRef]
- Sireteanu, T.; Solomon, O.; Mitu, A.-M.; Giuclea, M. A Linearization Method of Piecewise Linear Systems Based on Frequency Domain Characteristics with Application to Semi-Active Control of Vibration. J. Vib. Acoust. 2018, 140, 061006. [Google Scholar] [CrossRef]
- Sun, Y.-H.; Zhang, Y.-W.; Ding, H.; Chen, L.-Q. Nonlinear energy sink for a flywheel system vibration reduction. J. Sound Vib. 2018, 429, 305–324. [Google Scholar] [CrossRef]
- Chen, N.; Huang, D.; Tu, Y.; Wei, D.; Lin, X. A novel inertial parameter identification method for the ship-mounted Stewart platform based on a wave compensation platform. Measurement 2025, 242, 116010. [Google Scholar] [CrossRef]
- Li, Z.; Du, H.; Si, J.; Wang, Z.; Xiong, W. Rigid-flexible coupling dynamic modeling and validation of a helicopter rescue simulator based on an inverted Stewart platform. Ocean Eng. 2025, 319, 120164. [Google Scholar] [CrossRef]


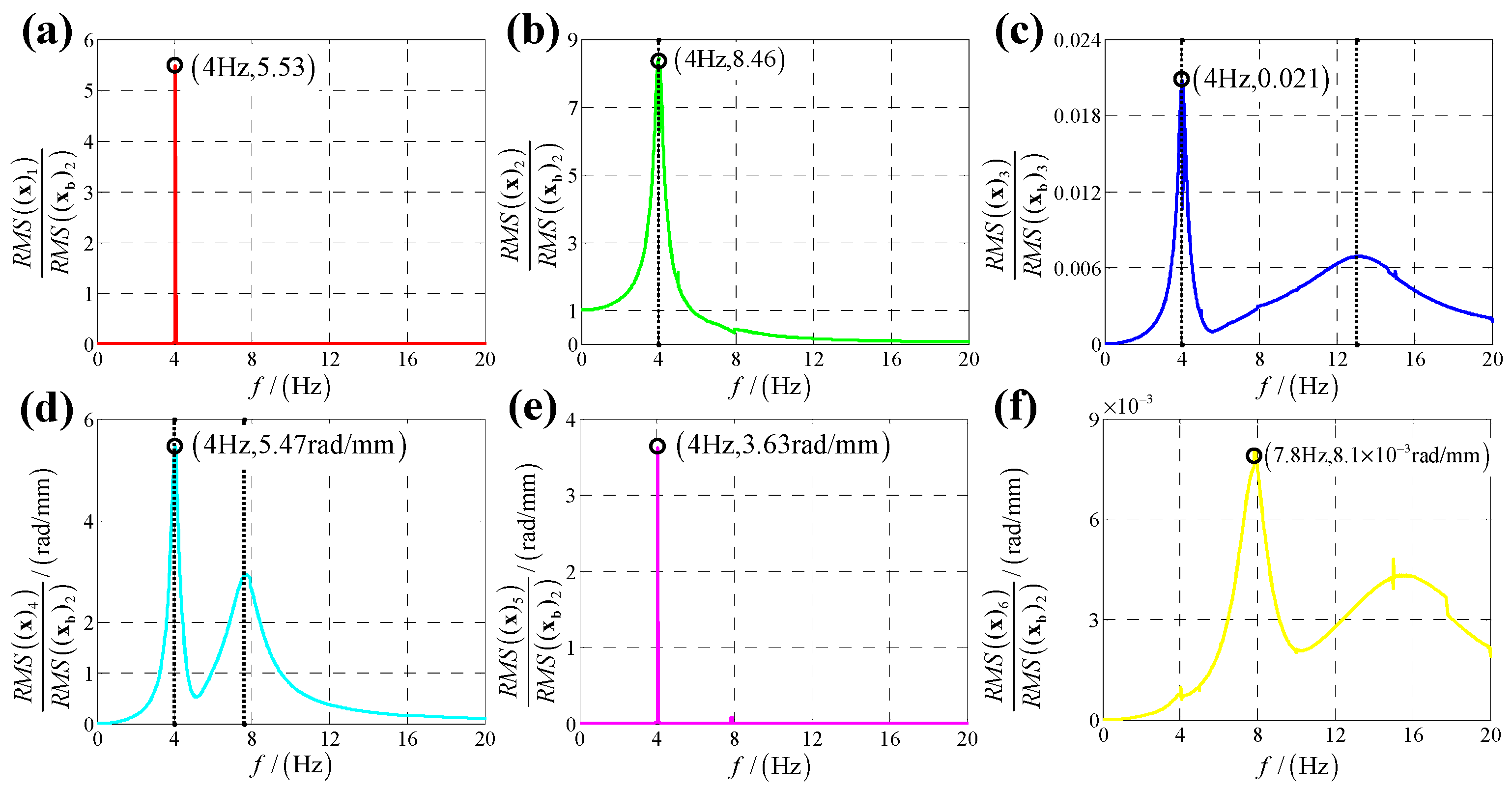

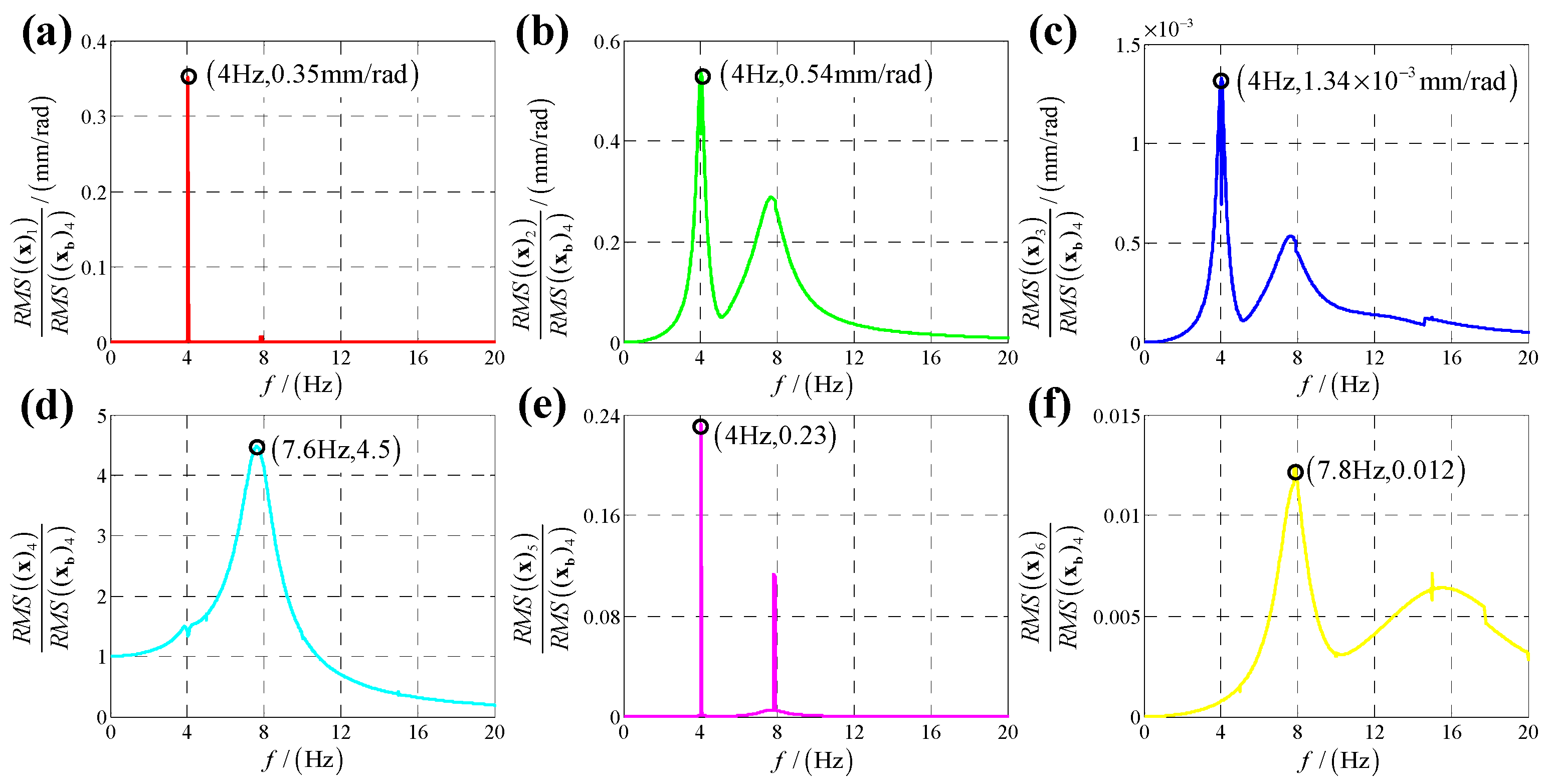
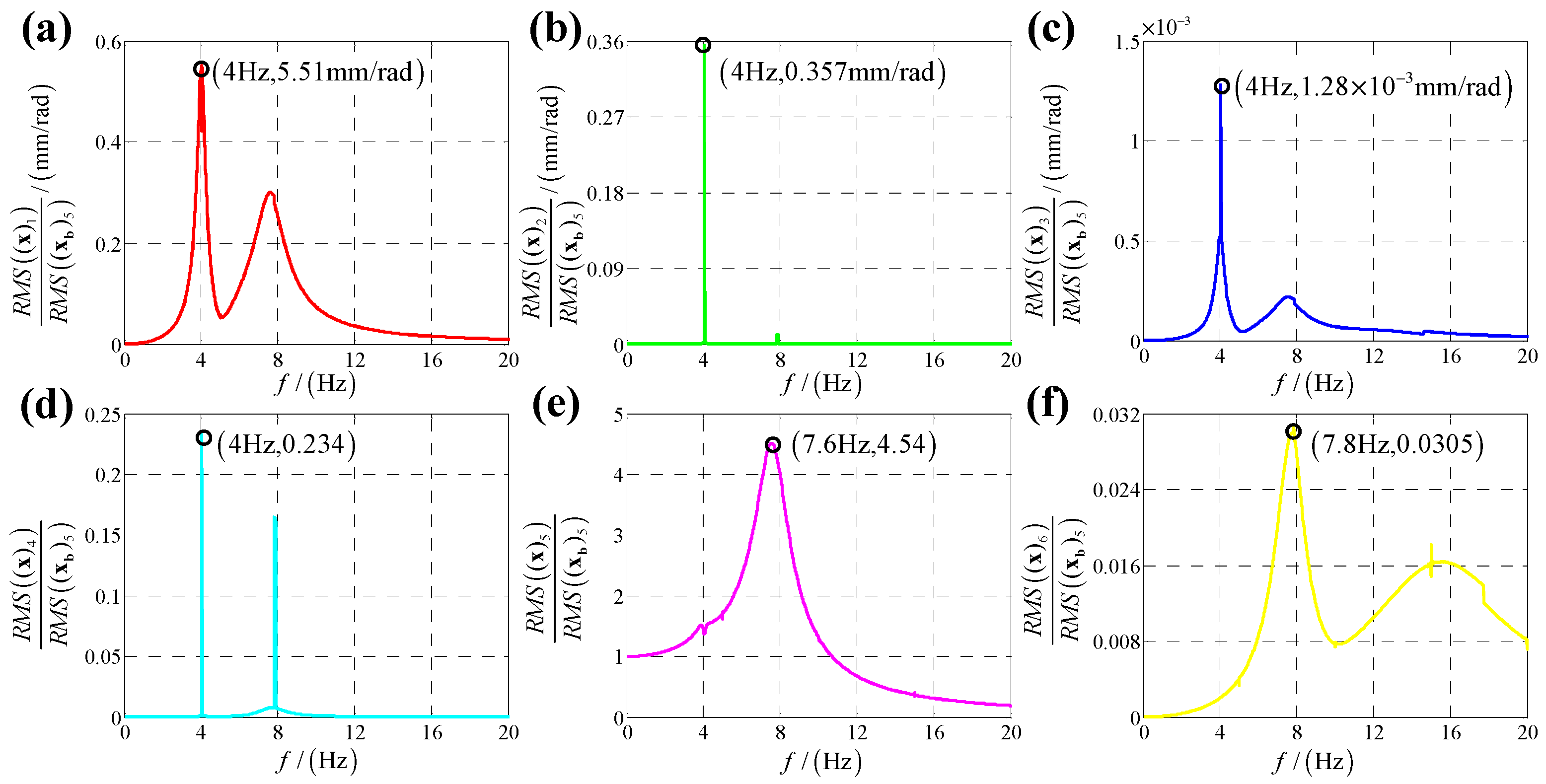
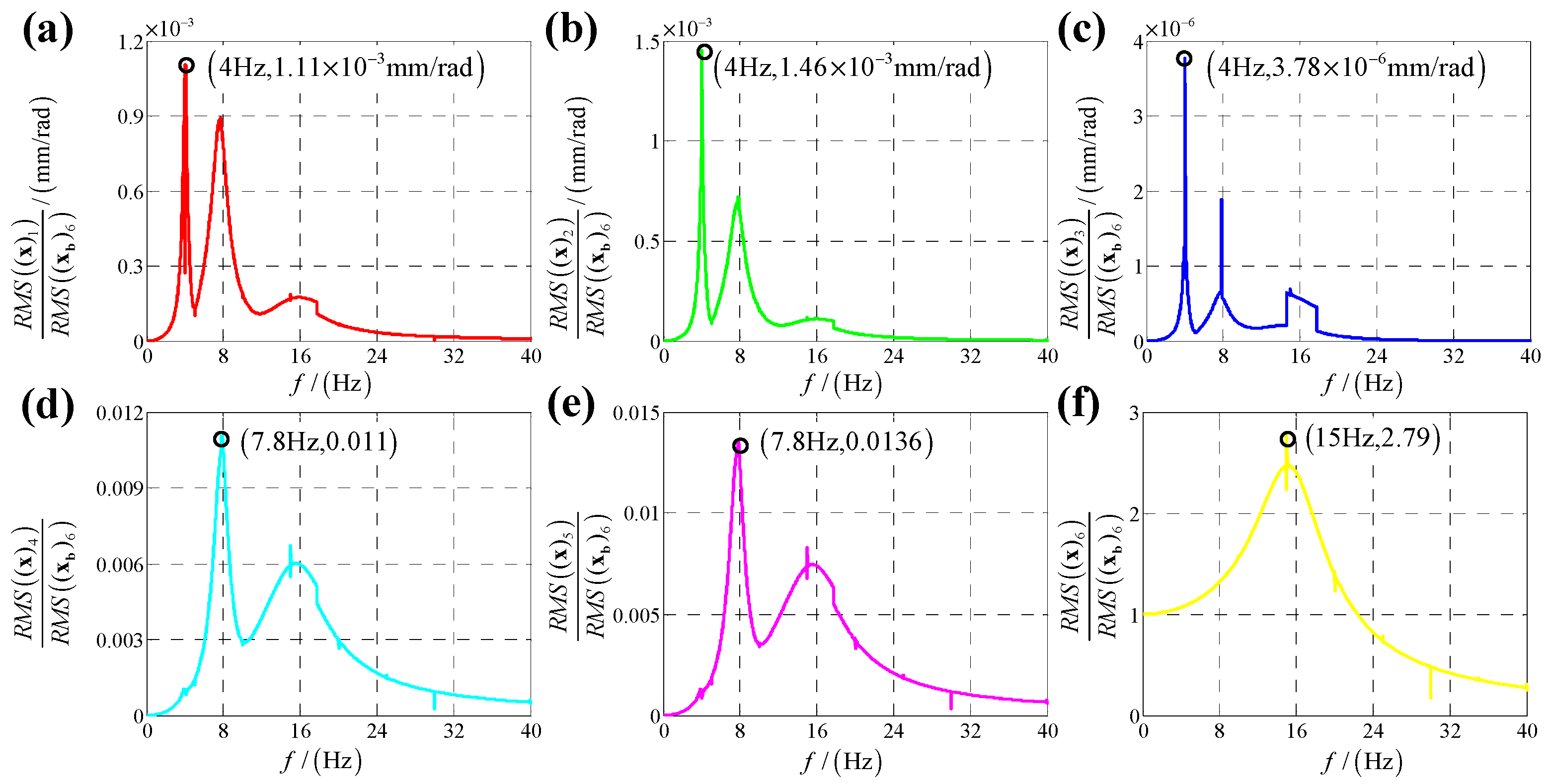

| /mm | /mm | /mm | /° | /° |
|---|---|---|---|---|
| 174.02 | 250.00 | 250.00 | 14.58 | 14.58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tu, Y.; Zhang, H.; Wu, H.; Li, Y.; Bao, B.; Lu, G.; Lin, H.; Chen, X.; Fan, J. Displacement Transmissibility Analysis of Stewart Platform Based SINS’s Bumper Under Base Vibration Excitation. Sensors 2025, 25, 3434. https://doi.org/10.3390/s25113434
Tu Y, Zhang H, Wu H, Li Y, Bao B, Lu G, Lin H, Chen X, Fan J. Displacement Transmissibility Analysis of Stewart Platform Based SINS’s Bumper Under Base Vibration Excitation. Sensors. 2025; 25(11):3434. https://doi.org/10.3390/s25113434
Chicago/Turabian StyleTu, Yongqiang, Haoran Zhang, Hao Wu, Yintao Li, Baohua Bao, Gang Lu, Hongwei Lin, Xinkai Chen, and Jianyu Fan. 2025. "Displacement Transmissibility Analysis of Stewart Platform Based SINS’s Bumper Under Base Vibration Excitation" Sensors 25, no. 11: 3434. https://doi.org/10.3390/s25113434
APA StyleTu, Y., Zhang, H., Wu, H., Li, Y., Bao, B., Lu, G., Lin, H., Chen, X., & Fan, J. (2025). Displacement Transmissibility Analysis of Stewart Platform Based SINS’s Bumper Under Base Vibration Excitation. Sensors, 25(11), 3434. https://doi.org/10.3390/s25113434





