Abstract
Entangled multiphoton is an ideal resource for quantum information technology. Here, narrow-bandwidth hyper-entangled quadphoton is theoretically demonstrated by quantizing degenerate Zeeman sub states through spontaneous eight-wave mixing (EWM) in a hot 85Rb. Polarization-based energy-time entanglement (output) under multiple polarized dressings is presented in detail with uncorrelated photons and Raman scattering suppressed. High-dimensional entanglement is contrived by passive non-Hermitian characteristic, and EWM-based quadphoton is genuine quadphoton with quadripartite entanglement. High quadphoton production rate is achieved from co-action of four strong input fields, and electromagnetically induced transparency (EIT) slow light effect. Atomic passive non-Hermitian characteristic provides the system with acute coherent tunability around exceptional points (EPs). The results unveil multiple coherent channels (~8) inducing oscillations with multiple periods (~19) in quantum correlations, and high-dimensional (~8) four-body entangled quantum network (capacity ~65536). Coexistent hyper and high-dimensional entanglements facilitate high quantum information capacity. The system can be converted among three working states under regulating passive non-Hermitian characteristic via triple polarized dressing. The research provides a promising approach for applying hyper-entangled multiphoton to tunable quantum networks with high information capacity, whose multi-partite entanglement and multiple-degree-of-freedom properties help optimize the accuracy of quantum sensors.
1. Introduction
Nonclassical multiphoton plays key roles on quantum information technology such as quantum network, obtaining quantum light sources with high-dimensional entanglement characteristics and greater information capacity has been the focus of quantum information research to realize breakthroughs [1,2]. Biphoton is generated via spontaneous parametric down-conversion (SPDC) [3] and four-wave mixing (FWM) [4]. Triphoton is generated by cascaded nonlinear parameter processes [5,6,7], post-selection [8], six-wave mixing (SWM) [9], etc. Attention is focused on quadphoton owing to increasing quantum information capacity which can be promoted by hyper [10] and high-dimensional entanglements [11], thus optimizing quantum communications [12,13].
SPDC-based biphoton is criticized for short coherent time and wide bandwidth. FWM-based biphoton and SWM-based triphoton feebly promote information capacity. Post-selection-based quadphoton is essentially biphoton which presents low generation efficiency. Moreover, bare quadphoton difficultly maximizes information capacity for lacking assisted means of hyper and high-dimensional entanglements.
Much theoretical and experimental work has been done on biphoton [14,15], triphoton [16,17,18,19] and multiphoton [20] which suffers natural physical inequality among photons. Hyperentangled [10] and polarization-entangled [21] biphoton are experimentally generated. x(5)-based polarization-entangled [18] or high-dimensional energy-time-entangled [19] triphoton is theoretically realized. To our knowledge, there is no study on x(7)-based hyperentangled and high-dimensional entangled quadphoton. Besides, atomic non-Hermitian system is less studied [22] comparing with other systems [23]. There is yet no tunable high-dimensional entanglement produced via atomic non-Hermitian characteristic.
EWM is a bright method to directly produce genuine quadphoton. Such approach has been theoretically presented in our previous work [24,25,26]. In this single physical process of EWM based on a pure high order nonlinearity (x(7)), the co-action of four strong input fields as well as EIT slow light effect endows the generated quadphoton with a natural high generation rate. For this quadphoton process, coexistent hyper and high-dimensional entanglements can be originally constructed when the coherent polarized dressing is used to control the degenerate Zeeman sub states in the atomic energy levels. Based on this, it is likely to build tunable high-dimensional entanglement, with passively regulating the atomic non-Hermitian characteristic.
In this paper, we theoretically generate x(7)-based energy-time-polarization-hyper-entangled quadphotons in 85Rb hot atomic vapor. The quadphotons’ generation mainly utilizes the Zeeman sub-state of the atom. A spatially separated optical pumping is used to suppress uncorrelated photons. We evaluate conditioned three-photon correlation, quad-photon nonclassical characteristics and correlation. Polarization-based energy-time entanglement is presented in the hyper-entanglement. The utilization of single, double, and triple polarized dressing is employed in the quantization of Zeeman sub-states at the high dimensional level. The construction of tunable high-dimensional entanglement is facilitated by the passive non-Hermitian characteristic of triply dressed atoms. The results show multiple coherent channels inducing Rabbi oscillations accompanied by multiple periods in quantum correlations, and high-dimensional four-body entangled quantum network elements. x(7)-based genuine quadphoton with high production rate, directly generated in single step, is capable of quadripartite entanglement source for quantum information. Coexistent hyper and high-dimensional entanglements, and triply dressed adjustable non-Hermitian characteristic make the quadphoton become a potential candidate for tunable quantum networks with high information capacity.
2. Basic Theory and Simulation
2.1. Quadphoton with Energy-Time-Polarization Hyper-Entanglement
In order to generate the hyper-entanglement, we make use of the degenerate Zeeman sub states of each hyperfine energy level of 85Rb (D1 line (795 nm), D2 line (780 nm), 776 nm). The Zeeman states with are coupled by a linearly polarized pump field and three coupling fields. Among them, the linearly polarized pump field is represented by the horizontal polarization H2; the coupled fields are represented by two vertical polarizations V1, V3 and one horizontal polarization H4. Given the fact that linearly polarized light can be decomposed into circularly polarized light, we can obtain the following relationships: , , and . It is important to note that two distinct types of circularly polarized modes exist, which correspond to the incidence of and , respectively. and are right circular polarization and left circular polarization, respectively.
The hyperfine energy levels are adopted as shown in Figure 1b, and considering that the polarizations of the S1-4 photons respectively follow the corresponding coupling and pump field in each incidence case, there are two kinds of coherent channels corresponding to the spontaneous processes defined as and . Thus, it allows two possible circularly polarized configurations and . Their output photons can be collected at the detectors.
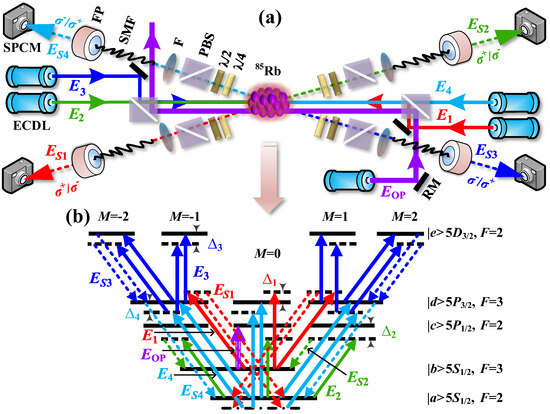
Figure 1.
The following scheme is proposed for the generation of hyperentangled quadphotons in a five-level atomic system. (a) Experimental setup. The generation of quadphotons is detected by four equidistant single-photon counting modules (SPCMs) situated at the core of an 85Rb vapor cell. The experimental setup includes a PBS (polarization beam splitter), an RM (reflective mirror), an SMF (single-mode fiber), a FP (Fabry-Perot cavity), a F (filter), an SPCM (single-photon counting module), and an ECDL (external cavity diode laser). (b) Energy-level diagram with two possible polarization configurations for the spontaneously emitted quadphotons S1-4 from 85Rb (D1 line (795 nm), D2 line (780 nm), 776 nm) five-level atomic system. A strong optical-pumping laser Eop is exploited to optically pump atoms from |b> to |a>, to suppress on-resonance Raman scattering of coupling beams [14].
Consequently, we can model energy-time-polarization hyper-entanglement by EWM process as
The entangled four-photons produced by the EWM process are denoted as S1-4 photons and measured by each of the four detectors. The obtained hyper-entangled quantum states are described as follows:
where ,. and can be viewed as polarization-based energy-time entanglement states, which have similar entanglement performance, here we mainly discuss the former state and relevant spontaneous process in detail.
2.2. The Schematic of Quadphoton Generation
A simplified experimental setup of quadphoton generation is illustrated in Figure 1a, where the occurrence of EWM process happens through 85Rb atomic vapor. With identical five-level atoms initially prepared in their ground level |a> (see Figure 1b), the atomic vapor is confined within a long and thin cylindrical volume. The power of pump beam E2 (horizontal polarization, ~795 nm, frequency ω2, wave vector k2, Rabi frequency G2) is about several milliwatts, where , is dipole moment between energy levels |i> and |j>. The power of coupling beams E1 (vertical polarization, ~780 nm, ω1, k1, G1), E3 (vertical polarization, ~776 nm, ω3, k3, G3) and E4 (horizontal polarization, ~780 nm, ω4, k4, G4) is over 10 milliwatts. The power of optical-pumping beam Eop (vertical polarization, ~795 nm) is over 30 milliwatts. E1, E4 and Eop counter-propagate with E2. E3 propagates in E2 direction. It should be noted that Eop is aligned parallel to E1–4 without overlapping. The schematic of quadphotons generated via a five-level atomic system is shown in Figure 1b. The role of E2 is to complete the process of atomic leaps |a>→|c> with detuning denoted as ∆2. Based on the above properties, this process significantly suppresses the quantum atomic noise and allows the atomic population to dominate in the ground state |a> [15] For the other three coupling beams Ei (i = 1, 3, 4), the detuning is denoted as (i = 1, 3, 4), corresponding to the atomic transitions |b>→|d>, |d>→|e>, and |a>→|d>, respectively. Here, is detuning defined as the frequency difference between the resonant transition frequency ωij and laser frequency ωi of the field Ei. The coupling beam E1 has been demonstrated to facilitate the EWM nonlinear process and to open the transparency window for S1 photons through the slow-light effect [19]. EOP is on resonance to the atomic transition |b>→|c>. The EWM process meets the energy conservation ћω1 + ћω2 + ћω3 + ћω4 = ћωS1 + ћωS2 + ћωS3 + ћωS4, where ωSi = ϖSi + δi. Then, with the phase-matching condition ћk1 + ћk2 + ћk3 + ћk4 = ћkS1 + ћkS2 + ћkS3 + ћkS4 and low-gain limit, the EWM process will occur spontaneously, which could generate entangled quadphotons S1–4 [24,25,26].
In the interaction picture, the effective interaction Hamiltonian of EWM process can be expressed as (ignoring the reflections from the systemic surfaces and using the rotating-wave approximation)
where vacuum permittivity is denoted by , volume illuminated by input beams E1–4 together is denoted by V, seventh-order nonlinear susceptibility is denoted by χ(7), positive-frequency part of input beam Ei is denoted by , quantum field amplitude of Si photon is denoted by , and Hermitian conjugate is denoted by H.c. is a constant, and is the cross-section area of single mode; The nonlinear parametric coupling coefficient is represented by . The central frequency of a Si photon is denoted by ϖSi. The speed of light in a vacuum, c, is also included in this equation. The electric field intensity is expressed as . The term Vq signifies the quantization volume. The longitudinal detuning function, denoted by , serves to determine the natural spectral width of quadphoton. is the phase mismatching of quadphoton, the phase-match condition holds perfectly when Δk is equal to 0, and ki is wavenumber of field; is the annihilation operator of the output mode for Si photon; Δω = ω1 + ω2 + ω3 + ω4 − ωS1 − ωS2 − ωS3 − ωS4.
Considering the first-order perturbation in the interaction picture, the photon state at the output surface is approximately the linear superposition of the vacuum state |0> and |ψ>. Given the unobservability of the vacuum state, it is set to one side and ignored in further analysis. The state |ψ> of quadphoton can be expressed as
Combining with Equations (3) and (4) [25], exp(−iΔωt) becomes 2πδ(Δω), which indicates the energy conservation of EWM process and leads to the frequency entanglement of the quadphoton state. As demonstrated in Equation (4), the quadphoton state exhibits entanglement in both frequency and wave number. This entanglement is illustrated by in the frequency domain, which is due to energy conservation. The wave number entanglement, denoted by , is an inherent property of the system under consideration. It is not possible to decompose into four independent functions, each containing only kS1–4. In the general noncollinear case, wave-number entanglement exerts a significant influence on the spatial correlation of quadphotons.
In order to engage in discourse on the optical properties of quadphotons generated via a five-level system, it is necessary to consider the measurement of the average quad-photon coincidence counting rate (Rcc). Rcc is a significant characterization metric of energy-time-entangled multiphotons [5,7,15]. From Rcc, we are able to obtain periods of oscillation, coherent time, and other crucial parameters. We suppose the detectors SPCM1-4 detect photons with frequency ωS1–4, respectively. Assuming perfect detection efficiency, Rcc is defined by
The fourth-order correlation function (CF), denoted G(4)(tS1,tS2,tS3,tS4), is the probability of four correlated coincidence events being detected jointly. According to Glauber’s theory, it can be written as:
where tSi = tSi0 − rSi/c, with rSi representing the length of Si’s optical path from the output surface of the medium to the detector. For the sake of simplicity, it is assumed that rS1 = rS2 = rS3 = rS4. is the amplitude of quadphoton, which can be expressed as
where P2 is a constant which absorbs all the constants and slowly varying terms. By using Equation (7), one can obtain
where τ1 = tS1 − tS4, τ2 = tS2 − tS4 and τ3 = tS3 − tS4 are the relative time. The S1-3 photons are used differently from the S4 photon, with the former being coincidence counting stop photons and the latter being coincidence counting trigger photon. In time domain, the wave function of quadphoton is a convolution of κ and Φ as . Where and .
2.3. Evaluation on the Correlations of Conditioned Three-Photon and Quadphoton
The correlation of conditioned three-photon is evaluated as Supplement S1. Checking the violation of Cauchy-Schwarz inequality (C.S.) is usually used to estimate the nonclassical behavior of multiphoton state. According to the inequality of for quadphoton, their correlated properties can be estimated through Equation (10).
where is the normalized cross-CF of quadphoton; is the normalized auto-CF of Si photon and can be obtained via a beam splitter. When the obtained C.S. is larger than 1, Cauchy-Schwarz inequality is violated, which indicates a strong nonclassical correlation in the quadphoton state.
The noise accompanying generation of quadphoton is mainly because of the third and fifth-order nonlinearity. Therefore, the actual Rcc of quadphoton can be written as
where is CF of SWM1 triphotons (k1 + k2 + k3 = kS1 + kS2 + kS3); is CF of SWM2 triphotons (k1 + k2 + k4 = kS1 + kS2 + kS4); is CF of SWM3 triphotons (k1 + k3 + k4 = kS1 + kS3 + kS4); is CF of SWM4 triphotons (k2 + k3 + k4 = kS2 + kS3 + kS4); is CF of phase conjugate FWM1 (PCFWM1) biphotons (k1 + k2 = kS1 + kS2); is CF of PCFWM2 biphotons (k1 + k3 = kS3 + kS4); is CF of self-diffraction FWM3 (SDFWM3) biphotons (k1 + k4 = kS1 + kS4); is CF of PCFWM4 biphotons (k2 + k4 = kS1 + kS2); is CF of PCFWM5 biphotons (k3 + k4 = kS3 + kS4); is CF of SDFWM6 biphotons (2k1 = kS1 + kaS1); is CF of SDFWM7 biphotons (2k2 = kS2 + kaS2); is CF of SDFWM8 biphotons (2k3 = kS3 + kaS3); is CF of SDFWM9 biphotons (2k4 = kS4 + kaS4); RS1–4 are the counting rates of uncorrelated single photons [27], which originate from S1-4 photons of SDFWM6-9 biphotons, respectively. Because the central frequency difference between aS1 and S4, aS2 and S3, aS3 and S2, aS4 and S1 photons, is more than 3 GHz, the noise of aS1-4 photons is filtered out by filters and narrowband etalon FPs before being detected by the SPCMs as illustrated in Figure 1a. In addition, triphotons of SWM1(2) and biphotons of PCFWM1(5) will pass through filters and FPs. However, one of triphotons of SWM3(4) will be filtered out by filter and FP, and another two photons will pass through another two filters and FPs; one of biphotons of PCFWM2(SDFWM3, PCFWM4) will be filtered out by filter and FP, and another photon will pass through another filter and FP. As a result, the actual Rcc of quadphoton (after filtering) can be rewritten as
where and is cross-CF of filtered triphotons of SWM3 and SWM4, respectively. R′S1–4 are the counting rates of uncorrelated single photons. R′S1 originates from S1 photons of biphotons of SDFWM3 and SDFWM6; R′S2 originates from S2 photons of biphotons of PCFWM4 and SDFWM7; R′S3 originates from S3 photons of biphotons of PCFWM2 and SDFWM8; R′S4 originates from S4 photons of biphotons of SDFWM3 and SDFWM9. Consequently, the accidental coincidence counting of quadphoton coincidence counting in actual measurements is caused by SWM1, SWM2, PCFWM1, PCFWM5, , , uncorrelated single photons, and dark count of SPCMs, which constitute the background of coincidence counting of quadphoton. In addition to using filters, FPs and optical pumping as depicted in Figure 1, the accidental coincidence counting can be effectively reduced by finely placing SPCMs at appropriate angles which satisfy the phase-matching condition of EWM process as soon as possible, however, dissatisfy the phase-matching conditions of SWM and FWM processes.
2.4. Optical Response and Coincidence Counts of Quadphoton
As in Equation (7), the amplitude of quadphoton is doubly determined by the nonlinear coefficient κ and longitudinal detuning function . In our case, Rabi frequency and linewidth are quite smaller than the phase-matching bandwidth and EIT bandwidth , approximates one [19]. The wave function of quadphoton can be expressed as . Consequently, one simply considers the nonlinear optical response.
Figure 2a–c show the rubidium atomic polarized energy-level diagrams of EWM in the “dressed-state” picture with multiple circularly polarized dressing fields. In Figure 2a, single circularly polarized dressing field E1 is introduced to generate multiple coherent channels. The energy level |d, M = 1⟩ is separated into energy levels |λ1±M⟩ by the dressing effect of E1. Consequently, the S1 photon acquires four dressed states: and . The S2 photon, in turn, has two dressed states: . The S3 photon has two states, and , and the S4 photon has one single state, , which can be derived from Equation (S6). The collective output states and their corresponding input states coalesce to form four distinct polarization-based coherent channels, a phenomenon that is governed by the principle of energy conservation. In Figure 2b, circularly polarized dressing field E4 with more power over Figure 2a is further added to generate more coherent channels. The energy level |d, M = −1⟩ is separated into energy levels |λ2±M⟩ by the dressing effect of E4. Consequently, the S1 photon has six dressed states: and . The S2 photon has two dressed states: . The S3 photon has two dressed states: and one bare state . In the case of the S4 photon, a single bare state, , can be derived from Equation (S7). The collective output states and their corresponding input states coalesce to comprise six polarization-based coherent channels, a phenomenon that is governed by the principle of energy conservation. In Figure 2c, we introduce the third circularly polarized dressing field E3 with more power over Figure 2b. In this case, the energy level |e, M = –2⟩ is divided into energy levels |λ3±M⟩ due to the dressing effect of E3. Consequently, the S1 photon possesses eight dressed states: and . The S2 photon has two dressed states, , and the S3 photon has four dressed states, and , and S4 photon has one bare state , which are derived from Equation (S8). Similarly, it can form eight polarization-based coherent channels with energy conservation. Where , ; , ; , ; , , , , , , .
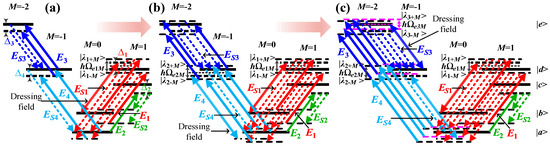
Figure 2.
Schemes for producing quadphotons with polarization-based energy-time entanglement of multi-channel EWM in five-level atomic system. (a–c) Evolution of coherent channels whose energy is conservative from the 85Rb atomic energy-level diagram by EWM. (a) The model under consideration comprises four channels, each characterized by four-dimensional quantized energy levels and a single circularly polarized dressing field. (b) The model under consideration comprises six channels, each characterized by six-dimensional quantized energy levels and double circularly polarized dressing fields. (c) eight channels in eight-dimensional quantized energy-levels with three circularly polarized dressing fields.
The perturbation chain is a suitable approach to directly present the relevant physical picture for demonstrating a multi-wave mixing process [28]. From Figure 2a, we can get the polarized perturbation chains as Equations (S4) and (S5). According to the polarized perturbation chains, the seventh-order nonlinear susceptibilities for the generated fields with single dressing (E1) (SM), double dressing (E1 and E4) (DM) and triple dressing (E1, E4 and E3) (TM) are defined in Equations (S6)–(S8), respectively. According to Equations (S6)–(S8), the resonant positions and line widths of S1-4 photons are as shown in Table S1.
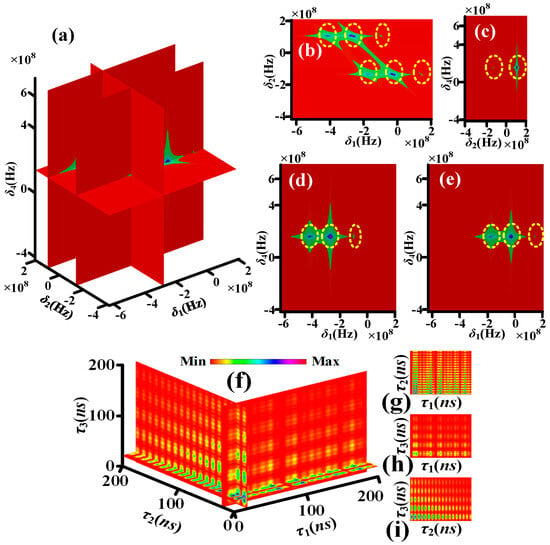
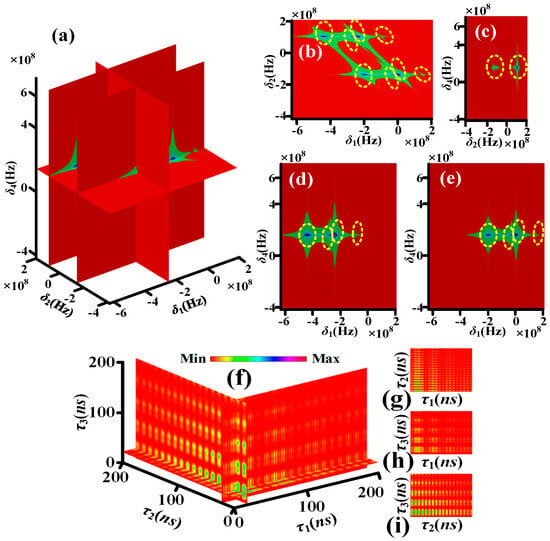
Figure 3a–e, simulated by Equation (S6), show the theoretical nonlinear susceptibility of quadphoton versus δ1, δ2 and δ4 controlled by single circularly polarized dressing field. Each yellow dotted circle contains one corresponding frequency mode. The four yellow dotted circles in δ1 direction of Figure 3b, two yellow dotted circles in δ1 direction of Figure 3d and two yellow dotted circles in δ1 direction of Figure 3e indicate S1 photon have four frequency modes. The two yellow dotted circles in δ2 direction of Figure 3b or Figure 3c indicate S2 photon have two frequency modes. The one yellow dotted circles in δ4 direction of Figure 3c, Figure 3d or Figure 3e indicates S4 photon has one frequency mode. It has been established that the S3 photon exhibits two distinct frequency modes in accordance with the energy conservation condition, δ1 + δ2 + δ3 + δ4 = 0. As illustrated in Figure 4a–e, the theoretical nonlinear susceptibility of the quadphoton is demonstrated versus δ1, δ2 and δ4, which are controlled by double circularly polarized dressing fields. This theoretical investigation was simulated using Equation (S7). The six yellow dotted circles in δ1 direction of Figure 4b, three yellow dotted circles in δ1 direction of Figure 4d and three yellow dotted circles in δ1 direction of Figure 4e indicate S1 photon have six frequency modes. The two yellow dotted circles in δ2 direction of Figure 4b or Figure 4c indicate S2 photon have two frequency modes. The one yellow dotted circles in δ4 direction of Figure 4c, Figure 4d or Figure 4e indicates S4 photon has one frequency mode. S3 photon has three frequency modes as per the energy conservation. Figure 5a–e, simulated by Equation (S8), show the theoretical nonlinear susceptibility of quadphoton versus δ1, δ2 and δ4 controlled by three circularly polarized dressing fields. The eight yellow dotted circles in δ1 direction of Figure 5b, four yellow dotted circles in δ1 direction of Figure 5d and four yellow dotted circles in δ1 direction of Figure 5e indicate S1 photon have eight frequency modes. The two yellow dotted circles in δ2 direction of Figure 5b or Figure 5c indicate S2 photon have two frequency modes. The one yellow dotted circles in δ4 direction of Figure 5c, Figure 5d or Figure 5e indicates S4 photon has one frequency mode. S3 photon has four frequency modes as per the energy conservation.
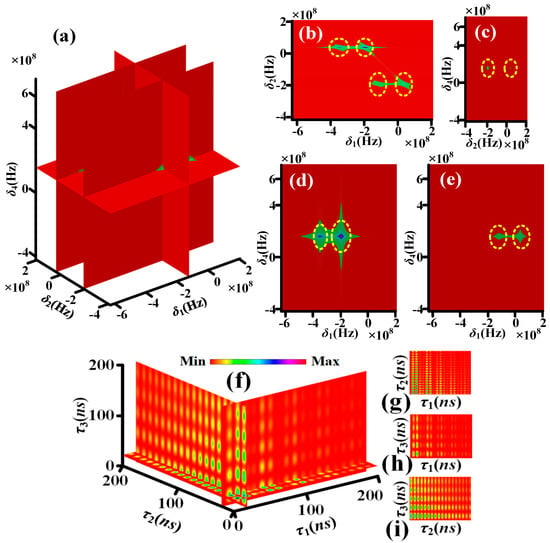
Figure 3.
(a) The seventh-order nonlinear susceptibility with single circularly polarized dressing field. (b) The nonlinear susceptibility in the flat of (a) with . (c) The nonlinear susceptibility in the flat of (a) with . (d) The nonlinear susceptibility in the flat of (a) with . (e) The nonlinear susceptibility in the flat of (a) with . The coincidence counting rate of quadphoton with single circularly polarized dressing field. (f) A sectional view of four-dimensional coincidence counting rate of quadphoton. (g) The coincidence counting rate of (f) in the and directions. (h) The same as (g), but in the and directions. (i) The same as (g), but in the and directions.
For modelling and demonstrating Rcc, polarization-based energy-time entanglement state with single, double and triple dressing can be modelled as Equations (S9)–(S11), respectively.
Based on the resonant position and line width of δi obtained from Table S1, the residue theorem is applied to integrate to obtain the quadphoton amplitude with single dressing (E1), double dressing (E1 and E4) and triple dressing (E1, E4 and E3) as Equations(S12)–(S14), respectively. Where τ1 = tS1 − tS4, τ2 = tS2 − tS4 and τ3 = tS3 − tS4. Afterwards, Rcc for quadphoton with single, double and triple dressing can be separately expressed as follows.
For characterizing the polarization-based energy-time-entangled quadphoton, we thus simulate Rcc according to Equations (13)–(15). Figure 3f shows the four-dimensional (4D) simulation of coincidence counting rate with single circularly polarized dressing field (Equation (13)). The wave form displays multiple decaying Rabi oscillations with four periods of , , and in τ1 direction of Figure 3f, Figure 3g or Figure 3h.
The Rabi oscillation, comprising four periods, is induced by the energy exchange and destructive interference among four polarization-based frequency modes of a single photon from four polarization-based coherent channels of energy conservation (C1–C4), as illustrated in Figure 2a. The wave form in τ2 (τ3) direction of Figure 3f, Figure 3g or Figure 3i (Figure 3f, Figure 3h or Figure 3i presents decaying Rabi oscillation with single period of (). This phenomenon is attributable to the energy exchange and destructive interference between two polarization-based frequency modes of S2 (S3) photons from C1–C4, as illustrated in Figure 2a. Figure 4f presents the 4D simulation of coincidence counting rate with double circularly polarized dressing fields (Equation (14)). The waveform displays multiple decaying Rabi oscillations with ten periods in the τ1 direction of Figure 4f, Figure 4g or Figure 4h. The ten periods are , , , , , , , , and . The Rabi oscillations with ten periods are induced via the energy exchange and destructive interference among six polarization-based frequency modes of S1 photon from six polarization-based coherent channels of energy conservation (C5–C10) schemed in Figure 2b. The wave form in τ2 direction of Figure 4f, Figure 4g or Figure 4i presents decaying Rabi oscillation with single period of . The wave form in τ3 direction of Figure 4f, Figure 4h or Figure 4i presents decaying Rabi oscillations with three periods of , and . The phenomenon is for the reason of the energy exchange and destructive interference between three polarization-based frequency modes of S3 photon from C5–C10 schemed in Figure 2b. Figure 5f reveals the 4D simulation of coincidence counting rate with triple circularly polarized dressing fields (Equation (15)). The wave form displays multiple decaying Rabi oscillations with nineteen periods in τ1 direction of Figure 5f, Figure 4g or Figure 4h. The nineteen periods are , , , , , , , , , , , , , , , , , , and . The Rabi oscillations, which exhibit nineteen periods, are induced through the energy exchange and destructive interference among eight polarization-based frequency modes of S1 photons from eight polarization-based coherent channels of energy conservation (C11–C18), as illustrated in Figure 2c. The wave form in τ2 direction of Figure 5f, Figure 5g or Figure 5i presents decaying Rabi oscillation with single period of . The wave form in τ3 direction of Figure 5f, Figure 5h or Figure 5i presents decaying Rabi oscillations with six periods of , , , , and . The phenomenon under investigation is attributed to the energy exchange and destructive interference between four polarization-based frequency modes of S3 photons from C11–C18, as depicted in Figure 2c. Indeed, distinguishing between these periods can be challenging. For instance, there are ten periods of S1 photon with double dressing fields, nineteen periods of S1 photon, and six periods of S3 photon with triple dressing fields. This difficulty arises from the presence of certain periods that are either too small or too large, several periods that are quite close together, and small periods that are covered by large periods.
2.5. The Generation of Polarization-Based High-Dimensional Entanglement Through Passive Non-Hermitian Processes
The EIT can not only promote the EWM process but also structure a passive non-Hermitian system. The polarized dressing terms , and of susceptibility in Equation (S8) are equivalent to EIT-based passive non-Hermitian system. By minimizing triple polarized dressing terms, the eigenvalues can be derived as Equations (S15) and (S16).
In Figures S1 and S2, the evolution of the real and imaginary parts of the eigenvalues is demonstrated in the parameter space [G1θM, G4θM, G3θM]. δ1i represents the ith eigenvalue of δ1. When [G1θM, G4θM, G3θM] = [, , ] = [0.5Γ21M, 0.5Γ11M, 0.38Γ41M] is satisfied, triple non-Hermitian EP1 (EP11, EP12), EP2 (EP21, EP22) and EP3 (EP31, EP32) emerge, being followed by the degeneracy of three pairs of eigenvalues. Where g1θM = , g4θM = , g3θM = . Thus, it can obtain three second-order non-Hermitian EPs. It has been demonstrated that, under certain conditions, the real parts of the eigenvalues undergo a process of splitting. These conditions include the satisfaction of the following inequalities: [G1θM, G4θM, G3θM] > [0.5Γ21M, 0.5Γ11M, 0.38Γ41M], as demonstrated in G1θM/Γ21M direction of the combination of Figures S1b,d (Figures S1j,l and S2b,d,j,l), G4θM/Γ11M direction of the combination of Figures S1b,j and S1d,l, as well as G3θM/Γ41M direction of the combination of Figures S2b,j and S2d,l; while the imaginary parts remain degenerate, as demonstrated in G1θM/Γ21M direction of the combination of Figure S1f,h (Figures S1n,p and S2f,h,m,p), G4θM/Γ11M direction of the combination of Figure S1f,n,h,p as well as G3θM/Γ41M direction of the combination of Figure S2f,n,h,p. The system exhibits three second-order non-Hermitian quasi parity–time (PT) symmetries. In the event of encountering the following relation, the imaginary parts of the eigenvalues undergo splitting: [G1θM, G4θM, G3θM] < [0.5Γ21M, 0.5Γ11M, 0.38Γ41M], as demonstrated in G1θM/Γ21M direction of the combination of Figure S1f,h (Figures S1n,p and S2f,h,n,p) G4θM/Γ11M direction of the combination of Figure S1f,n,h,p as well as G3θM/Γ41M direction of the combination of Figure S2f,n,h,p; while the real parts keep degenerate, as demonstrated in G1θM/Γ21M direction of the combination of Figure S1b,d (Figures S1j,l and S2b,d,j,l), G4θM/Γ11M direction of the combination of Figure S1b,j,d,l as well as G3θM/Γ41M direction of the combination of Figure S2b,j,d,l. The outcome of this process is the breakdown of three second-order non-Hermitian quasi-PT symmetries within the system. In summary, the evolution of three second-order non-Hermitian EPs can be controlled by regulating the triple-polarized dressing fields, thereby determining whether the breakdown of three second-order non-Hermitian quasi-PT symmetries occurs. Considering Equation (S8), δ2 and δ4 have two eigenvalues and one eigenvalue, respectively. The eigenvalues of δ3 can be thus obtained via the polarization-based energy conservation.
According to the above theory concerning the passive non-Hermitian system, in atomic polarized energy levels, we naturally structure multi-resonance and multi-absorptive coherent channels of quadphotons. As illustrated in Figure 6, the rubidium atomic polarized energy-level diagrams of multi-resonance and multi-absorptive coherent channels of quadphoton are depicted in the “dressed-state” picture with triple circularly polarized dressing fields. With [G1θM, G4θM, G3θM] > [0.5Γ21M, 0.5Γ11M, 0.38Γ41M], the real components of the energy levels |d, M = 1⟩, |d, M = −1⟩ and |e, M = –2⟩ are split into energy levels |λ1±M⟩, |λ2±M⟩ and |λ3±M⟩, as shown in Figure 6a. It is noteworthy that the corresponding imaginary components remain degenerate. Thus, S1 photon has eight resonance dressed states (, ) and two absorptive states (, ), S2 photon has two resonance dressed states and one absorptive state , S3 photon has four resonance dressed states (, ) and two absorptive states (, ), and S4 photon has one resonance state and one absorptive state . All output and compatible input states form eight polarization-based resonance coherent channels and two polarization-based absorptive coherent channels. When [G1θM, G4θM, G3θM] = [0.5Γ21M, 0.5Γ11M, 0.38Γ41M], the real and imaginary components of all energy levels remain degenerate, as demonstrated in Figure 6b. Consequently, the S1 photon exhibits two resonance states (, ), and two absorptive states (, ). The S2 photon has one additional resonance state, given by and one absorptive state . S3 photon has two resonance states (, ) and two absorptive states (, ), and S4 photon has one resonance state and one absorptive state . All output and matched input states form two polarization-based resonance coherent channels and two polarization-based absorptive coherent channels. It is evident that with [G1θM, G4θM, G3θM] < [0.5Γ21M, 0.5Γ11M, 0.38Γ41M], the imaginary components of the energy levels |d, M = 1⟩, |d, M = −1⟩ and |e, M = −2⟩ are split into energy levels |Г1 ± M⟩, |Г2 ± M⟩ and |Г3 ± M⟩ as illustrated in Figure 6c. It is important to note that the corresponding real components remain degenerate. Accordingly, S1 photon has eight absorptive dressed states (, ) and two resonance states (, ), S2 photon has two absorptive dressed states and one resonance state , S3 photon has four absorptive dressed states (, ) and two resonance states (, ), and S4 photon has one absorptive state and one resonance state . Similarly, it can generate eight polarization-based absorptive coherent channels and two polarization-based resonance coherent channels. Where , , , , , , , , , , , , , and . Table S2 supplies the relevant resonance and absorptive coherent channels of quadphotons in detail.
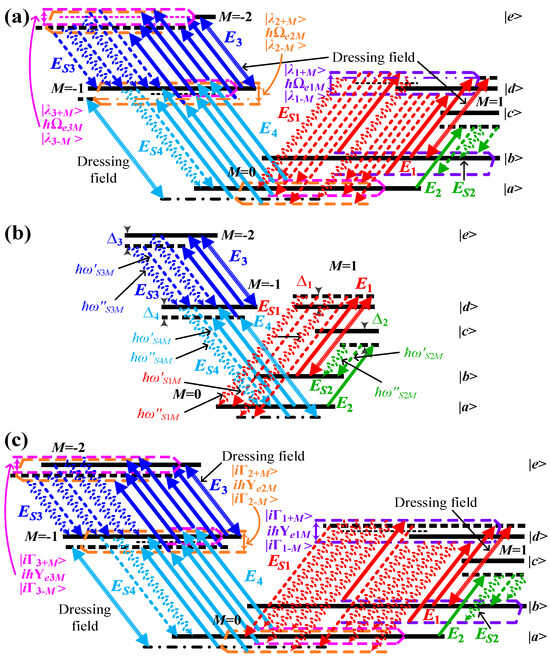
Figure 6.
Energy-level sketch of multi-resonance (real part) and multi-absorptive (imaginary part) coherent channels in the EWM process is presented herein. (a) Eight-resonance and two-absorptive channels at [G1θM, G4θM, G3θM] > [0.5Γ21M, 0.5Γ11M, 0.38Γ41M]. (b) two-resonance and two-absorptive channels at [G1θM, G4θM, G3θM] = [0.5Γ21M, 0.5Γ11M, 0.38Γ41M]. (c) Two-resonance and eight-absorptive channels at [G1θM, G4θM, G3θM] < [0.5Γ21M, 0.5Γ11M, 0.38Γ41M].
Ulteriorly, the preparative entanglement states are used to structure polarization-based high-dimensional four-body entangled quantum network element among Alice, Bob, Charlie and David. The states of S1–4 photons function as the information carriers for Alice, Bob, Charlie, and David, respectively. The states of the photons are represented by [G1θM, G4θM, G3θM] > [0.5Γ21M, 0.5Γ11M, 0.38Γ41M], as illustrated in Figure 7a, eight resonance dressed states of the S1 photon, two resonance dressed states of the S2 photon, four resonance dressed states of the S3 photon, and one resonance state of the S4 photon form an eight-resonance-channels-based eight-dimensional four-body entangled communication, with an information capacity of ~65536. Two absorptive states of the S1 photon, one absorptive state of the S2 photon, two absorptive states of the S3 photon, and one absorptive state of the S4 photon form a two-absorptive-channels-based two-dimensional four-body entangled communication, with an information capacity of ~16. With [G1θM, G4θM, G3θM] = [0.5Γ21M, 0.5Γ11M, 0.38Γ41M], as illustrated in Figure 7b, two resonance (absorptive) states of S1 photon, one resonance (absorptive) state of S2 photon, two resonance (absorptive) states of S3 photon, and one resonance (absorptive) state of S4 photon comprise two-resonance(absorptive)-channels-based two-dimensional four-body entangled communication, its information capacity is ~16. As illustrated in Figure 7c, the information capacity of this communication is maximized when the following conditions are met: [G1θM, G4θM, G3θM] < [0.5Γ21M, 0.5Γ11M, 0.38Γ41M] in which the eight absorptive dressed states of the S1 photon, the two absorptive dressed states of the S2 photon, the four absorptive dressed states of the S3 photon, and the one absorptive state of the S4 photon collectively constitute the eight-absorptive-channels-based eight-dimensional four-body entangled communication, with an information capacity of ~65,536. Analogously, this configuration can also facilitate two-resonance-channels-based two-dimensional four-body entangled communication, with an information capacity of ~16.
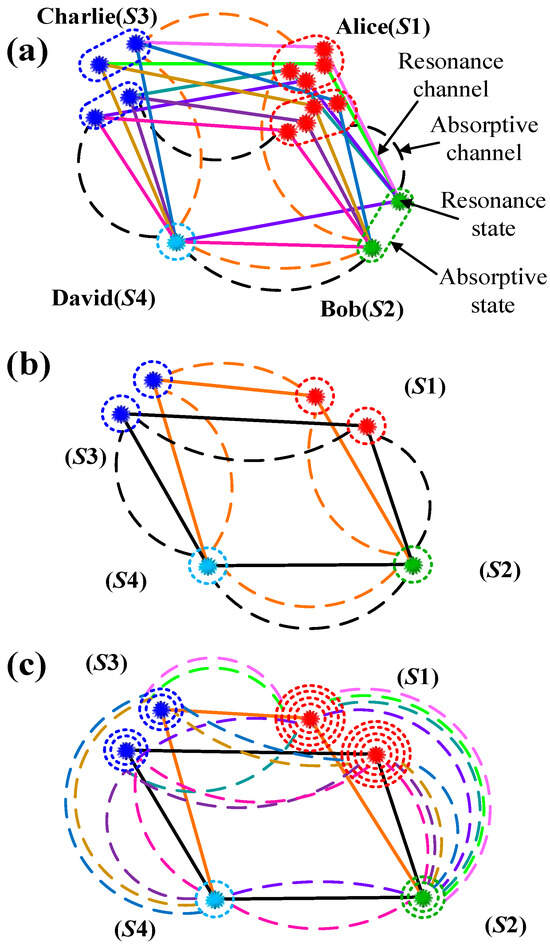
Figure 7.
As illustrated in (a–c), the model of a polarization-based high-dimensional four-body entangled quantum network has been constructed by applying the entanglement states depicted in Figure 6a–c.
3. Conclusions
In summary, we theoretically demonstrated EWM-based hyper-entangled quadphotons generation in 85Rb vapor. Polarization-based energy-time entanglement was obtained under single, double and triple circularly polarized dressing fields. We quantized the degenerate Zeeman sub states for quadphotons along with polarization-based energy-time entanglement, which formed multiple coherent channels. These coherent channels were regulated through dressing and assisted by polarized nonlinear susceptibilities while satisfying polarization-based energy conservation. Ulteriorly, polarization-based tunable high-dimensional four-body entanglement and quantum network elements were demonstrated through passive non-Hermitian characteristic by simulating multi-resonance (real part) and multi-absorptive (imaginary part) coherent channels under triple dressing regulation. The fine physical characteristics make the hyper-entangled quadphoton naturally serve as a significant entangled source. The predicted high information capacity is stimulated by coexistent hyper and high-dimensional entanglements of genuine quadphoton. The high producing efficiency is caused by four strong input fields, EIT slow light effect, and etc. The atomic passive non-Hermitian characteristic eventuates the system with a high tunability around EPs under triple dressing regulation. Eventually, the produced hyper-entangled quadphoton is potential to be applied in tunable four-body entangled quantum networks with high information capacity, whose multi-partite entanglement and multiple-degree-of-freedom properties help optimize the accuracy of quantum sensors.
Supplementary Materials
The following supporting information can be downloaded at: https://www.mdpi.com/article/10.3390/s25113425/s1.
Author Contributions
Validation, Z.F.; Formal analysis, G.L.; Investigation, Q.C.; Resources, Y.Z.; Data curation, S.L.; Writing—original draft, R.Z. and S.Z.; Writing—review & editing, R.Z., S.Z. and Y.Z.; Funding acquisition, Y.Z. All authors have read and agreed to the published version of the manuscript.
Funding
National Natural Science Foundation of China (62475208, 62475209, 12474392).
Data Availability Statement
Data underlying the results presented in this paper are not publicly available at this time but may be obtained from the authors upon reasonable request.
Conflicts of Interest
The authors declare no conflicts of interest.
References
- Kimble, H.J. The quantum internet. Nature 2008, 453, 1023. [Google Scholar] [CrossRef]
- Chang, K.-C.; Cheng, X.; Sarihan, M.C.; Wong, C.W. Recent advances in high-dimensional quantum frequency combs. Newton 2025, 1, 100024. [Google Scholar] [CrossRef]
- Burnham, D.C.; Weinberg, D.L. Observation of simultaneity in parametric production of optical photon pairs. Phys. Rev. Lett. 1970, 25, 84. [Google Scholar] [CrossRef]
- Balić, V.; Braje, D.A.; Kolchin, P.; Yin, G.Y.; Harris, S.E. Generation of paired photons with controllable waveforms. Phys. Rev. Lett. 2005, 94, 183601. [Google Scholar] [CrossRef]
- Hübel, H.; Hamel, D.R.; Fedrizzi, A.; Ramelow, S.; Resch, K.J.; Jennewein, T. Direct generation of photon triplets using cascaded photon-pair sources. Nature 2010, 466, 601. [Google Scholar] [CrossRef]
- Wen, J.; Oh, E.; Du, S. Tripartite entanglement generation via four-wave mixings: Narrowband triphoton W state. J. Opt. Soc. Am. B 2010, 27, A11. [Google Scholar] [CrossRef]
- Ding, D.-S.; Zhang, W.; Shi, S.; Zhou, Z.-Y.; Li, Y.; Shi, B.-S.; Guo, G.-C. Hybrid-cascaded generation of tripartite telecom photons using an atomic ensemble and a nonlinear waveguide. Optica 2015, 2, 642. [Google Scholar] [CrossRef]
- Bouwmeester, D.; Pan, J.W.; Daniell, M.; Weinfurter, H.; Zeilinger, A. Observation of three-photon Greenberger-Horne-Zeilinger entanglement. Phys. Rev. Lett. 1999, 82, 1345. [Google Scholar] [CrossRef]
- Zhang, S.; Li, W.; Li, K.; Li, Y.; Mu, F.; Feng, Y.; Liu, Y.; Zhang, Y. Triphoton correlations in six-wave mixing. Ann. Phys. 2020, 412, 168000. [Google Scholar] [CrossRef]
- Yan, H.; Zhang, S.; Chen, J.F.; Loy, M.M.T.; Wong, G.K.L.; Du, S. Generation of narrow-band hyperentangled nondegenerate paired photons. Phys. Rev. Lett. 2011, 106, 033601. [Google Scholar] [CrossRef]
- Zhang, Y.; Li, X.; Zhang, D.; Cheng, L.; Li, C.; Zhang, Y. Generation of high-dimensional energy-time-entangled photon pairs. Phys. Rev. A 2017, 96, 053849. [Google Scholar] [CrossRef]
- Lee, C.; Bunandar, D.; Zhang, Z.; Steinbrecher, G.R.; Ben Dixon, P.; Wong, F.N.C.; Shapiro, J.H.; Hamilton, S.A.; Englund, D. Large-alphabet encoding for higher-rate quantum key distribution. Opt. Express 2019, 27, 17539–17549. [Google Scholar] [CrossRef]
- Yang, S.; Sarihan, M.C.; Chang, K.-C.; Wong, C.W.; Dolecek, L. Efficient information reconciliation for energy-time entanglement quantum key distribution. In Proceedings of the 2019 53rd Asilomar Conference on Signals, Systems, and Computers, IEEE, Pacific Grove, CA, USA, 3–6 November 2019. [Google Scholar]
- Zhao, L.; Guo, X.; Sun, Y.; Su, Y.; Loy, M.M.T.; Du, S. Shaping the biphoton temporal waveform with spatial light modulation. Phys. Rev. Lett. 2015, 115, 193601. [Google Scholar] [CrossRef]
- Shu, C.; Chen, P.; Chow, T.K.A.; Zhu, L.; Xiao, Y.; Loy, M.M.T.; Du, S. Subnatural-linewidth biphotons from a doppler-broadened hot atomic vapour cell. Nat. Commun. 2016, 7, 12783. [Google Scholar] [CrossRef] [PubMed]
- Shalm, L.K.; Hamel, D.R.; Yan, Z.; Simon, C.; Resch, K.J.; Jennewein, T. Three-photon energy-time entanglement. Nature Phys. 2013, 9, 19. [Google Scholar] [CrossRef]
- Hamel, D.R.; Shalm, L.K.; Hübel, H.; Miller, A.J.; Marsili, F.; Verma, V.B.; Mirin, R.P.; Nam, S.W.; Resch, K.J.; Jennewein, T. Direct generation of three-photon polarization entanglement. Nat. Photon. 2014, 8, 801. [Google Scholar] [CrossRef]
- Lan, G.; Zhang, S.; Xiang, S.; Wang, S.; Luo, Z.; Ahmed, I.; Zhang, Y. Three-photon polarized entanglement and interference generated using six-wave mixing and polarized dressing atomic coherence control. OSA Contin. 2019, 2, 3153. [Google Scholar] [CrossRef]
- Li, K.; Cai, Y.; Wu, J.; Liu, Y.; Xiong, S.; Li, Y.; Zhang, Y. Three-body topology entanglement generation via a six-wave mixing: Competing and coexisting of linear and nonlinear optics responses in triphoton temporal correlation. Adv. Quantum Technol. 2020, 3, 1900119. [Google Scholar] [CrossRef]
- Yao, X.C.; Wang, T.X.; Xu, P.; Lu, H.; Pan, G.S.; Bao, X.H.; Peng, C.Z.; Lu, C.Y.; Chen, Y.A.; Pan, J.W. Observation of eight-photon entanglement. Nature Photon. 2012, 6, 225. [Google Scholar] [CrossRef]
- Liao, K.; Yan, H.; He, J.; Du, S.; Zhang, Z.M.; Zhu, S.L. Subnatural-linewidth polarization-entangled photon pairs with controllable temporal length. Phys. Rev. Lett. 2014, 112, 243602. [Google Scholar] [CrossRef]
- Wu, H.; Ruan, Y.; Li, Z.; Dong, M.X.; Cai, M.; Tang, J.; Tang, L.; Zhang, H.; Xiao, M.; Xia, K. Fundamental distinction of electromagnetically induced transparency and autler–townes splitting in breaking the time-reversal symmetry. Laser Photonics Rev. 2022, 16, 2100708. [Google Scholar] [CrossRef]
- Miri, M.A.; Alu, A. Exceptional points in optics and photonics. Science 2019, 363, 42. [Google Scholar] [CrossRef] [PubMed]
- Feng, Y.; Li, K.; Ahmed, I.; Li, Y.; Li, W.; Lan, G.; Zhang, Y. Generation of a quadphoton via seventh-order nonlinear susceptibility. Ann. Phys. 2019, 531, 1900072. [Google Scholar] [CrossRef]
- Li, Y.; Feng, Y.; Li, W.; Li, K.; Liu, Y.; Lan, Y.; Zhang, Y. Double-dressing tri and quad-photon correlations in spontaneous six and eightwave mixing. Phys. Scr. 2019, 94, 105802. [Google Scholar] [CrossRef]
- Li, S.; Li, Y.; Xiong, S.; Qin, Y.; Feng, Y.; Zhao, Y.; Yu, X.; Zhang, Y. Coherent control of multiphoton using multidressing fields. Ann. Phys. 2021, 533, 2100083. [Google Scholar] [CrossRef]
- Zhao, L.; Su, Y.; Du, S. Narrowband biphoton generation in the group delay regime. Phys. Rev. A 2016, 93, 033815. [Google Scholar] [CrossRef]
- Zhang, Y.; Brown, A.W.; Xiao, M. Opening four-wave mixing and six-wave mixing channels via dual electromagnetically induced transparency windows. Phys. Rev. Lett. 2007, 99, 123603. [Google Scholar] [CrossRef]
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).