Sliding Mode Observer with Gain Tuning Method for Passive Interferometric Fiber-Optic Gyroscope
Abstract
1. Introduction
Sliding Mode Control Principles
2. Experimental Setup
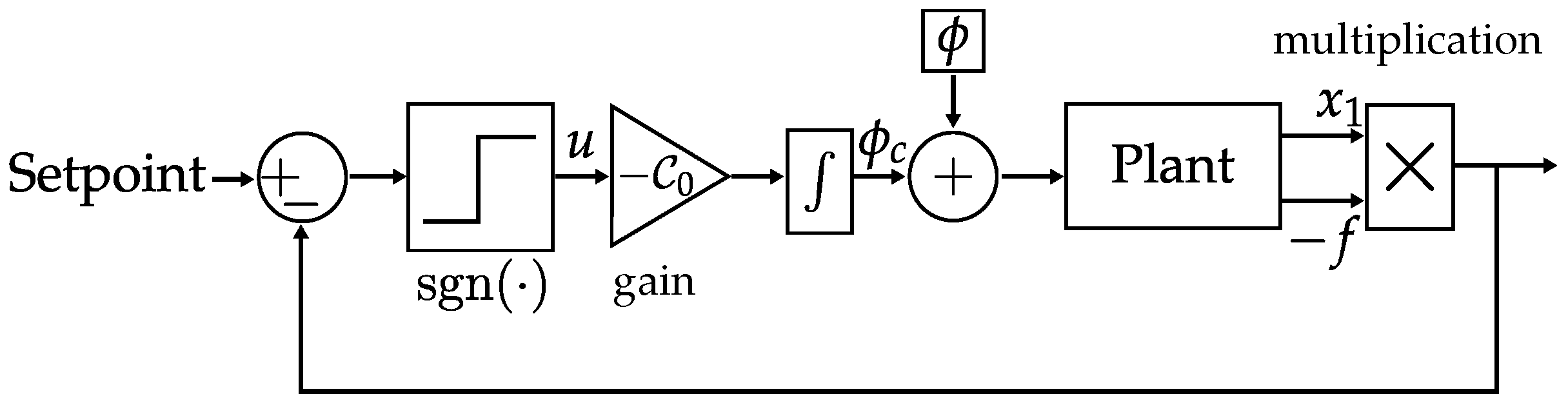
3. Sliding Mode Observer for IFOG
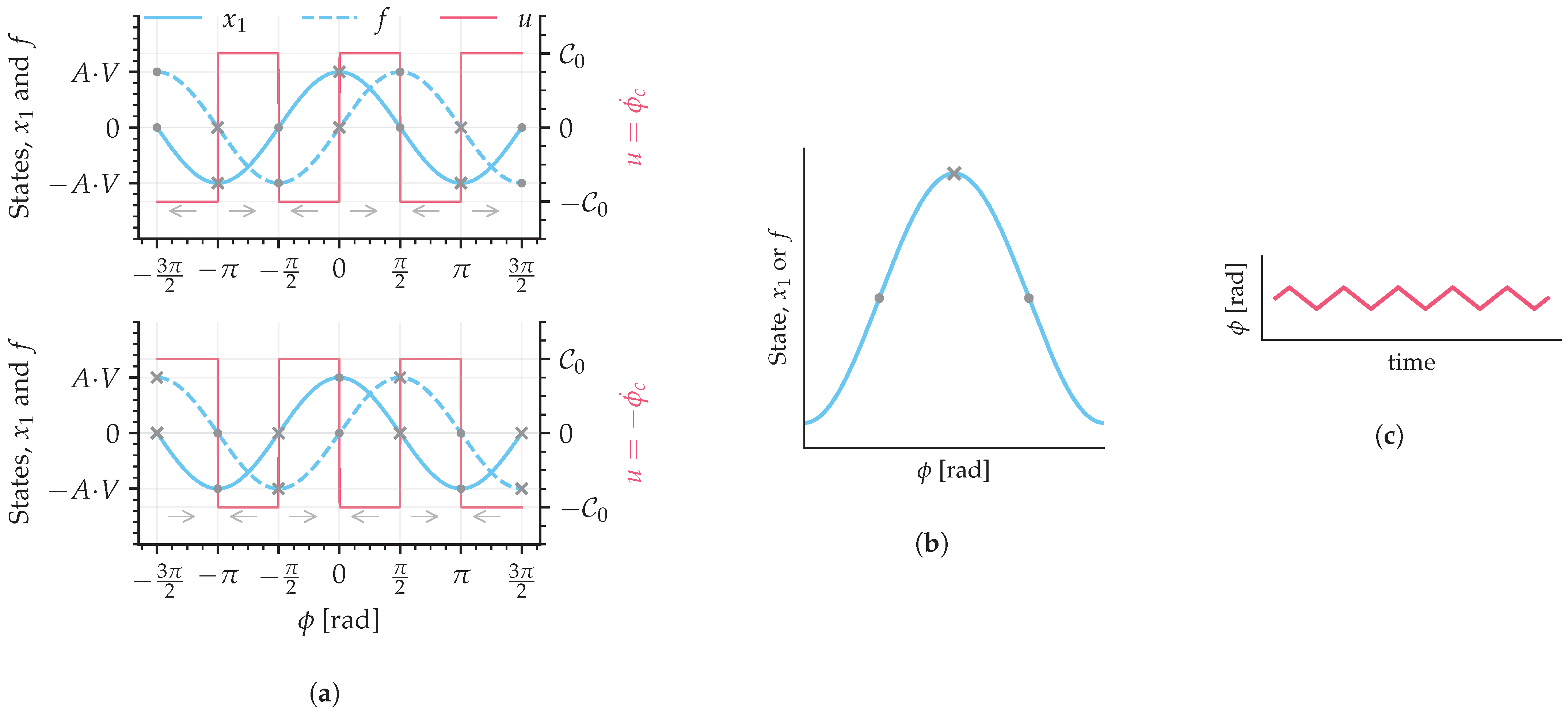
3.1. Sliding Mode Stability Analysis
3.2. Chattering Phenomenon
3.3. Calibration
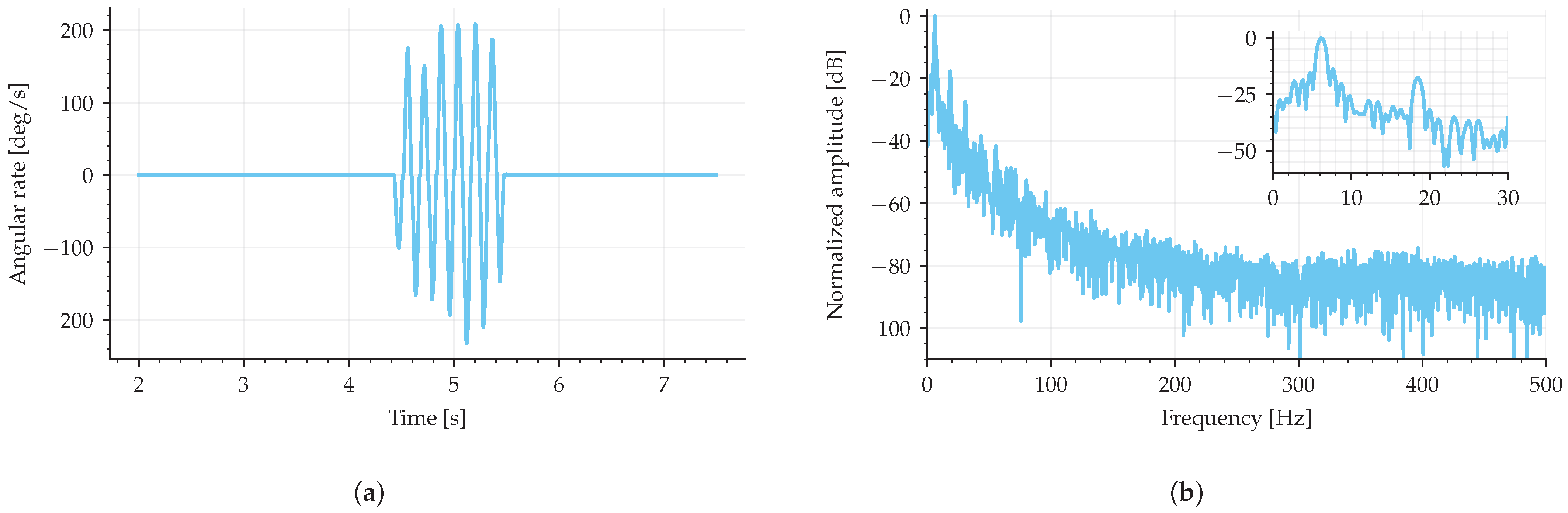
3.4. Minimum Sample Rate
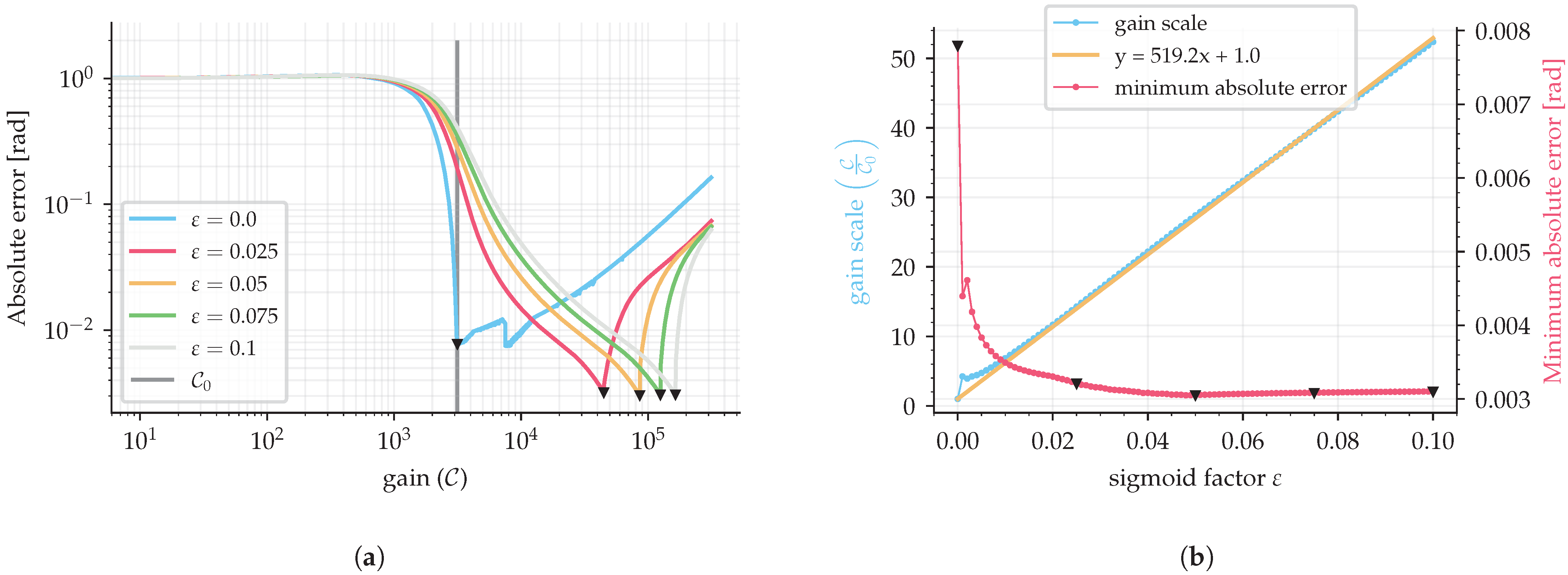
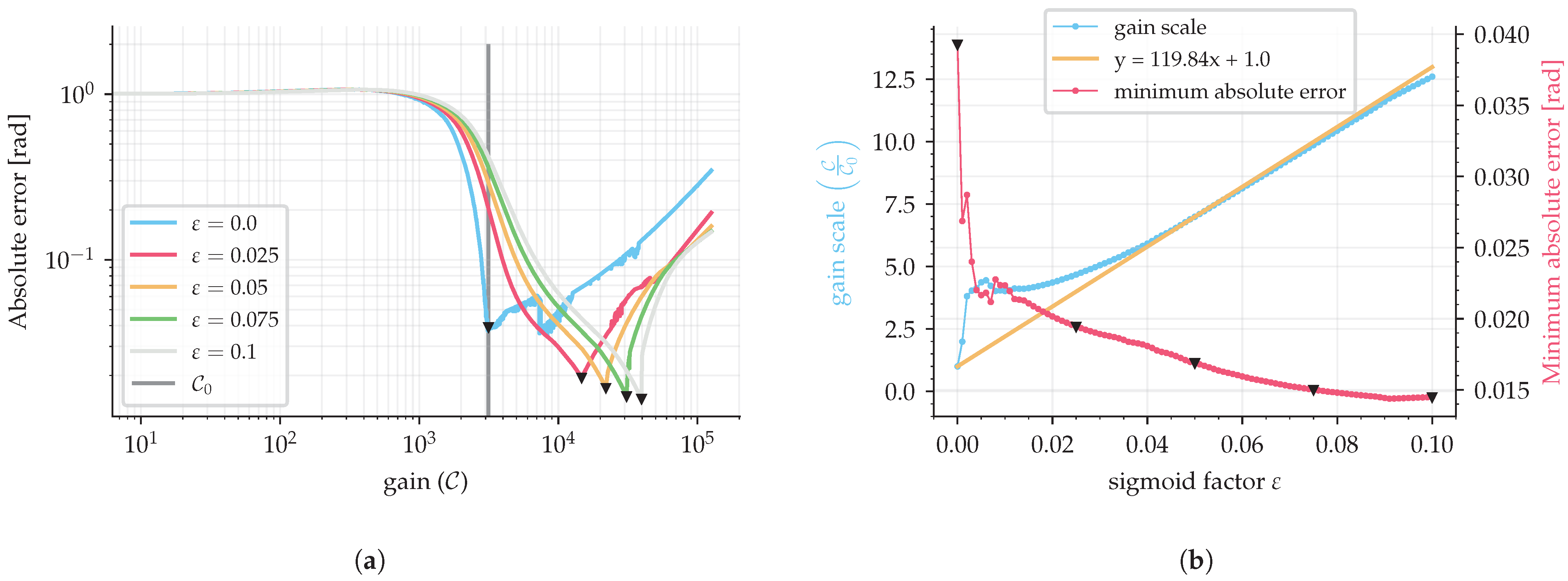
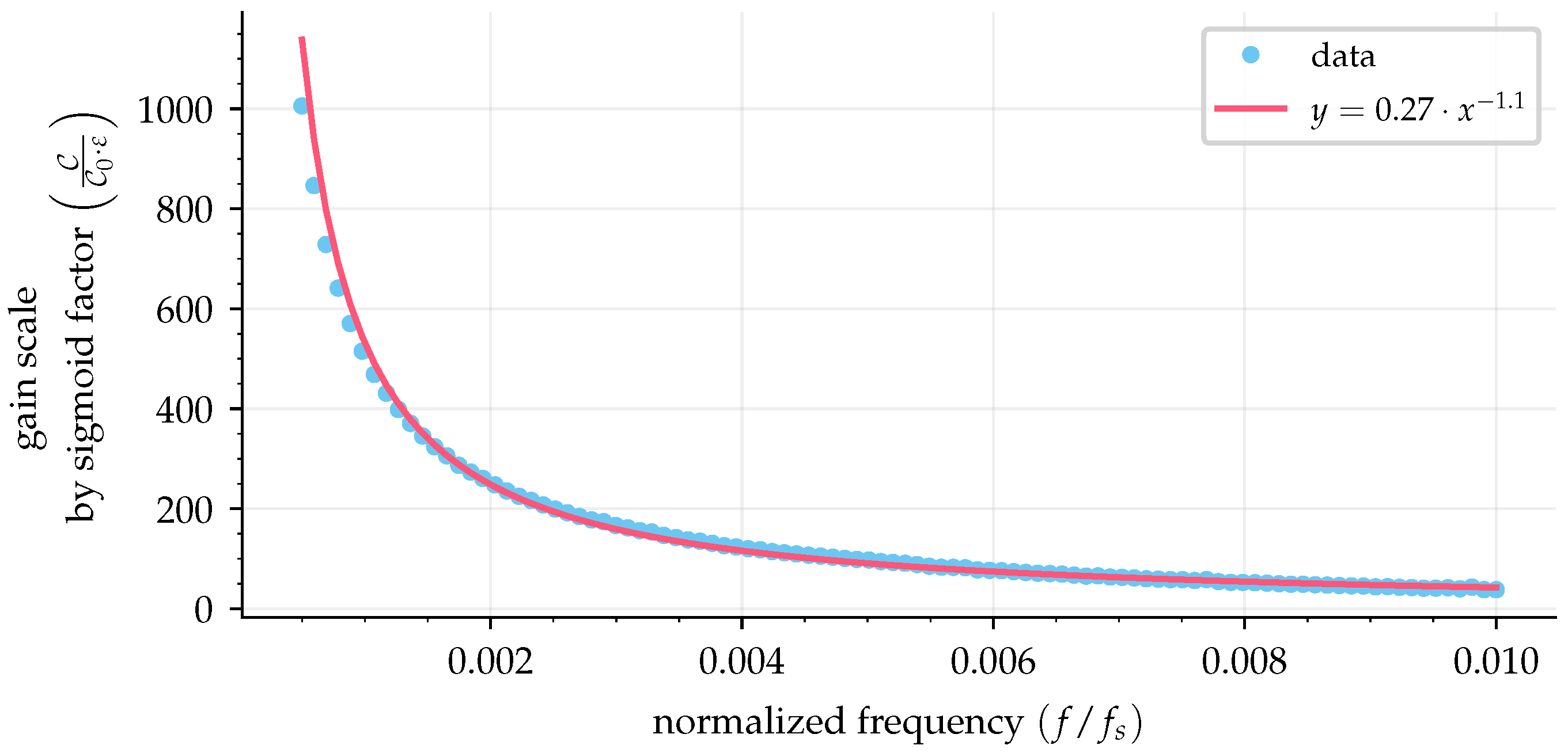
4. Sigmoid Gain Tuning
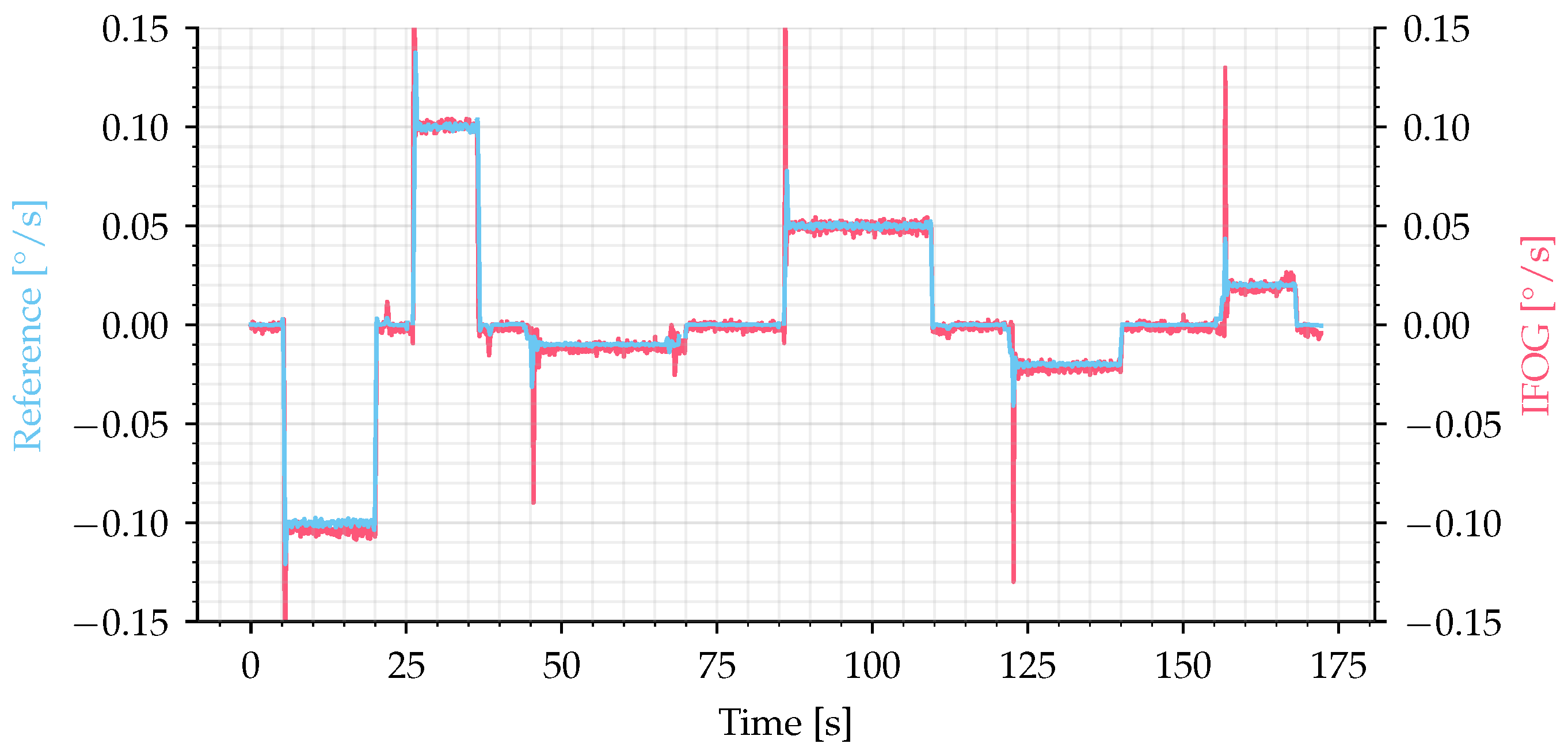
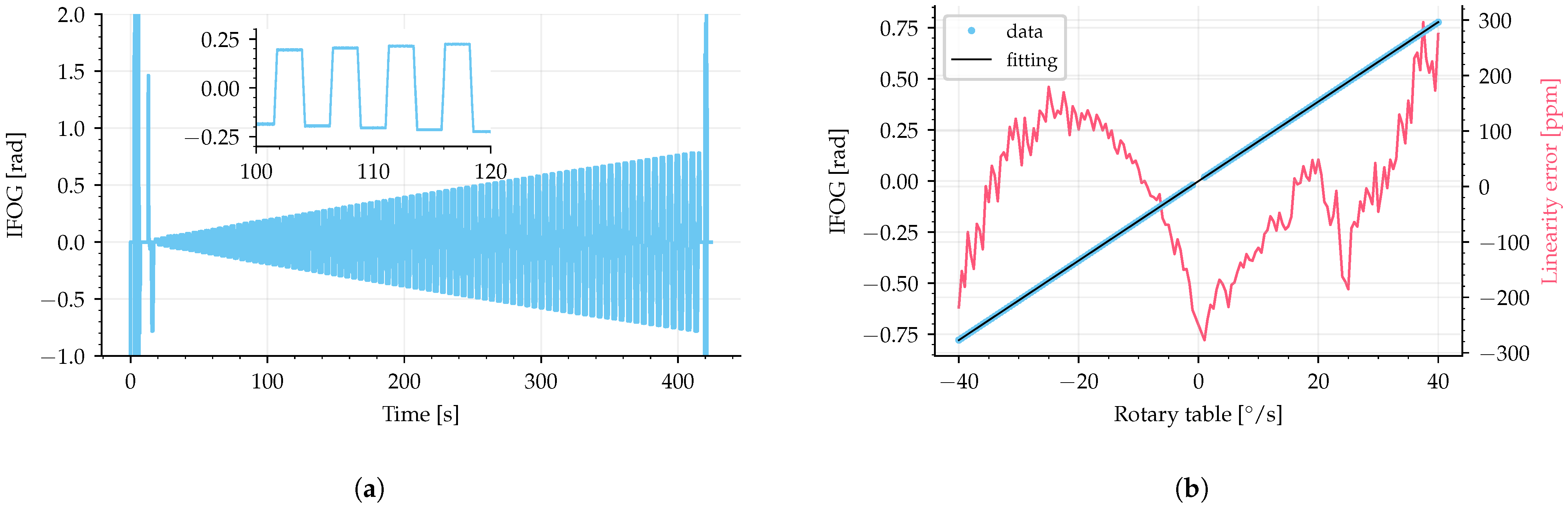
5. Results and Discussion
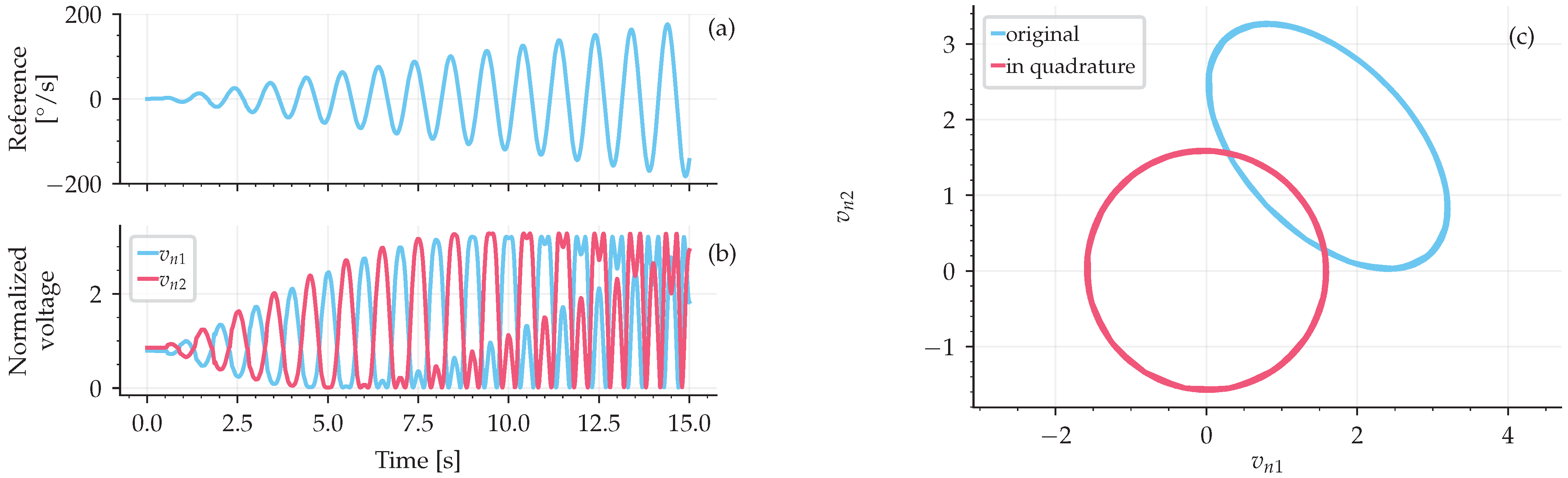
5.1. Simulation Results
5.2. Experimental Results
6. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Lee, H.; Utkin, V.I. Chattering suppression methods in sliding mode control systems. Annu. Rev. Control 2007, 31, 179–188. [Google Scholar] [CrossRef]
- Zeng, X.; Zhang, X.; Nan, F. The Sliding Mode Control for Piezoelectric Tip/Tilt Platform on Precision Motion Tracking. Actuators 2024, 13, 269. [Google Scholar] [CrossRef]
- Ruggiero, D.; Capello, E.; Novara, C.; Grzymisch, J. Design of Super-Twisting Sliding Mode Observer for LISA Mission Micro-Meteoroid Impact. In Proceedings of the 2023 American Control Conference (ACC), San Diego, CA, USA, 31 May–2 June 2023; pp. 4814–4819. [Google Scholar] [CrossRef]
- Zuo, Y.; Lai, C.; Iyer, K.L.V. A Review of Sliding Mode Observer Based Sensorless Control Methods for PMSM Drive. IEEE Trans. Power Electron. 2023, 38, 11352–11367. [Google Scholar] [CrossRef]
- Martin, R.I.; Sakamoto, J.M.S.; Teixeira, M.C.M.; Martinez, G.A.; Pereira, F.C.; Kitano, C. Nonlinear control system for optical interferometry based on variable structure control and sliding modes. Opt. Express 2017, 25, 6335–6348. [Google Scholar] [CrossRef]
- Martin, R.I.; Sakamoto, J.M.S.; Teixeira, M.C.M.; Kitano, C. Variable structure and sliding modes nonlinear control system applied to a fiber optic interferometer. In Proceedings of the Third International Conference on Applications of Optics and Photonics, Faro, Portugal, 22 August 2017; Volume 10453, pp. 459–463. [Google Scholar]
- Felão, L.H.V.; Martin, R.I.; Sakamoto, J.M.S.; Teixeira, M.C.M.; Kitano, C. Wide dynamic range quadrature interferometer with high-gain approach and sliding mode control. Opt. Express 2019, 27, 25031–25045. [Google Scholar] [CrossRef]
- Flores, G.; Rakotondrabe, M. Output Feedback Control for a Nonlinear Optical Interferometry System. IEEE Control Syst. Lett. 2021, 5, 1880–1885. [Google Scholar] [CrossRef]
- Felão, L.H.V.; Martin, R.I.; Martinez, G.A.; Sakamoto, J.M.S.; Teixeira, M.C.M.; Kitano, C. All digital sliding mode observer of a feedback-free interferometer for high dynamic range detection. Opt. Lett. 2022, 47, 3852–3855. [Google Scholar] [CrossRef]
- Lefèvre, H.C. The Fiber-Optic Gyroscope, 3rd ed.; Artech House: Norwood, Australia, 2022. [Google Scholar]
- Andronova, I.A.; Malykin, G.B. Physical problems of fiber gyroscopy based on the Sagnac effect. Physics-Uspekhi 2002, 45, 793. [Google Scholar] [CrossRef]
- Zhang, S.; Zhang, C.; Pan, X.; Song, N. High-performance fully differential photodiode amplifier for miniature fiber-optic gyroscopes. Opt. Express 2019, 27, 2125–2141. [Google Scholar] [CrossRef]
- Sheem, S.K. Fiber-optic gyroscope with [3×3] directional coupler. Appl. Phys. Lett. 1980, 37, 869–871. [Google Scholar] [CrossRef]
- Trommer, G.; Poisel, H.; Buhler, W.; Hartl, E.; Muller, R. Passive fiber optic gyroscope. Appl. Opt. 1990, 29, 5360–5365. [Google Scholar] [CrossRef] [PubMed]
- Hartl, E.; Trommer, G.F.; Mueller, R.; Poisel, H. Low-cost passive fiber optic gyroscope. In Proceedings of the Fiber Optic Gyros: 15th Anniversary Conference, Boston, MA, USA, 1–7 September 1991; Ezekiel, S., Udd, E., Eds.; SPIE: Bellingham, WA, USA, 1992; Volume 1585, pp. 405–416. [Google Scholar] [CrossRef]
- Trommer, G.F.; Mueller, R.; Opitz, S. Passive FOG IMU for short-range missile application: From qualification toward series production. In Proceedings of the Fiber Optic Gyros: 20th Anniversary Conference, Denver, CO, USA, 12 November 1996; Udd, E., Lefevre, H.C., Hotate, K., Eds.; SPIE: Bellingham, WA, USA, 1996. [Google Scholar] [CrossRef]
- Bechtle, J.; Trommer, G.F. A new measurement algorithm for the 3 × 3 fiber optic Sagnac interferometer. In Proceedings of the 17th International Conference on Optical Fibre Sensors, Bruges, Belgium, 23 May 2005. [Google Scholar] [CrossRef]
- Haywood, J.; Bassett, I.; Matar, M. Application of the NIMI technique to the 3 × 3 Sagnac fibre optic current sensor-experimental results. In Proceedings of the 2002 15th Optical Fiber Sensors Conference Technical Digest. OFS 2002 (Cat. No.02EX533), Portland, OR, USA, 10 May 2002; Volume 1, pp. 553–556. [Google Scholar] [CrossRef]
- Haywood, J.H.; Bassett, I.M.; Matar, M. Restoring reciprocity to the 3 × 3 Sagnac interferometer using the NIMI technique. In Proceedings of the 17th International Conference on Optical Fibre Sensors, Bruges, Belgium, 23 May 2005. [Google Scholar] [CrossRef]
- Windeck, F.; Tajmar, M. Characterization of a Passive 3 × 3 Fiber Optic Gyroscope for Cryogenic Applications at Liquid Nitrogen Temperatures. In Proceedings of the 2024 IEEE International Symposium on Inertial Sensors and Systems (INERTIAL), Hiroshima, Japan, 25–28 March 2024; pp. 1–4. [Google Scholar] [CrossRef]
- Chen, F.; Dunnigan, M. Comparative study of a sliding-mode observer and Kalman filters for full state estimation in an induction machine. IEE Proc.-Electr. Power Appl. 2002, 149, 53–64. [Google Scholar] [CrossRef]
- Slotine, J.J.E.; Li, W. Applied Nonlinear Control; Prentice Hall: Englewood Cliffs, NJ, USA, 1991. [Google Scholar]
- Quispe-Valencia, L.M.; Coradini, M.F.; Lyra, S.S.; Higuti, R.T.; Teixeira, M.C.; Kitano, C. Simulation of a sliding mode controller applied to an optical voltage sensor. In Proceedings of the XXV Congresso Brasileiro de Automática, SBA, Rio de Janeiro, Brazil, 15 October 2024. [Google Scholar]
- Coradini, M.F.; Felão, L.H.V.; Lyra, S.d.S.; Teixeira, M.C.M.; Kitano, C. Takagi–Sugeno Fuzzy Nonlinear Control System for Optical Interferometry. Sensors 2025, 25, 1853. [Google Scholar] [CrossRef] [PubMed]
- Heydemann, P.L.M. Determination and correction of quadrature fringe measurement errors in interferometers. Appl. Opt. 1981, 20, 3382–3384. [Google Scholar] [CrossRef]
- Felão, L.H.V. High Gain Approach and Sliding Mode Control Applied to Quadrature Interferometer. Ph.D. Thesis, Universidade Estadual Paulista (UNESP), Ilha Solteira, Brazil, 2019. [Google Scholar]
- Kyslan, K.; Petro, V.; Bober, P.; Šlapák, V.; Ďurovský, F.; Dybkowski, M.; Hric, M. A Comparative Study and Optimization of Switching Functions for Sliding-Mode Observer in Sensorless Control of PMSM. Energies 2022, 15, 2689. [Google Scholar] [CrossRef]
- Chi, S.; Zhang, Z.; Xu, L. Sliding-Mode Sensorless Control of Direct-Drive PM Synchronous Motors for Washing Machine Applications. IEEE Trans. Ind. Appl. 2009, 45, 582–590. [Google Scholar] [CrossRef]
- Kazraji, S.M.; Soflayi, R.B.; Sharifian, M.B.B. Sliding-Mode Observer for Speed and Position Sensorless Control of Linear-PMSM. Electr. Control Commun. Eng. 2014, 5, 20–26. [Google Scholar] [CrossRef]
- Tarchala, G.; Orlawska-Kowalska, T. Sliding mode speed observer for the induction motor drive with different sign function approximation forms and gain adaptation. Organ Stowarzyszenia Elektr. Pol. 2013, 1, 13. [Google Scholar]
- Alvarez-Rodríguez, S.; Flores, G. PID Principles to Obtain Adaptive Variable Gains for a Bi-order Sliding Mode Control. Int. J. Control Autom. Syst. 2020, 18, 2456–2467. [Google Scholar] [CrossRef]
- Nunes, G.F.S.; Sakamoto, J.M.S. Passive Interferometric Fiber-Optic Gyroscope for Aerospace Applications. In Proceedings of the 2024 Latin American Workshop on Optical Fiber Sensors (LAWOFS), Campinas, Brazil, 20 May 2024; pp. 1–2. [Google Scholar] [CrossRef]
- IEEE Std 528-2019; IEEE Standard for Inertial Sensor Terminology. IEEE: New York, NY, USA, 2019; pp. 1–35. [CrossRef]
- Wang, Q.; Yang, C.; Wang, X.; Wang, Z. All-digital signal-processing open-loop fiber-optic gyroscope with enlarged dynamic range. Opt. Lett. 2013, 38, 5422–5425. [Google Scholar] [CrossRef]
- Bacurau, R.M.; Dante, A.; Schlischting, M.W.; Spengler, A.W.; Ferreira, E.C. Two-level and two-period modulation for closed-loop interferometric fiber optic gyroscopes. Opt. Lett. 2018, 43, 2652–2655. [Google Scholar] [CrossRef] [PubMed]
- Ovchinnikov, K.A.; Gilev, D.G.; Krishtop, V.V.; Volyntsev, A.B.; Maximenko, V.A.; Garkushin, A.A.; Filatov, Y.V.; Kukaev, A.S.; Sevryugin, A.A.; Shalymov, E.V.; et al. A Prototype for a Passive Resonant Interferometric Fiber Optic Gyroscope with a 3 × 3 Directional Coupler. Sensors 2023, 23, 1319. [Google Scholar] [CrossRef] [PubMed]
- Martynov, D.; Brown, N.; Nolasco-Martinez, E.; Evans, M. Passive optical gyroscope with double homodyne readout. Opt. Lett. 2019, 44, 1584–1587. [Google Scholar] [CrossRef]
- Ameli, F.; Battaglieri, M.; Bondì, M.; Capodiferro, M.; Celentano, A.; Chiarusi, T.; Chiodi, G.; De Napoli, M.; Lunadei, R.; Marsicano, L.; et al. A low cost, high speed, multichannel analog to digital converter board. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2019, 936, 286–287. [Google Scholar] [CrossRef]
- Zhang, G.; Wang, X.; Zhao, Z.; Jiang, Y.; Jia, J.; Ge, Q.; Wu, X. Adaptive Ellipse Fitting Based Ameliorated Passive Interferometric Demodulation Scheme. J. Light. Technol. 2025, 43, 2912–2918. [Google Scholar] [CrossRef]
- Wu, Y.; Li, C.; Wang, C.; Jia, B. Self-calibration phase demodulation scheme for stabilization based on an auxiliary reference fiber-optic interferometer and ellipse fitting algorithm. Opt. Express 2023, 31, 4639–4651. [Google Scholar] [CrossRef]
- Nunes, G.F.S.; Palma, V.B.; Martin, R.I.; Felão, L.H.V.; Teixeira, M.C.M.; Kitano, C.; Cazo, R.M.; Sakamoto, J.M.S. Characterization of a thin-film metal-coated fiber optical phase modulator based on thermal effect with a nonlinear control interferometer. Appl. Opt. 2021, 60, 7611–7618. [Google Scholar] [CrossRef]







Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nunes, G.F.S.; Sakamoto, J.M.S. Sliding Mode Observer with Gain Tuning Method for Passive Interferometric Fiber-Optic Gyroscope. Sensors 2025, 25, 3385. https://doi.org/10.3390/s25113385
Nunes GFS, Sakamoto JMS. Sliding Mode Observer with Gain Tuning Method for Passive Interferometric Fiber-Optic Gyroscope. Sensors. 2025; 25(11):3385. https://doi.org/10.3390/s25113385
Chicago/Turabian StyleNunes, Gabriel F. S., and João M. S. Sakamoto. 2025. "Sliding Mode Observer with Gain Tuning Method for Passive Interferometric Fiber-Optic Gyroscope" Sensors 25, no. 11: 3385. https://doi.org/10.3390/s25113385
APA StyleNunes, G. F. S., & Sakamoto, J. M. S. (2025). Sliding Mode Observer with Gain Tuning Method for Passive Interferometric Fiber-Optic Gyroscope. Sensors, 25(11), 3385. https://doi.org/10.3390/s25113385




