Validity of a Single Inertial Measurement Unit to Measure Hip Range of Motion During Gait in Patients Undergoing Total Hip Arthroplasty
Abstract
1. Introduction
2. Materials and Methods
2.1. Participants
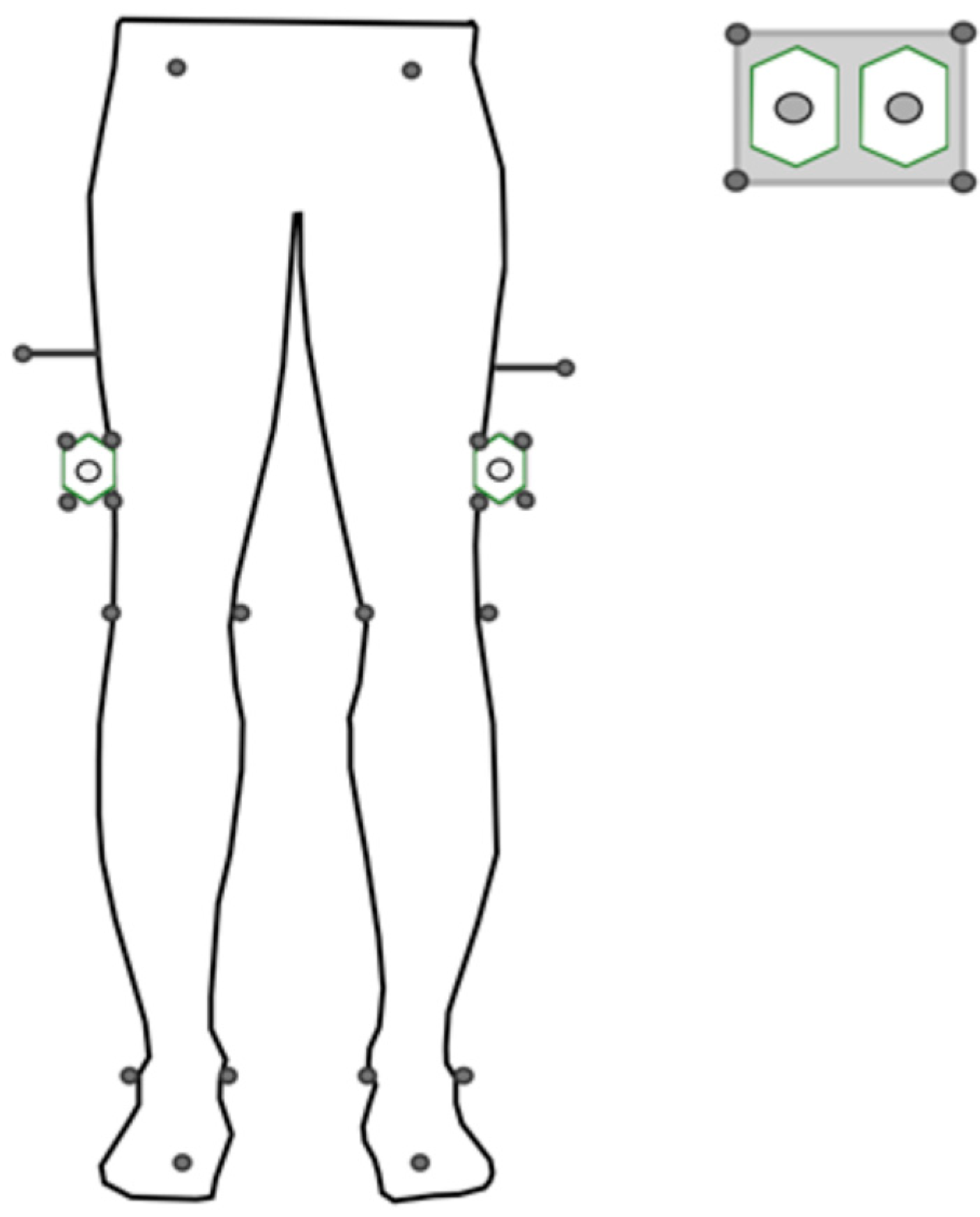
2.2. Equipment
2.3. Protocol
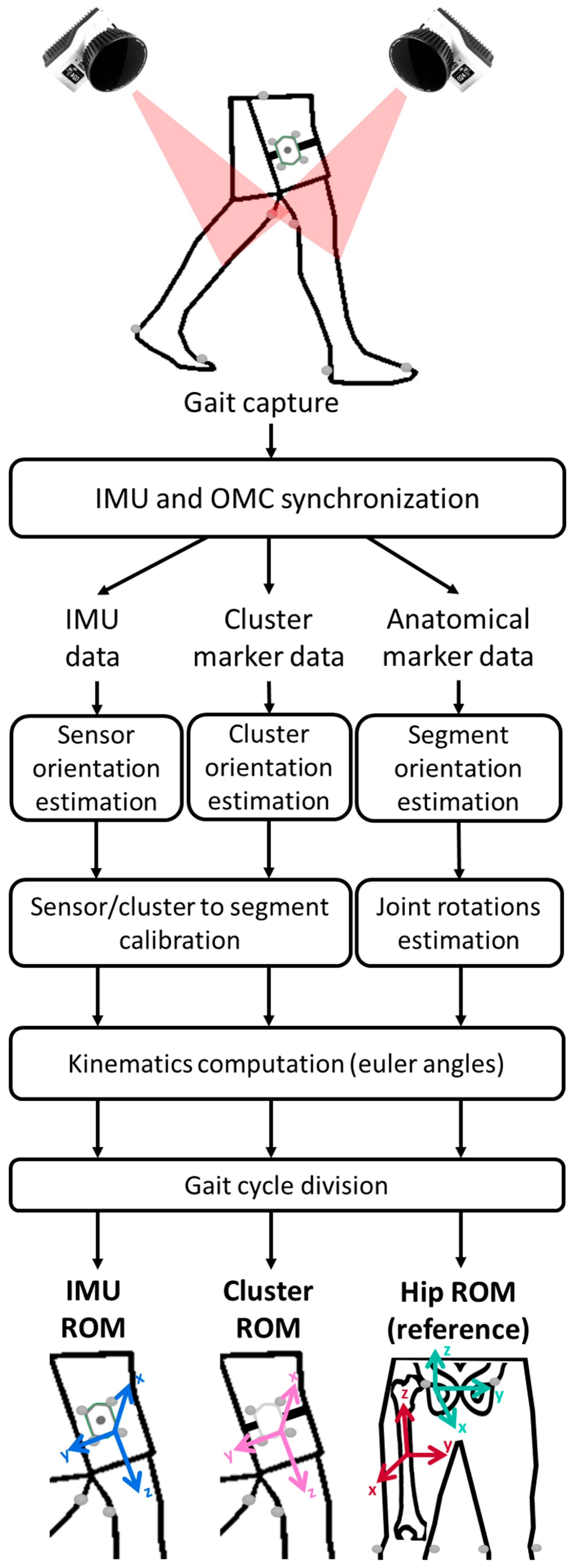
2.4. Pre-Processing
2.5. Data Processing
2.5.1. Cluster Orientations
2.5.2. Sensor-to-Segment Calibration
2.5.3. Kinematics Computation
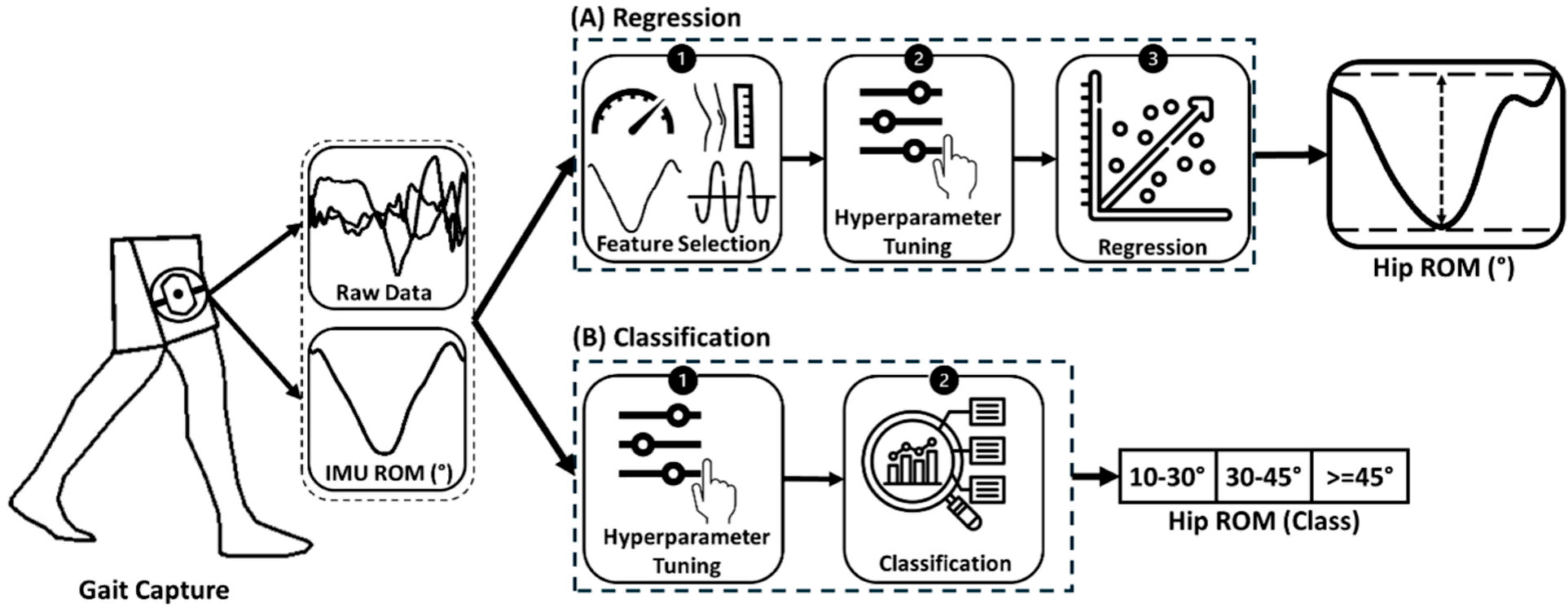
2.6. ML Models
2.6.1. Simple Linear Regression (SLR)
2.6.2. Multiple Linear Regression (MLR)
2.6.3. Random Forest
2.7. Network Architecture
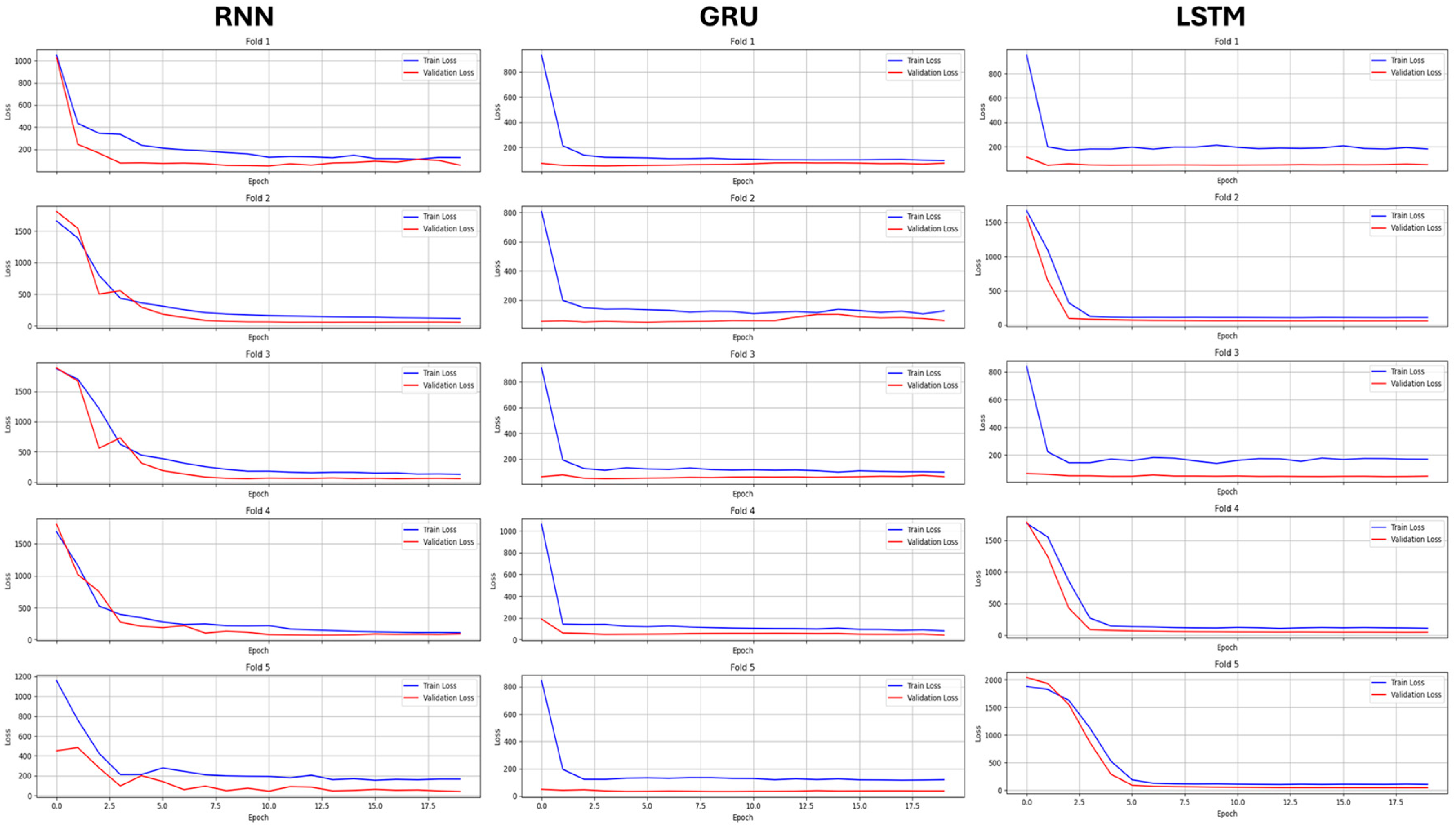
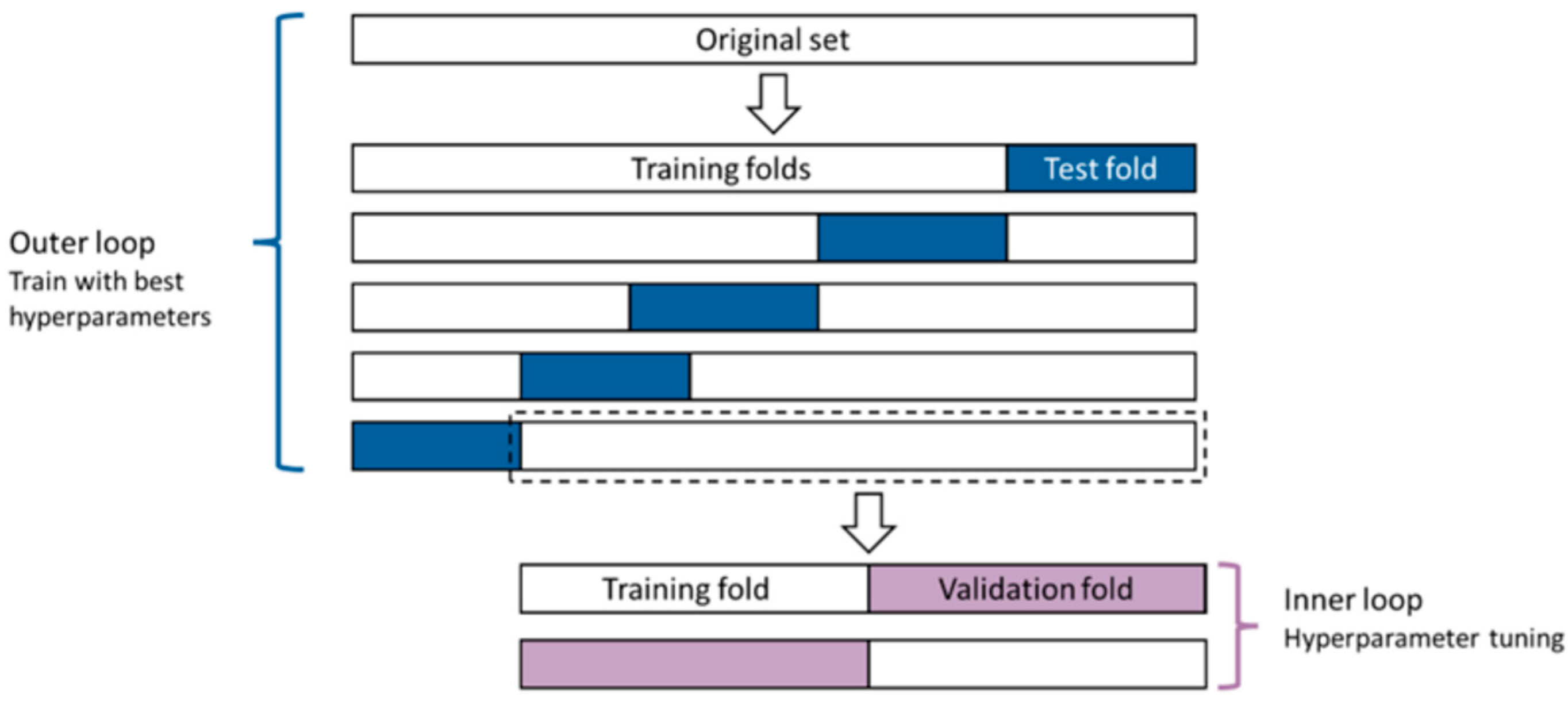
2.7.1. Hyperparameter Tuning
2.7.2. Model Training
2.8. Statistical Analysis
2.8.1. Normality and Significance Analysis of SFA Errors
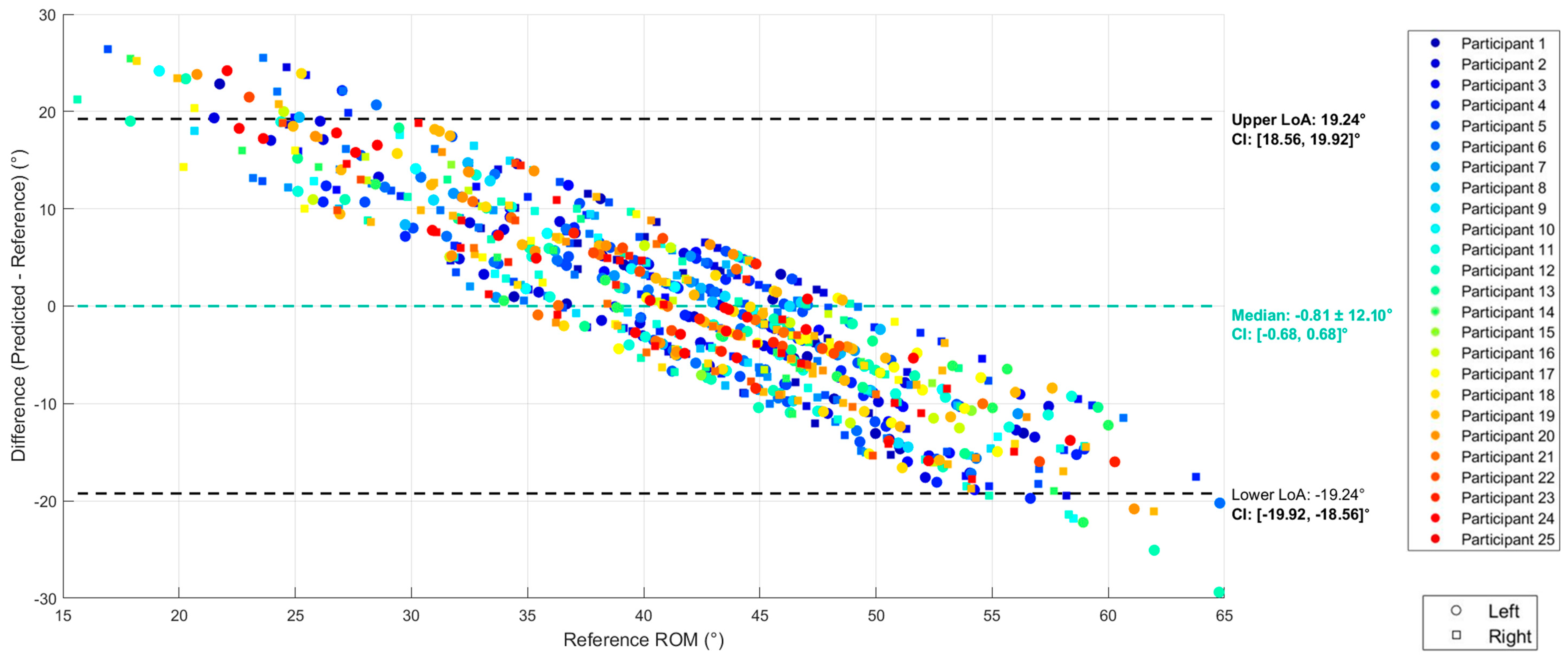
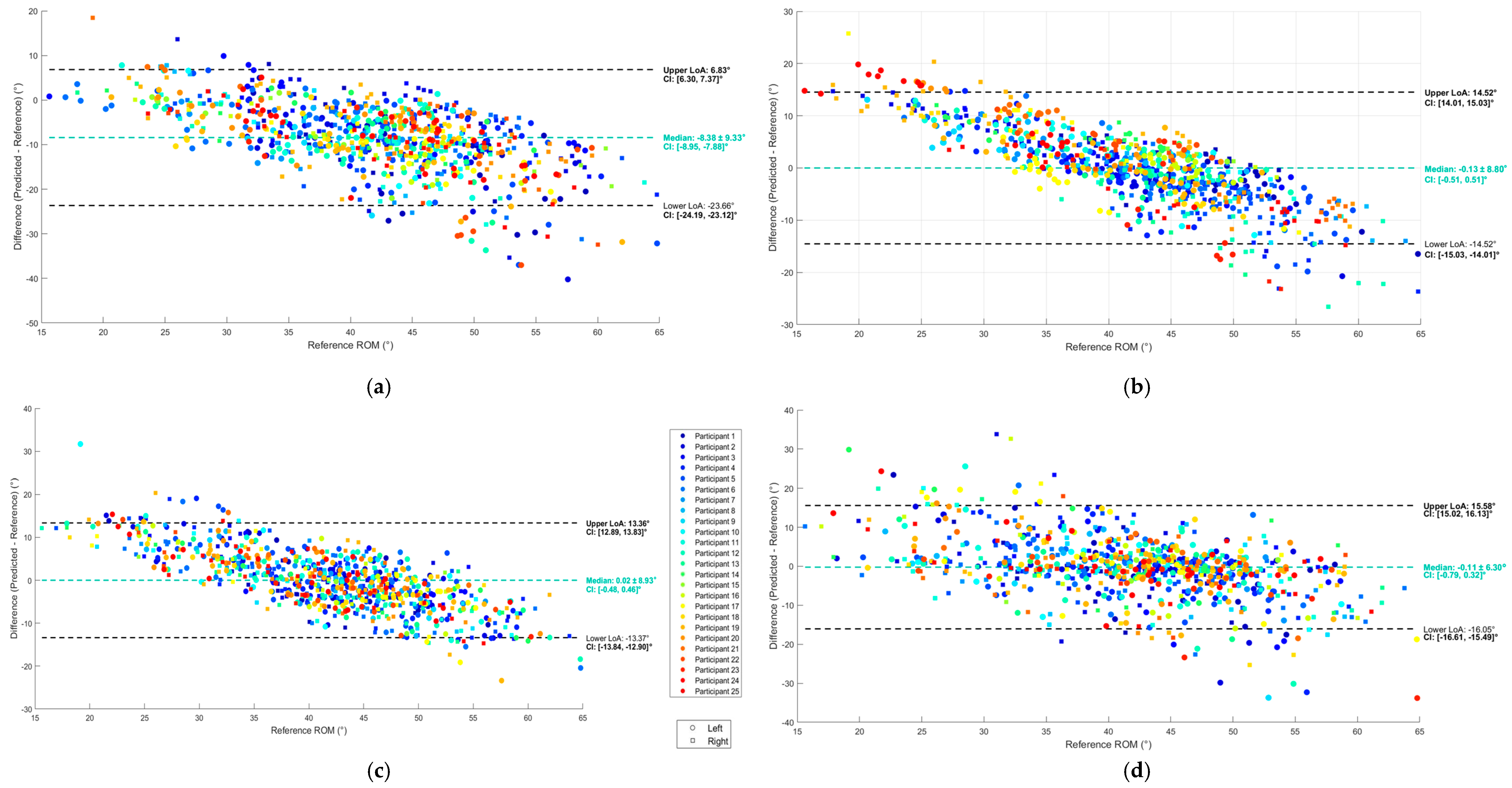
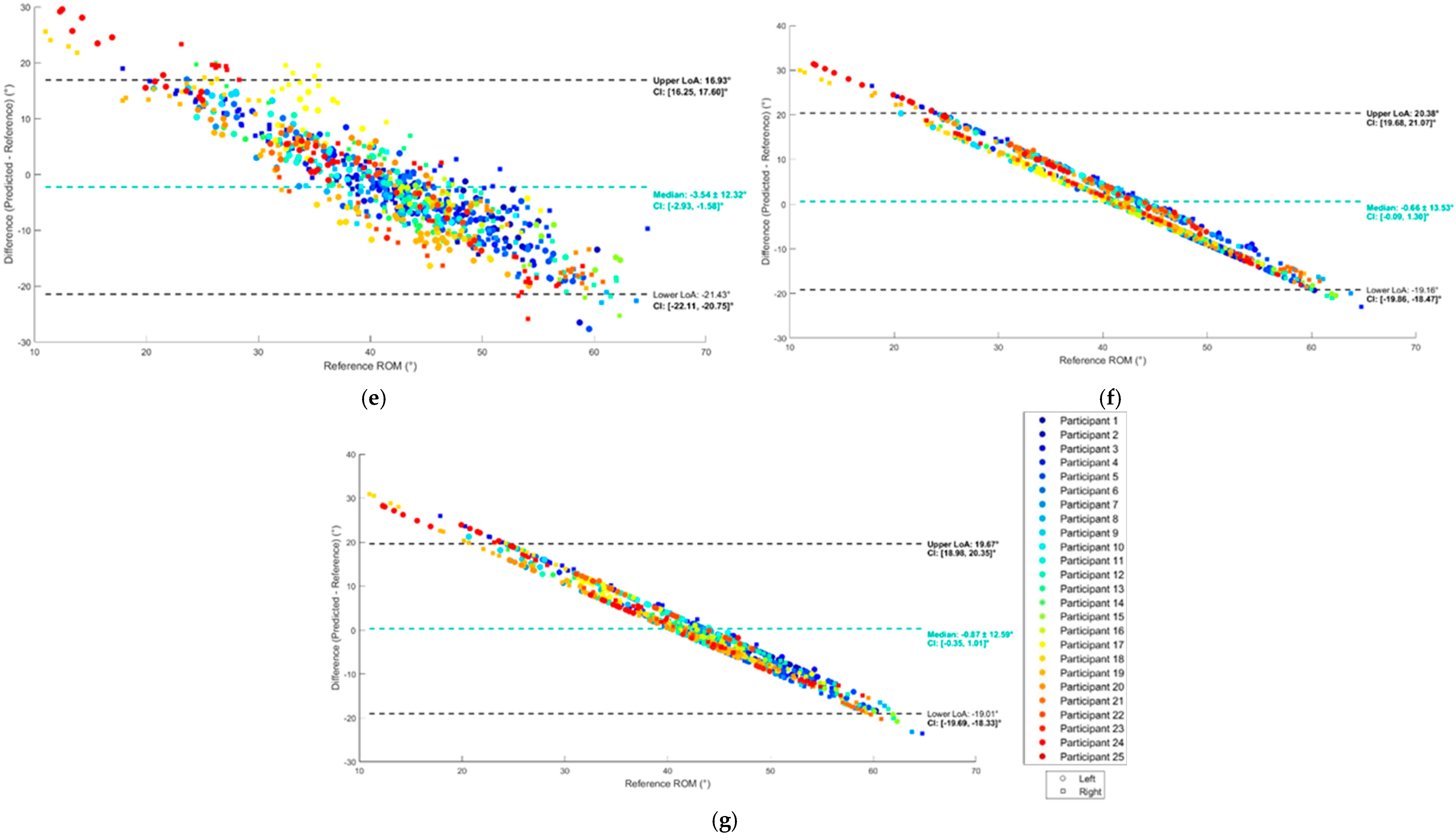
2.8.2. Evaluation of Validity
3. Results
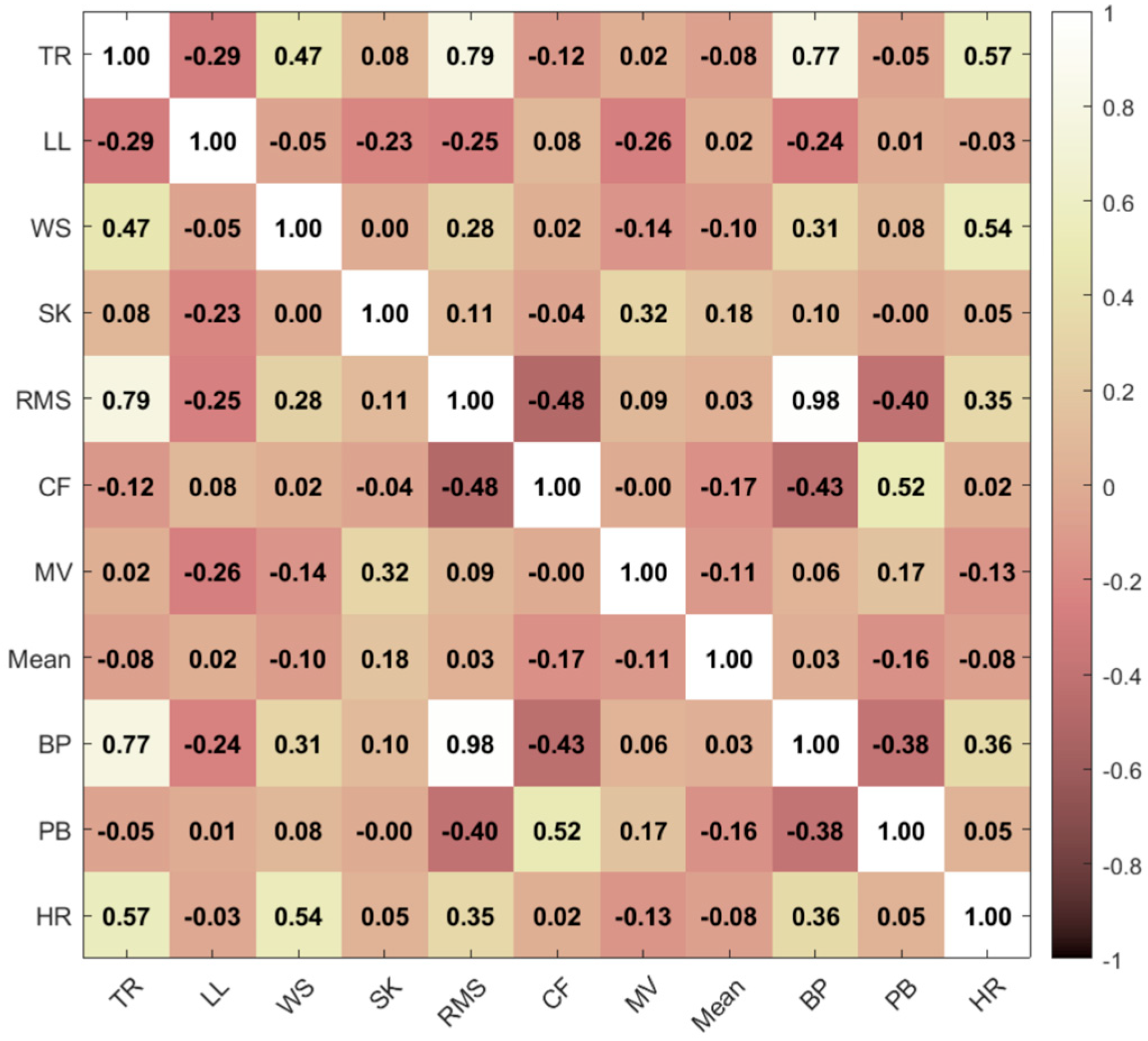
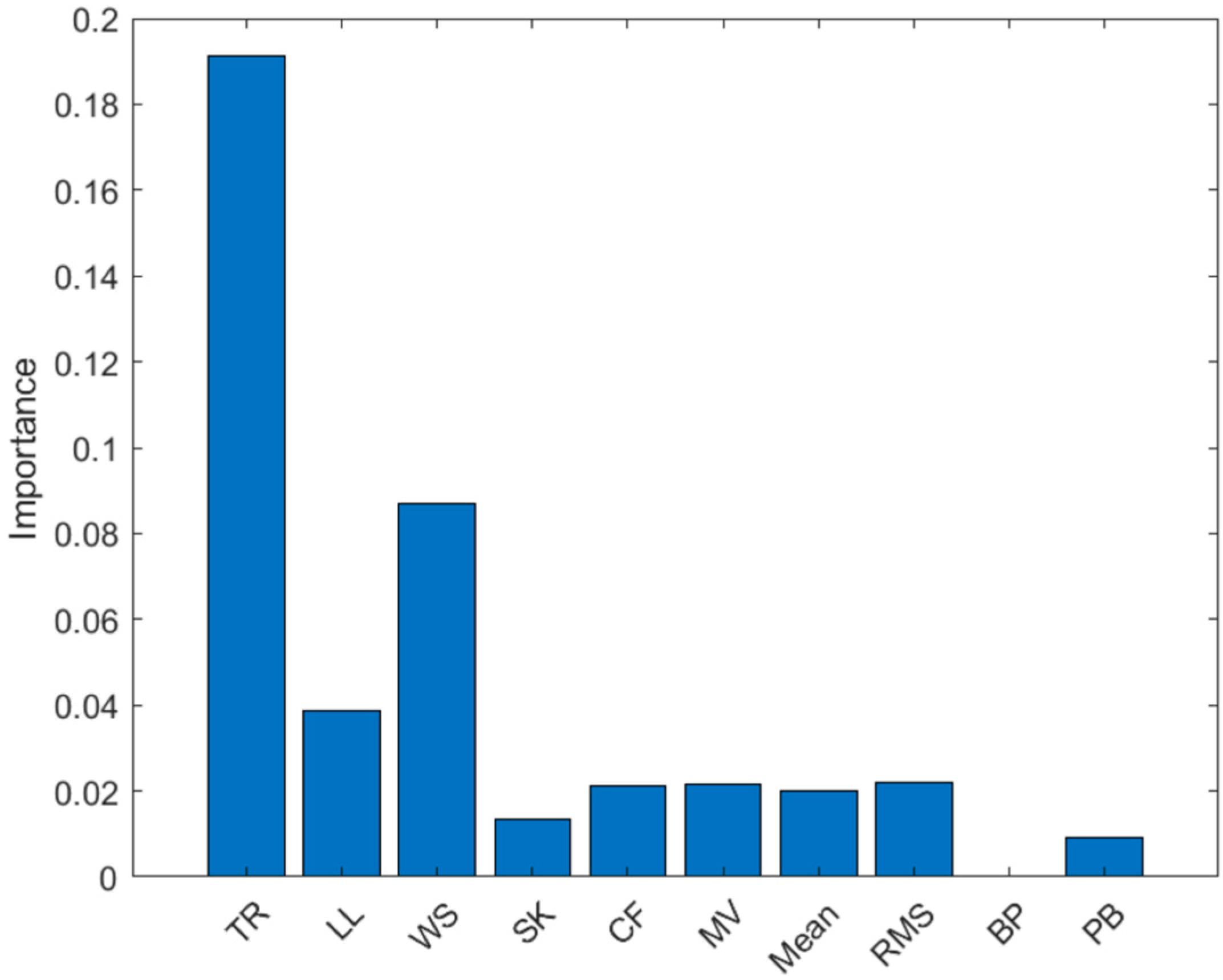
3.1. Feature Selection
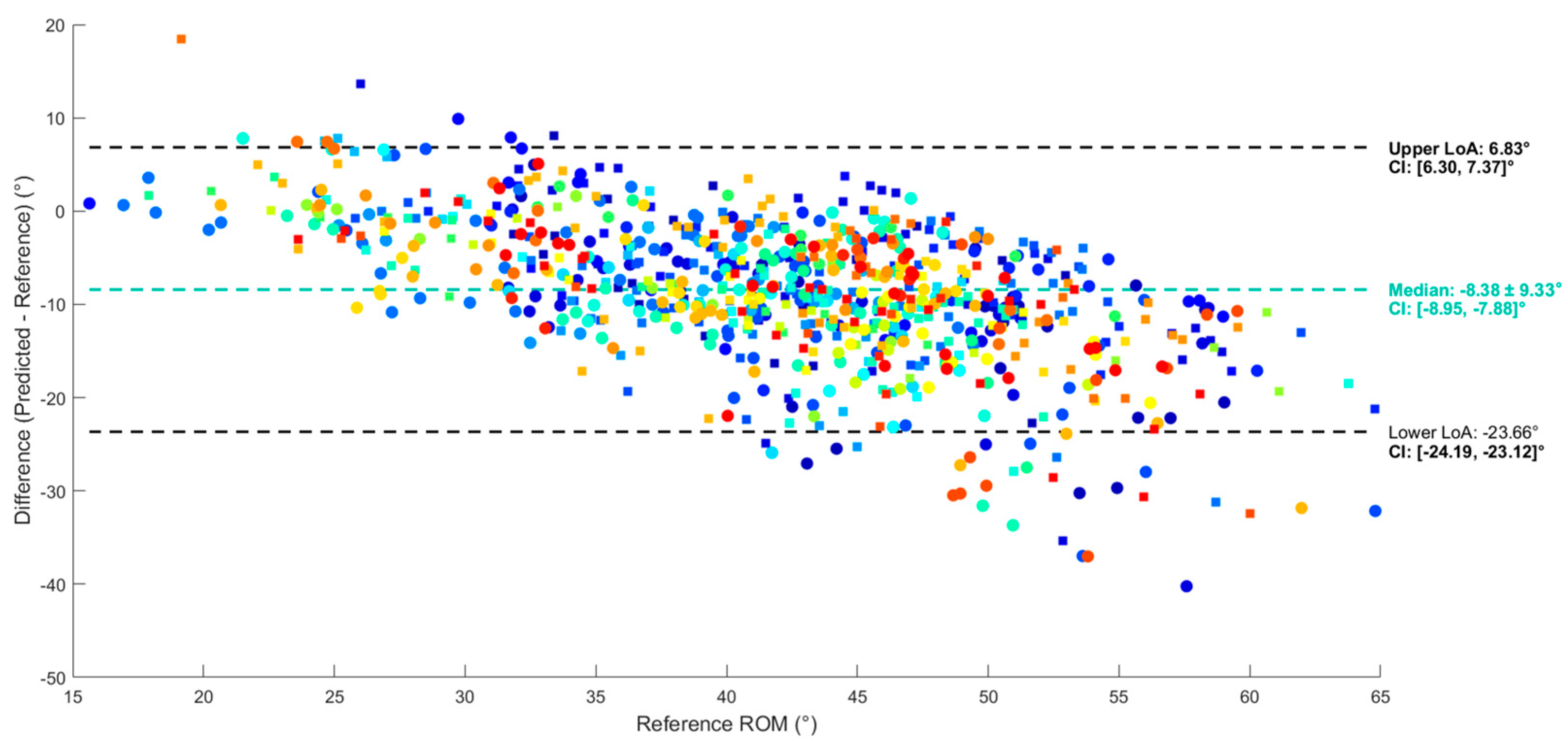
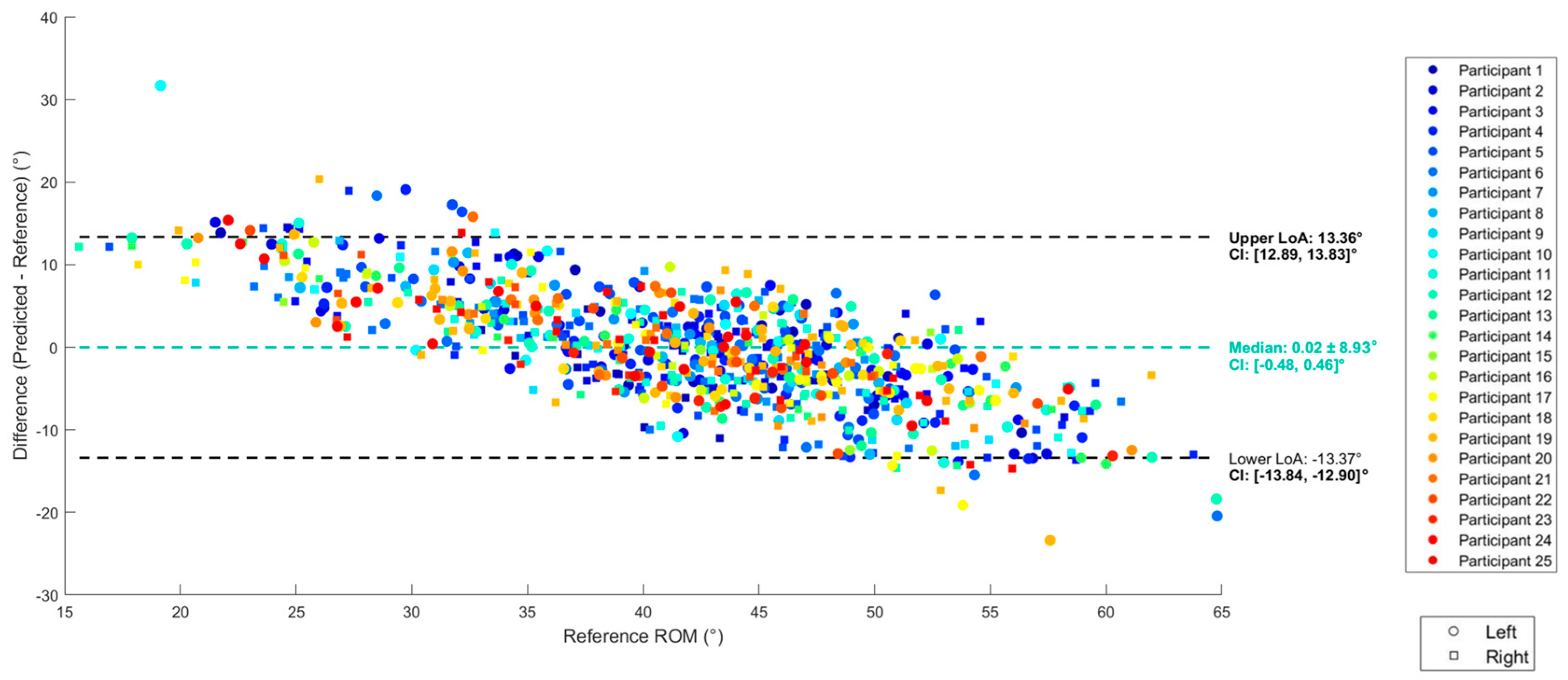
3.2. Regression
3.3. Classification
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A

| SFA | p1 | p2 | p3 | p4 | p5 | RMSE (°) |
|---|---|---|---|---|---|---|
| STR | NA | NA | NA | NA | NA | 7.6 |
| MAD (CF) | 0 | NA | NA | NA | NA | 4.4 |
| MAH (CF) | 1.2 × 10−5 | 0 | NA | NA | NA | 8.2 |
| VAK (KF) | 0.003 | 7.3 | 0.89 | NA | NA | 11.2 |
| GUO (KF) | 10−4 | 15.8 | 22.2 | NA | NA | 16.0 |
| VAC (CF) | 0.1 | 0 | 0.02 | 0.001 | 0.01 | 11.4 |
| Model | MAE (°) | R2 | LoA (°) | Computation Time (s) |
|---|---|---|---|---|
| SLR | 4.3 ± 0.7 | 0.30 | [−14.5, 14.5] | 0.06 |
| MLR | 4.2 ± 0.5 | 0.43 | [−13.4, 13.4] | 0.98 |
| RF | 3.2 ± 0.6 | 0.40 | [−15.5, 14.9] | 1680 |
| RNN | 7.0 ± 7.9 | −0.37 | [−21.4, 16.9] | 5212 |
| GRU | 7.0 ± 8.1 | −0.22 | [−19.2, 20.4] | 11,353 |
| LSTM | 6.6 ± 8.0 | −0.19 | [−19.0, 19.7] | 11,651 |
| Model | Accuracy (%) | Precision (%) | Recall (%) | F1-Score (%) | Computation Time (s) |
|---|---|---|---|---|---|
| RF | 0.59 | 0.60 | 0.59 | 0.58 | 480 |
| RNN | 0.48 | 0.49 | 0.48 | 0.47 | 7718 |
| GRU | 0.44 | 0.44 | 0.45 | 0.41 | 19,400 |
| LSTM | 0.40 | 0.35 | 0.40 | 0.35 | 62,280 |
References
- U.S. Food and Drug Administration. Osteoarthritis: A Serious Disease. Available online: https://oarsi.org/sites/oarsi/files/library/2018/pdf/oarsi_white_paper_oa_serious_disease121416_1.pdf (accessed on 6 March 2024).
- Ferguson, R.J.; Palmer, A.J.; Taylor, A.; Porter, M.L.; Malchau, H.; Glyn-Jones, S. Hip replacement. Lancet 2018, 392, 1662–1671. [Google Scholar] [CrossRef] [PubMed]
- Ewen, A.M.; Stewart, S.; Gibson, A.S.C.; Kashyap, S.N.; Caplan, N. Post-operative gait analysis in total hip replacement patients—A review of current literature and meta-analysis. Gait Posture 2012, 36, 1–6. [Google Scholar] [CrossRef] [PubMed]
- Vissers, M.M.; Bussmann, J.B.; Verhaar, J.A.; Arends, L.R.; Furlan, A.D.; Reijman, M. Recovery of Physical Functioning After Total Hip Arthroplasty: Systematic Review and Meta-Analysis of the Literature. Phys. Ther. 2011, 91, 615–629. [Google Scholar] [CrossRef] [PubMed]
- Ornetti, P.; Maillefert, J.-F.; Laroche, D.; Morisset, C.; Dougados, M.; Gossec, L. Gait analysis as a quantifiable outcome measure in hip or knee osteoarthritis: A systematic review. Jt. Bone Spine 2010, 77, 421–425. [Google Scholar] [CrossRef]
- Bergmann, J.H.M.; McGregor, A.H. Body-Worn Sensor Design: What Do Patients and Clinicians Want? Ann. Biomed. Eng. 2011, 39, 2299–2312. [Google Scholar] [CrossRef]
- Caruso, M.; Sabatini, A.M.; Laidig, D.; Seel, T.; Knaflitz, M.; Della Croce, U.; Cereatti, A. Analysis of the Accuracy of Ten Algorithms for Orientation Estimation Using Inertial and Magnetic Sensing under Optimal Conditions: One Size Does Not Fit All. Sensors 2021, 21, 2543. [Google Scholar] [CrossRef]
- Pacher, L.; Chatellier, C.; Vauzelle, R.; Fradet, L. Sensor-to-Segment Calibration Methodologies for Lower-Body Kinematic Analysis with Inertial Sensors: A Systematic Review. Sensors 2020, 20, 3322. [Google Scholar] [CrossRef]
- Carcreff, L.; Gerber, C.N.; Paraschiv-Ionescu, A.; De Coulon, G.; Newman, C.J.; Aminian, K.; Armand, S. Comparison of gait characteristics between clinical and daily life settings in children with cerebral palsy. Sci. Rep. 2020, 10, 1–11. [Google Scholar] [CrossRef]
- Warmerdam, E.; Hausdorff, J.M.; Atrsaei, A.; Zhou, Y.; Mirelman, A.; Aminian, K.; Espay, A.J.; Hansen, C.; Evers, L.J.W.; Keller, A.; et al. Long-term unsupervised mobility assessment in movement disorders. Lancet Neurol. 2020, 19, 462–470. [Google Scholar] [CrossRef]
- Zügner, R.; Tranberg, R.; Timperley, J.; Hodgins, D.; Mohaddes, M.; Kärrholm, J. Validation of inertial measurement units with optical tracking system in patients operated with Total hip arthroplasty. BMC Musculoskelet. Disord. 2019, 20, 1–8. [Google Scholar] [CrossRef]
- Piche, E.; Guilbot, M.; Chorin, F.; Guerin, O.; Zory, R.; Gerus, P. Validity and repeatability of a new inertial measurement unit system for gait analysis on kinematic parameters: Comparison with an optoelectronic system. Measurement 2022, 198, 111442. [Google Scholar] [CrossRef]
- Kirk, C.; Küderle, A.; Micó-Amigo, M.E.; Bonci, T.; Paraschiv-Ionescu, A.; Ullrich, M.; Soltani, A.; Gazit, E.; Salis, F.; Alcock, L.; et al. Estimating real-world walking speed from a single wearable device: Analytical pipeline, results and lessons learnt from the Mobilise-D technical validation study. arXiv 2023. [Google Scholar] [CrossRef]
- Kolk, S.; Minten, M.J.; van Bon, G.E.; Rijnen, W.H.; Geurts, A.C.; Verdonschot, N.; Weerdesteyn, V. Gait and gait-related activities of daily living after total hip arthroplasty: A systematic review. Clin. Biomech. 2014, 29, 705–718. [Google Scholar] [CrossRef]
- Fransen, B.L.; Pijnappels, M.; Butter, I.K.; Burger, B.J.; van Dieën, J.H.; Hoozemans, M.J.M. Patients’ perceived walking abilities, daily-life gait behavior and gait quality before and 3 months after total knee arthroplasty. Arch. Orthop. Trauma Surg. 2021, 142, 1189–1196. [Google Scholar] [CrossRef]
- Micó-Amigo, M.; Bonci, T.; Paraschiv-Ionescu, A.; Ullrich, M.; Kirk, C.; Soltani, A.; Küderle, A.; Gazit, E.; Salis, F.; Alcock, L.; et al. Assessing real-world gait with digital technology? Validation, insights and recommendations from the Mobilise-D consortium. arXiv 2022. [Google Scholar] [CrossRef]
- Paraschiv-Ionescu, A.; Newman, C.J.; Carcreff, L.; Gerber, C.N.; Armand, S.; Aminian, K. Locomotion and cadence detection using a single trunk-fixed accelerometer: Validity for children with cerebral palsy in daily life-like conditions. J. Neuroeng. Rehabilitation 2019, 16, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Bonnet, V.; Joukov, V.; Kulic, D.; Fraisse, P.; Ramdani, N.; Venture, G. Monitoring of Hip and Knee Joint Angles Using a Single Inertial Measurement Unit During Lower Limb Rehabilitation. IEEE Sensors J. 2015, 16, 1557–1564. [Google Scholar] [CrossRef]
- Sung, J.; Han, S.; Park, H.; Cho, H.-M.; Hwang, S.; Park, J.W.; Youn, I. Prediction of Lower Extremity Multi-Joint Angles during Overground Walking by Using a Single IMU with a Low Frequency Based on an LSTM Recurrent Neural Network. Sensors 2021, 22, 53. [Google Scholar] [CrossRef]
- Wang, J.; Xu, F.; Zhang, H.; Wang, B.; Deng, T.; Zhou, Z.; Li, K.; Nie, Y. Validity of an inertial measurement system to measure lower-limb kinematics in patients with hip and knee pathology. J. Biomech. 2024, 178, 112446. [Google Scholar] [CrossRef]
- Gurchiek, R.D.; Cheney, N.; McGinnis, R.S. Estimating Biomechanical Time-Series with Wearable Sensors: A Systematic Review of Machine Learning Techniques. Sensors 2019, 19, 5227. [Google Scholar] [CrossRef]
- Halilaj, E.; Rajagopal, A.; Fiterau, M.; Hicks, J.L.; Hastie, T.J.; Delp, S.L. Machine learning in human movement biomechanics: Best practices, common pitfalls, and new opportunities. J. Biomech. 2018, 81, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Argent, R.; Drummond, S.; Remus, A.; O’reilly, M.; Caulfield, B. Evaluating the use of machine learning in the assessment of joint angle using a single inertial sensor. J. Rehabilitation Assist. Technol. Eng. 2019, 6. [Google Scholar] [CrossRef]
- Dorschky, E.; Nitschke, M.; Martindale, C.F.; Bogert, A.J.v.D.; Koelewijn, A.D.; Eskofier, B.M. CNN-Based Estimation of Sagittal Plane Walking and Running Biomechanics From Measured and Simulated Inertial Sensor Data. Front. Bioeng. Biotechnol. 2020, 8, 604. [Google Scholar] [CrossRef] [PubMed]
- Tan, J.-S.; Tippaya, S.; Binnie, T.; Davey, P.; Napier, K.; Caneiro, J.P.; Kent, P.; Smith, A.; O’sullivan, P.; Campbell, A. Predicting Knee Joint Kinematics from Wearable Sensor Data in People with Knee Osteoarthritis and Clinical Considerations for Future Machine Learning Models. Sensors 2022, 22, 446. [Google Scholar] [CrossRef]
- McGinley, J.L.; Baker, R.; Wolfe, R.; Morris, M.E. The reliability of three-dimensional kinematic gait measurements: A systematic review. Gait Posture 2009, 29, 360–369. [Google Scholar] [CrossRef]
- Carcreff, L.; Payen, G.; Grouvel, G.; Massé, F.; Armand, S. Three-Dimensional Lower-Limb Kinematics from Accelerometers and Gyroscopes with Simple and Minimal Functional Calibration Tasks: Validation on Asymptomatic Participants. Sensors 2022, 22, 5657. [Google Scholar] [CrossRef]
- Leboeuf, F.; Baker, R.; Barré, A.; Reay, J.; Jones, R.; Sangeux, M. The conventional gait model, an open-source implementation that reproduces the past but prepares for the future. Gait Posture 2019, 69, 235–241. [Google Scholar] [CrossRef] [PubMed]
- Fonseca, M.; Dumas, R.; Armand, S. Automatic gait event detection in pathologic gait using an auto-selection approach among concurrent methods. Gait Posture 2022, 96, 271–274. [Google Scholar] [CrossRef]
- Cohen, J. Statistical power analysis. Curr. Dir. Psychol. Sci. 1992, 1, 98–101. [Google Scholar] [CrossRef]
- Breiman, L.; Freidman, H.; Olshen, R.A.; Stone, C.J. Classification and Regression Trees, 1st ed.; Chapman and Hall/CRC: New York, NY, USA, 1984. [Google Scholar]
- Biau, G. Analysis of a Random Forests Model. arXiv 2010. [Google Scholar] [CrossRef]
- Huang, Y.; He, Z.; Liu, Y.; Yang, R.; Zhang, X.; Cheng, G.; Yi, J.; Ferreira, J.P.; Liu, T. Real-Time Intended Knee Joint Motion Prediction by Deep-Recurrent Neural Networks. IEEE Sensors J. 2019, 19, 11503–11509. [Google Scholar] [CrossRef]
- Su, J.; Cheng, T.; Tan, X.; Li, M.; Zhang, B.; Zhao, X. A Recurrent Neural Network Based Prediction Method for Continuous Joint Angle Movement. In Proceedings of the 2023 IEEE 13th International Conference on CYBER Technology in Automation, Control, and Intelligent Systems (CYBER), Qinhuangdao, China, 11–14 July 2023; pp. 521–526. [Google Scholar]
- Mundt, M.; Johnson, W.R.; Potthast, W.; Markert, B.; Mian, A.; Alderson, J. A Comparison of Three Neural Network Approaches for Estimating Joint Angles and Moments from Inertial Measurement Units. Sensors 2021, 21, 4535. [Google Scholar] [CrossRef]
- McCabe, M.V.; Van Citters, D.W.; Chapman, R.M. Developing a method for quantifying hip joint angles and moments during walking using neural networks and wearables. Comput. Methods Biomech. Biomed. Eng. 2022, 26, 1–11. [Google Scholar] [CrossRef] [PubMed]
- Mobbs, A.; Kahn, M.; Williams, G.; Mentiplay, B.F.; Pua, Y.-H.; Clark, R.A. Machine learning for automating subjective clinical assessment of gait impairment in people with acquired brain injury—A comparison of an image extraction and classification system to expert scoring. J. Neuroeng. Rehabilitation 2024, 21, 1–11. [Google Scholar] [CrossRef]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014. [Google Scholar] [CrossRef]
- Gul, S.; Malik, M.I.; Khan, G.M.; Shafait, F. Multi-view gait recognition system using spatio-temporal features and deep learning. Expert Syst. Appl. 2021, 179. [Google Scholar] [CrossRef]
- Ambure, P.; Gajewicz-Skretna, A.; Cordeiro, M.N.D.S.; Roy, K. New Workflow for QSAR Model Development from Small Data Sets: Small Dataset Curator and Small Dataset Modeler. Integration of Data Curation, Exhaustive Double Cross-Validation, and a Set of Optimal Model Selection Techniques. J. Chem. Inf. Model. 2019, 59, 4070–4076. [Google Scholar] [CrossRef]
- Prodanovic, N.; Dzunic, D.; Kocovic, V.; Djordjevic, A.; Prodanovic, T.; Savic, S.P.; Devedzic, G. Application of the Random Forest Algorithm for Identifying Abnormal Patterns of Knee Joint Movement. In Proceedings of the 2024 26th International Conference on Digital Signal Processing and its Applications (DSPA), Moscow, Russia, 27–29 March 2024; pp. 1–4. [Google Scholar]
- de Vet, H.C.W.; Terwee, C.B.; Mokkink, L.B.; Knol, D.L. Measurement in Medicine; University Press: New York, NY, USA, 2011. [Google Scholar]
- Mundt, M.; Thomsen, W.; Witter, T.; Koeppe, A.; David, S.; Bamer, F.; Potthast, W.; Markert, B. Prediction of lower limb joint angles and moments during gait using artificial neural networks. Med Biol. Eng. Comput. 2019, 58, 211–225. [Google Scholar] [CrossRef]
- Renani, M.S.; Eustace, A.M.; Myers, C.A.; Clary, C.W. The Use of Synthetic IMU Signals in the Training of Deep Learning Models Significantly Improves the Accuracy of Joint Kinematic Predictions. Sensors 2021, 21, 5876. [Google Scholar] [CrossRef]
- Hernandez, V.; Dadkhah, D.; Babakeshizadeh, V.; Kulić, D. Lower body kinematics estimation from wearable sensors for walking and running: A deep learning approach. Gait Posture 2021, 83, 185–193. [Google Scholar] [CrossRef]
- Findlow, A.; Goulermas, J.; Nester, C.; Howard, D.; Kenney, L. Predicting lower limb joint kinematics using wearable motion sensors. Gait Posture 2008, 28, 120–126. [Google Scholar] [CrossRef] [PubMed]
- McCabe, M.V.; Van Citters, D.W.; Chapman, R.M. Hip Joint Angles and Moments during Stair Ascent Using Neural Networks and Wearable Sensors. Bioengineering 2023, 10, 784. [Google Scholar] [CrossRef] [PubMed]
- Lim, H.; Kim, B.; Park, S. Prediction of Lower Limb Kinetics and Kinematics during Walking by a Single IMU on the Lower Back Using Machine Learning. Sensors 2019, 20, 130. [Google Scholar] [CrossRef]
- Lübbeke, A.; Zimmermann-Sloutskis, D.; Stern, R.; Roussos, C.; Bonvin, A.; Perneger, T.; Peter, R.; Hoffmeyer, P. Physical Activity Before and After Primary Total Hip Arthroplasty: A Registry-Based Study. Arthritis Care Res. 2014, 66, 277–284. [Google Scholar] [CrossRef] [PubMed]
- Mahomed, N.N.; Arndt, D.C.; McGrory, B.J.; Harris, W.H. The Harris hip score: Comparison of patient self-report with surgeon assessment. J. Arthroplast. 2001, 16, 575–580. [Google Scholar] [CrossRef]
- Ancillao, A.; Tedesco, S.; Barton, J.; O’flynn, B. Indirect Measurement of Ground Reaction Forces and Moments by Means of Wearable Inertial Sensors: A Systematic Review. Sensors 2018, 18, 2564. [Google Scholar] [CrossRef]


Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alalem, N.; Gasparutto, X.; Rose-Dulcina, K.; DiGiovanni, P.; Hannouche, D.; Armand, S. Validity of a Single Inertial Measurement Unit to Measure Hip Range of Motion During Gait in Patients Undergoing Total Hip Arthroplasty. Sensors 2025, 25, 3363. https://doi.org/10.3390/s25113363
Alalem N, Gasparutto X, Rose-Dulcina K, DiGiovanni P, Hannouche D, Armand S. Validity of a Single Inertial Measurement Unit to Measure Hip Range of Motion During Gait in Patients Undergoing Total Hip Arthroplasty. Sensors. 2025; 25(11):3363. https://doi.org/10.3390/s25113363
Chicago/Turabian StyleAlalem, Noor, Xavier Gasparutto, Kevin Rose-Dulcina, Peter DiGiovanni, Didier Hannouche, and Stéphane Armand. 2025. "Validity of a Single Inertial Measurement Unit to Measure Hip Range of Motion During Gait in Patients Undergoing Total Hip Arthroplasty" Sensors 25, no. 11: 3363. https://doi.org/10.3390/s25113363
APA StyleAlalem, N., Gasparutto, X., Rose-Dulcina, K., DiGiovanni, P., Hannouche, D., & Armand, S. (2025). Validity of a Single Inertial Measurement Unit to Measure Hip Range of Motion During Gait in Patients Undergoing Total Hip Arthroplasty. Sensors, 25(11), 3363. https://doi.org/10.3390/s25113363






