Enhanced Channel Estimation for RIS-Assisted OTFS Systems by Introducing ELM Network
Abstract
1. Introduction
1.1. OTFS in High-Mobility Scenarios
1.2. The Integration of RIS with OTFS Modulation
1.3. CE Challenges and ML Methods
1.4. Motivation and Contributions
- We propose an enhanced CE method for RIS-assisted OTFS systems by introducing an ELM network. To the best of our knowledge, few works have exploited ELM-based CE for RIS-assisted OTFS systems. Although existing DL-based methods achieve effective CE in RIS-OTFS systems (e.g., [29]), the high processing complexity motivates the exploration of alternative methods to alleviate challenges such as intricate parameter tuning and long training time.
- To mitigate the limited learning capability of ELMs relative to deep networks, we incorporate a threshold-based feature extraction method that enhances input representation despite the reduced model complexity. This initial feature extraction takes into account the specificity of CE in OTFS systems, setting it apart from current ELM-based CE methods (e.g., [32]).
- We incorporate the cascaded channels of RIS into the representation of the DD domain equivalent channels of the OTFS systems. This enables the simplification of CE in high-mobility communication scenarios by leveraging the approximately time-invariant channel characteristics in the DD domain [35], and thus improves the CE accuracy of RIS-assisted OTFS systems [16].
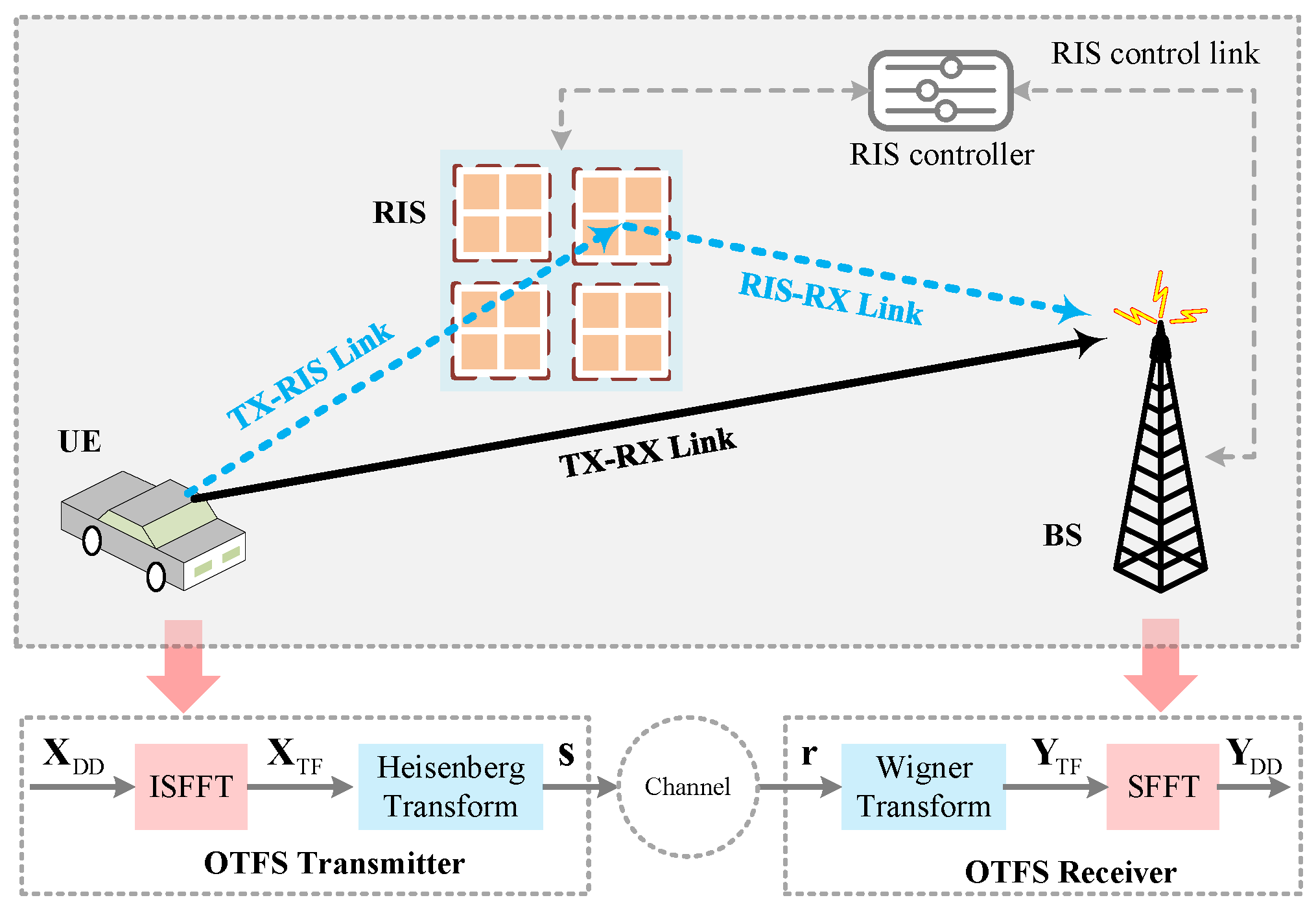
2. System Model
3. Enhanced CE by Introducing ELM Network
3.1. Pilot Placement
3.2. Initial Feature Extraction
3.3. CE Enhancement with ELM Network
| Algorithm 1 The algorithm of ELM-EnCE |
| Input: The received signal , the positive threshold , the input weights and biases of the ELM, and the number of training samples, i.e., Q.
Output: The output weight of the hidden layer (i.e., ), and the enhanced CE . Offline training: 1: for do 2: Collect the q-th training sample according to the equations from Equation (16) to Equation (18). 3: Calculate the hidden layer output according to Equation (19). 4: end for 5: Collect to form , i.e., Equation (20). 6: Calculate the output weight of the hidden layer (i.e., ) by using Equation (21). Online deployment: 7: By using Equations (13) and (14), we transform the received to the DD domain to obtain . 8: Estimate (i.e., the gain of the p-th path) according to Equation (16), i.e., the threshold-based estimation method. 9: Estimate the equivalent channel in the DD domain by using Equation (17). 10: Vectorize column-wise to obtain the initial feature matrix according to Equation (18). 11: Feed into the trained ELM network to obtain the enhanced CE . |
3.3.1. Network Architecture
3.3.2. Offline Training
3.3.3. Online Deployment
4. Results and Discussion
4.1. Parameter Settings
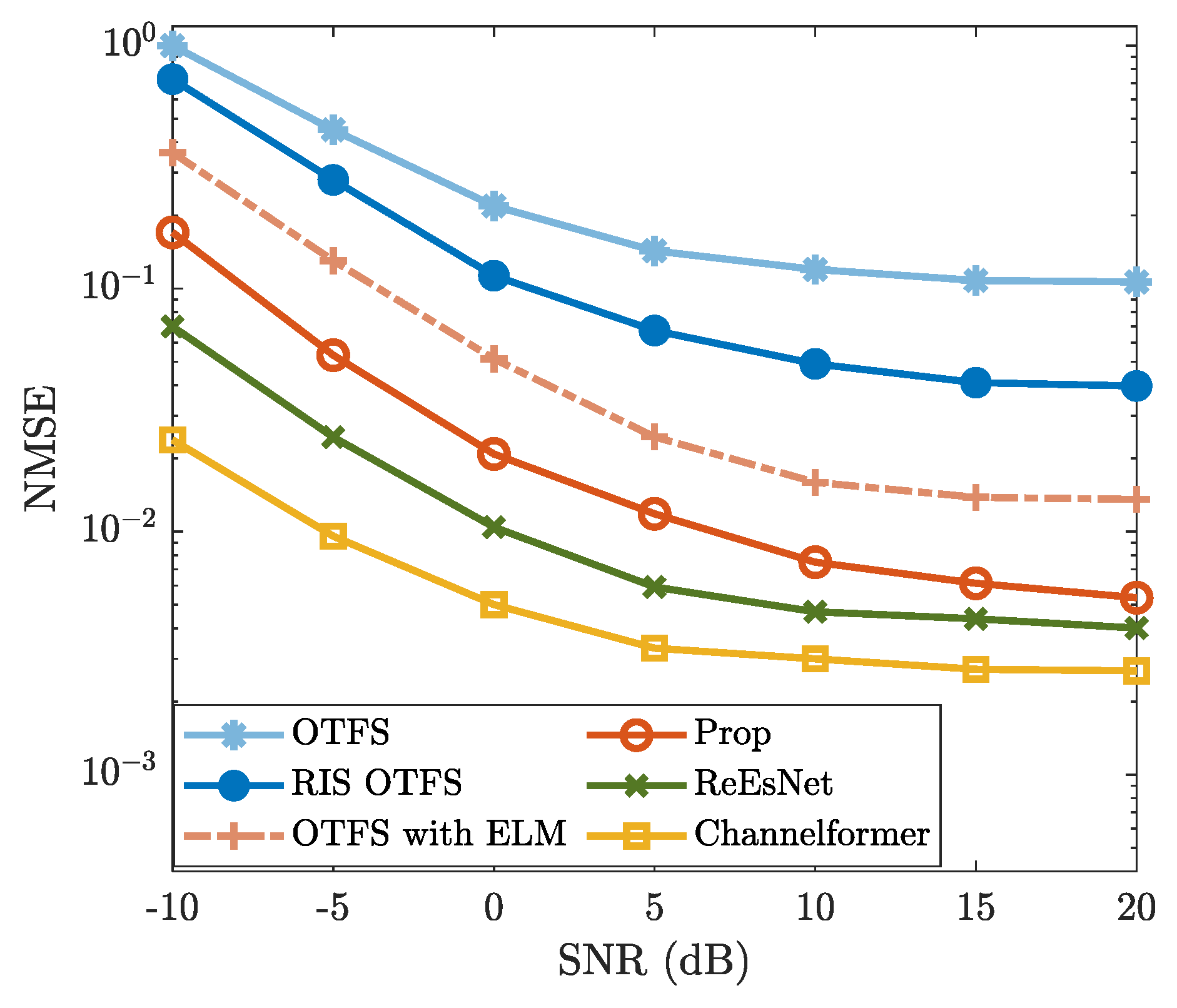
4.2. Effectiveness Analysis
4.3. Robustness Analysis
4.3.1. Robustness Against I
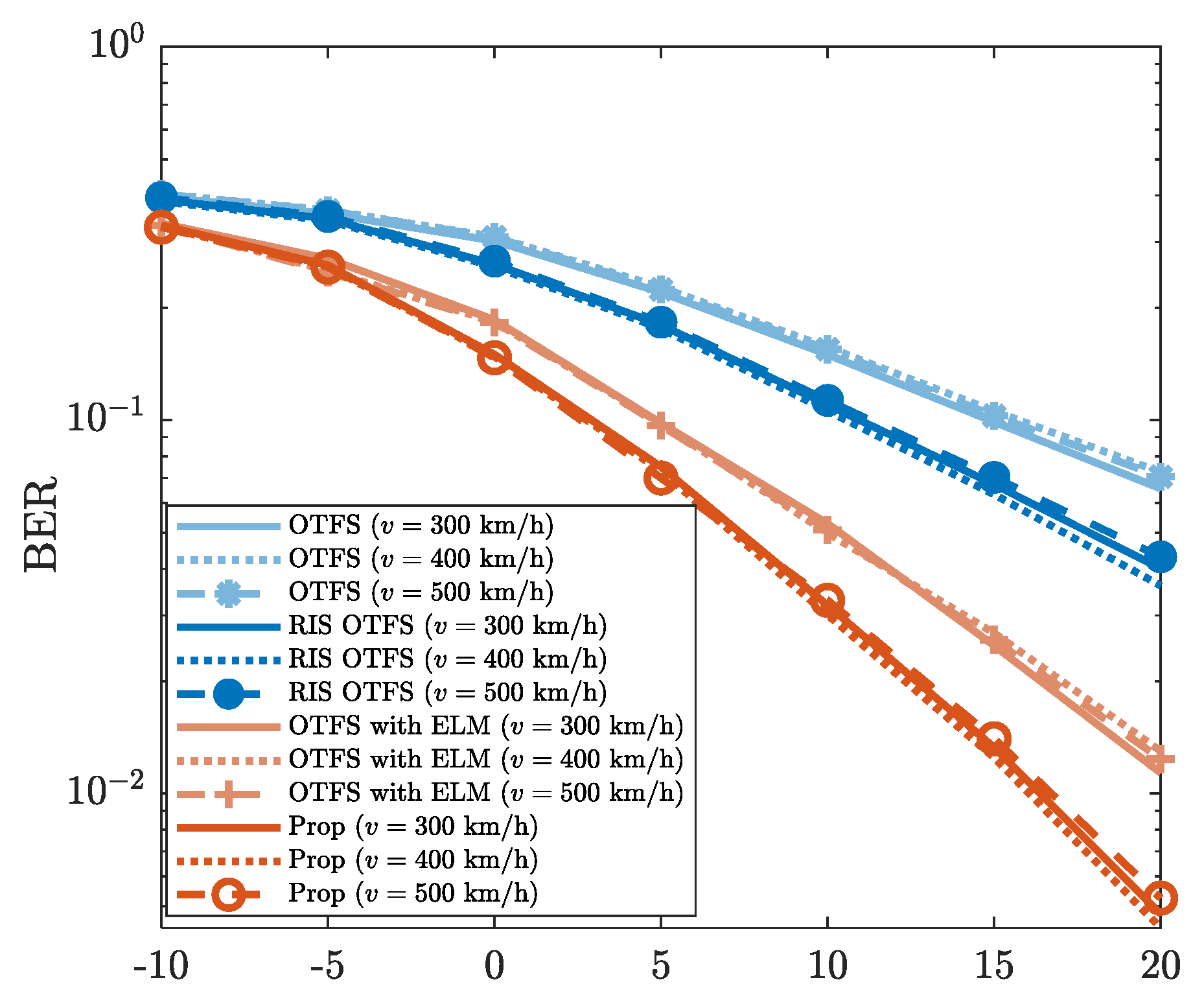
4.3.2. Robustness Against v
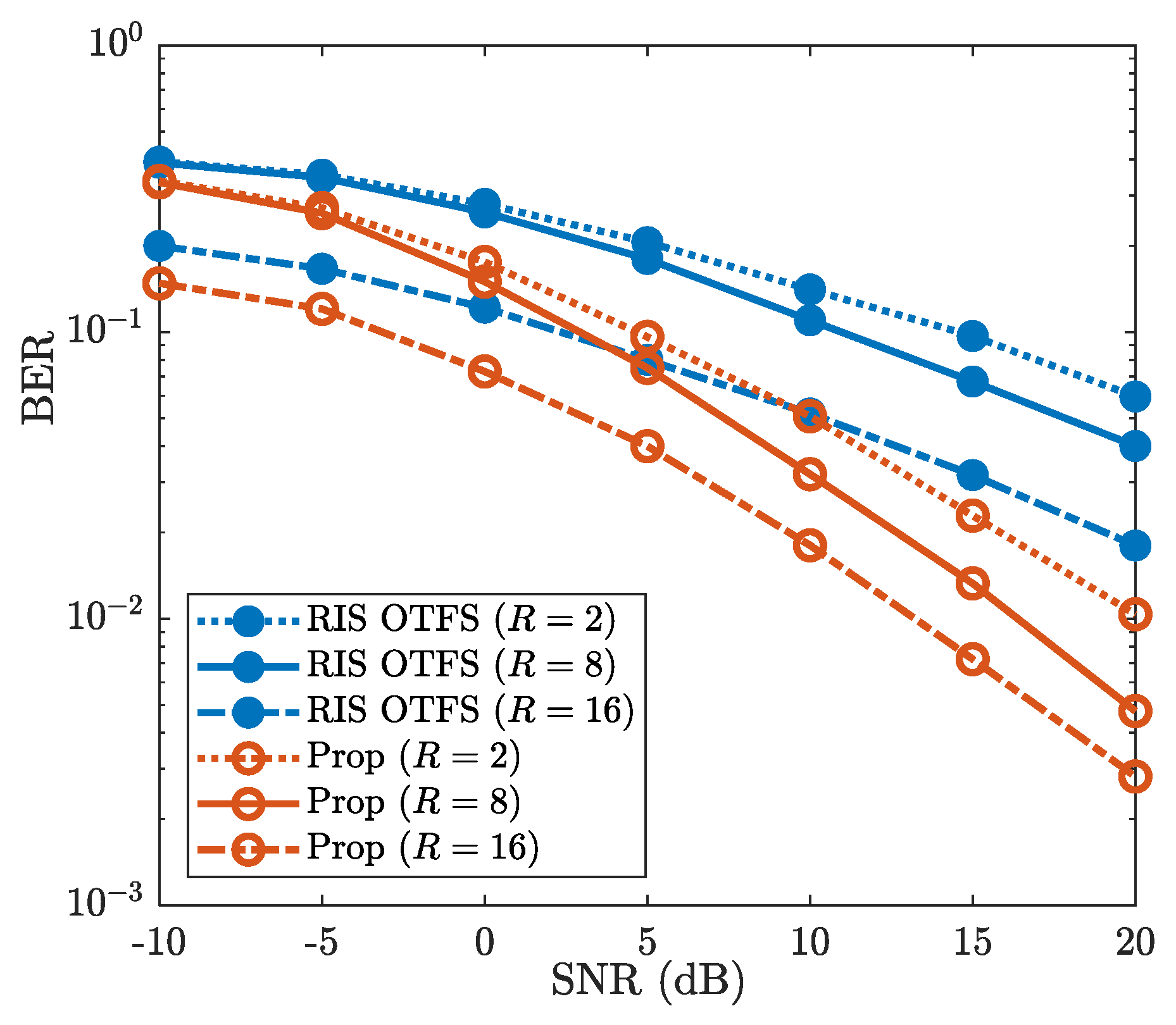
4.3.3. Robustness Against R
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, C.; You, X.; Gao, X.; Zhu, X.; Li, Z.; Zhang, C.; Wang, H.; Huang, Y.; Chen, Y.; Haas, H.; et al. On the road to 6G: Visions, requirements, key technologies, and testbeds. IEEE Commun. Surv. Tutor. 2023, 25, 905–974. [Google Scholar] [CrossRef]
- Gui, G.; Liu, M.; Tang, F.; Kato, N.; Adachi, F. 6G: Opening new horizons for integration of comfort, security, and intelligence. IEEE Wirel. Commun. 2020, 27, 126–132. [Google Scholar] [CrossRef]
- Tataria, H.; Shafi, M.; Dohler, M.; Sun, S. Six critical challenges for 6G wireless systems: A summary and some solutions. IEEE Veh. Technol. Mag. 2022, 17, 16–26. [Google Scholar] [CrossRef]
- Hadani, R.; Rakib, S.; Tsatsanis, M.; Monk, A.; Goldsmith, A.; Molisch, A.; Calderbank, R. Orthogonal time frequency space modulation. In Proceedings of the 2017 IEEE Wireless Communications and Networking Conference (WCNC), San Francisco, CA, USA, 19–22 March 2017; pp. 1–6. [Google Scholar]
- Raviteja, P.; Phan, K.; Hong, Y. Embedded pilot-aided channel estimation for OTFS in delay-doppler channels. IEEE Trans. Veh. Technol. 2019, 68, 4906–4917. [Google Scholar] [CrossRef]
- Thaj, T.; Viterbo, E. Low complexity iterative rake decision feedback equalizer for zero-padded OTFS systems. IEEE Trans. Veh. Technol. 2020, 69, 15606–15622. [Google Scholar] [CrossRef]
- Wei, Z.; Yuan, W.; Li, S.; Yuan, J.; Bharatula, G.; Hadani, R.; Hanzo, L. Orthogonal time-frequency space modulation: A promising next-generation waveform. IEEE Wirel. Commun. 2021, 28, 136–144. [Google Scholar] [CrossRef]
- Kamble, P.; Shaikh, A. 6G wireless networks: Vision, requirements, applications and challenges. In Proceedings of the 2022 5th International Conference on Advances in Science and Technology (ICAST), Mumbai, India, 2–3 December 2022; pp. 577–581. [Google Scholar]
- Chen, Z.; Han, C.; Wu, Y.; Li, L.; Huang, C.; Zhang, Z.; Wang, G.; Tong, W. Terahertz wireless communications for 2030 and beyond: A cutting-edge frontier. IEEE Commun. Mag. 2021, 59, 66–72. [Google Scholar] [CrossRef]
- Moltchanov, D.; Gaidamaka, Y.; Ostrikova, D.; Beschastnyi, V.; Koucheryavy, Y.; Samouylov, K. Ergodic outage and capacity of terahertz systems under micromobility and blockage impairments. IEEE Trans. Wirel. Commun. 2022, 21, 3024–3039. [Google Scholar] [CrossRef]
- Liu, Y.; Liu, X.; Mu, X.; Hou, T.; Xu, J.; Di Renzo, M.; AlDhahir, N. Reconfigurable intelligent surfaces: Principles and opportunities. IEEE Commun. Surv. Tutor. 2021, 23, 1546–1577. [Google Scholar] [CrossRef]
- Pan, C.; Ren, H.; Wang, K.; Kolb, J.; Elkashlan, M.; Chen, M.; Di Renzo, M.; Hao, Y.; Wang, J.; Swindlehurst, A.; et al. Reconfigurable intelligent surfaces for 6G systems: Principles, applications, and research directions. IEEE Commun. Mag. 2021, 59, 14–20. [Google Scholar] [CrossRef]
- Huang, C.; Zappone, A.; Alexandropoulos, G.; Debbah, M.; Yuen, C. Reconfigurable intelligent surfaces for energy efficiency in wireless communication. IEEE Trans. Wirel. Commun. 2019, 18, 4157–4170. [Google Scholar] [CrossRef]
- Xu, C.; Xiang, L.; An, J.; Dong, C.; Sugiura, S.; Maunder, R.; Yang, L.; Hanzo, L. OTFS-aided ris-assisted sagin systems outperform their ofdm counterparts in doubly selective high-doppler scenarios. IEEE Internet Things J. 2023, 10, 682–703. [Google Scholar] [CrossRef]
- Li, Z.; Yuan, W.; Li, B.; Wu, J.; You, C.; Meng, F. Reconfigurable intelligent surface aided OTFS: Transmission scheme and channel estimation. IEEE Internet Things J. 2023, 10, 19518–19532. [Google Scholar] [CrossRef]
- Li, M.; Zhang, S.; Ge, Y.; Gao, F.; Fan, P. Joint channel estimation and data detection for hybrid ris aided millimeter wave OTFS systems. IEEE Trans. Commun. 2022, 70, 6832–6848. [Google Scholar] [CrossRef]
- Shen, D.; Dai, L. Dimension reduced channel feedback for reconfigurable intelligent surface aided wireless communications. IEEE Trans. Commun. 2021, 69, 7748–7760. [Google Scholar] [CrossRef]
- Luo, J.; Wang, F.; Wang, S.; Wang, H.; Wang, D. Reconfigurable intelligent surface: Reflection design against passive eavesdropping. IEEE Trans. Wirel. Commun. 2021, 20, 3350–3364. [Google Scholar] [CrossRef]
- Zhang, Z.; Dai, L.; Chen, X.; Liu, C.; Yang, F.; Schober, R.; Poor, H. Active ris vs. passive ris: Which will prevail in 6G? IEEE Trans. Commun. 2023, 71, 1707–1725. [Google Scholar] [CrossRef]
- Xu, Y.; Xie, H.; Wu, Q.; Huang, C.; Yuen, C. Robust max-min energy efficiency for ris-aided hetnets with distortion noises. IEEE Trans. Commun. 2022, 70, 1457–1471. [Google Scholar] [CrossRef]
- Chen, M.; Challita, U.; Saad, W.; Yin, C.; Debbah, M. Artificial neural networks-based machine learning for wireless networks: A tutorial. IEEE Commun. Surv. Tutor. 2019, 21, 3039–3071. [Google Scholar] [CrossRef]
- Qing, C.; Dong, L.; Wang, L.; Wang, J.; Huang, C. Joint model and data-driven receiver design for data-dependent superimposed training scheme with imperfect hardware. IEEE Trans. Wirel. Commun. 2022, 21, 3779–3791. [Google Scholar] [CrossRef]
- Abid, M.; Talin, I.; Kadir, M. Reconfigurable intelligent surface-aided orthogonal time frequency space and its deep learning-based signal detection. IEEE Access 2023, 11, 47321–47338. [Google Scholar] [CrossRef]
- Ahmad, M.; Sarwar, M.S.; Shin, S.Y. Deep Learning Assisted Channel Estimation for Adaptive Parameter Selection in mMIMO-SEFDM. IEEE Internet Things J. 2025. early access. [Google Scholar] [CrossRef]
- Shen, W.; Qin, Z.; Nallanathan, A. Deep Learning for Super-Resolution Channel Estimation in Reconfigurable Intelligent Surface Aided Systems. IEEE Trans. Commun. 2023, 71, 1491–1503. [Google Scholar] [CrossRef]
- Elbir, A.M.; Papazafeiropoulos, A.; Kourtessis, P.; Chatzinotas, S. Deep Channel Learning for Large Intelligent Surfaces Aided mm-Wave Massive MIMO Systems. IEEE Trans. Wirel. Commun. 2020, 9, 1447–1451. [Google Scholar] [CrossRef]
- Liu, C.; Liu, X.; Ng, D.W.K.; Yuan, J. Deep Residual Learning for Channel Estimation in Intelligent Reflecting Surface-Assisted Multi-User Communications. IEEE Wirel. Commun. Lett. 2022, 21, 898–912. [Google Scholar] [CrossRef]
- Jin, Y.; Zhang, J.; Huang, C.; Yang, L.; Xiao, H.; Ai, B. Multiple Residual Dense Networks for Reconfigurable Intelligent Surfaces Cascaded Channel Estimation. IEEE Trans. Veh. Technol. 2022, 71, 2134–2139. [Google Scholar] [CrossRef]
- Singh, S.; Trivedi, A.; Saxena, D. Channel Estimation for IRS-Aided OTFS System Using Dilated Attention GAN. Trans. Emerg. Telecommun. Technol. 2024, 35, e70031. [Google Scholar] [CrossRef]
- Alzubaidi, L.; Zhang, J.; Humaidi, A.; Al-Dujaili, A.; Duan, Y.; Al-Shamma, O.; Santamaría, J.; Fadhel, M.; Al-Amidie, M.; Farhan, L. Review of deep learning: Concepts, cnn architectures, challenges, applications, future directions. J. Big Data 2021, 8, 1–74. [Google Scholar] [CrossRef]
- Tang, J.; Deng, C.; Huang, G. Extreme learning machine for multilayer perceptron. IEEE Trans. Neural Netw. Learn. Syst. 2016, 27, 809–821. [Google Scholar] [CrossRef] [PubMed]
- Qing, C.; Wang, L.; Dong, L.; Wang, J. Enhanced elm based channel estimation for ris-assisted ofdm systems with insufficient cp and imperfect hardware. IEEE Commun. Lett. 2022, 26, 153–157. [Google Scholar] [CrossRef]
- Liu, J.; Mei, K.; Zhang, X.; Ma, D.; Wei, J. Online extreme learning machine-based channel estimation and equalization for ofdm systems. IEEE Commun. Lett. 2019, 23, 1276–1279. [Google Scholar] [CrossRef]
- Carrera, D.; Zabala-Blanco, D.; Vargas-Rosales, C.; Azurdia-Meza, C. Extreme learning machine-based receiver for multi-user massive mimo systems. IEEE Commun. Lett. 2021, 25, 484–488. [Google Scholar] [CrossRef]
- Lampel, F.; Avarado, A.; Willems, F. On OTFS using the discrete Zak transform. In Proceedings of the 2022 IEEE International Conference on Communications Workshops (ICC Workshops), Seoul, Republic of Korea, 16–20 May 2022; pp. 729–734. [Google Scholar]
- Raviteja, P.; Hong, Y.; Viterbo, E.; Biglieri, E. Practical pulse-shaping waveforms for reduced-cyclic-prefix OTFS. IEEE Trans. Veh. Technol. 2018, 68, 957–961. [Google Scholar] [CrossRef]
- Zheng, B.; Zhang, R. Intelligent reflecting surface-enhanced ofdm: Channel estimation and reflection optimization. IEEE Wirel. Commun. Lett. 2020, 9, 518–522. [Google Scholar] [CrossRef]
- Zhang, H.; Huang, X.; Zhang, J. Comparison of OTFS diversity performance over slow and fast fading channels. In Proceedings of the 2019 IEEE/CIC International Conference on Communications in China (ICCC), Changchun, China, 11–13 August 2019; pp. 828–833. [Google Scholar]
- Habibi, S.; Chen, J.; Fang, F.; Wang, X. User-Specific Channel Estimation Overhead Optimization and Resource Allocation for Multi-User OTFS Systems. IEEE Commun. Lett. 2024, 28, 2126–2130. [Google Scholar] [CrossRef]
- Liu, R.; Huang, Y.; He, D.; Xu, Y.; Zhang, W. Optimizing Channel Estimation Overhead for OTFS with Prior Channel Statistics. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference, WCNC, Nanjing, China, 29 March–1 April 2021; pp. 1–6. [Google Scholar]
- Liu, H.; Liu, Y.; Yang, M.; Zhang, Q. On the characterizations of OTFS modulation over multipath rapid fading channel. IEEE Trans. Wirel. Commun. 2022, 22, 2008–2021. [Google Scholar] [CrossRef]
- Wang, T.; Fan, S.; Chen, H.; Xiao, Y.; Guan, X.; Song, W. Generalized approximate message passing detector for GSM-OTFS systems. IEEE Access 2022, 10, 22997–23007. [Google Scholar] [CrossRef]
- Li, L.; Chen, H.; Chang, H.-H.; Liu, L. Deep Residual Learning Meets OFDM Channel Estimation. IEEE Wirel. Commun. Lett. 2020, 9, 615–618. [Google Scholar] [CrossRef]
- Luan, D.; Thompson, J.S. Channelformer: Attention Based Neural Solution for Wireless Channel Estimation and Effective Online Training. IEEE Trans. Wirel. Commun. 2023, 22, 6562–6577. [Google Scholar] [CrossRef]
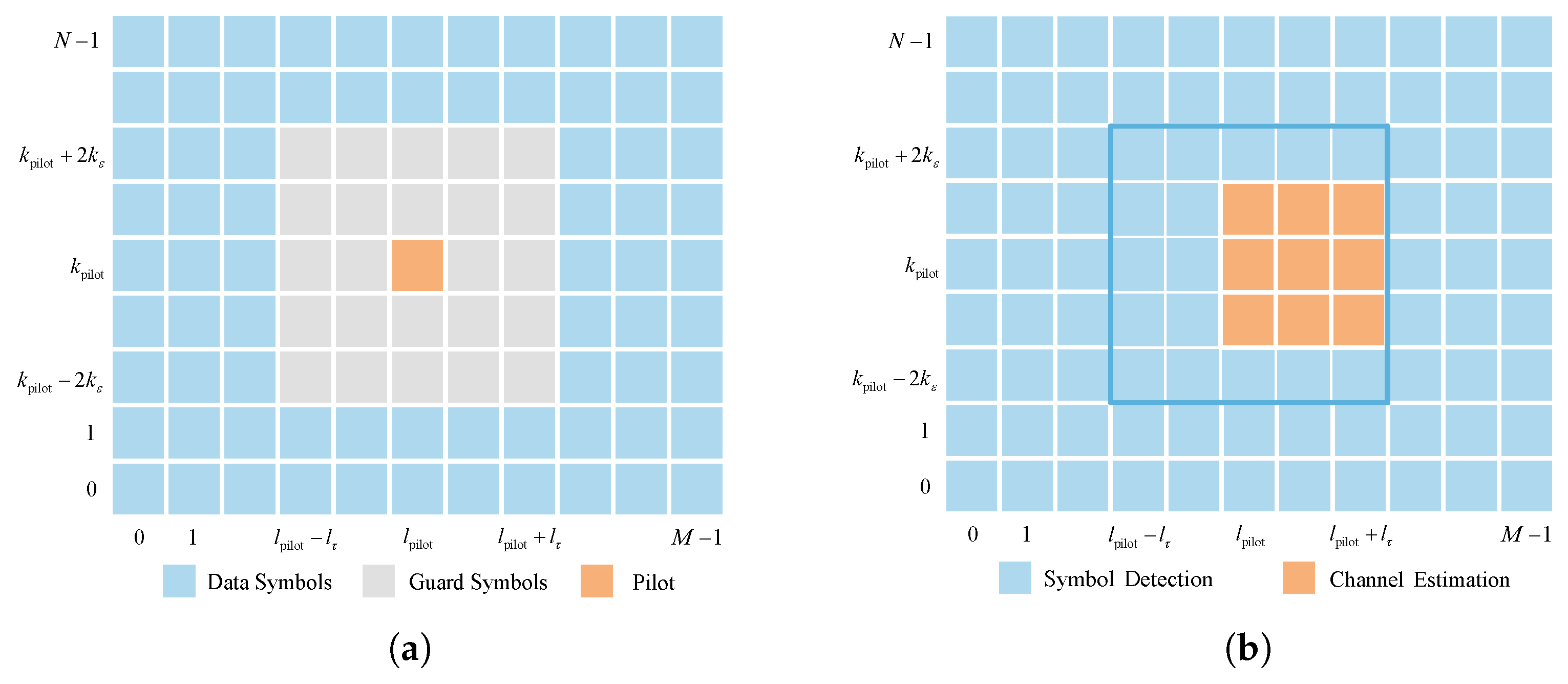




| Net1 | Net2 | ||||
|---|---|---|---|---|---|
| Layer | Neuron Size |
Activation Function | Layer | Neuron Size |
Activation Function |
| Input | Linear | Input | Linear | ||
| Hidden | Sigmoid | Hidden | Sigmoid | ||
| Output | Linear | Output | Linear | ||
| Channelformer | ReEsNet | ELM |
|---|---|---|
| 1835 | 1176 | 58 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, M.; Liu, Z.; Wang, L.; Hu, W.; Qing, C. Enhanced Channel Estimation for RIS-Assisted OTFS Systems by Introducing ELM Network. Sensors 2025, 25, 3292. https://doi.org/10.3390/s25113292
Zhang M, Liu Z, Wang L, Hu W, Qing C. Enhanced Channel Estimation for RIS-Assisted OTFS Systems by Introducing ELM Network. Sensors. 2025; 25(11):3292. https://doi.org/10.3390/s25113292
Chicago/Turabian StyleZhang, Mintao, Zhiying Liu, Li Wang, Wenquan Hu, and Chaojin Qing. 2025. "Enhanced Channel Estimation for RIS-Assisted OTFS Systems by Introducing ELM Network" Sensors 25, no. 11: 3292. https://doi.org/10.3390/s25113292
APA StyleZhang, M., Liu, Z., Wang, L., Hu, W., & Qing, C. (2025). Enhanced Channel Estimation for RIS-Assisted OTFS Systems by Introducing ELM Network. Sensors, 25(11), 3292. https://doi.org/10.3390/s25113292






