A Novel Variational Bayesian Method Based on Student’s t Noise for Underwater Localization
Abstract
1. Introduction
- To address the heavy-tailed noise problem caused by outlier interference, the SWVKF-ST is proposed. Student’s t-distribution is adopted to model the noise, and auxiliary random variables are introduced to approximate it as a Gaussian hierarchical distribution.
- The proposed SWVKF-ST algorithm achieves further adaptive parameter updates through smoothing estimation within a sliding window. Through VB iteration, the state, measurement noise covariance, and auxiliary random variables are jointly estimated online, effectively mitigating the influence of outliers and improving estimation accuracy.
- To correct the predicted state covariance, the proposed SWVKF-ST algorithm constructs multiple fading factors. The optimal estimation of the measurement noise covariance is embedded as a time-varying parameter into the suboptimal fading factor based on the strong tracking principle, thereby improving the correction accuracy of the predicted state covariance.
2. Problem Formulation
3. Proposed Method
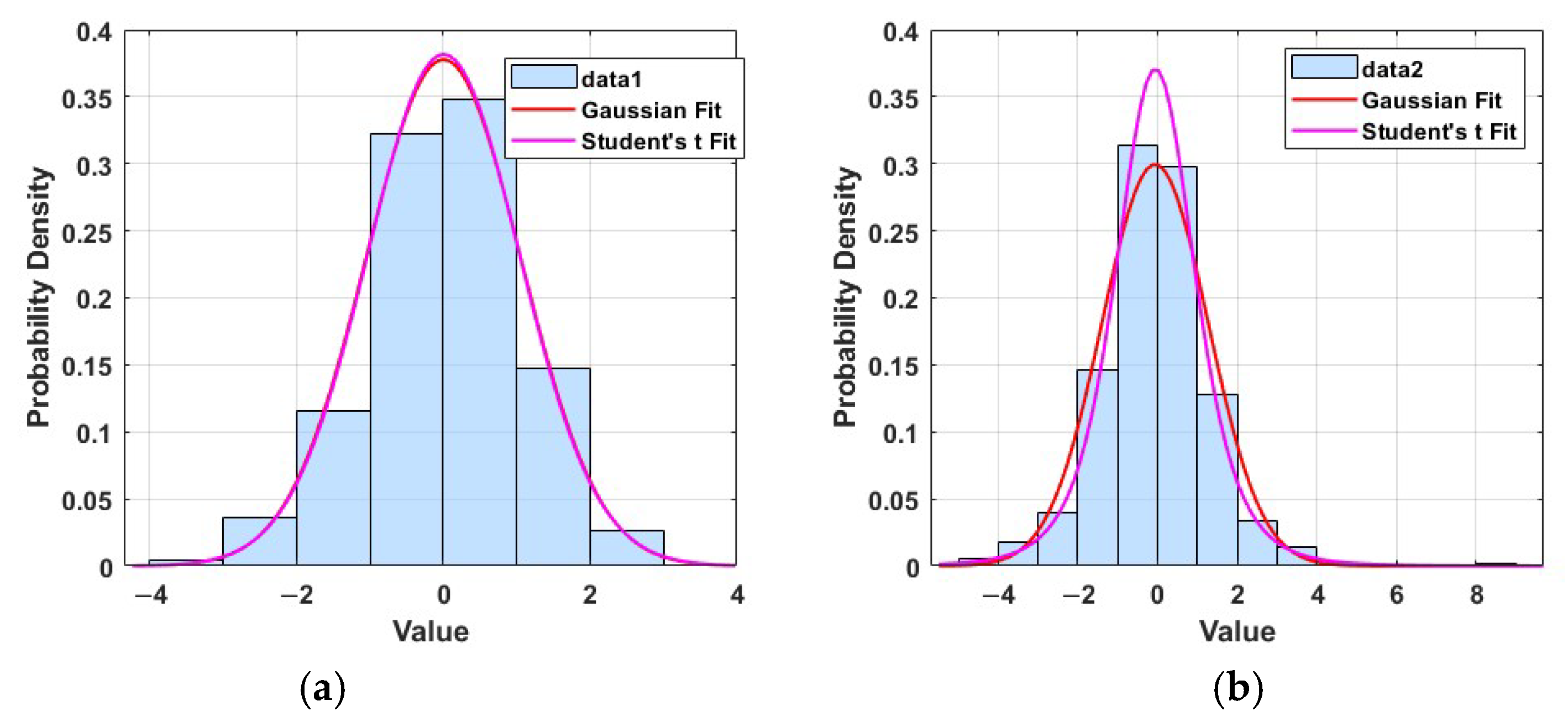
3.1. Noise Modeling
3.2. Variational Approximations
3.3. Construction of Multiple Fading Factors
| Algorithm 1 The proposed SWVKF-ST |
| Inputs: , , , , , , , , , , , . |
| Initialization: |
| For |
| , |
| End for |
| Calculate DOF parameters and inverse-scale matrices using (24)–(25) |
| Iteration: |
| For |
| Calculate the scale matrices and using (31)–(32) |
| Obtain the multiple fading factors by (11)–(15) |
| End for |
| For |
| Calculate and as (39)–(40) |
| Calculate the shape parameters and rate parameters using (44)–(47) |
| Calculate the expectations as (48)–(51) |
| If , the iteration is terminated |
| End for |
| , |
| , |
| , |
| Outputs:, , , . |
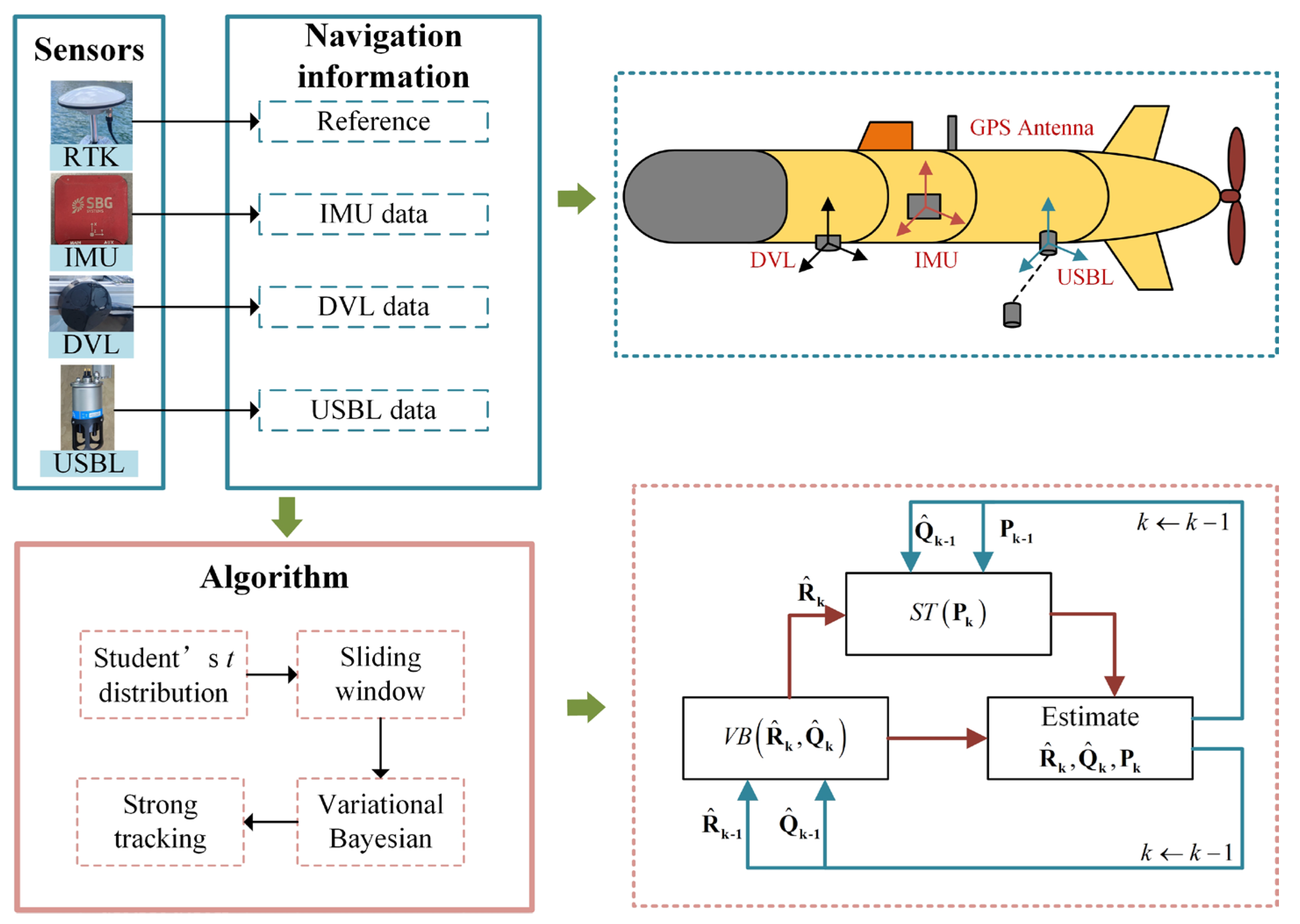
4. Simulations and Experiment
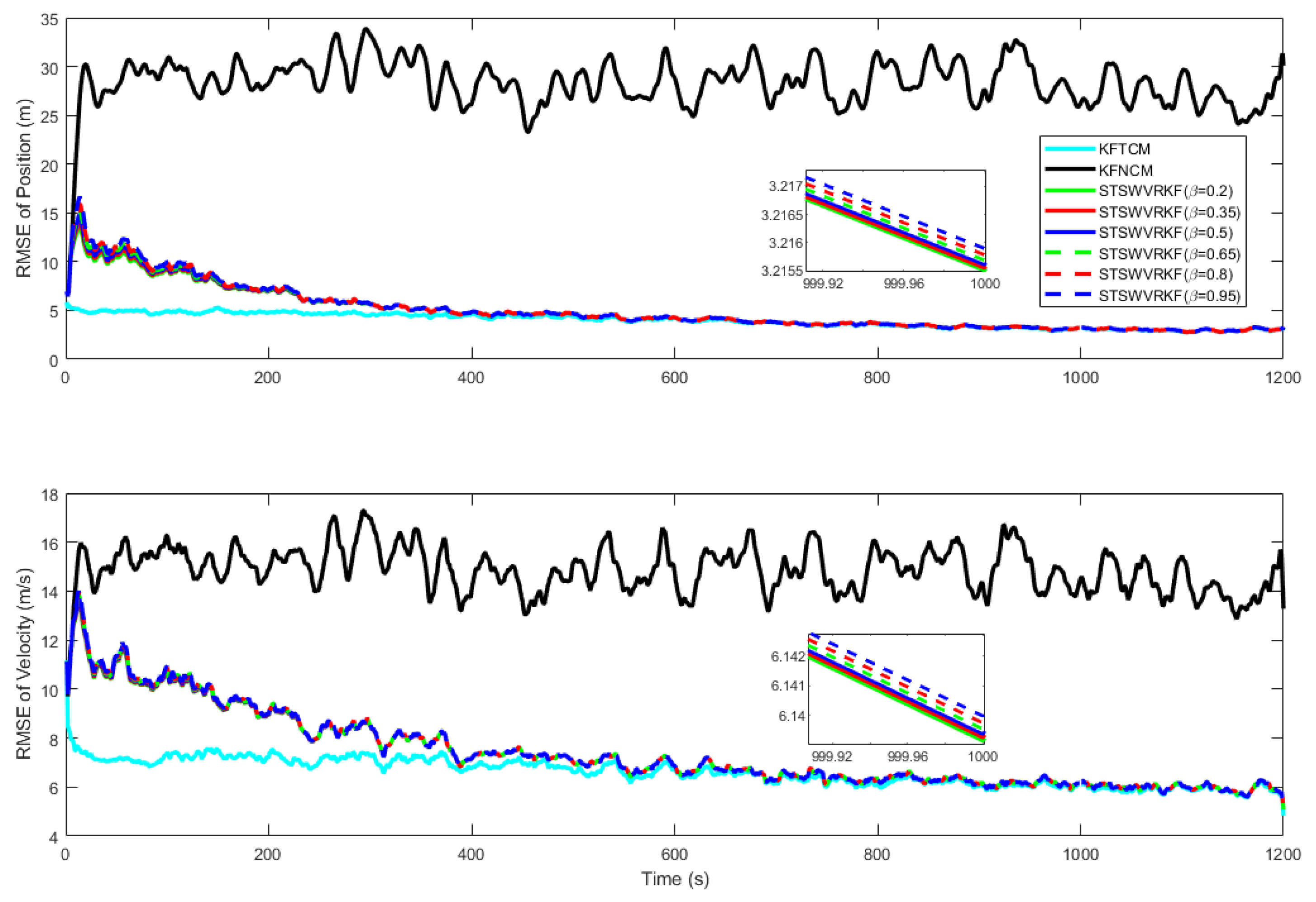
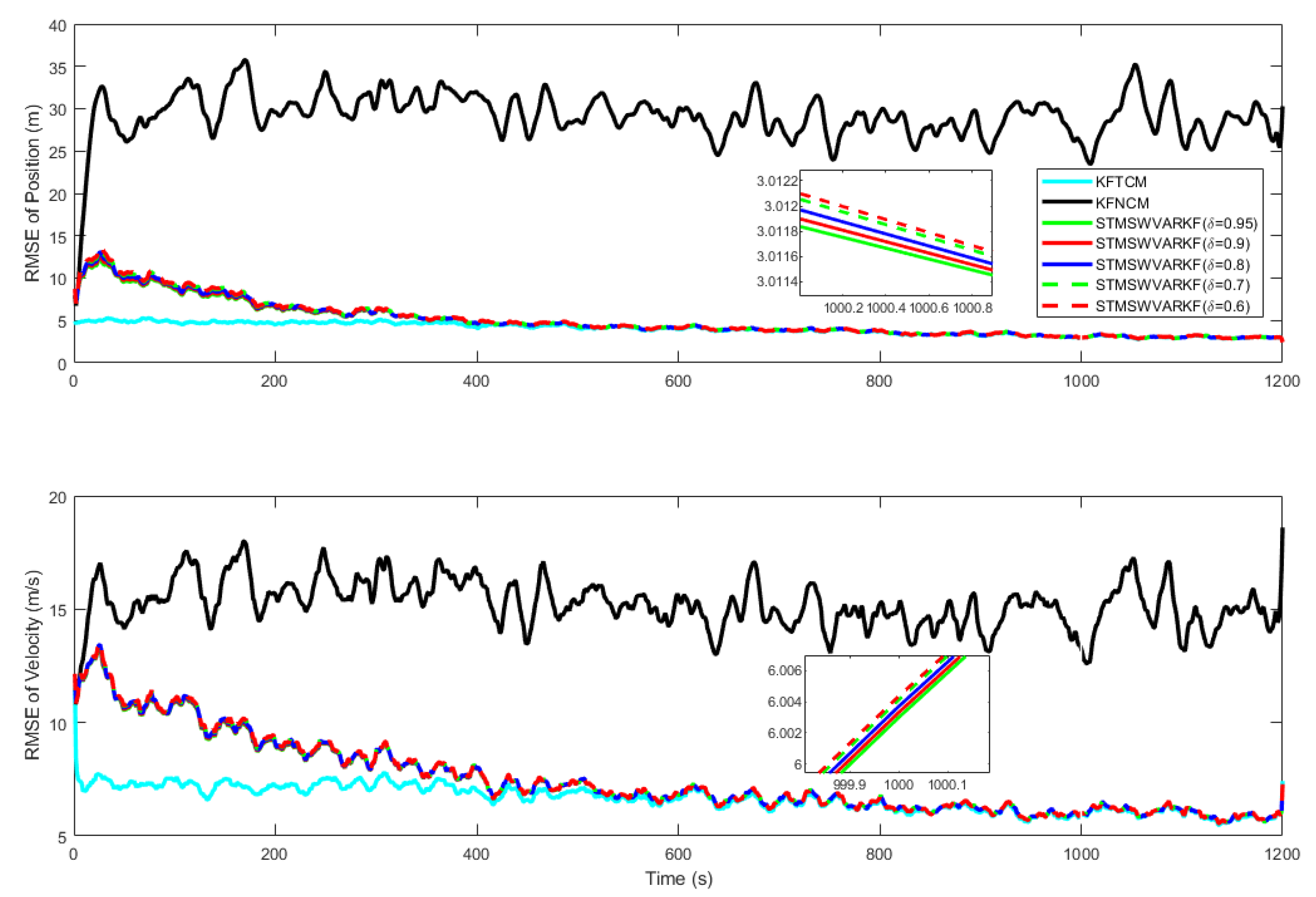
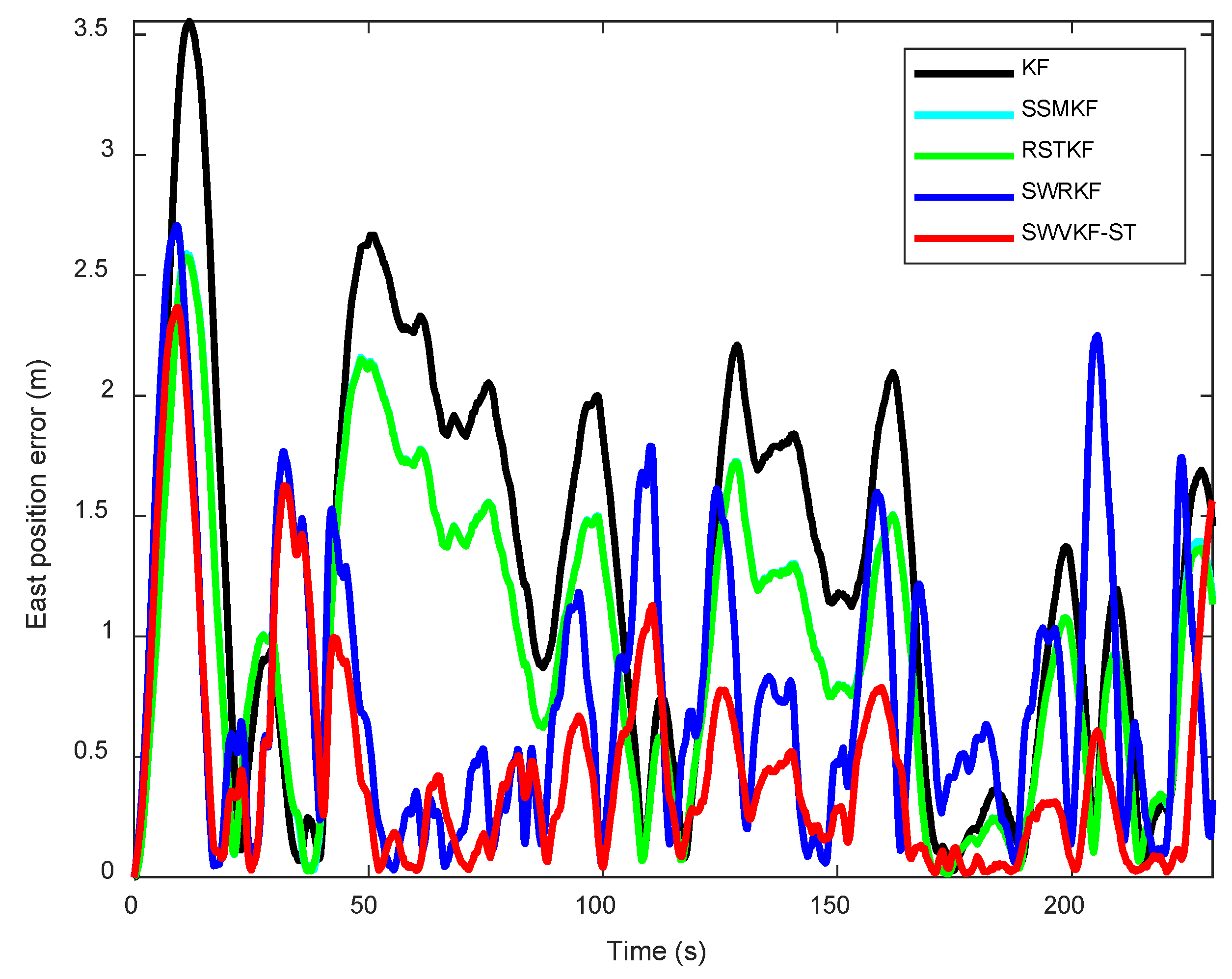
4.1. Simulations
4.2. Surface Vessel Test
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Wang, D.; Wang, B.; Huang, H.; Yao, Y.; Xu, X. Robust Filter Method for SINS/DVL/USBL Tight Integrated Navigation System. IEEE Sens. J. 2023, 23, 10912–10923. [Google Scholar] [CrossRef]
- Pang, W.; Zhu, D.; Sun, C. Multi-AUV Formation Reconfiguration Obstacle Avoidance Algorithm Based on Affine Transformation and Improved Artificial Potential Field Under Ocean Currents Disturbance. IEEE Trans. Autom. Sci. Eng. 2024, 21, 1469–1487. [Google Scholar] [CrossRef]
- Zhu, Y.; Zhang, T.; Cui, B.; Wei, X.; Jin, B. In-Motion Coarse Alignment for SINS/USBL Based on USBL Relative Position. IEEE Trans. Autom. Sci. Eng. 2025, 22, 1425–1434. [Google Scholar] [CrossRef]
- Bian, Y.; Li, R.; Wang, G.; Qin, X.; Hu, M.; Ding, R. Tightly Coupled Information Fusion for SINS/DVL/USBL Integrated Navigation of UUV. IEEE Trans. Instrum. Meas. 2023, 72, 8503213. [Google Scholar] [CrossRef]
- Wang, D.; Huang, H.; Wang, J.; Wang, B.; Wang, Y. The Fault Detection and Virtual Reconstruction Method for Underwater Navigation System. IEEE Trans. Instrum. Meas. 2025, 74, 8500312. [Google Scholar] [CrossRef]
- Wang, D.; Xu, X.S.; Yao, Y.Q.; Zhang, T.; Zhu, Y.Y. A Novel SINS/DVL Tightly Integrated Navigation Method for Complex Environment. IEEE Trans. Instrum. Meas. 2020, 69, 5183–5196. [Google Scholar] [CrossRef]
- Mu, X.; He, B.; Wu, S.; Zhang, X.; Song, Y.; Yan, T. A practical INS/GPS/DVL/PS integrated navigation algorithm and its application on Autonomous Underwater Vehicle. Appl. Ocean Res. 2021, 106, 102441. [Google Scholar] [CrossRef]
- Zhang, L.; Wu, X.; Gao, R.; Pan, L.; Zhang, Q. A multi-sensor fusion positioning approach for indoor mobile robot using factor graph. Measurement 2023, 216, 112926. [Google Scholar] [CrossRef]
- Shan, T.X.; Englot, B.; Meyers, D.; Wang, W.; Ratti, C.; Rus, D. LIO-SAM: Tightly-coupled Lidar Inertial Odometry via Smoothing and Mapping. In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Electr Network, Virtual, 24 October–24 January 2020. [Google Scholar]
- Qin, H.; Wang, X.; Wang, G.; Hu, M.; Bian, Y.; Qin, X.; Ding, R. A novel INS/USBL/DVL integrated navigation scheme against complex underwater environment. Ocean Eng. 2023, 286, 115485. [Google Scholar] [CrossRef]
- Dawson, E.; Rashed, M.A.; Abdelfatah, W.; Noureldin, A. Radar-Based Multisensor Fusion for Uninterrupted Reliable Positioning in GNSS-Denied Environments. IEEE Trans. Intell. Transp. Syst. 2022, 23, 23384–23398. [Google Scholar] [CrossRef]
- Kheirandish, M.; Yazdi, E.A.; Mohammadi, H.; Mohammadi, M. A fault-tolerant sensor fusion in mobile robots using multiple model Kalman filters. Robot. Auton. Syst. 2023, 161, 104343. [Google Scholar] [CrossRef]
- Huang, H.; Tang, J.; Liu, C.; Zhang, B.; Wang, B. Variational Bayesian-Based Filter for Inaccurate Input in Underwater Navigation. IEEE Trans. Veh. Technol. 2021, 70, 8441–8452. [Google Scholar] [CrossRef]
- Zhu, Z.; Liu, S.R.; Zhang, B.T. An improved Sage-Husa adaptive filtering algorithm. In Proceedings of the 31 Chinese Control Conference, Hefei, China, 25–27 July 2012. [Google Scholar]
- Toledo-Moreo, R.; Zamora-Izquierdo, M.A.; Ubeda-Minarro, B.; Gomez-Skarmeta, A.F. High-integrity IMM-EKF-based road vehicle navigation with low-cost GPS/SBAS/INS. IEEE Trans. Intell. Transp. Syst. 2007, 8, 491–511. [Google Scholar] [CrossRef]
- Wang, D.; Wang, B.; Huang, H.; Xu, B.; Zhang, H. A Novel SINS/DVL Integrated Navigation Method Based on Different Track Models for Complex Environment. IEEE Trans. Instrum. Meas. 2024, 73, 8501912. [Google Scholar] [CrossRef]
- Huang, Y.L.; Zhang, Y.G.; Li, N.; Wu, Z.M.; Chambers, J.A. A Novel Robust Student’s t-Based Kalman Filter. IEEE Trans. Aerosp. Electron. Syst. 2017, 53, 1545–1554. [Google Scholar] [CrossRef]
- Xu, H.; Duan, K.; Yuan, H.; Xie, W.; Wang, Y. Adaptive Fixed-Lag Smoothing Algorithms Based on the Variational Bayesian Method. IEEE Trans. Autom. Control 2021, 66, 4881–4887. [Google Scholar] [CrossRef]
- Xu, B.; Wang, X.; Guo, Y.; Zhang, J.; Razzaqi, A.A. A Novel Adaptive Filter for Cooperative Localization Under Time-Varying Delay and Non-Gaussian Noise. IEEE Trans. Instrum. Meas. 2021, 70, 9600615. [Google Scholar] [CrossRef]
- Huang, Y.; Zhu, F.; Jia, G.; Zhang, Y. A Slide Window Variational Adaptive Kalman Filter. IEEE Trans. Circuits Syst. II-Express Briefs 2020, 67, 3552–3556. [Google Scholar] [CrossRef]
- Fan, Y.; Qiao, S.; Wang, G.; Zhang, H. An Adaptive Variational Outlier-Robust Filter for Multisensor Distributed Fusion. IEEE Sens. J. 2024, 24, 4618–4627. [Google Scholar] [CrossRef]
- Pan, C.; Gao, J.; Li, Z.; Qian, N.; Li, F. Multiple fading factors-based strong tracking variational Bayesian adaptive Kalman filter. Measurement 2021, 176, 109139. [Google Scholar] [CrossRef]
- Zhu, F.; Huang, Y.; Xue, C.; Mihaylova, L.; Chambers, J. A Sliding Window Variational Outlier-Robust Kalman Filter Based on Student’s t-Noise Modeling. IEEE Trans. Aerosp. Electron. Syst. 2022, 58, 4835–4849. [Google Scholar] [CrossRef]
- Wang, K.; Wu, P.; Li, X.; He, S.; Li, J. An adaptive outlier-robust Kalman filter based on sliding window and Pearson type VII distribution modeling. Signal Process. 2024, 216, 109306. [Google Scholar] [CrossRef]
- Qiao, S.; Fan, Y.; Wang, G.; Mu, D.; He, Z. Modified Strong Tracking Slide Window Variational Adaptive Kalman Filter With Unknown Noise Statistics. IEEE Trans. Ind. Inform. 2023, 19, 8679–8690. [Google Scholar] [CrossRef]
- Yang, Y.X.; Xu, T.H. An adaptive Kalman filter based on sage windowing weights and variance components. J. Navig. 2003, 56, 231–240. [Google Scholar] [CrossRef]
- Huang, H.; Zhang, S.; Wang, D.; Ling, K.-V.; Liu, F.; He, X. A Novel Bayesian-Based Adaptive Algorithm Applied to Unobservable Sensor Measurement Information Loss for Underwater Navigation. IEEE Trans. Instrum. Meas. 2023, 72, 9514812. [Google Scholar] [CrossRef]
- Huang, Y.; Zhang, Y.; Wu, Z.; Li, N.; Chambers, J. A Novel Adaptive Kalman Filter With Inaccurate Process and Measurement Noise Covariance Matrices. IEEE Trans. Autom. Control 2018, 63, 594–601. [Google Scholar] [CrossRef]
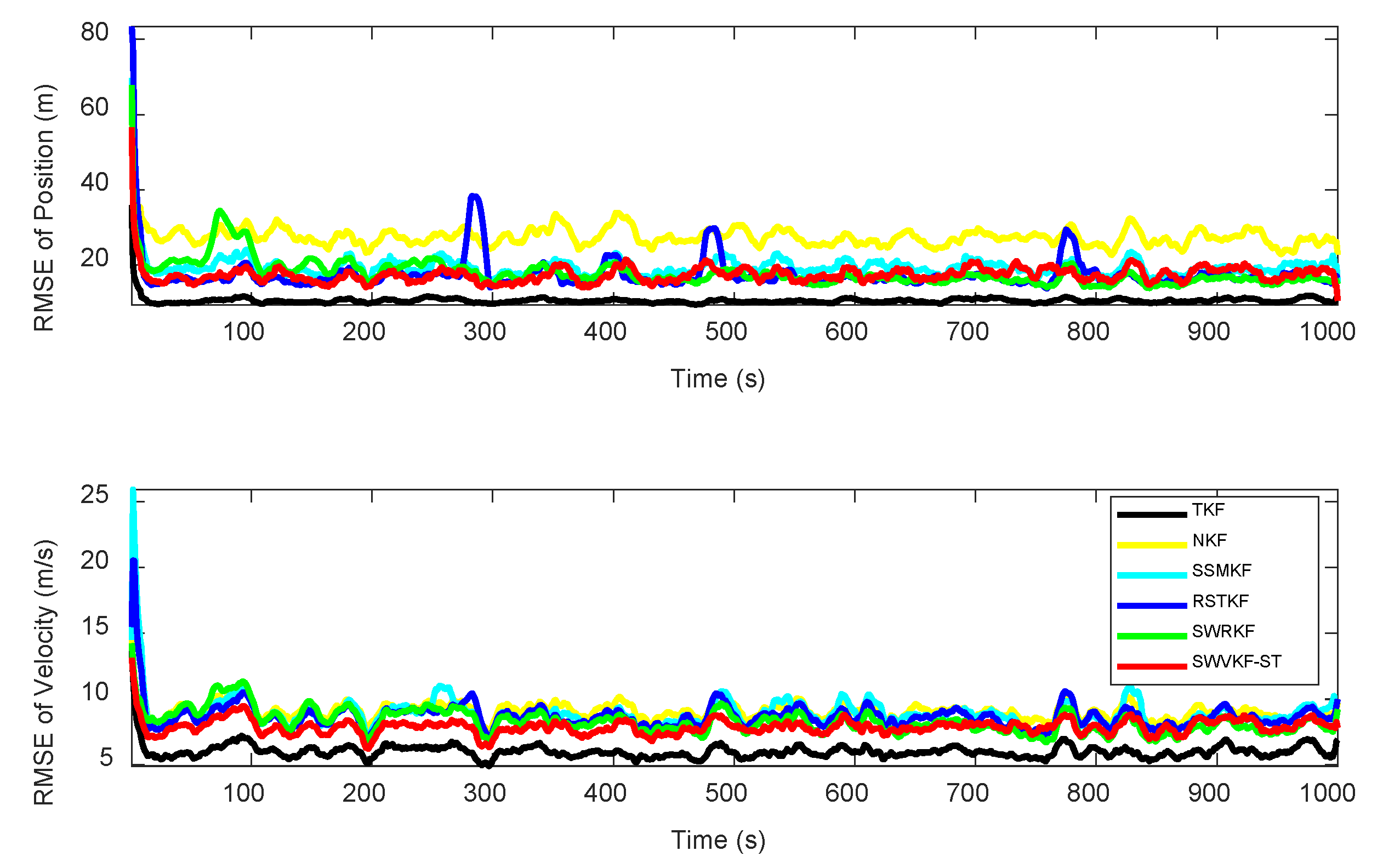
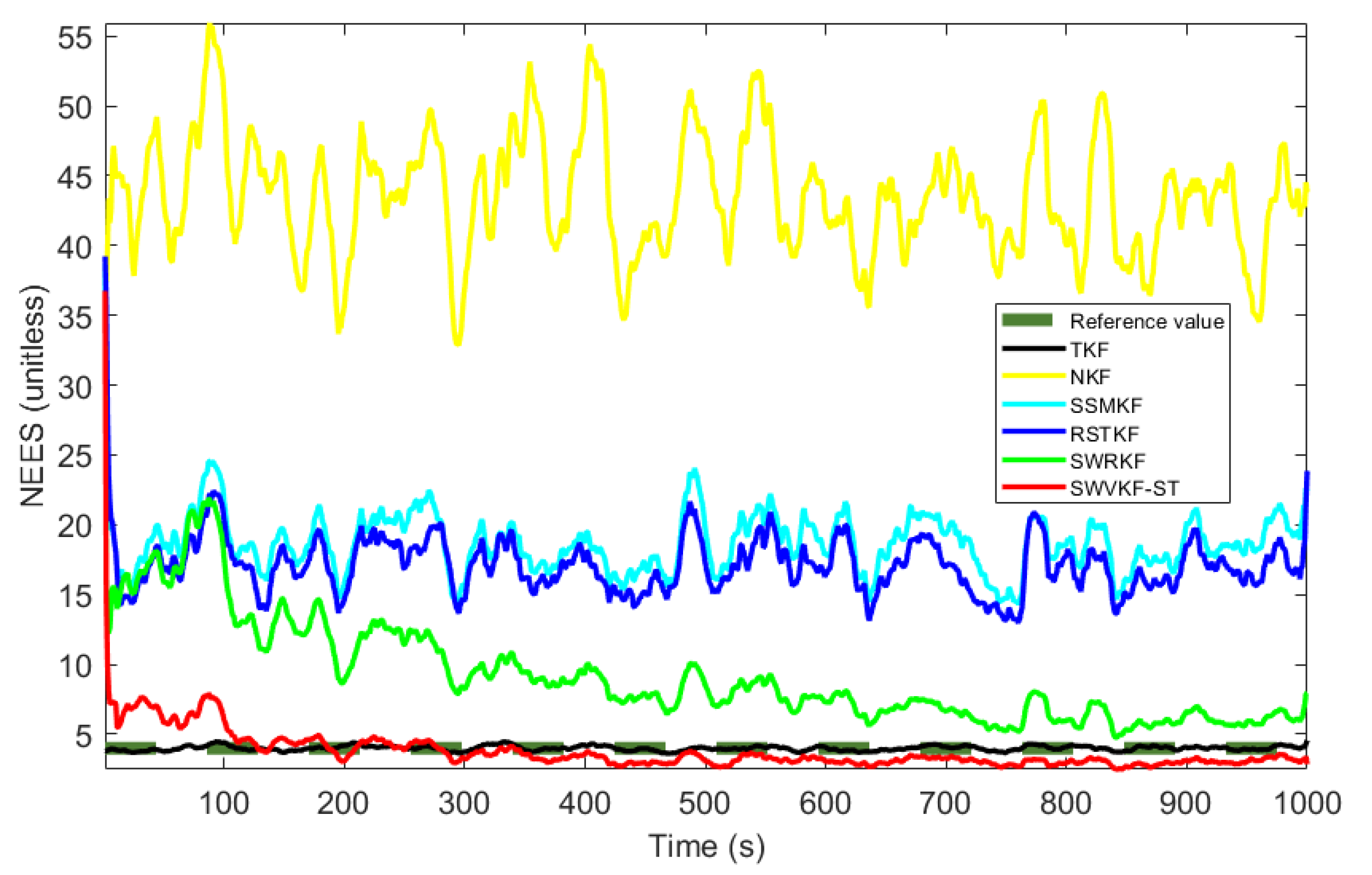

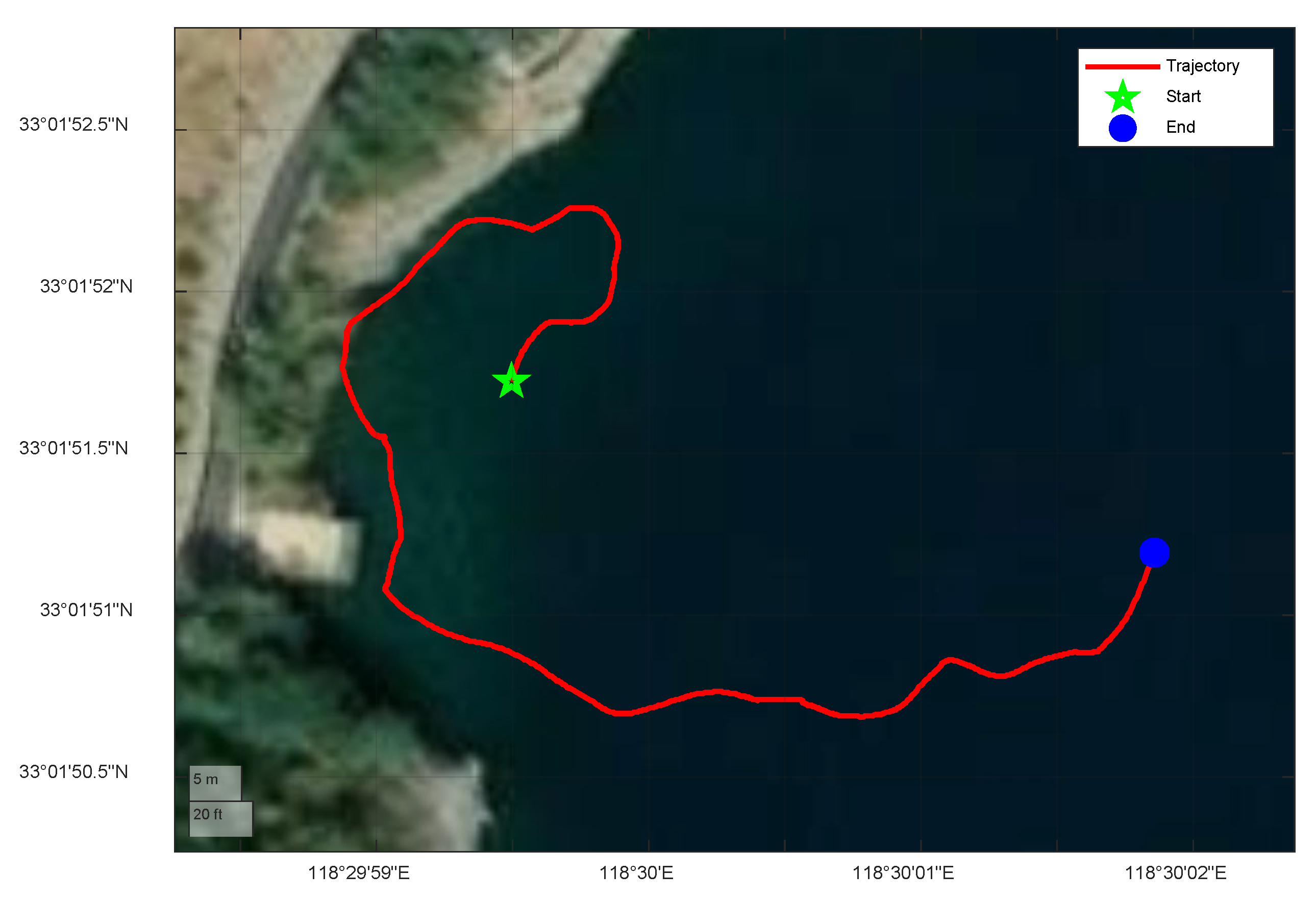
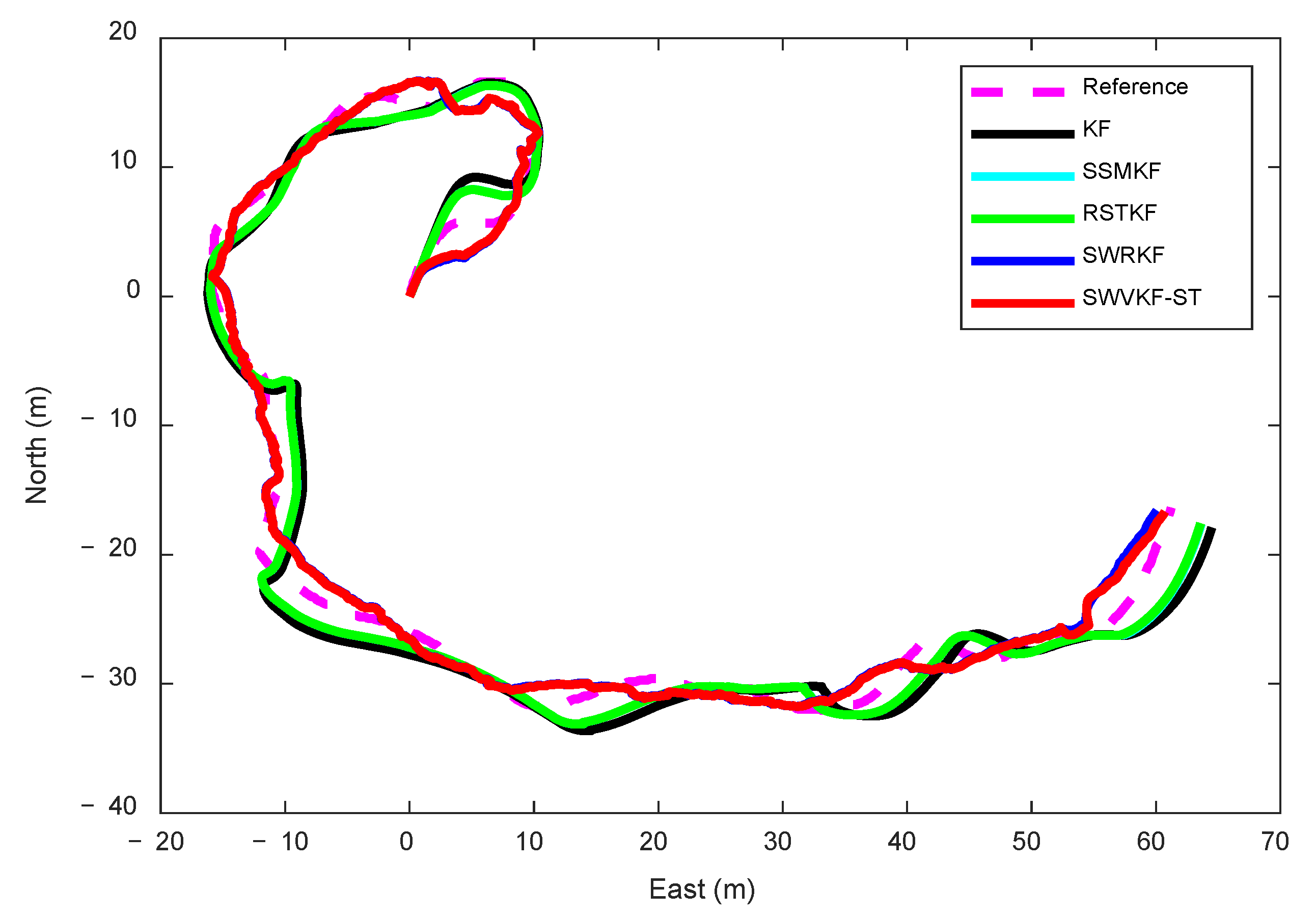

| Algorithms | ARMSEpos (m) | ARMSEvel (m/s) |
|---|---|---|
| TKF | 10.4871 | 6.0097 |
| NKF | 27.4480 | 9.1783 |
| SSMKF | 19.3816 | 8.9235 |
| RSTKF | 17.3648 | 8.6984 |
| SWRKF | 17.7961 | 8.3188 |
| SWVKF-ST | 17.3249 | 7.8931 |
| Algorithms | ANEES | Times (ms) |
|---|---|---|
| TKF | 3.9911 | 0.0078 |
| NKF | 43.5038 | 0.0078 |
| SSMKF | 18.6296 | 0.0656 |
| RSTKF | 17.0918 | 0.0982 |
| SWRKF | 9.2505 | 0.3865 |
| SWVKF-ST | 3.7192 | 0.4327 |
| Sensor | Specifications |
|---|---|
| IMU | Type: Ellipes−E Frequency: 200 Hz Gyroscope random walk: Gyroscope in run bias instability: Accelerometer random walk: Accelerometer in run bias instability: |
| DVL | Type: DVL−A50 Frequency: 10 Hz Velocity resolution: 0.1 mm/s Long term accuracy: 0.1% |
| RTK | Type: BYNAV X1 Frequency: 1 Hz Positioning accuracy: 1.5 cm |
| Algorithms | East Error | North Error |
|---|---|---|
| KF | 1.2554 | 1.8327 |
| SSMKF | 0.9588 | 1.3414 |
| RSTKF | 0.9547 | 1.3300 |
| SWRKF | 0.7406 | 0.9560 |
| STSWVRKF | 0.4509 | 0.7414 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Huang, H.; Zhang, Y.; Dong, C. A Novel Variational Bayesian Method Based on Student’s t Noise for Underwater Localization. Sensors 2025, 25, 3291. https://doi.org/10.3390/s25113291
Huang H, Zhang Y, Dong C. A Novel Variational Bayesian Method Based on Student’s t Noise for Underwater Localization. Sensors. 2025; 25(11):3291. https://doi.org/10.3390/s25113291
Chicago/Turabian StyleHuang, Haoqian, Yutong Zhang, and Chenhui Dong. 2025. "A Novel Variational Bayesian Method Based on Student’s t Noise for Underwater Localization" Sensors 25, no. 11: 3291. https://doi.org/10.3390/s25113291
APA StyleHuang, H., Zhang, Y., & Dong, C. (2025). A Novel Variational Bayesian Method Based on Student’s t Noise for Underwater Localization. Sensors, 25(11), 3291. https://doi.org/10.3390/s25113291






