Multiple-Cumulant-Matrices-Based Method for Exact NF Polarization Localization with COLD Array
Abstract
1. Introduction
2. Signal Model
3. The Proposed Method
3.1. Spatial Manifold Matrix Estimation
3.2. Polarization Parameters Estimation
3.3. Coarse Estimation
3.4. Fine Estimation
3.5. Asymptotic Variance for Joint Parameters
3.6. Computational Complexity
3.7. CRB Derivation
4. Simulation Results
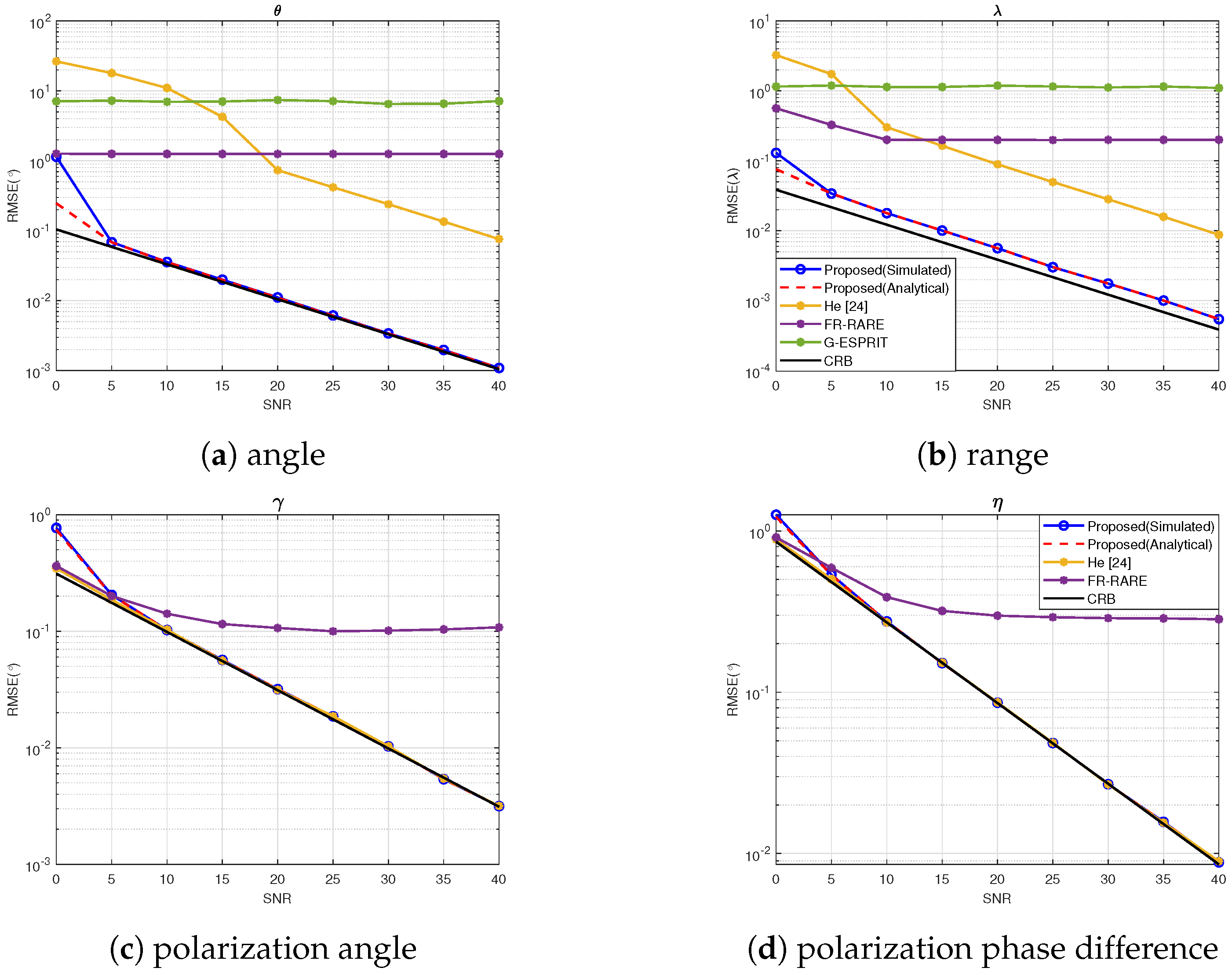
4.1. Experiment 1: RMSE vs. SNR
4.2. Experiment 2: Scatter for Spatial and Polarization
4.3. Experiment 3: RMSE vs. Path Loss Exponent
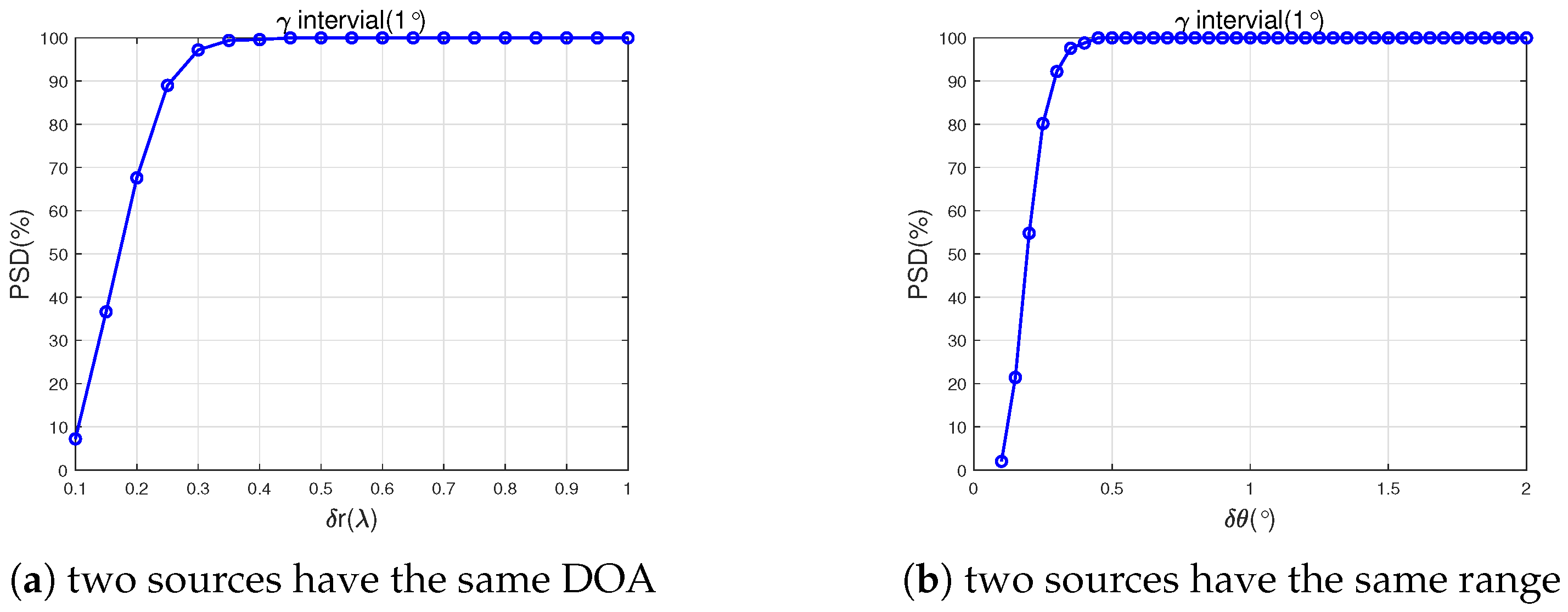
4.4. Experiment 4: Detection Capability for Closely Spaced Targets
4.5. Experiment 5: RMSE vs. Correlation Coefficient
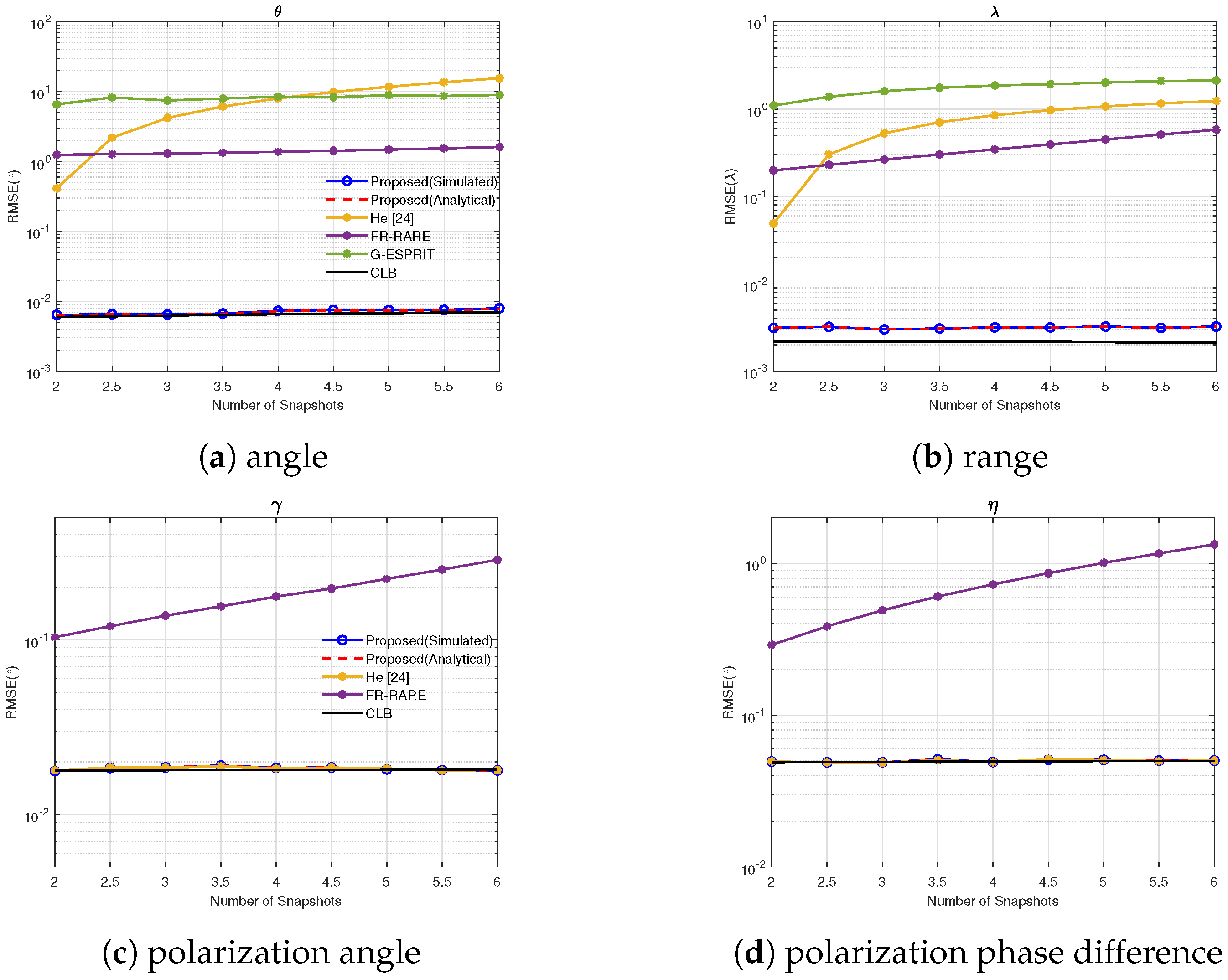
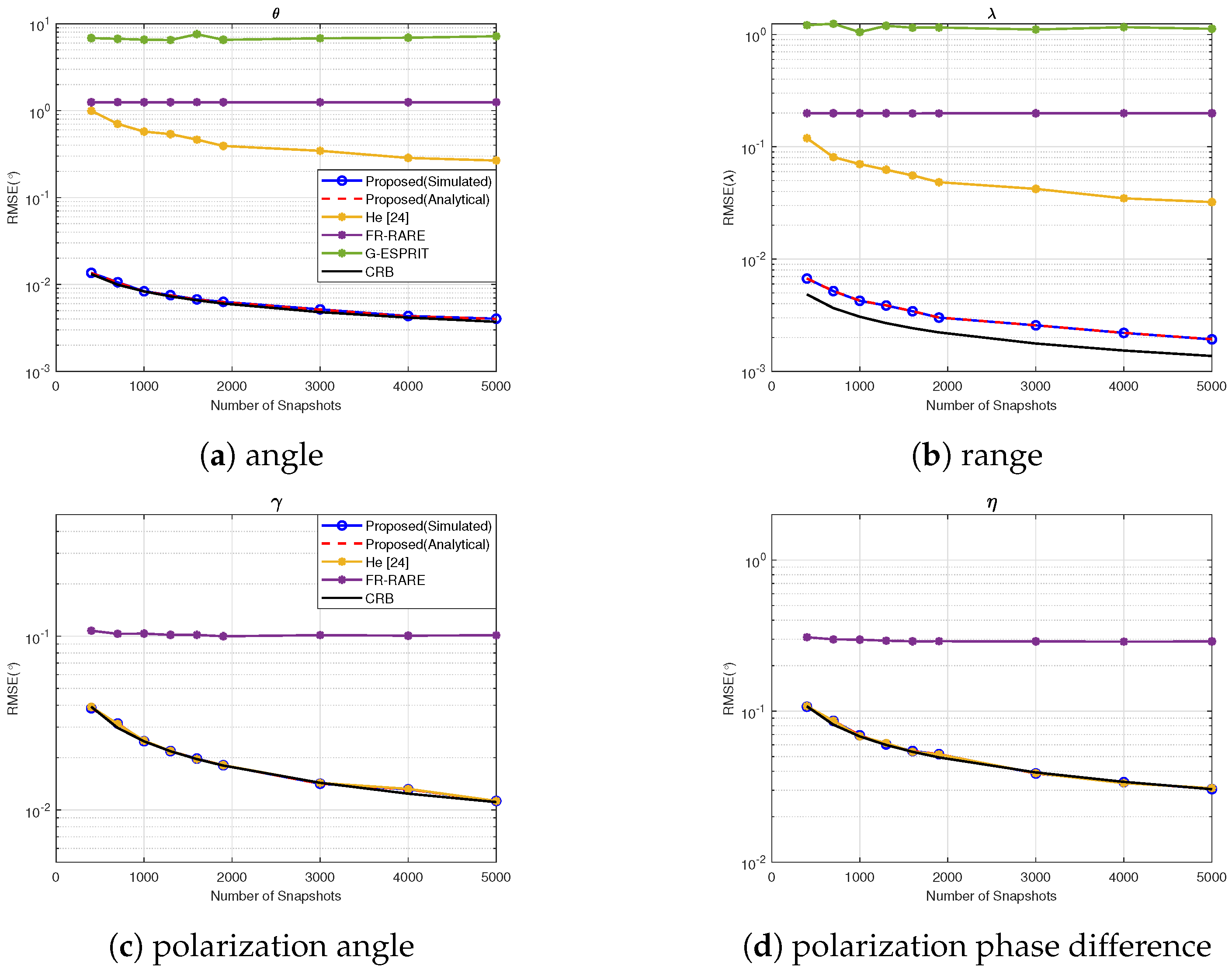
4.6. Experiment 6: RMSE vs. Snapshots
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Sakhnini, A.; De Bast, S.; Guenach, M.; Bourdoux, A.; Sahli, H.; Pollin, S. Near-Field Coherent Radar Sensing Using a Massive MIMO Communication Testbed. IEEE Trans. Wirel. Commun. 2022, 21, 6256–6270. [Google Scholar] [CrossRef]
- Ali, E.; Balfaqih, M.; Shglouf, I.; Alrayes, M.; Balfagih, Z. Two-Dimensional DOA Zero-Forcing Precoding for Enhanced Spectral Efficiency in Cell-Free Massive MIMO. In Proceedings of the 2025 22nd International Learning and Technology Conference, Jeddah, Saudi Arabia, 15–16 January 2025; Volume 22, pp. 164–169. [Google Scholar] [CrossRef]
- Chen, H.; Fang, J.; Wang, W.; Liu, W.; Tian, Y.; Wang, Q.; Wang, G. Near-Field Target Localization for EMVS-MIMO Radar with Arbitrary Configuration. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 5406–5417. [Google Scholar] [CrossRef]
- Weißer, F.; Utschick, W. DoA-Aided Channel Estimation for One-Bit Quantized Systems. In Proceedings of the 2025 14th International ITG Conference on Systems, Communications and Coding (SCC), Karlsruhe, Germany, 10–13 March 2025; pp. 1–6. [Google Scholar] [CrossRef]
- Elbir, A.M.; Celik, A.; Eltawil, A.M. NEAT-MUSIC: Auto-Calibration of DOA Estimation for Terahertz-Band Massive MIMO Systems. IEEE Wirel. Commun. Lett. 2024, 13, 451–455. [Google Scholar] [CrossRef]
- Buzzi, S.; Grossi, E.; Lops, M.; Venturino, L. Foundations of MIMO Radar Detection Aided by Reconfigurable Intelligent Surfaces. IEEE Trans. Signal Process. 2022, 70, 1749–1763. [Google Scholar] [CrossRef]
- Chen, H.; Yi, Z.; Jiang, Z.; Liu, W.; Tian, Y.; Wang, Q.; Wang, G. Spatial-Temporal-Based Underdetermined Near-Field 3-D Localization Employing a Nonuniform Cross Array. IEEE J. Sel. Top. Signal Process. 2024, 18, 561–571. [Google Scholar] [CrossRef]
- Chen, J.; Hudson, R.; Yao, K. Maximum-likelihood source localization and unknown sensor location estimation for wideband signals in the near-field. IEEE Trans. Signal Process. 2002, 50, 1843–1854. [Google Scholar] [CrossRef]
- Gao, F.; Gershman, A. A generalized ESPRIT approach to direction-of-arrival estimation. IEEE Signal Process. Lett. 2005, 12, 254–257. [Google Scholar] [CrossRef]
- Huang, Y.D.; Barkat, M. Near-field multiple source localization by passive sensor array. IEEE Trans. Antennas Propag. 1991, 39, 968–975. [Google Scholar] [CrossRef]
- He, J.; Swamy, M.N.S.; Ahmad, M.O. Efficient Application of MUSIC Algorithm Under the Coexistence of Far-Field and Near-Field Sources. IEEE Trans. Signal Process. 2012, 60, 2066–2070. [Google Scholar] [CrossRef]
- Zaman, F.; Akbar, S.; Akhtar, Z.; Phanomchoeng, G. Efficient Technique for Joint Parameter Estimation of Mixed Far Field Targets and Near Field Jammers in Phased Array Radar. IEEE Access 2025, 13, 55887–55898. [Google Scholar] [CrossRef]
- Yuen, N.; Friedlander, B. Performance analysis of higher order ESPRIT for localization of near-field sources. IEEE Trans. Signal Process. 1998, 46, 709–719. [Google Scholar] [CrossRef]
- Molaei, A.M.; del Hougne, P.; Fusco, V.; Yurduseven, O. Efficient Joint Estimation of DOA, Range and Reflectivity in Near-Field by Using Mixed-Order Statistics and a Symmetric MIMO Array. IEEE Trans. Veh. Technol. 2022, 71, 2824–2842. [Google Scholar] [CrossRef]
- Liang, J.; Liu, D. Passive Localization of Mixed Near-Field and Far-Field Sources Using Two-stage MUSIC Algorithm. IEEE Trans. Signal Process. 2010, 58, 108–120. [Google Scholar] [CrossRef]
- Friedlander, B. Localization of Signals in the Near-Field of an Antenna Array. IEEE Trans. Signal Process. 2019, 67, 3885–3893. [Google Scholar] [CrossRef]
- Fang, J.; Chen, H.; Liu, W.; Yang, S.; Yuen, C.; So, H.C. Three-Dimensional Localization of Mixed Near-Field and Far-Field Sources Based on a Unified Exact Propagation Model. IEEE Trans. Signal Process. 2025, 73, 245–258. [Google Scholar] [CrossRef]
- He, J.; Li, L.; Shu, T.; Truong, T.K. Mixed Near-Field and Far-Field Source Localization Based on Exact Spatial Propagation Geometry. IEEE Trans. Veh. Technol. 2021, 70, 3540–3551. [Google Scholar] [CrossRef]
- Jiang, Z.; Chen, H.; Liu, W.; Wang, G. 3-D temporal-spatial-based near-field source localization considering amplitude attenuation. Signal Process. 2022, 201, 108735. [Google Scholar] [CrossRef]
- Jin, L.; Chen, H.; Fang, J.; Liu, W.; Tian, Y.; Wang, G. Fourth-Order Cumulant Based 3-D Near-Field Underdetermined Parameter Estimation With Exact Spatial Propagation Model. In Proceedings of the ICASSP 2025—2025 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Hyderabad, India, 6–11 April 2025; pp. 1–5. [Google Scholar] [CrossRef]
- He, J.; Shu, T.; Li, L.; Truong, T.K. Mixed Near-Field and Far-Field Localization and Array Calibration With Partly Calibrated Arrays. IEEE Trans. Signal Process. 2022, 70, 2105–2118. [Google Scholar] [CrossRef]
- He, J.; Ahmad, M.O.; Swamy, M.N.S. Near-Field Localization of Partially Polarized Sources with a Cross-Dipole Array. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 857–870. [Google Scholar] [CrossRef]
- Tao, J.W.; Liu, L.; Lin, Z.Y. Joint DOA, Range, and Polarization Estimation in the Fresnel Region. IEEE Trans. Aerosp. Electron. Syst. 2011, 47, 2657–2672. [Google Scholar] [CrossRef]
- He, J.; Li, L.; Shu, T. Near-Field Parameter Estimation for Polarized Source Using Spatial Amplitude Ratio. IEEE Commun. Lett. 2020, 24, 1961–1965. [Google Scholar] [CrossRef]
- Mendel, J. Tutorial on higher-order statistics (spectra) in signal processing and system theory: Theoretical results and some applications. Proc. IEEE 1991, 79, 278–305. [Google Scholar] [CrossRef]
- Ma, H.; Tao, H.; Xie, J.; Cheng, X. Parameters Estimation of 3-D Near-Field Sources with Arbitrarily Spaced Electromagnetic Vector-Sensors. IEEE Commun. Lett. 2022, 26, 2764–2768. [Google Scholar] [CrossRef]



| Step | Operation |
|---|---|
| 1 | Construct via (9) and the long matrix |
| can be obtain via (10). | |
| 2 | Compute the covariance matrix and perform eigen-decomposition |
| to obtain signal subspace . | |
| 3 | Using the LS and eigen-decomposition, we can obtain |
| to construct . | |
| 4 | Extract and from to construct and . |
| Matrix is obtained by performing eigen-decomposition on matrix , | |
| where matrix can be obtain from (33). From the diagonal element of , | |
| we have the estimates and . | |
| 5 | for do |
| (1) The closed-form coarse estimation and can be obtained via (26) and (27). | |
| (2) Via (28) and (29), we can disambiguate the phase to construct matrices | |
| and . | |
| (3) Based on LS method, the fine estimation and can be obtained by | |
| solving (33). | |
| End for |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zheng, J.; Meng, H.; Luo, Z.; Wu, H.; Liu, W.; Chen, H. Multiple-Cumulant-Matrices-Based Method for Exact NF Polarization Localization with COLD Array. Sensors 2025, 25, 3244. https://doi.org/10.3390/s25103244
Zheng J, Meng H, Luo Z, Wu H, Liu W, Chen H. Multiple-Cumulant-Matrices-Based Method for Exact NF Polarization Localization with COLD Array. Sensors. 2025; 25(10):3244. https://doi.org/10.3390/s25103244
Chicago/Turabian StyleZheng, Jiefeng, Haifen Meng, Zhuang Luo, Huayue Wu, Weiyue Liu, and Hua Chen. 2025. "Multiple-Cumulant-Matrices-Based Method for Exact NF Polarization Localization with COLD Array" Sensors 25, no. 10: 3244. https://doi.org/10.3390/s25103244
APA StyleZheng, J., Meng, H., Luo, Z., Wu, H., Liu, W., & Chen, H. (2025). Multiple-Cumulant-Matrices-Based Method for Exact NF Polarization Localization with COLD Array. Sensors, 25(10), 3244. https://doi.org/10.3390/s25103244






