Fault Diagnosis of Switching Power Supplies Using Dynamic Wavelet Packet Transform and Optimized SVM
Abstract
1. Introduction
2. Materials and Methods
2.1. Fault Set Acquisition
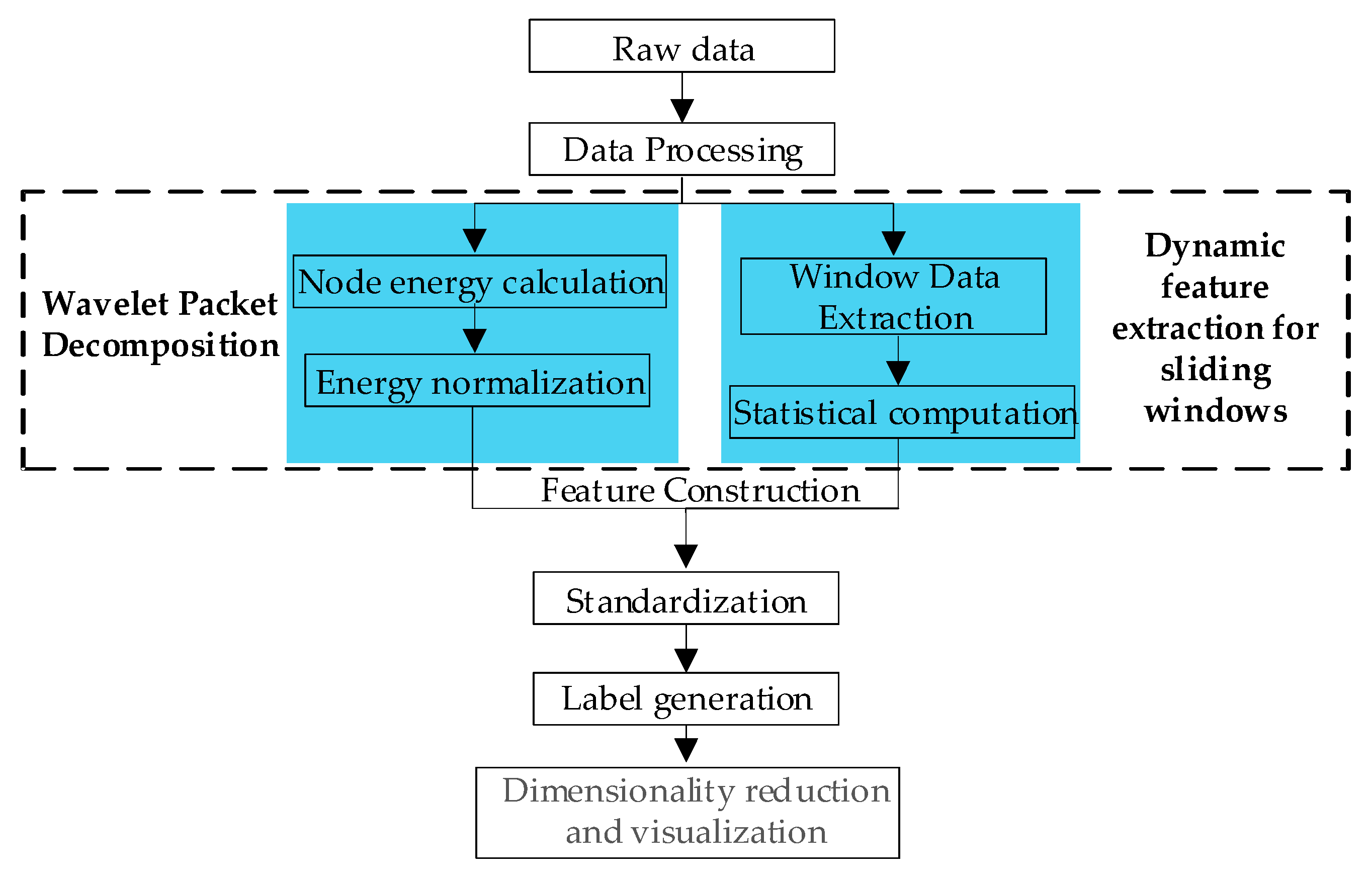
2.2. Fault Feature Extraction Method
2.2.1. Feature Extraction with Wavelet Packet Decomposition
- (1)
- Banding for wavelet packet decomposition
- (2)
- Node energy feature extraction
2.2.2. Dynamic Feature Extraction
- (1)
- Sliding window settings
- (2)
- Dynamic Mean Calculation
- (3)
- Dynamic standard deviation calculation
- (4)
- Skewness calculation
- (5)
- Kurtosis calculation
2.2.3. Fault Feature Vector Construction
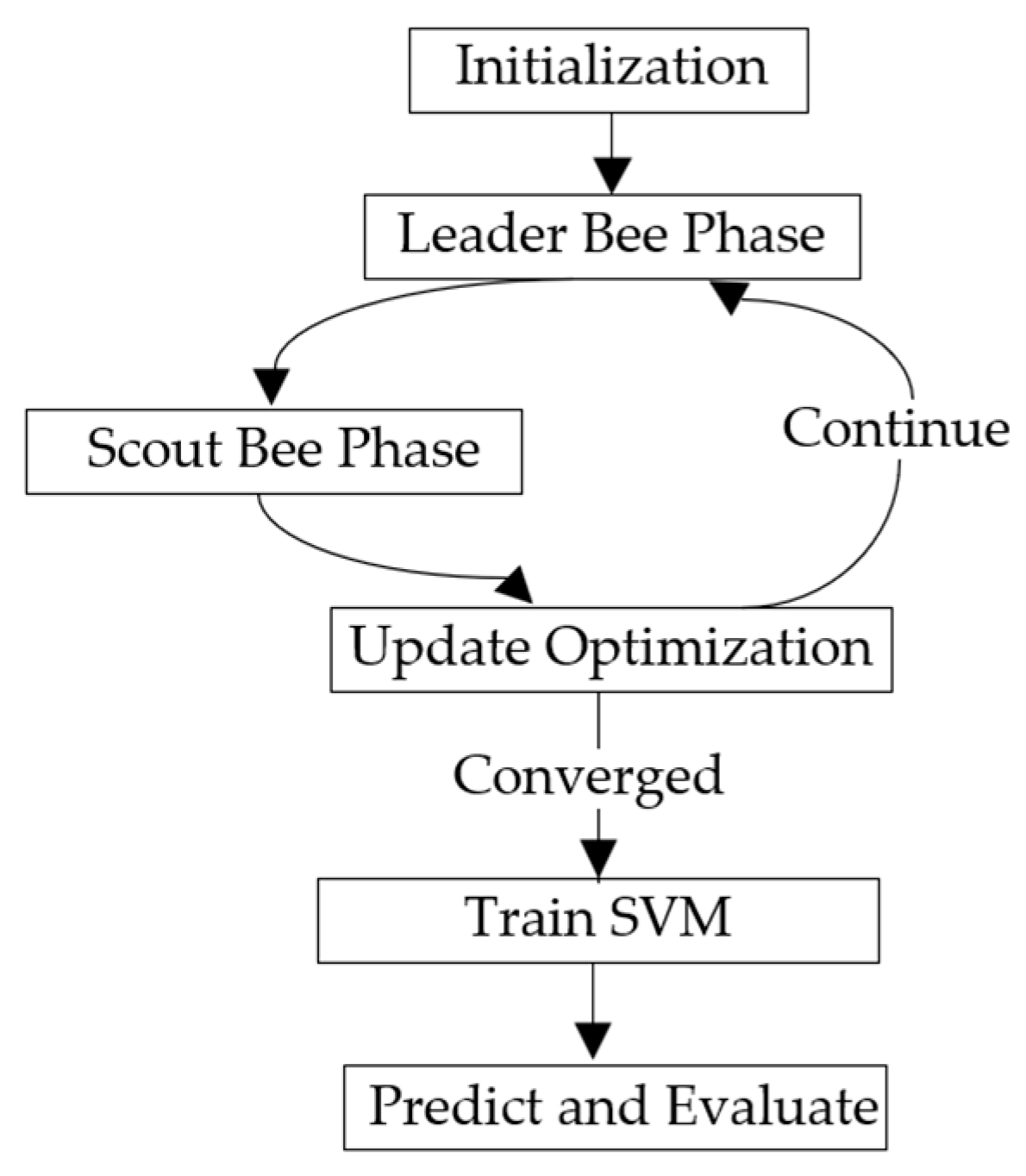
2.3. Troubleshooting Methods
- (1)
- Adaptive step-size adjustment strategy
- (2)
- Global optimal guidance search mechanism
- (3)
- Designing exponential mapping fitness functions
- (4)
- Scout Bee Local Reboot Strategy
3. Results and Discussion
3.1. Fault Feature Extraction
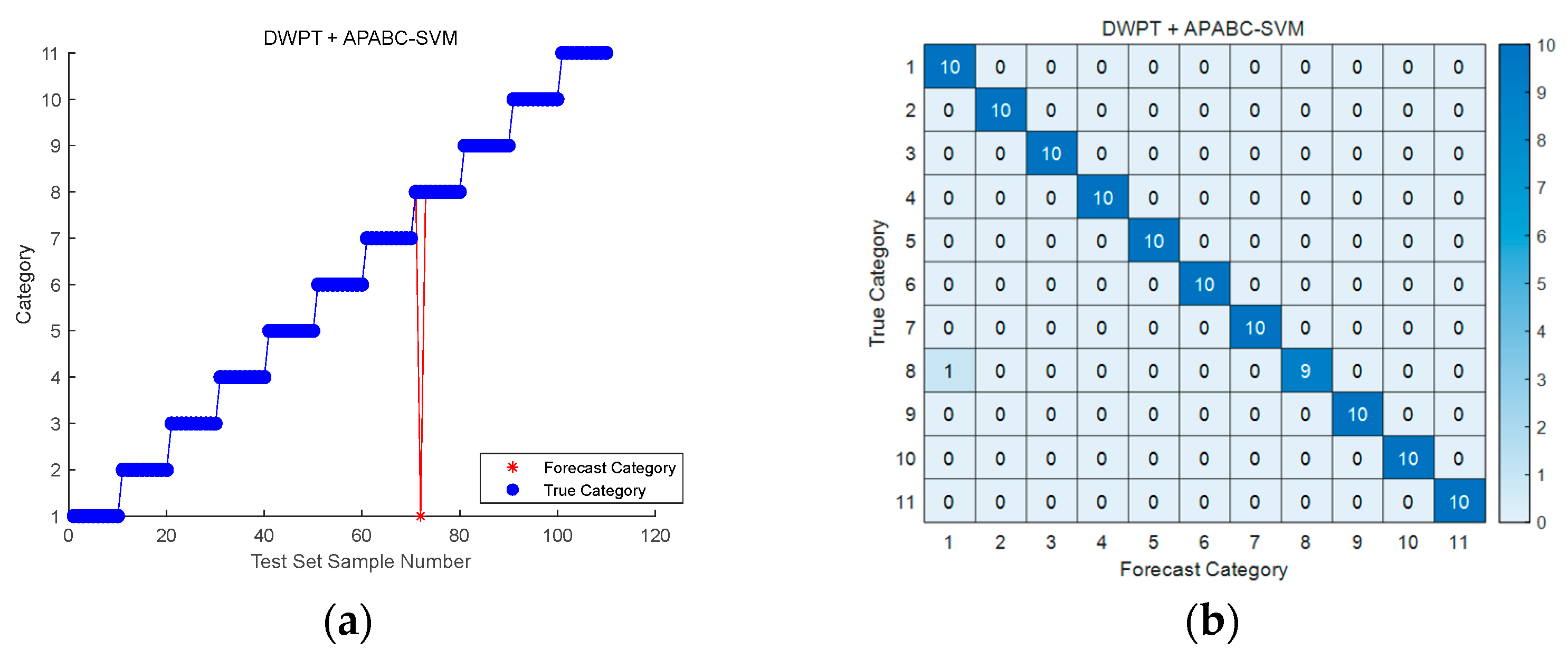
3.2. Troubleshooting Experiment Results
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| SMPS | Switching Mode Power Supply |
| SVM | Support Vector Machine |
| DWPT | Dynamic Wavelet Packet Transform |
| FFT | Fast Fourier Transform |
| WPT | Wavelet Packet Transform |
| WT | Wavelet Transform |
| PSO-SVM | Particle Swarm Optimized Support Vector Machine |
| APABC-SVM | Adaptive Improved Artificial Bee Colony Optimized Support Vector Machine |
| ABC-SVM | Artificial Bee Colony Optimized Support Vector Machine |
References
- Machowski, J.; Lubosny, Z.; Bialek, J.W.; Bumby, J.R. Power System Dynamics: Stability and Control; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kareem, A.B.; Akpudo, U.E.; Hur, J.W. An Integrated Cost-Aware Dual Monitoring Framework for SMPS Switching Device Diagnosis. Electronics 2021, 10, 2487. [Google Scholar] [CrossRef]
- Wang, F.; Wu, Y.; Bu, Y.; Pan, F.; Chen, D.; Lin, Z. Fault diagnosis of DCS SMPSs in nuclear power plants based on machine learning. Arab. J. Sci. Eng. 2024, 49, 6903–6922. [Google Scholar] [CrossRef]
- Kareem, A.B.; Hur, J.-W. Towards Data-Driven Fault Diagnostics Framework for SMPS-AEC Using Supervised Learning Algorithms. Electronics 2022, 11, 2492. Available online: https://www.mdpi.com/2079-9292/11/16/2492 (accessed on 6 March 2025). [CrossRef]
- Hadad, K.; Pourahmadi, M.; Majidi-Maraghi, H. Fault diagnosis and classification based on wavelet transform and neural network. Prog. Nucl. Energy 2011, 53, 41–47. [Google Scholar] [CrossRef]
- Tang, S.; Wang, H.; Wang, W.; Liu, C. A fault diagnosis method for active power factor correction power supply based on seagull algorithm optimized kernel-based extreme learning machine. Int. J. Circuit Theory Appl. 2024, 52, 1116–1135. [Google Scholar] [CrossRef]
- Liao, Y.; Zhang, Y. Rethinking Model-Based Fault Detection: Uncertainties, Risks, and Optimization Based on a Multilevel Converter Case Study. IEEE Trans. Power Electron. 2024, 39, 14229–14239. [Google Scholar] [CrossRef]
- Xie, D.; Lin, C.; Deng, Q.; Lin, H.; Cai, C.; Basler, T.; Ge, X. Simple Vector Calculation and Constraint-Based Fault-Tolerant Control for a Single-Phase CHBMC. IEEE Trans. Power Electron. 2025, 40, 2028–2041. [Google Scholar] [CrossRef]
- Zabihi, M.; Mehrizi, R.V.; Kasaiezadeh, A.; Pirani, M.; Khajepour, A. A Hybrid Model-Data Vehicle Sensor and Actuator Fault Detection and Diagnosis System. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8121–8133. [Google Scholar] [CrossRef]
- Zheng, L.; Jiang, Y.; Jiang, H.; Tang, C.; Jiao, W.; Shi, Z.; Rehman, A.U. Adaptive Dynamic Threshold Graph Neural Network: A Novel Deep Learning Framework for Cross-Condition Bearing Fault Diagnosis. Machines 2024, 12, 18. [Google Scholar] [CrossRef]
- Yang, W.; Qin, Y.; Huang, R.; Chen, Y. Adaptive feature extraction for entity relation extraction. Comput. Speech Lang. 2025, 89, 101712. [Google Scholar] [CrossRef]
- Jia, W.; Shi, H.; Dong, Z.; Zhang, X. A rolling bearing fault diagnosis framework under variable working conditions considers dynamic feature extraction. Eng. Appl. Artif. Intell. 2025, 146, 110255. [Google Scholar] [CrossRef]
- Zhan, Z.-H.; Shi, L.; Tan, K.C.; Zhang, J. A Survey on Evolutionary Computation for Complex Continuous Optimization. Artif. Intell. Rev. 2021, 55, 59–110. [Google Scholar] [CrossRef]
- Yang, X.; Huang, W.; Ye, M. Dynamic Personalized Federated Learning with Adaptive Differential Privacy. In Proceedings of the NeurIPS 2023 Conference, New Orleans, LA, USA, 10 December 2023; Available online: https://proceedings.neurips.cc/paper_files/paper/2023/hash/e4724af0e2a0d52ce5a0a4e084b87f59-Abstract-Conference.html (accessed on 6 March 2025).
- Qin, C.; Zhang, Y.; Bao, F.; Zhang, C.; Liu, P.; Liu, P. XGBoost Optimized by Adaptive Particle Swarm Optimization for Credit Scoring-qin-2021-Mathematical Problems in Engineering. Math. Probl. Eng. 2021, 2021, 6655510. [Google Scholar] [CrossRef]
- Kumar, S.; Kolekar, T.; Patil, S.; Bongale, A.; Kotecha, K.; Zaguia, A.; Prakash, C. A Low-Cost Multi-Sensor Data Acquisition System for Fault Detection in Fused Deposition Modelling. Sensors 2022, 22, 517. [Google Scholar] [CrossRef] [PubMed]
- Ai, S.; Song, J.; Cai, G.; Zhao, K. Active Fault-Tolerant Control for Quadrotor UAV Against Sensor Fault Diagnosed by the Auto Sequential Random Forest. Aerospace 2022, 9, 518. [Google Scholar] [CrossRef]
- Khemani, V.; Azarian, M.H.; Pecht, M.G. Learnable Wavelet Scattering Networks: Applications to Fault Diagnosis of Analog Circuits and Rotating Machinery. Electronics 2022, 11, 451. [Google Scholar] [CrossRef]
- He, Z.; Chu, P.; Li, C.; Zhang, K.; Wei, H.; Hu, Y. Compound fault diagnosis for photovoltaic arrays based on multi-label learning considering multiple faults coupling. Energy Convers. Manag. 2023, 279, 116742. [Google Scholar] [CrossRef]
- Dai, X.; Sun, M.; Deng, P.; Wang, R.; Su, Y. Asymmetric bidirectional capacitive power transfer method with push–pull full-bridge hybrid topology. IEEE Trans. Power Electron. 2022, 37, 13902–13913. [Google Scholar] [CrossRef]
- Musumeci, S.; Stella, F.; Mandrile, F.; Armando, E.; Fratta, A. Soft-Switching Full-Bridge Topology with AC Distribution Solution in Power Converters’ Auxiliary Power Supplies. Electronics 2022, 11, 884. [Google Scholar] [CrossRef]
- Chen, J.; Xu, J.; Wang, Y. Seamless control of full-bridge and half-bridge topology morphing LLC converter based on state plane analysis. IEEE Trans. Power Electron. 2024, 39, 198–211. [Google Scholar] [CrossRef]
- Ekici, S.; Yildirim, S.; Poyraz, M. Energy and entropy-based feature extraction for locating fault on transmission lines by using neural network and wavelet packet decomposition. Expert Syst. Appl. 2008, 34, 2937–2944. [Google Scholar] [CrossRef]
- Parmar, U.; Pandya, D.H. Comparison of the Supervised Machine Learning Techniques Using WPT for the Fault Diagnosis of Cylindrical Roller Bearing. Int. J. Eng. Sci. Technol. 2021, 13, 2. [Google Scholar] [CrossRef]
- Wang, X.; Shi, T.; Liao, G.; Zhang, Y.; Hong, Y.; Chen, K. Using Wavelet Packet Transform for Surface Roughness Evaluation and Texture Extraction. Sensors 2017, 17, 933. [Google Scholar] [CrossRef]
- Smith, W.A.; Fan, Z.Q.; Peng, Z.X.; Li, H.Z.; Randall, R.B. Optimised Spectral Kurtosis for Bearing Diagnostics Under Electromagnetic Interference-ScienceDirect. Mech. Syst. Signal Process. 2016, 75, 371–394. [Google Scholar] [CrossRef]
- Yang, D.M. The detection of motor bearing fault with maximal overlap discrete wavelet packet transform and teager energy adaptive spectral kurtosis. Sensors 2021, 21, 6895. [Google Scholar] [CrossRef]
- Yang, C.Z.; Fang, L.C.; Fei, B.J.; Yu, Q.; Wei, H. Multi-Level Contour Combination Features for Shape Recognition-ScienceDirect. Comput. Vis. Image Underst. 2023, 229, 103650. [Google Scholar] [CrossRef]
- Shi, Q.; Fan, Y.; Zhang, D.; Guo, H.; Liu, J. K-means ship trajectory clustering algorithm based on trajectory image similarity. In Proceedings of the Third International Conference on Digital Signal and Computer Communications (DSCC 2023), Xi’an, China, 21–23 April 2023; SPIE: Bellingham, WA, USA, 2023; Volume 12716, pp. 30–38. [Google Scholar]
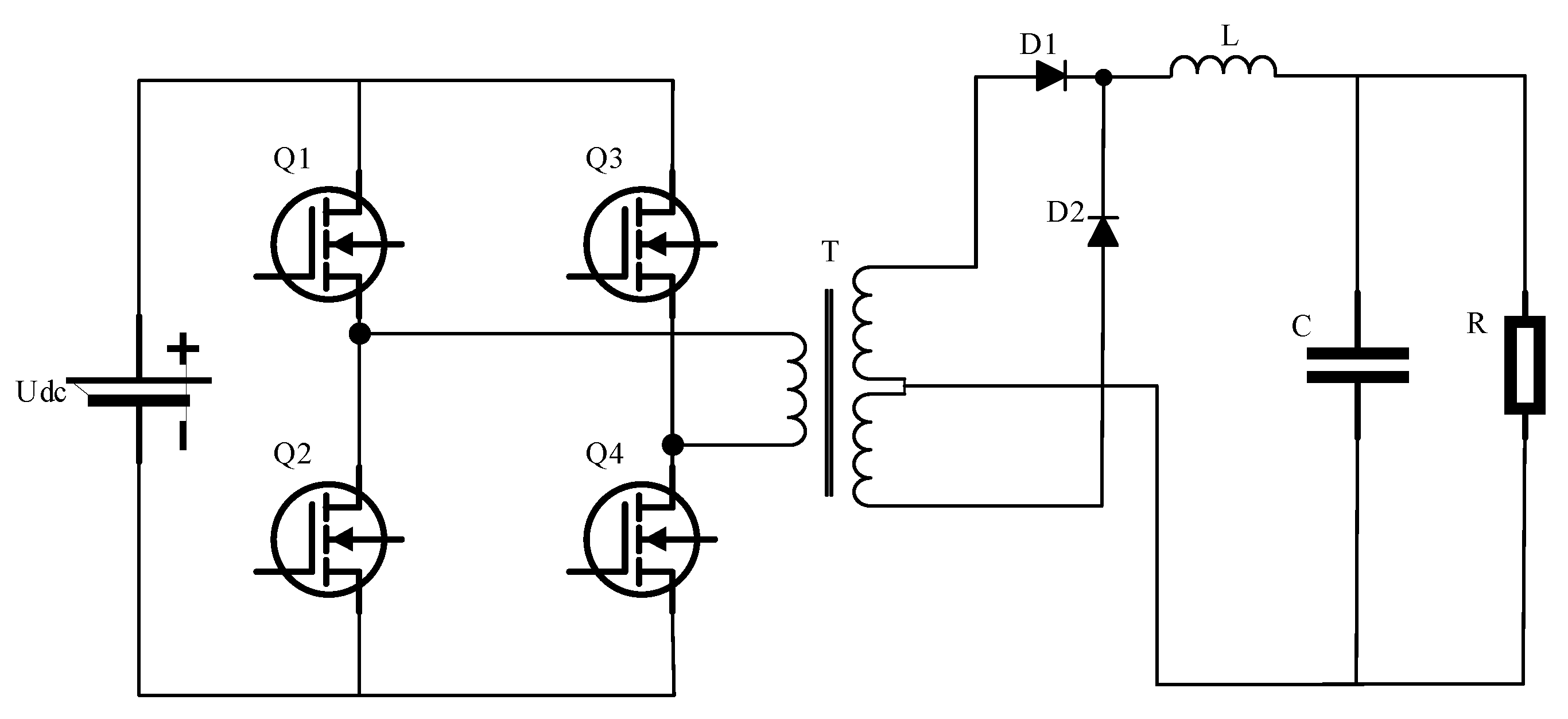


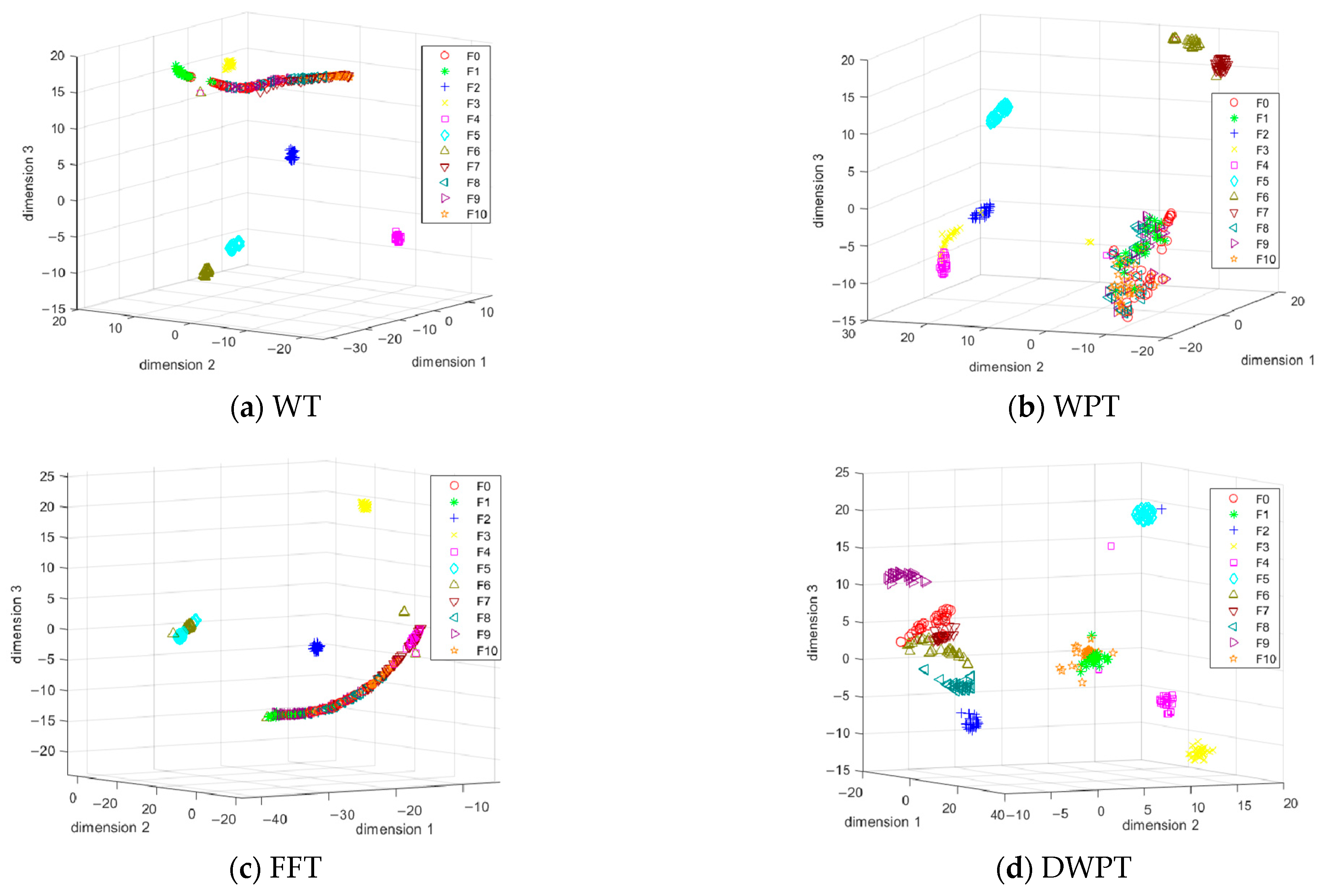
| Trouble Code | Defective Element | Failure Mode |
|---|---|---|
| F0 | - | trouble free |
| F1 | MOSFET Q1 | short circuit |
| F2 | MOSFET Q1 | open circuit |
| F3 | Diode D1 | short circuit |
| F4 | Diode D1 | open circuit |
| F5 | Capacitor C | open circuit |
| F6 | Capacitor C | reduced capacity |
| F7 | Capacitor C | increased capacity |
| F8 | Resistor R | reduced resistance |
| F9 | Resistor R | increased resistance |
| F10 | MOSFET Q1Q3 | short circuit |
| Feature Extraction Methods | Classification Method | Training Time/s | Test Time/s | Accuracy |
|---|---|---|---|---|
| DWPT | Decision Tree | 0.5402 | 0.0503 | 86.364% |
| DWPT | SVM | 0.2909 | 0.1070 | 72.73% |
| DWPT | PSO-SVM | 0.2376 | 0.1117 | 91.818% |
| DWPT | ABC-SVM | 0.3072 | 0.1108 | 98.182% |
| DWPT | APABC-SVM | 0.2309 | 0.1018 | 99.091% |
| FFT | APABC-SVM | 0.1675 | 0.0135 | 77.273% |
| WPT | APABC-SVM | 0.1714 | 0.0152 | 59.091% |
| WT | APABC-SVM | 0.1789 | 0.0153 | 79.091% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xu, J.; Zhu, J.; Wang, Z. Fault Diagnosis of Switching Power Supplies Using Dynamic Wavelet Packet Transform and Optimized SVM. Sensors 2025, 25, 3236. https://doi.org/10.3390/s25103236
Xu J, Zhu J, Wang Z. Fault Diagnosis of Switching Power Supplies Using Dynamic Wavelet Packet Transform and Optimized SVM. Sensors. 2025; 25(10):3236. https://doi.org/10.3390/s25103236
Chicago/Turabian StyleXu, Jie, Jingjing Zhu, and Zhifeng Wang. 2025. "Fault Diagnosis of Switching Power Supplies Using Dynamic Wavelet Packet Transform and Optimized SVM" Sensors 25, no. 10: 3236. https://doi.org/10.3390/s25103236
APA StyleXu, J., Zhu, J., & Wang, Z. (2025). Fault Diagnosis of Switching Power Supplies Using Dynamic Wavelet Packet Transform and Optimized SVM. Sensors, 25(10), 3236. https://doi.org/10.3390/s25103236





