Fabric Tactile Prediction Method Based on Spider Diagram
Abstract
1. Introduction
2. Experimental and Method
2.1. Fabrics Samples
2.2. Instruments
2.2.1. Subjective Testing Platform
2.2.2. POD (Pin on Disk) Tribometer
2.2.3. KES-FB Fabric Style Analyzer
2.2.4. Self-Made Testing Device for Fabric Tensile Properties
2.2.5. Self-Made Testing Device for Thermal Properties of Fabrics
2.3. Experimental Procedure and Method
2.3.1. Fabric Touch Evaluation Test
2.3.2. POD Tribometer Experiment
2.3.3. Bending Experiment
2.3.4. Tensile Experiment
2.3.5. Heat Conduction Experiment
3. Results and Discussions
3.1. Fabric Touch Evaluation Experiment
3.2. Construction and Analysis of Physical Property Spider Diagrams
3.3. Degree of Influence of Physical Properties on Subjective Evaluations
3.4. Spider Diagram-Based Prediction for Comprehensive Evaluation
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Silva, S.C.; Rocha, T.V.; De Cicco, R.; Galhanone, R.F.; Manzini Ferreira Mattos, L.T. Need for Touch and Haptic Imagery: An Investigation in Online Fashion Shopping. J. Retail. Consum. Serv. 2021, 59, 102378. [Google Scholar] [CrossRef]
- Liao, X.; Li, Y.; Hu, J.; Li, Q.; Wu, X. Psychophysical Relations between Interacted Fabric Thermal-Tactile Properties and Psychological Touch Perceptions. J. Sens. Stud. 2016, 31, 181–192. [Google Scholar] [CrossRef]
- Han, B.; Li, P.; Liu, X. Effect of Tactile Imagery on Consumers’ Online Purchase Intention of Clothing. J. Shanghai Univ. Eng. Technol. 2024, 38, 212–217. [Google Scholar]
- Yang, D.; Du, Z.Q.; Liu, G.; Lin, X. Fabric Tactile Style Grade Evaluation Based on the CHES-FY System. J. Silk 2022, 59, 82–90. [Google Scholar]
- Wang, Y.M. Research Progress on Factors and Evaluation Methods of Fabric Hand Feel. Text. Lead. 2024, 2024, 68–71. [Google Scholar] [CrossRef]
- Ahirwar, M.; Behera, B.K. Fabric Hand Research Translates Senses into Numbers—A Review. J. Text. Inst. 2022, 113, 2531–2548. [Google Scholar] [CrossRef]
- Musa, A.B.H.; Malengier, B.; Vasile, S.; Van Langenhove, L.; De Raeve, A. Analysis and Comparison of Thickness and Bending Measurements from Fabric Touch Tester (FTT) and Standard Methods. Autex Res. J. 2018, 18, 51–60. [Google Scholar] [CrossRef]
- Liao, X.; Li, Y.; Hu, J.; Wu, X.; Li, Q. A Simultaneous Measurement Method to Characterize Touch Properties of Textile Materials. Fibers Polym. 2014, 15, 1548–1559. [Google Scholar] [CrossRef]
- Vasile, S.; Malengier, B.; De Raeve, A.; Deruyck, F. Influence of Selected Production Parameters on the Hand of Mattress Knitted Fabrics Assessed by the Fabric Touch Tester. Text. Res. J. 2019, 89, 98–112. [Google Scholar] [CrossRef]
- Akgül, E.; Kizilkaya Aydoğan, E.; Sinanoğlu, C. Investigation of Different Denim Fabrics with Fabric Touch Tester and Sensory Evaluation. J. Nat. Fibers 2022, 19, 5551–5565. [Google Scholar] [CrossRef]
- Sun, Y.; Zhang, M.; Liu, G.; Du, Z. Measurement of Fabric Handle Characteristics Based on the Quick-Intelligent Handle Evaluation System for Fabrics (QIHES-F). Text. Res. J. 2019, 89, 3374–3386. [Google Scholar] [CrossRef]
- Chu, X.X.; Xiao, H.; Fan, J. Subjective and Objective Evaluation and Determination of Fabric Cooling Grade. J. Text. Res. 2019, 40, 105–113. [Google Scholar] [CrossRef]
- Beyene, K.A.; Muhammed, N. Linear Model Equation for Prediction and Evaluation of Surface Roughness of Plain-Woven Fabric. Tekst. Konfeksiyon 2023, 33, 88–94. [Google Scholar] [CrossRef]
- Shao, Y.; Sun, Y.; Zheng, D.; Liu, G.; Du, Z.; Liu, J.; Wang, M. Tactile Comfort Characterization of Knitted Fabrics Based on the Ring-Shaped Style Tester. Text. Res. J. 2021, 91, 766–777. [Google Scholar] [CrossRef]
- Ding, S.; Pan, Y.; Zhao, X. Humanoid Identification of Fabric Material Properties by Vibration Spectrum Analysis. Sensors 2018, 18, 1820. [Google Scholar] [CrossRef] [PubMed]
- Zhao, C.; Liu, X.J.; Dai, J.Y.; Wang, G.B. Fabric Style Evaluation of Cotton Fabric Based on KES System. Cotton Text. Technol. 2018, 46, 58–62. [Google Scholar]
- Liu, K.X.; Qiu, Y.P.; Chen, S.; Xacker, S.T. Research Progress on Factors and Evaluation Methods of Fabric Hand Feel. J. Donghua Univ. (Nat. Sci.) 2024, 1–8. [Google Scholar] [CrossRef]
- Ding, S.Y. Study on Tactile Vibration Information Acquisition and Material Characteristic Recognition Based on Reciprocating Friction. Ph.D. Thesis, Harbin Institute of Technology, Harbin, China, 2018. [Google Scholar] [CrossRef]
- Duan, H.Q.; Xu, W.; Wang, Z.W. Development of a Novel Fabric Thermal Transfer Performance Tester. Shanghai Text. Sci. Technol. 2003, 53–54, 62. [Google Scholar] [CrossRef]
- Tu, L.X.; Shen, H.; Wang, F.M. Test Method and Characterization of Textile’s Cool Sensation Based on Single Flat Fabric Thermal Performance Tester. J. Donghua Univ. (Nat. Sci.) 2019, 45, 658–664. [Google Scholar]
- Sun, Y. Characterization and Modeling of Fabric Hand Feel and Mechanical Properties. Ph.D. Thesis, Donghua University, Shanghai, China, 2023. [Google Scholar] [CrossRef]
- Takasaki, M.; Sakurai, M.; Oomori, A.; Watanabe, S.; Nishikawa, S.; Miyake, H. Relationship between Subjective and Objective Evaluations of Knitted Fabrics for Summer Garments. J. Fiber Sci. Technol. 2020, 76, 50–62. [Google Scholar] [CrossRef]



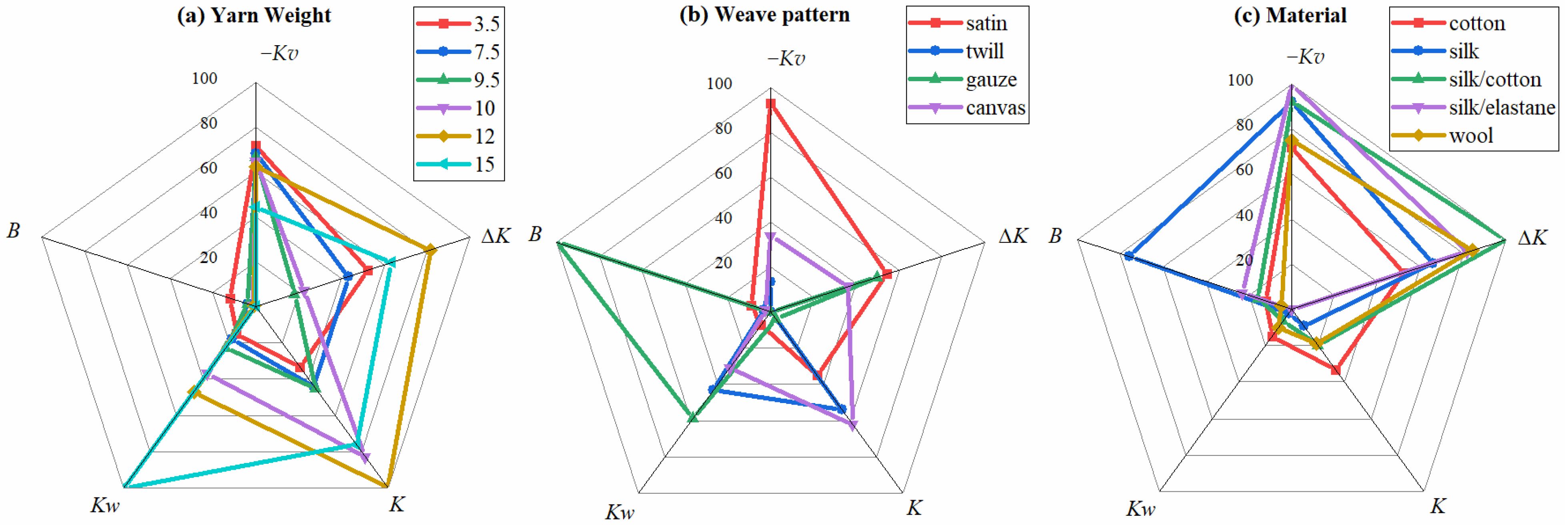


| Samples | S(FFT2) Slope Kv | S(FFT) Slope Kw | Bending Property B | Coefficient of Elasticity K | Differential Rate of Warming ΔK |
|---|---|---|---|---|---|
| 3.5 | 215.53 | 3.59 | 17.20 | 7272.73 | 7.45 |
| 7.5 | 242.92 | 4.15 | 6.03 | 9049.77 | 7.25 |
| 9.5 | 253.48 | 5.13 | 5.53 | 9259.26 | 6.7 |
| 10 | 267.85 | 7.86 | 2.57 | 15,625 | 6.8 |
| 12 | 282.8 | 9.81 | 1.51 | 18,518.5 | 8.1 |
| 15 | 412.56 | 20.14 | 0.61 | 14,492.8 | 7.7 |
| canvas | 486.41 | 6.72 | 3.79 | 12,121.2 | 7.1 |
| twill | 632.55 | 9.11 | 5.01 | 10,695.2 | 6.3 |
| gauze | 727.61 | 12.12 | 139.61 | 2259.89 | 7.4 |
| satin | 64.39 | 2.08 | 13.41 | 7547.17 | 7.5 |
| silk | 69.97 | 1.16 | 105.94 | 3149.61 | 7.75 |
| silk/cotton | 71.43 | 1.96 | 22.42 | 4975.12 | 8.5 |
| silk/elastane | 15.41 | 0.71 | 32.51 | 1610.31 | 8.1 |
| wool | 192.32 | 2.67 | 7.63 | 4784.69 | 8.15 |
| cotton | 215.53 | 3.58 | 17.20 | 7272.73 | 7.45 |
| Physical Property | Grading Criteria (X is Normalized) | ||||
|---|---|---|---|---|---|
| Roughness | Level 1 | Level 2 | Level 3 | Level 4 | Level 5 |
| Fullness | 0 ≤ X ≤ 10 | 10 < X ≤ 20 | 20 < X ≤ 30 | 30 < X ≤ 40 | 40 < X ≤ 50 |
| Bendability | |||||
| Elasticity | Level 6 | Level 7 | Level 8 | Level 9 | Level 10 |
| Thermal-conductivity | 50 < X ≤ 60 | 60 < X ≤ 70 | 70 < X ≤ 80 | 80 < X ≤ 90 | 90 < X ≤ 100 |
| Physical Property | Undetermined Parameters | R-Squared | |||||
|---|---|---|---|---|---|---|---|
| −Kv | ΔK | K | 0.1357 | 0.1305 | 0.0788 | 60.5963 | 0.1693 |
| ΔK | K | Kw | 1.0978 | 0.0117 | 0.0143 | 68.4913 | 0.0386 |
| K | Kw | B | 0.1362 | 0.1048 | 0.4041 | 66.4129 | 0.2212 |
| Kw | B | −Kv | 0.2472 | 0.1816 | 0.2208 | 64.1700 | 0.4386 |
| B | −Kv | ΔK | 0.1717 | 0.1588 | 0.0647 | 63.4502 | 0.2411 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Xie, R.; Ding, S.; Cheng, Z.; Ma, L.; Yang, Y. Fabric Tactile Prediction Method Based on Spider Diagram. Sensors 2025, 25, 3187. https://doi.org/10.3390/s25103187
Xie R, Ding S, Cheng Z, Ma L, Yang Y. Fabric Tactile Prediction Method Based on Spider Diagram. Sensors. 2025; 25(10):3187. https://doi.org/10.3390/s25103187
Chicago/Turabian StyleXie, Ruifeng, Shuyang Ding, Zeyu Cheng, Luowei Ma, and Yanzhu Yang. 2025. "Fabric Tactile Prediction Method Based on Spider Diagram" Sensors 25, no. 10: 3187. https://doi.org/10.3390/s25103187
APA StyleXie, R., Ding, S., Cheng, Z., Ma, L., & Yang, Y. (2025). Fabric Tactile Prediction Method Based on Spider Diagram. Sensors, 25(10), 3187. https://doi.org/10.3390/s25103187






