Depth Perception Based on the Interaction of Binocular Disparity and Motion Parallax Cues in Three-Dimensional Space
Abstract
1. Introduction
2. Research Trends of Depth Perception
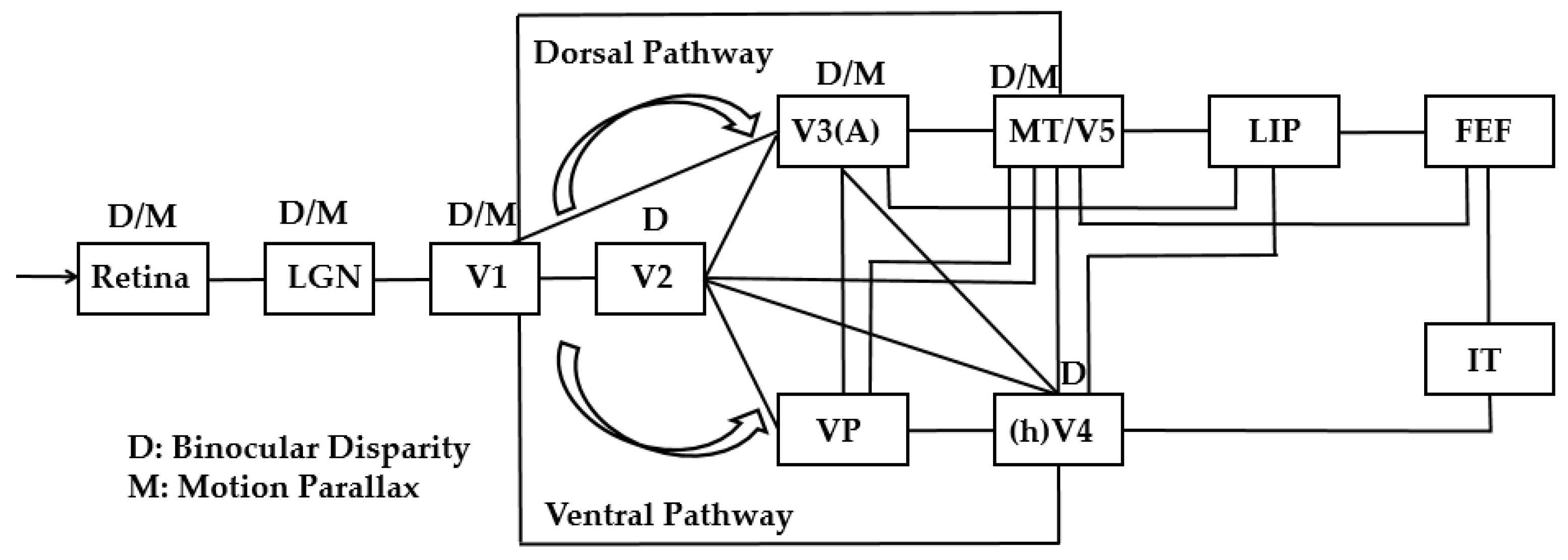
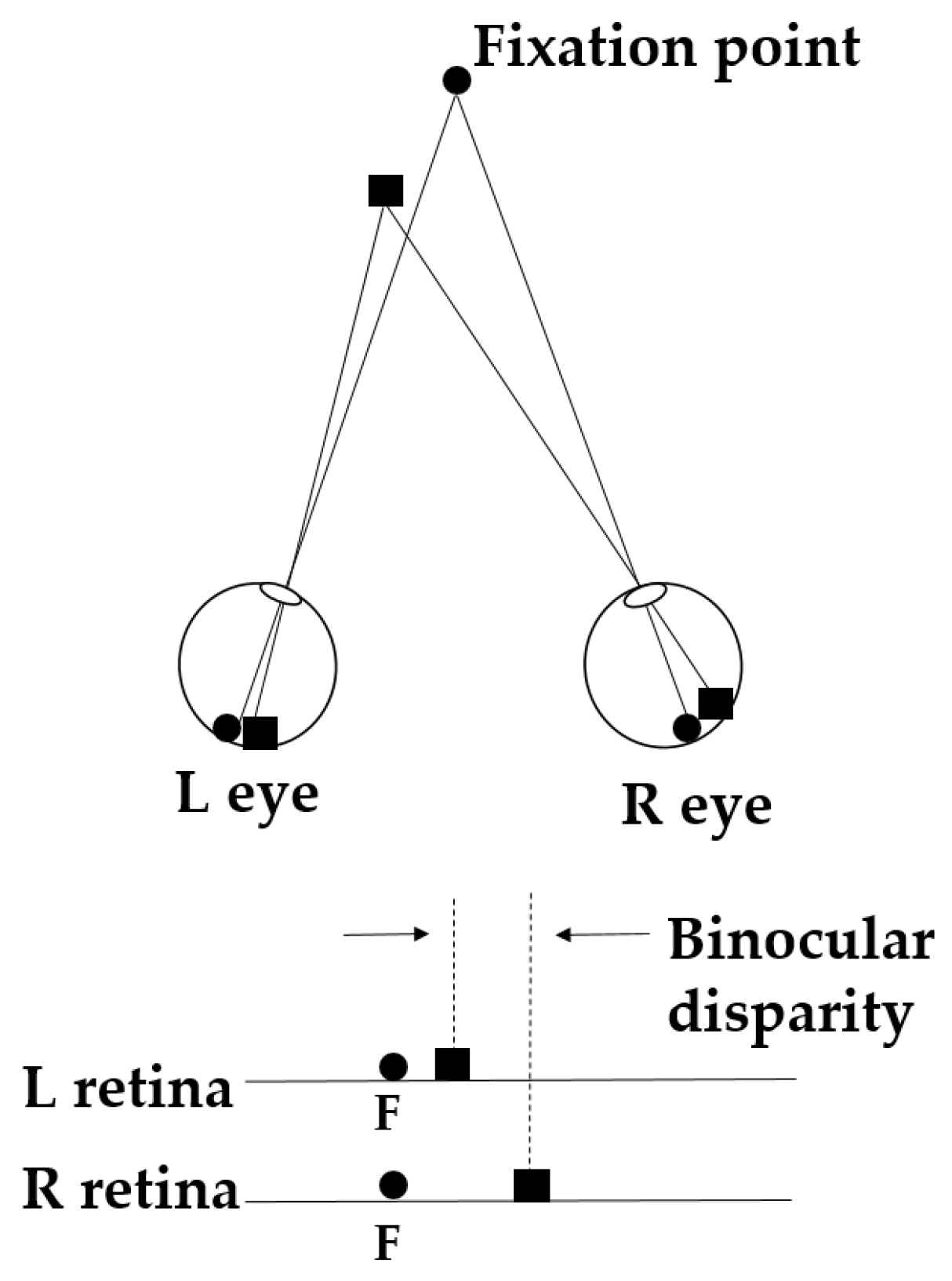
3. The Mechanism of Binocular Disparity Cue
4. The Mechanism of Motion Parallax Cue
5. Models of Depth Perception Based on Interaction Between Binocular Disparity and Motion Parallax Cues
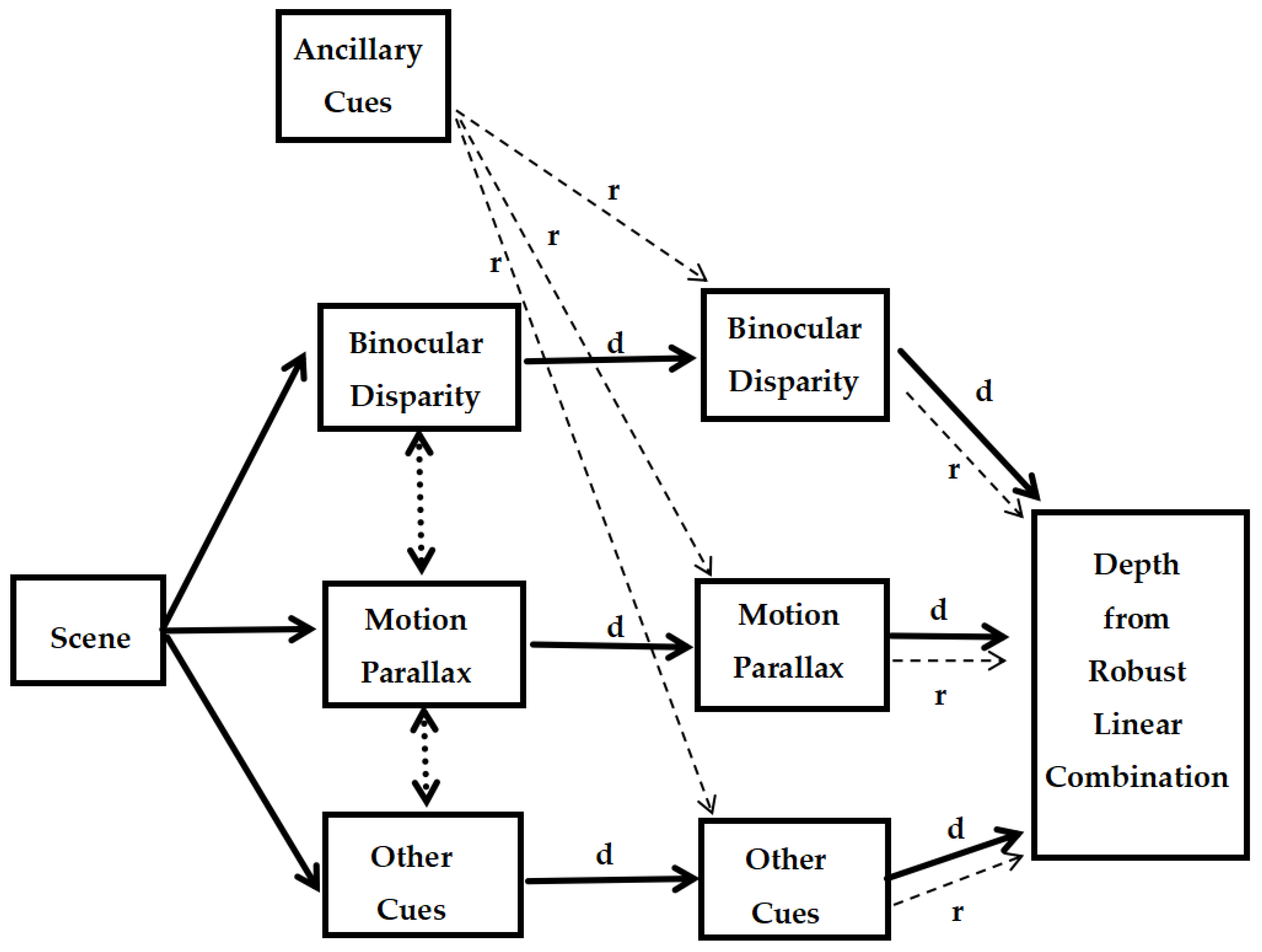
5.1. The WF Model
5.2. The MWF Model
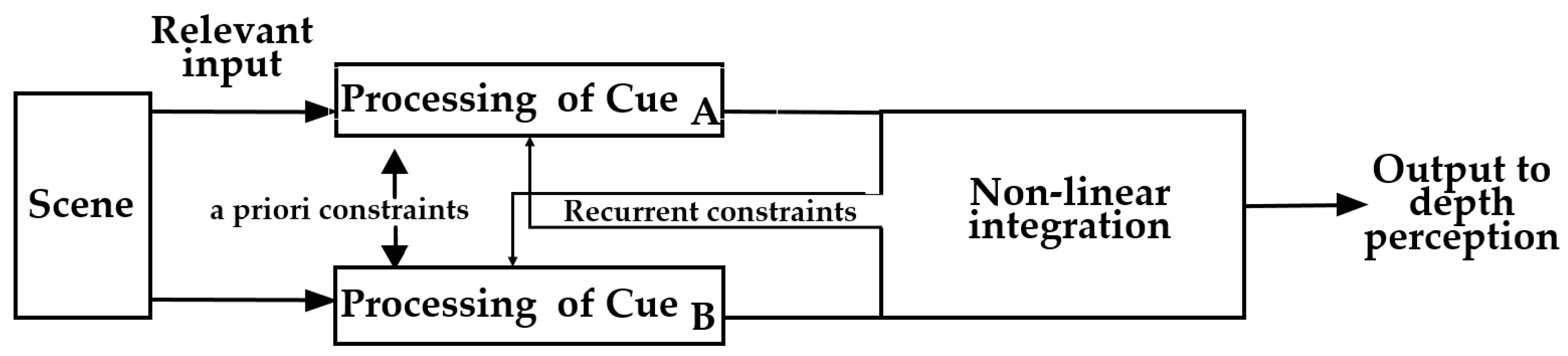
5.3. The SF Model
5.4. The IC Model
5.5. Comparisons and Applications of Above Models
5.5.1. Comparisons of Above Models
5.5.2. Applications of Above Models
6. Open Research Challenges and Future Direction
6.1. Open Research Challenges
- (1)
- How to apply depth perception models to improve the realistic experience of depth perception in 3D space
- (2)
- How to build up depth perception models for applications in complex 3D scenarios
- (3)
- How to improve the performance of human–computer interaction via the study of depth perception in 3D space
6.2. Future Directions
- (1)
- Exploring methods for easier manipulating depth cue signals in stereoscopic images
- (2)
- Adopting deep learning methods to construct models with multiple cues and/or factors and predict perceived depth for human visual system in complex 3D scenarios
7. Summary
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Correction Statement
References
- Brenner, E.; Smeets, J.B. Depth perception. In Stevens’ Handbook of Experimental Psychology and Cognitive Neuroscience: Sensation, Perception, and Attention; Wiley: Hoboken, NJ, USA, 2018; pp. 385–414. [Google Scholar]
- Howard, I.P.; Rogers, B.J. Perceiving in Depth, Volume 2: Stereoscopic Vision; OUP: Oxford, UK, 2012. [Google Scholar]
- Kim, H.R.; Angelaki, D.E.; DeAngelis, G.C. The neural basis of depth perception from motion parallax. Philos. Trans. R. Soc. B Biol. Sci. 2016, 371, 20150256. [Google Scholar] [CrossRef]
- Howard, I.P. Perceiving in depth, Vol. 3: Other Mechanisms of Depth Perception; Oxford University Press: Oxford, UK, 2012. [Google Scholar]
- Welchman, A.E. The human brain in depth: How we see in 3D. Annu. Rev. Vis. Sci. 2016, 2, 345–376. [Google Scholar] [CrossRef]
- Howard, I.P.; Rogers, B.J. Binocular Vision and Stereopsis; Oxford University Press: Oxford, UK, 1995. [Google Scholar]
- Lillakas, L.; Ono, H.; Ujike, H.; Wade, N. On the definition of motion parallax. Vision 2004, 16, 83–92. [Google Scholar]
- Wang, S.; Ming, H.; Wang, A.; Xu, L.; Zhang, T. Three-Dimensional Display Based on Human Visual Perception. Chin. J. Lasers 2014, 41, 209007. [Google Scholar] [CrossRef]
- Lambooij, M.; IJsselsteijn, W.; Fortuin, M.; Heynderickx, I. Visual discomfort and visual fatigue of stereoscopic displays: A review. J. Imaging Sci. Technol. 2009, 53, 30201. [Google Scholar] [CrossRef]
- Koulieris, G.-A.; Bui, B.; Banks, M.S.; Drettakis, G. Accommodation and comfort in head-mounted displays. ACM Trans. Graph. (TOG) 2017, 36, 1–11. [Google Scholar] [CrossRef]
- Guo, M.; Yue, K.; Hu, H.; Lu, K.; Han, Y.; Chen, S.; Liu, Y. Neural research on depth perception and stereoscopic visual fatigue in virtual reality. Brain Sci. 2022, 12, 1231. [Google Scholar] [CrossRef] [PubMed]
- Lang, M.; Hornung, A.; Wang, O.; Poulakos, S.; Smolic, A.; Gross, M. Nonlinear disparity mapping for stereoscopic 3D. ACM Trans. Graph. (TOG) 2010, 29, 1–10. [Google Scholar] [CrossRef]
- Kellnhofer, P.; Didyk, P.; Ritschel, T.; Masia, B.; Myszkowski, K.; Seidel, H.-P. Motion parallax in stereo 3D: Model and applications. ACM Trans. Graph. (TOG) 2016, 35, 1–12. [Google Scholar] [CrossRef]
- Julesz, B. Binocular Depth Perception without Familiarity Cues: Random-dot stereo images with controlled spatial and temporal properties clarify problems in stereopsis. Science 1964, 145, 356–362. [Google Scholar] [CrossRef]
- Tyler, C.W. Depth perception in disparity gratings. Nature 1974, 251, 140–142. [Google Scholar] [CrossRef] [PubMed]
- Rogers, B.; Graham, M. Motion parallax as an independent cue for depth perception. Perception 1979, 8, 125–134. [Google Scholar] [CrossRef]
- Chen, N.; Chen, Z.; Fang, F. Functional specialization in human dorsal pathway for stereoscopic depth processing. Exp. Brain Res. 2020, 238, 2581–2588. [Google Scholar] [CrossRef] [PubMed]
- Li, Z.; Cui, Y.; Zhou, T.; Jiang, Y.; Wang, Y.; Yan, Y.; Nebeling, M.; Shi, Y. Color-to-depth mappings as depth cues in virtual reality. In Proceedings of the 35th Annual ACM Symposium on User Interface Software and Technology, 29 October–2 November 2022; pp. 1–14. [Google Scholar]
- Bailey, R.; Grimm, C.; Davoli, C.; Abrams, R. The Effect of Object Color on Depth Ordering; Technical Report WUCSE-2007-21; Department of Computer Science & Engineering, Washington University in St. Louis: St. Louis, MO, USA, 2007. [Google Scholar]
- Bradshaw, M.F.; Rogers, B.J. The interaction of binocular disparity and motion parallax in the computation of depth. Vis. Res. 1996, 36, 3457–3468. [Google Scholar] [CrossRef] [PubMed]
- Bradshaw, M.F.; Hibbard, P.B.; Parton, A.D.; Rose, D.; Langley, K. Surface orientation, modulation frequency and the detection and perception of depth defined by binocular disparity and motion parallax. Vis. Res. 2006, 46, 2636–2644. [Google Scholar] [CrossRef]
- Domini, F.; Caudek, C.; Tassinari, H. Stereo and motion information are not independently processed by the visual system. Vis. Res. 2006, 46, 1707–1723. [Google Scholar] [CrossRef]
- Minini, L.; Parker, A.J.; Bridge, H. Neural modulation by binocular disparity greatest in human dorsal visual stream. J. Neurophysiol. 2010, 104, 169–178. [Google Scholar] [CrossRef]
- DeAngelis, G.C.; Cumming, B.G.; Newsome, W.T. Cortical area MT and the perception of stereoscopic depth. Nature 1998, 394, 677–680. [Google Scholar] [CrossRef]
- Uka, T.; DeAngelis, G.C. Linking neural representation to function in stereoscopic depth perception: Roles of the middle temporal area in coarse versus fine disparity discrimination. J. Neurosci. 2006, 26, 6791–6802. [Google Scholar] [CrossRef]
- Nadler, J.W.; Angelaki, D.E.; DeAngelis, G.C. A neural representation of depth from motion parallax in macaque visual cortex. Nature 2008, 452, 642–645. [Google Scholar] [CrossRef]
- Kim, H.R.; Angelaki, D.E.; DeAngelis, G.C. A functional link between MT neurons and depth perception based on motion parallax. J. Neurosci. 2015, 35, 2766–2777. [Google Scholar] [CrossRef] [PubMed]
- Xu, Z.-X.; DeAngelis, G.C. Neural mechanism for coding depth from motion parallax in area MT: Gain modulation or tuning shifts? J. Neurosci. 2022, 42, 1235–1253. [Google Scholar] [CrossRef] [PubMed]
- Li, Z. Understanding Vision: Theory, Models, and Data; Oxford University Press: Oxford, UK, 2014. [Google Scholar]
- Qian, N. Binocular disparity and the perception of depth. Neuron 1997, 18, 359–368. [Google Scholar] [CrossRef] [PubMed]
- Nawrot, M.; Stroyan, K. The motion/pursuit law for visual depth perception from motion parallax. Vis. Res. 2009, 49, 1969–1978. [Google Scholar] [CrossRef]
- Dosher, B.A.; Sperling, G.; Wurst, S.A. Tradeoffs between stereopsis and proximity luminance covariance as determinants of perceived 3D structure. Vis. Res. 1986, 26, 973–990. [Google Scholar] [CrossRef]
- Rogers, B.J.; Collett, T.S. The appearance of surfaces specified by motion parallax and binocular disparity. Q. J. Exp. Psychol. Sect. A-Hum. Exp. Psychol. 1989, 41, 697–717. [Google Scholar] [CrossRef]
- Landy, M.S.; Maloney, L.T.; Johnston, E.B.; Young, M. Measurement and modeling of depth cue combination: In defense of weak fusion. Vis. Res. 1995, 35, 389–412. [Google Scholar] [CrossRef]
- Wheatstone, C., XVIII. Contributions to the physiology of vision.—Part the first. On some remarkable, and hitherto unobserved, phenomena of binocular vision. Philos. Trans. R. Soc. Lond. 1838, 128, 371–394. [Google Scholar]
- Hibbard, P.B. Binocular energy responses to natural images. Vis. Res. 2008, 48, 1427–1439. [Google Scholar] [CrossRef]
- Kytö, M.; Nuutinen, M.; Oittinen, P. Method for measuring stereo camera depth accuracy based on stereoscopic vision. In Proceedings of the Three-Dimensional Imaging, Interaction, and Measurement, San Francisco, CA, USA, 24–27 January 2011; pp. 168–176. [Google Scholar]
- Gillam, B.; Palmisano, S.A.; Govan, D.G. Depth interval estimates from motion parallax and binocular disparity beyond interaction space. Perception 2011, 40, 39–49. [Google Scholar] [CrossRef]
- He, S.; Shigemasu, H.; Ishikawa, Y.; Dai, C. Effects of Different Cues on Object Depth Perception in Three-Dimensional Space. Acta Opt. Sin. 2019, 39, 1033002. [Google Scholar]
- Hibbard, P.B.; Bouzit, S. Stereoscopic correspondence for ambiguous targets is affected by elevation and fixation distance. Spat. Vis. 2005, 18, 399–411. [Google Scholar]
- Sprague, W.W.; Cooper, E.A.; Tošić, I.; Banks, M.S. Stereopsis is adaptive for the natural environment. Sci. Adv. 2015, 1, e1400254. [Google Scholar] [CrossRef] [PubMed]
- Jordan III, J.R.; Geisler, W.S.; Bovik, A.C. Color as a source of information in the stereo correspondence process. Vis. Res. 1990, 30, 1955–1970. [Google Scholar] [CrossRef]
- Simmons, D.R.; Kingdom, F.A. Contrast thresholds for stereoscopic depth identification with isoluminant and isochromatic stimuli. Vis. Res. 1994, 34, 2971–2982. [Google Scholar] [CrossRef] [PubMed]
- Burge, J.; McCann, B.C.; Geisler, W.S. Estimating 3D tilt from local image cues in natural scenes. J. Vis. 2016, 16, 2. [Google Scholar] [CrossRef]
- Burge, J.; Fowlkes, C.C.; Banks, M.S. Natural-scene statistics predict how the figure–ground cue of convexity affects human depth perception. J. Neurosci. 2010, 30, 7269–7280. [Google Scholar] [CrossRef]
- Qiu, F.T.; Von Der Heydt, R. Figure and ground in the visual cortex: V2 combines stereoscopic cues with Gestalt rules. Neuron 2005, 47, 155–166. [Google Scholar] [CrossRef]
- Cottereau, B.R.; McKee, S.P.; Ales, J.M.; Norcia, A.M. Disparity-tuned population responses from human visual cortex. J. Neurosci. 2011, 31, 954–965. [Google Scholar] [CrossRef]
- Potetz, B.; Lee, T.S. Statistical correlations between two-dimensional images and three-dimensional structures in natural scenes. JOSA A 2003, 20, 1292–1303. [Google Scholar] [CrossRef]
- Samonds, J.M.; Potetz, B.R.; Lee, T.S. Relative luminance and binocular disparity preferences are correlated in macaque primary visual cortex, matching natural scene statistics. Proc. Natl. Acad. Sci. USA 2012, 109, 6313–6318. [Google Scholar] [CrossRef]
- Snowden, R.J.; Snowden, R.; Thompson, P.; Troscianko, T. Basic Vision: An Introduction to Visual Perception; Oxford University Press: Oxford, UK, 2012; pp. 220–222. [Google Scholar]
- Von Helmholtz, H. Helmholtz’s Treatise on Physiological Optics; Optical Society of America: Rochester, NY, USA, 1925; Volume 3. [Google Scholar]
- Gibson, E.J.; Gibson, J.J.; Smith, O.W.; Flock, H. Motion parallax as a determinant of perceived depth. J. Exp. Psychol. 1959, 58, 40. [Google Scholar] [CrossRef] [PubMed]
- Epstein, W.; Park, J. Examination of Gibson’s psychophysical hypothesis. Psychol. Bull. 1964, 62, 180. [Google Scholar] [CrossRef]
- Gogel, W.C.; Tietz, J.D. Eye fixation and attention as modifiers of perceived distance. Percept. Mot. Ski. 1977, 45, 343–362. [Google Scholar] [CrossRef]
- de la Malla, C.; Buiteman, S.; Otters, W.; Smeets, J.B.J.; Brenner, E. How various aspects of motion parallax influence distance judgments, even when we think we are standing still. J. Vis. 2016, 16, 8. [Google Scholar] [CrossRef] [PubMed]
- Fulvio, J.M.; Miao, H.; Rokers, B. Head jitter enhances three-dimensional motion perception. J. Vis. 2021, 21, 12. [Google Scholar] [CrossRef] [PubMed]
- Dokka, K.; MacNeilage, P.R.; DeAngelis, G.C.; Angelaki, D.E. Estimating distance during self-motion: A role for visual-vestibular interactions. J. Vis. 2011, 11, 1–16. [Google Scholar] [CrossRef]
- Buckthought, A.; Yoonessi, A.; Baker, C.L. Dynamic perspective cues enhance depth perception from motion parallax. J. Vis. 2017, 17, 10. [Google Scholar] [CrossRef]
- Norman, J.F.; Clayton, A.M.; Shular, C.F.; Thompson, S.R. Aging and the perception of depth and 3-D shape from motion parallax. Psychol. Aging 2004, 19, 506. [Google Scholar] [CrossRef]
- Ono, H.; Wade, N.J. Depth and motion perceptions produced by motion parallax. Teach. Psychol. 2006, 33, 199–202. [Google Scholar]
- Mansour, M.; Davidson, P.; Stepanov, O.; Piche, R. Relative Importance of Binocular Disparity and Motion Parallax for Depth Estimation: A Computer Vision Approach. Remote Sens. 2019, 11, 1990. [Google Scholar] [CrossRef]
- Johnston, E.B.; Cumming, B.G.; Landy, M.S. Integration of stereopsis and motion shape cues. Vis. Res. 1994, 34, 2259–2275. [Google Scholar] [CrossRef]
- Ichikawa, M.; Saida, S.; Osa, A.; Munechika, K. Integration of binocular disparity and monocular cues at near threshold level. Vis. Res. 2003, 43, 2439–2449. [Google Scholar] [CrossRef] [PubMed]
- Maloney, L.T.; Landy, M.S. A statistical framework for robust fusion of depth information. In Proceedings of the Visual Communications and Image Processing IV, Tokyo, Japan, 8–11 December 2024; pp. 1154–1163. [Google Scholar]
- Fine, I.; Jacobs, R.A. Modeling the combination of motion, stereo, and vergence angle cues to visual depth. Neural Comput. 1999, 11, 1297–1330. [Google Scholar] [CrossRef] [PubMed]
- Clark, J.; Yuille, A. Data Fusion for Sensory Information Processing Systems; Springer: Boston, MA, USA, 1990; pp. 71–104. [Google Scholar]
- Nakayama, K.; Shimojo, S. Experiencing and perceiving visual surfaces. Science 1992, 257, 1357–1363. [Google Scholar] [CrossRef] [PubMed]
- Domini, F.; Caudek, C. The intrinsic constraint model and Fechnerian sensory scaling. J. Vis. 2009, 9, 25. [Google Scholar] [CrossRef]
- Tassinari, H.; Domini, F.; Caudek, C. The intrinsic constraint model for stereo-motion integration. Perception 2008, 37, 79–95. [Google Scholar] [CrossRef]
- Domini, F. The case against probabilistic inference: A new deterministic theory of 3D visual processing. Philos. Trans. R. Soc. B 2023, 378, 20210458. [Google Scholar] [CrossRef]
- MacKenzie, K.J.; Murray, R.F.; Wilcox, L.M. The intrinsic constraint approach to cue combination: An empirical and theoretical evaluation. J. Vis. 2008, 8, 5. [Google Scholar] [CrossRef]
- Kemp, J.T.; Cesanek, E.; Domini, F. Perceiving depth from texture and disparity cues: Evidence for a non-probabilistic account of cue integration. J. Vis. 2023, 23, 13. [Google Scholar] [CrossRef]
- Temel, D.; Lin, Q.; Zhang, G.; AlRegib, G. Modified weak fusion model for depthless streaming of 3D videos. In Proceedings of the 2013 IEEE International Conference on Multimedia and Expo Workshops (ICMEW), San Jose, CA, USA, 15–19 July 2023; pp. 1–6. [Google Scholar]
- Campagnoli, C.; Hung, B.; Domini, F. Explicit and implicit depth-cue integration: Evidence of systematic biases with real objects. Vis. Res. 2022, 190, 107961. [Google Scholar] [CrossRef] [PubMed]
- Peters, T.M.; Linte, C.A.; Yaniv, Z.; Williams, J. Mixed and Augmented Reality in Medicine; CRC Press: Boca Raton, FL, USA, 2018. [Google Scholar]
- Cheng, L.Y.; Lin, C.J. The effects of depth perception viewing on hand–eye coordination in virtual reality environments. J. Soc. Inf. Disp. 2021, 29, 801–817. [Google Scholar] [CrossRef]
- Chapiro, A.; O’Sullivan, C.; Jarosz, W.; Gross, M.H.; Smolic, A. Stereo from Shading. In Proceedings of the EGSR (EI&I), Zaragoza, Spain, 19–21 June 2013; pp. 119–125. [Google Scholar]
- Didyk, P.; Ritschel, T.; Eisemann, E.; Myszkowski, K.; Seidel, H.-P. Apparent stereo: The cornsweet illusion can enhance perceived depth. In Proceedings of the Human Vision and Electronic Imaging XVII, Burlingame, CA, USA, 22–26 January 2012; pp. 180–191. [Google Scholar]
- Chen, Z.; Guo, X.; Li, S.; Yang, Y.; Yu, J. Deep eyes: Joint depth inference using monocular and binocular cues. Neurocomputing 2021, 453, 812–824. [Google Scholar] [CrossRef]
- Ming, Y.; Meng, X.; Fan, C.; Yu, H. Deep learning for monocular depth estimation: A review. Neurocomputing 2021, 438, 14–33. [Google Scholar] [CrossRef]
- Almasre, M.A.; Al-Nuaim, H. Comparison of four SVM classifiers used with depth sensors to recognize Arabic sign language words. Computers 2017, 6, 20. [Google Scholar] [CrossRef]




| Model | Main Procedure | Characteristics | Validation Results |
|---|---|---|---|
| WF [32,33,34,63,64] | (1) Linear average | (1) Modular | (1) In the no-noise condition, each model performs well. (2) While after adding noise, the WMF model performs best in depth judgement task; but in some conditions, the prediction of the MWF model was inconsistent with the psychophysical data. |
| (2) Cue independent (no interaction) | |||
| SF [34,63,66,67] | (1) A priori constraints | (1) Non-modular | |
| (2) Recurrent constraints | (2) Unconstrained nonlinear interaction | ||
| MWF [34,65] | (1) Cue promotion | (1) Modular | |
| (2) Dynamic weighting | (2) Constrained nonlinear interaction | ||
| IC [22,68,70,72] | (1) Affine reconstruction | (1) Non-modular for cues | The IC model could explain both findings which were in support of the MLE model, or contradicted the MLE model. |
| (2) Depth interpretation | (2) Concern of reducing the measurement noise |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Li, S.; He, S.; Dong, Y.; Dai, C.; Liu, J.; Wang, Y.; Shigemasu, H. Depth Perception Based on the Interaction of Binocular Disparity and Motion Parallax Cues in Three-Dimensional Space. Sensors 2025, 25, 3171. https://doi.org/10.3390/s25103171
Li S, He S, Dong Y, Dai C, Liu J, Wang Y, Shigemasu H. Depth Perception Based on the Interaction of Binocular Disparity and Motion Parallax Cues in Three-Dimensional Space. Sensors. 2025; 25(10):3171. https://doi.org/10.3390/s25103171
Chicago/Turabian StyleLi, Shuai, Shufang He, Yuanrui Dong, Caihong Dai, Jinyuan Liu, Yanfei Wang, and Hiroaki Shigemasu. 2025. "Depth Perception Based on the Interaction of Binocular Disparity and Motion Parallax Cues in Three-Dimensional Space" Sensors 25, no. 10: 3171. https://doi.org/10.3390/s25103171
APA StyleLi, S., He, S., Dong, Y., Dai, C., Liu, J., Wang, Y., & Shigemasu, H. (2025). Depth Perception Based on the Interaction of Binocular Disparity and Motion Parallax Cues in Three-Dimensional Space. Sensors, 25(10), 3171. https://doi.org/10.3390/s25103171





