Analyzing Breathing Patterns in the Breaststroke Technique Through Dual-Media Kinematics and Fractal Dimension
Abstract
1. Introduction
2. Methods
2.1. Participants
2.2. Intervention Program
2.3. Motion Capture System
2.4. Data Collection Procedures
2.5. Data Analysis and Processing
2.6. Statistical Analysis
3. Results
4. Discussion
5. Limitations and Future Research
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1
 | ||
| # | Marker Name | Description |
| 1 | HeadFront | Forehead, above the nose. |
| 2 | HeadL, HeadR | Just above the ear center. |
| 3 | HeadFront | On top of the head vertically above the ears. |
| 4 | LShoulderTop, RShoulderTop | On top of the shoulder (bony prominence). |
| 5 | LElbowOut, RElbowOut | On the outside of the elbow (bony prominence). |
| 6 | LElbowIn, RElbowIn | On the inside of the elbow (bony prominence). |
| 7 | LWristIn, RWristIn | On the inside of the wrist (bony prominence on the thumb side). |
| 8 | LWristOut, RWristOut | On the outside of the wrist (bony prominence on the pinky side). |
| 9 | Chest | Upper part of the sternum. |
| 10 | WaistLFront, WaistRFront | On the front of the pelvis (bony prominence). |
| 11 | LThighFrontHigh, RThighFrontHigh | Top of the thigh. |
| 12 | LThighFrontLow, RThighFrontLow | Above the kneecap. |
| 13 | LKneeOut, RKneeOut | On the outside of the knee (bony prominence). |
| 14 | LKneeIn, RKneeIn | On the inside of the knee (bony prominence). |
| 15 | LShinFrontHigh, RShinFrontHigh | Front of the shin. |
| 16 | LAnkleOut, RAnkleOut | On the outside of the ankle. |
| 17 | LAnkleIn, RAnkleIn | On the inside of the ankle. |
| 18 | LForefoot5, RForefoot5 | Base of the toes on the outside. |
| 19 | LForefoot2, RForefoot2 | Top of the foot tip. |
| 20 | LForefoot1, RForefoot1 | Base of the toes on the inside. |
| 21 | SpineThoracic2 | On the 2nd prominence below the biggest prominence on the top of the spine. |
| 22 | LArm, RArm | On the back of the upper arm. |
| 23 | LHand2, RHand2 | Just below the index finger’s knuckle. |
| 24 | LHand5, RHand5 | Just below the pinky finger’s knuckle. |
| 25 | SpineThoracic12 | A few cm below the midpoint of the lower tip of the shoulder blades. |
| 26 | WaistBack | On the midpoint between the two prominences on the back of the pelvis. |
| 27 | WaistL, WaistR | On the sides of the pelvis (bony prominence). |
| 28 | LHeelBack, RHeelBack | Back of the heel. |
| Note: the prefixes “L” and “R” denote left and right sides. | ||
Appendix A.2
| Variables | Schematic Presentation |
|---|---|
| Hand variables | |
|  |
|  |
|  |
|  |
|  |
|  |
|  |
| Foot variables | |
|  |
|  |
|  |
|  |
|  |
|  |
|  |
| Head variables | |
|  |
|  |
|  |
|  |
| Center of mass variables | |
|  |
|  |
| 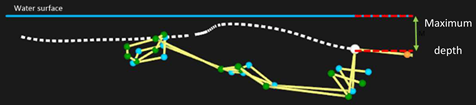 |
References
- Toussaint, H.M.; Beek, P.J. Biomechanics of competitive front crawl swimming. Sports Med. 1992, 13, 8–24. [Google Scholar] [CrossRef] [PubMed]
- Pendergast, D.; Mollendorf, J.; Zamparo, P.; Termin, A.; Bushnell, D.; Paschke, D. The influence of drag on human locomotion in water. Undersea Hyperb. Med. 2005, 32, 45–57. [Google Scholar]
- Cardelli, C.; Lerda, R.; Chollet, D. Analysis of breathing in the crawl as a function of skill and stroke characteristics. Percept. Mot. Ski. 2000, 90, 979–987. [Google Scholar] [CrossRef] [PubMed]
- Pedersen, T.; Kjendlie, P.-L. The effect of the breathing action on velocity in front crawl sprinting. Port. J. Sport Sci. 2006, 6, 75–77. [Google Scholar]
- Alves, F.; Cunha, P.; Gomes-Pereira, J. Kinematic changes with inspiratory actions in butterfly swimming. In Biomechanics and Medicine in Swimming VIII; Keskinen, K.L., Komi, P.V., Hollander, A.P., Eds.; University of Jyvaskyla: Jyvaskyla, Finland, 1999; pp. 9–14. [Google Scholar]
- Hahn, A.; Krug, T. Application of knowledge gained from the coordination of partial movements in breaststroke and butterfly swimming for the development of technical training. In Biomechanics and Medicine in Swimming V1; Taylor & Francis: Abingdon, UK, 2013; pp. 144–148. [Google Scholar]
- Fernandes, A.; Costa, M.J.; Mezêncio, B.; Vilas-Boas, J.P.; Fernandes, R.J. Breaststroke and butterfly intercycle kinematic variation according to different competitive levels with Statistical Parametric Mapping analysis. J. Biomech. 2024, 176, 112380. [Google Scholar] [CrossRef]
- Seifert, L.; Chollet, D.; Sanders, R. Does breathing disturb coordination in butterfly? Int. J. Sports Med. 2010, 31, 167–173. [Google Scholar] [CrossRef][Green Version]
- Couto, J.G.M.; Franken, M.; Castro, F.A.d.S. Influence of different breathing patterns on front crawl kinematics. Rev. Bras. De Cineantropometria E Desempenho Hum. 2014, 17, 82–90. [Google Scholar] [CrossRef]
- McCabe, C.B.; Sanders, R.H.; Psycharakis, S.G. Upper limb kinematic differences between breathing and non-breathing conditions in front crawl sprint swimming. J. Biomech. 2015, 48, 3995–4001. [Google Scholar] [CrossRef] [PubMed]
- Zompanakis, I.; Papadimitriou, K.; Georgios, T.; Dimitrios, L. The effects of reduced breathing on swimming performance and on blood lactate concentration in 25 and 50 m breaststroke swimming at maximal intensity. JSR 2020, 27, 2. [Google Scholar]
- Alves, M.; Barbosa, T.M.; Vilas-Boas, J.P. Exploring the impact of breathing patterns on active drag in breaststroke swimming. J. Biomech. 2024, 177, 112390. [Google Scholar] [CrossRef]
- Fernandes, A.; Goethel, M.; Marinho, D.A.; Mezêncio, B.; Vilas-Boas, J.P.; Fernandes, R.J. Velocity variability and performance in backstroke in elite and good-level swimmers. Int. J. Environ. Res. Public Health 2022, 19, 6744. [Google Scholar] [CrossRef]
- Barbosa, T.M.; Bragada, J.A.; Reis, V.M.; Marinho, D.A.; Carvalho, C.; Silva, A.J. Energetics and biomechanics as determining factors of swimming performance: Updating the state of the art. J. Sci. Med. Sport 2010, 13, 262–269. [Google Scholar] [CrossRef] [PubMed]
- Barbosa, T.M.; Morouço, P.G.F.; Jesus, S.; Feitosa, W.G.; Costa, M.J.; Marinho, D.A.; Silva, A.; Garrido, N.D. The interaction between intra-cyclic variation of the velocity and mean swimming velocity in young competitive swimmers. Int. J. Sports Med. 2013, 34, 123–130. [Google Scholar] [CrossRef] [PubMed]
- Vilas-Boas, J.P. Speed fluctuations and energy cost of different breaststroke techniques. In Biomechanics and Medicine in Swimming VII; Routledge: New York, NY, USA, 1996; Volume 7, pp. 167–171. [Google Scholar]
- Barbosa, T.M.; Lima, F.; Portela, A.; Novais, D.; Machado, L.; Colaco, P.; Goncalves, R.F.; Keskinen, K.L.; Vilas-Boas, J.P. Relationships between energy cost, swimmming velocity and speed fluctuation in competitive swimming strokes. Biomech. Med. Swim. X 2006, 6 (Suppl. S2), 192–194. [Google Scholar]
- Figueiredo, P.; Kjendlie, P.L.; Vilas-Boas, J.P.; Fernandes, R.J. Intracycle velocity variation of the body centre of mass in front crawl. Int. J. Sports Med. 2012, 33, 285–290. [Google Scholar] [CrossRef]
- Matsuda, Y.; Yamada, Y.; Ikuta, Y.; Nomura, T.; Oda, S. Intracyclic velocity variation and arm coordination for different skilled swimmers in the front crawl. J. Hum. Kinet. 2014, 44, 67. [Google Scholar] [CrossRef][Green Version]
- Miller, D.I. Biomechanics of Swimming. Exerc. Sport Sci. Rev. 1975, 3, 219–248. [Google Scholar] [CrossRef]
- De Jesus, K.; Sanders, R.; De Jesus, K.; Ribeiro, J.; Figueiredo, P.; Vilas-Boas, J.P.; Fernandes, R.J. The effect of intensity on 3-dimensional kinematics and coordination in front-crawl swimming. Int. J. Sports Physiol. Perform. 2016, 11, 768–775. [Google Scholar] [CrossRef]
- Psycharakis, S.G.; Naemi, R.; Connaboy, C.; McCabe, C.; Sanders, R.H. Three-dimensional analysis of intracycle velocity fluctuations in frontcrawl swimming. Scand. J. Med. Sci. Sports 2010, 20, 128–135. [Google Scholar] [CrossRef] [PubMed]
- Schnitzler, C.; Seifert, L.; Ernwein, V.; Chollet, D. Arm coordination adaptations assessment in swimming. Int. J. Sports Med. 2008, 29, 480–486. [Google Scholar] [CrossRef]
- Vieira, L.; Soares, S.; Costa, M.J.; Fernandes, R.J.; Ferreira, F.A.; Goethel, M.; Vilas-Boas, J.P. Comparação da velocidade intracíclica de nado obtida por unidade inercial e por velocímetro. Motricidade 2024, 20, 1–3. [Google Scholar]
- Barbosa, T.; Morais, J.; Bartolomeu, R.; Costa, M. Comparison of fractal dimension among swimmers with different levels of expertise. Motricidade 2017, 13, 127. [Google Scholar]
- Bravi, A.; Longtin, A.; Seely, A.J. Review and classification of variability analysis techniques with clinical applications. Biomed. Eng. Online 2011, 10, 90. [Google Scholar] [CrossRef]
- Den Hartigh, R.J.; Cox, R.F.; Gernigon, C.; Van Yperen, N.W.; Van Geert, P.L. Pink noise in rowing ergometer performance and the role of skill level. Mot. Control 2015, 19, 355–369. [Google Scholar] [CrossRef]
- Hoos, O.; Boeselt, T.; Steiner, M.; Hottenrott, K.; Beneke, R. Long-range correlations and complex regulation of pacing in long-distance road racing. Int. J. Sports Physiol. Perform. 2014, 9, 544–553. [Google Scholar] [CrossRef]
- Slopecki, M.; Clément, J.; Charbonneau, M.; Côté, J.N. The impact of limb symmetry on stroke-to-stroke movement variability in para-swimmers during an adapted aerobic step test. ISBS Proc. Arch. 2024, 42, 862. [Google Scholar]
- Tucker, R.; Bester, A.; Lambert, E.V.; Noakes, T.D.; Vaughan, C.L.; Gibson, A.S.C. Non-random fluctuations in power output during self-paced exercise. Br. J. Sports Med. 2006, 40, 912–917. [Google Scholar] [CrossRef]
- Guadagnoli, M.A.; Lee, T.D. Challenge point: A framework for conceptualizing the effects of various practice conditions in motor learning. J. Mot. Behav. 2004, 36, 212–224. [Google Scholar] [CrossRef]
- Qualisys. Sports Marker Set. 2021. Available online: https://cdn-content.qualisys.com/2021/11/Sports-Marker-Set.pdf (accessed on 9 May 2025).
- Andersen, J.; Sinclair, P.; Fernandes, R.J.; Vilas-Boas, J.P.; Sanders, R. Is torso twist production the primary role of the torso muscles in front crawl swimming? Sports Biomech. 2023, 22, 1602–1616. [Google Scholar] [CrossRef]
- Toubekis, A.G.; Adam, G.V.; Douda, H.T.; Antoniou, P.D.; Douroundos, I.I.; Tokmakidis, S.P. Repeated sprint swimming performance after low-or high-intensity active and passive recoveries. J. Strength Cond. Res. 2011, 25, 109–116. [Google Scholar] [CrossRef]
- Roithner, R.; Schwameder, H.; Mueller, E. Determination of optimal filter parameters for filtering kinematic walking data using Butterworth low pass filter. In ISBS-Conference Proceedings Archive; OJS: Phoenix, AZ, USA, 2000. [Google Scholar]
- Vilas-Boas, J.P. Caracterização Biofísica de três Variantes da Técnica de Bruços. 1993. Available online: https://repositorio-aberto.up.pt/handle/10216/93621 (accessed on 9 May 2025).
- Higuchi, T. Approach to an irregular time series on the basis of the fractal theory. Phys. D Nonlinear Phenom. 1988, 31, 277–283. [Google Scholar] [CrossRef]
- Barbosa, T.M.; Goh, W.X.; Morais, J.E.; Costa, M.J.; Pendergast, D. Comparison of classical kinematics, entropy, and fractal properties as measures of complexity of the motor system in swimming. Front. Psychol. 2016, 7, 1566. [Google Scholar] [CrossRef] [PubMed]
- Ferguson, C.J. An effect size primer: A guide for clinicians and researchers. In Methodological Issues and Strategies in Clinical Research; American Psychological Association: Washington, DC, USA, 2016. [Google Scholar]
- Kjendlie, P.L.; Stallman, R.K. Drag characteristics of competitive swimming children and adults. J. Appl. Biomech. 2008, 24, 35–42. [Google Scholar] [CrossRef] [PubMed]
- Chatard, J.C.; Padilla, S.; Cazorla, G.; Lacour, J.R. Infuence of body height, weight, hydrostatic lift and training on the energy cost of front crawl. NZ J. Sports Med. 1985, 13, 82–84. [Google Scholar]
- Kjendlie, P.L.; Ingjer, F.; Madsen, O.; Stallman, R.K.; Stray-Gundersen, J. Differences in the energy cost between children and adults during front crawl swimming. Eur. J. Appl. Physiol. 2004, 91, 473–480. [Google Scholar] [CrossRef]
- Kjendlie, P.L.; Ingjer, F.; Stallman, R.K.; Stray-Gundersen, J. Factors affecting swimming economy in children and adults. Eur. J. Appl. Physiol. 2004, 93, 65–74. [Google Scholar] [CrossRef]
- Persyn, U.; Colman, V.; Ungerechts, B. Diagnosis & Advice in the Undulating Strokes. Coaches’ Information Service-Website. 2005. Online Version 12/02/2007. Available online: http://www.coachesinfo.com (accessed on 15 January 2025).
- Sanders, R.H. Breaststroke technique variations among New Zealand Pan Pacific squad swimmers. In Biomechanics and Medicine in Swimming VII; Routledge: New York, NY, USA, 1996; pp. 64–69. [Google Scholar]
- Gourgoulis, V.; Koulexidis, S.; Gketzenis, P.; Tzouras, G. Intracyclic velocity variation of the center of mass and hip in breaststroke swimming with maximal intensity. J. Strength Cond. Res. 2018, 32, 830–840. [Google Scholar] [CrossRef]
- Vilas-Boas, J.P.; Fernandes, R.J.; Barbosa, T.M. Intra-cycle velocity variations, swimming economy, performance and training in swimming. In The World Book of Swimming: From Science to Performance; Nova Science Publishers, Hauppauge: New York, NY, 2011; pp. 119–134. [Google Scholar]
- Figueiredo, P.; Marques, E.A.; Vilas-Boas, J.P.; Fernandes, R.J. Methods of intracycle velocity variation assessment in front crawl. In Proceedings of the International Society of Biomechanics, Natal, Brazil, 4–9 August 2013. [Google Scholar]
- Gonjo, T.; Fernandes, R.J.; Vilas-Boas, J.P.; Sanders, R. Is the use of the coefficient of variation a valid way to assess the swimming intra-cycle velocity fluctuation? J. Sci. Med. Sport 2023, 26, 328–334. [Google Scholar] [CrossRef]
- Castiglioni, P.; Di Rienzo, M.; Parati, G.; Faini, A. Fractal dimension of mean arterial pressure and heart-rate time series from ambulatory blood pressure monitoring devices. In Proceedings of the 2011 Computing in Cardiology, Hangzhou, China, 18–21 September 2011; IEEE: New York, NY, USA, 2011; pp. 593–596. [Google Scholar]
- Barbosa, T.M.; Goh, W.X.; Morais, J.E.; Costa, M.J. Variation of linear and nonlinear parameters in the swim strokes according to the level of expertise. Mot. Control 2017, 21, 312–326. [Google Scholar] [CrossRef]



| Variables | Breathing Cycle | Non-Breathing Cycle | Breathing Cycle Following a Non-Breathing Cycle | F | ŋ2 | |
|---|---|---|---|---|---|---|
| Mean ± SD [95%Cl] | Mean ± SD [95%Cl] | Mean ± SD [95%Cl] | ||||
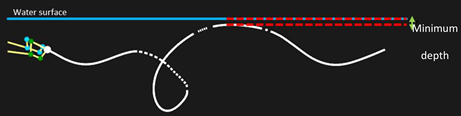
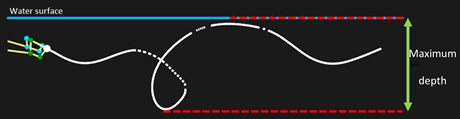
| Hands motor path | Min depth (m) | −0.02 ± 0.05 | −0.03 ± 0.05 | −0.03 ± 0.09 | 0.435 | 0.025 |
| [−0.01 ± −0.03] | [−0.01 ± −0.04] | [0 ± −0.06] | ||||
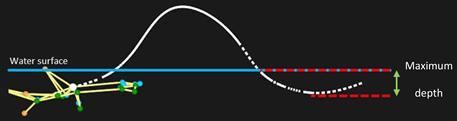
| Max depth (m) | −0.34 ± 0.05 | −0.35 ± 0.05 | −0.32 ± 0.08 | 2.124 | 0.111 | |
| [−0.33 ± −0.35] | [−0.34 ± −0.37] | [−0.3 ± −0.35] | ||||
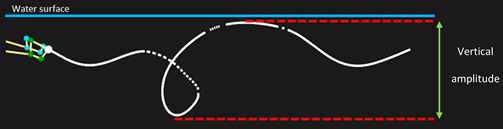
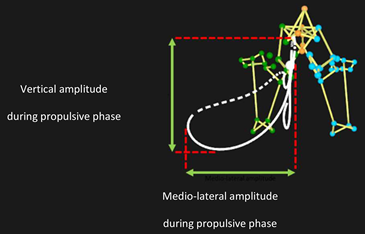
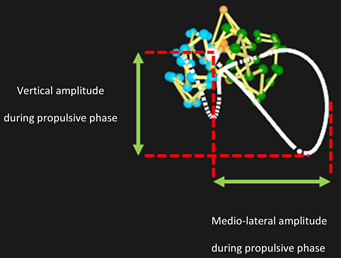
| Vertical amplitude (m) | 0.32 ± 0.08 | 0.33 ± 0.08 | 0.29 ± 0.15 | 1.577 | 0.085 | |
| [0.34; 0.31] | [0.35; 0.30] | [0.34; 0.25] | ||||
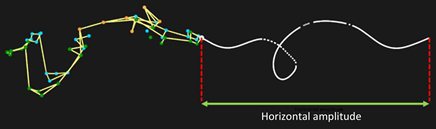
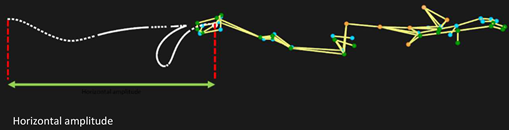
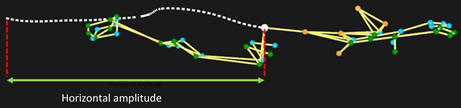
| Horizontal amplitude (m) | 1.11 ± 0.23 | 1.13 ± 0.24 | 1.11 ± 0.21 | 0.319 | 0.018 | |
| [1.16; 1.06] | [1.20; 1.06] | [1.17; 1.04] | ||||
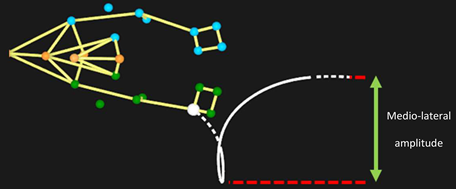
| Medio-lateral amplitude (m) | 0.40 ± 0.06 c | 0.40 ± 0.06 | 0.38 ± 0.06 a | 5.667 | 0.250 | |
| [0.41; 0.39] | [0.42; 0.38] | [0.40; 0.37] | ||||
| Horizontality index | 1.46 ± 0.32 | 1.38 ± 0.37 | 1.39 ± 0.30 | 0.0078 | 0.205 | |
| [1.53; 1.39] | [1.49; 1.27] | [1.49; 1.29] | ||||
| Antero-posterior stabilization index in the sagittal plane | 1.03 ± 0.76 | 0.90 ± 0.48 | 1.03 ± 1.10 | 0.2379 | 0.004 | |
| [1.18; 0.87] | [1.04; 0.76] | [1.39; 0.68] | ||||
| Feet motor path | Min depth (m) | −0.15 ± 0.04 | −0.13 ± 0.04 | −0.13 ± 0.03 | 0.594 | 0.034 |
| [−0.14 ± −0.16] | [−0.12 ± −0.14] | [−0.12 ± −0.14] | ||||
| Max depth (m) | −0.43 ± 0.07 | −0.43 ± 0.06 | −0.42 ± 0.06 | 1.840 | 0.098 | |
| [−0.42 ± −0.45] | [−0.42 ± −0.45] | [−0.41 ± −0.44] | ||||
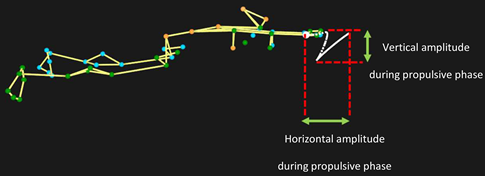
| Vertical amplitude (m) | 0.28 ± 0.04 | 0.30 ± 0.05 | 0.29 ± 0.04 | 1.842 | 0.100 | |
| [0.29; 0.27] | [0.32; 0.29] | [0.30; 0.28] | ||||
| Horizontal amplitude (m) | 1.20 ± 0.21 | 1.16 ± 0.22 | 1.12 ± 0.23 | 1.603 | 0.086 | |
| [1.24; 1.16] | [1.22; 1.10] | [1.20; 1.05] | ||||
| Medio-lateral amplitude (m) | 0.35 ± 0.05 | 0.35 ± 0.07 | 0.35 ± 0.05 | 0.831 | 0.047 | |
| [0.36; 0.34] | [0.37; 0.33] | [0.37; 0.34] | ||||
| Horizontality index | 1.09 ± 0.25 | 1.10 ± 0.27 | 1.10 ± 0.22 | 3.722 | 0.057 | |
| [1.14; 1.04] | [1.17; 1.02] | [1.17; 1.03] | ||||
| Antero-posterior stabilization index in the sagittal plane | 8.76 ± 22.70 | 9.60 ± 22.29 | 9.82 ± 13.24 | 2.890 | 0.045 | |
| [13.40; 4.12] | [16.11; 3.08] | [14.15; 5.50] | ||||
| Head motor path | Min depth (m) | 0.26 ± 0.04 b,c | 0.14 ± 0.08 a,c | 0.26 ± 0.04 a,b | 25.096 | 0.596 |
| [0.27 ± 0.25] | [0.16 ± 0.12] | [0.27 ± 0.25] | ||||
| Max depth (m) | −0.15 ± 0.06 b | −0.18 ± 0.05 a,c | −0.15 ± 0.05 b | 7.925 | 0.318 | |
| [−0.13 ± −0.16] | [−0.16 ± −0.19] | [−0.13 ± −0.16] | ||||
| Vertical amplitude (m) | 0.40 ± 0.09 b | 0.32 ± 0.10 a,c | 0.41 ± 0.07 b | 8.919 | 0.344 | |
| [0.42; 0.39] | [0.35; 0.29] | [0.43; 0.39] | ||||
| Horizontal amplitude (m) | 1.13 ± 0.22 | 1.15 ± 0.22 | 1.11 ± 0.20 | 0.963 | 0.054 | |
| [1.17; 1.08] | [1.22; 1.09] | [1.17; 1.04] | ||||
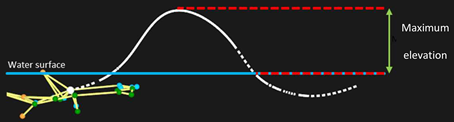
| Horizontal amplitude of the motor path of the head out of the water (m) | 0.63 ± 0.08 b | 0.45 ± 0.10 a,c | 0.62 ± 0.08 b | 32.378 | 0.656 | |
| [0.65; 0.62] | [0.48; 0.42] | [0.65; 0.60] | ||||
| CoM motor path | Min depth (m) | −0.13 ± 0.02 | −0.13 ± 0.05 | −0.11 ± 0.07 | 0.672 | 0.038 |
| [−0.12 ± −0.13] | [−0.11 ± −0.14] | [−0.09 ± −0.13] | ||||
| Max depth (m) | −0.23 ± 0.03 | −0.23 ± 0.03 | −0.23 ± 0.03 | 1.674 | 0.090 | |
| [−0.23 ± −0.24] | [−0.23 ± −0.24] | [−0.22 ± −0.24] | ||||
| Vertical amplitude (m) | 0.11 ± 0.02 | 0.11 ± 0.04 | 0.13 ± 0.06 | 3.559 | 0.173 | |
| [0.11; 0.10] | [0.12; 0.09] | [0.14; 0.11] | ||||
| Horizontal amplitude (m) | 1.14 ± 0.20 | 1.15 ± 0.21 | 1.11 ± 0.19 | 0.617 | 0.035 | |
| [1.18; 1.10] | [1.21; 1.08] | [1.17; 1.05] |
| Variables | Breathing Cycle | Non-Breathing Cycle | Breathing Cycle Following a Non-Breathing Cycle | F | ŋ2 | ||
|---|---|---|---|---|---|---|---|
| Mean ± SD [95%Cl] | Mean ± SD [95%Cl] | Mean ± SD [95%Cl] | |||||
| Hand | Max | X | 1.39 ± 0.47 | 1.47 ± 0.26 | 1.38 ± 0.2 | 3.039 | 0.152 |
| [1.49; 1.29] | [1.54; 1.39] | [1.44; 1.31] | |||||
| Y | 2.54 ± 0.84 | 2.61 ± 0.61 | 2.54 ± 0.61 | 1.847 | 0.098 | ||
| [2.71; 2.36] | [2.79; 2.43] | [2.74; 2.34] | |||||
| Z | 1.64 ± 0.61 | 1.65 ± 0.47 | 1.7 ± 0.43 | 0.783 | 0.044 | ||
| [1.77; 1.52] | [1.79; 1.51] | [1.84; 1.56] | |||||
| Mean | X | −0.01 ± 0.03 | −0.01 ± 0.03 | 0 ± 0.02 | 0.861 | 0.048 | |
| [−0.01; −0.02] | [0; −0.02] | [0; −0.01] | |||||
| Y | 0.93 ± 0.14 | 0.95 ± 0.13 | 0.93 ± 0.12 | 1.263 | 0.069 | ||
| [0.96; 0.90] | [0.98; 0.91] | [0.97; 0.89] | |||||
| Z | 0 ± 0.04 | 0 ± 0.04 | 0 ± 0.04 | 0.058 | 0.003 | ||
| [0.01; −0.01] | [0.01; −0.02] | [0.01; −0.01] | |||||
| Min | X | −1.92; 0.34 | −1.99; 0.36 | −1.88; 0.31 | 2.973 | 0.149 | |
| [−1.85; −1.99] | [−1.88; −2.09] | [−1.78; −1.98] | |||||
| Y | −0.85 ± 0.25 | −0.96 ± 0.27 | −0.95 ± 0.23 | 0.698 | 0.039 | ||
| [−0.80; −0.90] | [−0.88; −1.04] | [−0.88; −1.03] | |||||
| Z | −1.25 ± 0.25 | −1.26 ± 0.25 | −1.22 ± 0.16 | 0.928 | 0.052 | ||
| [−1.2; −1.31] | [−1.19; −1.33] | [−1.17; −1.27] | |||||
| Feet | Max | X | 1.26 ± 0.25 | 1.36 ± 0.25 | 1.34 ± 0.21 | 0.612 | 0.035 |
| [1.31; 1.21] | [1.43; 1.28] | [1.41; 1.27] | |||||
| Y | 2.32 ± 0.29 | 2.36 ± 0.26 | 2.32 ± 0.26 | 3.772 | 0.180 | ||
| [2.38; 2.26] | [2.44; 2.28] | [2.41; 2.24] | |||||
| Z | 0.77 ± 0.27 b | 0.98 ± 0.35 a,c | 0.81 ± 0.29 b | 4.482 | 0.209 | ||
| [0.82; 0.71] | [1.08; 0.88] | [0.91; 0.72] | |||||
| Mean | X | −0.01 ± 0.1 | −0.01 ± 0.1 | 0.01 ± 0.07 | 1.127 | 0.062 | |
| [0.01; −0.03] | [0.02; −0.04] | [0.03; −0.01] | |||||
| Y | 1.01 ± 0.20 | 0.98 ± 0.20 | 0.94 ± 0.18 | 3.046 | 0.152 | ||
| [1.05; 0.97] | [1.04; 0.92] | [1.00; 0.88] | |||||
| Z | 0.04 ± 0.1 | 0.03 ± 0.09 c | −0.01 ± 0.07 b | 5.496 | 0.244 | ||
| [0.06; 0.02] | [0.06; 0.01] | [0.01; −0.04] | |||||
| Min | X | −1.46 ± 0.33 | −1.57 ± 0.39 | −1.5 ± 0.28 | 0.934 | 0.052 | |
| [−1.4; −1.53] | [−1.46; −1.68] | [−1.41; −1.59] | |||||
| Y | −1.54 ± 0.61 | −1.76 ± 0.53 | −1.75 ± 0.54 | 1.696 | 0.091 | ||
| [−1.41; −1.66] | [−1.6; −1.91] | [−1.58; −1.93] | |||||
| Z | −1.64 ± 0.47 | −1.85 ± 0.54 | −1.82 ± 0.38 | 3.613 | 0.175 | ||
| [−1.54; −1.73] | [−1.7; −2.01] | [−1.69; −1.95] | |||||
| Head | Max | X | 0.12 ± 0.07 | 0.12 ± 0.08 | 0.13 ± 0.08 | 0.612 | 0.035 |
| [0.13; 0.1] | [0.15; 0.1] | [0.15; 0.1] | |||||
| Y | 1.27 ± 0.23 | 1.30 ± 0.17 | 1.31 ± 0.23 | 0.284 | 0.016 | ||
| [1.32; 1.23] | [1.35; 1.25] | [1.38; 1.23] | |||||
| Z | 1.17; 0.26 | 1.01; 0.3 c | 1.20 ± 0.25 b | 3.830 | 0.184 | ||
| [1.22; 1.12] | [1.1; 0.92] | [1.28; 1.12] | |||||
| Mean | X | 0.02 ± 0.03 b | 0.02 ± 0.04 a | 0.02 ± 0.04 | 3.726 | 0.180 | |
| [0.02; 0.01] | [0.03; 0.01] | [0.03; 0.01] | |||||
| Y | 0.94 ± 0.14 | 0.97 ± 0.13 c | 0.93 ± 0.13b | 4.101 | 0.194 | ||
| [0.97; 0.91] | [1.00; 0.93] | [0.97; 0.88] | |||||
| Z | 0.02 ± 0.06 | −0.01 ± 0.09 | 0.02 ± 0.07 | 1.166 | 0.064 | ||
| [0.03; 0] | [0.01; −0.04] | [0.04; 0] | |||||
| Min | X | −0.07 ± 0.06 | −0.08 ± 0.05 | −0.08 ± 0.04 | 3.083 | 0.154 | |
| [−0.06; −0.09] | [−0.07; −0.1] | [−0.07; −0.09] | |||||
| Y | 0.58 ± 0.13 | 0.53 ± 0.17 | 0.53 ± 0.16 | 1.615 | 0.087 | ||
| [0.6; 0.55] | [0.58; 0.48] | [0.59; 0.48] | |||||
| Z | −1.25 ± 0.39 | −1.06 ± 0.37 c | −1.32 ± 0.33 b | 3.507 | 0.171 | ||
| [−1.17; −1.33] | [−0.96; −1.17] | [−1.22; −1.43] | |||||
| CoM | Max | X | 0.06 ± 0.04 | 0.07 ± 0.04 | 0.07 ± 0.04 | 1.290 | 0.071 |
| [0.07; 0.05] | [0.08; 0.05] | [0.08; 0.05] | |||||
| Y | 1.24 ± 0.17 b | 1.30 ± 0.18 a,c | 1.24 ± 0.16 b | 7.180 | 0.297 | ||
| [1.27; 1.21] | [1.35; 1.25] | [1.29; 1.18] | |||||
| Z | 0.30 ± 0.06 | 0.32 ± 0.07 | 0.32 ± 0.07 | 3.090 | 0.154 | ||
| [0.31; 0.29] | [0.34; 0.29] | [0.34; 0.3] | |||||
| Mean | X | 0.01 ± 0.04 | 0.01 ± 0.03 | 0.02 ± 0.04 | 3.124 | 0.155 | |
| [0.02; 0.01] | [0.02; 0.01] | [0.03; 0.01] | |||||
| Y | 0.94 ± 0.14 | 0.96 ± 0.13 | 0.93 ± 0.13 | 2.459 | 0.126 | ||
| [0.97; 0.91] | [1.00; 0.92] | [0.97; 0.89] | |||||
| Z | −0.01 ± 0.07 | 0 ± 0.03 | 0 ± 0.02 | 0.570 | 0.032 | ||
| [0.01; −0.02] | [0; −0.01] | [0; −0.01] | |||||
| Min | X | −0.02 ± 0.04 b,c | −0.04 ± 0.04 a | −0.04 ± 0.04 a | 6.094 | 0.264 | |
| [−0.02; −0.03] | [−0.02; −0.05] | [−0.02; −0.05] | |||||
| Y | 0.51 ± 0.12 | 0.50 ± 0.14 | 0.49 ± 0.13 | 0.884 | 0.049 | ||
| [0.54; 0.48] | [0.54; 0.46] | [0.54; 0.45] | |||||
| Z | −0.36 ± 0.07 c | −0.38 ± 0.09 | −0.43 ± 0.11 a | 5.931 | 0.259 | ||
| [−0.35; −0.38] | [−0.35; −0.4] | [−0.39; −0.46] | |||||
| Variables | Breathing Cycle | Non-Breathing Cycle | Breathing Cycle Following a Non-Breathing Cycle | F | ŋ2 |
|---|---|---|---|---|---|
| Mean ± SD [95%Cl] | Mean ± SD [95%Cl] | Mean ± SD [95%Cl] | |||
| Hip angle (°) | 49.80 ± 8.70 | 50.90 ± 7.60 | 50.80 ± 7.50 | 0.852 | 0.048 |
| [51.60; 48.00] | [53.10; 48.70] | [53.30; 48.40] | |||
| Knee angle (°) | 137.00 ± 10.10 | 141.00 ± 11.90 | 141.10 ± 10.2 | 0.532 | 0.030 |
| [139.00; 134.90] | [144.50; 137.50] | [144.50; 137.80] | |||
| Thorax angle (°) | 44.10 ± 9.70 | 45.00 ± 13.30 | 47.10 ± 11.5 | 1.195 | 0.066 |
| [46.10; 42.10] | [48.90; 41.20] | [50.90; 43.30] |
| Variables | Breathing Cycle | Non-Breathing Cycle | Breathing Cycle Following a Non-Breathing Cycle | F | ŋ2 |
|---|---|---|---|---|---|
| Mean ± SD [95%Cl] | Mean ± SD [95%Cl] | Mean ± SD [95%Cl] | |||
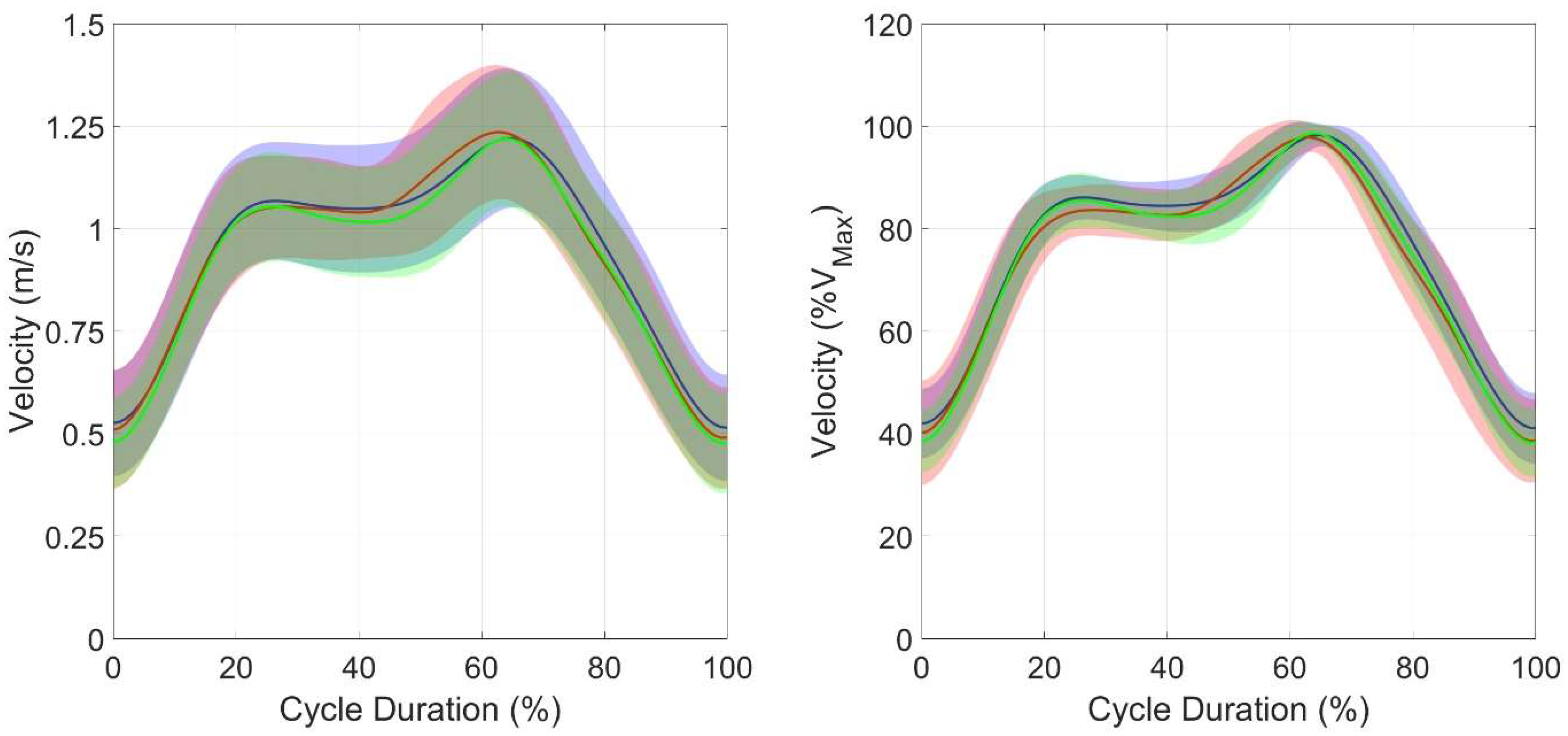
| dv (%) | 4.43 ± 6.77 | 3.74 ± 4.38 | 4.45 ± 5.51 | 0.275 | 0.052 |
| [7.86; 1.01] | [5.96; 1.53] | [7.57; 1.34] | |||
| Fractal dimension | 1.269 ± 0.095 | 1.291 ± 0.095 | 1.313 ± 0.079 | 0.891 | 0.050 |
| [1.288; 1.249] | [1.319; 1.264] | [1.339; 1.287] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Alves, M.; Fonseca, P.; Fernandes, A.; Brito, A.V.; Barbosa, T.M.; Vilas-Boas, J.P. Analyzing Breathing Patterns in the Breaststroke Technique Through Dual-Media Kinematics and Fractal Dimension. Sensors 2025, 25, 3104. https://doi.org/10.3390/s25103104
Alves M, Fonseca P, Fernandes A, Brito AV, Barbosa TM, Vilas-Boas JP. Analyzing Breathing Patterns in the Breaststroke Technique Through Dual-Media Kinematics and Fractal Dimension. Sensors. 2025; 25(10):3104. https://doi.org/10.3390/s25103104
Chicago/Turabian StyleAlves, Miriam, Pedro Fonseca, Aléxia Fernandes, André V. Brito, Tiago M. Barbosa, and João Paulo Vilas-Boas. 2025. "Analyzing Breathing Patterns in the Breaststroke Technique Through Dual-Media Kinematics and Fractal Dimension" Sensors 25, no. 10: 3104. https://doi.org/10.3390/s25103104
APA StyleAlves, M., Fonseca, P., Fernandes, A., Brito, A. V., Barbosa, T. M., & Vilas-Boas, J. P. (2025). Analyzing Breathing Patterns in the Breaststroke Technique Through Dual-Media Kinematics and Fractal Dimension. Sensors, 25(10), 3104. https://doi.org/10.3390/s25103104







