Design and Realization of a High-Q Grounded Tunable Active Inductor for 5G NR (FR1) Transceiver Front-End Applications
Abstract
1. Introduction
- −
- −
- Current differencing transconductance amplifiers (CDTAs) [10];
- −
- −
- Differential voltage current conveyors (DVCCs) [13];
- −
- Differential current conveyors (DCCIIs) [14];
- −
- Fully differential current conveyors (FDCCIIs) [15];
- −
- Second-generation current conveyors (CCIIs) [16];
- −
- Third-generation current conveyors (CCIIIs) [17];
- −
- −
- Four-terminal floating nullors (FTFNs) [21];
- −
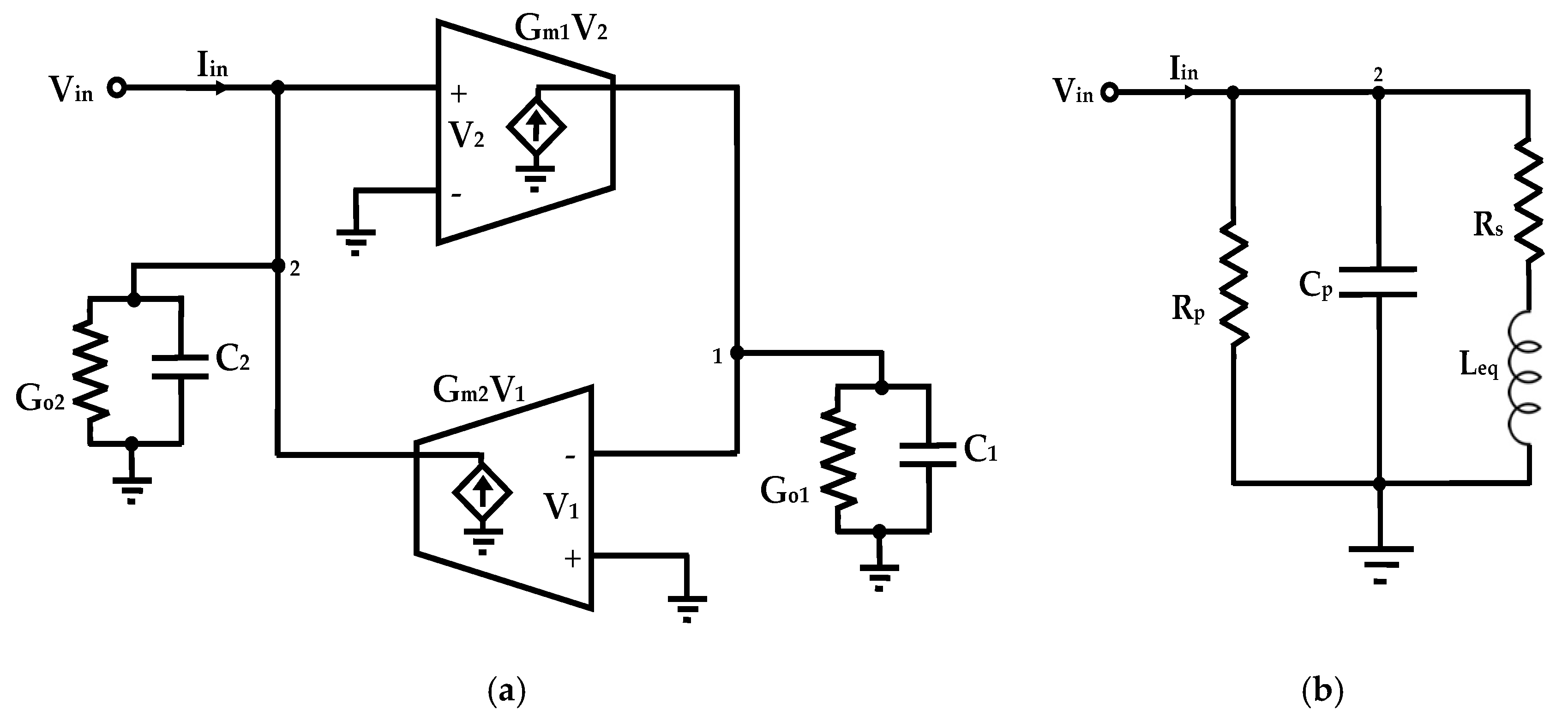
2. Grounded Gyrator-C-Based Tunable Active Inductor
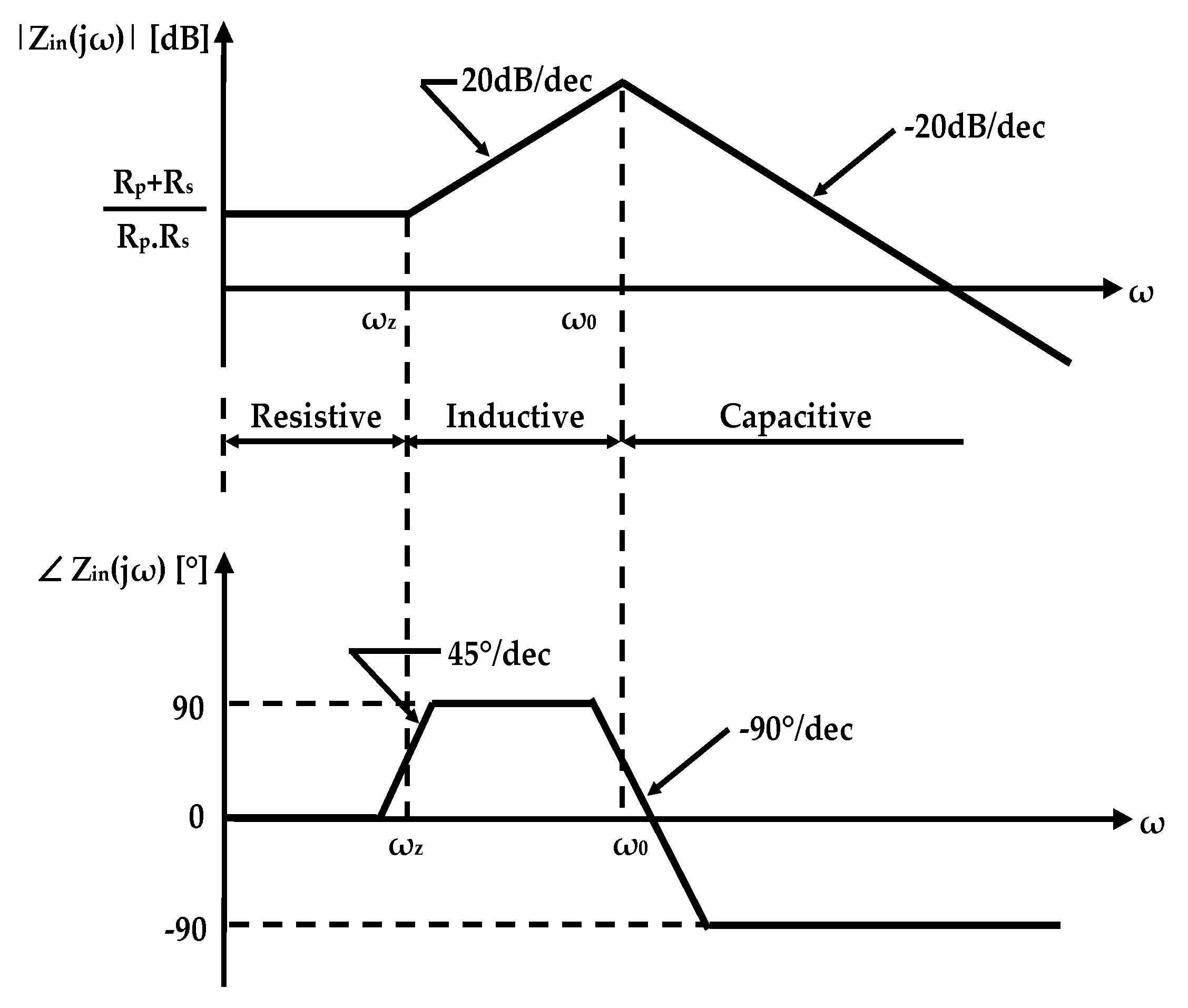
2.1. Basic Concept
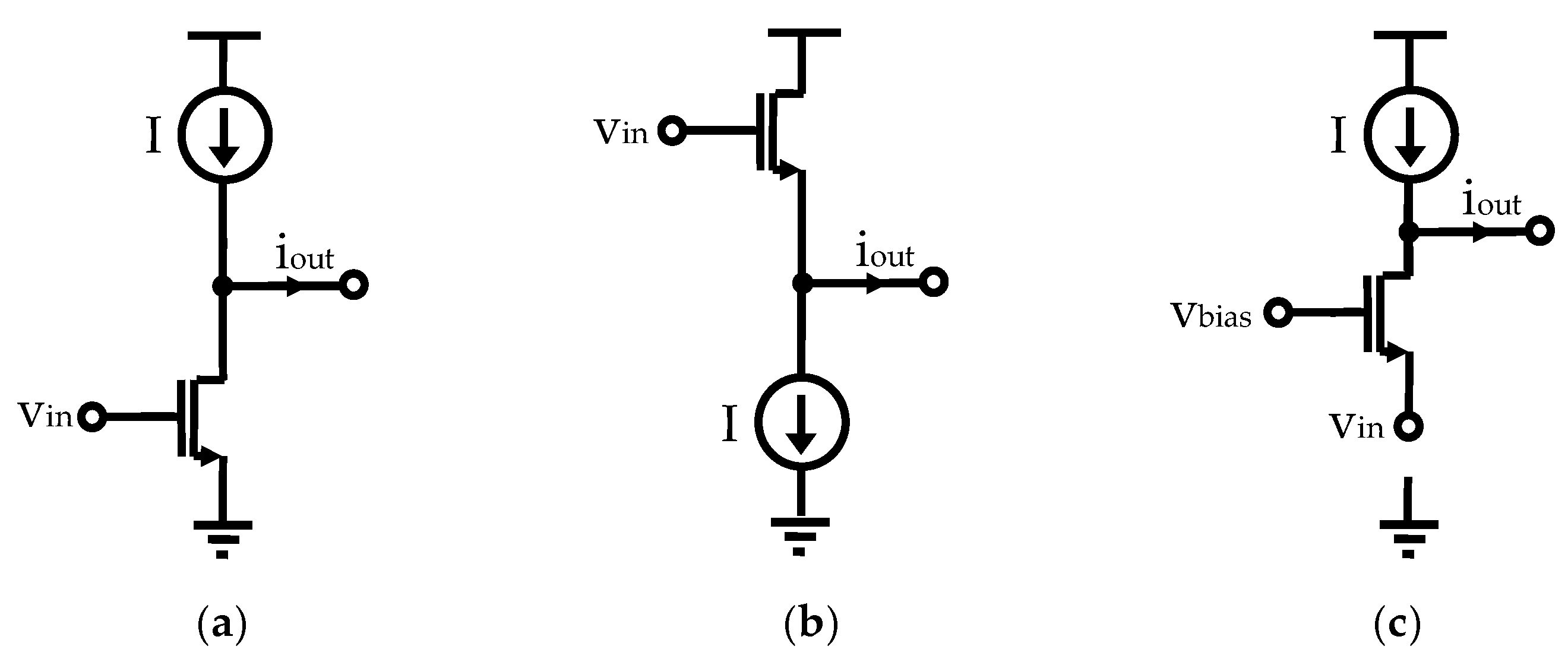
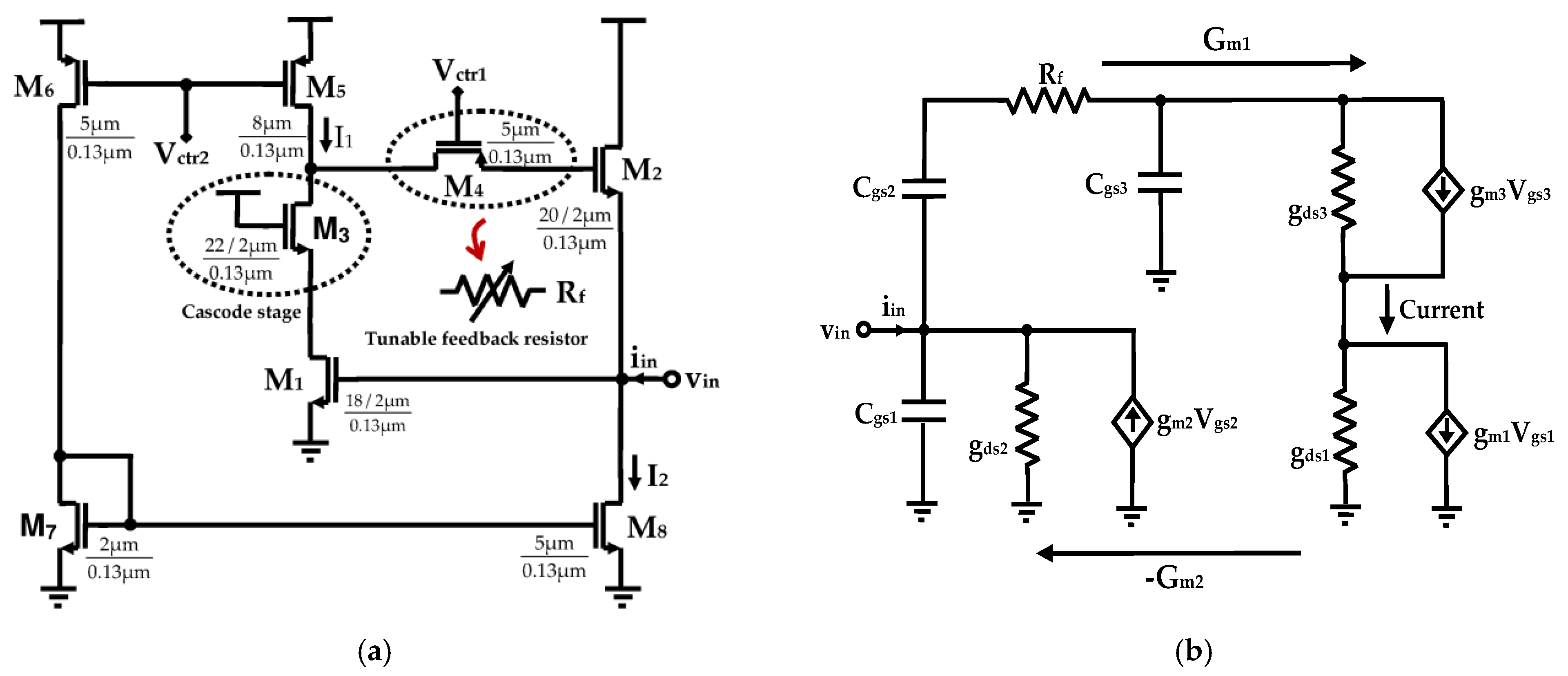
2.2. Proposed Grounded Tunable Active Inductor
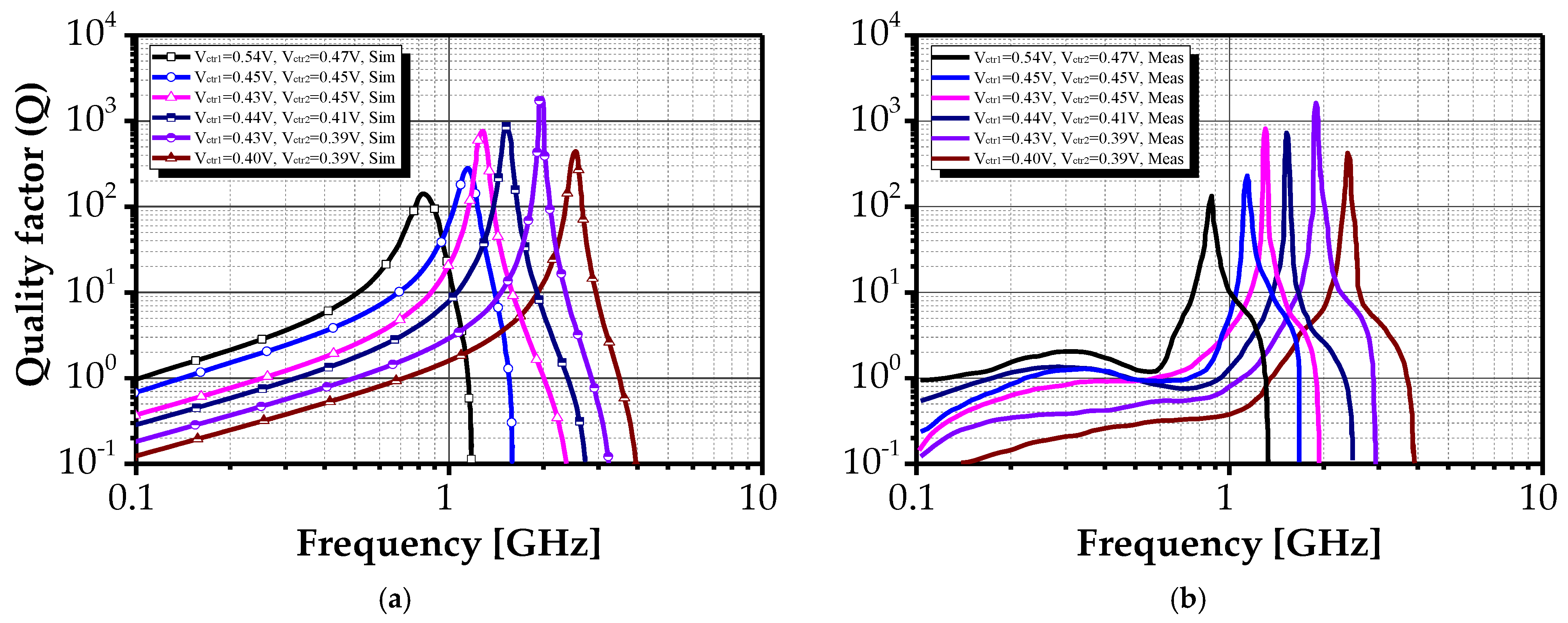
3. Experimental Results
4. Conclusions and Future Works
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| RF | Radio frequency |
| CMOS | Complementary metal-oxide semiconductor |
| AI | Active inductor |
| GSG | Ground–signal–ground |
| SRF | Self-resonant frequency |
| NR | New Radio |
| FR1 | Frequency Range 1 |
| 5G | Fifth generation |
| FDD | Frequency Division Duplex |
| TDD | Time Division Duplex |
| LNA | Low-noise amplifier |
| VCO | Voltage-controlled oscillator |
| NIC | Negative impedance converter |
| FinFET | Fin field-effect transistor |
| SOI | Silicon-on-insulator |
| GaN | Gallium nitride |
| KCL | Kirchhoff’s Current Law |
| CD | Common drain |
| CG | Common gate |
| CS | Common source |
| TAI | Tunable active inductor |
| DC | Direct current |
| VNA | Vector network analyzer |
| PVT | Process–voltage–temperature |
| 4G | Fourth generation |
| ISM | Industrial, scientific, and medical |
References
- Holma, H.; Toskala, A.; Nakamura, T. 5G Technology: 3GPP New Radio, 1st ed.; John Wiley & Sons: Hoboken, NJ, USA, 2020. [Google Scholar]
- Kim, Y.; Kim, Y.; Oh, J.; Ji, H.; Yeo, J.; Choi, S.; Ryu, H.; Noh, H.; Kim, T.; Sun, F.; et al. New radio (NR) and its evolution toward 5G-advanced. IEEE Wirel. Commun. 2019, 26, 2–7. [Google Scholar] [CrossRef]
- Lin, X.; Li, J.; Baldemair, R.; Cheng, J.F.T.; Parkvall, S.; Larsson, D.C.; Koorapaty, H.; Frenne, M.; Falahati, S.; Grovlen, A.; et al. 5G new radio: Unveiling the essentials of the next generation wireless access technology. IEEE Commun. Stand. Mag. 2019, 3, 30–37. [Google Scholar] [CrossRef]
- Ahmadi, S. 5G NR: Architecture, Technology, Implementation, and Operation of 3GPP New Radio Standards, 1st ed.; Academic Press: Cambridge, MA, USA, 2019. [Google Scholar]
- Chen, J.; Liou, J.J. On-chip spiral inductors for RF applications: An overview. J. Semicond. Technol. Sci. 2004, 4, 149–167. [Google Scholar]
- Yuce, E.; Minaei, S. Other Active Devices. In Passive and Active Circuits by Example, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2024. [Google Scholar]
- Yuce, E.; Minaei, S. A modified CFOA and its applications to simulated inductors, capacitance multipliers, and analog filters. IEEE Trans. Circuits Syst. I Regul. Pap. 2008, 55, 266–275. [Google Scholar] [CrossRef]
- Dogan, M.; Yuce, E. CFOA based a new grounded inductor simulator and its applications. Microelectron. J. 2019, 90, 297–305. [Google Scholar] [CrossRef]
- Kacar, F.; Kuntman, H. CFOA-based lossless and lossy inductance simulators. Radioengineering 2011, 20, 627–631. [Google Scholar]
- Bang, J.; Ryu, I.H. Design of A 10MHz Bandpass Filter Using Grounding and Floating CDTA Active Inductors. J. Korea Acad.-Ind. Coop. Soc. 2014, 15, 6804–6809. [Google Scholar]
- Jaikla, W.; Biolek, D.; Siripongdee, S.; Bajer, J. High input impedance voltage-mode biquad filter using VD-DIBAs. Radioengineering 2014, 23, 914–921. [Google Scholar]
- Jaikla, W.; Bunrueangsak, S.; Khateb, F.; Kulej, T.; Suwanjan, P.; Supavarasuwat, P. Inductance simulators and their application to the 4th order elliptic lowpass ladder filter using CMOS VD-DIBAs. Electronics 2021, 10, 684. [Google Scholar] [CrossRef]
- Singh, Y.S.; Ranjan, A.; Adhikari, S.; Shimray, B.A. A lossless active inductor design using single ZC-VDCC: Grounded and floating mode. IETE J. Res. 2024, 70, 623–637. [Google Scholar] [CrossRef]
- Metin, B.; Herencsar, N.; Koton, J.; Horng, J.W. DCCII-based novel lossless grounded inductance simulators with no element matching constrains. Radioengineering 2014, 23, 532–539. [Google Scholar]
- Gür, F.; Anday, F. Simulation of a novel current-mode universal filter using FDCCIIs. Analog Integr. Circuits Signal Process. 2009, 60, 231–236. [Google Scholar] [CrossRef]
- Ferri, G.; Guerrini, N.; Silverii, E.; Tatone, A. Vibration damping using CCII-based inductance simulators. IEEE Trans. Instrum. Meas. 2008, 57, 907–914. [Google Scholar] [CrossRef]
- Senani, R.; Bhaskar, D.R.; Singh, A.K. Current Conveyors: Variants, Applications and Hardware Implementations, 1st ed.; Springer: Berlin/Heidelberg, Germany, 2014. [Google Scholar]
- Ibrahim, M.A.; Minaei, S.; Yuce, E.; Herencsar, N.; Koton, J. Lossy/Lossless Floating/Grounded Inductance Simulation Using One DDCC. Radioengineering 2012, 21, 3–10. [Google Scholar]
- Abaci, A.; Yuce, E. Single DDCC− based simulated floating inductors and their applications. IET Circuits Devices Syst. 2020, 14, 796–804. [Google Scholar] [CrossRef]
- Kumari, S.; Nand, D. Realization of nth Order Wave Active Low-Pass Filter Using Differential Difference Current Conveyor. J. Circuits Syst. Comput. 2024, 33, 2450180. [Google Scholar] [CrossRef]
- Tarunkumar, H.; Shantikumar Singh, Y.; Ranjan, A. An active inductor employing a new four terminal floating nullor transconductance amplifier (FTFNTA). Int. J. Electron. 2020, 107, 683–702. [Google Scholar] [CrossRef]
- Rani, M.; Kaur, P.A. Review of Active Inductors based on the Gyrator-C Principle. In Latest Trends in Engineering and Technology, 1st ed.; CRC Press: London, UK, 2024; pp. 205–213. [Google Scholar]
- Yuan, F. CMOS Active Inductors and Transformers: Principle, Implementation and Applications, 1st ed.; Springer: New York, NY, USA, 2008. [Google Scholar]
- Yücehan, T.; Yüce, E. A Lossless Simulated Floating Inductor Based on the Second-Generation Current Conveyors. Electrica 2025, 25, 1–13. [Google Scholar]
- Hsiao, C.C.; Kuo, C.W.; Ho, C.C.; Chan, Y.J. Improved quality-factor of 0.18-μm CMOS active inductor by a feedback resistance design. IEEE Microw. Wirel. Compon. Lett. 2002, 12, 467–469. [Google Scholar] [CrossRef]
- Yuce, E.; Alpaslan, H.; Minaei, S.; Ayten, U.E. A new simulated grounded inductor based on two NICs, two resistors and a grounded capacitor. Circuits Syst. Signal Process. 2021, 40, 5847–5863. [Google Scholar] [CrossRef]
- Behera, P.; Siddique, A.; Delwar, T.S.; Biswal, M.R.; Choi, Y.; Ryu, J.Y. A novel 65 nm active-inductor-based VCO with improved Q-factor for 24 GHz automotive radar applications. Sensors 2022, 22, 4701. [Google Scholar] [CrossRef] [PubMed]
- Gorjizad, Z.; Shojaee, A.; Abrishamifar, A. A compact and tunable active inductor-based bandpass filter with high quality factor for Wireless LAN applications. AEU—Int. J. Electron. Commun. 2024, 187, 155540. [Google Scholar] [CrossRef]
- Demirel, H.; Ahmed, A. New FinFet Transistor Implementation of Floating and Grounded Inductance Simulator Based on Active Elements. Gazi Mühendislik Bilimleri Dergisi 2024, 9, 647–653. [Google Scholar] [CrossRef]
- Yang, R.; Li, J.; Qian, H.; Han, Z. SOI active and passive integrated devices for RFIC applications. In Proceedings of the 7th International Conference on Solid-State and Integrated Circuits Technology, Beijing, China, 18–21 October 2004; Volume 1, pp. 186–189. [Google Scholar]
- Herbert, T.B.; Hyland, J.S.; Abdullah, S.; Wight, J.; Amaya, R.E. An active bandpass filter for LTE/WLAN applications using robust active inductors in gallium nitride. IEEE Trans. Circuits Syst. II Express Briefs 2021, 68, 2252–2256. [Google Scholar] [CrossRef]
- Ismail, M.; Wassenaar, R.; Morrison, W. A high-speed continuous-time bandpass VHF filter in MOS technology. In Proceedings of the 1991 IEEE International Symposium on Circuits and Systems (ISCAS), Singapore, 11–14 June 1991; pp. 1761–1764. [Google Scholar]
- Ler, C.L.; A’ain, A.K.B.; Kordesch, A.V. CMOS active inductor linearity improvement using feed-forward current source technique. IEEE Trans. Microw. Theory Tech. 2009, 57, 1915–1924. [Google Scholar] [CrossRef]
- Mukhopadhyay, R.; Park, Y.; Sen, P.; Srirattana, N.; Lee, J.; Lee, C.H.; Nuttinck, S.; Joseph, A.; Cressler, J.; Laskar, J. Reconfigurable RFICs in Si-based technologies for a compact intelligent RF front-end. IEEE Trans. Microw. Theory Tech. 2005, 53, 81–93. [Google Scholar] [CrossRef]
- Zaiden, D.M.; Grandfield, J.E.; Weller, T.M.; Mumcu, G. Compact and wideband MMIC phase shifters using tunable active inductor-loaded all-pass networks. IEEE Trans. Microw. Theory Tech. 2017, 66, 1047–1057. [Google Scholar] [CrossRef]
- Hwang, K.S.; Cho, C.S.; Lee, J.W.; Kim, J. High quality-factor and inductance of symmetric differential-pair structure active inductor using a feedback resistance design. In Proceedings of the IEEE MTT-S International Microwave Symposium Digest, Atlanta, GA, USA, 15–20 June 2008; pp. 1059–1062. [Google Scholar]
- Ghadiri, A.; Moez, K. Wideband active inductor and negative capacitance for broadband RF and microwave applications. IEEE Trans. Compon. Packag. Manuf. Technol. 2014, 4, 1808–1814. [Google Scholar] [CrossRef]
- Bhattacharya, R.; Basu, A.; Koul, S.K. A highly linear CMOS active inductor and its application in filters and power dividers. IEEE Microw. Wirel. Compon. Lett. 2015, 25, 715–717. [Google Scholar] [CrossRef]
- Pakasiri, C.; Hsu, K.C.; Wang, S. A Compact 0.73~3.1 GHz CMOS VCO Based on Active-Inductor and Active-Resistor Topology. J. Low Power Electron. Appl. 2024, 14, 18. [Google Scholar] [CrossRef]
- Saad, S.; Mhiri, M.; Hammadi, A.B.; Besbes, K. A new low-power, high-Q, wide tunable CMOS active inductor for RF applications. IETE J. Res. 2016, 62, 265–273. [Google Scholar] [CrossRef]
- Koo, J.; An, B.; Jeong, Y. Wideband CMOS high-Q 2-port active inductor using parallel LC resonance Circuit. In Proceedings of the Asia-Pacific Microwave Conference (APMC), New Delhi, India, 5–9 December 2016; pp. 1–4. [Google Scholar]

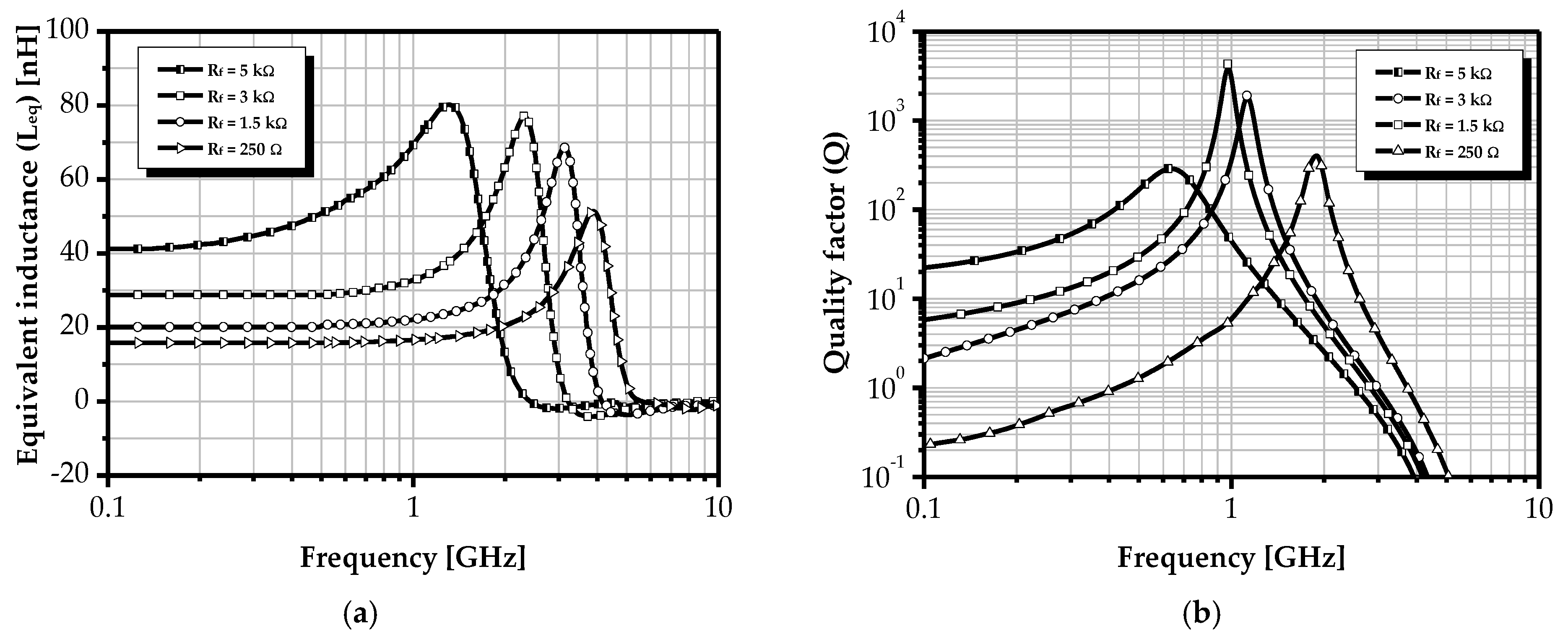


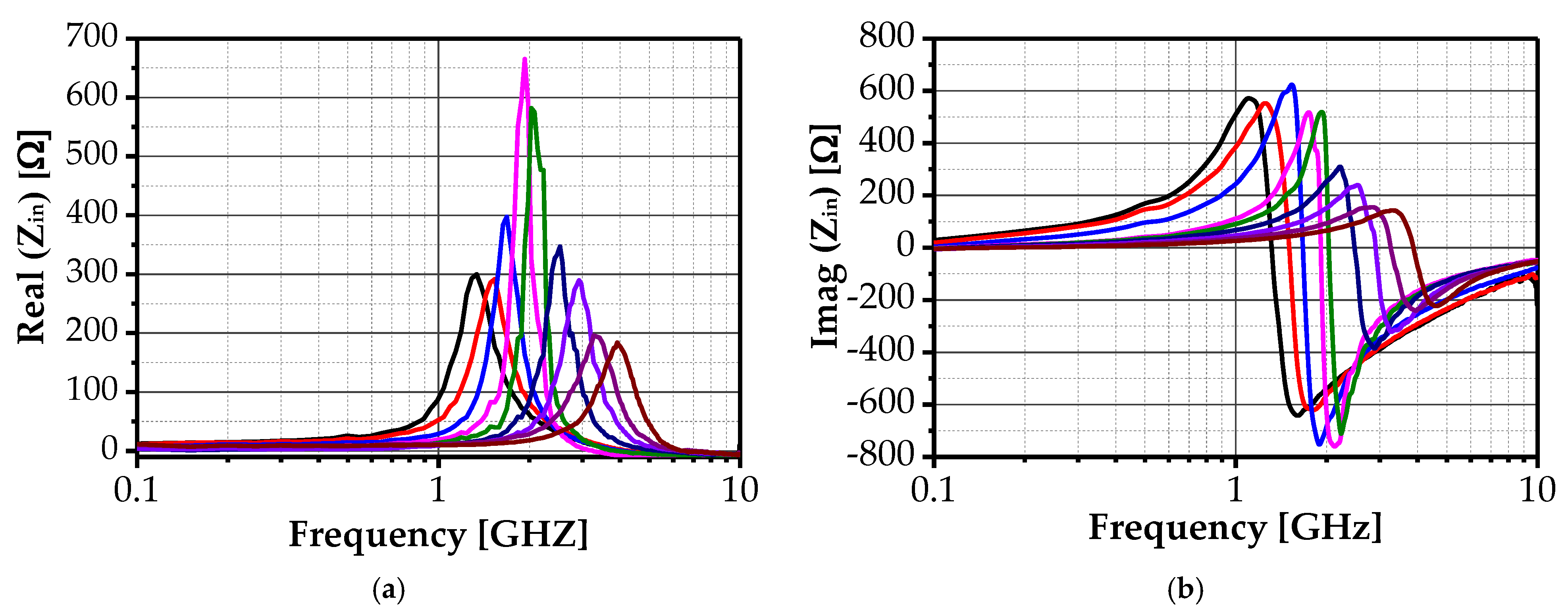
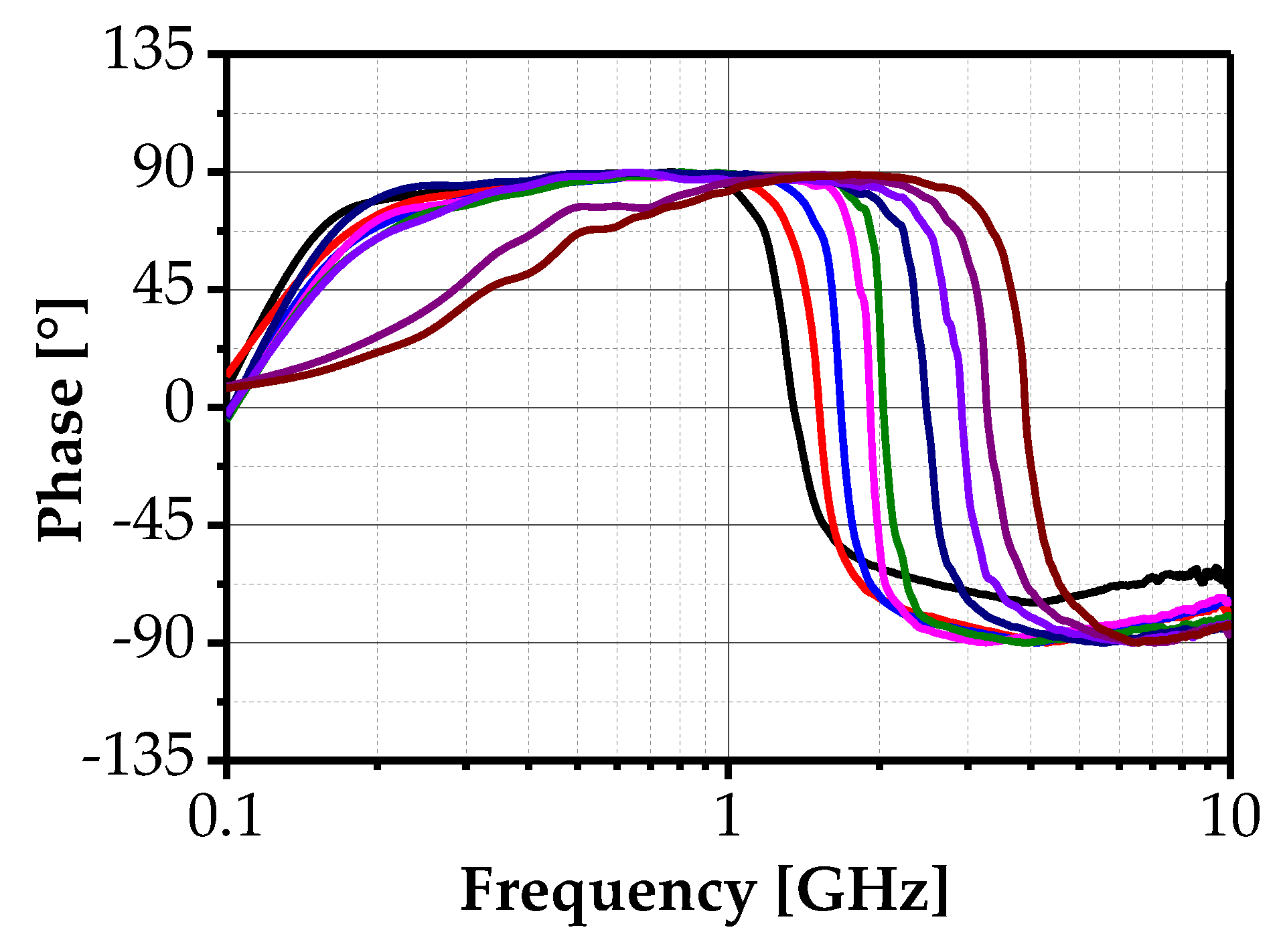
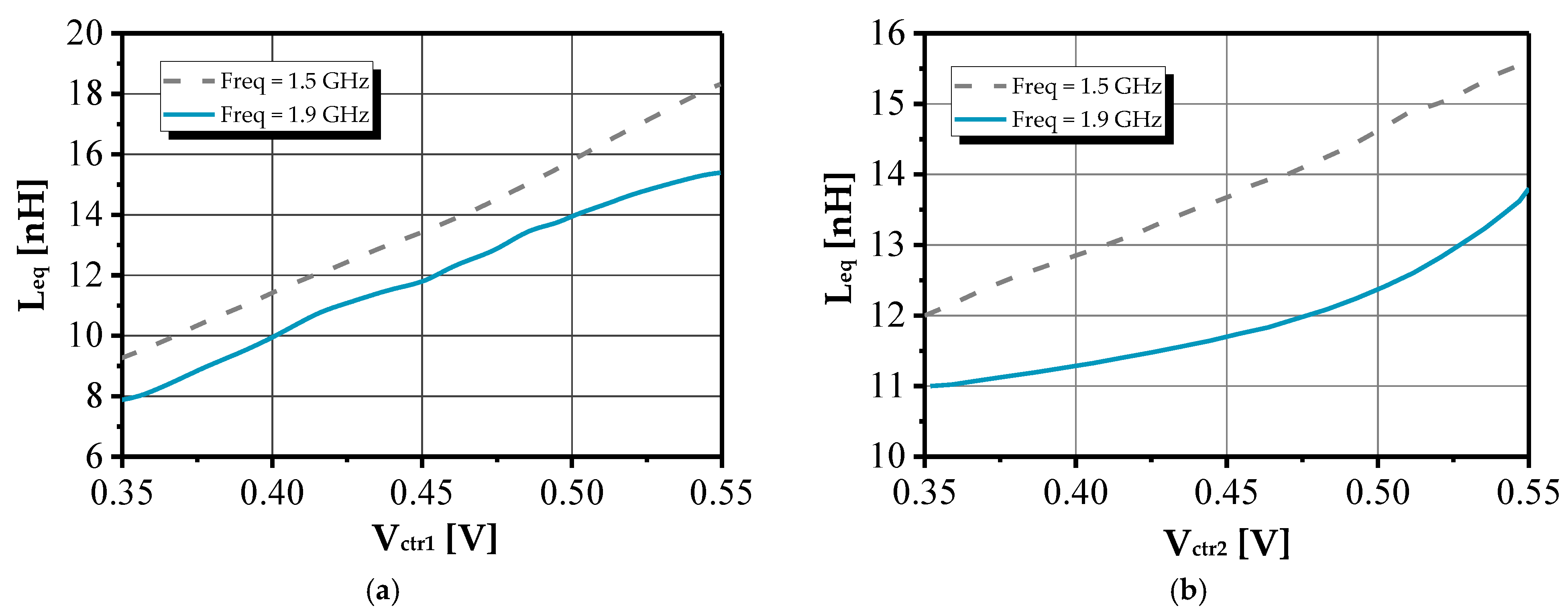

| gm | ωz | ω0 | Rs | Leq | Q |
| + | ↓ | ↑ | ↓↓ | ↓↓ | ↑↑ |
| − | ↑ | ↓ | ↑↑ | ↑↑ | ↓↓ |
| Rf | ωz | ω0 | Rs | Leq | Q |
| + | ↓↓ | ↑ | ↓ | ↓ | ↑↓ |
| − | ↑↑ | ↓ | ↑ | ↑ | ↓↑ |
| Ref. | Topology | Verification | Leq (nH) | Qmax | SRF (GHz) | PDC (mW) | Area (µm²) | CMOS Process (nm) | VDD (V) |
|---|---|---|---|---|---|---|---|---|---|
| [25] | Gyrator-C | Meas. | 5.7 | 70 | 2.5 | 8 | 88 × 90 + | 180 | 2.0 |
| [28] | Gyrator-C | Sim. | 191.7 | 286 | 4.81 | - | - | 65 | 1.2 |
| [36] | Gyrator-C | Meas. | 27 | 28 | 1.5 | 4 | 0.1 × 0.1 mm2 * | 180 | 1.8 |
| [37] | Gyrator-C | Meas. | 0.65–1 | 45 | >8 | 21 | 390 × 290 + | 130 | 1.5 |
| [38] | Gyrator-C | Meas. | 0.8–3.5 | 70 | 3.5 | 16 | 8800 + | 180 | 3.3 |
| [39] | Gyrator-C | Meas. | 2.5–5 | 740 | >6 | - | - | 180 | 1.6 |
| [40] | Gyrator-C | Sim. | 3.55–26 | 895 | 5.5 | 0.5 | 22 × 27.5 + | 90 | 1.0 |
| [41] | Gyrator-C | Meas. | 22 | 450 | 10 | 3.6 | 0.2 × 0.3 + | 65 | 1.2 |
| This work | Gyrator-C | Meas. | 6.7–84.4 | 1586 | 3.96 | 2 | 12.2 × 25.3 + | 130 | 1.0 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Saad, S.; Ben Hammadi, A.; Haddad, F. Design and Realization of a High-Q Grounded Tunable Active Inductor for 5G NR (FR1) Transceiver Front-End Applications. Sensors 2025, 25, 3070. https://doi.org/10.3390/s25103070
Saad S, Ben Hammadi A, Haddad F. Design and Realization of a High-Q Grounded Tunable Active Inductor for 5G NR (FR1) Transceiver Front-End Applications. Sensors. 2025; 25(10):3070. https://doi.org/10.3390/s25103070
Chicago/Turabian StyleSaad, Sehmi, Aymen Ben Hammadi, and Fayrouz Haddad. 2025. "Design and Realization of a High-Q Grounded Tunable Active Inductor for 5G NR (FR1) Transceiver Front-End Applications" Sensors 25, no. 10: 3070. https://doi.org/10.3390/s25103070
APA StyleSaad, S., Ben Hammadi, A., & Haddad, F. (2025). Design and Realization of a High-Q Grounded Tunable Active Inductor for 5G NR (FR1) Transceiver Front-End Applications. Sensors, 25(10), 3070. https://doi.org/10.3390/s25103070






