Laser Transmission Characteristics of Seawater for Underwater Wireless Optical Communication
Abstract
1. Introduction
2. Method
2.1. Monte Carlo Simulation
2.1.1. Photon Transmission Distance
2.1.2. Types of Photon Interactions
2.1.3. Photon Scattering Direction
2.2. Simulation Settings
3. Results and Discussion
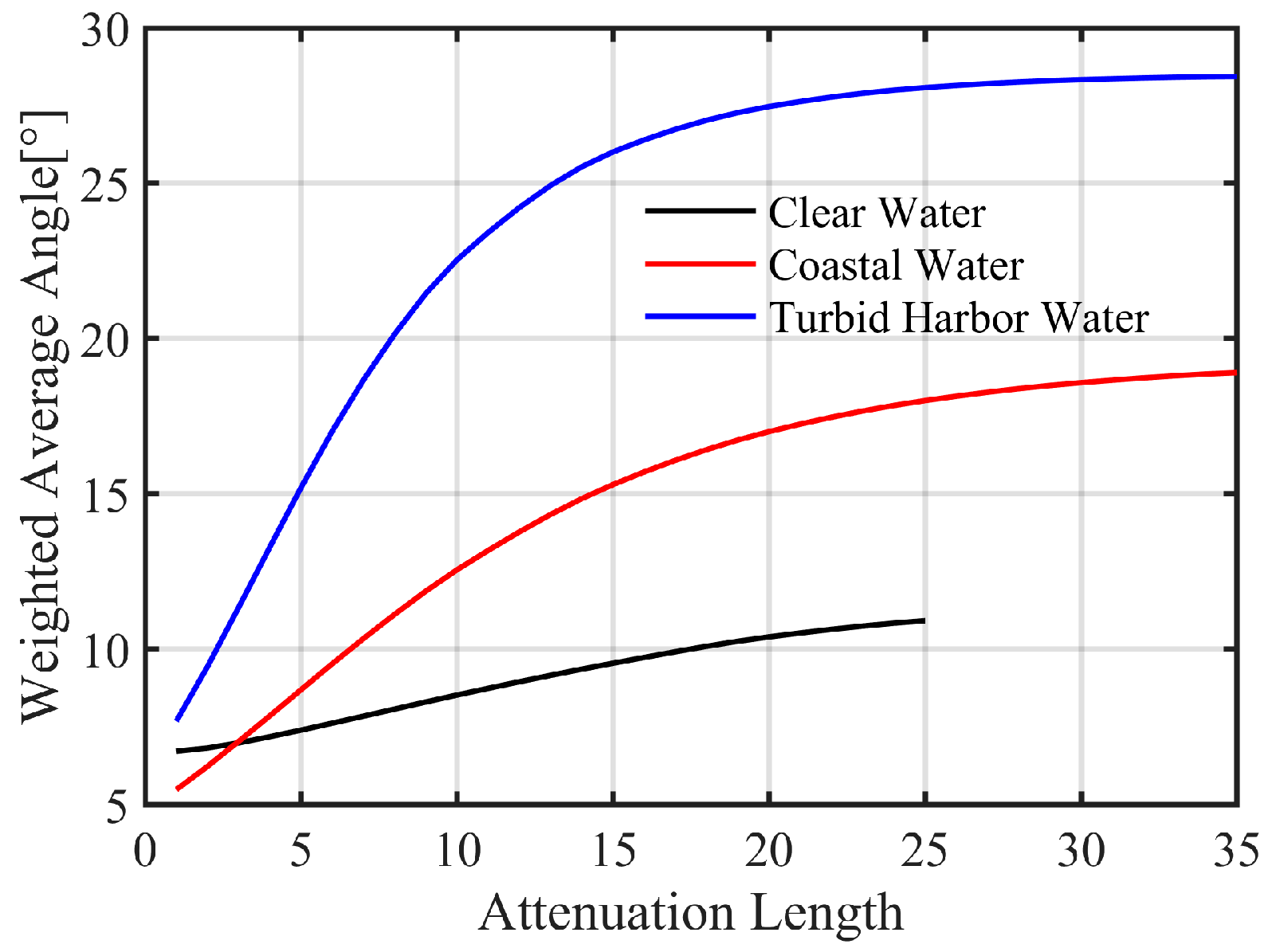
3.1. Average AOA
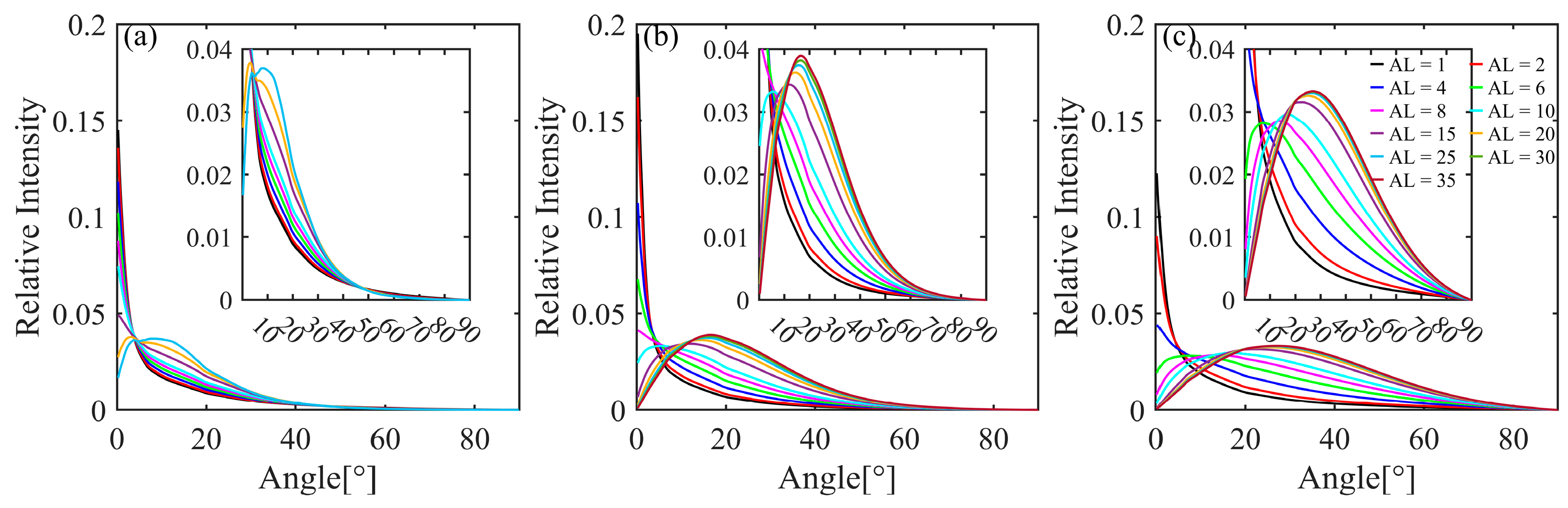
3.1.1. AOA Distribution on the Whole Receiving Plane
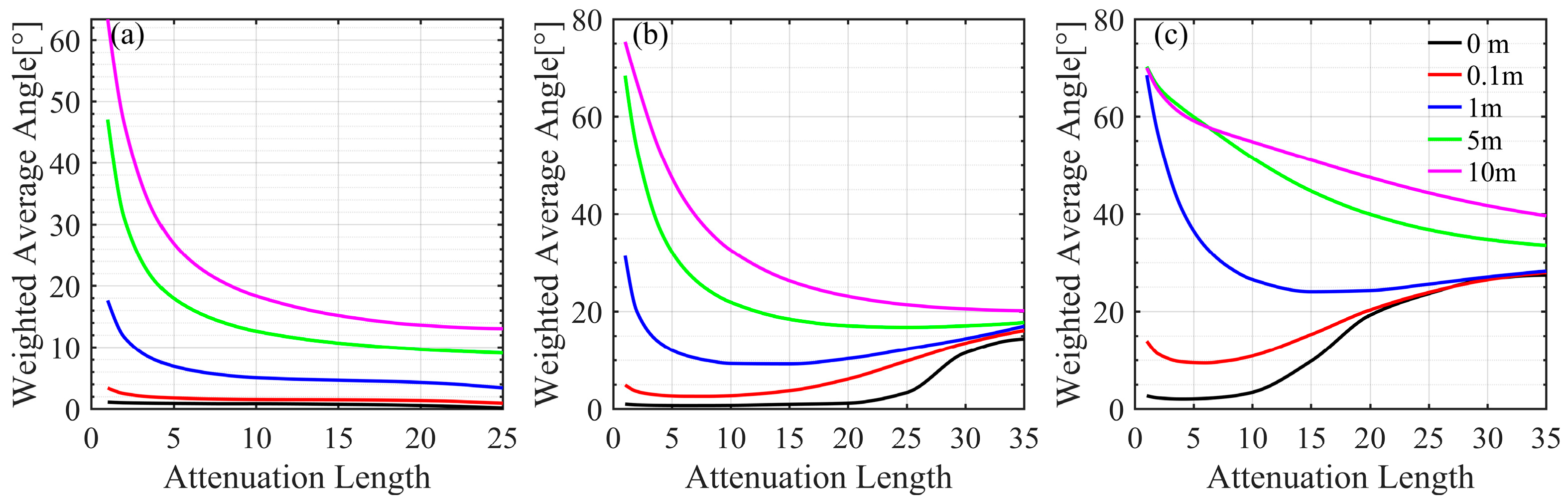
3.1.2. Average AOA at Different Offsets on the Receiving Plane
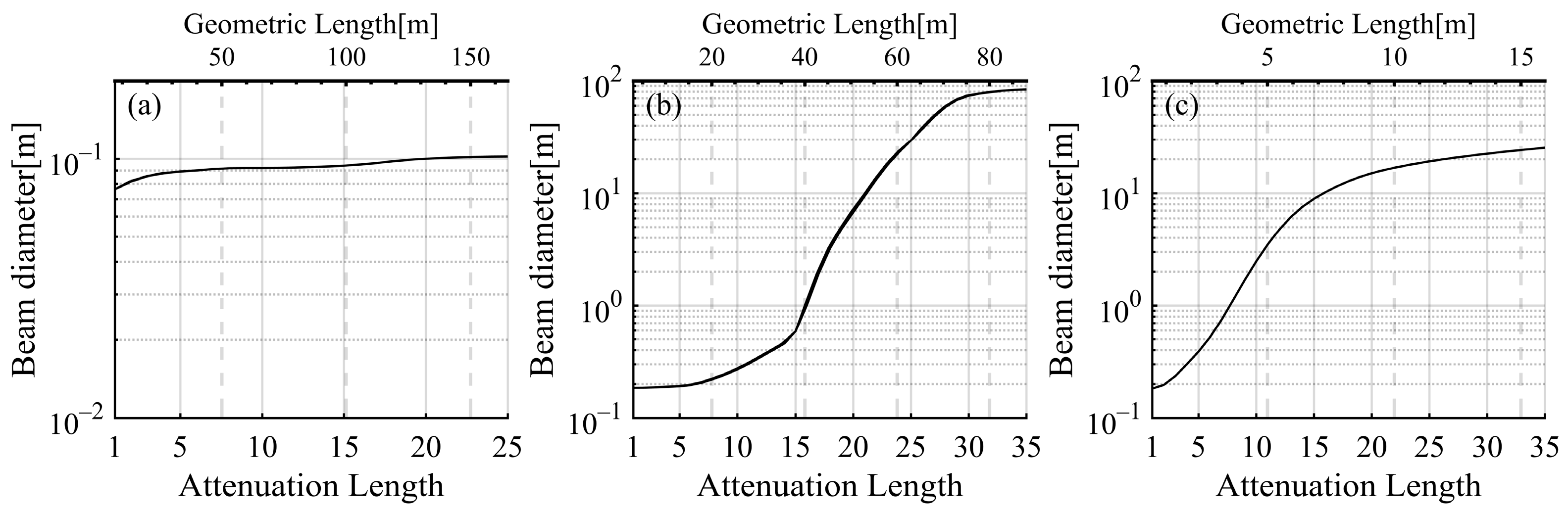
3.2. Beam Spreading
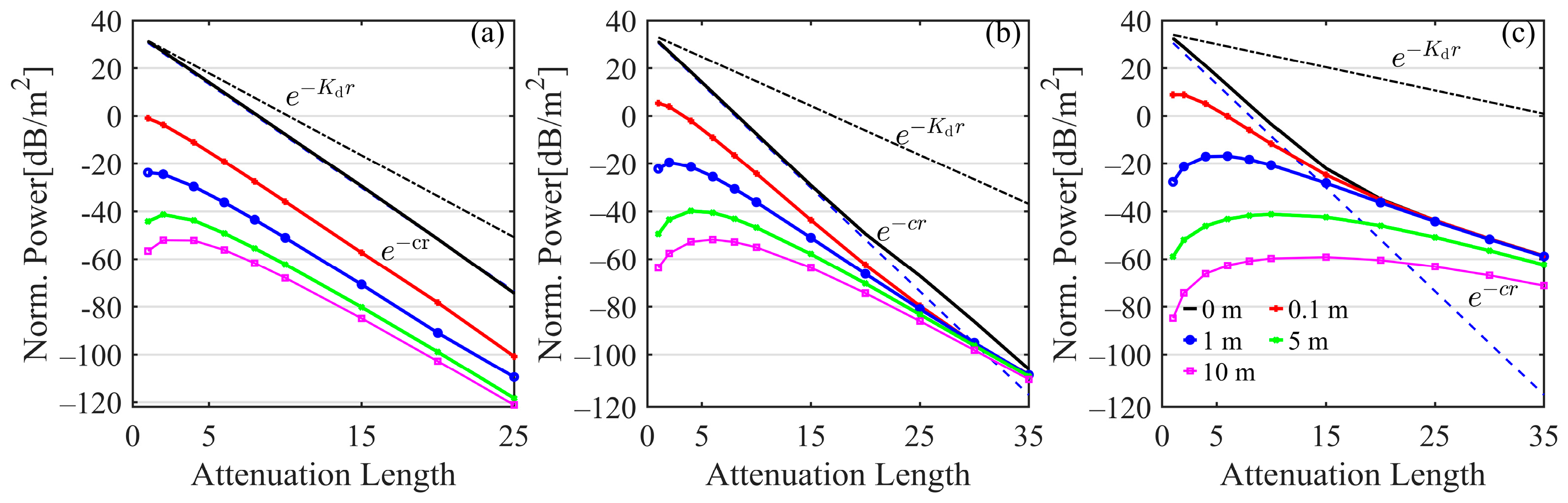
3.3. Channel Loss
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| UWOC | Underwater Wireless Optical Communication |
| LD | Laser Diode |
| LED | Light-Emitting Diode |
| BER | Bit Error Rate |
| SNR | Signal-to-Noise Ratio |
| FOV | Field of View |
| AOA | Angle of Arrival |
| FWHM | Full Width at Half Maxima |
| IOPs | Inherent Optical Properties |
| SSA | Single Scattering Albedo |
| VSF | Volume Scattering Function |
| SPF | Scattering Phase Function |
| Probability Density Function | |
| CDF | Cumulative Distribution Function |
References
- Schirripa Spagnolo, G.; Cozzella, L.; Leccese, F. Underwater Optical Wireless Communications: Overview. Sensors 2020, 20, 2261. [Google Scholar] [CrossRef] [PubMed]
- Ali, M.F.; Jayakody, D.N.K.; Li, Y. Recent Trends in Underwater Visible Light Communication (UVLC) Systems. IEEE Access 2022, 10, 22169–22225. [Google Scholar] [CrossRef]
- Zhu, S.; Chen, X.; Liu, X.; Zhang, G.; Tian, P. Recent Progress in and Perspectives of Underwater Wireless Optical Communication. Prog. Quantum Electron. 2020, 73, 100274. [Google Scholar] [CrossRef]
- Duntley, S.Q. Light in the Sea. J. Opt. Soc. Am. 1963, 53, 214–233. [Google Scholar] [CrossRef]
- BlueComm 200. Available online: https://www.sonardyne.com/product/blue-comm/ (accessed on 14 April 2025).
- Li, S.; Qu, W.; Liu, C.; Qiu, T.; Zhao, Z. Survey on High Reliability Wireless Communication for Underwater Sensor Networks. J. Netw. Comput. Appl. 2019, 148, 102446. [Google Scholar] [CrossRef]
- Li, C.-Y.; Huang, X.-H.; Lu, H.-H.; Huang, Y.-C.; Huang, Q.-P.; Tu, S.-C. A WDM PAM4 FSO–UWOC Integrated System With a Channel Capacity of 100 Gb/s. J. Lightwave Technol. 2020, 38, 1766–1776. [Google Scholar] [CrossRef]
- Dong, X.; Zhang, K.; Sun, C.; Zhang, J.; Zhang, A.; Wang, L. Towards 250-m Gigabits-per-Second Underwater Wireless Optical Communication Using a Low-Complexity ANN Equalizer. Opt. Express 2025, 33, 2321–2337. [Google Scholar] [CrossRef]
- Elamassie, M.; Miramirkhani, F.; Uysal, M. Performance Characterization of Underwater Visible Light Communication. IEEE Trans. Commun. 2019, 67, 543–552. [Google Scholar] [CrossRef]
- Tian, P.; Chen, H.; Wang, P.; Liu, X.; Chen, X.; Zhou, G.; Zhang, S.; Lu, J.; Qiu, P.; Qian, Z.; et al. Absorption and Scattering Effects of Maalox, Chlorophyll, and Sea Salt on a Micro-LED-Based Underwater Wireless Optical Communication [Invited]. Chin. Opt. Lett. 2019, 17, 100010. [Google Scholar] [CrossRef]
- Kumar, S.; Prince, S.; Venkata Aravind, J.; Kumar, G.S. Analysis on the Effect of Salinity in Underwater Wireless Optical Communication. Mar. Geores. Geotechnol. 2020, 38, 291–301. [Google Scholar] [CrossRef]
- Sahoo, R.; Shanmugam, P. Effect of the Complex Air–Sea Interface on a Hybrid Atmosphere-Underwater Optical Wireless Communications System. Opt. Commun. 2022, 510, 127941. [Google Scholar] [CrossRef]
- Kou, L.; Zhang, J.; Zhang, P.; Yang, Y.; He, F. Composite Channel Modeling for Underwater Optical Wireless Communication and Analysis of Multiple Scattering Characteristics. Opt. Express 2023, 31, 11320–11334. [Google Scholar] [CrossRef] [PubMed]
- Yi, X.; Liu, J.; Liu, Y.; Ata, Y. Monte-Carlo Based Vertical Underwater Optical Communication Performance Analysis with Chlorophyll Depth Profiles. Opt. Express 2023, 31, 41684–41700. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.; Lu, C.; Li, S.; Xu, Z. 100 m/500 Mbps Underwater Optical Wireless Communication Using an NRZ-OOK Modulated 520 Nm Laser Diode. Opt. Express 2019, 27, 12171. [Google Scholar] [CrossRef] [PubMed]
- Perera, A.; Katz, M.; Godaliyadda, R.; Häkkinen, J.; Strömmer, E. Light-Based Internet of Things: Implementation of an Optically Connected Energy-Autonomous Node. In Proceedings of the 2021 IEEE Wireless Communications and Networking Conference (WCNC), Nanjing, China, 29 March–1 April 2021. [Google Scholar]
- AL-Din, M.B.; Alkareem, R.A.S.A.; Mazin Ali, A. Ali Transmission of 10 Gb/s For Underwater Optical Wireless Communication System. J. Opt. 2024. [Google Scholar] [CrossRef]
- Salman, M.; Bolboli, J.; Naik, R.P.; Chung, W.-Y. Aqua-Sense: Relay-Based Underwater Optical Wireless Communication for IoUT Monitoring. IEEE Open J. Commun. Soc. 2024, 5, 1358–1375. [Google Scholar] [CrossRef]
- Bertocco, M.; Brighente, A.; Peruzzi, G.; Pozzebon, A.; Tormena, N.; Trivellin, N. Fear of the Dark: Exploring PV-Powered IoT Nodes for VLC and Energy Harvesting. In Proceedings of the 2024 IEEE International Workshop on Metrology for the Sea, Learning to Measure Sea Health Parameters (MetroSea). Portorose, Slovenia, 14–16 October 2024. [Google Scholar]
- Han, T.; Ding, P.; Liu, N.; Wang, Z.; Li, Z.; Ru, Z.; Song, H.; Yin, Z. Design and Implementation of a High-Reliability Underwater Wireless Optical Communication System Based on FPGA. Appl. Sci. 2025, 15, 3544. [Google Scholar] [CrossRef]
- Mehta, H.; Kumar, R.; Prakriya, S. Performance Analysis of an Underwater Partitioned IRS-Assisted VLC Link with Energy Harvesting. In Proceedings of the 2025 17th International Conference on COMmunication Systems and NETworks (COMSNETS), Bengaluru, India, 6–10 January 2025. [Google Scholar]
- Salcedo-Serrano, P.; Boluda-Ruiz, R.; Garrido-Balsells, J.M.; García-Zambrana, A.; Castillo-Vázquez, B.; Puerta-Notario, A.; Hranilovic, S. UOWC Spatial Diversity Techniques over Hostile Maritime Environments: An Approach under Imperfect CSI and per-Source Power Constraints. Opt. Express 2024, 32, 42347–42367. [Google Scholar] [CrossRef]
- Cochenour, B.M.; Mullen, L.J.; Laux, A.E. Characterization of the Beam-Spread Function for Underwater Wireless Optical Communications Links. IEEE J. Ocean. Eng. 2008, 33, 513–521. [Google Scholar] [CrossRef]
- Sahu, S.K.; Shanmugam, P. A Theoretical Study on the Impact of Particle Scattering on the Channel Characteristics of Underwater Optical Communication System. Opt. Commun. 2018, 408, 3–14. [Google Scholar] [CrossRef]
- Ramley, I.; Alzayed, H.M.; Al-Hadeethi, Y.; Chen, M.; Barasheed, A.Z. An Overview of Underwater Optical Wireless Communication Channel Simulations with a Focus on the Monte Carlo Method. Mathematics 2024, 12, 3904. [Google Scholar] [CrossRef]
- Wang, X.; Zhang, M.; Zhou, H.; Ren, X. Performance Analysis and Design Considerations of the Shallow Underwater Optical Wireless Communication System with Solar Noises Utilizing a Photon Tracing-Based Simulation Platform. Electronics 2021, 10, 632. [Google Scholar] [CrossRef]
- Huang, J.; Wen, G.; Dai, J.; Zhang, L.; Wang, J. Channel Model and Performance Analysis of Long-Range Deep Sea Wireless Photon-Counting Communication. Opt. Commun. 2020, 473, 125989. [Google Scholar] [CrossRef]
- Qadar, R.; Kasi, M.K.; Ayub, S.; Kakar, F.A. Monte Carlo–Based Channel Estimation and Performance Evaluation for UWOC Links under Geometric Losses. Int. J. Commun. Syst. 2018, 31, e3527. [Google Scholar] [CrossRef]
- Chen, P.; Pan, D.; Mao, Z.; Liu, H. Semi-Analytic Monte Carlo Model for Oceanographic Lidar Systems: Lookup Table Method Used for Randomly Choosing Scattering Angles. Appl. Sci. 2019, 9, 48. [Google Scholar] [CrossRef]
- Boluda-Ruiz, R.; Rico-Pinazo, P.; Castillo-Vazquez, B.; Garcia-Zambrana, A.; Qaraqe, K. Impulse Response Modeling of Underwater Optical Scattering Channels for Wireless Communication. IEEE Photonics J. 2020, 12, 7904414. [Google Scholar] [CrossRef]
- Qin, J.; Fu, M.; Sun, M.; Zhen, C.; Ji, R.; Zheng, B. Simulation of Beam Characteristics in Long-Distance Underwater Optical Communication. In Proceedings of the Global Oceans 2020: Singapore—U.S. Gulf Coast, Singapore, 5–14 October 2020. [Google Scholar]
- Cox, W.; Muth, J. Simulating Channel Losses in an Underwater Optical Communication System. J. Opt. Soc. Am. A Opt. Image Sci. Vis. 2014, 31, 920–934. [Google Scholar] [CrossRef]
- Zhang, H.; Hui, L.; Dong, Y. Angle of Arrival Analysis for Underwater Wireless Optical Links. IEEE Commun. Lett. 2015, 19, 2162–2165. [Google Scholar] [CrossRef]
- Ding, H.; Chen, G.; Majumdar, A.K.; Sadler, B.M.; Xu, Z. Modeling of Non-Line-of-Sight Ultraviolet Scattering Channels for Communication. IEEE J. Sel. Areas Commun. 2009, 27, 1535–1544. [Google Scholar] [CrossRef]
- Shetty, C.S.S.; Naik, R.P.; Acharya, U.S.; Chung, W.-Y. Performance Analysis of Underwater Vertical Wireless Optical Communication System in the Presence of Weak Turbulence, Pointing Errors and Attenuation Losses. Opt. Quantum Electron. 2023, 55, 1. [Google Scholar] [CrossRef]
- Sun, X.; Kang, C.H.; Kong, M.; Alkhazragi, O.; Guo, Y.; Ouhssain, M.; Weng, Y.; Jones, B.H.; Ng, T.K.; Ooi, B.S. A Review on Practical Considerations and Solutions in Underwater Wireless Optical Communication. J. Lightwave Technol. 2020, 38, 421–431. [Google Scholar] [CrossRef]
- Ocean Optics Web Book. Available online: https://www.oceanopticsbook.info/ (accessed on 24 April 2025).
- Leathers, R.A.; Downes, T.V.; Davis, C.O.; Mobley, C.D. Monte Carlo Radiative Transfer Simulations for Ocean Optics: A Practical Guide; Defense Technical Information Center: Fort Belvoir, VA, USA, 2004; pp. 1–50.
- Mobley, C.D. (Ed.) Radiative Transfer Theory. In The Oceanic Optics Book; International Ocean Colour Coordinating Group (IOCCG): Dartmouth, NS, Canada, 2022; pp. 323–354. [Google Scholar]
- Mobley, C.D. Light and Water: Radiative Transfer in Natural Waters; Academic Press: Cambridge, MA, USA, 1994; ISBN 978-0-12-502750-2. [Google Scholar]
- Petzold, T.J. Volume Scattering Functions for Selected Ocean Waters; Scripps Institution of Oceanography: San Diego, CA, USA, 1972. [Google Scholar]
- Mobley, C.D. (Ed.) The Oceanic Optics Book; International Ocean Colour Coordinating Group (IOCCG): Dartmouth, NS, Canada, 2022. [Google Scholar]
- Preisendorfer, R.W. Optical Properties at Extreme Depths. In Hydrologic Optics; Water and Sediment Quality Modeling and Criteria Materials; U.S. Department of Commerce; National Oceanic and Atmospheric Administration; Environmental Research Laboratories; Pacific Marine Environmental Laboratory: Honolulu, HI, USA, 1976; Volume 5, pp. 183–259. [Google Scholar]
- Preisendorfer, R.W. Hydrologic Optics. Volume V. Properties; Water and Sediment Quality Modeling and Criteria Materials; U.S. Department of Commerce; National Oceanic and Atmospheric Administration; Environmental Research Laboratories; Pacific Marine Environmental Laboratory: Honolulu, HI, USA, 1976; Volume 5.
- Zaneveld, J.R.V. An Asymptotic Closure Theory for Irradiance in the Sea and Its Inversion to Obtain the Inherent Optical Properties. Limnol. Oceanogr. 1989, 34, 1442–1452. [Google Scholar] [CrossRef]
- Marinyuk, V.V.; Rogozkin, D.B.; Sheberstov, S.V. Optical Beam Spread in Seawater. Opt. Commun. 2025, 574, 131098. [Google Scholar] [CrossRef]



| Symbols | Descriptions | Unit |
|---|---|---|
| Offset relative to the beam center on the receiving plane | m | |
| Transmission distance | m | |
| Absorption coefficient | m−1 | |
| Scattering coefficient | m−1 | |
| Attenuation coefficient, | m−1 | |
| Optical path length, | ||
| Uniform random variable distributed between 0 and 1 | ||
| Probability density distribution function of a certain sampling variable | ||
| Cumulative distribution function of a certain sampling variable | ||
| Radiance | W m−2 sr−1 | |
| Scattering angle | ° | |
| Azimuth angle | ° | |
| Direction vector of a photon | ||
| Single scattering albedo (SSA), | ||
| Volume scattering function (VSF) | m−1 sr−1 | |
| Scattering phase function (SPF), | sr−1 | |
| Downwelling diffuse attenuation coefficient | m−1 |
| Water Type | () | () | () | ||
|---|---|---|---|---|---|
| Clear Water | 0.114 | 0.037 | 0.151 | 0.120 | 0.25 |
| Coastal Water | 0.179 | 0.220 | 0.399 | 0.189 | 0.55 |
| Turbid Harbor Water | 0.366 | 1.829 | 2.195 | 0.493 | 0.83 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Yuan, R.; Zhang, T.; Li, C.; Gao, H.; Hu, L. Laser Transmission Characteristics of Seawater for Underwater Wireless Optical Communication. Sensors 2025, 25, 3057. https://doi.org/10.3390/s25103057
Yuan R, Zhang T, Li C, Gao H, Hu L. Laser Transmission Characteristics of Seawater for Underwater Wireless Optical Communication. Sensors. 2025; 25(10):3057. https://doi.org/10.3390/s25103057
Chicago/Turabian StyleYuan, Ruiman, Tinglu Zhang, Cong Li, Hong Gao, and Lianbo Hu. 2025. "Laser Transmission Characteristics of Seawater for Underwater Wireless Optical Communication" Sensors 25, no. 10: 3057. https://doi.org/10.3390/s25103057
APA StyleYuan, R., Zhang, T., Li, C., Gao, H., & Hu, L. (2025). Laser Transmission Characteristics of Seawater for Underwater Wireless Optical Communication. Sensors, 25(10), 3057. https://doi.org/10.3390/s25103057





