A Novel Algorithm for Adaptive Detection and Tracking of Extended Targets Using Millimeter-Wave Imaging Radar
Abstract
1. Introduction
- Utilizing the statistical properties of ETs in radar imaging, a two-dimensional Gaussian mixture model (2D-GMM) is constructed to represent the target distribution. The target distribution information is extracted from the radar images generated in each coherent processing interval (CPI) through a 2D-KDE approach. This model is highly applicable to most targets in high-resolution radar sensing scenarios and provides an accurate representation of the target scattering distribution characteristics.
- We propose an adaptive ET detection and tracking algorithm based on scattering point shift (SPS). In addition to rigid targets, this algorithm can effectively handle complex targets with independently moving internal modules, demonstrating a robust performance. By simultaneously performing tracking and detection, the proposed algorithm achieves higher efficiency and lower information loss compared to traditional track-after-detect approaches.
- The effectiveness of the proposed algorithm is jointly validated through simulations and field measurements, demonstrating its feasibility for practical applications.
2. Materials and Methods
2.1. Signal Model and Algorithm Framework
2.1.1. LFMCW Radar Echo Signal Model
2.1.2. Backprojection Imaging
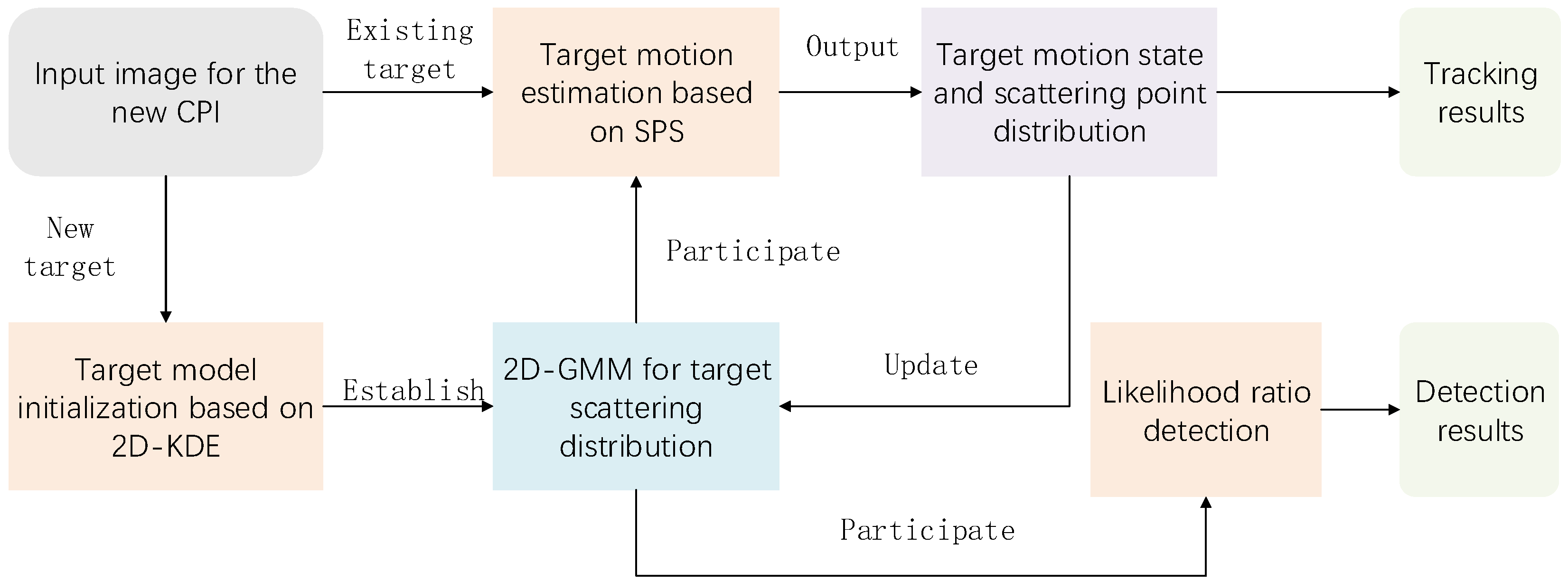
2.1.3. Algorithm Framework
2.2. Adaptive Detection and Tracking Algorithm for ETs
2.2.1. 2D-GMM for ETs
2.2.2. Target Model Initialization Based on 2D-KDE
- Initialize the parameters: corresponds to the normalized amplitudes of the K peak points in the image, represents , the positions of these peak points, and is initialized based on the range resolution and angular resolution ;
- The iterative process begins, with i serving as the iteration counter;
- The probability that all imaging region units belong to each scattering point model is computed. Here, , acting as a latent variable in the model, quantifies the membership degree of each data point within the Gaussian component:
- Following the update of the membership degree parameter, the weight is updated. Specifically, the weight of the k-th distribution is derived by aggregating the membership degrees of all data points assigned to the k-th distribution:
- The center of each distribution is updated by weighting the coordinates using the integrated normalized amplitude of the pixel points. The center is then computed by maximizing the expected likelihood based on the membership degree :
- The distribution covariance matrix is updated as follows:
- Steps 3 to 6 are repeated until the weight , center , and distribution covariance matrix converge. The convergence condition is defined as:
2.2.3. Target Motion Estimation Based on SPS
2.2.4. Likelihood Ratio Detection
3. Results and Discussion
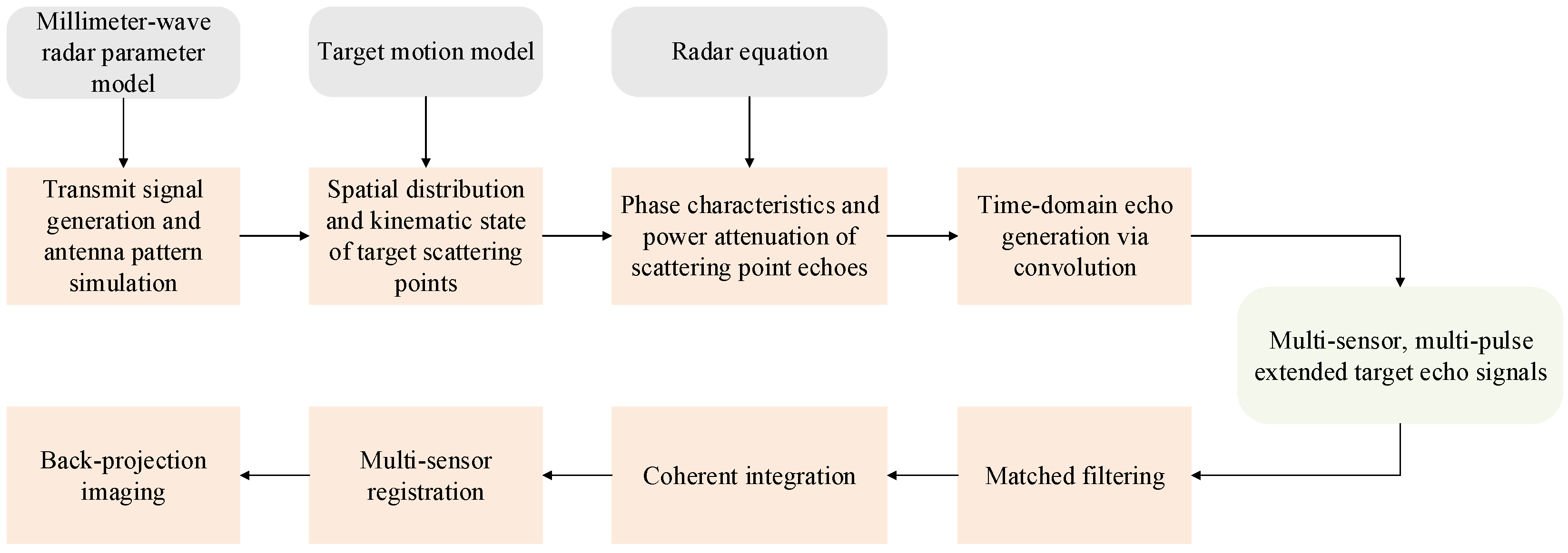
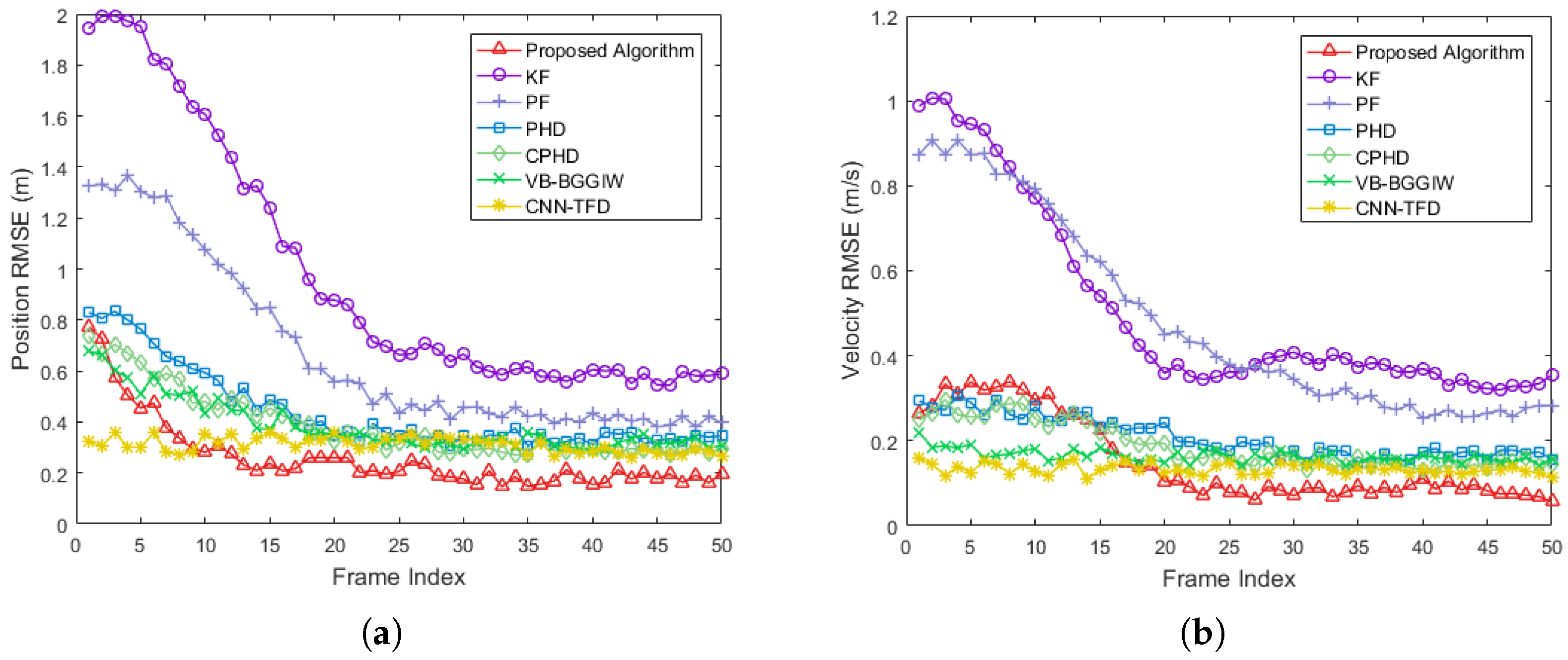
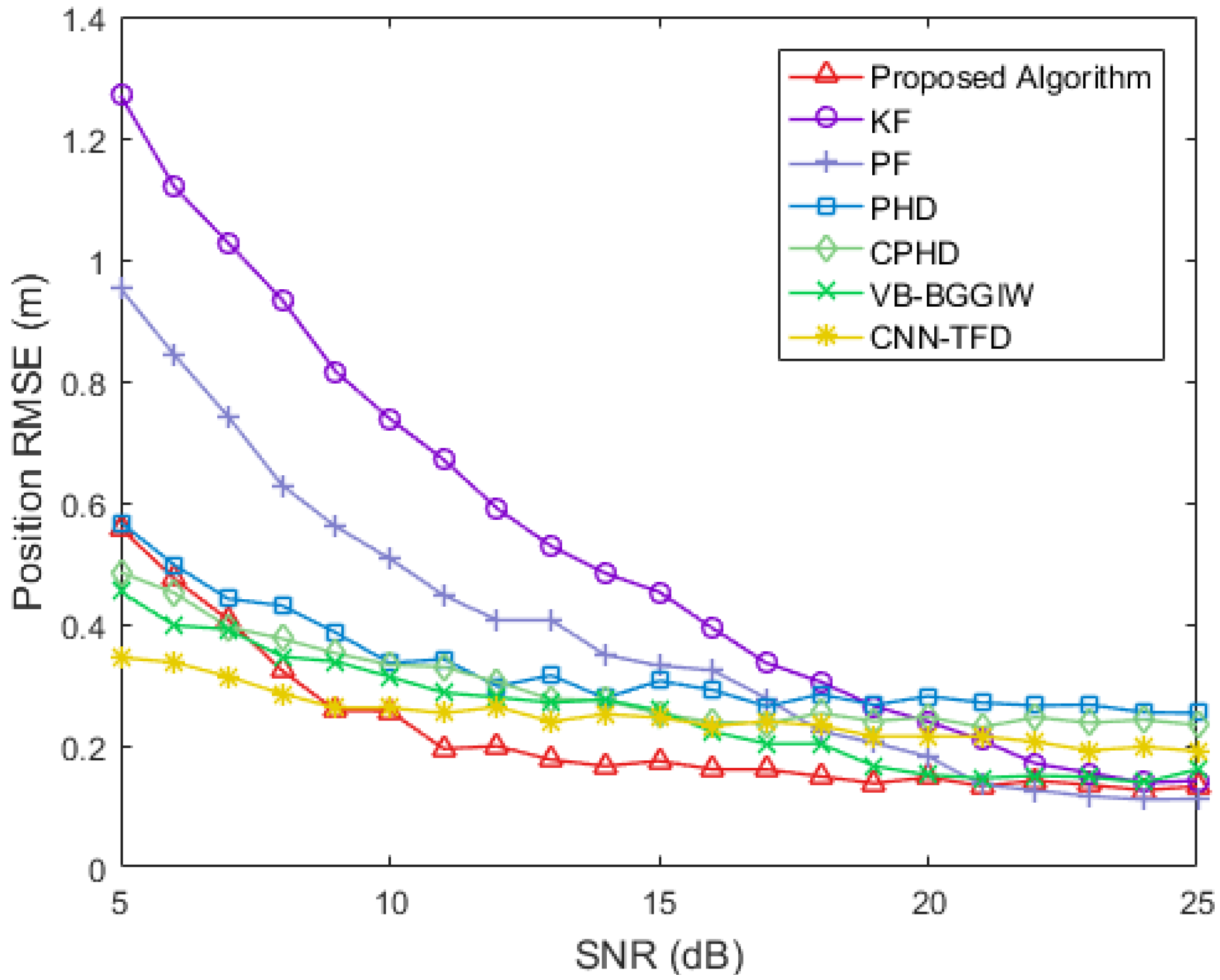
3.1. Simulation Experiment
- Transmitting the signal generation and antenna pattern simulation based on configured radar parameters (carrier frequency, bandwidth, pulse width, PRF, modulation scheme);
- The determination of scattering point spatial distribution and kinematic states according to the target motion model;
- The calculation of time delays, phase shifts, and echo power attenuation;
- The generation of time-domain echoes through the convolution of scattering point distribution with reflection signals;
- Final output of multi-sensor, multi-pulse echo signals per CPI.
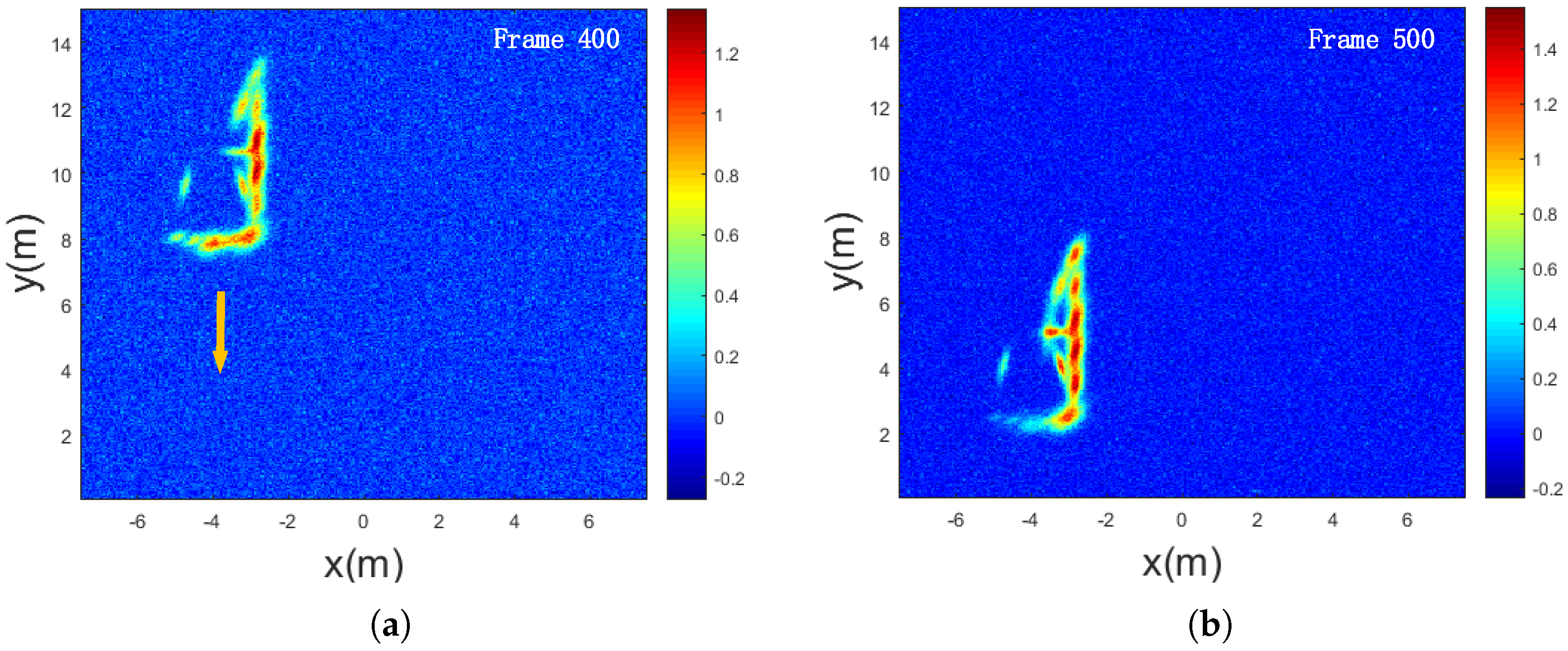
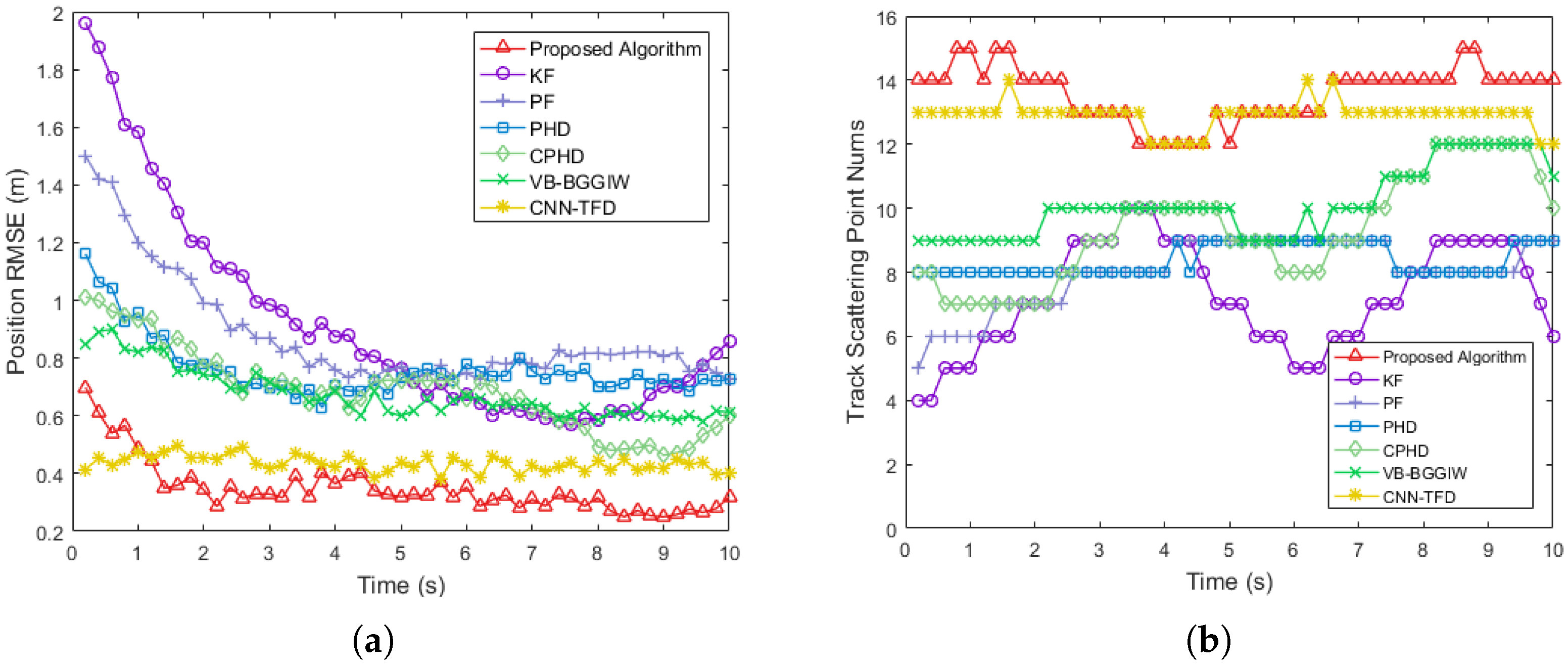
3.2. Field Experiment
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
Abbreviations
| ETs | Extended targets |
| SPS | Scattering Point Shift |
| 2D-KDE | Two-dimensional kernel density estimation |
| mmWave | Millimeter-wave |
| LFMCW | Linear Frequency Modulated Continuous Wave |
| KF | Kalman Filter |
| PF | Particle filter |
| RFS | Random Finite Set |
| ETT | Extended Target Tracking |
| PHD | Probability Hypothesis Density |
| CPHD | Cardinalized Probability Hypothesis Density |
| 2D-GMM | Two-dimensional Gaussian mixture model |
| CPI | Coherent processing interval |
| SNR | Signal-to-noise ratio |
| EM | Expectation-Maximization |
| AWGN | Additive white Gaussian noise |
| RMSE | Root mean square error |
References
- Gao, X.; Roy, S.; Xing, G. MIMO-SAR: A Hierarchical High-Resolution Imaging Algorithm for mmWave FMCW Radar in Autonomous Driving. IEEE Trans. Veh. Technol. 2021, 70, 7322–7334. [Google Scholar] [CrossRef]
- Kosuge, A.; Suehiro, S.; Hamada, M.; Kuroda, T. mmWave-YOLO: A mmWave Imaging Radar-Based Real-Time Multiclass Object Recognition System for ADAS Applications. IEEE Trans. Instrum. Meas. 2022, 71, 2509810. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, Q.; Hong, R. A Novel Monopulse Angle Estimation Method for Wideband LFM Radars. Sensors 2016, 16, 817. [Google Scholar] [CrossRef] [PubMed]
- Richards, M.A. Fundamentals of Radar Signal Processing, 2nd ed.; McGraw-Hill Education: New York, NY, USA, 2014; pp. 10–126. [Google Scholar]
- Jiao, H.; Yan, J.; Pu, W.; Chen, Y.; Liu, H.; Greco, M.S. Wideband Sensor Resource Allocation for Extended Target Tracking and Classification. IEEE Trans. Signal Process. 2025, 73, 55–66. [Google Scholar] [CrossRef]
- Liu, M.; Zhao, K.; Zhang, Y.; Gao, Y.; Zhang, T. Feature Aided Extended Target Tracking For High Resolution Radar. In Proceedings of the 2021 33rd Chinese Control and Decision Conference (CCDC), Kunming, China, 22–24 May 2021. [Google Scholar]
- Wang, S.; Men, C.; Li, R.; Yeo, T.-S. A Maneuvering Extended Target Tracking IMM Algorithm Based on Second-Order EKF. IEEE Trans. Instrum. Meas. 2024, 73, 8505011. [Google Scholar] [CrossRef]
- Sang, H.; Zheng, R.; Cheng, H.; Meng, X.; Li, L.; Qi, J. A Review of Point Target and Extended Target Tracking Algorithms. In Proceedings of the 2024 3rd International Conference on Image Processing and Media Computing (ICIPMC), Hefei, China, 17–19 May 2024. [Google Scholar]
- Brooker, G. Introduction to Sensors for Ranging and Imaging; SciTech Publishing: Chennai, India, 2013; pp. 21–139. [Google Scholar]
- Liu, Q.; Cheng, Y.; Cao, K.; Liu, K. Radar 3-D Forward-Looking Imaging for Extended Targets Based on Attribute Scattering Model. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3502305. [Google Scholar] [CrossRef]
- Yoon, Y.S.; Amin, M.G. High resolution through-the-wall radar imaging using extended target model. In Proceedings of the 2008 IEEE Radar Conference, Rome, Italy, 26–30 May 2008. [Google Scholar]
- Liu, B.; Tharmarasa, R.; Jassemi, R.; Brown, D. RFS-Based Multiple Extended Target Tracking with Resolved Multipath Detections in Clutter. IEEE Trans. Intell. Transp. Syst. 2023, 24, 10400–10409. [Google Scholar] [CrossRef]
- Zhong, Z.; Meng, H.; Wang, X. Extended target tracking using an IMM based Rao-Blackwellised unscented Kalman filter. In Proceedings of the 2008 9th International Conference on Signal Processing, Beijing, China, 26–29 October 2008. [Google Scholar]
- Xu, J. Extended Target Tracking Using a Gaussian Mixture Model and Kalman Filter. IEEE Trans. Signal Process. 2017, 65, 1001–1011. [Google Scholar]
- Liu, H. Extended Target Tracking Using Gaussian Mixture Model and Particle Filter. IEEE Trans. Aerosp. Electron. Syst. 2016, 52, 1097–1107. [Google Scholar]
- Wu, W.; Liu, D.; Sun, J. Multihypothesis Multimodel Elliptic Radon Transform for Low-Observability Maneuvering Range-Ambiguity Target Detection. IEEE Trans. Aerosp. Electron. Syst. 2024, 60, 4088–4104. [Google Scholar] [CrossRef]
- Yang, S.; Baum, M. Metrics for performance evaluation of elliptic extended object tracking methods. In Proceedings of the 2016 IEEE International Conference on Multisensor Fusion and Integration for Intelligent Systems (MFI), Baden-Baden, Germany, 19–21 September 2016. [Google Scholar]
- Shen, X.; Song, Z.; Fan, H. PHD filter for single extended target tracking. In Proceedings of the 2016 CIE International Conference on Radar (RADAR), Guangzhou, China, 10–13 October 2016. [Google Scholar]
- Beard, M.; Reuter, S. Multiple Extended Target Tracking with Labeled Random Finite Sets. IEEE Trans. Signal Process. 2016, 64, 1638–1653. [Google Scholar] [CrossRef]
- Granstrom, K.; Lundquist, C.; Orguner, O. Extended Target Tracking using a Gaussian-Mixture PHD Filter. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 3268–3286. [Google Scholar] [CrossRef]
- Chen, Y.; Liu, W. Multiple extended target tracking based on GLMB filter and gibbs sampler. In Proceedings of the 2017 International Conference on Control, Automation and Information Sciences (ICCAIS), Chiang Mai, Thailand, 31 October–1 November 2017. [Google Scholar]
- Eryildirim, A.; Guldogan, M.B. A Bernoulli Filter for Extended Target Tracking Using Random Matrices in a UWB Sensor Network. IEEE Sens. J. 2016, 16, 4362–4373. [Google Scholar] [CrossRef]
- Yuan, Y.; Ma, S. Joint Multi-Target Tracking and Identification for Distributed Radars Using Bayesian Binary Test. In Proceedings of the 2024 IEEE Radar Conference, Denver, CO, USA, 6–10 May 2024. [Google Scholar]
- Beard, M. Bayesian Multi-Target Tracking with Merged Measurements Using Labelled Random Finite Sets. IEEE Trans. Signal Process. 2015, 63, 1433–1447. [Google Scholar] [CrossRef]
- Yang, X.; Jiao, Q. Variational Approximation for Extended Target Tracking in Clutter with Random Matrix. In Proceedings of the 2021 International Conference on Control, Automation and Information Sciences (ICCAIS), Xi’an, China, 14–17 October 2021. [Google Scholar]
- Zhao, L. Deep Learning for Radar Target Detection and Tracking: A Survey. IEEE Trans. Signal Process. 2020, 68, 3520–3537. [Google Scholar]
- Ding, M.; Ding, Y.; Peng, Y. CNN-Based Time–Frequency Image Enhancement Algorithm for Target Tracking Using Doppler Through-Wall Radar. IEEE Geosci. Remote Sens. Lett. 2023, 20, 3505305. [Google Scholar] [CrossRef]
- Zhu, Y. UAV Trajectory Tracking via RNN-Enhanced IMM-KF with ADS-B Data. In Proceedings of the 2024 IEEE Wireless Communications and Networking Conference (WCNC), Dubai, United Arab Emirates, 21–24 April 2024. [Google Scholar]
- Zhang, Y. Robust Extended Target Tracking in Cluttered Environments. IEEE Trans. Aerosp. Electron. Syst. 2018, 54, 1540–1550. [Google Scholar]
- Huang, X. Multi-target Tracking of Extended Targets Using a Hybrid Filter. IEEE Trans. Radar Syst. 2019, 40, 123–134. [Google Scholar]
- Seng, C.H.; Bouzerdoum, A.; Amin, M.G.; Ahmad, F. A Gaussian-Rayleigh mixture modeling approach for through-the-wall radar image segmentation. In Proceedings of the 2012 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Kyoto, Japan, 25–30 March 2012; pp. 877–880. [Google Scholar]
- Kilaru, V.; Amin, M.G.; Ahmad, F.; Sévigny, P.; DiFilippo, D. Gaussian mixture model based features for stationary human identification in urban radar imagery. In Proceedings of the 2014 IEEE Radar Conference, Cincinnati, OH, USA, 19–23 May 2014; pp. 0426–0430. [Google Scholar]
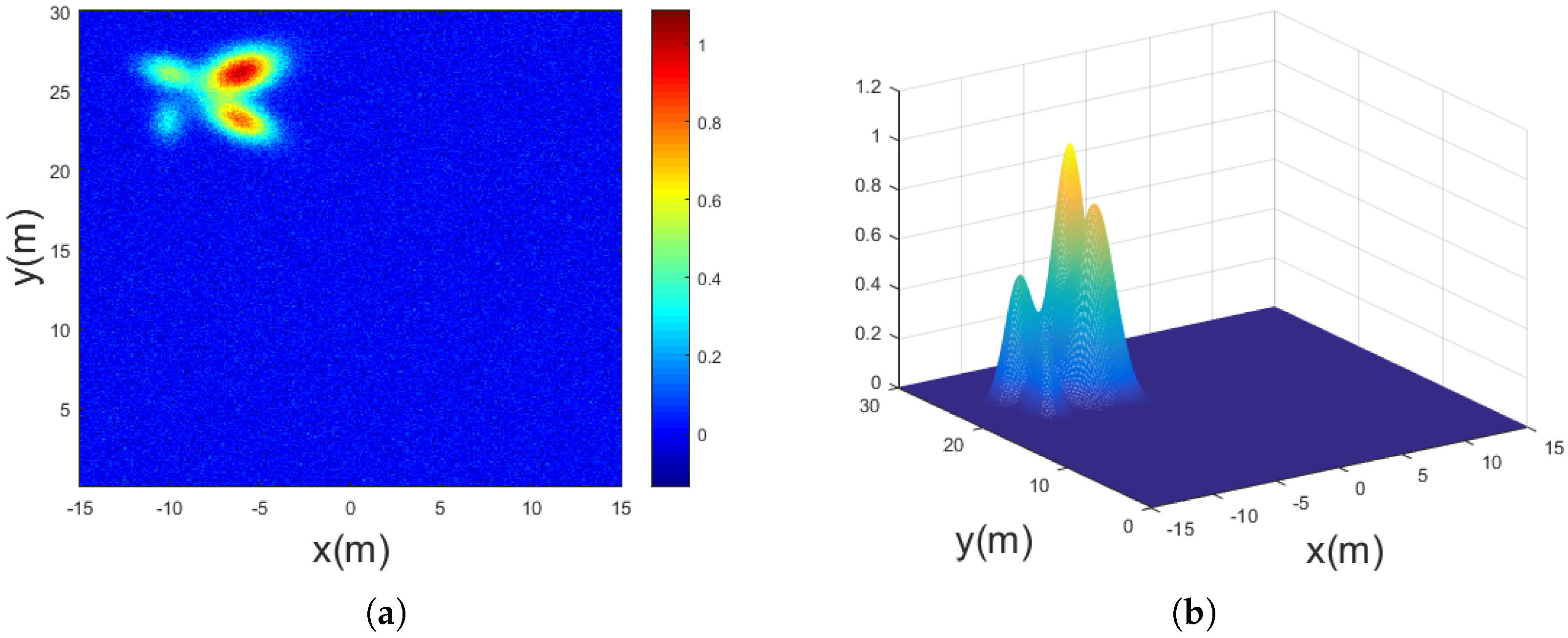
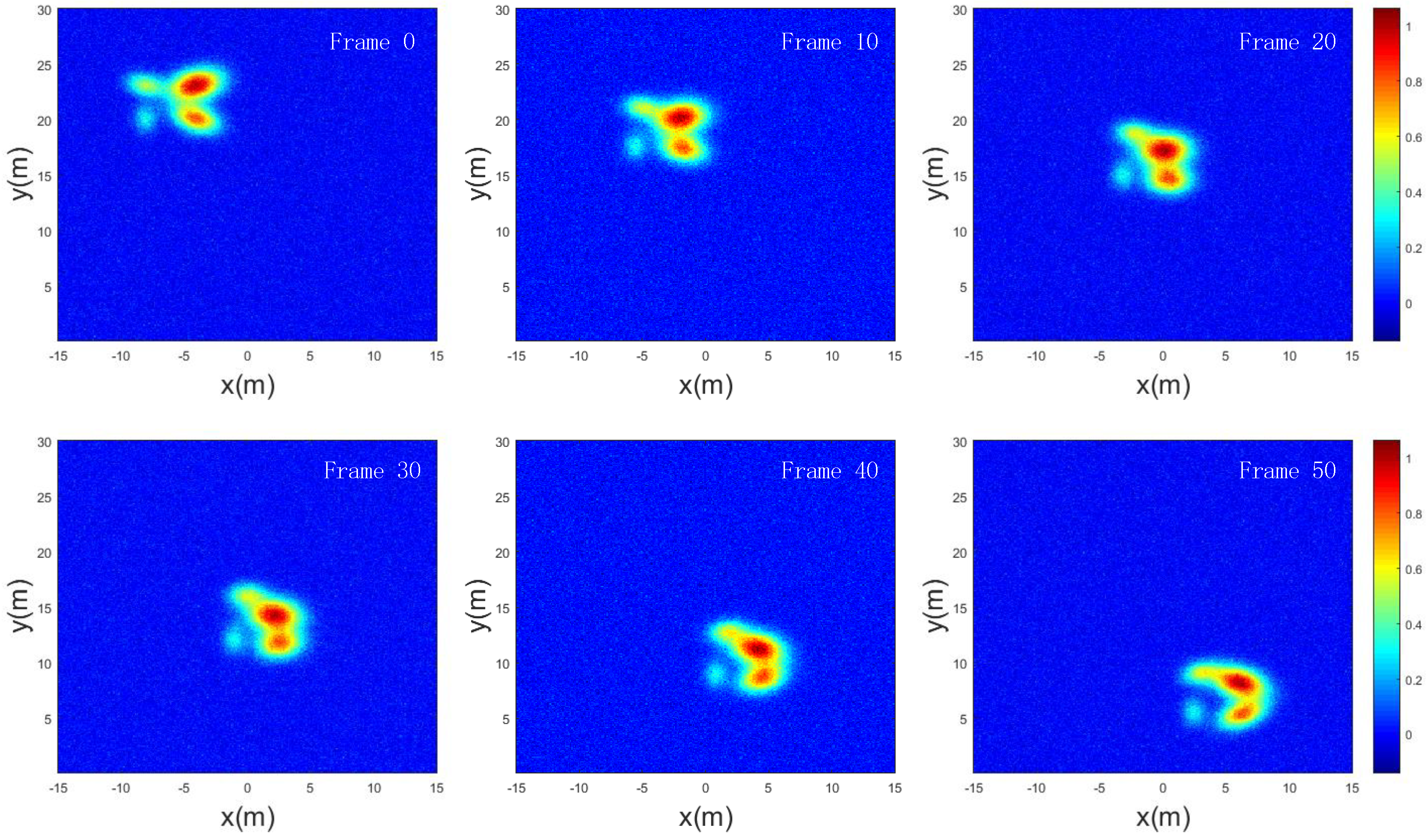

| Parameter | True Values | Estimated Values |
|---|---|---|
| Scattering point 1 | ||
| Peak value | 1.0 | 1.0 |
| Central position | [−6, 26] | [−6, 26] |
| Covariance matrix | [2 0.5; 0.5 1] | [1.98 0.53; 0.51 0.99] |
| Scattering point 2 | ||
| Peak value | 0.5 | 0.51 |
| Central position | [−10, 26] | [−9.9, 25.9] |
| Covariance matrix | [1 −0.2; −0.2 0.5] | [0.96 −0.2; −0.19 0.5] |
| Scattering point 3 | ||
| Peak value | 0.8 | 0.81 |
| Central position | [−6, 23] | [−6, 23.1] |
| Covariance matrix | [1.5 −0.5; −0.5 0.8] | [1.51 −0.49; −0.5 0.78] |
| Scattering point 4 | ||
| Peak value | 0.3 | 0.29 |
| Central position | [−10, 23] | [−9.8, 23] |
| Covariance matrix | [0.4 0; 0 0.8] | [0.38 0.03; 0.01 0.83] |
| Symbol | Parameter | Value |
|---|---|---|
| Carrier frequency | 76–80 GHz | |
| B | Bandwidth of the signal | 1 GHz |
| Sampling rate | 1.5 GHz | |
| Coherent processing interval | 20 ms |
| Method | Computational Times (ms) |
|---|---|
| SPS | 15.7 |
| KF | 5.1 |
| PF | 204.4 |
| PHD | 241.6 |
| CPHD | 288.7 |
| VB-BGGIW | 183.5 |
| CNN-TFD | 325.2 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, G.; Shi, W.; Shen, X.; Miao, Q.; Xie, C.; Chen, L. A Novel Algorithm for Adaptive Detection and Tracking of Extended Targets Using Millimeter-Wave Imaging Radar. Sensors 2025, 25, 3029. https://doi.org/10.3390/s25103029
Zhang G, Shi W, Shen X, Miao Q, Xie C, Chen L. A Novel Algorithm for Adaptive Detection and Tracking of Extended Targets Using Millimeter-Wave Imaging Radar. Sensors. 2025; 25(10):3029. https://doi.org/10.3390/s25103029
Chicago/Turabian StyleZhang, Ge, Weimin Shi, Xiaofeng Shen, Qilong Miao, Chenfei Xie, and Lu Chen. 2025. "A Novel Algorithm for Adaptive Detection and Tracking of Extended Targets Using Millimeter-Wave Imaging Radar" Sensors 25, no. 10: 3029. https://doi.org/10.3390/s25103029
APA StyleZhang, G., Shi, W., Shen, X., Miao, Q., Xie, C., & Chen, L. (2025). A Novel Algorithm for Adaptive Detection and Tracking of Extended Targets Using Millimeter-Wave Imaging Radar. Sensors, 25(10), 3029. https://doi.org/10.3390/s25103029









