Sensing-Aided Communication Method for Distributed Radar Communication System
Abstract
1. Introduction
- Joint Optimization of Communication and Sensing: This paper proposes a novel approach to optimize both communication performance and sensing accuracy simultaneously. Traditional methods usually adopt a two-step optimization strategy, that is, optimization of the communication performance independently, and then optimization of the sensing performance or vice versa, which makes it difficult to take into account the interaction between the two in the optimization process. It is easy to produce suboptimal overall performance. Differing from this approach, the proposed method dynamically coordinates the power allocation strategy by considering both communication and sensing performance indicators in a single optimization framework, so as to realize the true joint optimization of communication and sensing performance and ensure coordination and optimality of the overall system.
- Advanced Interference and Fading Adaptation: The work introduces an interference-aware power control strategy and a fading-aware resource allocation mechanism that effectively reduces interference and adapts to fading channels, ensuring robust communication and efficient power allocation. The proposed scheme outperforms existing methods in terms of communication rates and interference management, particularly under severe multipath fading conditions. In addition, the joint optimization framework helps to avoid wastage of power resources, ensures that limited power resources are optimally allocated between communication and sensing tasks, and improves the overall efficiency of power utilization.
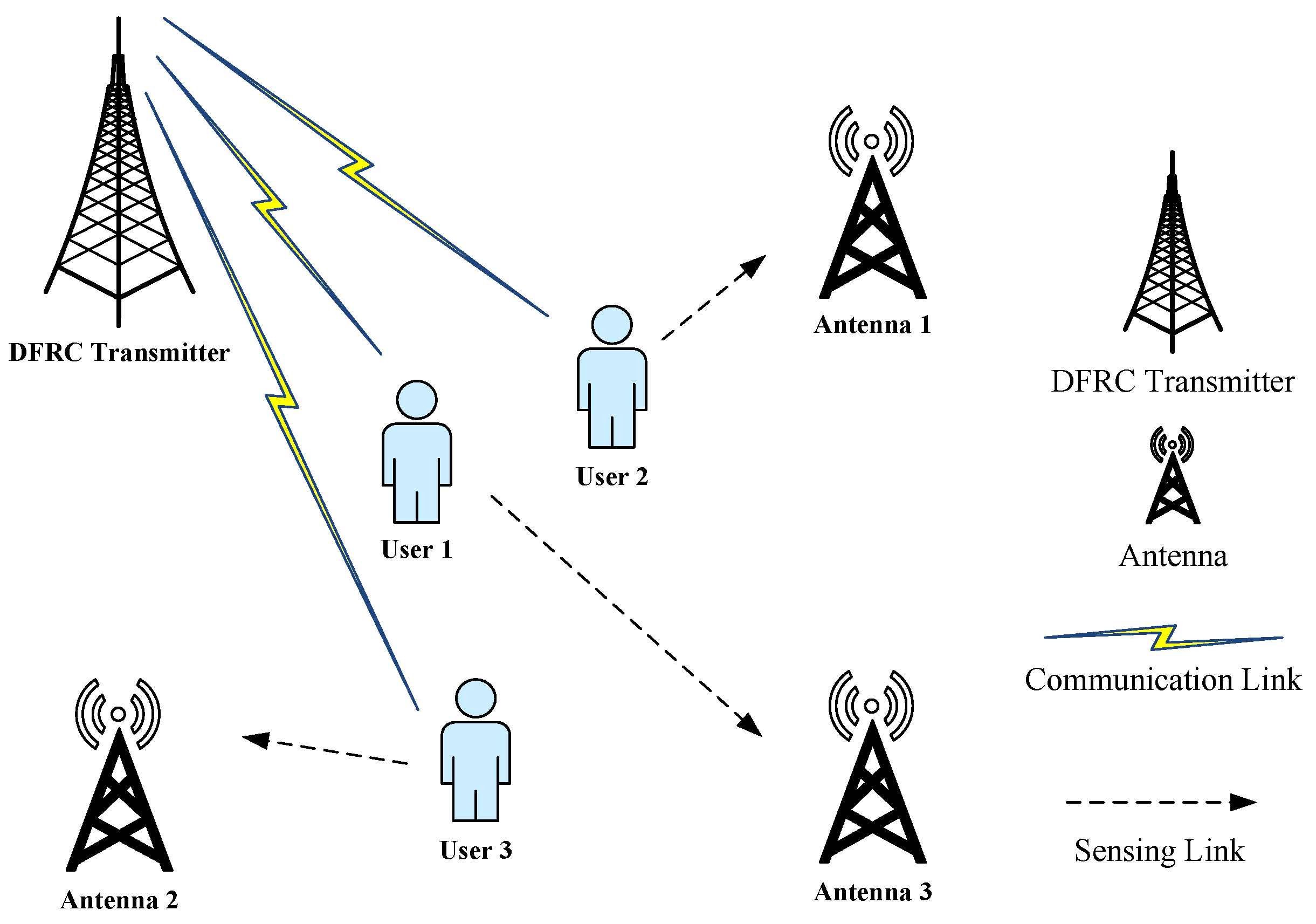
2. System Model and Problem Formulation
2.1. Mobility Model
2.2. Signal Power Transmission Model
2.3. Signal Multipath Fading Model
3. Problem Analysis and Algorithm Analysis
3.1. Establishment of Constraint Model
3.2. Convergence and Complexity Analysis
| Algorithm 1 WMMSE-SCA Algorithm |
|
3.3. Performance and Robustness Analysis
4. Performance and Simulation Analysis
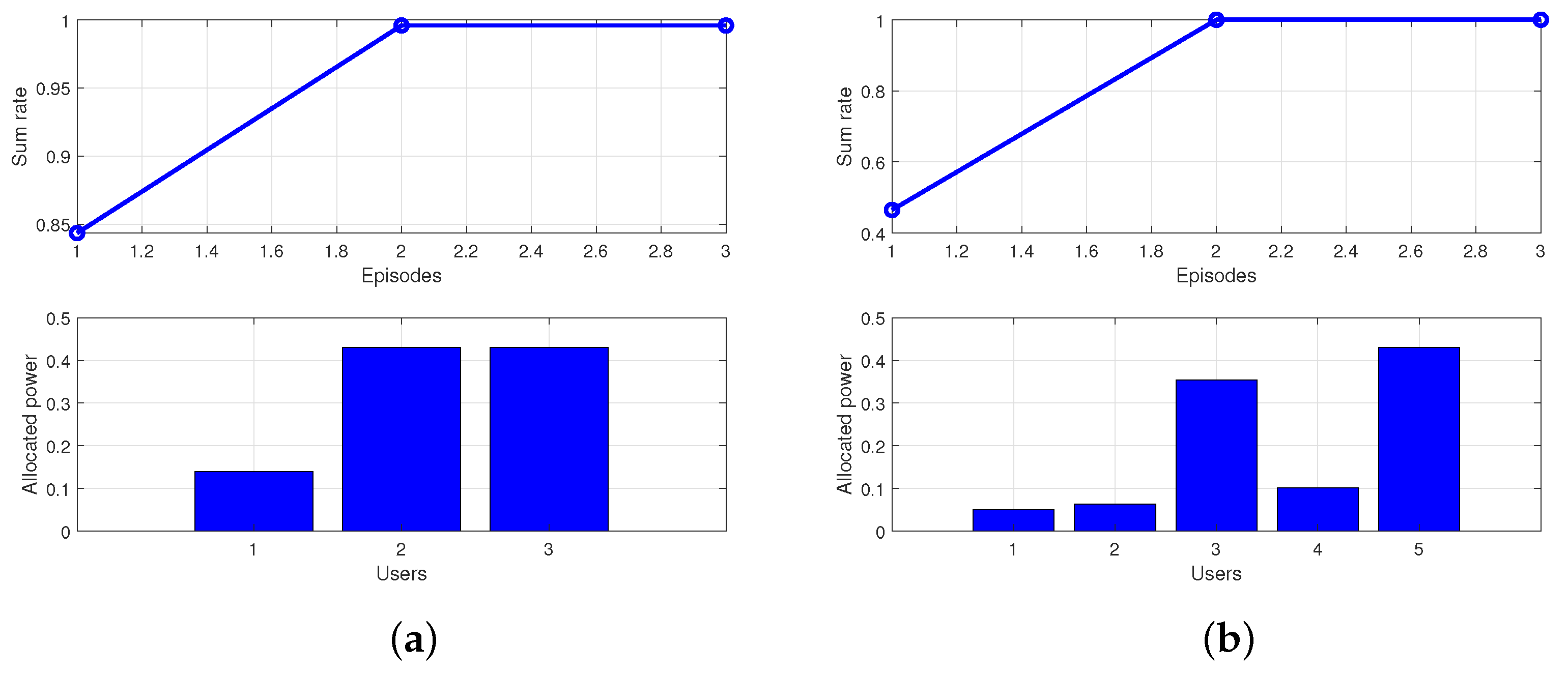
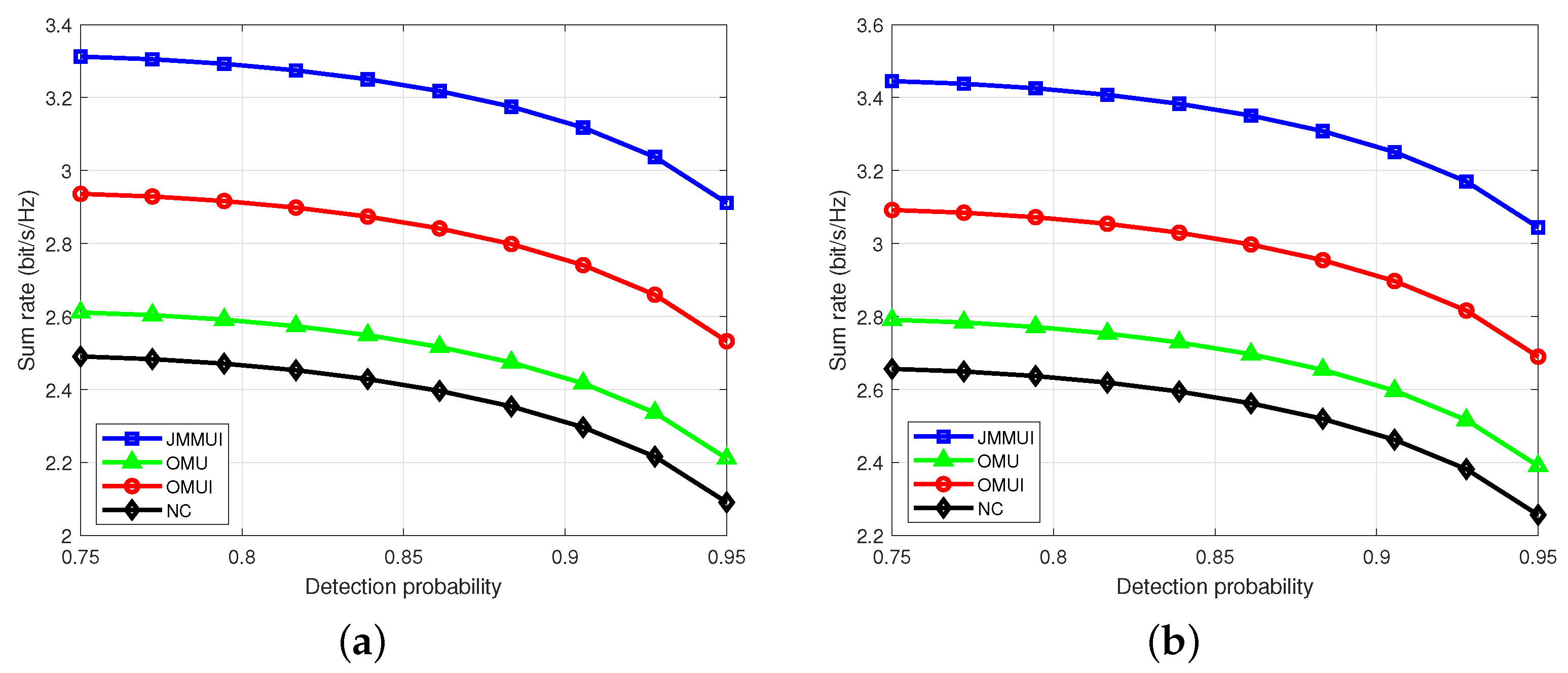
4.1. Different Detection Probability Constraints
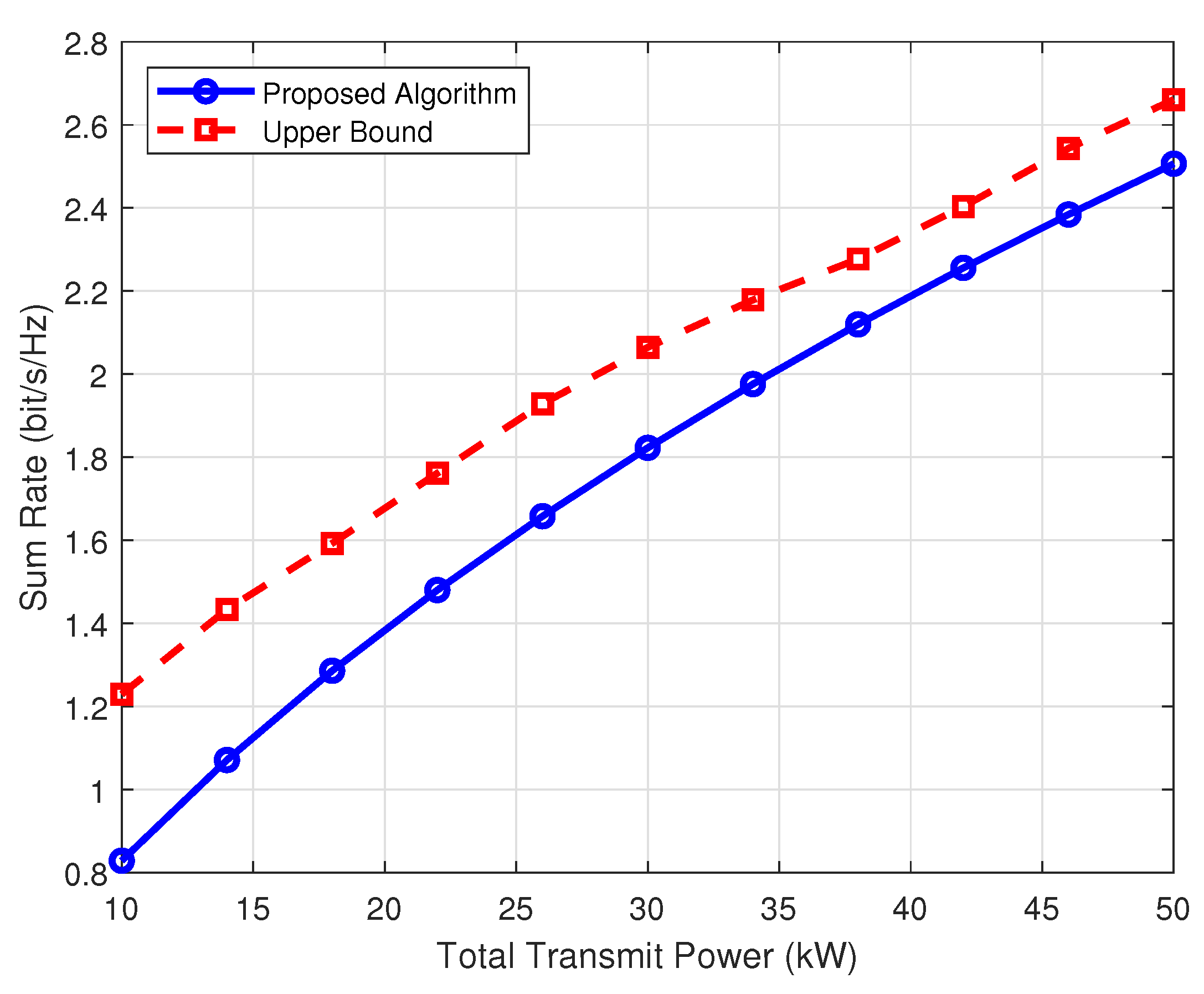
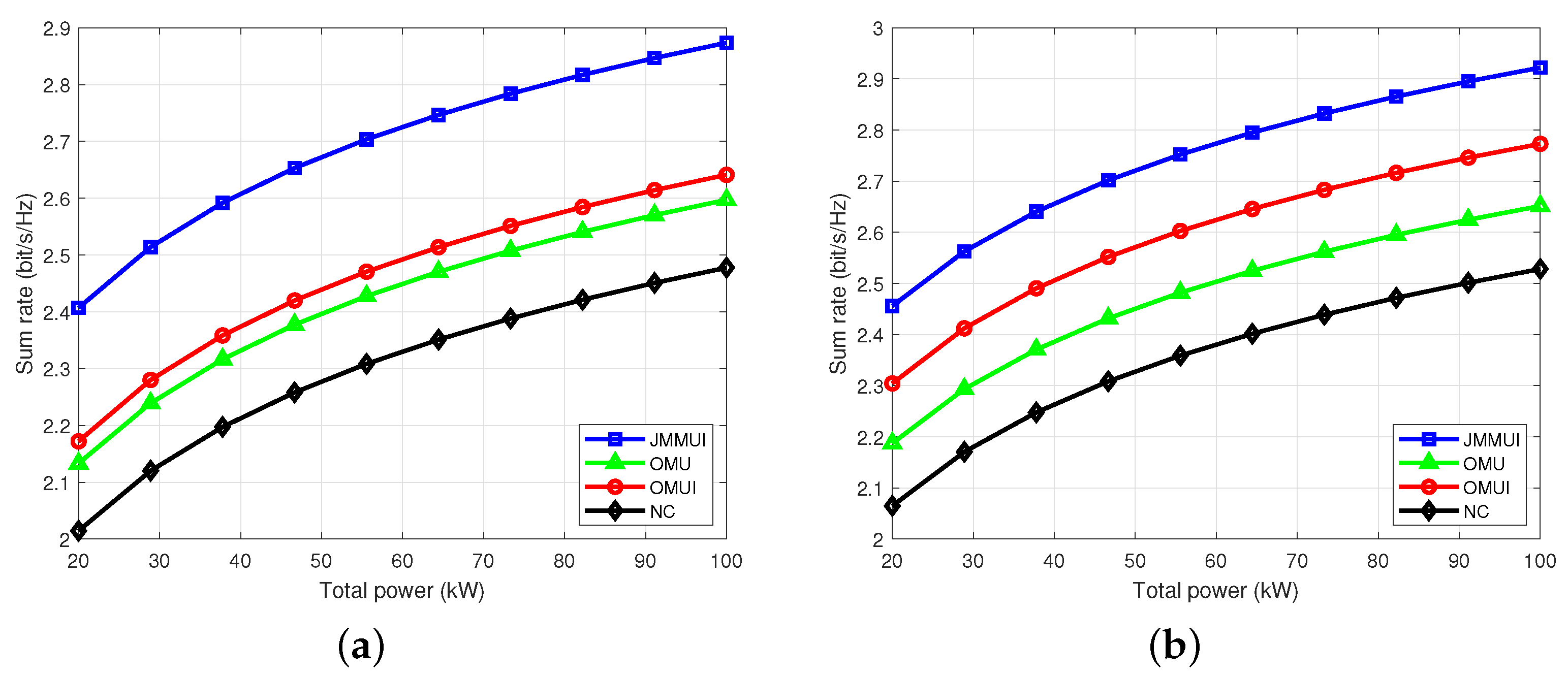
4.2. Different Total Power Constraints
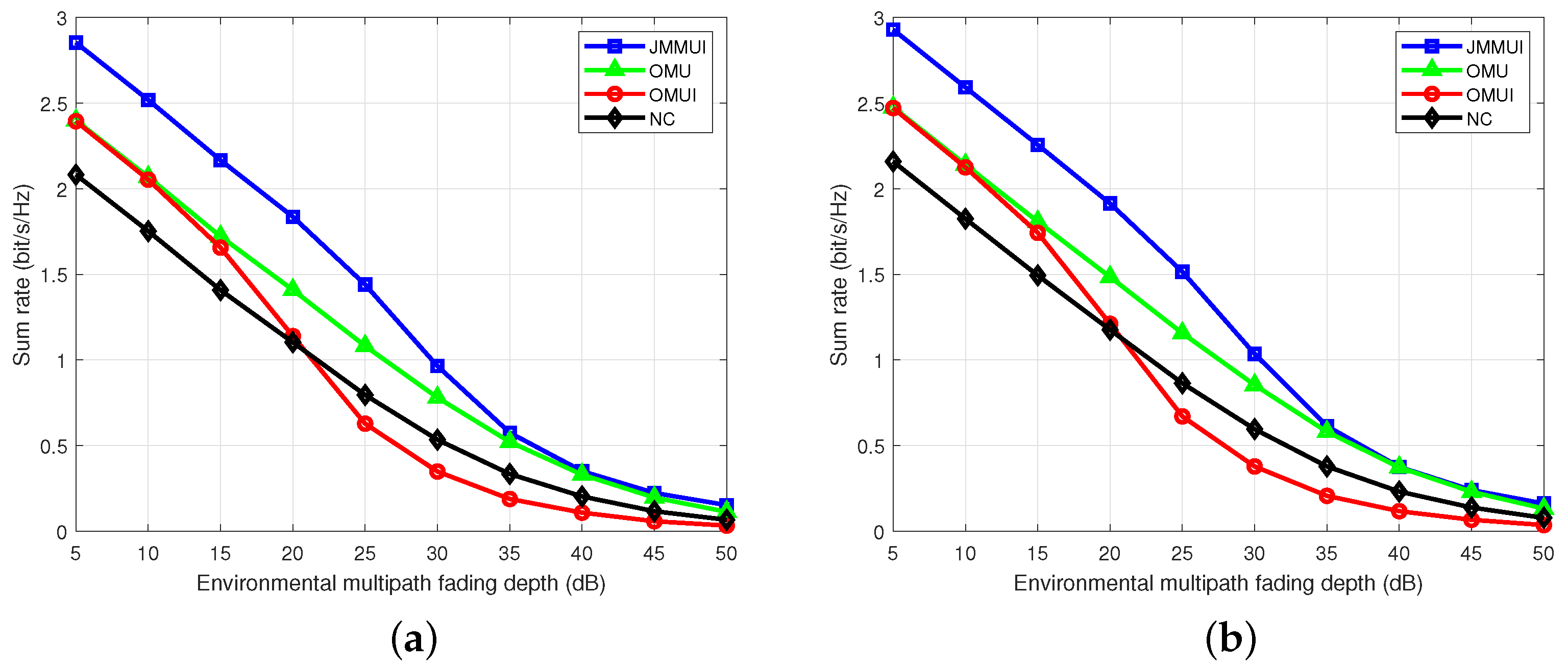
4.3. Complex Urban Environment Simulation
4.4. Simulation Analysis Summary
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Saad, W.; Bennis, M.; Chen, M. A Vision of 6G Wireless Systems: Applications, Trends, Technologies, and Open Research Problems. IEEE Netw. 2020, 34, 134–142. [Google Scholar] [CrossRef]
- Paul, B.; Chiriyath, A.R.; Bliss, D.W. Survey of RF Communications and Sensing Convergence Research. IEEE Access 2017, 5, 252–270. [Google Scholar] [CrossRef]
- Chiriyath, A.R.; Paul, B.; Bliss, D.W. Radar-Communications Convergence: Coexistence, Cooperation, and Co-Design. IEEE Trans. Cogn. Commun. Netw. 2017, 3, 1–12. [Google Scholar] [CrossRef]
- Hassanien, A.; Amin, M.G.; Aboutanios, E.; Himed, B. Dual-Function Radar Communication Systems: A Solution to the Spectrum Congestion Problem. IEEE Signal Process. Mag. 2019, 36, 115–126. [Google Scholar] [CrossRef]
- Mealey, R.M. A Method for Calculating Error Probabilities in a Radar Communication System. IEEE Trans. Space Electron. Telem. 1963, 9, 37–42. [Google Scholar] [CrossRef]
- Huang, Y.; Fang, Y.; Li, X.; Xu, J. Coordinated Power Control for Network Integrated Sensing and Communication. IEEE Trans. Veh. Technol. 2022, 71, 13361–13365. [Google Scholar] [CrossRef]
- Sturm, C.; Wiesbeck, W. Waveform Design and Signal Processing Aspects for Fusion of Wireless Communications and Radar Sensing. Proc. IEEE 2011, 99, 1236–1259. [Google Scholar] [CrossRef]
- Wymeersch, H.; Seco-Granados, G.; Destino, G.; Dardari, D.; Tufvesson, F. 5G mmWave Positioning for Vehicular Networks. IEEE Wirel. Commun. 2017, 24, 80–86. [Google Scholar] [CrossRef]
- Chen, L.; Liu, K.; Gao, Q.; Wang, X.; Zhang, Z. Enhancing Integrated Sensing and Communication (ISAC) Performance for a Searching–Deciding Alternation Radar-Comm System with Multi-Dimension Point Cloud Data. Remote Sens. 2024, 16, 3242. [Google Scholar] [CrossRef]
- Zhao, X.; Liu, H.; Gong, S.; Ju, X.; Xing, C.; Zhao, N. Dual-Functional MIMO Beamforming Optimization for RIS-Aided Integrated Sensing and Communication. IEEE Trans. Commun. 2024, 72, 5411–5427. [Google Scholar] [CrossRef]
- Choi, J.; Va, V.; Gonzalez-Prelcic, N.; Daniels, R.; Bhat, C.R.; Heath, R.W. Millimeter-Wave Vehicular Communication to Support Massive Automotive Sensing. IEEE Commun. Mag. 2016, 54, 160–167. [Google Scholar] [CrossRef]
- Zhang, A.; Rahman, M.L.; Huang, X.; Guo, Y.J.; Chen, S.; Heath, R.W. Perceptive Mobile Networks: Cellular Networks With Radio Vision via Joint Communication and Radar Sensing. IEEE Veh. Technol. Mag. 2021, 16, 20–30. [Google Scholar] [CrossRef]
- Dou, C.; Huang, N.; Wu, Y.; Qian, L.; Quek, T.Q.S. Sensing-Efficient NOMA-Aided Integrated Sensing and Communication: A Joint Sensing Scheduling and Beamforming Optimization. IEEE Trans. Veh. Technol. 2023, 72, 13591–13603. [Google Scholar] [CrossRef]
- Huang, N.; Dong, H.; Dou, C.; Wu, Y.; Qian, L.; Ma, S.; Lu, R. Edge Intelligence Oriented Integrated Sensing and Communication: A Multi-Cell Cooperative Approach. IEEE Trans. Veh. Technol. 2024, 73, 8810–8824. [Google Scholar] [CrossRef]
- Zhang, R.; Wu, W.; Chen, X.; Gao, Z.; Cai, Y. Terahertz Integrated Sensing and Communication-Empowered UAVs in 6G: A Transceiver Design Perspective. IEEE Vehicular Technology Magazine, 2025. [CrossRef]
- Xia, W.; Quek, T.Q.S.; Guo, K.; Wen, W.; Yang, H.H.; Zhu, H. Multi-Armed Bandit-Based Client Scheduling for Federated Learning. IEEE Trans. Wirel. Commun. 2020, 19, 7108–7123. [Google Scholar] [CrossRef]
- Bazzi, A.; Chafii, M. Low Dynamic Range for RIS-Aided Bistatic Integrated Sensing and Communication. IEEE J. Sel. Areas Commun. 2025, 43, 912–927. [Google Scholar] [CrossRef]
- Xia, W.; Wen, W.; Wong, K.K.; Quek, T.Q.; Zhang, J.; Zhu, H. Federated-Learning-Based Client Scheduling for Low-Latency Wireless Communications. IEEE Wirel. Commun. 2021, 28, 32–38. [Google Scholar] [CrossRef]
- Liu, F.; Garcia-Rodriguez, A.; Masouros, C.; Geraci, G. Interfering Channel Estimation in Radar-Cellular Coexistence: How Much Information Do We Need? IEEE Trans. Wirel. Commun. 2019, 18, 4238–4253. [Google Scholar] [CrossRef]
- Xu, Z.; Petropulu, A.; Sun, S. A Joint Design of MIMO-OFDM Dual-Function Radar Communication System Using Generalized Spatial Modulation. In Proceedings of the 2020 IEEE Radar Conference (RadarConf20), Florence, Italy, 21–25 September 2020; pp. 1–6. [Google Scholar] [CrossRef]
- Lu, S.; Liu, F.; Li, Y.; Zhang, K.; Huang, H.; Zou, J.; Li, X.; Dong, Y.; Dong, F.; Zhu, J.; et al. Integrated Sensing and Communications: Recent Advances and Ten Open Challenges. IEEE Internet Things J. 2024, 11, 19094–19120. [Google Scholar] [CrossRef]
- Liu, F.; Masouros, C.; Petropulu, A.P.; Griffiths, H.; Hanzo, L. Joint Radar and Communication Design: Applications, State-of-the-Art, and the Road Ahead. IEEE Trans. Commun. 2020, 68, 3834–3862. [Google Scholar] [CrossRef]
- Feng, Z.; Fang, Z.; Wei, Z.; Chen, X.; Quan, Z.; Ji, D. Joint radar and communication: A survey. China Commun. 2020, 17, 1–27. [Google Scholar] [CrossRef]
- Sakhnini, A.; Bourdoux, A.; Pollin, S. A Distributed Radar and Communication System with Interference Cancellation and Power Control. Authorea Prepr. 2024, 24, 955–968. [Google Scholar] [CrossRef]
- Martone, A.F.; Gallagher, K.A.; Sherbondy, K.D. Joint Radar and Communication System Optimization for Spectrum Sharing. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–6. [Google Scholar] [CrossRef]
- Zhang, J.A.; Huang, X.; Guo, Y.J.; Yuan, J.; Heath, R.W. Multibeam for Joint Communication and Radar Sensing Using Steerable Analog Antenna Arrays. IEEE Trans. Veh. Technol. 2019, 68, 671–685. [Google Scholar] [CrossRef]
- Rahman, M.L.; Zhang, J.A.; Huang, X.; Guo, Y.J.; Heath, R.W. Framework for a Perceptive Mobile Network Using Joint Communication and Radar Sensing. IEEE Trans. Aerosp. Electron. Syst. 2020, 56, 1926–1941. [Google Scholar] [CrossRef]
- Liu, F.; Yuan, W.; Masouros, C.; Yuan, J. Radar-Assisted Predictive Beamforming for Vehicular Links: Communication Served by Sensing. IEEE Trans. Wirel. Commun. 2020, 19, 7704–7719. [Google Scholar] [CrossRef]
- Khawar, A.; Abdelhadi, A.; Clancy, C. Target Detection Performance of Spectrum Sharing MIMO Radars. IEEE Sens. J. 2015, 15, 4928–4940. [Google Scholar] [CrossRef]
- Haitao, Z.; Zhongzheng, D.; Qin, W.; Wenchao, X.; Bo, X.; Hongbo, Z. Antenna Selection Method for Distributed Dual-Function Radar Communication in MIMO System. Chin. J. Electron. 2025, 34, 1–11. [Google Scholar] [CrossRef]
- Nartasilpa, N.; Salim, A.; Tuninetti, D.; Devroye, N. Communications System Performance and Design in the Presence of Radar Interference. IEEE Trans. Commun. 2018, 66, 4170–4185. [Google Scholar] [CrossRef]
- Zheng, L.; Lops, M.; Wang, X. Adaptive Interference Removal for Uncoordinated Radar/Communication Coexistence. IEEE J. Sel. Top. Signal Process. 2018, 12, 45–60. [Google Scholar] [CrossRef]
- Ahmed, A.; Zhang, Y.D.; Himed, B. Distributed Dual-Function Radar-Communication MIMO System with Optimized Resource Allocation. In Proceedings of the 2019 IEEE Radar Conference (RadarConf), Boston, MA, USA, 22–26 April 2019; pp. 1–5. [Google Scholar] [CrossRef]
- Shi, Q.; Razaviyayn, M.; Luo, Z.Q.; He, C. An Iteratively Weighted MMSE Approach to Distributed Sum-Utility Maximization for a MIMO Interfering Broadcast Channel. IEEE Trans. Signal Process. 2011, 59, 4331–4340. [Google Scholar] [CrossRef]
- Tse, D.; Viswanath, P. Fundamentals of Wireless Communication; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]

| Parameter | Value | Units |
|---|---|---|
| The coordinates of antenna 1 | ||
| The coordinates of antenna 2 | ||
| The coordinates of antenna 3 | ||
| The coordinates of antenna 4 | ||
| The coordinates of user 1 | ||
| The coordinates of user 2 | ||
| The coordinates of user 3 | ||
| The speed of users | ||
| Angle of motion direction relative to X-axis |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, X.; Xia, S.; Ding, Z.; Wang, Q.; Xia, W.; Zhao, H. Sensing-Aided Communication Method for Distributed Radar Communication System. Sensors 2025, 25, 3028. https://doi.org/10.3390/s25103028
Wang X, Xia S, Ding Z, Wang Q, Xia W, Zhao H. Sensing-Aided Communication Method for Distributed Radar Communication System. Sensors. 2025; 25(10):3028. https://doi.org/10.3390/s25103028
Chicago/Turabian StyleWang, Xinren, Sisi Xia, Zhongzheng Ding, Qin Wang, Wenchao Xia, and Haitao Zhao. 2025. "Sensing-Aided Communication Method for Distributed Radar Communication System" Sensors 25, no. 10: 3028. https://doi.org/10.3390/s25103028
APA StyleWang, X., Xia, S., Ding, Z., Wang, Q., Xia, W., & Zhao, H. (2025). Sensing-Aided Communication Method for Distributed Radar Communication System. Sensors, 25(10), 3028. https://doi.org/10.3390/s25103028








