Comparative Assessment of Neural Radiance Fields and 3D Gaussian Splatting for Point Cloud Generation from UAV Imagery
Abstract
1. Introduction
2. Related Works
3. Materials and Methods
3.1. Study Area and Data Capturing
3.2. Neural Radiance Fields (NeRF)
3.3. 3D Gaussian Splatting (3DGS)
3.4. Structure from Motion (SfM)
3.5. Evaluation Metrics
4. Results
4.1. Accuracy Assessment of Photogrammetric Point Clouds
4.2. Assessment of Rendering Quality
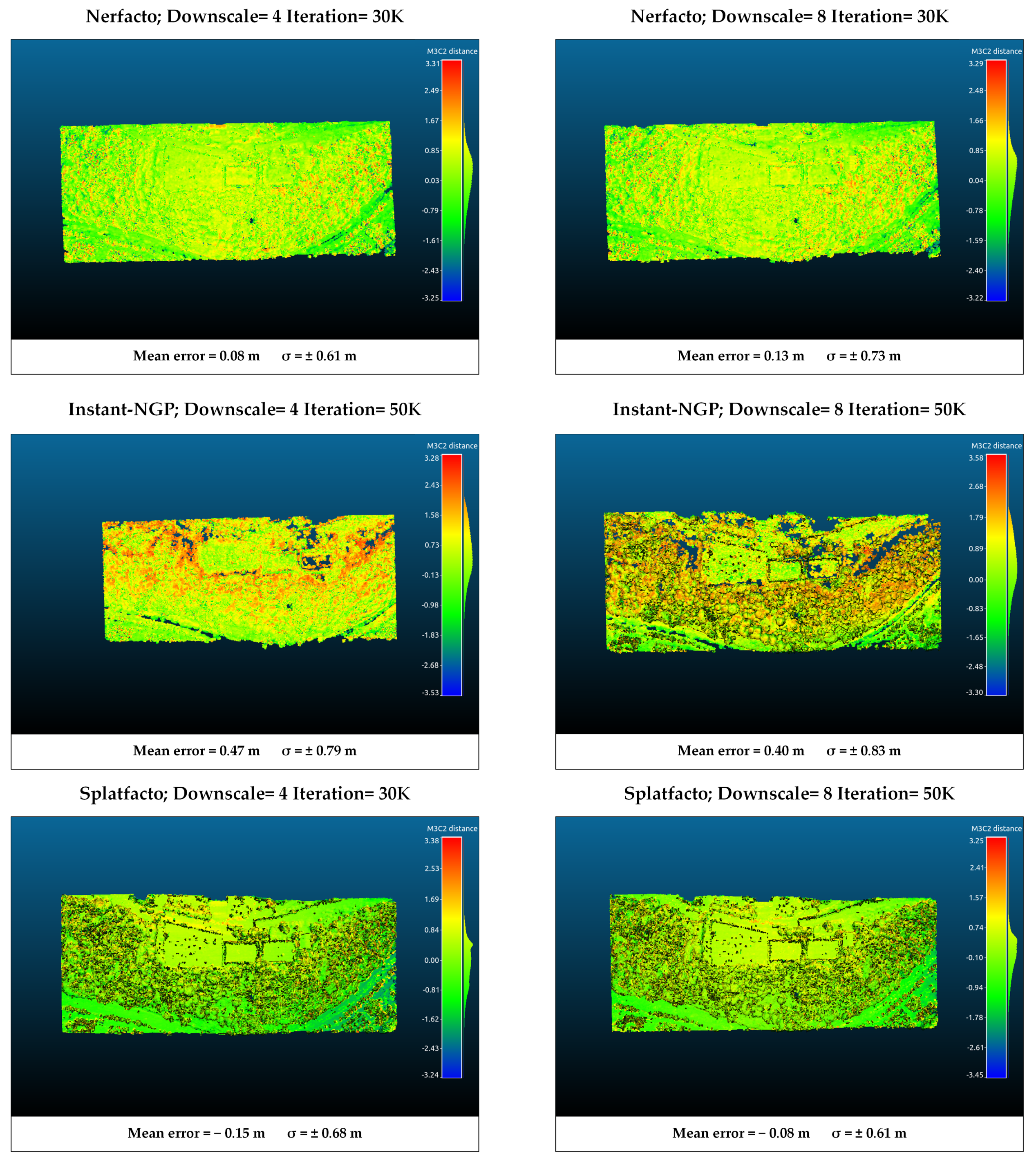
4.3. M3C2 Distance Analysis
4.4. Cross-Section Analysis
5. Discussion
6. Conclusions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| UAV | Unmanned Aerial Vehicle |
| NeRF | Neural Radiance Field |
| 3DGS | Three-dimensional gaussian splatting |
| 3D | Three-dimensional |
| AI | Artificial intelligence |
| SfM | Structure-from-Motion |
| MVS | MultiView Stereo |
| M3C2 | Multiscale Model-to-Model Cloud Comparison |
| LiDAR | Light Detection and Ranging |
| TDOM | True digital orthophoto map |
| RTK | Real time kinematic |
| 5D | Five-dimensional |
| GPU | Graphics processing unit |
| VR | Virtual reality |
| SIFT | Scale-invariant feature transform |
| PnP | Perspective-n-points |
| PSNR | Peak signal-to-noise ratio |
| SSIM | Structural similarity index measure |
| LPIPS | Learned perceptual image patch similarity |
| MSE | Mean square error |
| ICP | Iterative closest point |
| GCP | Ground control point |
References
- Li, Y.; Zeng, Q.; Shao, C.; Zhuo, P.; Li, B.; Sun, K. UAV Localization Method with Keypoints on the Edges of Semantic Objects for Low-Altitude Economy. Drones 2025, 9, 14. [Google Scholar] [CrossRef]
- Atik, M.E.; Arkali, M. Comparative Assessment of the Effect of Positioning Techniques and Ground Control Point Distribution Models on the Accuracy of UAV-Based Photogrammetric Production. Drones 2025, 9, 15. [Google Scholar] [CrossRef]
- Atik, M.E.; Arkali, M.; Atik, S.O. Impact of UAV-Derived RTK/PPK Products on Geometric Correction of VHR Satellite Imagery. Drones 2025, 9, 291. [Google Scholar] [CrossRef]
- Jiang, S.; Jiang, W.; Wang, L. Unmanned Aerial Vehicle-Based Photogrammetric 3D Mapping: A survey of techniques, applications, and challenges. IEEE Geosci. Remote Sens. Mag. 2022, 10, 135–171. [Google Scholar] [CrossRef]
- Kerle, N.; Nex, F.; Duarte, D.; Vetrivel, A. UAV-based structural damage mapping—Results from 6 years of research in two European projects. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2019, XLII-3/W8, 187–194. [Google Scholar] [CrossRef]
- Jiang, C.; Shao, H. Fast 3D Reconstruction of UAV Images Based on Neural Radiance Field. Appl. Sci. 2023, 13, 10174. [Google Scholar] [CrossRef]
- Croce, V.; Billi, D.; Caroti, G.; Piemonte, A.; De Luca, L.; Véron, P. Comparative Assessment of Neural Radiance Fields and Photogrammetry in Digital Heritage: Impact of Varying Image Conditions on 3D Reconstruction. Remote Sens. 2024, 16, 301. [Google Scholar] [CrossRef]
- Remondino, F.; Karami, A.; Yan, Z.; Mazzacca, G.; Rigon, S.; Qin, R. A Critical Analysis of NeRF-Based 3D Reconstruction. Remote Sens. 2023, 15, 3585. [Google Scholar] [CrossRef]
- Mildenhall, B.; Srinivasan, P.P.; Tancik, M.; Barron, J.T.; Ramamoorthi, R.; Ng, R. NeRF: Representing scenes as neural radiance fields for view synthesis. Commun. ACM 2022, 65, 99–106. [Google Scholar] [CrossRef]
- Kerbl, B.; Kopanas, G.; Leimkuehler, T.; Drettakis, G. 3D Gaussian Splatting for Real-Time Radiance Field Rendering. ACM Trans. Graph. 2023, 42, 1–14. [Google Scholar] [CrossRef]
- Levoy, M.; Hanrahan, P. Light Field Rendering. In Seminal Graphics Papers: Pushing the Boundaries, Volume 2, 1st ed.; Whitton, M.C., Ed.; ACM: New York, NY, USA, 2023; pp. 441–452. [Google Scholar] [CrossRef]
- Wang, W. Real-Time Fast 3D Reconstruction of Heritage Buildings Based on 3D Gaussian Splashing. In Proceedings of the 2024 IEEE 2nd International Conference on Sensors, Electronics and Computer Engineering (ICSECE), Jinzhou, China, 29–31 October 2024; pp. 1014–1018. [Google Scholar] [CrossRef]
- Tancik, M.; Weber, E.; Ng, E.; Li, R.; Yi, B.; Wang, T.; Kristoffersen, A.; Austin, J.; Salahi, K.; Ahuja, A.; et al. Nerfstudio: A Modular Framework for Neural Radiance Field Development. In Proceedings of the Special Interest Group on Computer Graphics and Interactive Techniques Conference, Los Angeles, CA, USA, 6–10 August 2023; pp. 1–12. [Google Scholar] [CrossRef]
- Schonberger, J.L.; Frahm, J.M. Structure-from-Motion Revisited. In Proceedings of the 2016 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 27–30 June 2016; pp. 4104–4113. [Google Scholar] [CrossRef]
- Yao, Y.; Luo, Z.; Li, S.; Fang, T.; Quan, L. MVSNet: Depth Inference for Unstructured Multi-view Stereo. In Proceedings of the Computer Vision—ECCV 2018, Munich, Germany, 8–14 September 2018; Ferrari, V., Hebert, M., Sminchisescu, C., Weiss, Y., Eds.; Lecture Notes in Computer Science. Springer International Publishing: Cham, Switzerland, 2018; Volume 11212, pp. 785–801. [Google Scholar] [CrossRef]
- Fan, H.; Su, H.; Guibas, L. A Point Set Generation Network for 3D Object Reconstruction from a Single Image. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Honolulu, HI, USA, 21–26 July 2017; pp. 2463–2471. [Google Scholar] [CrossRef]
- Maturana, D.; Scherer, S. VoxNet: A 3D Convolutional Neural Network for real-time object recognition. In Proceedings of the 2015 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Hamburg, Germany, 17 December 2015; pp. 922–928. [Google Scholar] [CrossRef]
- Groueix, T.; Fisher, M.; Kim, V.G.; Russell, B.C.; Aubry, M. A Papier-Mache Approach to Learning 3D Surface Generation. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–22 June 2018; pp. 216–224. [Google Scholar] [CrossRef]
- Barron, J.T.; Mildenhall, B.; Tancik, M.; Hedman, P.; Martin-Brualla, R.; Srinivasan, P.P. Mip-NeRF: A Multiscale Representation for Anti-Aliasing Neural Radiance Fields. In Proceedings of the 2021 IEEE/CVF International Conference on Computer Vision (ICCV), Montreal, QC, Canada, 10–17 October 2021; pp. 5835–5844. [Google Scholar] [CrossRef]
- Barron, J.T.; Mildenhall, B.; Verbin, D.; Srinivasan, P.P.; Hedman, P. Mip-NeRF 360: Unbounded Anti-Aliased Neural Radiance Fields. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition (CVPR), New Orleans, LA, USA, 18–24 June 2022; pp. 5460–5469. [Google Scholar] [CrossRef]
- Müller, T.; Evans, A.; Schied, C.; Keller, A. Instant neural graphics primitives with a multiresolution hash encoding. ACM Trans. Graph. 2022, 41, 1–15. [Google Scholar] [CrossRef]
- Condorelli, F.; Rinaudo, F.; Salvadore, F.; Tagliaventi, S. A comparison between 3D reconstruction using NeRF Neural Networks and MVS algorithms on cultural heritage images. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2021, XLIII-B2-2021, 565–570. [Google Scholar] [CrossRef]
- Murtiyoso, A.; Grussenmeyer, P. Initial assessment on the use of state-of-the-art NeRF neural network 3D reconstruction for heritage documentation. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-M-2-2023, 1113–1118. [Google Scholar] [CrossRef]
- Balloni, E.; Gorgoglione, L.; Paolanti, M.; Mancini, A.; Pierdicca, R. Few shot photogrametry: A comparison between NeRF and MVS-SFM for the documentation of cultural heritage. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2023, XLVIII-M-2- 2023, 155–162. [Google Scholar] [CrossRef]
- Chen, G.; Wang, W. A Survey on 3D Gaussian Splatting. arXiv 2024, arXiv:2401.03890. [Google Scholar] [CrossRef]
- Basso, A.; Condorelli, F.; Giordano, A.; Morena, S.; Perticarini, M. Evolution of rendering based on radiance fields. The Palermo case study for a comparison between NeRF and Gaussian Splatting. Int. Arch. Photogramm. Remote Sens. Spat. Inf. Sci. 2024, XLVIII-2/W4-2024, 57–64. [Google Scholar] [CrossRef]
- Huang, H.; Tian, G.; Chen, C. Evaluating the Point Cloud of Individual Trees Generated from Images Based on Neural Radiance Fields (NeRF) Method. Remote Sens. 2024, 16, 967. [Google Scholar] [CrossRef]
- Wei, J.; Zhu, G.; Chen, X. NeRF-Based Large-Scale Urban True Digital Orthophoto Map Generation Method. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 1070–1084. [Google Scholar] [CrossRef]
- Tang, J.; Gao, Y.; Yang, D.; Yan, L.; Yue, Y.; Yang, Y. DroneSplat: 3D Gaussian Splatting for Robust 3D Reconstruction from In-the-Wild Drone Imagery. arXiv 2025, arXiv:2503.16964. [Google Scholar] [CrossRef]
- Qian, J.; Yan, Y.; Gao, F.; Ge, B.; Wei, M.; Shangguan, B.; He, G. C3DGS: Compressing 3D Gaussian Model for Surface Reconstruction of Large-Scale Scenes Based on Multiview UAV Images. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2025, 18, 4396–4409. [Google Scholar] [CrossRef]
- Jia, Z.; Wang, B.; Chen, C. Drone-NeRF: Efficient NeRF based 3D scene reconstruction for large-scale drone survey. Image Vis. Comput. 2024, 143, 104920. [Google Scholar] [CrossRef]
- Li, L.; Zhang, Y.; Jiang, Z.; Wang, Z.; Zhang, L.; Gao, H. Unmanned Aerial Vehicle-Neural Radiance Field (UAV-NeRF): Learning Multiview Drone Three-Dimensional Reconstruction with Neural Radiance Field. Remote Sens. 2024, 16, 4168. [Google Scholar] [CrossRef]
- Wang, T.; Yang, J.; Cai, Z.; Chi, X.; Huang, H.; Deng, F. True orthophoto generation from unmanned aerial vehicle imagery using neural radiance fields with multi-resolution hash encoding. J. Appl. Remote Sens. 2024, 18, 046507. [Google Scholar] [CrossRef]
- Chen, S.; Yan, Q.; Qu, Y.; Gao, W.; Yang, J.; Deng, F. Ortho-NeRF: Generating a true digital orthophoto map using the neural radiance field from unmanned aerial vehicle images. Geo-Spat. Inf. Sci. 2024, 1–20. [Google Scholar] [CrossRef]
- Wu, Y.; Liu, J.; Ji, S. 3D Gaussian Splatting for Large-scale Surface Reconstruction from Aerial Images. arXiv 2024, arXiv:2409.00381. [Google Scholar] [CrossRef]
- Ham, Y.; Michalkiewicz, M.; Balakrishnan, G. DRAGON: Drone and Ground Gaussian Splatting for 3D Building Reconstruction. In Proceedings of the 2024 IEEE International Conference on Computational Photography (ICCP), Lausanne, Switzerland, 22–24 July 2024; pp. 1–12. [Google Scholar] [CrossRef]
- Mari, R.; Facciolo, G.; Ehret, T. Sat-NeRF: Learning Multi-View Satellite Photogrammetry With Transient Objects and Shadow Modeling Using RPC Cameras. In Proceedings of the 2022 IEEE/CVF Conference on Computer Vision and Pattern Recognition Workshops (CVPRW), New Orleans, LA, USA, 19–20 June 2022; pp. 1310–1320. [Google Scholar] [CrossRef]
- Arslan, O. UAV Photogrammetry as a Photogrammetric Computer Vision Technique. Turk. J. Unmanned Aer. Veh. 2023, 5, 59–71. [Google Scholar] [CrossRef]
- Lowe, D.G. Distinctive Image Features from Scale-Invariant Keypoints. Int. J. Comput. Vis. 2004, 60, 91–110. [Google Scholar] [CrossRef]
- Chen, K.; Reichard, G.; Akanmu, A.; Xu, X. Geo-registering UAV-captured close-range images to GIS-based spatial model for building façade inspections. Autom. Constr. 2021, 122, 103503. [Google Scholar] [CrossRef]
- Zhao, S.; Kang, F.; Li, J.; Ma, C. Structural health monitoring and inspection of dams based on UAV photogrammetry with image 3D reconstruction. Autom. Constr. 2021, 130, 103832. [Google Scholar] [CrossRef]
- Hore, A.; Ziou, D. Image Quality Metrics: PSNR vs. SSIM. In Proceedings of the 2010 20th International Conference on Pattern Recognition, Istanbul, Turkey, 23–26 August 2010; pp. 2366–2369. [Google Scholar] [CrossRef]
- Wang, Z.; Bovik, A.; Sheikh, H.; Simoncelli, E. Image quality assessment: From error visibility to structural similarity. IEEE Trans. Image Process. 2004, 13, 600–612. [Google Scholar] [CrossRef]
- Zhang, R.; Isola, P.; Efros, A.A.; Shechtman, E.; Wang, O. The Unreasonable Effectiveness of Deep Features as a Perceptual Metric. In Proceedings of the 2018 IEEE/CVF Conference on Computer Vision and Pattern Recognition, Salt Lake City, UT, USA, 18–23 June 2018; pp. 586–595. [Google Scholar] [CrossRef]
- Fang, X.; Zhang, Y.; Tan, H.; Liu, C.; Yang, X. Performance Evaluation and Optimization of 3D Gaussian Splatting in Indoor Scene Generation and Rendering. ISPRS Int. J. Geo-Inf. 2025, 14, 21. [Google Scholar] [CrossRef]
- Duan, D.; Deng, Y.; Zhang, J.; Wang, J.; Dong, P. Influence of VF and SOR-Filtering Methods on Tree Height Inversion Using Unmanned Aerial Vehicle LiDAR Data. Drones 2024, 8, 119. [Google Scholar] [CrossRef]
- Atik, M.E.; Duran, Z. 3D facial recognition using local feature-based methods and accuracy assessment. J. Fac. Eng. Archit. Gazi Univ. 2020, 36, 359–372. [Google Scholar] [CrossRef]
- Guo, Y.; Bennamoun, M.; Sohel, F.; Lu, M.; Wan, J.; Kwok, N.M. A Comprehensive Performance Evaluation of 3D Local Feature Descriptors. Int. J. Comput. Vis. 2016, 116, 66–89. [Google Scholar] [CrossRef]
- Lague, D.; Brodu, N.; Leroux, J. Accurate 3D comparison of complex topography with terrestrial laser scanner: Application to the Rangitikei canyon (N-Z). ISPRS J. Photogramm. Remote Sens. 2013, 82, 10–26. [Google Scholar] [CrossRef]












| Point ID | Error X (m) | Error Y (m) | Error Z (m) |
|---|---|---|---|
| PN1 | −0.028 | 0.002 | −0.141 |
| PN2 | −0.026 | 0.067 | −0.154 |
| PN3 | −0.01 | 0.014 | −0.066 |
| PN4 | −0.02 | 0.036 | −0.065 |
| PN5 | −0.046 | 0.057 | −0.112 |
| PN6 | 0.002 | 0.025 | −0.111 |
| PN7 | −0.03 | 0.033 | −0.13 |
| PN8 | −0.034 | −0.017 | −0.116 |
| PN9 | −0.010 | 0.003 | −0.268 |
| RMSE | 0.026 | 0.035 | 0.141 |
| Point ID | Error X (m) | Error Y (m) | Error Z (m) |
|---|---|---|---|
| PN1 | −0.019 | 0.018 | 0.068 |
| PN2 | −0.044 | 0.015 | 0.187 |
| PN3 | −0.015 | 0.002 | 0.209 |
| PN4 | 0.009 | −0.029 | 0.175 |
| PN5 | −0.016 | 0.01 | 0.187 |
| PN6 | −0.007 | 0.023 | 0.16 |
| PN7 | −0.004 | −0.017 | 0.372 |
| PN8 | 0.015 | −0.009 | 0.359 |
| RMSE | 0.020 | 0.017 | 0.240 |
| Method | Number of Iterations | Downscale (4) | Downscale (8) | ||||
|---|---|---|---|---|---|---|---|
| PSNR | SSIM | LPIPS | PSNR | SSIM | LPIPS | ||
| 5K | 16.1579 | 0.4472 | 0.7103 | 16.9832 | 0.4814 | 0.4958 | |
| Nerfacto | 30K | 16.3759 | 0.4533 | 0.5684 | 16.9837 | 0.4826 | 0.3699 |
| 50K | 16.2834 | 0.4431 | 0.5416 | 16.8934 | 0.4773 | 0.3426 | |
| 5K | 18.5218 | 0.5394 | 0.6403 | 18.8985 | 0.6161 | 0.4424 | |
| Instant-NGP | 30K | 18.9743 | 0.5937 | 0.5194 | 19.6127 | 0.6848 | 0.3363 |
| 50K | 18.7872 | 0.5961 | 0.5078 | 19.3977 | 0.6878 | 0.3236 | |
| 5K | 20.5129 | 0.6644 | 0.4734 | 21.1858 | 0.7182 | 0.3325 | |
| Gaussian Splatting | 30K | 23.0607 | 0.8318 | 0.2224 | 23.5486 | 0.8542 | 0.1444 |
| 50K | 23.2573 | 0.8359 | 0.2114 | 23.8038 | 0.8572 | 0.1388 | |
| Method | Number of Iterations | Downscale (4) | Downscale (8) | ||||
|---|---|---|---|---|---|---|---|
| PSNR | SSIM | LPIPS | PSNR | SSIM | LPIPS | ||
| 5K | 19.9150 | 0.4104 | 0.6216 | 20.8616 | 0.5137 | 0.3584 | |
| Nerfacto | 30K | 20.0619 | 0.4233 | 0.4746 | 20.6049 | 0.5018 | 0.2466 |
| 50K | 18.7324 | 0.3550 | 0.4482 | 20.5677 | 0.4954 | 0.2296 | |
| 5K | 21.6822 | 0.4952 | 0.5761 | 23.2117 | 0.6546 | 0.3547 | |
| Instant-NGP | 30K | 22.7156 | 0.5703 | 0.4610 | 24.6328 | 0.7586 | 0.2535 |
| 50K | 22.9457 | 0.5857 | 0.4397 | 24.7991 | 0.7715 | 0.2399 | |
| 5K | 23.3103 | 0.6733 | 0.4077 | 24.4501 | 0.7713 | 0.2512 | |
| Splatfacto | 30K | 27.6840 | 0.8898 | 0.0959 | 28.9073 | 0.9186 | 0.0589 |
| 50K | 27.5989 | 0.8887 | 0.0919 | 28.9315 | 0.9180 | 0.0561 | |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2025 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Atik, M.E. Comparative Assessment of Neural Radiance Fields and 3D Gaussian Splatting for Point Cloud Generation from UAV Imagery. Sensors 2025, 25, 2995. https://doi.org/10.3390/s25102995
Atik ME. Comparative Assessment of Neural Radiance Fields and 3D Gaussian Splatting for Point Cloud Generation from UAV Imagery. Sensors. 2025; 25(10):2995. https://doi.org/10.3390/s25102995
Chicago/Turabian StyleAtik, Muhammed Enes. 2025. "Comparative Assessment of Neural Radiance Fields and 3D Gaussian Splatting for Point Cloud Generation from UAV Imagery" Sensors 25, no. 10: 2995. https://doi.org/10.3390/s25102995
APA StyleAtik, M. E. (2025). Comparative Assessment of Neural Radiance Fields and 3D Gaussian Splatting for Point Cloud Generation from UAV Imagery. Sensors, 25(10), 2995. https://doi.org/10.3390/s25102995






