Square Root Unscented Kalman Filter-Based Multiple-Model Fault Diagnosis of PEM Fuel Cells
Abstract
1. Introduction
- To develop a diagnostic oriented multi-scale PEMFC catalytic degradation model that investigates the failure mechanisms of catalytic degradation through platinum dissolution and platinum oxide formation [25] on overall stack performance. The model can be used to generate reference data to test the proposed fault diagnosis system in effectively detecting catalytic degradation in PEM fuel cells.
- To implement the principles of multiple-model fault diagnosis, first introduced in [26], combined with the SRUKF as a Bayes’ filter for the diagnosis of fuel cell systems in dynamic operations [27]. Fundamentally, the main task of multiple-model fault diagnosis schemes is to select the underlying model which most likely represents the current system state.
2. Materials and Methods
2.1. Multi-Scale PEMFC Catalytic Degradation Model
- Gases behave like ideal gases.
- PEMFC is an isothermal system.
- The anodic overpotential is neglected.
- All cells in the stack are homogeneous.
- The catalyst layer is composed of spherically shaped carbon supported platinum particles.
- Platinum dissolution and platinum oxide formation and reduction are the only mechanisms responsible for catalytic degradation.
2.1.1. Macroscopic Model
2.1.2. Microscopic Model
2.2. Vehicle Model
2.3. Design of Fault Diagnosis Models
2.3.1. Flooding
2.3.2. Catalytic Degradation
2.4. Fault Diagnosis Scheme
2.4.1. Square Root Unscented Kalman Filter
| Algorithm 1 Square root unscented Kalman filter |
Sigma point calculation and time update |
2.4.2. Bayesian Model Selection Method
3. Results
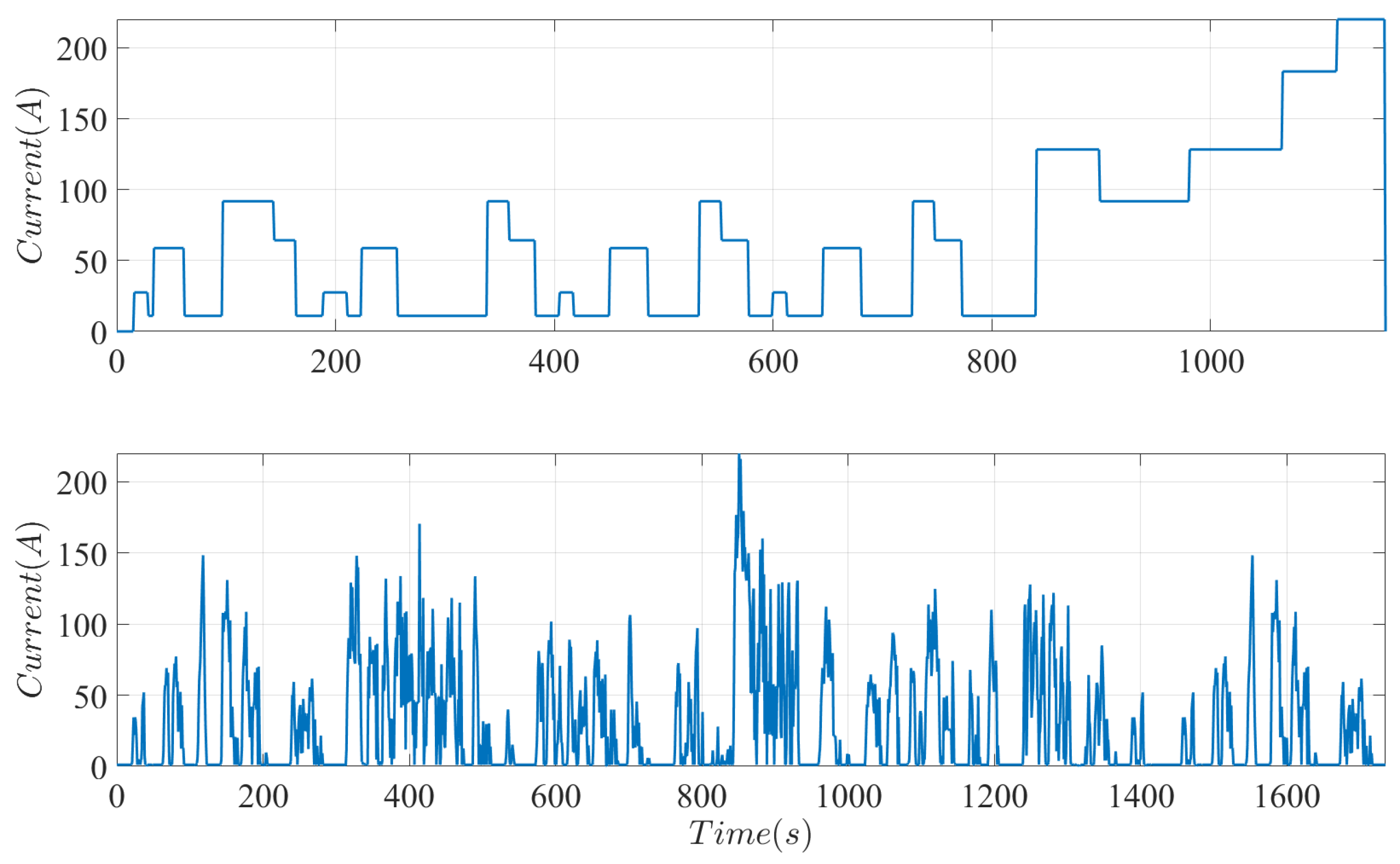
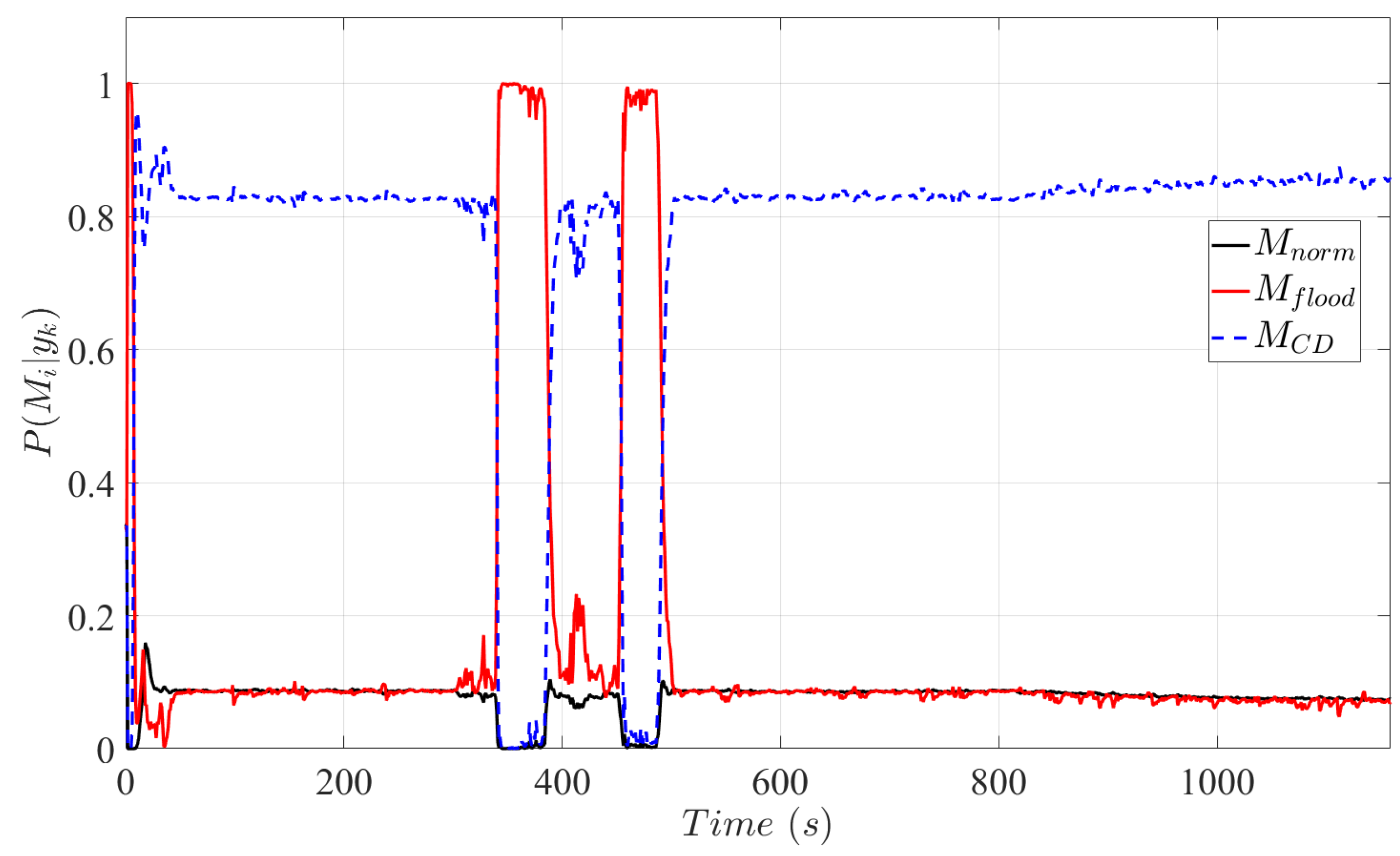
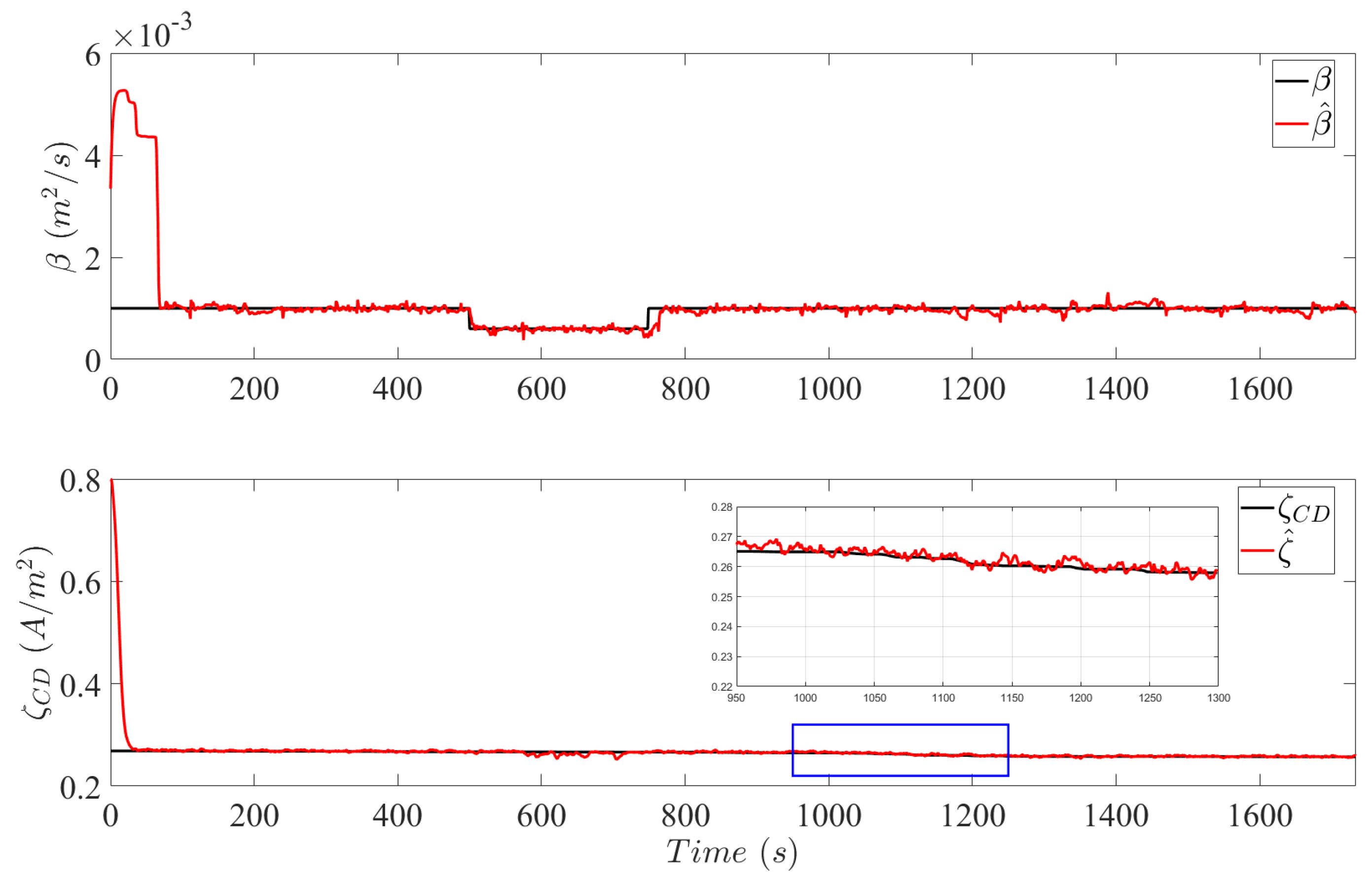
3.1. NEDC Driving Cycle
3.2. LA92 Cycle
4. Conclusions
Author Contributions
Funding
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
| Annotation | Description | Value |
|---|---|---|
| Vehicle Model | ||
| Vehicle Mass | 10,000 kg | |
| Drag Coefficient | 0.51 | |
| Frontal Cross-Sectional area | 6 m2 | |
| Open-Circuit Voltage | 1.229 V | |
| Roll Resistance coefficient | 0.013 | |
| Number of Cells | 370 | |
| Macroscopic Model | ||
| Electrode Surface Area | 0.0053 m2 | |
| Mass Transfer Coefficient | 1 × 10−3 m3/s | |
| Cathode Double Layer Capacitance | 2 A/m2 | |
| Ohmic Resistances | 0.0022 Ohms | |
| Exchange Current Density | 0.8 A/m2 | |
| Gas Bulk Volume | 2 m3 | |
| Electrode Bulk Volume | 2 m3 | |
| Gas Constant | 8.314 | |
| F | Faradays Constant | 8.314 |
| T | Stack Temperature | 353 |
| Mass Transfer Coefficient of Oxygen Oxidation Reaction | 0.5 | |
| Reference Oxygen Concentration | 8 mol/m3 | |
| Microscopic Model | ||
| Reaction Rate Constant of Platinum Dissolution | ||
| Reaction Rate Constant of Platinum Oxide formation | 1.36 | |
| Reaction Rate Constant of Platinum Oxide Dissolution | 1.6 | |
| Thermodynamic Reversible of Pt Dissolution | 1.188 V | |
| Thermodynamic Reversible of PtO Formation | 0.98 V | |
| Anodic Mass Transfer Coefficient of Reaction (12) | 0.5 | |
| Anodic Mass Transfer Coefficient of Reaction (13) | 0.35 | |
| Cathodic Mass Transfer Coefficient of Reaction (13) | 0.15 | |
| Surface Tension of Pt | 2.37 J/m2 | |
| Surface Tension of Pt | 2.37 J/m2 | |
| Surface Tension of PtO | 1 J/m2 | |
| Electrochemical Potential of PtO of Pt | 42.3 J/mol | |
| Molecular Weight of Pt | 195 g/mol | |
| Molecular Weight of PtO | 227 g/mol | |
| Density of Pt | 21 g/m3 | |
| Density of PtO | 14.1 g/m3 | |
| PtO-PtO Interaction Parameter | 30 J/mol | |
| Reference Proton Concentration | 444 mol/m3 | |
| Moles of Active Sites per Platinum Area | 2.18 | |
References
- Federal Ministry for Economic Affairs and Climate Action. National Hydrogen Strategy Update; Annual Report of the National Hydrogen Strategy NHS2023; Federal Ministry for Economic Affairs and Climate Action: Berlin, Germany, 2023. [Google Scholar]
- Marcinkoski, J.; Vijayagopal, R.; Adams, J.; James, B.; Kopasz, J.; Ahluwalia, R. DOE Advanced Truck Technologies; Technical Report Record 19006; U.S Department of Energy: Washington, DC, USA, 2019.
- Pei, P.; Chen, H. Main Factors Affecting the Lifetime of Proton Exchange Membrane fuel Cells in Vehicle Applications: A review. Appl. Energy 2014, 125, 60–75. [Google Scholar] [CrossRef]
- Zhao, J.; Tu, Z.; Chan, S.H. Carbon corrosion mechanism and mitigation strategies in a proton exchange membrane fuel cell (PEMFC): A review. J. Power Sources 2021, 488, 229434. [Google Scholar] [CrossRef]
- Futter, G. Physical Modeling of Pemfc Performance and Chemical Degradation. Ph.D. Thesis, University of Stuttgart, Stuttgart, Germany, 2019. [Google Scholar]
- Baroody, H.A.; Kjeang, E. Predicting platinum dissolution and performance degradation under drive cycle operation of polymer electrolyte fuel cells. J. Electrochem. Soc. 2021, 168. [Google Scholar] [CrossRef]
- Steiner, N.Y.; Hissel, D.; Moçotéguy, P.; Candusso, D. Non intrusive diagnosis of polymer electrolyte fuel cells by wavelet packet transform. Int. J. Hydrogen Energy 2011, 36, 740–746. [Google Scholar] [CrossRef]
- Ibrahim, M.; Antoni, U.; Steiner, N.Y.; Jemei, S.; Kokonendji, C.; Ludwig, B.; Moçotéguy, P.; Hissel, D. Signal-based Diagnostics by Wavelet Transform for Proton Exchange Membrane Fuel Cell. Energy Procedia 2015, 74, 1508–1516. [Google Scholar] [CrossRef]
- Damour, C.; Benne, M.; Grondin-Perez, B.; Bessafi, M.; Hissel, D.; Chabriat, J.P. Polymer Electrolyte Membrane Fuel Cell Fault Diagnosis based on Empirical Mode Decomposition. J. Power Sources 2015, 299, 596–603. [Google Scholar] [CrossRef]
- Chen, J.; Zhou, B. Diagnosis of PEM fuel cell stack dynamic behaviors. J. Power Sources 2008, 177, 83–95. [Google Scholar] [CrossRef]
- Li, Z.; Outbib, R.; Giurgea, S.; Hissel, D. Diagnosis for PEMFC systems: A data-driven approach with the capabilities of online adaptation and novel fault detection. IEEE Trans. Ind. Electron. 2015, 62, 5164–5174. [Google Scholar] [CrossRef]
- Lu, J.; Gao, Y.; Zhang, L.; Li, K.; Yin, C. PEMFC water management fault diagnosis method based on principal component analysis and support vector data description. In Proceedings of the IECON 2021–47th Annual Conference of the IEEE Industrial Electronics Society, Toronto, ON, Canada, 13–16 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1–8. [Google Scholar]
- Benmouna, A.; Becherif, M.; Depernet, D.; Gustin, F.; Ramadan, H.; Fukuhara, S. Fault diagnosis methods for proton exchange membrane fuel cell system. Int. J. Hydrogen Energy 2017, 42, 1534–1543. [Google Scholar] [CrossRef]
- Rodat, S.; Sailler, S.; Druart, F.; Thivel, P.X.; Bultel, Y.; Ozil, P. EIS Measurements in the Diagnosis of the Environment within a PEMFC Stack. J. Appl. Electrochem. 2010, 40, 911–920. [Google Scholar] [CrossRef]
- Hernandez, A.; Hissel, D.; Outbib, R. Modeling and Fault Diagnosis of a Polymer Electrolyte Fuel Cell using Electrical Equivalent Analysis. IEEE Trans. Energy Convers. 2009, 25, 148–160. [Google Scholar] [CrossRef]
- Pivac, I.; Bezmalinović, D.; Barbir, F. Catalyst Degradation Diagnostics of Proton Exchange Membrane Fuel Cells using Electrochemical Impedance Spectroscopy. Int. J. Hydrogen Energy 2018, 43, 13512–13520. [Google Scholar] [CrossRef]
- Cadet, C.; Jemei, S.; Druart, F.; Hissel, D. Diagnostic tools for PEMFCs: From conception to implementation. Int. J. Hydrogen Energy 2014, 39, 10613–10626. [Google Scholar] [CrossRef]
- Petrone, R.; Zheng, Z.; Hissel, D.; Péra, M.C.; Pianese, C.; Sorrentino, M.; Becherif, M.; Yousfi-Steiner, N. A Review on Model-Based Diagnosis Methodologies for PEMFCs. Int. J. Hydrogen Energy 2013, 38, 7077–7091. [Google Scholar] [CrossRef]
- Escobet, T.; Feroldi, D.; De Lira, S.; Puig, V.; Quevedo, J.; Riera, J.; Serra, M. Model-based Fault diagnosis in PEM Fuel Cell Systems. J. Power Sources 2009, 192, 216–223. [Google Scholar] [CrossRef]
- Zhang, X.; Pisu, P. An Unscented Kalman Filter Based On-line Diagnostic Approach for PEM Fuel Cell Flooding. Int. J. Progn. Health Manag. 2014, 4. [Google Scholar] [CrossRef]
- De Lira, S.; Puig, V.; Quevedo, J.; Husar, A. LPV Observer Design for PEM Fuel Cell System: Application to Fault Detection. J. Power Sources 2011, 196, 4298–4305. [Google Scholar] [CrossRef]
- Ariza, E.; Correcher, A.; Vargas-Salgado, C. PEMFCs Model-Based Fault Diagnosis: A Proposal Based on Virtual and Real Sensors Data Fusion. Sensors 2023, 23, 7383. [Google Scholar] [CrossRef] [PubMed]
- Allam, A.; Mangold, M.; Zhang, P. Fault Diagnosis of PEM Fuel Cells: An Assessment of two Bayes’ Filters. IFAC-PapersOnLine 2024, 58, 473–478. [Google Scholar] [CrossRef]
- Ding, S.X. Model-Based Fault Diagnosis Techniques: Design Schemes, Algorithms, and Tools; Springer: Heidelberg, Germany, 2013. [Google Scholar]
- Darling, R.M.; Meyers, J.P. Kinetic Model of platinum Dissolution in PEMFCs. J. Electrochem. Soc. 2003, 150, A1523. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Van Der Merwe, R.; Wan, E.A. The Square-Root Unscented Kalman Filter for State and Parameter-Estimation. In Proceedings of the 2001 IEEE International Conference on Acoustics, Speech, and Signal Processing, Salt Lake City, UT, USA, 7–11 May 2001; pp. 3461–3464. [Google Scholar]
- Wang, Y.; Meng, D.; Li, R.; Zhou, Y.; Zhang, X. Multi-fault diagnosis of interacting multiple model batteries based on low inertia noise reduction. IEEE Access 2021, 9, 18465–18480. [Google Scholar] [CrossRef]
- Pandy, A.; Yang, Z.; Gummalla, M.; Atrazhev, V.V.; Kuzminyh, N.Y.; Sultanov, V.I.; Burlatsky, S. A carbon corrosion model to evaluate the effect of steady state and transient operation of a polymer electrolyte membrane fuel cell. J. Electrochem. Soc. 2013, 160, F972. [Google Scholar] [CrossRef]
- Rinaldo, S.G.; Stumper, J.; Eikerling, M. Physical theory of platinum nanoparticle dissolution in polymer electrolyte fuel cells. J. Phys. Chem. C 2010, 114, 5773–5785. [Google Scholar] [CrossRef]
- Kneer, A.; Wagner, N. A semi-empirical catalyst degradation model based on voltage cycling under automotive operating conditions in PEM fuel cells. J. Electrochem. Soc. 2019, 166, F120. [Google Scholar] [CrossRef]
- You, H.; Fu, J.; Li, X. Research on ecsa degradation model for pem fuel cell under vehicle conditions. In Proceedings of the 2020 4th CAA International Conference on Vehicular Control and Intelligence (CVCI), Hangzhou, China, 18–20 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 573–577. [Google Scholar]
- Jahnke, T.; Futter, G.A.; Baricci, A.; Rabissi, C.; Casalegno, A. Physical modeling of catalyst degradation in low temperature fuel cells: Platinum oxidation, dissolution, particle growth and platinum band formation. J. Electrochem. Soc. 2019, 167, 013523. [Google Scholar] [CrossRef]
- Kregar, A.; Tavčar, G.; Kravos, A.; Katrašnik, T. Predictive system-level modeling framework for transient operation and cathode platinum degradation of high temperature proton exchange membrane fuel cells. Appl. Energy 2020, 263, 114547. [Google Scholar] [CrossRef]
- Moein-Jahromi, M.; Kermani, M.; Movahed, S. Degradation Forecast for PEMFC Cathode-Catalysts Under Cyclic Loads. J. Power Sources 2017, 359, 611–625. [Google Scholar] [CrossRef]
- Robin, C.; Gerard, M.; Franco, A.A.; Schott, P. Multi-scale Coupling between Two Dynamical Models for PEMFC Aging Prediction. Int. J. Hydrogen Energy 2013, 38, 4675–4688. [Google Scholar] [CrossRef]
- Allam, A.; Mangold, M.; Zhang, P. Fault Diagnosis of Proton Exchange Membrane Fuel Cells. In Proceedings of the 5th International Conference on Control and Fault-Tolerant Systems, Saint-Raphael, France, 29 September–1 October 2021; pp. 366–371. [Google Scholar]
- Yousfi-Steiner, N.; Moçotéguy, P.; Candusso, D.; Hissel, D. A Review on Polymer Electrolyte Membrane Fuel Cell Catalyst Degradation and Starvation Issues: Causes, Consequences and Diagnostic for Mitigation. J. Power Sources 2009, 194, 130–145. [Google Scholar] [CrossRef]
- Lemoine-Nava, R.; Hanke-Rauschenbach, R.; Mangold, M.; Sundmacher, K. The gas diffusion layer in polymer electrolyte membrane fuel cells: A process model of the two-phase flow. Int. J. Hydrogen Energy 2011, 36, 1637–1653. [Google Scholar] [CrossRef]
- Grötsch, M.; Hanke-Rauschenbach, R.; Mangold, M. Bifurcation Analysis of a Two-Phase PEMFC Model. J. Fuel Cell Sci. Technol. 2008, 5, 021001. [Google Scholar] [CrossRef]
- Yousfi-Steiner, N.; Moçotéguy, P.; Candusso, D.; Hissel, D.; Hernandez, A.; Aslanides, A. A review on PEM voltage degradation associated with water management: Impacts, influent factors and characterization. J. Power Sources 2008, 183, 260–274. [Google Scholar] [CrossRef]
- Yamada, H.; Hatanaka, T.; Murata, H.; Morimoto, Y. Measurement of flooding in gas diffusion layers of polymer electrolyte fuel cells with conventional flow field. J. Electrochem. Soc. 2006, 153, A1748. [Google Scholar] [CrossRef]
- Aguilar, J.A.; Andrade-Cetto, J.; Husar, A. Control-oriented Estimation of the Exchange Current Density in PEM Fuel Cells via Stochastic Filtering. Int. J. Energy Res. 2022, 46, 22516–22529. [Google Scholar] [CrossRef]
- Larminie, J.; Dicks, A.; McDonald, M.S. Fuel Cell Systems Explained; John Wiley: Chichester, UK, 2003; Volume 2. [Google Scholar]
- Blackmore, L.; Williams, B. Finite Horizon Control Design for Optimal Discrimination between Several Models. In Proceedings of the 45th IEEE Conference on Decision and Control, San Diego, CA, USA, 13–15 December 2006; pp. 1147–1152. [Google Scholar]
- Gadsden, S.A.; Song, Y.; Habibi, S.R. Novel Model-Based Estimators for the Purposes of Fault Detection and Diagnosis. IEEE/ASME Trans. Mechatron. 2013, 18, 1237–1249. [Google Scholar] [CrossRef]
- Zhang, K.; Jiang, B.; Chen, F. Multiple-Model-Based Diagnosis of multiple faults with high-speed train applications using second-level adaptation. IEEE Trans. Ind. Electron. 2020, 68, 6257–6266. [Google Scholar] [CrossRef]
- Julier, S.J. The Scaled Unscented Transformation. In Proceedings of the 2002 American Control Conference, Anchorage, AK, USA, 8–10 May 2002; pp. 4555–4559. [Google Scholar]
- Julier, S.J.; Uhlmann, J.K.; Durrant-Whyte, H.F. A new approach for filtering nonlinear systems. In Proceedings of the 1995 American Control Conference-ACC’95, Washington, DC, USA, 21–23 June 1995; IEEE: Piscataway, NJ, USA, 1995; Volume 3, pp. 1628–1632. [Google Scholar]
- Tsotridis, G.; Pilenga, A.; De Marco, G.; Malkow, T. EU Harmonised Test Protocols for PEMFC MEA Testing in Single Cell Configuration for Automotive Applications; Publications Office of the European Union Luxembourg: Luxembourg, 2015. [Google Scholar]
- Guilminot, E.; Corcella, A.; Chatenet, M.; Maillard, F.; Charlot, F.; Berthomé, G.; Iojoiu, C.; Sanchez, J.Y.; Rossinot, E.; Claude, E. Membrane and active layer degradation upon PEMFC steady-state operation: I. platinum dissolution and redistribution within the MEA. J. Electrochem. Soc. 2007, 154, B1106. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Allam, A.; Mangold, M.; Zhang, P. Square Root Unscented Kalman Filter-Based Multiple-Model Fault Diagnosis of PEM Fuel Cells. Sensors 2025, 25, 29. https://doi.org/10.3390/s25010029
Allam A, Mangold M, Zhang P. Square Root Unscented Kalman Filter-Based Multiple-Model Fault Diagnosis of PEM Fuel Cells. Sensors. 2025; 25(1):29. https://doi.org/10.3390/s25010029
Chicago/Turabian StyleAllam, Abdulrahman, Michael Mangold, and Ping Zhang. 2025. "Square Root Unscented Kalman Filter-Based Multiple-Model Fault Diagnosis of PEM Fuel Cells" Sensors 25, no. 1: 29. https://doi.org/10.3390/s25010029
APA StyleAllam, A., Mangold, M., & Zhang, P. (2025). Square Root Unscented Kalman Filter-Based Multiple-Model Fault Diagnosis of PEM Fuel Cells. Sensors, 25(1), 29. https://doi.org/10.3390/s25010029





