Phased Array Ultrasonic Method for Robotic Preload Measurement in Offshore Wind Turbine Bolted Connections
Abstract
1. Introduction
2. Theoretical Background
3. Methodology and Experimental Setup
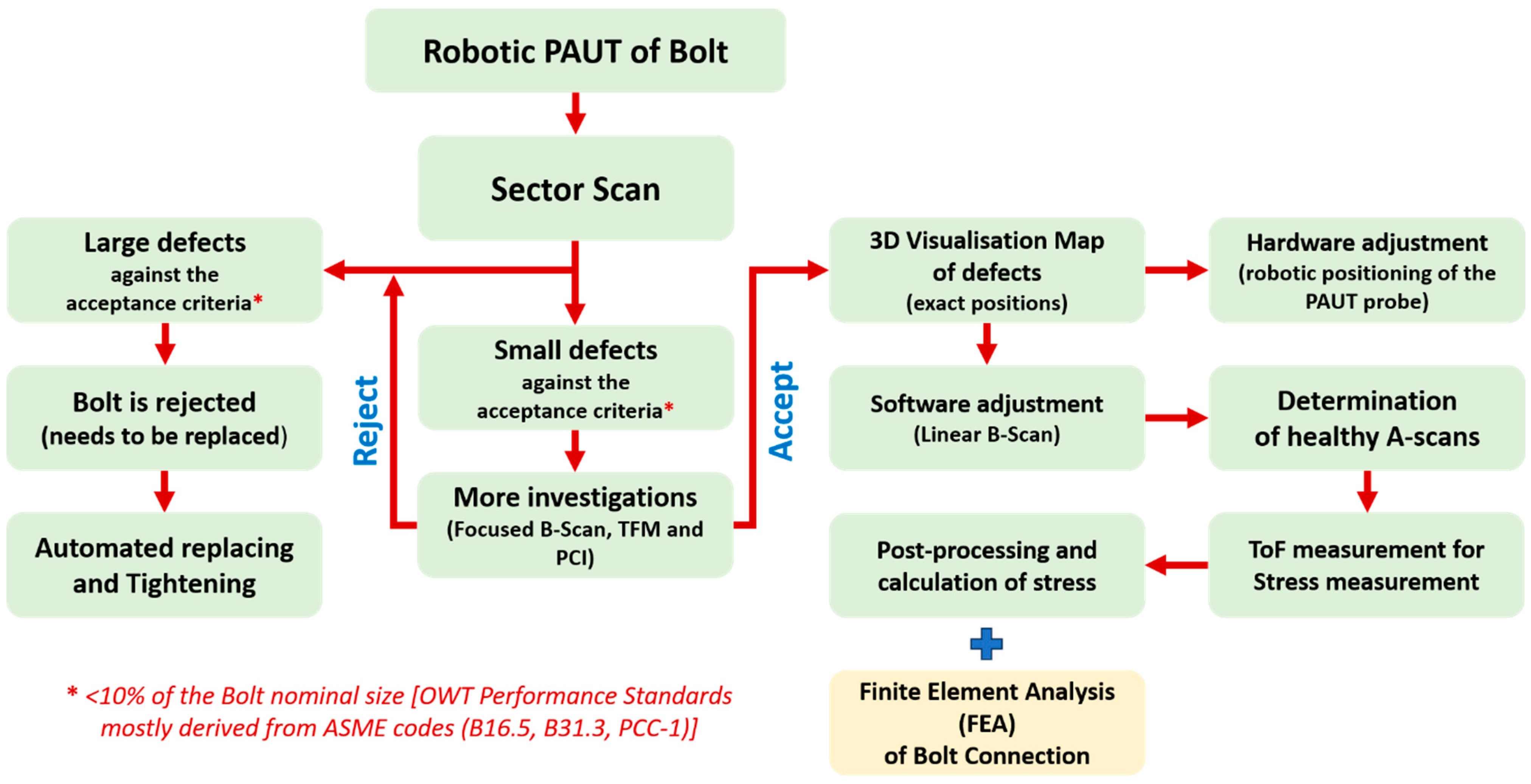
3.1. Methodology
- (1)
- A sector scan is performed to simultaneously inspect the bolt threads and the internal volume for defects, and the acceptance criteria are evaluated to determine if the defects meet the requirements. The acceptance criteria, based on industry performance standards from ASME codes (B16.5 [24], B31.3 [25], and PCC-1 [2]), state that the defect size should be within 10% of the nominal bolt size. In this paper, the bolt under investigation is M36, and small defects are defined as having a size of less than 3.6 mm.
- (2)
- Even if the bolt is rejected due to larger defects exceeding 3.6 mm, the automation process discussed in this paper remains valuable as it enables automatic replacement of the bolt. However, this automatic replacement is beyond the scope of this paper and will not be discussed.
- (3)
- This paper primarily focuses on small defects, as it is believed that they can still affect ultrasonic stress measurements.
- (4)
- To ensure small defects meet the acceptance criteria, the unique advantages of PAUT over single-element transducers (such as TFM, PCI and Focused B-Scan) are employed for comprehensive investigations. This is crucial to mitigate potential misinterpretations of defect size caused by low SNR and other inspection challenges encountered during in situ testing of OWTs. If a large defect is detected at this stage, the procedure described in Point 2 will be repeated.
- (5)
- If the defect is deemed acceptable after this in-depth study, a 3D volumetric scanning image is generated using the PAUT system.
- (6)
- The PAUT probe position is adjusted by a robotic system based on the 3D image of the bolt defects, aiming to minimize the interference of small defects with the ultrasonic wave propagation inside the bolt. This adjustment process is referred to as hardware adjustment in this paper.
- (7)
- In cases where complete hardware adjustment is not feasible, meaning that some defects still obstruct the acoustic path, software adjustment is implemented. Since the ultrasonic array can generate multiple acoustic paths, only the acoustic paths free from defects obstructing the backwall are considered in the next stages. These selected paths are termed “healthy A-scans” (see Figure 2).
- (8)
- Time-of-Flight (ToF) measurements required for stress calculation are exclusively conducted on the healthy A-scans.
- (9)
- The final step involves post-processing and utilising acoustoelasticity for stress calculations.
3.2. The Influence of Small Defects on the Stress
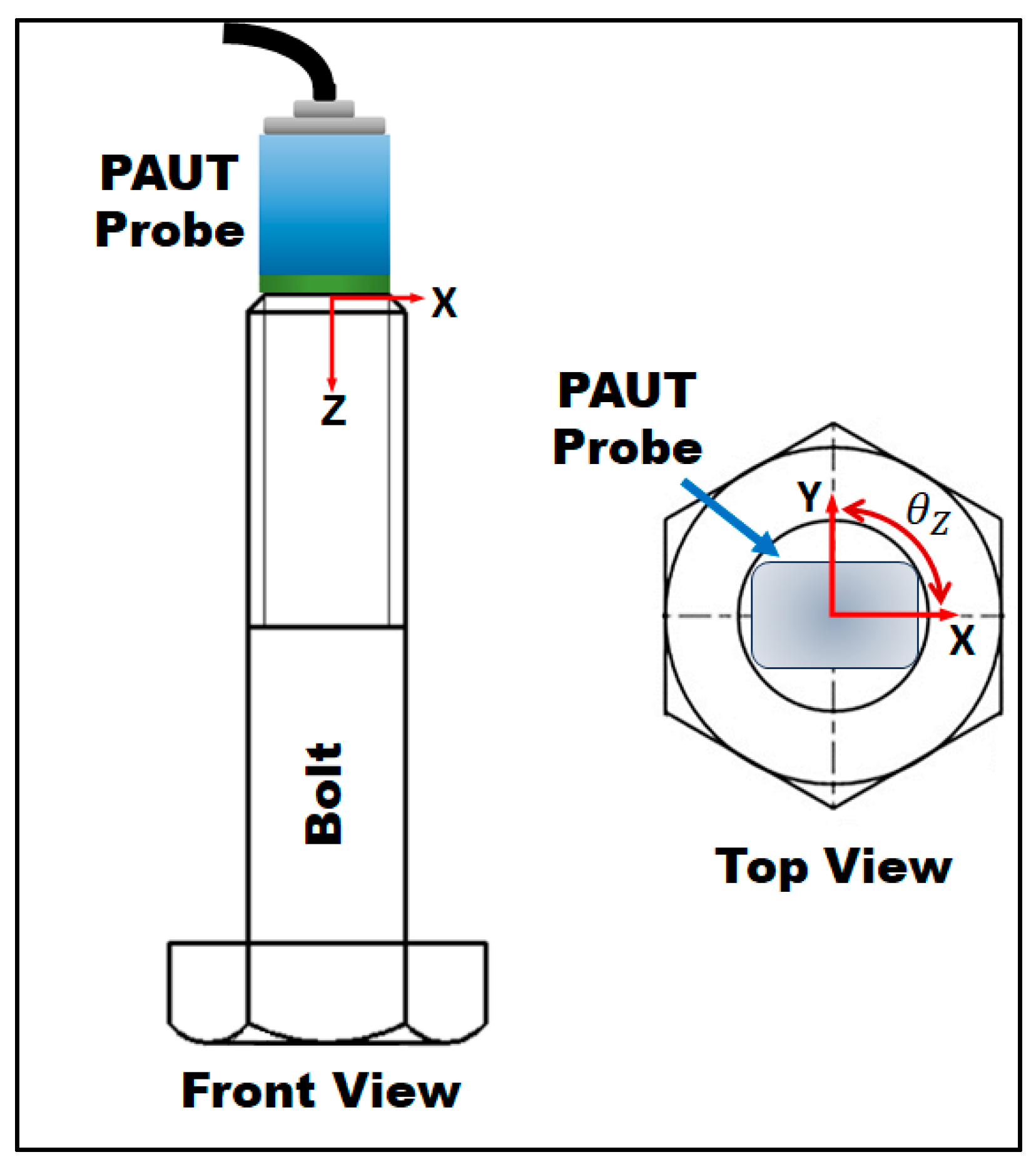
3.3. Experimental Setup for Robotic PAUT of Bolt
4. Results and Discussions
4.1. The Influence of Small Defects on the Stress and Advantages of the PAUT System
4.2. The Benefit of Robotics for Preload Measurement in OWT Bolted Connections
4.3. Robotic PAUT of Bolt
4.3.1. Sector Scan
4.3.2. Further Investigations (Focused B-Scan, TFM and PCI)
4.3.3. Hardware and Software Adjustment for Stress Measurement
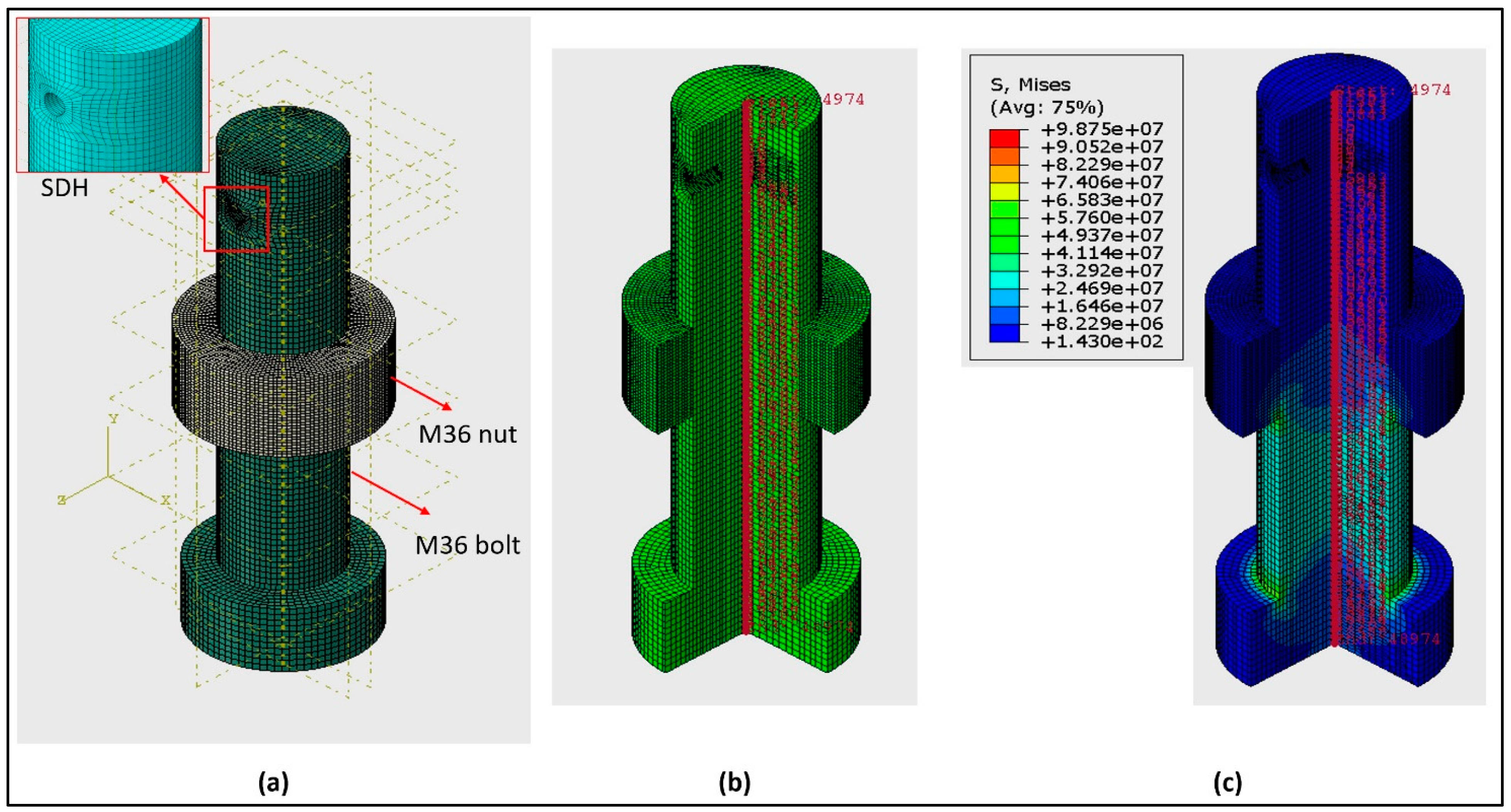
4.3.4. Finite Element Analysis
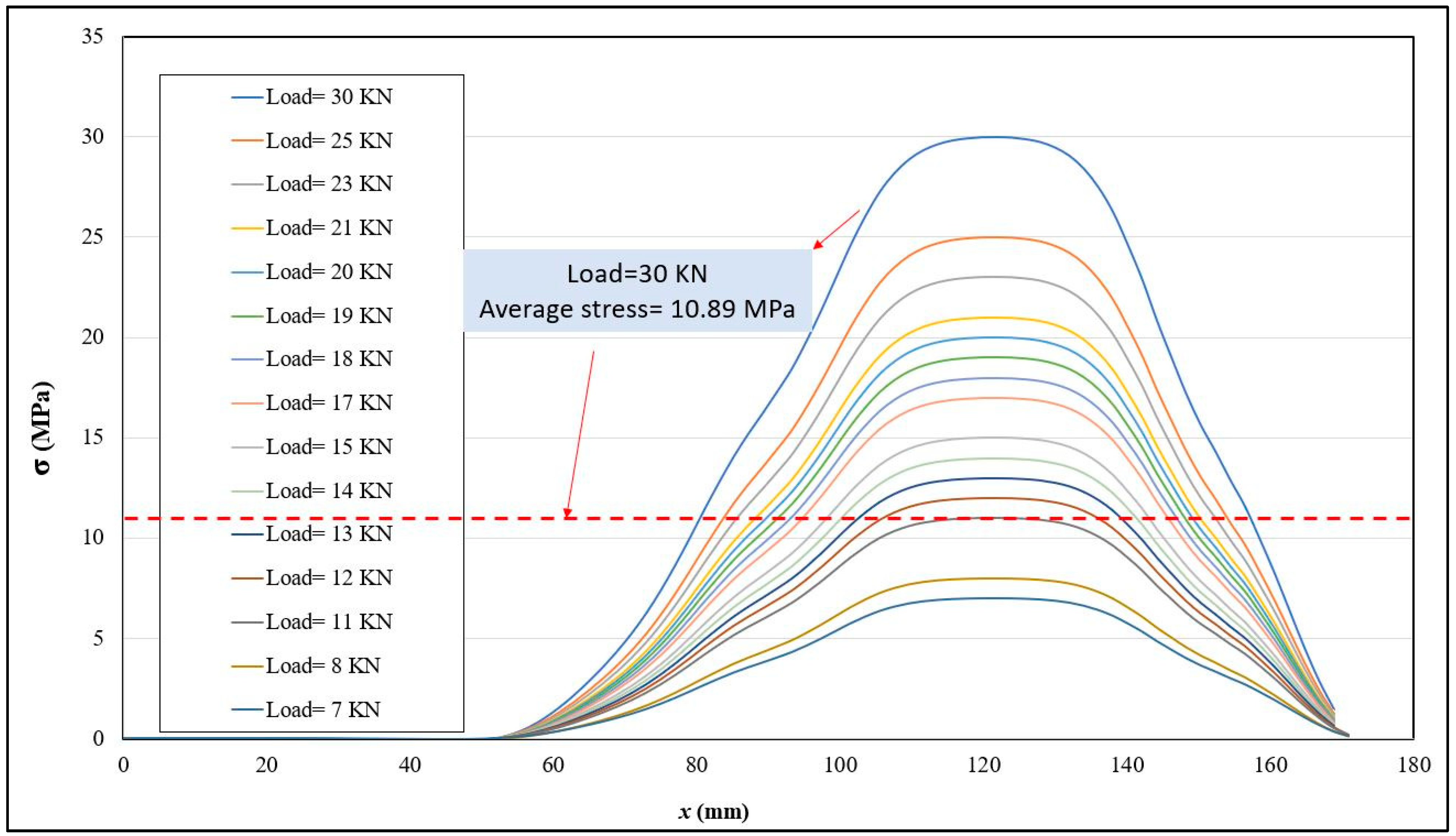
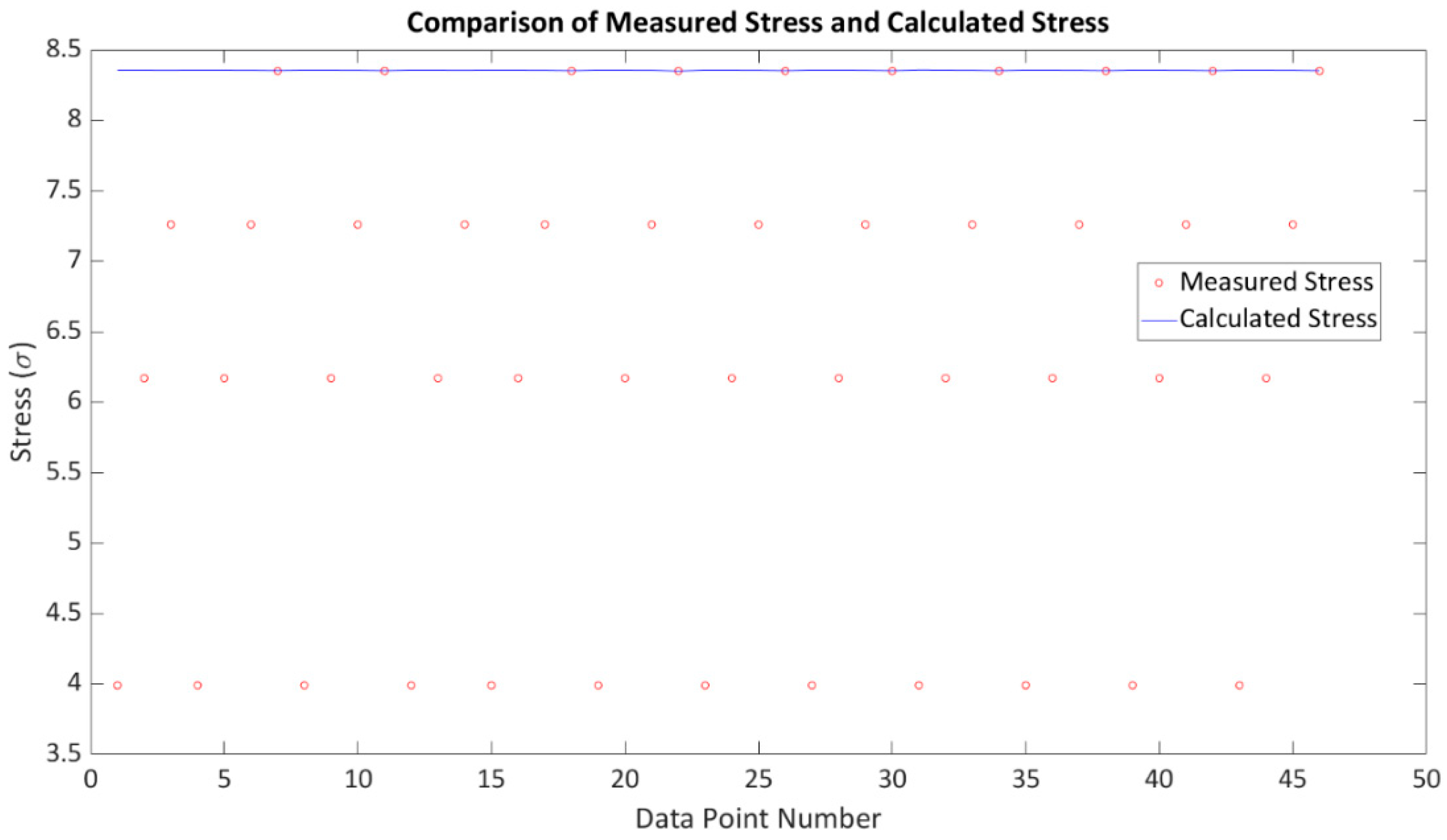
4.3.5. Stress Measurement Using the PAUT Method
- (a)
- Single-Element Transducer (manual scanning): With a single-element transducer, only a single set of data points for Time of Flight (ToF) and stress measurements can be obtained. As the dataset is limited, the approach involves directly solving the equations for A, B, and C using numerical methods such as Newton–Raphson or optimization algorithms. The single-element transducer approach offers simplicity and ease of implementation. It requires minimal data processing and computational resources. However, its accuracy and reliability may be limited due to the small dataset and potential uncertainties associated with manual scanning.
- (b)
- Robotic Phased Array (FMC approach): Utilising a robotic phased array with FMC enables the acquisition of a significantly larger dataset. Compared to the single-element transducer case, a 20-element array, as utilised in this study, can generate a dataset that is 400 times larger (20 × 20). Moreover, with the robotic system, the data acquisition can be repeated multiple times at each increment to enhance the dataset. In this case, regression analysis or curve-fitting techniques can be employed to estimate the coefficients A, B, and C based on the extended dataset. The curve-fitting approach provides a more accurate and statistically robust estimation of the coefficients. The primary advantage of the robotic phased array with FMC lies in the significantly increased dataset, which improves the accuracy of coefficient estimation. The larger number of data points allows for capturing finer details, reducing the impact of noise or outliers. Additionally, the FMC technique enables advanced imaging capabilities to create high-resolution stress distribution maps, providing valuable insights into the behaviour of the bolt.
- (1)
- Simultaneous defect detection and stress measurement: The PAUT system allowed us to leverage advanced features such as the TFM to accurately locate defects. This precise defect mapping facilitated subsequent hardware and software adjustments.
- (2)
- Utilisation of extensive data: The abundant data obtained through PAUT enabled us to solve the nonlinear acoustoelastic equations using numerical methods.
- (3)
- Accurate stress measurement in the correct position: With the hardware and software adjustments in place, we achieved an average measurement error of 5%, demonstrating the effectiveness of the robotic PAUT approach. Conversely, the single-element approach exhibited measurement errors ranging from 5% to 200%.
4.3.6. Disadvantages of the Robotic PAUT Approach in Offshore Applications
- (a)
- Costs: The implementation of robotic PAUT requires substantial investments in various aspects, including hardware such as robots, phased array probes, controllers, load cells, and force/torque sensors. Additionally, software resources such as LabView 2023, MATLAB R2023b, and Finite Element (FE) software (Abaqus 2023) are necessary. Moreover, the employment of highly skilled personnel adept in data interpretation, numerical modelling, and coding is vital, as exemplified in this study. The financial outlay for this approach can be up to four times greater than that of a manual system employing a single-element transducer.
- (b)
- Deployment: It is crucial to recognise that deploying robots and PAUT systems in offshore facilities presents significant challenges. Maintaining the operational integrity of such sophisticated systems requires dedicated efforts and regular maintenance tasks for turbine operation management.
4.3.7. Mobile Robotics, Machine Learning-Enabled Technologies, and Continuous Monitoring
- (a)
- Exposure to corrosive environments necessitates continuous integrity monitoring to mitigate loss of preload from bi-metallic connections. Automated testing enables periodic assurance against corrosion-induced bolt failures.
- (b)
- Modular structural design involving numerous bolted flange joints is critical for turbines withstanding fluctuating gravitational and aerodynamic loads over decades. This work facilitates condition monitoring with prognostic abilities for these safety-critical bolts.
- (c)
- Commitments to minimize operator time offshore drive innovations for remote asset management. The proposed robotics-enabled solution promises capabilities aligning with this strategic objective.
4.3.8. Mitigating Offshore Bolt-Corrosion Challenges with Robotic PAUT
4.3.9. Alternative Approaches to Robotic PAUT
5. Conclusions
- Comprehensive and accurate defect detection is critical prior to preload measurement to ensure reliable results. Acceptable defects, smaller than the defined criteria, impact stress measurement, while bolts with significant defects are rejected, obviating the need for further stress measurement.
- Robotic preload measurement ensures consistent probe pressure and uniform couplant-layer thickness, and maintains consistency between calibration and in situ stress measurement regarding position and orientation. The study demonstrated that a change in orientation can lead to up to 140 MPa error in bolt stress measurement.
- Considering the average stress is vital for comparison with ultrasonic data. FEA can be employed to provide such information.
- The advantages of the robotic PAUT method over the single-element approach were discussed. These advantages include incorporating nonlinearity into the equations, simultaneous defect detection and stress measurement, hardware and software adjustments, and, most importantly, a substantial improvement in measurement accuracy.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- BS EN 14399-1:2015; High-Strength Structural Bolting Assemblies for Preloading—General Requirements. British-Standards-Institution: London, UK, 2015.
- ASME PCC-1; Pressure Boundary Bolted Flange Joint Assembly. ASME: New York, NY, USA, 2022.
- Pan, Q.; Pan, R.; Shao, C.; Chang, M.; Xu, X. Research Review of Principles and Methods for Ultrasonic Measurement of Axial Stress in Bolts. Chin. J. Mech. Eng. 2020, 33, 1–16. [Google Scholar] [CrossRef]
- Jahani, K.; Langlois, R.G.; Afagh, F.F. Structural dynamics of offshore Wind Turbines: A review. Ocean Eng. 2022, 251, 111136. [Google Scholar] [CrossRef]
- Gollub, P.; Jensen, J.F.; Giese, D.; Güres, S. Flanged foundation connection of the Offshore Wind Farm Amrumbank West—Concept, approval, design, tests and installation. Stahlbau 2014, 83, 522–528. [Google Scholar] [CrossRef]
- Ma, H.; Yang, J. A novel hybrid monopile foundation for offshore wind turbines. Ocean Eng. 2020, 198, 106963. [Google Scholar] [CrossRef]
- Gupta, B.K.; Basu, D. Offshore wind turbine monopile foundations: Design perspectives. Ocean Eng. 2020, 213, 107514. [Google Scholar] [CrossRef]
- Wang, B.; Wang, J.; Guan, Y.; Ren, L.; Ning, K.; Zhang, W. Study on the safety performance of large offshore wind turbine coupling. Ocean Eng. 2023, 279, 114525. [Google Scholar] [CrossRef]
- Lin, M.S.-M.; Lu, B.-S. Risk assessment and management n the offshore wind power industry: A focus on component handling operations in ports. Saf. Sci. 2023, 167, 106286. [Google Scholar] [CrossRef]
- Mehmanparast, A.; Lotfian, S.; Vipin, S.P. A Review of Challenges and Opportunities Associated with Bolted Flange Connections in the Offshore Wind Industry. Metals 2020, 10, 732. [Google Scholar] [CrossRef]
- Ahn, J.-H.; You, J.M.; Huh, J.; Kim, I.-T.; Jeong, Y.-S. Residual clamping force of bolt connections caused by sectional damage of nuts. J. Constr. Steel Res. 2017, 136, 204–214. [Google Scholar] [CrossRef]
- Den Otter, C.; Maljaars, J. Preload loss of stainless steel bolts in aluminium plated slip resistant connections. Thin-Walled Struct. 2020, 157, 106984. [Google Scholar] [CrossRef]
- Jhang, K.-Y.; Quan, H.-H.; Ha, J.; Kim, N.-Y. Estimation of clamping force in high-tension bolts through ultrasonic velocity measurement. Ultrasonics 2006, 44, e1339–e1342. [Google Scholar] [CrossRef]
- Cawley, P. Non-destructive testing—Current capabilities and future directions. Proc. Inst. Mech. Eng. Part L J. Mater. Des. Appl. 2001, 215, 213–223. [Google Scholar]
- Drinkwater, B.W.; Wilcox, P.D. Ultrasonic arrays for non-destructive evaluation: A review. NDT E Int. 2006, 39, 525–541. [Google Scholar] [CrossRef]
- Holmes, C.; Drinkwater, B.W.; Wilcox, P.D. Post-processing of the full matrix of ultrasonic transmit–receive array data for non-destructive evaluation. NDT E Int. 2005, 38, 701–711. [Google Scholar] [CrossRef]
- Holmes, C.; Drinkwater, B.W.; Wilcox, P.D. Advanced post-processing for scanned ultrasonic arrays: Application to defect detection and classification in non-destructive evaluation. Ultrasonics 2008, 48, 636–642. [Google Scholar] [CrossRef] [PubMed]
- Mendelsohn, Y.; Wiener-Avnear, E. Simulations of circular 2D phase-array ultrasonic imaging transducers. Ultrasonics 2002, 39, 657–666. [Google Scholar] [CrossRef] [PubMed]
- Camacho, J.; Fritsch, C.; Fernandez-Cruza, J.; Parrilla, M. Phase Coherence Imaging: Principles, applications and current developments. Proc. Meet. Acoust. 2019, 38, 055012. [Google Scholar]
- Javadi, Y.; Hutchison, A.; Singh, J.; Mohseni, E.; Rahimi, S.; Mehnen, J.; Macleod, C.N.; Pierce, S.G.; Tant, K.M.M.; Gachagan, A. Feasibility Study of Residual Stress Measurement Using Phased Array Ultrasonic Method. In Proceedings of the 11th International Conference on Residual Stress, Nancy, France, 27 March 2022. [Google Scholar]
- Hughes, D.S.; Kelly, J.L. Second-Order Elastic Deformation of Solids. Phys. Rev. B 1953, 92, 1145–1149. [Google Scholar] [CrossRef]
- Murnaghan, F.D. Finite Deformations of an Elastic Solid. Am. J. Math. 1937, 59, 235. [Google Scholar] [CrossRef]
- Javadi, Y.; Hutchison, A.; Zimermann, R.; Lines, D.; Sweeney, N.E.; Vasilev, M.; Mohseni, E.; Vithanage, R.K.W.; MacLeod, C.N.; Pierce, G.; et al. Development of a Phased Array Ultrasonic System for Residual Stress Measurement in Welding and Additive Manufacturing. In Proceedings of the ASME 2022 Pressure Vessels & Piping Conference, Las Vegas, NE, USA, 17–22 July 2022. [Google Scholar]
- ASME B16.5; Pipe Flanges and Flanged Fittings: NPS 1/2 through NPS 24, Metric/Inch Standard. ASME: New York, NY, USA, 2021.
- ASME B31.3:2022; Process Piping Code Changes. ASME: New York, NY, USA, 2022.
- Withers, P.J.; Turski, M.; Edwards, L.; Bouchard, P.J.; Buttle, D.J. Recent advances in residual stress measurement. Int. J. Press. Vessel. Pip. 2008, 85, 118–127. [Google Scholar] [CrossRef]
- Rossini, N.; Dassisti, M.; Benyounis, K.; Olabi, A. Methods of measuring residual stresses in components. Mater. Des. 2012, 35, 572–588. [Google Scholar] [CrossRef]
- Bray, D.E.; Junghans, P. Application of the LCR ultrasonic technique for evaluation of post-weld heat treatment in steel plates. NDT E Int. 1995, 28, 235–242. [Google Scholar] [CrossRef]
- Egle, D.M.; Bray, D.E. Measurement of acoustoelastic and third-order elastic constants for rail steel. J. Acoust. Soc. Am. 1976, 60, 741–744. [Google Scholar] [CrossRef]
- Zhou, L.; Chen, S.X.; Choy, A.; Ni, Y.Q. Monitoring of Rail Bolted Joint Looseness with Pzt Network-Based Emi Technique under a Deep Learning Framework. In Proceedings of the 12th International Workshop on Structural Health Monitoring: Enabling Intelligent Life-Cycle Health Management for Industry Internet of Things (IIOT), IWSHM2019, Stanford, CA, USA, 10–17 September 2019; pp. 2841–2848. [Google Scholar]
- Chen, D.; Huo, L.; Song, G. High resolution bolt pre-load looseness monitoring using coda wave interferometry. Struct. Health Monit. 2021, 21, 1959–1972. [Google Scholar] [CrossRef]
- Ihn, J.-B.; Chang, F.-K. Pitch-catch Active Sensing Methods in Structural Health Monitoring for Aircraft Structures. Struct. Health Monit. 2008, 7, 5–19. [Google Scholar] [CrossRef]










| Test #1 (µs) | Test #2 (µs) | |
|---|---|---|
| t1 | 62.93 | 62.91 |
| t2 | 123.92 | 123.91 |
| Difference (Δt) | 60.99 | 61.00 |
| Test #A (µs) | Test #B: Different Pressure (µs) | Test #C: Different Orientation (µs) | |
|---|---|---|---|
| t1 | 62.91 | 62.91 | 62.88 |
| t2 | 123.91 | 123.91 | 123.86 |
| Difference (Δt) | 61.00 | 61.00 | 60.98 |
| Washer-Shaped Loadcell Reading | Stress Based on the Loadcell Reading | Average of Stress Based on FEA | Stress Measured by the PAUT Method | Stress Measured with the Assumption of Single Element |
|---|---|---|---|---|
| 23 KN | 23 MPa | 8.35 MPa | 8 MPa | 4–11 MPa |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Javadi, Y.; Mills, B.; MacLeod, C.; Lines, D.; Abad, F.; Lotfian, S.; Mehmanparast, A.; Pierce, G.; Brennan, F.; Gachagan, A.; et al. Phased Array Ultrasonic Method for Robotic Preload Measurement in Offshore Wind Turbine Bolted Connections. Sensors 2024, 24, 1421. https://doi.org/10.3390/s24051421
Javadi Y, Mills B, MacLeod C, Lines D, Abad F, Lotfian S, Mehmanparast A, Pierce G, Brennan F, Gachagan A, et al. Phased Array Ultrasonic Method for Robotic Preload Measurement in Offshore Wind Turbine Bolted Connections. Sensors. 2024; 24(5):1421. https://doi.org/10.3390/s24051421
Chicago/Turabian StyleJavadi, Yashar, Brandon Mills, Charles MacLeod, David Lines, Farhad Abad, Saeid Lotfian, Ali Mehmanparast, Gareth Pierce, Feargal Brennan, Anthony Gachagan, and et al. 2024. "Phased Array Ultrasonic Method for Robotic Preload Measurement in Offshore Wind Turbine Bolted Connections" Sensors 24, no. 5: 1421. https://doi.org/10.3390/s24051421
APA StyleJavadi, Y., Mills, B., MacLeod, C., Lines, D., Abad, F., Lotfian, S., Mehmanparast, A., Pierce, G., Brennan, F., Gachagan, A., & Mineo, C. (2024). Phased Array Ultrasonic Method for Robotic Preload Measurement in Offshore Wind Turbine Bolted Connections. Sensors, 24(5), 1421. https://doi.org/10.3390/s24051421














