Custom Loss Functions in XGBoost Algorithm for Enhanced Critical Error Mitigation in Drill-Wear Analysis of Melamine-Faced Chipboard
Abstract
1. Introduction
2. Materials and Methods
2.1. Data Collection
2.2. Feature Extraction Techniques
2.2.1. 2-D Morlet Wavelets in Wavelet Scattering Image Decomposition
| Algorithm 1 Wavelet Feature Extraction from Images |
|
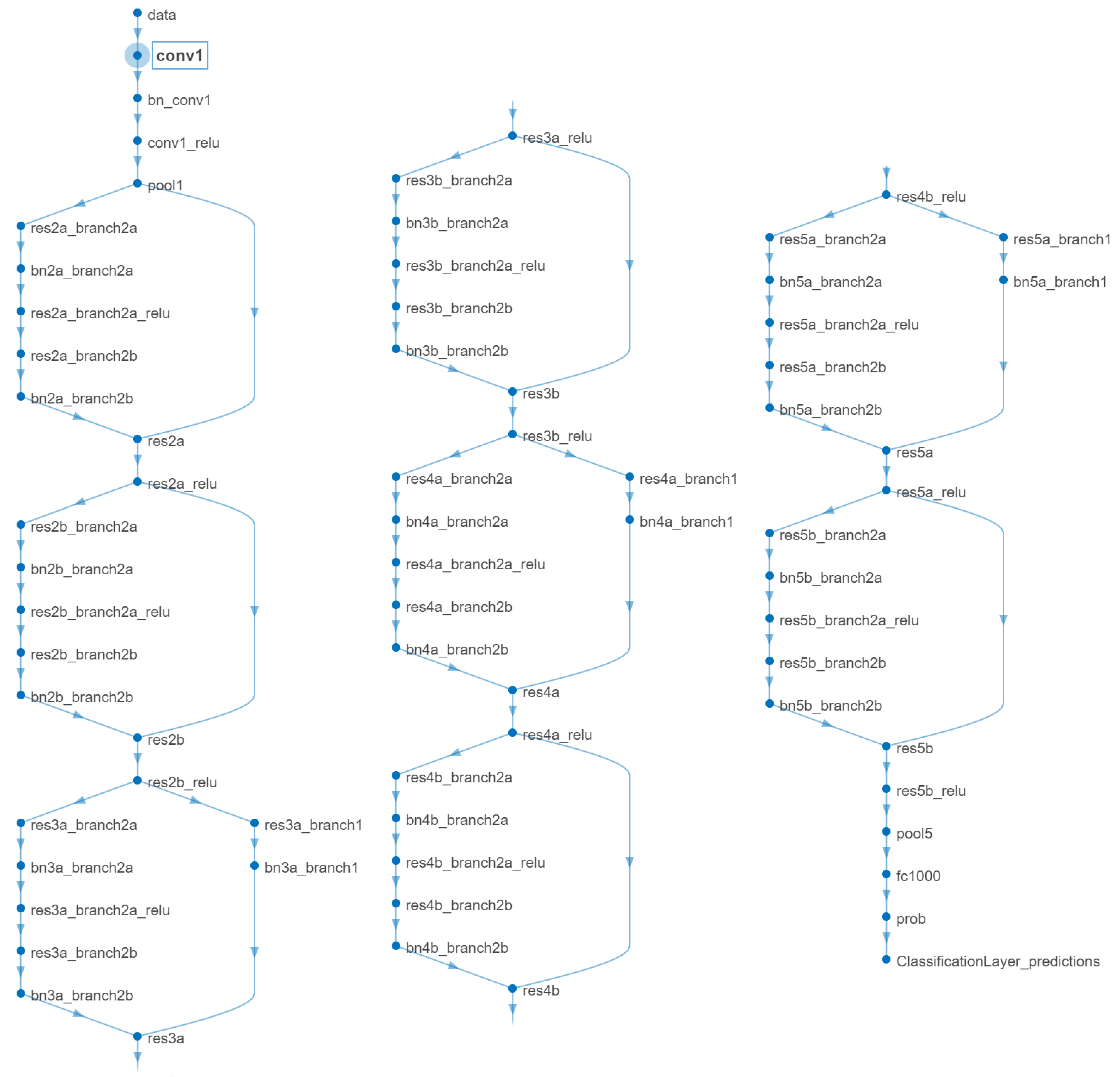
2.2.2. Pretrained Network: ResNet-18 for Extracting Lower-Level and High-Level Features
2.2.3. High-Level Features Feature Extraction Using Pretrained Convolutional Networks
| Algorithm 2 CNN Feature Extraction Using ResNet-18’s 35th/68th Layer |
|
2.2.4. Low-Level Extracting of Features Using ResNet-18’s 35th Layer
2.2.5. Manually Defined Feature Set
- Diameter of the smallest circle encompassing the hole;
- Diameter of the largest circle that can fit inside the hole;
- Variation in hole diameters;
- Total area covered by holes;
- Area of the convex hull;
- Total perimeter length;
- Length of the longest axis of the ellipse fitting the image;
- Length of the shortest axis of the ellipse fitting the image;
- Solidity (ratio of area to convex hull area).
| Algorithm 3 Generation of Individual Image Features Using Custom Method |
|
2.2.6. Histogram of Oriented Gradients (HOG) for Feature Extraction
| Algorithm 4 Extract HOG Features |
|
2.3. Extreme Gradient Boosting—XGBoost
2.4. Key Features of XGBoost
- Regularization: This includes L1 (Lasso Regression) and L2 (Ridge Regression) regularization, which helps in reducing overfitting.
- Handling Sparse Data: XGBoost is designed to handle sparse data from the ground up.
- Tree Pruning: XGBoost uses a depth-first approach for tree pruning, unlike the level-wise approach, making it more efficient.
- Handling Missing Values: XGBoost has an in-built routine to handle missing values.
- System Optimization: The system is optimized for distributed computing and can handle large datasets efficiently.
- Number of Boosting Stages (M) = 50;
- Loss Function = ‘log-loss’;
- Maximum Depth of Trees = 3;
- Learning Rate = 0.1;
- Minimum Samples per Leaf = 1.
2.5. Loss Functions
- Addressing Class Imbalance: Loss function modification can help address the class imbalance by assigning higher penalties for errors in underrepresented classes. This ensures that the model does not overlook these classes during the learning process.
- Focusing on Critical Errors: In many real-world applications, certain misclassifications are more costly than others. Customized loss functions can be designed to impose heavier penalties for specific types of critical errors, thereby reducing their occurrence.
- Improving Model Sensitivity: Modifying loss functions can improve the model’s sensitivity towards edge classes, enhancing its ability to detect and correctly classify instances belonging to these classes.
2.6. XGBoost’s Default Loss Function for Multi-Class Classification
Pseudocode for ‘multi:softprob’
| Algorithm 5 Pseudocode for multi:softprob in XGBoost |
|
2.7. Weighted Softmax Loss Variant 1
| Algorithm 6 Weighted Softmax Loss Function—Variant 1 |
|
2.7.1. Softmax Transformation
2.7.2. Gradient and Hessian Initialization
2.7.3. Weight Assignment
- Classes 0 and 1: ;
- Classes 0 and 2: ;
- Classes 1 and 2: .
2.7.4. Gradient and Hessian Computation
2.8. Weighted Softmax Loss Function—Variant 2
Modified Weight Assignment
- Classes 0 and 1: ;
- Classes 0 and 2: ;
- Classes 1 and 2: .
2.9. Weighted Softmax Loss Function—Variant 3
Modified Weight Assignment
- Classes 0 and 1: ;
- Classes 0 and 2: ;
- Classes 1 and 2: .
2.10. Weighted Softmax Loss Function—Variant 4
Modified Weight Assignment
- Classes 0 and 1: ;
- Classes 0 and 2: ;
- Classes 1 and 2: .
2.11. Weighted Softmax Loss Function—Variant 5
Modified Weight Assignment
- Classes 0 and 1:
- Classes 0 and 2:
- Classes 1 and 2:
2.12. Weighted Softmax Loss Function with Edge Penalty
2.12.1. Modified Weight Assignment
- Classes 0 and 1: ;
- Classes 0 and 2: ;
- Classes 1 and 2: .
2.12.2. Algorithm of Weighted Softmax Loss Function with Edge Penalty
| Algorithm 7 Weighted Softmax Loss with Edge Penalty |
|
2.13. Adaptive Weighted Softmax Loss Function
2.13.1. Computing Adaptive Weights
2.13.2. Focal Loss Modification
2.13.3. Algorithm of Adaptive Weighted Softmax Loss Function
| Algorithm 8 Compute Adaptive Weights |
|
| Algorithm 9 Adaptive Weighted Softmax Loss with Focal Modification |
|
3. Numerical Experiments
- Inherent Feature Handling Capabilities of XGBoost: XGBoost is well-known for its ability to handle a large number of features efficiently. It automatically assigns a score to each feature based on its importance, effectively doing an internal form of feature selection during the learning process. Given this capability, we believed that an additional explicit feature selection step might not significantly improve the performance.
- Complexity of the Data: The dataset in our study was complex, with features extracted from five different methods. Each feature potentially carried unique information that could be crucial for accurate classification. We wanted to ensure that the model had access to all available information before making any decision to exclude features.
- Avoiding Potential Loss of Information: Feature selection, especially if not done carefully, can lead to the loss of important information that could be valuable for the model. Given the critical nature of our task—drill-wear analysis—we could not afford to lose potentially subtle yet important signals that might be present in the less prominent features.
- Computational Resources: We had access to sufficient computational resources to handle the complexity and size of our dataset without the need for feature reduction. This allowed us to train the XGBoost model on the full set of features without concerns about computational efficiency or training time.
- Ensuring Model Robustness: By using the complete set of features, we aimed to develop a model that is robust and can generalize well across different scenarios. Reducing the feature space might lead to a model that is overly optimized for the specific characteristics of the training data, potentially reducing its effectiveness on new, unseen data.
- Processor: AMD RYZEN THREADRIPPER 2990WX (32C 64T) 4.3 GHz;
- Motherboard: AsRock X399 TAICHI;
- Memory: 8 × ADATA XPG SPECTRIX DDR4 16 GB D41 3000 MHz (128 GB RAM);
- Graphics Card: 2 × Nvidia GeForce RTX Titan 24 GB GDDR6 (48 GB RAM);
- Drive SSD: 2 × WD BLACK 1 TB WDS100T3X0C1TB (PCIE);
- Drive HDD: 1 × WD RED PRO 8 TB WD8003FFBX 3.5” (SATA);
- Power Supply: BE QUIET! DARK POWER PRO 11 1000 W;
- Cooling: BE QUIET! Silent Loop BW003 280 mm;
- Network: 10GbE SFP+.
4. Results and Discussion
4.1. Advantages and Limitations of the Proposed Work
4.1.1. Advantages
- Enhanced Accuracy for Critical Classes: By customizing loss functions, the model demonstrates improved classification accuracy, especially for critical edge classes, which are essential in industrial applications for maintaining production quality.
- Flexibility in Addressing Class Imbalance: The adaptive nature of the proposed loss functions effectively addresses the challenges posed by imbalanced datasets, a common issue in real-world scenarios.
- Context-Specific Model Optimization: Tailoring loss functions according to the specific needs of the application allows for a more nuanced and effective model compared to standard approaches.
- Improved Decision-Making in Industrial Settings: The refined predictions offered by the model facilitate better decision-making processes, crucial in high-stakes industrial environments such as furniture manufacturing.
4.1.2. Limitations
- Increased Computational Complexity: Custom loss functions, particularly those involving adaptive weights and focal modifications, demand higher computational resources, potentially impacting the efficiency of the model.
- Overfitting Risks: The model’s heightened sensitivity to specific classes might lead to overfitting, particularly when dealing with small or highly specific datasets.
- Dependency on Expert Knowledge: The effectiveness of the approach relies heavily on domain expertise for accurately defining and tuning the custom loss functions.
- Limited Generalizability: While effective in the specific context of drill-wear analysis, the approach may not be directly applicable or as effective in other domains without significant modifications.
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Byrne, G.; Dornfeld, D.; Inasaki, I.; Ketteler, G.; König, W.; Teti, R. Tool condition monitoring (TCM)—The status of research and industrial application. CIRP Ann. 1995, 44, 541–567. [Google Scholar] [CrossRef]
- Liu, T.I.; Jolley, B. Tool condition monitoring (TCM) using neural networks. Int. J. Adv. Manuf. Technol. 2015, 78, 1999–2007. [Google Scholar] [CrossRef]
- Mohamed, A.; Hassan, M.; M’Saoubi, R.; Attia, H. Tool condition monitoring for high-performance machining systems—A review. Sensors 2022, 22, 2206. [Google Scholar] [CrossRef]
- Schueller, A.; Saldaña, C. Indirect Tool Condition Monitoring Using Ensemble Machine Learning Techniques. J. Manuf. Sci. Eng. 2023, 145, 011006. [Google Scholar] [CrossRef]
- Lemaster, R.L.; Tee, L.B.; Dornfeld, D.A. Monitoring tool wear during wood machining with acoustic emission. Wear 1985, 101, 273–282. [Google Scholar] [CrossRef]
- Kun, W.; Qi, S.; Cheng, W.; Chunjie, L. Influence of pneumatic pressure on delamination factor of drilling medium density fiberboard. Wood Res. 2015, 60, 429–440. [Google Scholar]
- Szwajka, K.; Trzepieciński, T. Effect of tool material on tool wear and delamination during machining of particleboard. J. Wood Sci. 2016, 62, 305–315. [Google Scholar] [CrossRef]
- Szwajka, K.; Trzepieciński, T. An examination of the tool life and surface quality during drilling melamine faced chipboard. Wood Res. 2017, 62, 307–318. [Google Scholar]
- Śmietańska, K.; Podziewski, P.; Bator, M.; Górski, J. Automated monitoring of delamination factor during up (conventional) and down (climb) milling of melamine-faced MDF using image processing methods. Eur. J. Wood Wood Prod. 2020, 78, 613–615. [Google Scholar] [CrossRef]
- Swiderski, B.; Antoniuk, I.; Kurek, J.; Bukowski, M.; Gorski, J.; Jegorowa, A. Tool Condition Monitoring for the Chipboard Drilling Process Using Automatic, Signal-based Tool State Evaluation. BioResources 2022, 17, 5349–5371. [Google Scholar] [CrossRef]
- Bukowski, M.; Kurek, J.; Antoniuk, I.; Jegorowa, A. Decision Confidence Assessment in Multi-Class Classification. Sensors 2021, 21, 3834. [Google Scholar] [CrossRef]
- Król, P.M.; Szymona, K. Methodology evaluation of computer vision small-dimension hole localization. Wood Mater. Sci. Eng. 2023, 18, 184–192. [Google Scholar] [CrossRef]
- Osowski, S.; Kurek, J.; Kruk, M.; Górski, J.; Hoser, P.; Wieczorek, G.; Jegorowa, A.; Wilkowski, J.; Śmietańska, K.; Kossakowska, J. Developing automatic recognition system of drill wear in standard laminated chipboard drilling process. Bull. Pol. Acad. Sci. Tech. Sci. 2016, 64, 633–640. [Google Scholar] [CrossRef][Green Version]
- Kuo, R. Multi-sensor integration for on-line tool wear estimation through artificial neural networks and fuzzy neural network. Eng. Appl. Artif. Intell. 2000, 13, 249–261. [Google Scholar] [CrossRef]
- Jemielniak, K.; Urbański, T.; Kossakowska, J.; Bombiński, S. Tool condition monitoring based on numerous signal features. Int. J. Adv. Manuf. Technol. 2012, 59, 73–81. [Google Scholar] [CrossRef]
- Panda, S.; Singh, A.; Chakraborty, D.; Pal, S. Drill wear monitoring using back propagation neural network. J. Mater. Process. Technol. 2006, 172, 283–290. [Google Scholar] [CrossRef]
- Jegorowa, A.; Górski, J.; Kurek, J.; Kruk, M. Initial study on the use of support vector machine (SVM) in tool condition monitoring in chipboard drilling. Eur. J. Wood Wood Prod. 2019, 77, 957–959. [Google Scholar] [CrossRef]
- Nasir, V.; Cool, J.; Sassani, F. Intelligent machining monitoring using sound signal processed with the wavelet method and a self-organizing neural network. IEEE Robot. Autom. Lett. 2019, 4, 3449–3456. [Google Scholar] [CrossRef]
- Nasir, V.; Sassani, F. A review on deep learning in machining and tool monitoring: Methods, opportunities, and challenges. Int. J. Adv. Manuf. Technol. 2021, 115, 2683–2709. [Google Scholar] [CrossRef]
- Ibrahim, I.; Khairuddin, A.; Abu Talip, M.; Arof, H.; Yusof, R. Tree species recognition system based on macroscopic image analysis. Wood Sci. Technol. 2017, 51, 431–444. [Google Scholar] [CrossRef]
- Kurek, J.; Swiderski, B.; Jegorowa, A.; Kruk, M.; Osowski, S. Deep learning in assessment of drill condition on the basis of images of drilled holes. In Proceedings of the 8th International Conference on Graphic and Image Processing (ICGIP 2016), Tokyo, Japan, 29–31 October 2016; Volume 10225, pp. 375–381. [Google Scholar] [CrossRef]
- Kurek, J.; Wieczorek, G.; Kruk, B.; Jegorowa, A.; Osowski, S. Transfer learning in recognition of drill wear using convolutional neural network. In Proceedings of the 18th International Conference on Computational Problems of Electrical Engineering (CPEE), Kutna Hora, Czech Republic, 11–13 September 2017; pp. 1–4. [Google Scholar] [CrossRef]
- Kurek, J.; Antoniuk, I.; Górski, J.; Jegorowa, A.; Świderski, B.; Kruk, M.; Wieczorek, G.; Pach, J.; Orłowski, A.; Aleksiejuk-Gawron, J. Classifiers Ensemble of Transfer Learning for Improved Drill Wear Classification using Convolutional Neural Network. Mach. Graph. Vis. 2019, 28, 13–23. [Google Scholar] [CrossRef]
- Kurek, J.; Antoniuk, I.; Górski, J.; Jegorowa, A.; Świderski, B.; Kruk, M.; Wieczorek, G.; Pach, J.; Orłowski, A.; Aleksiejuk-Gawron, J. Data Augmentation Techniques for Transfer Learning Improvement in Drill Wear Classification Using Convolutional Neural Network. Mach. Graph. Vis. 2019, 28, 3–12. [Google Scholar] [CrossRef]
- Wieczorek, G.; Chlebus, M.; Gajda, J.; Chyrowicz, K.; Kontna, K.; Korycki, M.; Jegorowa, A.; Kruk, M. Multiclass image classification using gans and cnn based on holes drilled in laminated chipboard. Sensors 2021, 21, 8077. [Google Scholar] [CrossRef] [PubMed]
- Jegorowa, A.; Kurek, J.; Antoniuk, I.; Dołowa, W.; Bukowski, M.; Czarniak, P. Deep learning methods for drill wear classification based on images of holes drilled in melamine faced chipboard. Wood Sci. Technol. 2021, 55, 271–293. [Google Scholar] [CrossRef]
- Jegorowa, A.; Antoniuk, I.; Kurek, J.; Bukowski, M.; Dołowa, W.; Czarniak, P. Time-efficient approach to drill condition monitoring based on images of holes drilled in melamine faced chipboard. BioResources 2020, 15, 9611. [Google Scholar] [CrossRef]
- Kurek, J.; Antoniuk, I.; Świderski, B.; Jegorowa, A.; Bukowski, M. Application of Siamese Networks to the Recognition of the Drill Wear State Based on Images of Drilled Holes. Sensors 2020, 20, 6978. [Google Scholar] [CrossRef]
- Kurek, J.; Osowski, S. Support vector machine for fault diagnosis of the broken rotor bars of squirrel-cage induction motor. Neural Comput. Appl. 2010, 19, 557–564. [Google Scholar] [CrossRef]
- Jegorowa, A.; Kurek, J.; Kruk, M.; Górski, J. The Use of Multilayer Perceptron (MLP) to Reduce Delamination during Drilling into Melamine Faced Chipboard. Forests 2022, 13, 933. [Google Scholar] [CrossRef]
- Jegorowa, A.; Górski, J.; Kurek, J.; Kruk, M. Use of nearest neighbors (k-NN) algorithm in tool condition identification in the case of drilling in melamine faced particleboard. Maderas. Cienc. Y Tecnol. 2020, 22, 189–196. [Google Scholar] [CrossRef]
- Kurek, J. Hybrid Approach Towards the Assessment of a Drill Condition Using Deep Learning and the Support Vector Machine. In Proceedings of the 22nd International Computer Science and Engineering Conference (ICSEC), Chiang Mai, Thailand, 21–24 November 2018; pp. 1–5. [Google Scholar] [CrossRef]
- Amal Asselman, M.K.; Aammou, S. Enhancing the prediction of student performance based on the machine learning XGBoost algorithm. Interact. Learn. Environ. 2023, 31, 3360–3379. [Google Scholar] [CrossRef]
- Ben Jabeur, S.; Stef, N.; Carmona, P. Bankruptcy Prediction using the XGBoost Algorithm and Variable Importance Feature Engineering. Comput. Econ. 2023, 61, 715–741. [Google Scholar] [CrossRef]
- Wang, T.; Bian, Y.; Zhang, Y.; Hou, X. Classification of earthquakes, explosions and mining-induced earthquakes based on XGBoost algorithm. Comput. Geosci. 2023, 170, 105242. [Google Scholar] [CrossRef]
- Lei, Y.; Shen, Z.; Tian, F.; Yang, X.; Wang, F.; Pan, R.; Wang, H.; Jiao, S.; Kou, W. Fire risk level prediction of timber heritage buildings based on entropy and XGBoost. J. Cult. Herit. 2023, 63, 11–22. [Google Scholar] [CrossRef]
- Ibrahim, A.A.; Elzaridi, K.M.A. XGBoost algorithm for orecasting electricity consumption of Germany. AURUM J. Eng. Syst. Archit. 2023, 7, 99–108. [Google Scholar] [CrossRef]
- Naik, D.; Kiran, R. A Novel Sensitivity-based Method for Feature Selection. J. Big Data 2021, 8, 128. [Google Scholar] [CrossRef]
- Asheghi, R.; Hosseini, S.A.; Saneie, M.; Shahri, A.A. Updating the neural network sediment load models using different sensitivity analysis methods: A regional application. J. Hydroinform. 2020, 22, 562–577. [Google Scholar] [CrossRef]
- Yeung, D.; Cloete, I.; Shi, D.; Ng, W. Sensitivity Analysis for Neural Networks; Springer: Berlin/Heidelberg, Germany, 2010. [Google Scholar] [CrossRef]
- Abbaszadeh Shahri, A.; Shan, C.; Larsson, S. A Novel Approach to Uncertainty Quantification in Groundwater Table Modeling by Automated Predictive Deep Learning. Nat. Resour. Res. 2022, 31, 1351–1373. [Google Scholar] [CrossRef]
- Ghaderi, A.; Abbaszadeh Shahri, A.; Larsson, S. A visualized hybrid intelligent model to delineate Swedish fine-grained soil layers using clay sensitivity. CATENA 2022, 214, 106289. [Google Scholar] [CrossRef]
- Czarniak, P.; Szymanowski, K.; Panjan, P. Characteristic of the wear of a tool coating based on amorphous carbon during chipboard milling. Ann. Wars. Univ. Life Sci. SGGW For. Wood Technol. 2020, 111, 53–59. [Google Scholar] [CrossRef]
- Czarniak, P.; Szymanowski, K.; Panjan, P. Influence of the microstructure of tool coatings based on Ti and Al on the blunting process during chipboard processing. Ann. Wars. Univ. Life Sci. SGGW For. Wood Technol. 2020, 112, 54–59. [Google Scholar] [CrossRef]
- Wieloch, G.; Szymanowski, K. Condition of edges of particle board laminated after saws on a panel saw. Trieskové A Beztrieskové Obrábanie Dreva = Chip Chipless Woodwork. Process. 2018, 11, 197–204. [Google Scholar]
- Pfleiderer. Meblarstwo i Wykończenie Wnętrz. 2023. Available online: https://www.pfleiderer.pl/en/produkty/MEBLARSTWO-I-WYKONCZENIE-WNETRZ/plyty-laminowane (accessed on 17 December 2023).
- Kruk, M.; Kurek, J.; Osowski, S.; Koktysz, R.; Swiderski, B.; Markiewicz, T. Ensemble of classifiers and wavelet transformation for improved recognition of Fuhrman grading in clear-cell renal carcinoma. Biocybern. Biomed. Eng. 2017, 37, 357–364. [Google Scholar] [CrossRef]
- PyWavelets Development Team. PyWavelets Documentation. 2023. Available online: https://pywavelets.readthedocs.io (accessed on 17 December 2023).
- Grossmann, A.; Kronland-Martinet, R.; Morlet, J. Reading and understanding continuous wavelet transforms. In Wavelets; Springer: Berlin/Heidelberg, Germany, 1990; pp. 2–20. [Google Scholar] [CrossRef]
- Büssow, R. An algorithm for the continuous Morlet wavelet transform. Mech. Syst. Signal Process. 2007, 21, 2970–2979. [Google Scholar] [CrossRef]
- ImageNet Project. ImageNet. 2023. Available online: https://www.image-net.org (accessed on 18 December 2023).
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep Residual Learning for Image Recognition. arXiv 2015, arXiv:1512.03385. [Google Scholar] [CrossRef]
- Chandola, Y.; Virmani, J.; Bhadauria, H.; Kumar, P. Chapter 4—End-to-end pre-trained CNN-based computer-aided classification system design for chest radiographs. In Deep Learning for Chest Radiographs; Academic Press: Cambridge, MA, USA, 2021; pp. 117–140. [Google Scholar] [CrossRef]
- Nazir, M.; Jan, Z.; Sajjad, M. Facial expression recognition using histogram of oriented gradients based transformed features. Clust. Comput. 2018, 21, 539–548. [Google Scholar] [CrossRef]
- Déniz, O.; Bueno, G.; Salido, J.; De la Torre, F. Face recognition using Histograms of Oriented Gradients. Pattern Recognit. Lett. 2011, 32, 1598–1603. [Google Scholar] [CrossRef]
- Jafari, F.; Basu, A. Saliency-Driven Hand Gesture Recognition Incorporating Histogram of Oriented Gradients (HOG) and Deep Learning. Sensors 2023, 23, 7790. [Google Scholar] [CrossRef] [PubMed]
- Dias, C.G.; Rodrigues, K.L.; Menegasse, N.C.; Alves, W.A.L.; Da Silva, L.C. Histogram of Oriented Gradients for Rotor Speed Estimation in Three-Phase Induction Motors. IEEE Trans. Instrum. Meas. 2023, 72, 7503811. [Google Scholar] [CrossRef]
- Bhattarai, B.; Subedi, R.; Gaire, R.R.; Vazquez, E.; Stoyanov, D. Histogram of Oriented Gradients meet deep learning: A novel multi-task deep network for 2D surgical image semantic segmentation. Med. Image Anal. 2023, 85, 102747. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. Xgboost: A Scalable Tree Boosting System; Association for Computing Machinery: New York, NY, USA, 2016. [Google Scholar] [CrossRef]
- Friedman, J.; Hastie, T.; Tibshirani, R. Additive logistic regression: A statistical view of boosting (With discussion and a rejoinder by the authors). Ann. Stat. 2000, 28, 337–407. [Google Scholar] [CrossRef]
- Friedman, J. Greedy Function Approximation: A Gradient Boosting Machine. Ann. Stat. 2001, 29, 1189–1232. [Google Scholar] [CrossRef]
- Friedman, J. Stochastic gradient boosting. Comput. Stat. Data Anal. 2002, 38, 367–378. [Google Scholar] [CrossRef]
- Sharma, N.; Anju; Juneja, A. Extreme Gradient Boosting with Squared Logistic Loss Function. In Machine Intelligence and Signal Analysis; Tanveer, M., Pachori, R.B., Eds.; Springer: Singapore, 2019; pp. 313–322. [Google Scholar] [CrossRef]
- Python API Reference of Xgboost. Available online: https://xgboost.readthedocs.io/en/stable/python/python_api.html (accessed on 1 December 2023).
- Mohiuddin, G.; Lin, Z.; Zheng, J.; Wu, J.; Li, W.; Fang, Y.; Wang, S.; Chen, J.; Zeng, X. Intrusion Detection using hybridized Meta-heuristic techniques with Weighted XGBoost Classifier. Expert Syst. Appl. 2023, 232, 120596. [Google Scholar] [CrossRef]
- Vadhwani, D.; Thakor, D. Prediction of extent of damage in vehicle during crash using improved XGBoost model. Int. J. Crashworthiness 2023, 28, 299–305. [Google Scholar] [CrossRef]
- Tian, J.; Tsai, P.W.; Zhang, K.; Cai, X.; Xiao, H.; Yu, K.; Zhao, W.; Chen, J. Synergetic Focal Loss for Imbalanced Classification in Federated XGBoost. IEEE Trans. Artif. Intell. 2023, 1–13. [Google Scholar] [CrossRef]
- Chen, T.; Guestrin, C. XGBoost: A Scalable Tree Boosting System. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD ’16), New York, NY, USA, 13–17 August 2016; pp. 785–794. [Google Scholar] [CrossRef]
- Goodfellow, I.; Bengio, Y.; Courville, A. Deep Learning; Chapter 6.2.2.3 Softmax Units for Multinoulli Output Distributions; MIT Press: Cambridge, MA, USA, 2016; pp. 180–184. [Google Scholar] [CrossRef]
- Mushava, J.; Murray, M. Flexible loss functions for binary classification in gradient-boosted decision trees: An application to credit scoring. Expert Syst. Appl. 2024, 238, 121876. [Google Scholar] [CrossRef]
- Legate, G.; Caccia, L.; Belilovsky, E. Re-weighted softmax cross-entropy to control forgetting in federated learning. arXiv 2023, arXiv:2304.05260. [Google Scholar] [CrossRef]
- Wang, C.; Deng, C.; Wang, S. Imbalance-XGBoost: Leveraging weighted and focal losses for binary label-imbalanced classification with XGBoost. Pattern Recognit. Lett. 2020, 136, 190–197. [Google Scholar] [CrossRef]
- Ye, M.; Zhu, L.; Li, X.; Ke, Y.; Huang, Y.; Chen, B.; Yu, H.; Li, H.; Feng, H. Estimation of the soil arsenic concentration using a geographically weighted XGBoost model based on hyperspectral data. Sci. Total Environ. 2023, 858, 159798. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, X.; Chen, B.; Zhang, R.; She, W.; Tian, Z. A combination of XGBoost and FocalLoss-based cable aging state assessment method. In Proceedings of the 5th International Conference on Information Science, Electrical, and Automation Engineering (ISEAE 2023), Wuhan, China, 24–26 March 2023; SPIE: Bellingham, DC, USA, 2023; Volume 12748, pp. 724–730. [Google Scholar]
- Fan, C.; Li, C.; Peng, Y.; Shen, Y.; Cao, G.; Li, S. Fault Diagnosis of Vibration Sensors Based on Triage Loss Function-Improved XGBoost. Electronics 2023, 12, 4442. [Google Scholar] [CrossRef]
- GitHub—Dmlc/Xgboost: Scalable, Portable and Distributed Gradient Boosting (GBDT, GBRT or GBM) Library, for Python, R, Java, Scala, C++ and More. Runs on Single Machine, Hadoop, Spark, Dask, Flink and DataFlow—github.com. Available online: https://github.com/dmlc/xgboost (accessed on 1 January 2024).






| Drill Number | Green Class | Yellow Class | Red Class | Total |
|---|---|---|---|---|
| Drill 1 | 840 | 420 | 406 | 1666 |
| Drill 2 | 840 | 700 | 280 | 1820 |
| Drill 3 | 700 | 560 | 420 | 1680 |
| Drill 4 | 840 | 560 | 280 | 1680 |
| Drill 5 | 560 | 560 | 560 | 1680 |
| Total | 3780 | 2800 | 1946 | 8526 |
| No. | Layer’s Name | Layer’s Type | Description | Total Learnables |
|---|---|---|---|---|
| 1 | data | Image Input | 224 × 224 × 3 images with ‘zscore’ normalization | 0 |
| 2 | conv1 | 2-D Convolution | 64 7 × 7 × 3 convolutions with stride [2 2] and padding [3 3 3 3] | 9472 |
| 3 | bn_conv1 | Batch Normalization | Batch normalization with 64 channels | 128 |
| 4 | conv1_relu | ReLU | ReLU | 0 |
| 5 | pool1 | 2-D Max Pooling | 3 × 3 max pooling with stride [2 2] and padding [1 1 1 1] | 0 |
| 6 | res2a_branch2a | 2-D Convolution | 64 3 × 3 × 64 convolutions with stride [1 1] and padding [1 1 1 1] | 36,928 |
| 7 | bn2a_branch2a | Batch Normalization | Batch normalization with 64 channels | 128 |
| 8 | res2a_branch2a_relu | ReLU | ReLU | 0 |
| 9 | res2a_branch2b | 2-D Convolution | 64 3 × 3 × 64 convolutions with stride [1 1] and padding [1 1 1 1] | 36,928 |
| 10 | bn2a_branch2b | Batch Normalization | Batch normalization with 64 channels | 128 |
| 11 | res2a | Addition | Element-wise addition of 2 inputs | 0 |
| 12 | res2a_relu | ReLU | ReLU | 0 |
| 13 | res2b_branch2a | 2-D Convolution | 64 3 × 3 × 64 convolutions with stride [1 1] and padding [1 1 1 1] | 36,928 |
| 14 | bn2b_branch2a | Batch Normalization | Batch normalization with 64 channels | 128 |
| 15 | res2b_branch2a_relu | ReLU | ReLU | 0 |
| 16 | res2b_branch2b | 2-D Convolution | 64 3 × 3 × 64 convolutions with stride [1 1] and padding [1 1 1 1] | 36,928 |
| 17 | bn2b_branch2b | Batch Normalization | Batch normalization with 64 channels | 128 |
| 18 | res2b | Addition | Element-wise addition of 2 inputs | 0 |
| 19 | res2b_relu | ReLU | ReLU | 0 |
| 20 | res3a_branch2a | 2-D Convolution | 128 3 × 3 × 64 convolutions with stride [2 2] and padding [1 1 1 1] | 73,856 |
| 21 | bn3a_branch2a | Batch Normalization | Batch normalization with 128 channels | 256 |
| 22 | res3a_branch2a_relu | ReLU | ReLU | 0 |
| 23 | res3a_branch2b | 2-D Convolution | 128 3 × 3 × 128 convolutions with stride [1 1] and padding [1 1 1 1] | 147,584 |
| 24 | bn3a_branch2b | Batch Normalization | Batch normalization with 128 channels | 256 |
| 25 | res3a_branch1 | 2-D Convolution | 128 1 × 1 × 64 convolutions with stride [2 2] and padding [0 0 0 0] | 8320 |
| 26 | bn3a_branch1 | Batch Normalization | Batch normalization with 128 channels | 256 |
| 27 | res3a | Addition | Element-wise addition of 2 inputs | 0 |
| 28 | res3a_relu | ReLU | ReLU | 0 |
| 29 | res3b_branch2a | 2-D Convolution | 128 3 × 3 × 128 convolutions with stride [1 1] and padding [1 1 1 1] | 147,584 |
| 30 | bn3b_branch2a | Batch Normalization | Batch normalization with 128 channels | 256 |
| 31 | res3b_branch2a_relu | ReLU | ReLU | 0 |
| 32 | res3b_branch2b | 2-D Convolution | 128 3 × 3 × 128 convolutions with stride [1 1] and padding [1 1 1 1] | 147,584 |
| 33 | bn3b_branch2b | Batch Normalization | Batch normalization with 128 channels | 256 |
| 34 | res3b | Addition | Element-wise addition of 2 inputs | 0 |
| 35 | res3b_relu | ReLU | ReLU | 0 |
| 36 | res4a_branch2a | 2-D Convolution | 256 3 × 3 × 128 convolutions with stride [2 2] and padding [1 1 1 1] | 295,168 |
| 37 | bn4a_branch2a | Batch Normalization | Batch normalization with 256 channels | 512 |
| 38 | res4a_branch2a_relu | ReLU | ReLU | 0 |
| 39 | res4a_branch2b | 2-D Convolution | 256 3 × 3 × 256 convolutions with stride [1 1] and padding [1 1 1 1] | 590,080 |
| 40 | bn4a_branch2b | Batch Normalization | Batch normalization with 256 channels | 512 |
| 41 | res4a_branch1 | 2-D Convolution | 256 1 × 1 × 128 convolutions with stride [2 2] and padding [0 0 0 0] | 33,024 |
| 42 | bn4a_branch1 | Batch Normalization | Batch normalization with 256 channels | 512 |
| 43 | res4a | Addition | Element-wise addition of 2 inputs | 0 |
| 44 | res4a_relu | ReLU | ReLU | 0 |
| 45 | res4b_branch2a | 2-D Convolution | 256 3 × 3 × 256 convolutions with stride [1 1] and padding [1 1 1 1] | 590,080 |
| 46 | bn4b_branch2a | Batch Normalization | Batch normalization with 256 channels | 512 |
| 47 | res4b_branch2a_relu | ReLU | ReLU | 0 |
| 48 | res4b_branch2b | 2-D Convolution | 256 3 × 3 × 256 convolutions with stride [1 1] and padding [1 1 1 1] | 590,080 |
| 49 | bn4b_branch2b | Batch Normalization | Batch normalization with 256 channels | 512 |
| 50 | res4b | Addition | Element-wise addition of 2 inputs | 0 |
| 51 | res4b_relu | ReLU | ReLU | 0 |
| 52 | res5a_branch2a | 2-D Convolution | 512 3 × 3 × 256 convolutions with stride [2 2] and padding [1 1 1 1] | 1,180,160 |
| 53 | bn5a_branch2a | Batch Normalization | Batch normalization with 512 channels | 1024 |
| 54 | res5a_branch2a_relu | ReLU | ReLU | 0 |
| 55 | res5a_branch2b | 2-D Convolution | 512 3 × 3 × 512 convolutions with stride [1 1] and padding [1 1 1 1] | 2,359,808 |
| 56 | bn5a_branch2b | Batch Normalization | Batch normalization with 512 channels | 1024 |
| 57 | res5a_branch1 | 2-D Convolution | 512 1 × 1 × 256 convolutions with stride [2 2] and padding [0 0 0 0] | 131,584 |
| 58 | bn5a_branch1 | Batch Normalization | Batch normalization with 512 channels | 1024 |
| 59 | res5a | Addition | Element-wise addition of 2 inputs | 0 |
| 60 | res5a_relu | ReLU | ReLU | 0 |
| 61 | res5b_branch2a | 2-D Convolution | 512 3 × 3 × 512 convolutions with stride [1 1] and padding [1 1 1 1] | 2,359,808 |
| 62 | bn5b_branch2a | Batch Normalization | Batch normalization with 512 channels | 1024 |
| 63 | res5b_branch2a_relu | ReLU | ReLU | 0 |
| 64 | res5b_branch2b | 2-D Convolution | 512 3 × 3 × 512 convolutions with stride [1 1] and padding [1 1 1 1] | 2,359,808 |
| 65 | bn5b_branch2b | Batch Normalization | Batch normalization with 512 channels | 1024 |
| 66 | res5b | Addition | Element-wise addition of 2 inputs | 0 |
| 67 | res5b_relu | ReLU | ReLU | 0 |
| 68 | pool5 | 2-D Global Average Pooling | 2-D global average pooling | 0 |
| 69 | fc1000 | Fully Connected | 1000 fully connected layer | 513,000 |
| 70 | prob | Softmax | softmax | 0 |
| 71 | ClassificationLayer _predictions | Classification Output | crossentropyex with ‘tench’ and 999 other classes | 0 |
| Loss Function for XGBoost | Green-Red Error | Red-Green Error | Total Critical Errors | Accuracy | Time |
|---|---|---|---|---|---|
| Default Softmax Loss | 552 | 598 | 1150 | 64.29% | 199 s |
| Weighted Softmax Loss V1 | 683 | 457 | 1140 | 62.73% | 215 s |
| Weighted Softmax Loss V2 | 603 | 458 | 1061 | 61.44% | 214 s |
| Weighted Softmax Loss V3 | 544 | 429 | 973 | 61.08% | 217 s |
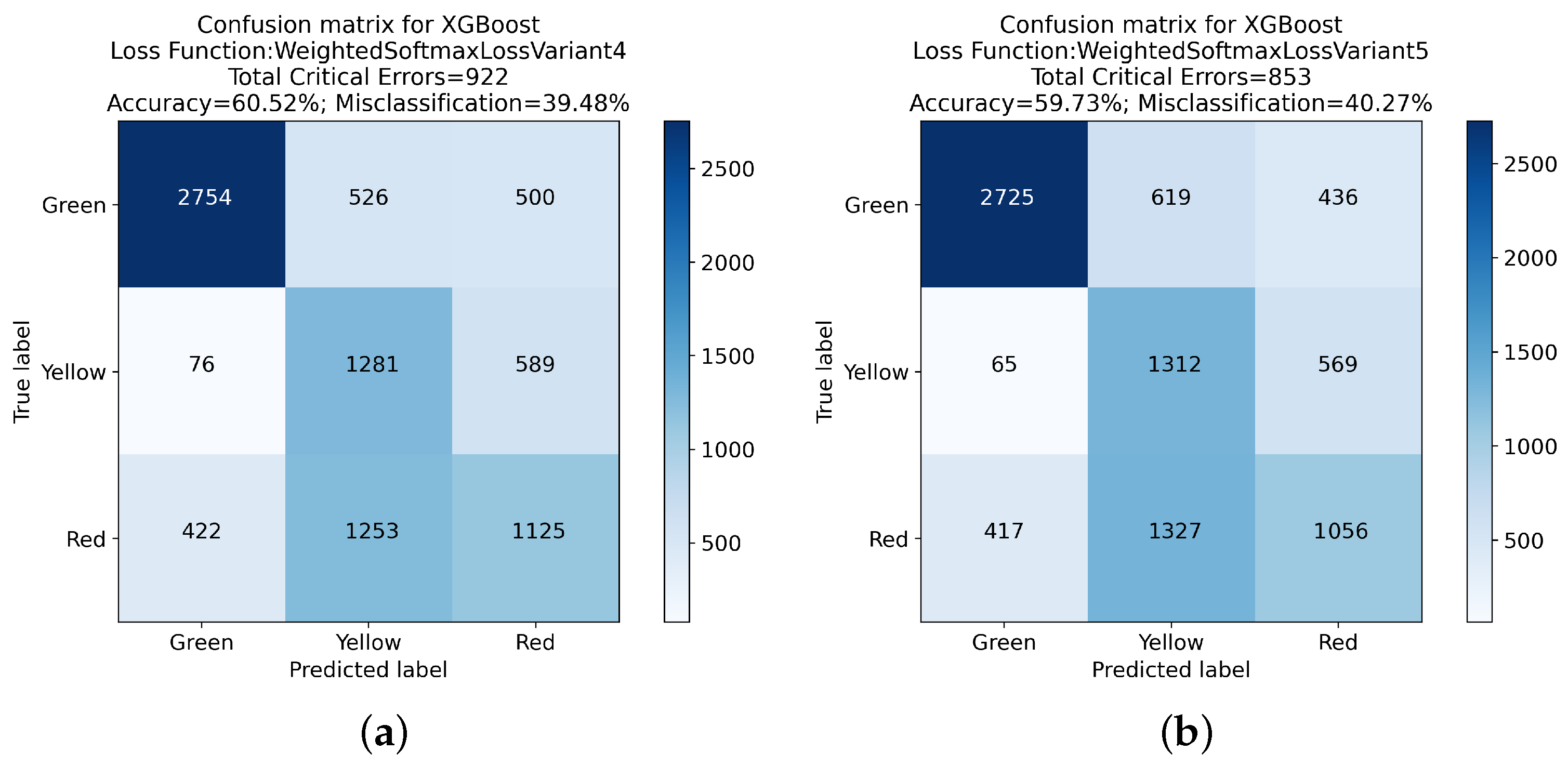
| Weighted Softmax Loss V4 | 500 | 422 | 922 | 60.52% | 223 s |
| Weighted Softmax Loss V5 | 436 | 417 | 853 | 59.73% | 218 s |
| Weighted Softmax Loss With Edge Penalty | 460 | 413 | 873 | 60.59% | 232 s |
| Adaptive Weighted Softmax Loss | 406 | 318 | 724 | 56.08% | 473 s |
| Class | Precision | Sensitivity | F1 Score | Specificity |
|---|---|---|---|---|
| Green | 81.68% | 79.95% | 80.80% | 85.71% |
| Yellow | 51.12% | 59.61% | 55.04% | 83.15% |
| Red | 50.80% | 46.39% | 48.50% | 78.03% |
| Class | Precision | Sensitivity | F1 Score | Specificity |
|---|---|---|---|---|
| Green | 83.85% | 74.15% | 78.70% | 88.62% |
| Yellow | 48.08% | 59.15% | 53.04% | 81.11% |
| Red | 49.98% | 49.79% | 49.88% | 75.64% |
| Class | Precision | Sensitivity | F1 Score | Specificity |
|---|---|---|---|---|
| Green | 83.77% | 73.47% | 78.28% | 88.66% |
| Yellow | 44.70% | 60.95% | 51.58% | 77.71% |
| Red | 49.84% | 45.54% | 47.59% | 77.59% |
| Class | Precision | Sensitivity | F1 Score | Specificity |
|---|---|---|---|---|
| Green | 84.44% | 72.91% | 78.25% | 89.30% |
| Yellow | 43.10% | 64.08% | 51.54% | 74.98% |
| Red | 50.87% | 43.04% | 46.62% | 79.67% |
| Class | Precision | Sensitivity | F1 Score | Specificity |
|---|---|---|---|---|
| Green | 84.69% | 72.86% | 78.33% | 89.51% |
| Yellow | 41.86% | 65.83% | 51.18% | 72.96% |
| Red | 50.81% | 40.18% | 44.87% | 80.98% |
| Class | Precision | Sensitivity | F1 Score | Specificity |
|---|---|---|---|---|
| Green | 84.97% | 72.09% | 78.00% | 89.84% |
| Yellow | 40.27% | 67.42% | 50.42% | 70.43% |
| Red | 51.24% | 37.71% | 43.45% | 82.45% |
| Class | Precision | Sensitivity | F1 Score | Specificity |
|---|---|---|---|---|
| Green | 73.37% | 72.46% | 72.91% | 81.08% |
| Yellow | 70.72% | 66.29% | 68.44% | 89.89% |
| Red | 38.30% | 40.61% | 39.42% | 71.88% |
| Class | Precision | Sensitivity | F1 Score | Specificity |
|---|---|---|---|---|
| Green | 69.80% | 68.17% | 68.98% | 79.71% |
| Yellow | 75.03% | 69.94% | 72.39% | 90.15% |
| Red | 27.91% | 30.11% | 28.97% | 68.72% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bukowski, M.; Kurek, J.; Świderski, B.; Jegorowa, A. Custom Loss Functions in XGBoost Algorithm for Enhanced Critical Error Mitigation in Drill-Wear Analysis of Melamine-Faced Chipboard. Sensors 2024, 24, 1092. https://doi.org/10.3390/s24041092
Bukowski M, Kurek J, Świderski B, Jegorowa A. Custom Loss Functions in XGBoost Algorithm for Enhanced Critical Error Mitigation in Drill-Wear Analysis of Melamine-Faced Chipboard. Sensors. 2024; 24(4):1092. https://doi.org/10.3390/s24041092
Chicago/Turabian StyleBukowski, Michał, Jarosław Kurek, Bartosz Świderski, and Albina Jegorowa. 2024. "Custom Loss Functions in XGBoost Algorithm for Enhanced Critical Error Mitigation in Drill-Wear Analysis of Melamine-Faced Chipboard" Sensors 24, no. 4: 1092. https://doi.org/10.3390/s24041092
APA StyleBukowski, M., Kurek, J., Świderski, B., & Jegorowa, A. (2024). Custom Loss Functions in XGBoost Algorithm for Enhanced Critical Error Mitigation in Drill-Wear Analysis of Melamine-Faced Chipboard. Sensors, 24(4), 1092. https://doi.org/10.3390/s24041092









