Comparative Analysis of Integrated Filtering Methods Using UWB Localization in Indoor Environment
Abstract
1. Introduction
2. Related Works
- This research enhances the development of UWB (ultra-wideband) localization systems by building on previous studies and suggesting innovative integrated filtering techniques for indoor localization. The investigation examines the use of moving average filter (MVG), Kalman filter (KF), and extended Kalman filter (EKF) algorithms, along with a pioneering integrated filtering strategy integrating a low-pass filter (LPF) into MVG, KF, and EKF. Our work aims to enhance solutions for improving UWB localization accuracy.
- This integration aims to enhance accuracy and minimize noise in filtering algorithms. Consequently, our approach effectively reduces high-frequency inference and noise. In contrast to existing probabilistic techniques such as particle filter, Bayesian filter, and support vector machine, which exhibit computational complexity and limited generalization ability, our proposed model is mathematical. This eliminates the need for computational complexity or training, allowing for easy generalization to various paths, including square, circular, and free paths.
3. Working Methodology
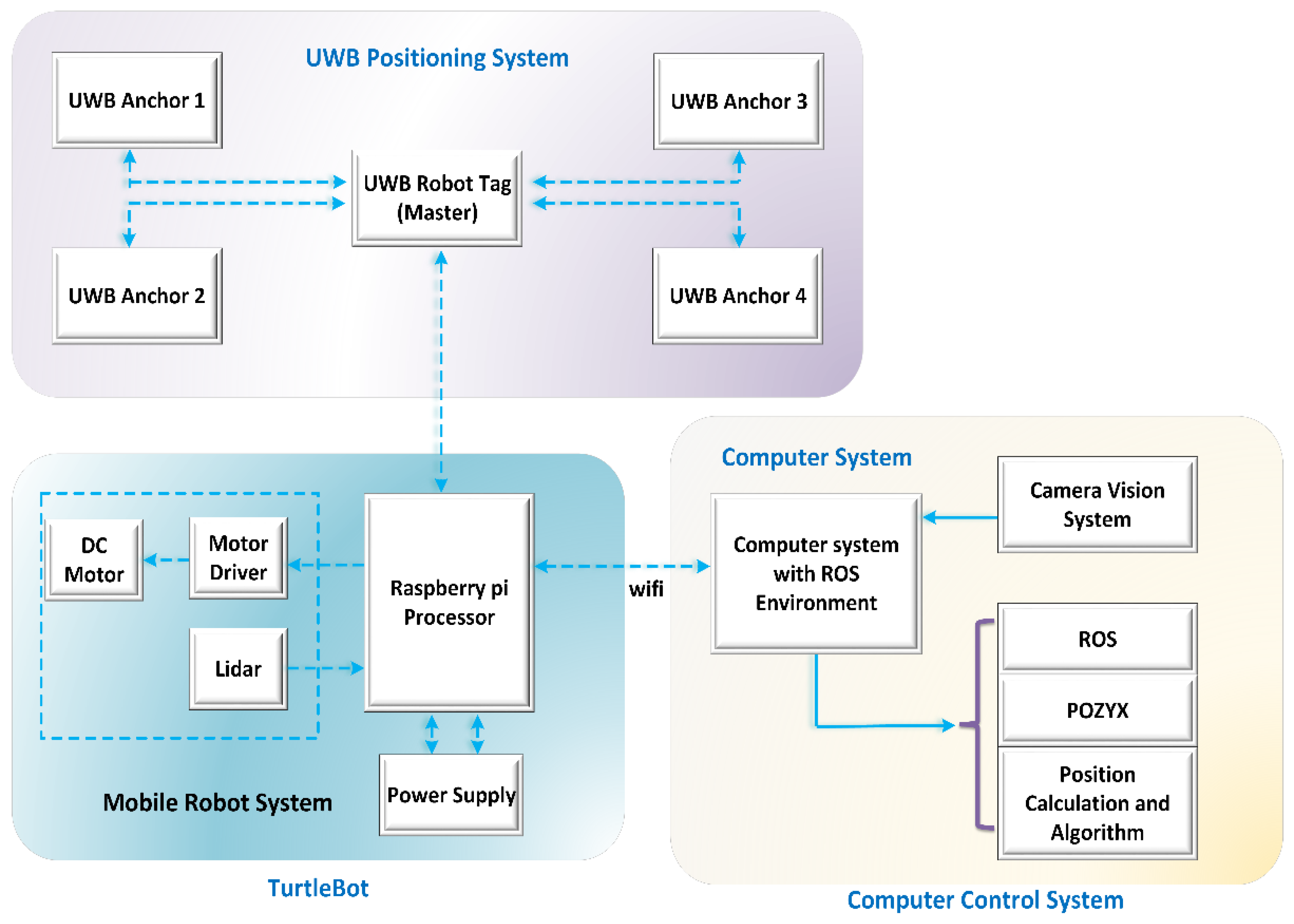
3.1. System Architecture
3.2. UWB System
3.3. Visual Tracking System
3.4. ROS Ecosystem
3.5. System Flowchart
4. Filtering Algorithm
5. Proposed Algorithm
5.1. Low-Pass Filter and Moving Average Filter (LPF + MVG)
| Algorithm 1 LPF + MVG | |||||
| 1: 2: 3: 4: | Input: data = , LPF–Averaging filter (data) filtered_data = [] For i in range (len(data)); | ||||
| 5: | Measurement (TOF ()); | ||||
| 6: | Lateration (); | ||||
| 7: | LPF–Averaging filter () | ||||
| 8: | { | ||||
| 9: | if no valid data, then | ||||
| 10: | return state: link failure or system failure | ||||
| 11: | else | ||||
| 12: 13: 14: 15: | Averaging (); ∖∖calculate the expected value of the range average_value = np.mean(data[start:end]) filtered_data = filtered_data.append(average_value) return: filtered_data | ||||
| 16: | end if | ||||
| 17: | } | ||||
| 18: | Lateration (); | ||||
| 19: | LPF–Averaging filter (); | ||||
| 20: | Print (filtered_data) | ||||
| 21: | End for | ||||
5.2. Low-Pass Filter and Kalman Filter (LPF + KF)
| Algorithm 2 LPF + KF | |||||
| 1: 2: 3: 4: | Input: data = , LPF–Kalman filter (data) filtered_data = [] For i in range (len(data)); | ||||
| 5: | Measurement (TOF()); | ||||
| 6: | LPF–Kalman filter () | ||||
| 7: | { | ||||
| 8: | if (Positions out of bound then | ||||
| 9: | return | ||||
| 10: | else | ||||
| 11: 12: 13: 14: 15: 16: 17: 18: 19: 20: 21: | LPF–Kalman filter (); ∖∖calculate the expected value of the range State Estimate = Process Noise Correction Step Predict Step filtered_data return: filtered_data | ||||
| 22: | end if | ||||
| 23: | } | ||||
| 24: | LPF–Kalman filter (); | ||||
| 25: | Print (filtered_data) | ||||
| 26: | End for | ||||
5.3. Low-Pass Filter in Extended Kalman Filter (LPF + EKF)
| Algorithm 3 LPF + EKF | |||||
| 1: 2: 3: 4: | Input: data = , LPF–Extended Kalman filter (data) filtered_data = [] For i in range (len(data)); | ||||
| 5: | Measurement (TOF ()); | ||||
| 6: | LPF–Extended Kalman filter () | ||||
| 7: | { | ||||
| 8: | if (Positions out of bound then | ||||
| 9: | return | ||||
| 10: | else | ||||
| 11: 12: 13: 14: 15: 16: 17: 18: 19: 2 0: 21: 22: | LPF–Extended Kalman filter (); ∖∖calculate the expected robot’s position and velocity range State Estimate = Process Noise Correction Step Predict Step filtered_data return: filtered_data | ||||
| 23: | end if | ||||
| 24: | } | ||||
| 25: | LPF–Extended Kalman filter (); | ||||
| 26: | Print (filtered_data) | ||||
| 27: | End for | ||||
6. Experimental Setup
6.1. Hardware Setup
6.2. Environment
6.2.1. Calibration
6.2.2. Localization
7. Experiment and Results
7.1. Experiment
7.2. Results
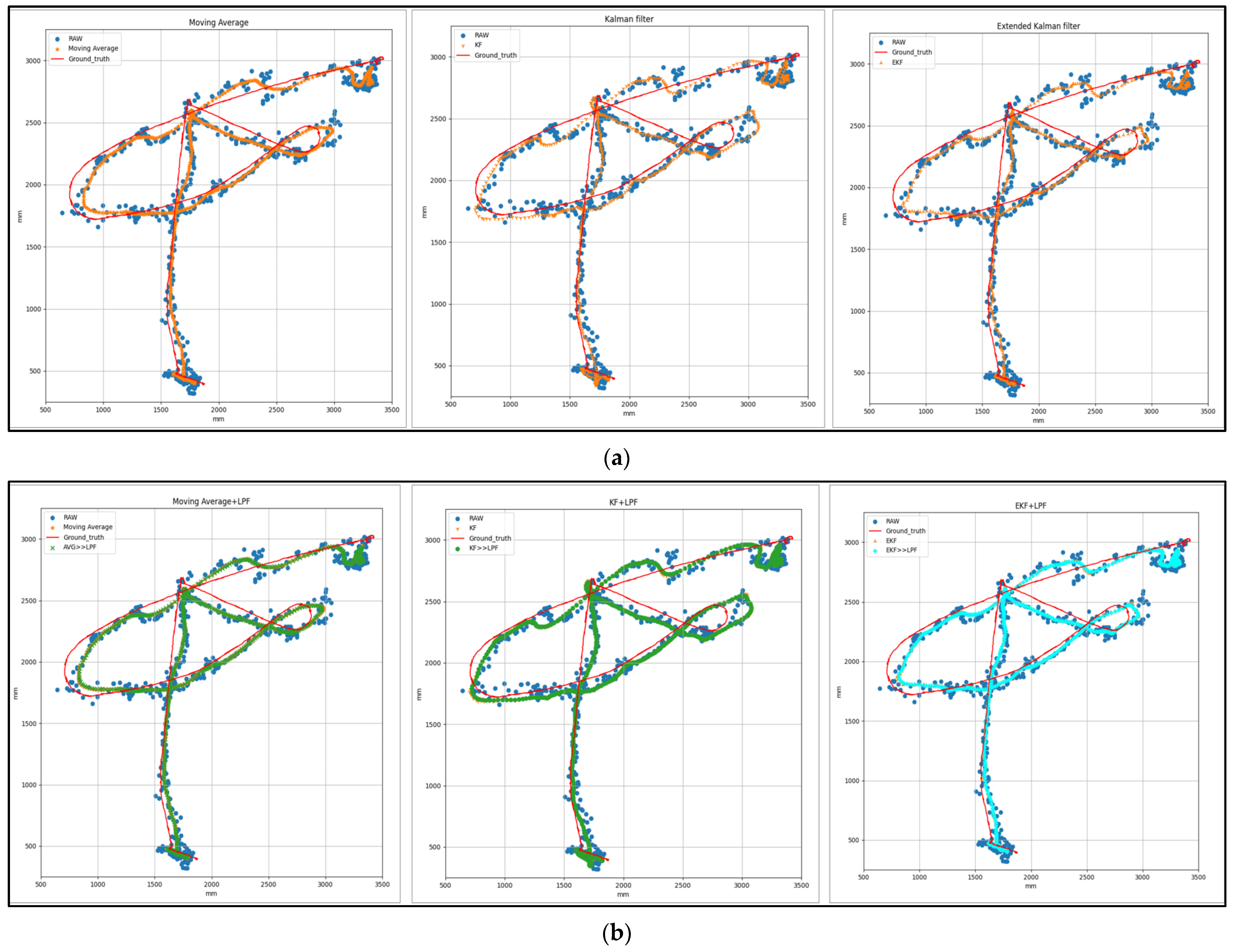
7.2.1. Target 1—Square Path with (MVG, KF, EKF and MVG + LPF, KF + LPF, EKF + LPF) Filtering
7.2.2. Target 2—Circular Path with (MVG, KF, EKF and MVG + LPF, KF + LPF, EKF + LPF) Filtering
7.2.3. Target 3—Free Path with (MVG, KF, EKF and MVG + LPF, KF + LPF, EKF + LPF) Filtering
7.2.4. RMSE ABS Error and SD (Circular, Square, and Free Path)
7.2.5. MAPE for Circular, Square, and Free Path
7.2.6. Overall Error % for Circular, Square, and Free Path
7.2.7. Comparison with Existing Methods
8. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Rawat, P.; Singh, K.D.; Chaouchi, H.; Bonnin, J.M. Wireless Sensor Networks: A Survey on Recent Developments and Potential Synergies. J. Supercomput. 2014, 68, 1–48. [Google Scholar] [CrossRef]
- Huang, B.; Zhao, J.; Liu, J. A Survey of Simultaneous Localization and Mapping with an Envision in 6G Wireless Networks. arXiv 2019, arXiv:1909.05214. [Google Scholar]
- Tang, J.; Zhang, Z.; Feng, S.; Zhao, M.; Xie, Z.; Liu, H. A Wireless Sensor Network-based Indoor Localization System for Emergency Application Use. In Proceedings of the 2nd International Conference on Mechanical, Electronic, Control and Automation Engineering (MECAE 2017), Beijing, China, 25–26 March 2017; pp. 338–341. [Google Scholar] [CrossRef]
- Liu, H.; Darabi, H.; Banerjee, P.; Liu, J. Survey of Wireless Indoor Positioning Techniques and Systems. IEEE Trans. Syst. Man Cybern. Part C Appl. Rev. 2007, 37, 1067–1080. [Google Scholar] [CrossRef]
- Hajjaj, M.; Miki, M.; Shimohara, K. Distributed Intelligent Lighting System using BLE at the Workplace. In Proceedings of the 2019 IEEE 8th Global Conference on Consumer Electronics (GCCE), Osaka, Japan, 15–18 October 2019; pp. 453–456. [Google Scholar] [CrossRef]
- Li, W.; Jia, Y.; Du, J. Distributed consensus extended Kalman filter: A variance-constrained approach. IET Control. Theory Appl. 2017, 11, 382–389. [Google Scholar] [CrossRef]
- Crețu-Sîrcu, A.L.; Schiøler, H.; Cederholm, J.P.; Sîrcu, I.; Schjørring, A.; Larrad, I.R.; Berardinelli, G.; Madsen, O. Evaluation and Comparison of Ultrasonic and UWB Technology for Indoor Localization in an Industrial Environment. Sensors 2022, 22, 2927. [Google Scholar] [CrossRef] [PubMed]
- McLoughlin, B.J.; Pointon, H.A.G.; McLoughlin, J.P.; Shaw, A.; Bezombes, F.A. Uncertainty Characterisation of Mobile Robot Localisation Techniques Using Optical Surveying Grade Instruments. Sensors 2018, 18, 2274. [Google Scholar] [CrossRef] [PubMed]
- Jan, B.; Farman, H.; Javed, H.; Montrucchio, B.; Khan, M.; Ali, S. Energy Efficient Hierarchical Clustering Approaches in Wireless Sensor Networks: A Survey. Wirel. Commun. Mob. Comput. 2017, 2017, 6457942. [Google Scholar] [CrossRef]
- Geng, C.; Abrudan, T.E.; Kolmonen, V.-M.; Huang, H. Experimental Study on Probabilistic ToA and AoA Joint Localization in Real Indoor Environments. In Proceedings of the ICC 2021—IEEE International Conference on Communications, Montreal, QC, Canada, 14–23 June 2021. [Google Scholar]
- Xiong, W.; Bordoy, J.; Gabbrielli, A.; Fischer, G.; Jan Schott, D.; Höflinger, F.; Wendeberg, J.; Schindelhauer, C.; Johann Rupitsch, S. Two Efficient and Easy-to-Use NLOS Mitigation Solutions to Indoor 3-D AOA-Based Localization. In Proceedings of the 2021 International Conference on Indoor Positioning and Indoor Navigation (IPIN), Lloret de Mar, Spain, 29 November–2 December 2021. [Google Scholar]
- Horiba, M.; Okamoto, E.; Shinohara, T.; Matsumura, K. An Improved NLOS Detection Scheme for Hy-brid-TOA/AOA-Based Localization in Indoor Environments. In Proceedings of the 2013 IEEE International Conference on Ultra-Wideband (ICUWB), Sydney, Australia, 15–18 September 2013; pp. 37–42. [Google Scholar]
- O’Lone, C.E.; Dhillon, H.S.; Buehrer, R.M. Characterizing the First-Arriving Multipath Component in 5G Millimeter Wave Networks: TOA, AOA, and Non-Line-of-Sight Bias. IEEE Trans. Wirel. Commun. 2022, 21, 1602–1620. [Google Scholar] [CrossRef]
- Abbas, H.A.; Boskany, N.W.; Ghafoor, K.Z.; Rawat, D.B. Wi-Fi Based Accurate Indoor Localization System Using SVM and LSTM Algorithms. In Proceedings of the 2021 IEEE 22nd International Conference on Information Reuse and Integration for Data Science (IRI), Las Vegas, NV, USA, 10–12 August 2021; pp. 416–422. [Google Scholar]
- Chriki, A.; Touati, H.; Snoussi, H. SVM-Based Indoor Localization in Wireless Sensor Networks. In Proceedings of the 2017 13th International Wireless Communications and Mobile Computing Conference (IWCMC), Valencia, Spain, 26–30 June 2017; pp. 1144–1149. [Google Scholar]
- Zhou, G.; Luo, J.; Xu, S.; Zhang, S.; Meng, S.; Xiang, K. An EKF-Based Multiple Data Fusion for Mobile Robot Indoor Localization. Assem. Autom. 2021, 41, 274–282. [Google Scholar] [CrossRef]
- Yang, T.; Cabani, A.; Chafouk, H. A Survey of Recent Indoor Localization Scenarios and Methodologies. Sensors 2021, 21, 8086. [Google Scholar] [CrossRef]
- Geng, M.; Wang, Y.; Tian, Y.; Huang, T. CNUSVM: Hybrid CNN-Uneven SVM Model for Imbalanced Visual Learning. In Proceedings of the 2016 IEEE Second International Conference on Multimedia Big Data (BigMM), Taipei, Taiwan, 20–22 April 2016; pp. 186–193. [Google Scholar]
- Oajsalee, S.; Tantrairatn, S.; Khaengkarn, S. Study of ROS Based Localization and Mapping for Closed Area Survey. In Proceedings of the 2019 IEEE 5th International Conference on Mechatronics System and Robots (ICMSR), Singapore, 3–5 May 2019; pp. 24–28. [Google Scholar]
- DeStefano, P.; Siebert, C.; Widenhorn, R. Using a local positioning system to track 2D motion. Phys. Teach. 2019, 57, 508–509. [Google Scholar] [CrossRef]
- Gezici, S.; Tian, Z.; Giannakis, G.B.; Kobayashi, H.; Molisch, A.F.; Poor, H.V.; Sahinoglu, Z. Localization via Ultra-Wideband Radios: A Look at Positioning Aspects for Future Sensor Networks. IEEE Signal Process. Mag. 2005, 22, 70–84. [Google Scholar] [CrossRef]
- Krishnan, S.; Sharma, P.; Guoping, Z.; Hwee Woon, O. A UWB Based Localization System for Indoor Robot Navigation. In Proceedings of the 2007 IEEE International Conference on Ultra-Wideband, Singapore, 24–26 September 2007. [Google Scholar]
- Wang, Y.; Jie, H.; Cheng, L. A Fusion Localization Method Based on a Robust Extended Kalman Filter and Track-Quality for Wireless Sensor Networks. Sensors 2019, 19, 3638. [Google Scholar] [CrossRef] [PubMed]
- Mahdi, A.A.; Chalechale, A.; Abdelraouf, A. A Hybrid Indoor Positioning Model for Critical Situations Based on Localization Technologies. Mob. Inf. Syst. 2022, 2022, 8033380. [Google Scholar] [CrossRef]
- Nagel, H.-H.; Haag, M. Bias-Corrected Optical Flow Estimation for Road Vehicle Tracking. In Proceedings of the Sixth International Conference on Computer Vision (IEEE Cat. No.98CH36271), Bombay, India, 7 January 1998. [Google Scholar]
- Oğuz Ekim, P. ROS Ekosistemi Ile Robotik Uygulamalar Için UWB, LiDAR ve Odometriye Dayalı Ko-numlandırma ve İlklendirme Algoritmaları. Eur. J. Sci. Technol. 2020, 343–350. [Google Scholar] [CrossRef]
- Li, J.; Gao, T.; Wang, X.; Bai, D.; Guo, W. The IMU/UWB/Odometer Fusion Positioning Algorithm Based on EKF. J. Phys. Conf. Ser. 2022, 2369, 012092. [Google Scholar] [CrossRef]
- Queralta, J.P.; Martínez Almansa, C.; Schiano, F.; Floreano, D.; Westerlund, T. UWB-Based System for UAV Localization in GNSS-Denied Environments: Characterization and Dataset. In Proceedings of the 2020 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Las Vegas, NV, USA, 24 October 2020–24 January 2021; Available online: https://ieeexplore.ieee.org/abstract/document/9341042/ (accessed on 22 November 2022).
- Long, Z.; Xiang, Y.; Lei, X.; Li, Y.; Hu, Z.; Dai, X. Integrated Indoor Positioning System of Greenhouse Robot Based on UWB/IMU/ODOM/LIDAR. Sensors 2022, 22, 4819. [Google Scholar] [CrossRef] [PubMed]
- Alatise, M.; Hancke, G. Pose Estimation of a Mobile Robot Based on Fusion of IMU Data and Vision Data Using an Extended Kalman Filter. Sensors 2017, 17, 2164. [Google Scholar] [CrossRef] [PubMed]
- Xing, B.; Zhu, Q.; Pan, F.; Feng, X. Marker-Based Multi-Sensor Fusion Indoor Localization System for Micro Air Vehicles. Sensors 2018, 18, 1706. [Google Scholar] [CrossRef]
- Yi, D.H.; Lee, T.J.; Dan Cho, D. A New Localization System for Indoor Service Robots in Low Luminance and Slippery Indoor Environment Using a Focal Optical Flow Sensor Based Sensor Fusion. Sensors 2018, 18, 171. [Google Scholar] [CrossRef]
- Chen, L.; Hu, H.; McDonald-Maier, K. EKF Based Mobile Robot Localization. In Proceedings of the Proceedings—3rd International Conference on Emerging Security Technologies, EST 2012, Lisbon, Portugal, 5–7 September 2012; pp. 149–154. [Google Scholar]
- 2011 International Conference on Indoor Positioning and Indoor Navigation; Institute of Electrical and Electronics Engineering: New York, NY, USA, 2011; ISBN 9781457718045.
- Sesyuk, A.; Ioannou, S.; Raspopoulos, M. A Survey of 3D Indoor Localization Systems and Technologies. Sensors 2022, 22, 9380. [Google Scholar] [CrossRef] [PubMed]
- Dai, Y. Research on Robot Positioning and Navigation Algorithm Based on SLAM. Wirel. Commun. Mob. Comput. 2022, 2022, 3340529. [Google Scholar] [CrossRef]
- Huang, J.-D.; Qian, S. Ultra-wideband indoor localization method based on Kalman filtering and Taylor algorithm. In Proceedings of the 3rd International Conference on Internet of Things and Smart City (IoTSC 2023), Chongqing, China, 24–26 March 2023; Volume 12708, p. 127080T. [Google Scholar] [CrossRef]
- Ziegler, M.; Kianfar, A.E.; Hartmann, T.; Clausen, E. Development and Evaluation of a Uwb-based Indoor Positioning System for Underground Mine Environments. Min. Metall. Explor. 2023, 40, 1021–1040. [Google Scholar] [CrossRef]
- Borhan, N.; Saleh, I.; Yunus, A.; Rahiman, W.; Novaliendry, D.; Risfendra. Reducing UWB Indoor Localization Error Using the Fusion of Kalman Filter with Moving Average Filter. In Proceedings of the 2023 IEEE International Conference on Automatic Control and Intelligent Systems (I2CACIS), Shah Alam, Malaysia, 17 June 2023; pp. 55–59. [Google Scholar] [CrossRef]













| Hardware Components | Description |
|---|---|
| UWB Localization System |
|
| Camera |
|
| TurtleBot |
|
| Computer/Processing Unit |
|
| UWB Anchors and Tags |
|
| Power Supply |
|
| Communication Interface |
|
| Mounting Hardware |
|
| Trajectory | Distance | Speed | Max. (mm) | Min. (mm) | |Max.–Min.| (mm) | Mean (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | X | Y | |||
| Square | 2 m | 0.5 m/s | 180.82 | 371.07 | 0.12 | 0.12 | 179.9 | 371.85 | 52.19 | 89.09 |
| Square (LPF) | 2 m | 0.5 m/s | 163.81 | 273.09 | 0.13 | 0.09 | 163.68 | 273 | 46.4 | 70.36 |
| Trajectory | Distance | Speed | Max. (mm) | Min. (mm) | |Max.–Min.| (mm) | Mean (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | X | Y | |||
| Circular | 2.2 m | 0.5 m/s | 166.38 | 341.05 | 0.46 | 0.58 | 165.91 | 340.47 | 56.34 | 100.5 |
| Circular (LPF) | 2.2 m | 0.5 m/s | 158.51 | 286.22 | 0.52 | 0.81 | 157.99 | 285.4 | 157.99 | 285.4 |
| Trajectory | Distance | Speed | Max. (mm) | Min. (mm) | |Max.–Min.| (mm) | Mean (mm) | ||||
|---|---|---|---|---|---|---|---|---|---|---|
| X | Y | X | Y | X | Y | X | Y | |||
| Free | 5 m | 0.5 m/s | 310.84 | 197.99 | 0.3 | 0.2 | 310.55 | 197.78 | 88.84 | 84.36 |
| Free (LPF) | 5 m | 0.5 m/s | 256.74 | 166.50 | 0.74 | 0.36 | 255.99 | 166.13 | 76.25 | 74.07 |
| Trajectory Square Path | MVG | KF | EKF | MVG + LFP | KF + LPF | EKF + LPF | ||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| MAPE % | X | Y | X | Y | X | Y | X | Y | X | Y | X | Y |
| 2.82% | 3.88% | 2.04% | 4.37% | 1.18% | 3.36% | 2.50% | 3.19% | 1.71% | 3.36% | 1.20% | 2.68% | |
| Trajectory Circular Path | MVG | KF | EKF | MVG + LFP | KF + LPF | EKF + LPF | ||||||
| MAPE % | X | Y | X | Y | X | Y | X | Y | X | Y | X | Y |
| 4.51% | 4.39% | 2.95% | 3.56% | 1.76% | 3.30% | 4.0% | 4.16% | 2.56% | 3.30% | 1.92% | 2.38% | |
| Trajectory Free Path | MVG | KF | EKF | MVG + LFP | KF + LPF | EKF + LPF | ||||||
| MAPE % | X | Y | X | Y | X | Y | X | Y | X | Y | X | Y |
| 7.20% | 5.54% | 5.43% | 4.36% | 3.59% | 3.47% | 6.17% | 5.05% | 4.48% | 3.37% | 3.13% | 3.51% | |
| Trajectory Square Path | MVG | KF | EKF | MVG + LFP | KF + LPF | EKF + LPF |
|---|---|---|---|---|---|---|
| Overall Error % | 4.76% | 4.22% | 2.86% | 4.09% | 3.39% | 2.54% |
| Trajectory Circular Path | MVG | KF | EKF | MVG+LFP | KF+LPF | EKF+LPF |
| Overall Error % | 6.70% | 4.73% | 3.41% | 6.08% | 4.21% | 3.11% |
| Trajectory Free Path | MVG | KF | EKF | MVG+LFP | KF+LPF | EKF+LPF |
| Overall Error % | 9.97% | 7.61% | 5.32% | 8.69% | 6.16% | 4.88% |
| Method | Comparison |
|---|---|
| Reducing UWB Indoor Localization Error Using the Fusion of a Kalman Filter with a Moving Average Filter [39] | Average Error (m) |
| Kalman Filter = 0.065 m Moving Average = 0.057 m | |
| Our Proposed Method (MVG, KF+LPF) | Kalman Filter = 0.068 m, Kalman Filter + LPF = 0.062 m Moving Average = 0.064 m, Moving Average + LPF = 0.054 m |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ranjan, R.; Shin, D.; Jung, Y.; Kim, S.; Yun, J.-H.; Kim, C.-H.; Lee, S.; Kye, J. Comparative Analysis of Integrated Filtering Methods Using UWB Localization in Indoor Environment. Sensors 2024, 24, 1052. https://doi.org/10.3390/s24041052
Ranjan R, Shin D, Jung Y, Kim S, Yun J-H, Kim C-H, Lee S, Kye J. Comparative Analysis of Integrated Filtering Methods Using UWB Localization in Indoor Environment. Sensors. 2024; 24(4):1052. https://doi.org/10.3390/s24041052
Chicago/Turabian StyleRanjan, Rahul, Donggyu Shin, Yoonsik Jung, Sanghyun Kim, Jong-Hwan Yun, Chang-Hyun Kim, Seungjae Lee, and Joongeup Kye. 2024. "Comparative Analysis of Integrated Filtering Methods Using UWB Localization in Indoor Environment" Sensors 24, no. 4: 1052. https://doi.org/10.3390/s24041052
APA StyleRanjan, R., Shin, D., Jung, Y., Kim, S., Yun, J.-H., Kim, C.-H., Lee, S., & Kye, J. (2024). Comparative Analysis of Integrated Filtering Methods Using UWB Localization in Indoor Environment. Sensors, 24(4), 1052. https://doi.org/10.3390/s24041052






