Structural Design and Electromagnetic Performance Analysis of Octupole Active Radial Magnetic Bearing
Abstract
:1. Introduction
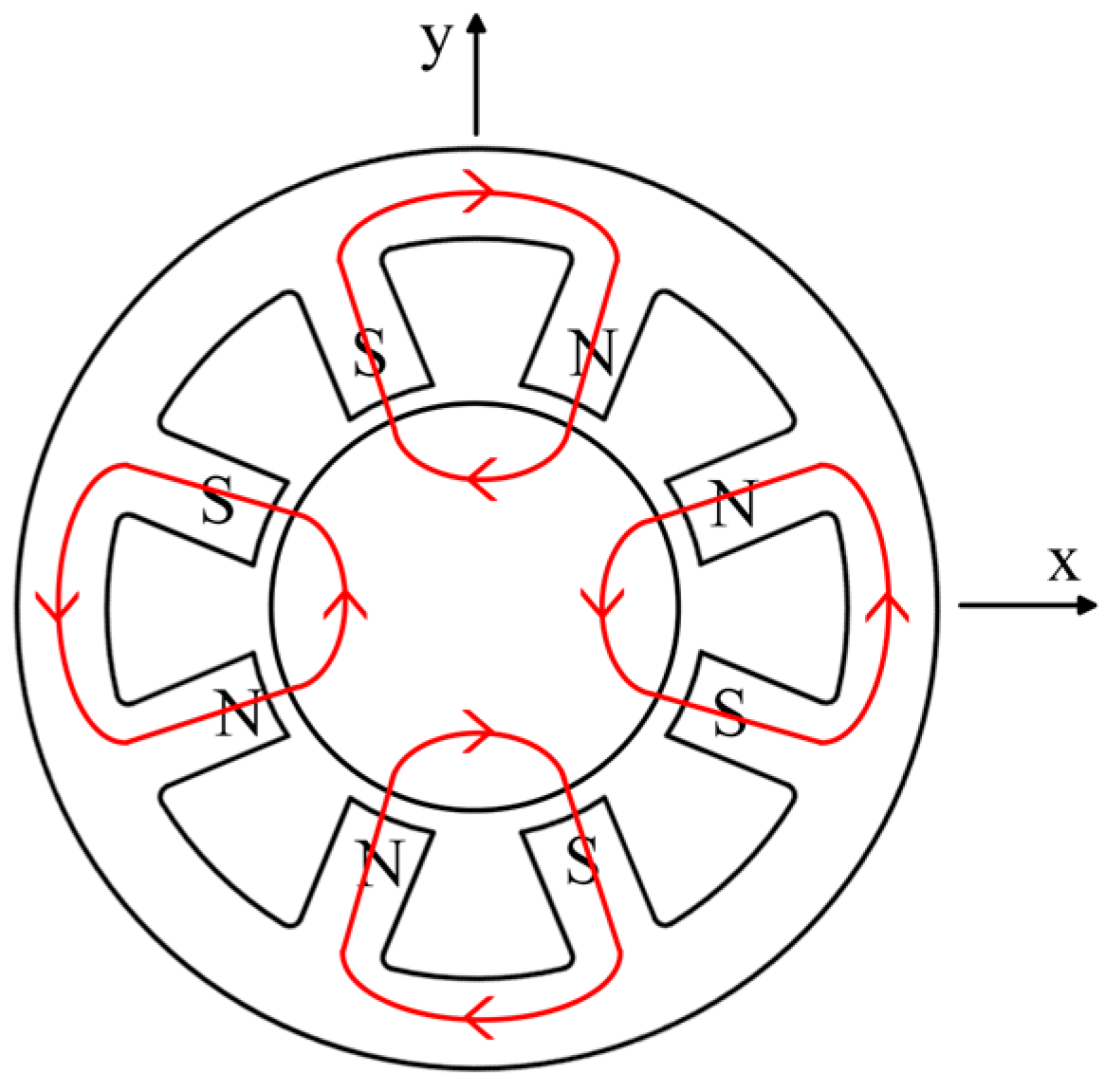
2. Structure and Working Principle
2.1. Structure Composition
2.2. Working Principle
3. Modelling and Design of Main Parameters
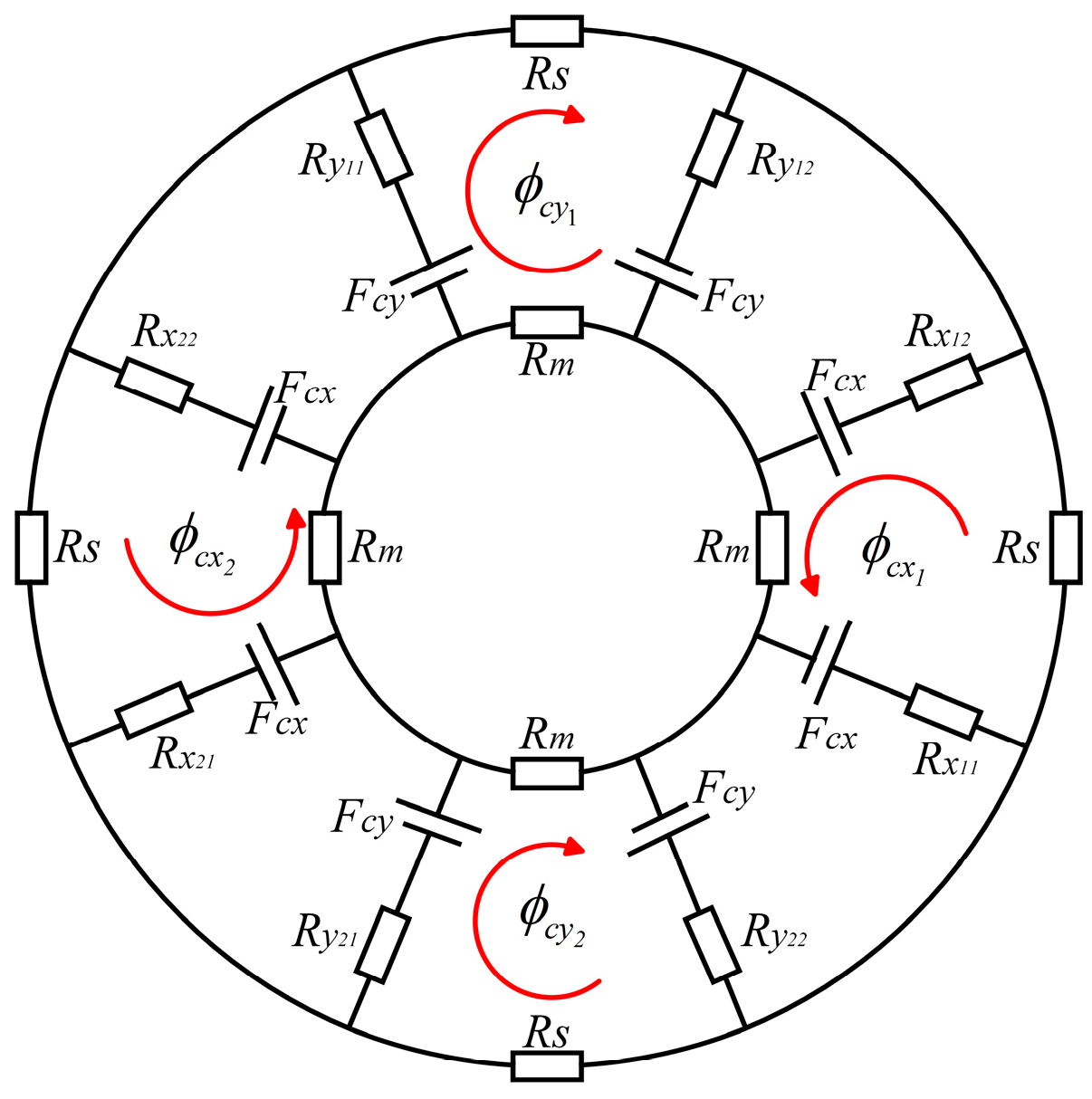
3.1. To Establish the Equivalent Magnetic Circuit Model of the ARMB
3.2. Main Parameter Design
3.2.1. Air Gap Bias Flux Density
3.2.2. Control Current
3.2.3. Coil Fixing Bracket
3.3. FE Model
4. Electromagnetic Property Analysis
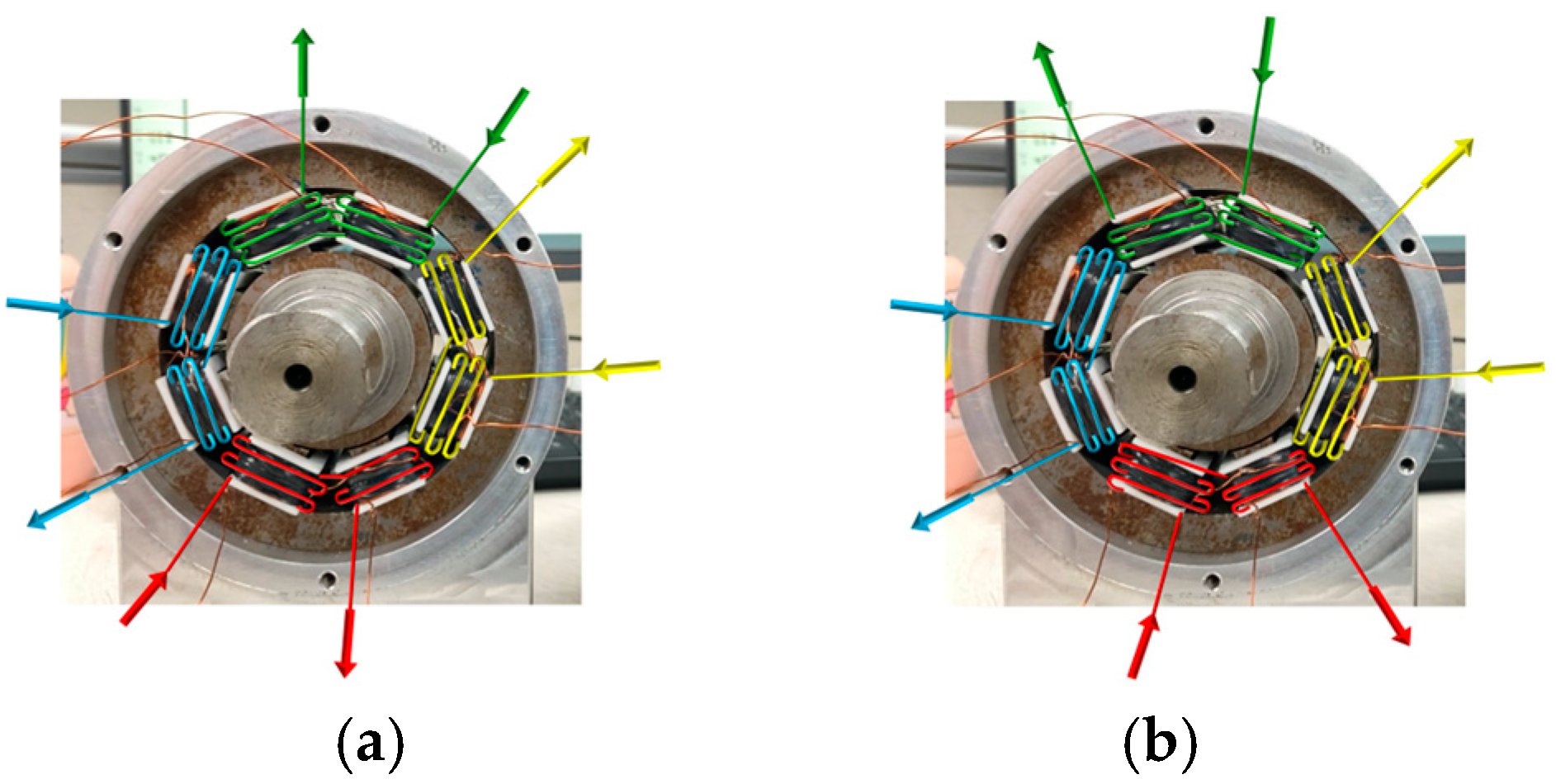
4.1. Magnetic Pole Arrangement–Magnetic Circuit Coupling Relationship
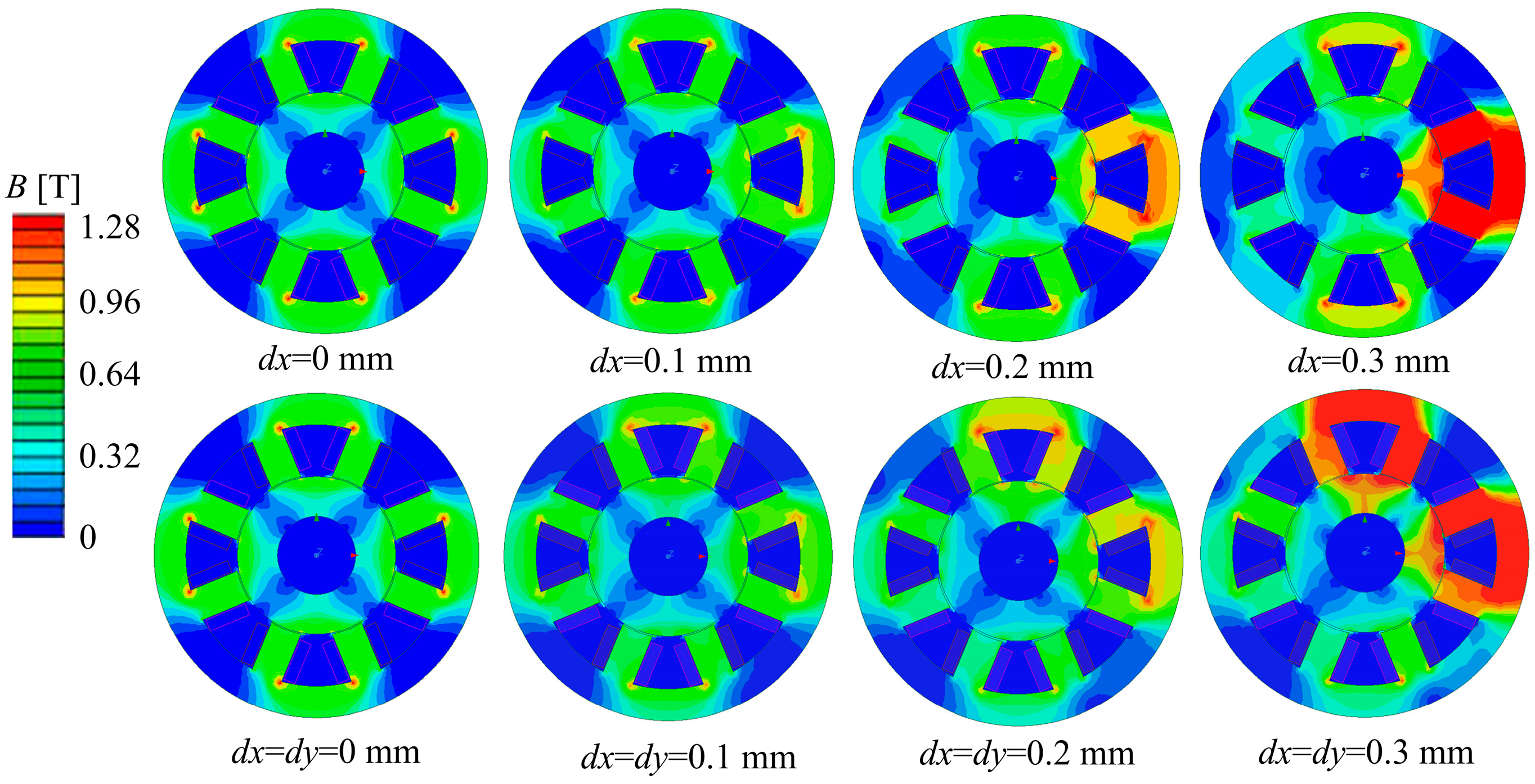
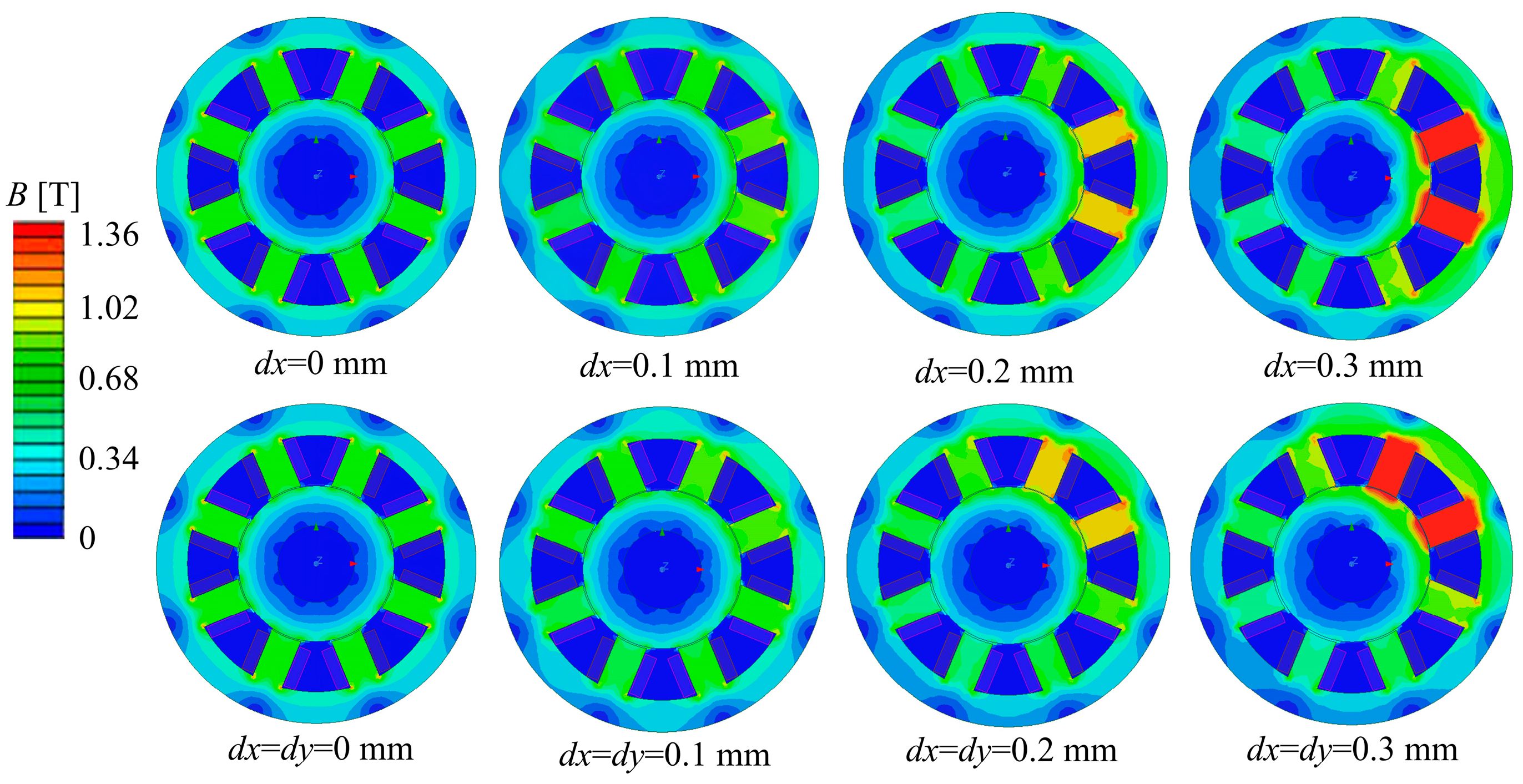
4.2. Unbalanced Disturbance of the Rotor–Magnetic Field Strength at the Air Gap Relationship
4.3. NNSS and NSNS Magnetic Pole Forms–Electromagnetic Force Relationship
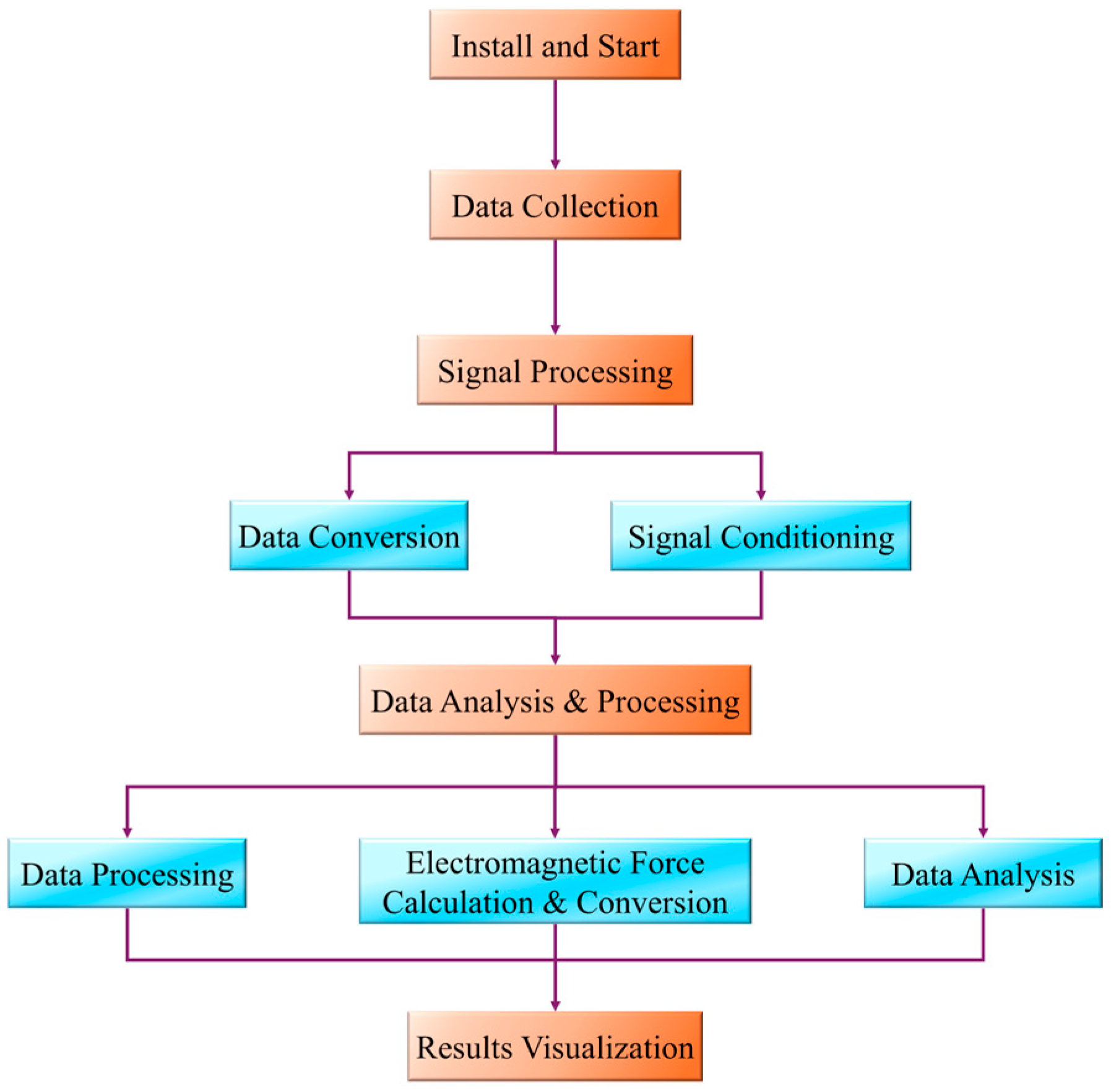
5. Experiment and Results
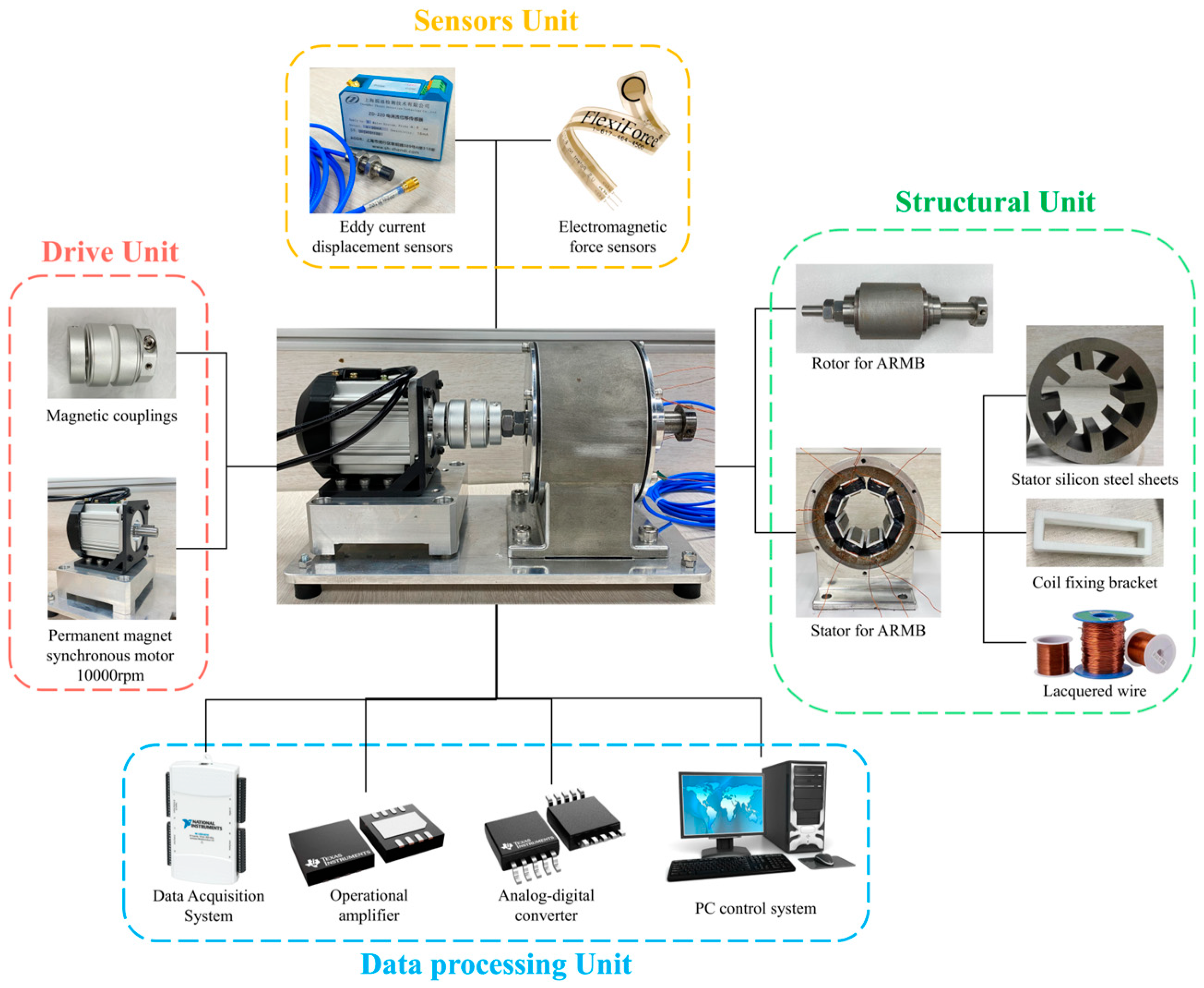
5.1. Experimental Modeling
5.2. Experimental Testing
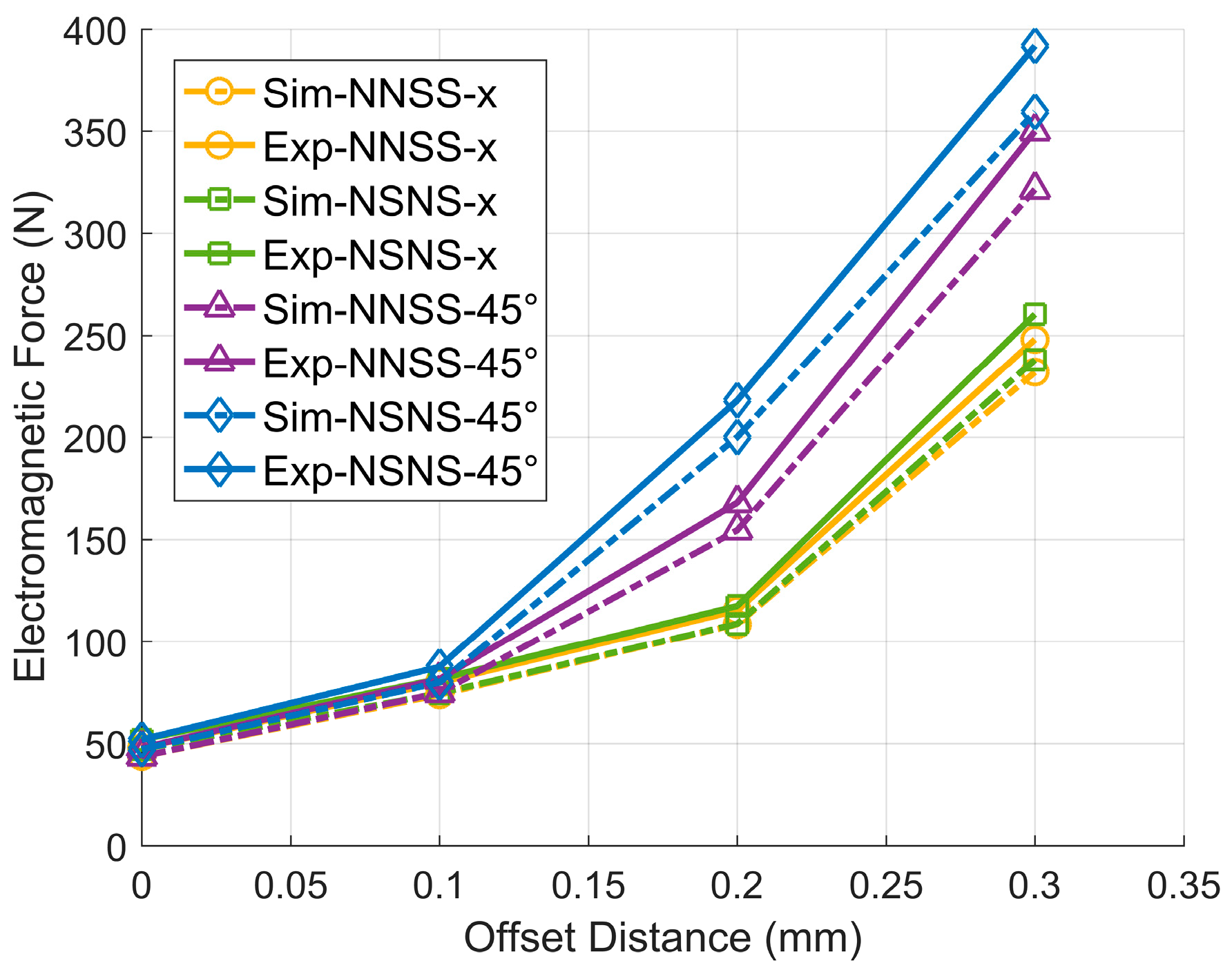
5.3. Experimental Results and Analysis
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Huang, Z.; Li, C.; Zhou, Z.; Liu, B.; Zhang, Y.; Yang, M.; Gao, T.; Liu, M.; Zhang, N.; Sharma, S.; et al. Magnetic Bearing: Structure, Model, and Control Strategy. Int. J. Adv. Manuf. Technol. 2024, 131, 3287–3333. [Google Scholar] [CrossRef]
- Debnath, S.; Das, U.; Biswas, P.K.; Aljafari, B.; Thanikanti, S.B. Design and Control of Multicoil Active Magnetic Bearing System for High-Speed Application. Energies 2023, 16, 4447. [Google Scholar] [CrossRef]
- He, F.; Xie, G.; Luo, J. Electrical Bearing Failures in Electric Vehicles. Friction 2020, 8, 4–28. [Google Scholar] [CrossRef]
- Cai, W.; Wu, X.; Zhou, M.; Liang, Y.; Wang, Y. Review and Development of Electric Motor Systems and Electric Powertrains for New Energy Vehicles. Automot. Innov. 2021, 4, 3–22. [Google Scholar] [CrossRef]
- Ma, J.; Xue, Y.; Han, Q.; Li, X.; Yu, C. Motor Bearing Damage Induced by Bearing Current: A Review. Machines 2022, 10, 1167. [Google Scholar] [CrossRef]
- El Hadraoui, H.; Zegrari, M.; Chebak, A.; Laayati, O.; Guennouni, N. A Multi-Criteria Analysis and Trends of Electric Motors for Electric Vehicles. World Electr. Veh. J. 2022, 13, 65. [Google Scholar] [CrossRef]
- Peng, Y. Seismic Mitigation Analysis of Base-Isolated Structure with Sliding Magnetic Bearings Considering Local-Site Conditions. J. Build. Eng. 2024, 91, 109662. [Google Scholar] [CrossRef]
- Zhang, T.; Le, Q.; Zhu, W. Structure and Suspension Force Analysis of Six-Pole Five Degrees of Freedom AC Hybrid Magnetic Bearing. IEEE Trans. Magn. 2021, 57, 8001404. [Google Scholar] [CrossRef]
- Han, X.; Liu, G.; Le, Y.; Dong, B.; Zheng, S. Unbalanced Magnetic Pull Disturbance Compensation of Magnetic Bearing Systems in MSCCs. IEEE Trans. Ind. Electron. 2023, 70, 4088–4097. [Google Scholar] [CrossRef]
- Taniguchi, R.; Ishida, S.; Yagi, K.; Ohashi, S. Analysis of the Amount of Flux Variation on the HTS Surface by the Oscillation of HTS Magnetic Bearing Rotor. IEEE Trans. Magn. 2023, 59, 8001004. [Google Scholar] [CrossRef]
- Xu, B.; Zhou, J.; Xu, L. Vibration Suppression for a Slice Rotor Supported by Active Magnetic Bearings Based on Fractional-Order Adaptive Backstepping Control. Mech. Syst. Signal Process. 2024, 210, 111160. [Google Scholar] [CrossRef]
- Sun, X.; Chen, L.; Jiang, H.; Yang, Z.; Chen, J.; Zhang, W. High-Performance Control for a Bearingless Permanent-Magnet Synchronous Motor Using Neural Network Inverse Scheme Plus Internal Model Controllers. IEEE Trans. Ind. Electron. 2016, 63, 3479–3488. [Google Scholar] [CrossRef]
- Wu, Y.; Ren, G.P.; Zhang, H.T. Dual-Mode Predictive Control of a Rotor Suspension System. Sci. China Inf. Sci. 2020, 63, 112204. [Google Scholar] [CrossRef]
- Zhu, R.; Xu, W.; Ye, C.; Zhu, J.; Lei, G.; Li, X. Design Optimization of a Novel Heteropolar Radial Hybrid Magnetic Bearing Using Magnetic Circuit Model. IEEE Trans. Magn. 2018, 54, 8201105. [Google Scholar] [CrossRef]
- Zhang, H.; Cheng, M.; Zhou, X.; Feng, L.; Feng, K. Investigations on the Nonlinear Dynamic Characteristics of a Rotor Supported by Hybrid Foil Magnetic Bearings. Nonlinear Dyn. 2023, 111, 14879–14899. [Google Scholar] [CrossRef]
- Li, X.; Palazzolo, A.; Wang, Z. A Combination 5-DOF Active Magnetic Bearing for Energy Storage Flywheels. IEEE Trans. Transp. Electrif. 2021, 7, 2344–2355. [Google Scholar] [CrossRef]
- Hsiao, D.C.; Hsieh, M.F. Design and Implementation of Novel Homopolar Magnetic Bearings Incorporated in Reaction Wheel for Satellite Attitude Control. IEEE Access 2023, 11, 66374–66381. [Google Scholar] [CrossRef]
- Su, Z.; Wang, D.; Chen, J.; Zhang, X.; Wu, L. Improving Operational Performance of Magnetically Suspended Flywheel with PM-Biased Magnetic Bearings Using Adaptive Resonant Controller and Nonlinear Compensation Method. IEEE Trans. Magn. 2016, 52, 8300304. [Google Scholar] [CrossRef]
- Yu, Y.; Zhang, W.; Sun, Y.; Xu, P. Basic Characteristics and Design of a Novel Hybrid Magnetic Bearing for Wind Turbines. Energies 2016, 9, 905. [Google Scholar] [CrossRef]
- Wajnert, D.; Tomczuk, B. Two Models for Time—Domain Simulation of Hybrid Magnetic Bearing’s Characteristics. Sensors 2022, 22, 1567. [Google Scholar] [CrossRef] [PubMed]
- Ueno, S.; Enokizono, M.; Mori, Y.; Yamazaki, K. Vector Magnetic Characteristics of Ultra-Thin Electrical Steel Sheet for Development of High-Efficiency High-Speed Motor. IEEE Trans. Magn. 2017, 53, 6300604. [Google Scholar] [CrossRef]
- Ding, W.; Yang, S.; Hu, Y. Development and Investigation on Segmented-Stator Hybrid-Excitation Switched Reluctance Machines with Different Rotor Pole Number. IEEE Trans. Ind. Electron. 2018, 65, 3784–3794. [Google Scholar] [CrossRef]
- Kang, J.; Huang, X.; Xia, C.; Huang, D.; Wang, F. Ultralocal Model-Free Adaptive Supertwisting Nonsingular Terminal Sliding Mode Control for Magnetic Levitation System. IEEE Trans. Ind. Electron. 2024, 71, 5187–5194. [Google Scholar] [CrossRef]
- Hwang, C.C.; Hung, S.S.; Liu, C.T.; Cheng, S.P. Optimal Design of a High Speed SPM Motor for Machine Tool Applications. IEEE Trans. Magn. 2014, 50, 4002304. [Google Scholar] [CrossRef]
- Srichiangsa, T.; Gunda, S.N.; Sugimoto, H.; Fujii, Y.; Kiyota, K.; Asama, J.; Chiba, A. Comparison of Acoustic Noise and Vibration in Ball-Bearing-Supported Motors and One-Axis Actively Positioned Single-Drive Bearingless Motor With Two Radial Permanent-Magnet Passive Magnetic Bearings. IEEE Open J. Ind. Appl. 2023, 4, 35–48. [Google Scholar] [CrossRef]
- Matsuzaki, T.; Takemoto, M.; Ogasawara, S.; Ota, S.; Oi, K.; Matsuhashi, D. Novel Structure of Three-Axis Active-Control-Type Magnetic Bearing for Reducing Rotor Iron Loss. IEEE Trans. Magn. 2016, 52, 8105404. [Google Scholar] [CrossRef]
- Han, B.; Chen, Y.; Zheng, S.; Li, M.; Xie, J. Whirl Mode Suppression for AMB-Rotor Systems in Control Moment Gyros Considering Significant Gyroscopic Effects. IEEE Trans. Ind. Electron. 2021, 68, 4249–4258. [Google Scholar] [CrossRef]
- Huang, X. Modeling and Optimization of Electromagnetic Conversion Coupling Coefficient Based on Maxwell’s Magnetic Field Theory. J. Vib. Eng. Technol. 2024, 12, 2659–2675. [Google Scholar] [CrossRef]
- Zhang, H.; Wang, Y.P.; Tuo, J.; Yang, M.; Ma, Y.; Xu, J. Magnetic Field and Electromagnetic Performance Analysis of Permanent Magnet Machines with Segmented Halbach Array. COMPEL—Int. J. Comput. Math. Electr. Electron. Eng. 2022, 41, 357–380. [Google Scholar] [CrossRef]
- Li, B.; Zhang, P.; Li, P.; Liu, Z.; Li, W.; Zhang, J. Research on Magnetic-Thermal-Force Multi-Physical Field Coupling of a High-Frequency Transformer with Different Winding Arrangements. Electronics 2023, 12, 5008. [Google Scholar] [CrossRef]
- Maslen, E.H.; Schweitzer, G. (Eds.) Magnetic Bearings; Springer: Berlin/Heidelberg, Germany, 2009; ISBN 978-3-642-00496-4. [Google Scholar]
- Li, Q.; Hu, Y.; Wu, H. Structure Design and Optimization of the Radial Magnetic Bearing. Actuators 2023, 12, 27. [Google Scholar] [CrossRef]
- Kandil, A.; Hou, L.; Sharaf, M.; Arafa, A.A. Configuration Angle Effect on the Control Process of an Oscillatory Rotor in 8-Pole Active Magnetic Bearings. AIMS Math. 2024, 9, 12928–12963. [Google Scholar] [CrossRef]
- Ye, X.; Le, Q.; Zhou, Z. A Novel Homopolar Four Degrees of Freedom Hybrid Magnetic Bearing. IEEE Trans. Magn. 2020, 56, 6703404. [Google Scholar] [CrossRef]
- Noh, M.D.; Jeong, W. Design and Unbiased Control of Nine-Pole Radial Magnetic Bearing. Actuators 2023, 12, 458. [Google Scholar] [CrossRef]
- Satapathy, S.C.; Bheema Rao, N.; Srinivas Kumar, S.; Dharma Raj, C.; Malleswara Rao, V.; Sarma, G.V.K. Microelectronics, Electromagnetics and Telecommunications, Proceedings of the ICMEET 2015; Lecture Notes in Electrical Engineering; Springer: New Delhi, India, 2015; Volume 372. [Google Scholar]
- Luo, C.; Zhang, K.; Duan, J.; Jing, Y. Study of Permanent Magnet Electrodynamic Suspension System with a Novel Halbach Array. J. Electr. Eng. Technol. 2020, 15, 969–977. [Google Scholar] [CrossRef]
- Tang, J.; Wang, K.; Xiang, B. Stable Control of High-Speed Rotor Suspended by Superconducting Magnetic Bearings and Active Magnetic Bearings. IEEE Trans. Ind. Electron. 2017, 64, 3319–3328. [Google Scholar] [CrossRef]
- Jones, W. Earnshaw’s Theorem and the Stability of Matter; IOP Publishing Ltd.: Bristol, UK, 1980; Volume 1. [Google Scholar]
- Lahdo, M.; Strohla, T.; Kovalev, S. Repulsive Magnetic Levitation Force Calculation for a High Precision 6-DoF Magnetic Levitation Positioning System. IEEE Trans. Magn. 2017, 53, 7200106. [Google Scholar] [CrossRef]
- Liu, L.; Qiu, H. Study on the Influence of Magnetic Circuit Saturation on Suspension Performance of Bearingless Permanent Magnet Synchronous Motor. J. Electr. Eng. Technol. 2024, 19, 2377–2386. [Google Scholar] [CrossRef]








| Parameter | Value |
|---|---|
| Height of coil fixing bracket, h | 14 mm |
| Top thickness of coil fixing bracket, h1 | 0.3 mm |
| Bottom thickness of coil fixed support, h2 | 0.4 mm |
| Thickness of each side of coil fixing bracket, t | 3.3 mm |
| Wall thickness of each side of coil fixing bracket, t1 | 0.3 mm |
| Parameter | Value |
|---|---|
| Inner diameter of the stator core, d | 61 mm |
| Outer diameter of the stator core, D | 123 mm |
| Width of the magnetic pole, b | 12 mm |
| Width of the yoke, c | 12 mm |
| Diameter of the rotor, D0 | 60 mm |
| Radial air gap length, δ0 | 0.5 mm |
| Bias flux density, B0 | 0.3 T |
| Control current of the coil, I | 2.5 A |
| Coil turns of each magnet, N | 90 |
| Occupy ratio, λ | 0.7 |
| x-Axis Direction Offset (dx)/mm | 0 | 0.1 | 0.2 | 0.3 | |
| NSNS | 47.082 | 74.431 | 108.637 | 237.957 | |
| NNSS | 43.541 | 73.749 | 108.459 | 231.827 | |
| 45° Direction Offset (dx = dy)/mm | 0 | 0.1 | 0.2 | 0.3 | |
| NSNS | 47.082 | 79.725 | 199.980 | 359.214 | |
| NNSS | 43.541 | 74.652 | 154.459 | 321.351 | |
| Form | Offset (mm) | Direction | Exp1 (N) | Exp2 (N) | Exp3 (N) | Exp4 (N) | Exp5 (N) | Average (N) | Inaccuracy |
|---|---|---|---|---|---|---|---|---|---|
| NNSS | 0 | 47.461 | 47.146 | 48.876 | 49.013 | 46.482 | 47.796 | 9.77% | |
| 0.1 | x-axis | 81.125 | 80.519 | 78.034 | 79.481 | 79.346 | 79.701 | 8.07% | |
| 45° | 81.565 | 81.022 | 80.571 | 81.543 | 82.006 | 81.341 | 8.96% | ||
| 0.2 | x-axis | 118.618 | 115.951 | 102.115 | 120.008 | 119.171 | 115.173 | 6.19% | |
| 45° | 169.005 | 167.375 | 169.852 | 165.844 | 170.489 | 168.513 | 8.71% | ||
| 0.3 | x-axis | 239.771 | 249.249 | 250.186 | 248.005 | 252.713 | 247.984 | 6.97% | |
| 45° | 348.265 | 352.146 | 349.855 | 352.564 | 350.112 | 350.589 | 8.85% | ||
| NSNS | 0 | 51.781 | 52.016 | 50.842 | 51.143 | 53.004 | 51.757 | 9.93% | |
| 0.1 | x-axis | 82.010 | 81.941 | 81.636 | 80.841 | 81.007 | 81.487 | 9.47% | |
| 45° | 87.477 | 86.748 | 87.512 | 87.228 | 88.014 | 87.396 | 9.62% | ||
| 0.2 | x-axis | 118.871 | 115.657 | 113.180 | 119.204 | 120.006 | 117.384 | 8.05% | |
| 45° | 218.633 | 218.418 | 216.984 | 217.511 | 218.010 | 217.910 | 8.97% | ||
| 0.3 | x-axis | 261.875 | 258.831 | 261.146 | 260.664 | 259.042 | 260.312 | 9.39% | |
| 45° | 390.517 | 389.772 | 390.159 | 392.114 | 390.106 | 390.534 | 9.08% |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, Q.; Lu, Y.; Shao, Z. Structural Design and Electromagnetic Performance Analysis of Octupole Active Radial Magnetic Bearing. Sensors 2024, 24, 8200. https://doi.org/10.3390/s24248200
Zhu Q, Lu Y, Shao Z. Structural Design and Electromagnetic Performance Analysis of Octupole Active Radial Magnetic Bearing. Sensors. 2024; 24(24):8200. https://doi.org/10.3390/s24248200
Chicago/Turabian StyleZhu, Qixuan, Yujun Lu, and Zhongkui Shao. 2024. "Structural Design and Electromagnetic Performance Analysis of Octupole Active Radial Magnetic Bearing" Sensors 24, no. 24: 8200. https://doi.org/10.3390/s24248200
APA StyleZhu, Q., Lu, Y., & Shao, Z. (2024). Structural Design and Electromagnetic Performance Analysis of Octupole Active Radial Magnetic Bearing. Sensors, 24(24), 8200. https://doi.org/10.3390/s24248200





