A Noise Reduction Method for Signal Reconstruction and Error Compensation of a Maglev Gyroscope Under Persistent External Interference
Abstract
1. Introduction
2. Principles of Azimuth Measurement and Error Analysis for Maglev Gyroscope Torque Sensors
2.1. Azimuth Measurement Principle
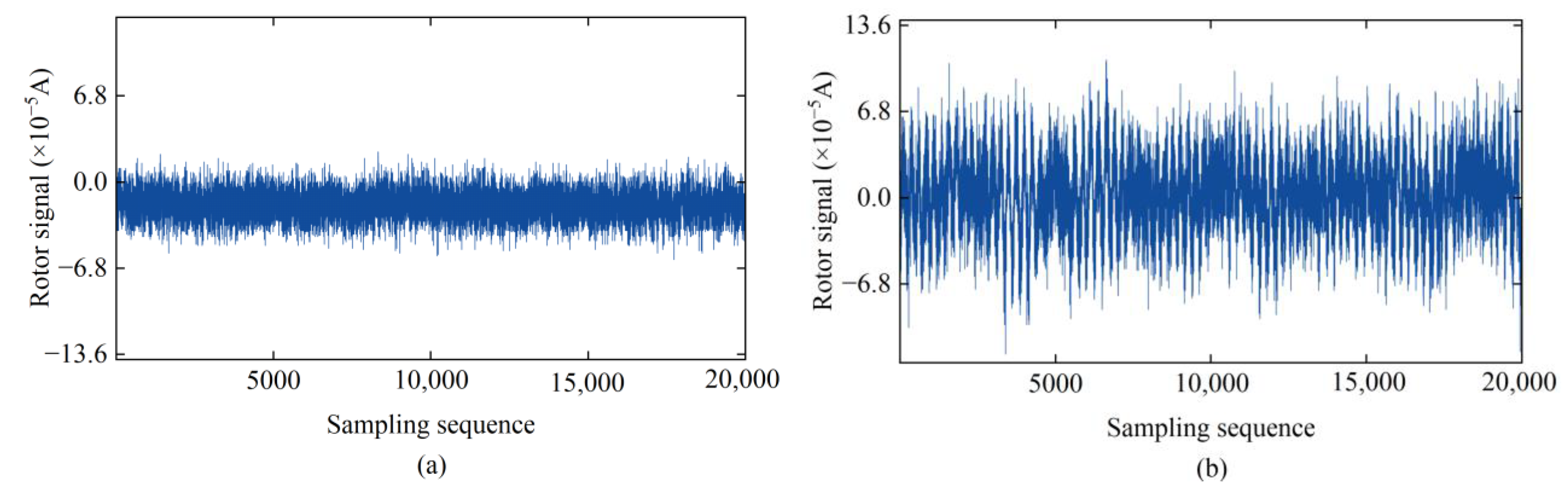
2.2. Analysis of Rotor Signal Error Under Continuous Disturbance of External Environment
3. Method
3.1. Basic Principles of the Variational Mode Decomposition Algorithm
3.2. Particle Swarm Optimization Algorithm
3.3. Signal Trend Term Extraction Method
3.4. The Specific Steps of the Rotor Signal Denoising Method
- (1)
- Constructing the APVMD model: Firstly, initialize the state of the particle swarm, where the position of each particle represents a configuration of a set of and parameters. Perform VMD on the rotor signal, and determine the optimal fitness function of the particle swarm by comparing the dispersion entropy corresponding to each particle. Continuously update the particle velocity, position, and iterate the best fitness function until the preset number of iterations is reached. After the iteration, the particle position corresponding to the optimal fitness function is the optimal parameter combination.
- (2)
- Rotor signal decomposition: The APVMD is used to decompose the rotor signal into IMF components with different center frequencies.
- (3)
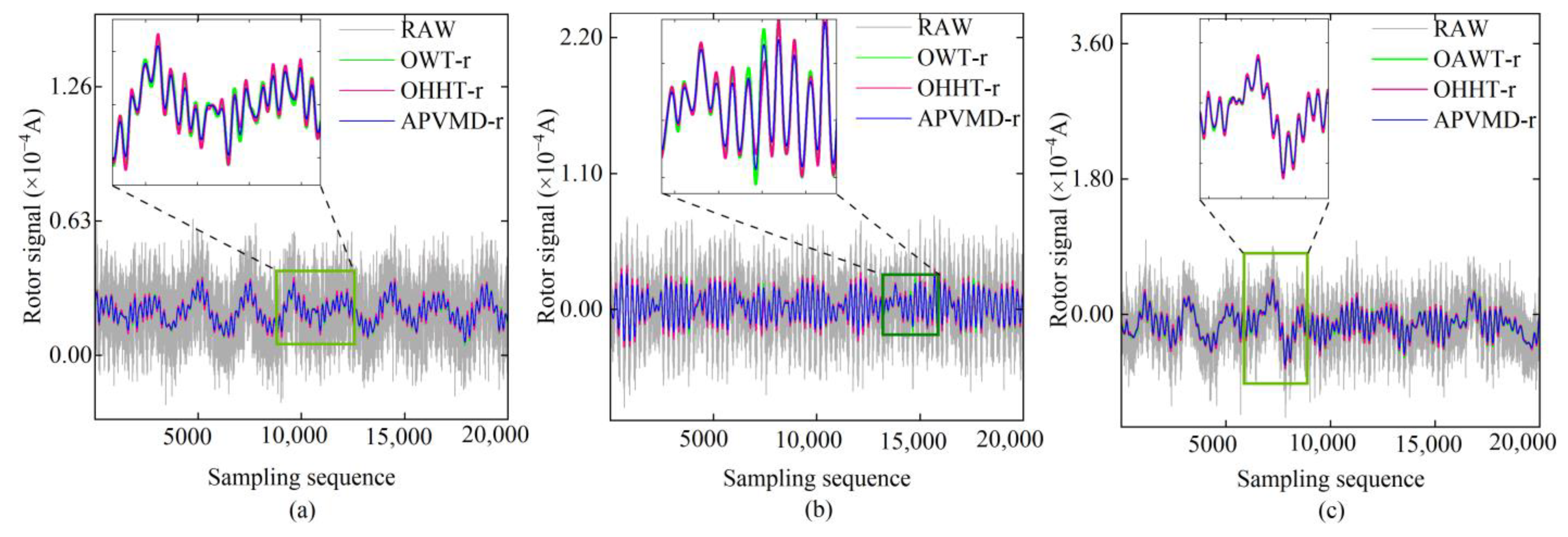
- Signal component reconstruction: Using multi-scale sample entropy as the discriminant criterion, the noise IMF components are removed, and the remaining signal IMF components are accumulated to reconstruct the signal, denoted as APVMD-r. At this point, most of the high-frequency noise in the reconstructed signal has been effectively removed.
- (4)
- Reconstructed signal error compensation: Perform EMD on APVMD-r, and the extracted residual component accurately reflects the accurate trend information of the reconstructed signal. Calculate the mean of the trend term of the reconstructed signal and compensate for the error of the reconstructed signal to correct its overall offset, thereby obtaining the final compensated signal APVMD-c. At this point, the noise reduction processing of the rotor signal is completed.
- (5)
- Calculation of the gyroscope’s north azimuth: According to the principle of orientation measurement by the gyroscope torque sensor, the compensated signal APVMD-c is considered as the filtered rotor signal and substituted into Formula (3) for calculation, thereby obtaining the processed gyroscope’s north azimuth.
4. Results and Analysis
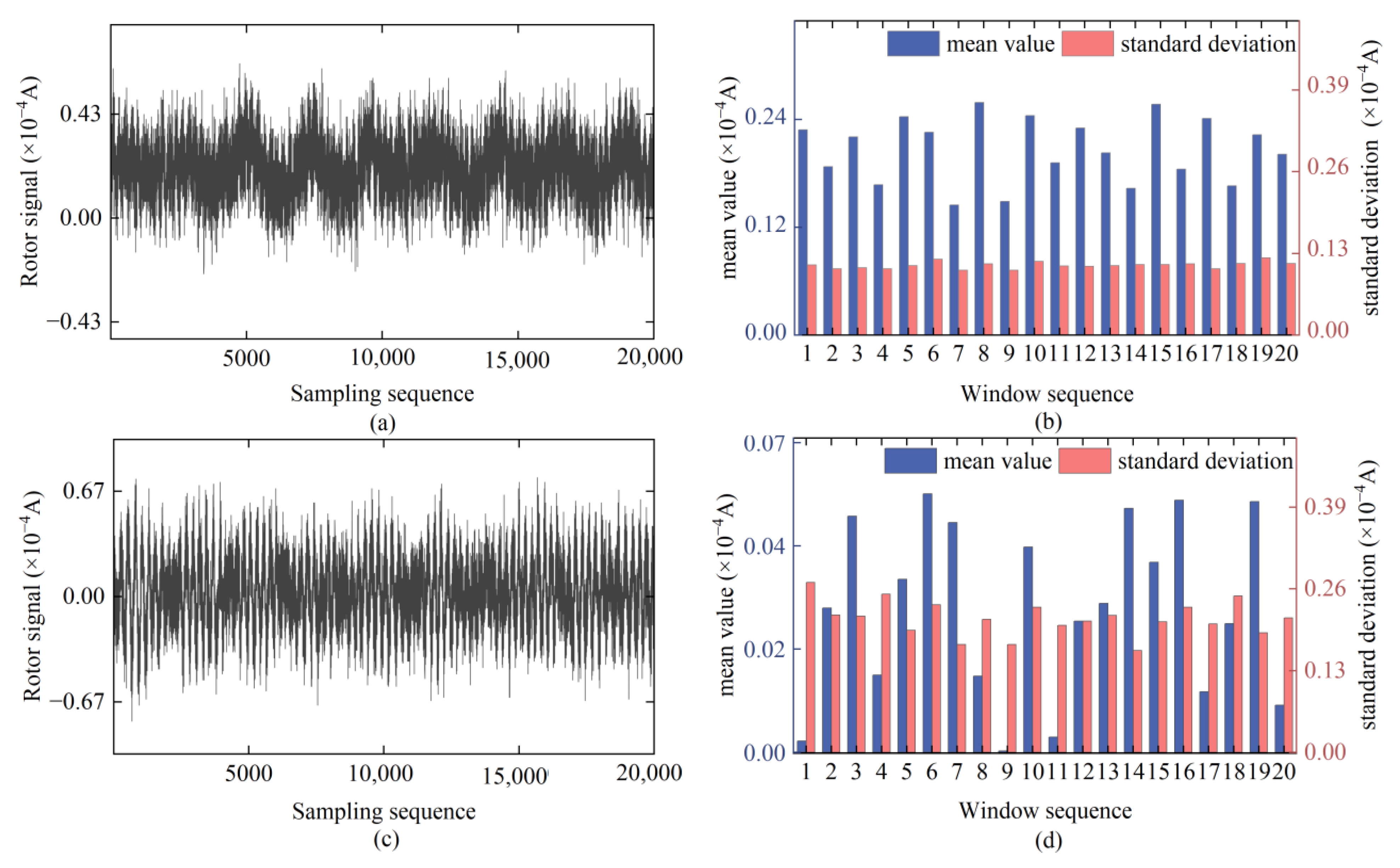
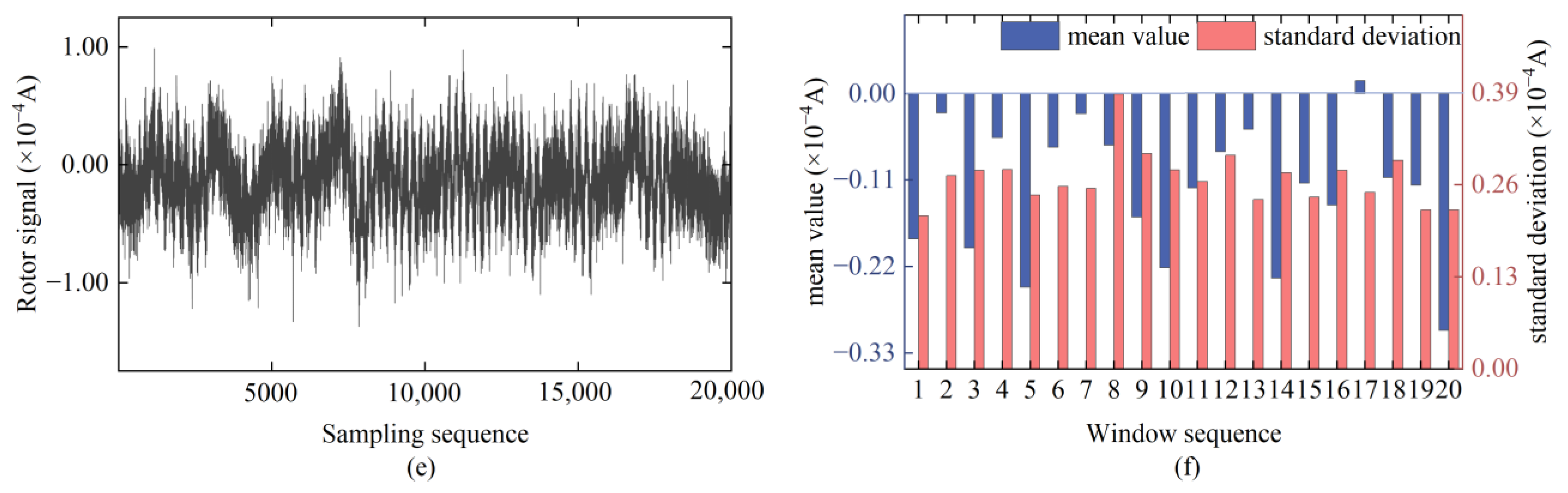
4.1. Experimental Data and Evaluation Indicators
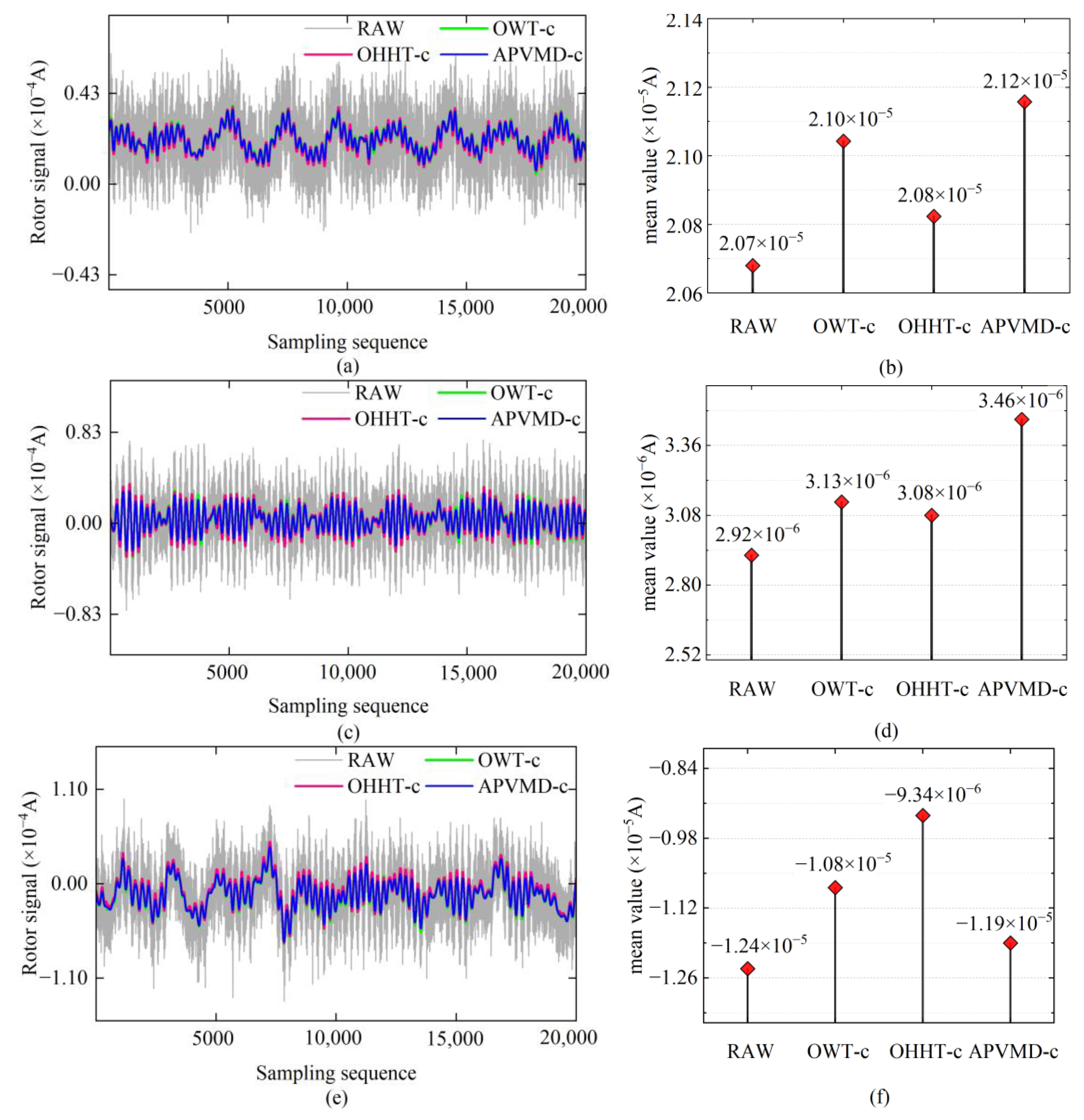
4.2. Rotor Signal Noise Reduction Processing and Result Analysis
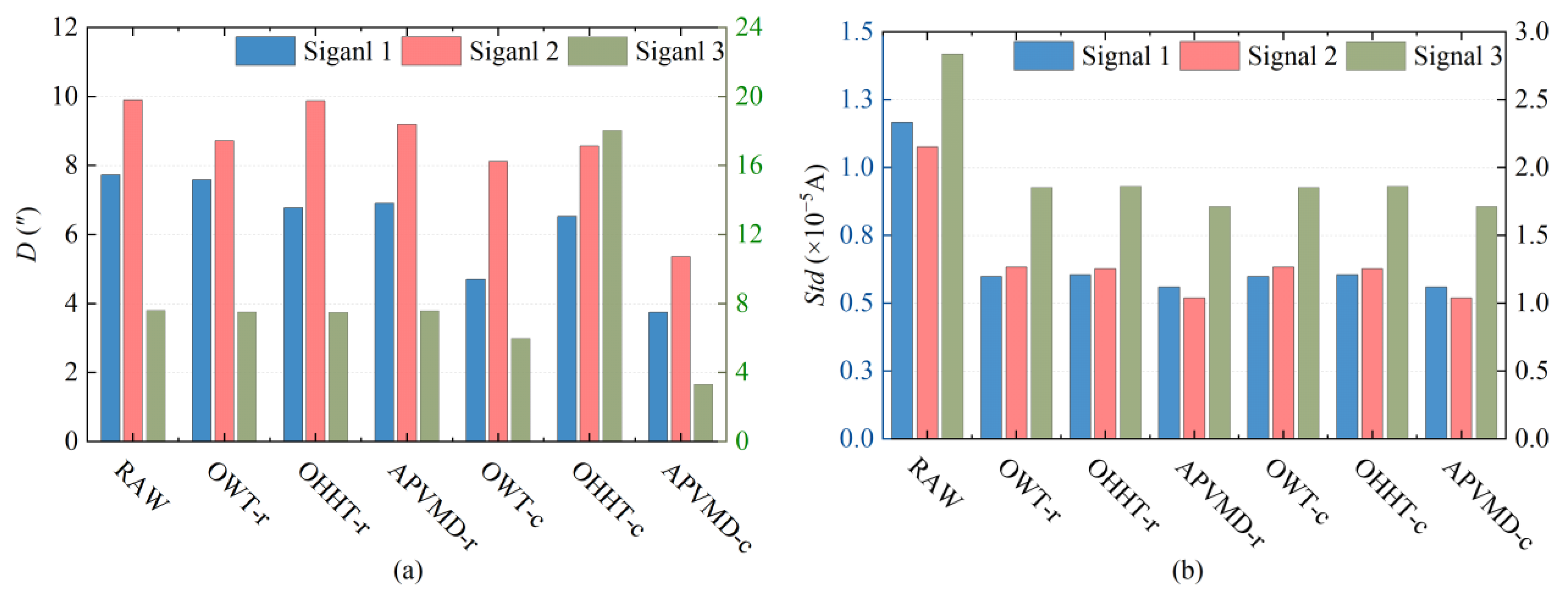
4.3. Noise Reduction Results for All Sampled Rotor Signals
5. Conclusions
- (1)
- The parameters of the VMD model were optimized using the APSO algorithm, which outperformed the genetic algorithm (GA), whale optimization algorithm (WOA), and standard PSO in terms of convergence speed and optimization precision, making it suitable for parameter optimization of VMD for various types of rotor signals.
- (2)
- The signal decomposition using the APVMD algorithm resulted in reconstructed signals with the lowest dispersion and accurate trend information. The corresponding compensation signals effectively corrected the overall offset error of the rotor signals. Field experimental data showed that the APVMD noise reduction method reduced the Std of the rotor signals by an average of 46.10% and improved the measurement accuracy of the north azimuth by an average of 45.63%. Its noise reduction performance surpassed that of the other four algorithms.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Luo, J.; Wang, Z.; Shen, C.; Kuijper, A.; Wen, Z.; Liu, S. Modeling and Implementation of Multi-Position Non-Continuous Rotation Gyroscope North Finder. Sensors 2016, 16, 1513. [Google Scholar] [CrossRef] [PubMed]
- Han, S.; Ren, X.; Lu, J.; Dong, J. An Orientation Navigation Approach Based on INS and Odometer Integration for Underground Unmanned Excavating Machine. IEEE Trans. Veh. Technol. 2020, 69, 10772–10786. [Google Scholar] [CrossRef]
- Velasco-Gomez, J.; Prieto, J.F.; Molina, I.; Herrero, T.; Fabrega, J.; Perez-Martin, E. Use of the gyrotheodolite in underground networks of long high-speed railway tunnels. Surv. Rev. 2016, 48, 329–337. [Google Scholar] [CrossRef]
- Tian, Y.-M.; Liu, S.-W.; Bai, Y.-C. New method of rough north seeking applied in gyro-theodolite. J. Chin. Inert. Technol. 2009, 17, 441–443, 448. [Google Scholar]
- Ma, J.; Yang, Z.; Shi, Z.; Liu, C.; Yin, H.; Zhang, X. Adjustment options for a survey network with magnetic levitation gyro data in an immersed under-sea tunnel. Surv. Rev. 2019, 51, 373–386. [Google Scholar] [CrossRef]
- Shi, Z.; Yang, Z.; He, K. Azimuth information processing optimization method for a magnetically suspended gyroscope. J. Intell. Fuzzy Syst. 2018, 34, 787–796. [Google Scholar] [CrossRef]
- Wang, Y.; Yang, Z.; Shi, Z.; Ma, J.; Liu, D.; Shi, L. Periodic error detection and separation of magnetic levitation gyroscope signals based on continuous wavelet transform and singular spectrum analysis. Meas. Sci. Technol. 2022, 33, 065107. [Google Scholar] [CrossRef]
- Shi, Z.; Yang, Z.; Ma, J. The detection method of maglev gyroscope abnormal data based on the characteristics of two positioning. Sci. Surv. Mapp. 2015, 40, 102–105, 109. [Google Scholar]
- Li, H.; Yang, Z.; Shi, Z. Data Preprocessing of Magnetic Suspension Gyro-Total-Station by Vondrak Filter. In Proceedings of the International Conference on Structures and Building Materials (ICSBM 2013), Guiyang, China, 9–10 March 2013; pp. 2099–2102. [Google Scholar]
- Qin, P. Study on Noise Reduction of Precision Magnetic Suspension Gyroscope Observation Value Based on the Fractal Filtering. Master’s Thesis, Chang’an University, Xi’an, China, 2014. [Google Scholar]
- Ma, J.; Yang, Z.; Shi, Z.; Zhang, X.; Liu, C. Application and Optimization of Wavelet Transform Filter for North-Seeking Gyroscope Sensor Exposed to Vibration. Sensors 2019, 19, 3624. [Google Scholar] [CrossRef]
- Zhang, X. Research on Data Processing of Maglev Gyroscope Based on Frequency Domain Analysis and Multivariate Filtering. Master’s Thesis, Chang’an University, Xi’an, China, 2019. [Google Scholar]
- Wang, Y.; Yang, Z.; Ma, J.; Shi, Z.; Liu, D.; Shi, L.; Li, H. A Novel Method for Automatic Detection and Elimination of the Jumps Caused by the Instantaneous Disturbance Torque in the Maglev Gyro Signal. Sensors 2023, 23, 2763. [Google Scholar] [CrossRef]
- Dragomiretskiy, K.; Zosso, D. Variational Mode Decomposition. IEEE Trans. Signal Process. 2014, 62, 531–544. [Google Scholar] [CrossRef]
- Wang, Y.; Markert, R.; Xiang, J.; Zheng, W. Research on variational mode decomposition and its application in detecting rub-impact fault of the rotor system. Mech. Syst. Sig. Process. 2015, 60–61, 243–251. [Google Scholar] [CrossRef]
- Zhang, Y.; Pan, G.; Chen, B.; Han, J.; Zhao, Y.; Zhang, C. Short-term wind speed prediction model based on GA-ANN improved by VMD. Renew. Energy 2020, 156, 1373–1388. [Google Scholar] [CrossRef]
- Diao, X.; Jiang, J.; Shen, G.; Chi, Z.; Wang, Z.; Ni, L.; Mebarki, A.; Bian, H.; Hao, Y. An improved variational mode decomposition method based on particle swarm optimization for leak detection of liquid pipelines. Mech. Syst. Sig. Process. 2020, 143, 106787. [Google Scholar] [CrossRef]
- Yi, C.; Lv, Y.; Dang, Z. A Fault Diagnosis Scheme for Rolling Bearing Based on Particle Swarm Optimization in Variational Mode Decomposition. Shock Vib. 2016, 2016, 9372691. [Google Scholar] [CrossRef]
- Mirjalili, S.; Lewis, A. The Whale Optimization Algorithm. Adv. Eng. Softw. 2016, 95, 51–67. [Google Scholar] [CrossRef]
- Kumar, A.; Zhou, Y.; Xiang, J. Optimization of VMD using kernel-based mutual information for the extraction of weak features to detect bearing defects. Measurement 2021, 168, 108402. [Google Scholar] [CrossRef]
- Zhou, Z.; Yang, Z.; Peng, F. Analysis and Modeling of Directional Error of Maglev Gyro Total Station. J. Geod. Geodyn. 2013, 33, 155–159. [Google Scholar]
- Zhou, Z.; Yang, Z.; Li, X. Maglev gyro total station errors modeling by time series analysis. Sci. Surv. Mapp. 2013, 38, 16–18. [Google Scholar]
- Shi, Z.; Ma, J.; Yang, Z. A Study on the Optimized Adjustment Method of Maglev Gyro Control Traverse Under Non-Weighted Measurement in Long and Large Tunnels. Mod. Tunn. Technol. 2016, 53, 44–47. [Google Scholar]
- Ma, J. Research on Key Technology of Maglev Gyroscope Orientation Measurement for Super Long Tunnel Under Complex Environment. Ph.D. Thesis, Chang’an University, Xi’an, China, 2019. [Google Scholar]
- Wang, Y.; Markert, R. Filter bank property of variational mode decomposition and its applications. Signal Process. 2016, 120, 509–521. [Google Scholar] [CrossRef]
- Wang, Y. An Adaptive Variational Mode Decomposition Technique with Differential Evolution Algorithm and Its Application Analysis. Shock Vib. 2021, 2021, 2030128. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the ICNN’95—International Conference on Neural Networks, Perth, Australia, 27 November–1 December 1995; Volume 1944, pp. 1942–1948. [Google Scholar]
- Li, W.; Zhao, W.; Cheng, S.; Zhang, H.; Yi, Z.; Sun, T.; Wu, P.; Zeng, Q.; Raza, R. Tunable metamaterial absorption device based on Fabry-Perot resonance as temperature and refractive index sensing. Opt. Lasers Eng. 2024, 181, 108368. [Google Scholar] [CrossRef]
- Xiaosong, H.; Shengbo, L.; Huei, P. A comparative study of equivalent circuit models for Li-ion batteries. J. Power Sources 2012, 198, 359–367. [Google Scholar] [CrossRef]
- Yan, C.; Zou, Y.; Wu, Z.; Maleki, A. Effect of various design configurations and operating conditions for optimization of a wind/solar/hydrogen/fuel cell hybrid microgrid system by a bio-inspired algorithm. Int. J. Hydrogen Energy 2024, 60, 378–391. [Google Scholar] [CrossRef]
- Jain, M.; Saihjpal, V.; Singh, N.; Singh, S.B. An Overview of Variants and Advancements of PSO Algorithm. Appl. Sci. 2022, 12, 8392. [Google Scholar] [CrossRef]
- Huang, N.E.; Shen, Z.; Long, S.R.; Wu, M.C.; Shih, H.H.; Zheng, Q.; Yen, N.C.; Tung, C.C.; Liu, H.H. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis. Proc. R. Soc. Math. Phys. Eng. Sci. 1998, 454, 903–995. [Google Scholar] [CrossRef]
- Ben Ali, J.; Fnaiech, N.; Saidi, L.; Chebel-Morello, B.; Fnaiech, F. Application of empirical mode decomposition and artificial neural network for automatic bearing fault diagnosis based on vibration signals. Appl. Acoust. 2015, 89, 16–27. [Google Scholar] [CrossRef]
- Zhang, S.; He, Y.; Li, Z.; Hou, X.; Qu, W.; Nan, Y. EMD for Noise Reduction of GPS Time Series. J. Geod. Geodyn. 2017, 37, 1248–1252. [Google Scholar]
- Yang, Q.; Qin, X.; Liu, Z.; Sun, Y.; Zhang, Q. Detrend of Vibration Signals Based on EMD-SSSC Decomposition. Noise Vib. Control. 2024, 44, 187–191. [Google Scholar]
- Luo, Y.; Li, Z.; Liang, X.; Li, C.; Hu, F. Multi-Fractal Detrended Fluctuation Analysis Method for Non-Stationary Time Series Based on EMD-LS. Acta Electron. Sin. 2021, 49, 2323–2329. [Google Scholar]





| IMF1 | IMF2 | IMF3 | IMF4 | IMF5 | IMF6 | IMF7 | IMF8 | IMF9 | IMF10 | |
|---|---|---|---|---|---|---|---|---|---|---|
| Signal 1 | 0.7545 | 0.7828 | 0.7822 | 0.7945 | 0.8056 | 0.8104 | 0.7835 | 0.8003 | 0.4169 | -- |
| Signal 2 | 0.7602 | 0.7833 | 0.7807 | 0.7769 | 0.7887 | 0.7889 | 0.7803 | 0.7936 | 0.4559 | 0.5048 |
| Signal 3 | 0.7503 | 0.7804 | 0.7768 | 0.8108 | 0.7915 | 0.7969 | 0.7952 | 0.8105 | 0.5534 | 0.5525 |
| Scheme | RAW | OWT | OHHT | GVMD | WVMD | APVMD | Signal Type |
|---|---|---|---|---|---|---|---|
| Sets | |||||||
| 1 | 7.74 | 4.71 | 6.53 | 4.02 | 4.39 | 3.75 | Periodic |
| 2 | 9.91 | 8.12 | 8.57 | -- | 6.18 | 5.36 | Jitter |
| 3 | 7.61 | 5.98 | -- | -- | 3.91 | 3.32 | Mixed |
| 4 | 6.53 | 3.87 | 4.26 | 4.38 | 3.64 | 3.18 | Mixed |
| 5 | 5.39 | 4.99 | 3.12 | 5.01 | 3.72 | 2.07 | Jitter |
| 6 | 6.97 | 2.62 | 5.41 | 2.48 | 3.09 | 2.12 | Periodic |
| 7 | 9.12 | -- | -- | -- | -- | 6.89 | Jitter |
| 8 | 6.47 | -- | 4.07 | 5.41 | 4.58 | 3.04 | Mixed |
| 9 | 4.81 | 4.04 | 3.64 | 2.72 | 2.79 | 2.74 | Mixed |
| 10 | 8.34 | 4.94 | 5.07 | 5.83 | 5.22 | 4.87 | Jitter |
| 11 | 5.23 | 4.83 | 4.67 | 5.02 | 3.84 | 3.40 | Mixed |
| 12 | 7.89 | 6.07 | 3.57 | 2.94 | 4.03 | 2.26 | Periodic |
| 13 | 7.82 | 6.23 | -- | 6.01 | 6.77 | 5.79 | Periodic |
| 14 | 8.29 | 3.19 | -- | -- | -- | 6.41 | Mixed |
| 15 | 3.77 | -- | -- | 3.13 | 3.09 | 2.38 | Periodic |
| Number of effective denoise | -- | 12 | 10 | 11 | 13 | 15 | -- |
| Mean value | 7.06 | 4.97 | 4.89 | 4.27 | 4.25 | 3.84 | -- |
| Improvement | -- | 31.14% | 29.40% | 33.84% | 37.56% | 45.63% | -- |
| Scheme | RAW Signal | OWT | OHHT | GVMD | WVMD | APVMD | Signal Type |
|---|---|---|---|---|---|---|---|
| Sets | |||||||
| 1 | 1.17 | 0.60 | 0.60 | 0.56 | 0.57 | 0.56 | Periodic |
| 2 | 2.15 | 1.27 | 1.26 | 1.04 | 1.05 | 1.04 | Jitter |
| 3 | 2.84 | 1.85 | 1.86 | 1.82 | 1.72 | 1.71 | Mixed |
| 4 | 1.77 | 1.37 | 1.37 | 1.35 | 1.35 | 1.34 | Mixed |
| 5 | 2.83 | 1.58 | 1.59 | 1.37 | 1.35 | 1.33 | Jitter |
| 6 | 2.30 | 1.26 | 1.26 | 1.24 | 1.24 | 1.23 | Periodic |
| 7 | 3.03 | 2.08 | 2.08 | 1.97 | 1.93 | 1.92 | Jitter |
| 8 | 2.39 | 1.69 | 1.69 | 1.65 | 1.55 | 1.54 | Mixed |
| 9 | 3.39 | 2.26 | 2.23 | 1.98 | 1.97 | 1.97 | Mixed |
| 10 | 1.85 | 1.05 | 1.06 | 0.81 | 0.80 | 0.80 | Jitter |
| 11 | 1.26 | 0.61 | 0.64 | 0.51 | 0.51 | 0.50 | Mixed |
| 12 | 1.94 | 1.06 | 1.07 | 1.06 | 1.07 | 1.05 | Periodic |
| 13 | 1.70 | 0.48 | 0.51 | 0.49 | 0.47 | 0.46 | Periodic |
| 14 | 2.73 | 1.55 | 1.57 | 1.53 | 1.45 | 1.44 | Mixed |
| 15 | 1.81 | 0.95 | 0.96 | 0.94 | 0.95 | 0.95 | Periodic |
| Mean value | 2.21 | 1.31 | 1.32 | 1.22 | 1.20 | 1.19 | -- |
| Improvement | -- | 40.69% | 40.41% | 44.74% | 45.78% | 46.10% | -- |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Liu, D.; Shi, Z.; Yang, Z.; Zou, C. A Noise Reduction Method for Signal Reconstruction and Error Compensation of a Maglev Gyroscope Under Persistent External Interference. Sensors 2024, 24, 8005. https://doi.org/10.3390/s24248005
Liu D, Shi Z, Yang Z, Zou C. A Noise Reduction Method for Signal Reconstruction and Error Compensation of a Maglev Gyroscope Under Persistent External Interference. Sensors. 2024; 24(24):8005. https://doi.org/10.3390/s24248005
Chicago/Turabian StyleLiu, Di, Zhen Shi, Ziyi Yang, and Chenxi Zou. 2024. "A Noise Reduction Method for Signal Reconstruction and Error Compensation of a Maglev Gyroscope Under Persistent External Interference" Sensors 24, no. 24: 8005. https://doi.org/10.3390/s24248005
APA StyleLiu, D., Shi, Z., Yang, Z., & Zou, C. (2024). A Noise Reduction Method for Signal Reconstruction and Error Compensation of a Maglev Gyroscope Under Persistent External Interference. Sensors, 24(24), 8005. https://doi.org/10.3390/s24248005





