Investigations on the Performance of a 5 mm CdTe Timepix3 Detector for Compton Imaging Applications
Abstract
:1. Introduction
2. Materials and Methods
2.1. Timepix3
2.2. Sensor Characterization
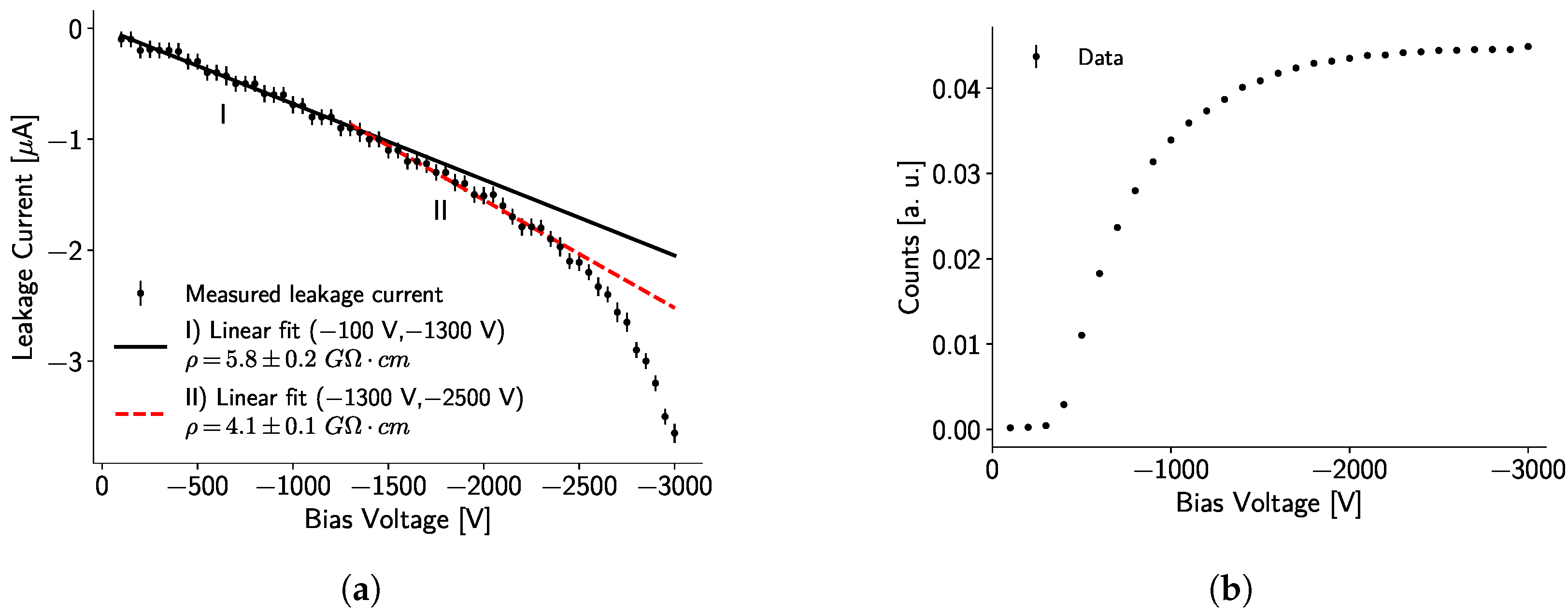
2.2.1. Current–Voltage Characteristics
2.2.2. Electron Mobility–Lifetime Product
2.2.3. Count Rate Homogeneity
2.3. Energy Calibration
2.4. Detector Characterization
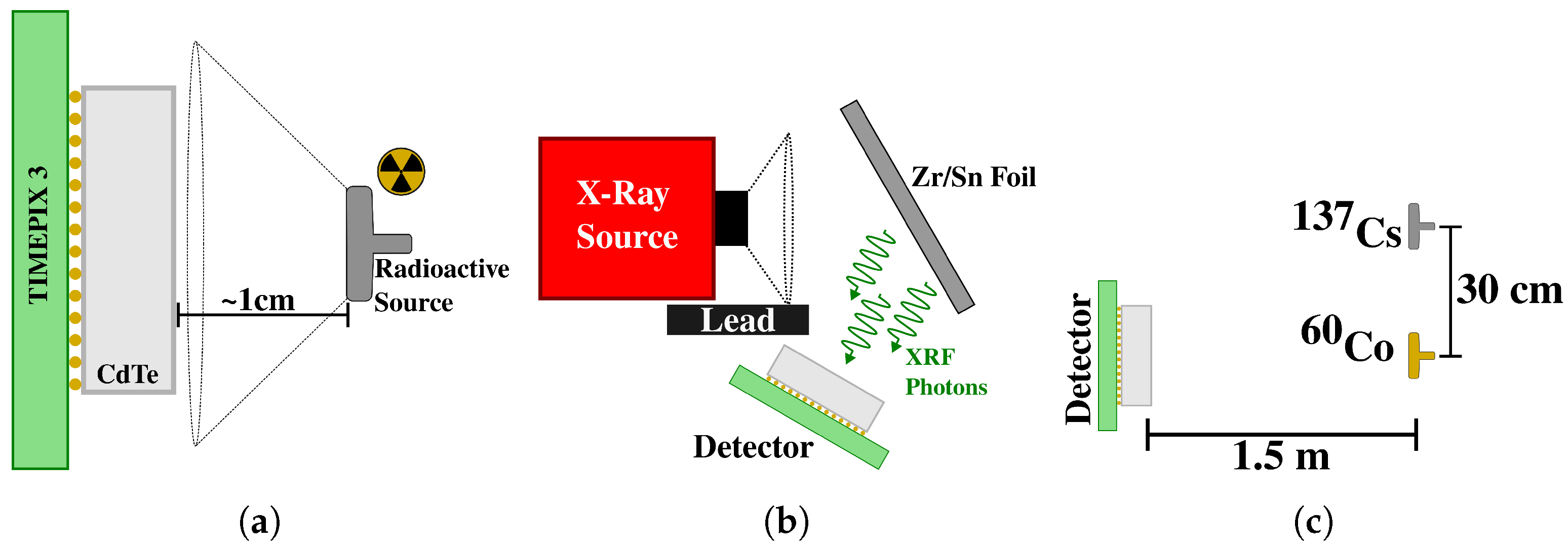
2.5. Compton Camera Application
3. Results
3.1. Sensor Characterization
3.1.1. Current-Voltage Characteristics
3.1.2. Electron Mobility–Lifetime Product
3.1.3. Count Rate Homogeneity
3.2. Energy Calibration
3.2.1. Back-Side Calibration
3.2.2. Front-Side Calibration
3.2.3. Calibrations Comparison
3.3. Detector Characterization
3.3.1. Energy Resolution
3.3.2. Drift Time
3.4. Compton Camera Application
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- BASE. Nuclear Phase-Out. 2024. Available online: https://www.base.bund.de/EN/ns/nuclear-phase-out/nuclear-phase-out_node.html (accessed on 29 May 2024).
- Laraia, M. (Ed.) Advances and Innovations in Nuclear Decommissioning; Woodhead Publishing Series in Energy; Woodhead: Cambridge, UK, 2017. [Google Scholar]
- Amgarou, K.; Aspe, F.; Idoeta, R.; Herranz, M. Recommendations for the Selection of in Situ Measurement Techniques for Radiological Characterization in Nuclear/Radiological Installations under Decommissioning and Dismantling Processes. Prog. Nucl. Energy 2021, 137, 103761. [Google Scholar] [CrossRef]
- Crompton, A.J.; Gamage, K.A.A.; Jenkins, A.; Taylor, C.J. Alpha Particle Detection Using Alpha-Induced Air Radioluminescence: A Review and Future Prospects for Preliminary Radiological Characterisation for Nuclear Facilities Decommissioning. Sensors 2018, 18, 1015. [Google Scholar] [CrossRef]
- Fey, J.; Procz, S.; Schütz, M.K.; Schoepff, V.; Carrel, F.; Useche, J.S.; Fauler, A.; Fiederle, M. CdTe Sensor Configurations for Robot Assisted Photon Counting Gamma Camera. J. Instrum. 2021, 16, T07010. [Google Scholar] [CrossRef]
- Benmahi, K.; Schoepff, V.; Amoyal, G.; Carrel, F.; Plagnard, J.; Bourbottea, J.M. Localization of Radioactive Sources by Multimodal Imaging Using a Single Gamma Camera. IEEE Trans. Nucl. Sci. 2024, 1. [Google Scholar] [CrossRef]
- Poikela, T.; Plosila, J.; Westerlund, T.; Campbell, M.; de Gaspari, M.; Llopart, X.; Gromov, V.; Kluit, R.; van Beuzekom, M.; Zappon, F.; et al. Timepix3: A 65K Channel Hybrid Pixel Readout Chip with Simultaneous ToA/ToT and Sparse Readout. J. Instrum. 2014, 9, C05013. [Google Scholar] [CrossRef]
- Turecek, D.; Jakubek, J.; Trojanova, E.; Sefc, L. Compton Camera Based on Timepix3 Technology. J. Instrum. 2018, 13, C11022. [Google Scholar] [CrossRef]
- Turecek, D.; Jakubek, J.; Trojanova, E.; Sefc, L. Single Layer Compton Camera Based on Timepix3 Technology. J. Instrum. 2020, 15, C01014. [Google Scholar] [CrossRef]
- Baca, T.; Stibinger, P.; Doubravova, D.; Turecek, D.; Solc, J.; Rusnak, J.; Saska, M.; Jakubek, J. Gamma Radiation Source Localization for Micro Aerial Vehicles with a Miniature Single-Detector Compton Event Camera. In Proceedings of the 2021 International Conference on Unmanned Aircraft Systems (ICUAS), Athens, Greece, 15–18 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 338–346. [Google Scholar] [CrossRef]
- Smolyanskiy, P.; Bergmann, B.; Burian, P.; Cherlin, A.; Jelínek, J.; Maneuski, D.; Pospíšil, S.; O’Shea, V. Characterization of a 5 Mm Thick CZT-Timepix3 Pixel Detector for Energy-Dispersive Gamma-Ray and Particle Tracking. Phys. Scr. 2024, 99, 015301. [Google Scholar] [CrossRef]
- Procz, S.; Roque, G.; Avila, C.; Racedo, J.; Rueda, R.; Santos, I.; Fiederle, M. Investigation of CdTe, GaAs, Se and Si as Sensor Materials for Mammography. IEEE Trans. Med. Imaging 2020, 39, 3766–3778. [Google Scholar] [CrossRef] [PubMed]
- Advafab. Advafab | World-Class Semiconductor Solutions. Available online: https://advafab.com/ (accessed on 4 June 2024).
- Jakubek, J. Precise Energy Calibration of Pixel Detector Working in Time-over-Threshold Mode. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2011, 633, S262–S266. [Google Scholar] [CrossRef]
- Procz, S.; Lubke, J.; Zwerger, A.; Mix, M.; Fiederle, M. Optimization of Medipix-2 Threshold Masks for Spectroscopic x-Ray Imaging. IEEE Trans. Nucl. Sci. 2009, 56, 1795–1799. [Google Scholar] [CrossRef]
- Turecek, D.; Jakubek, J.; Soukup, P. USB 3.0 Readout and Time-Walk Correction Method for Timepix3 Detector. J. Instrum. 2016, 11, C12065. [Google Scholar] [CrossRef]
- Advacam. ADVACAM Radiation Imaging Solutions—Semiconductor Photon Counting Cameras. Available online: https://advacam.com/ (accessed on 4 June 2024).
- Hamann, E. Characterization of High Resistivity GaAs as Sensor Material for Photon Counting Semiconductor Pixel Detectors. Ph.D. Thesis, Albert-Ludwigs-University, Freiburg, Germany, 2013. [Google Scholar]
- Greiffenberg, D.; Andrä, M.; Barten, R.; Bergamaschi, A.; Busca, P.; Brückner, M.; Alvarez, S.C.; Chsherbakov, I.; Dinapoli, R.; Fajardo, P.; et al. Characterization of GaAs:Cr Sensors Using the Charge-Integrating JUNGFRAU Readout Chip. J. Instrum. 2019, 14, P05020. [Google Scholar] [CrossRef]
- Fey, J.; Procz, S.; Schütz, M.K.; Fiederle, M. Investigations on Performance and Spectroscopic Capabilities of a 3 Mm CdTe Timepix Detector. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2020, 977, 164308. [Google Scholar] [CrossRef]
- Microfocus X-Ray Source L10321 | Hamamatsu Photonics. Available online: https://www.hamamatsu.com/us/en/product/light-and-radiation-sources/microfocus-x-ray-source/L10321.html (accessed on 3 December 2024).
- Mundy, D.W.; Herman, M.G. An Accelerated Threshold-Based Back-Projection Algorithm for Compton Camera Image Reconstruction. Med Phys. 2011, 38, 15–22. [Google Scholar] [CrossRef]
- Etxebeste, A.; Dauvergne, D.; Fontana, M.; Létang, J.M.; Llosá, G.; Munoz, E.; Oliver, J.F.; Testa, É.; Sarrut, D. CCMod: A GATE Module for Compton Camera Imaging Simulation. Phys. Med. Biol. 2020, 65, 055004. [Google Scholar] [CrossRef] [PubMed]
- Jan, S.; Santin, G.; Strul, D.; Staelens, S.; Assié, K.; Autret, D.; Avner, S.; Barbier, R.; Bardiès, M.; Bloomfield, P.M.; et al. GATE: A Simulation Toolkit for PET and SPECT. Phys. Med. Biol. 2004, 49, 4543–4561. [Google Scholar] [CrossRef] [PubMed]
- Greiffenberg, D.; Fauler, A.; Zwerger, A.; Fiederle, M. Energy Resolution and Transport Properties of CdTe-Timepix-Assemblies. J. Instrum. 2011, 6, C01058. [Google Scholar] [CrossRef]
- Useche Parra, J.S.; Schütz, M.; Roque, G.; Fey, J.; Avila, C.; Fiederle, M.; Procz, S. Dose Estimation in X-ray Backscatter Imaging with Timepix3 and TLD Detectors. J. Instrum. 2023, 18, P05042. [Google Scholar] [CrossRef]
- Maneuski, D.; Astromskas, V.; Fröjdh, E.; Fröjdh, C.; Gimenez, E.N.; Marchal, J.; O’Shea, V.; Stewart, G.; Tartoni, N.; Wilhelm, H.; et al. Imaging and Spectroscopic Performance Studies of Pixellated CdTe Timepix Detector. J. Instrum. 2012, 7, C01038. [Google Scholar] [CrossRef]
- Amoyal, G.; Menesguen, Y.; Schoepff, V.; Carrel, F.; Michel, M.; Angélique, J.C.; Blanc de Lanaute, N. Evaluation of Timepix3 Si and CdTe Hybrid-Pixel Detectors’ Spectrometric Performances on X- and Gamma-Rays. IEEE Trans. Nucl. Sci. 2021, 68, 229–235. [Google Scholar] [CrossRef]
- Bergmann, B.; Burian, P.; Manek, P.; Pospisil, S. 3D Reconstruction of Particle Tracks in a 2 Mm Thick CdTe Hybrid Pixel Detector. Eur. Phys. J. C 2019, 79, 165. [Google Scholar] [CrossRef]
- Urban, M.; Nentvich, O.; Marek, L.; Hudec, R.; Sieger, L. Timepix3: Temperature Influence on Radiation Energy Measurement with Si Sensor. Sensors 2023, 23, 2201. [Google Scholar] [CrossRef] [PubMed]
- Del Sordo, S.; Abbene, L.; Caroli, E.; Mancini, A.M.; Zappettini, A.; Ubertini, P. Progress in the Development of CdTe and CdZnTe Semiconductor Radiation Detectors for Astrophysical and Medical Applications. Sensors 2009, 9, 3491–3526. [Google Scholar] [CrossRef] [PubMed]
- Sellin, P.; Davies, A.; Lohstroh, A.; Ozsan, M.; Parkin, J. Drift Mobility and Mobility-Lifetime Products in CdTe:Cl Grown by the Travelling Heater Method. IEEE Trans. Nucl. Sci. 2005, 52, 3074–3078. [Google Scholar] [CrossRef]
- Amoyal, G.; Schoepff, V.; Carrel, F.; Michel, M.; Blanc de Lanaute, N.; Angélique, J.C. Development of a Hybrid Gamma Camera Based on Timepix3 for Nuclear Industry Applications. Nucl. Instrum. Methods Phys. Res. Sect. A Accel. Spectrometers Detect. Assoc. Equip. 2021, 987, 164838. [Google Scholar] [CrossRef]
- Amoyal, G.; Schoepff, V.; Carrel, F.; Tondut, L.; Helbert, C.; Fiederle, M.; Fauler, A.; Plagnard, J.; Abou-Khalil, R.; Mekhalfa, Z.; et al. Nanopix-v1: A Compact Miniaturized Coded-Aperture Gamma Imager. Nucl. Instrum. Methods Phys. Res. Sect. A: Accel. Spectrometers, Detect. Assoc. Equip. 2024, 1068, 169718. [Google Scholar] [CrossRef]
- Xu, D.; He, Z.; Lehner, C.E.; Zhang, F. 4-Pi Compton Imaging with Single 3D Position-Sensitive CdZnTe Detector. In Proceedings of the Hard X-Ray and Gamma-Ray Detector Physics VI, Denver, CO, USA, 2–6 August 2004; SPIE: St Bellingham, WA, USA, 2004; Volume 5540, pp. 144–155. [Google Scholar] [CrossRef]
- Xu, D.; He, Z. Filtered Back-Projection in4piCompton Imaging With a Single 3D Position Sensitive CdZnTe Detector. IEEE Trans. Nucl. Sci. 2006, 53, 2787–2796. [Google Scholar] [CrossRef]
- Haefner, A.; Gunter, D.; Barnowski, R.; Vetter, K. A Filtered Back-Projection Algorithm for 4π Compton Camera Data. IEEE Trans. Nucl. Sci. 2015, 62, 1911–1917. [Google Scholar] [CrossRef]
- Wilderman, S.; Clinthorne, N.; Fessler, J.; Rogers, W. List-Mode Maximum Likelihood Reconstruction of Compton Scatter Camera Images in Nuclear Medicine. In Proceedings of the 1998 IEEE Nuclear Science Symposium Conference Record. 1998 IEEE Nuclear Science Symposium and Medical Imaging Conference (Cat. No. 98CH36255), Toronto, ON, Canada, 8–14 November 1998; Volume 3, pp. 1716–1720. [Google Scholar] [CrossRef]









Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Useche Parra, J.S.; Roque, G.; Schütz, M.K.; Fiederle, M.; Procz, S. Investigations on the Performance of a 5 mm CdTe Timepix3 Detector for Compton Imaging Applications. Sensors 2024, 24, 7974. https://doi.org/10.3390/s24247974
Useche Parra JS, Roque G, Schütz MK, Fiederle M, Procz S. Investigations on the Performance of a 5 mm CdTe Timepix3 Detector for Compton Imaging Applications. Sensors. 2024; 24(24):7974. https://doi.org/10.3390/s24247974
Chicago/Turabian StyleUseche Parra, Juan S., Gerardo Roque, Michael K. Schütz, Michael Fiederle, and Simon Procz. 2024. "Investigations on the Performance of a 5 mm CdTe Timepix3 Detector for Compton Imaging Applications" Sensors 24, no. 24: 7974. https://doi.org/10.3390/s24247974
APA StyleUseche Parra, J. S., Roque, G., Schütz, M. K., Fiederle, M., & Procz, S. (2024). Investigations on the Performance of a 5 mm CdTe Timepix3 Detector for Compton Imaging Applications. Sensors, 24(24), 7974. https://doi.org/10.3390/s24247974





