Advanced Trajectory Planning and Control for Autonomous Vehicles with Quintic Polynomials
Abstract
:1. Introduction
- To achieve a smooth trajectory transition and ensure occupant comfort and safety, an ideal trajectory is designed using the quintic polynomial method;
- A fuzzy PID controller is designed to overcome the tuning challenges and enhance the robustness of the controller;
- The superiority and effectiveness of the proposed method are validated through testing on an intelligent experimental vehicle.
2. Model Establishment and Trajectory Generation
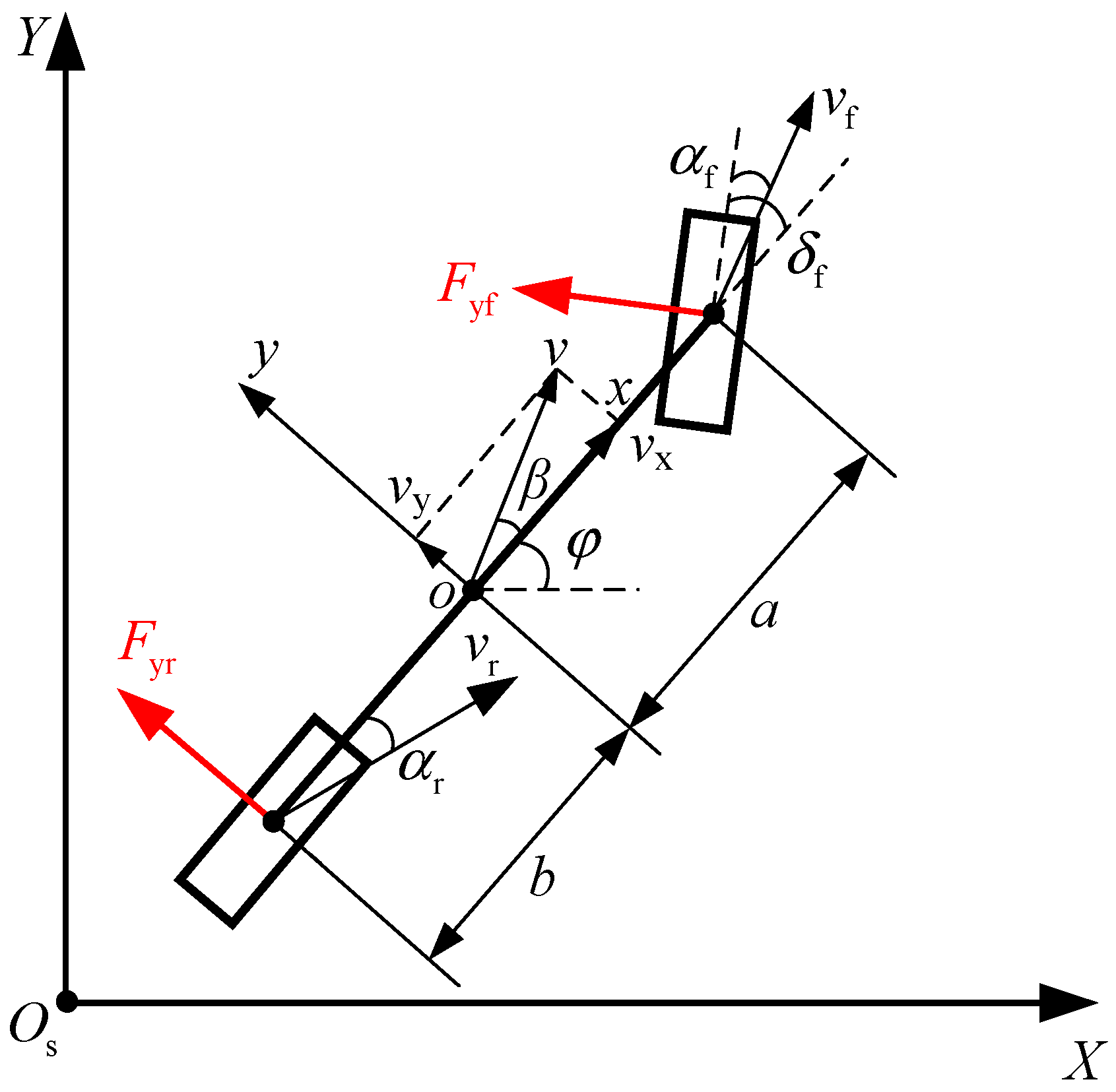
2.1. Vehicle Dynamics Model
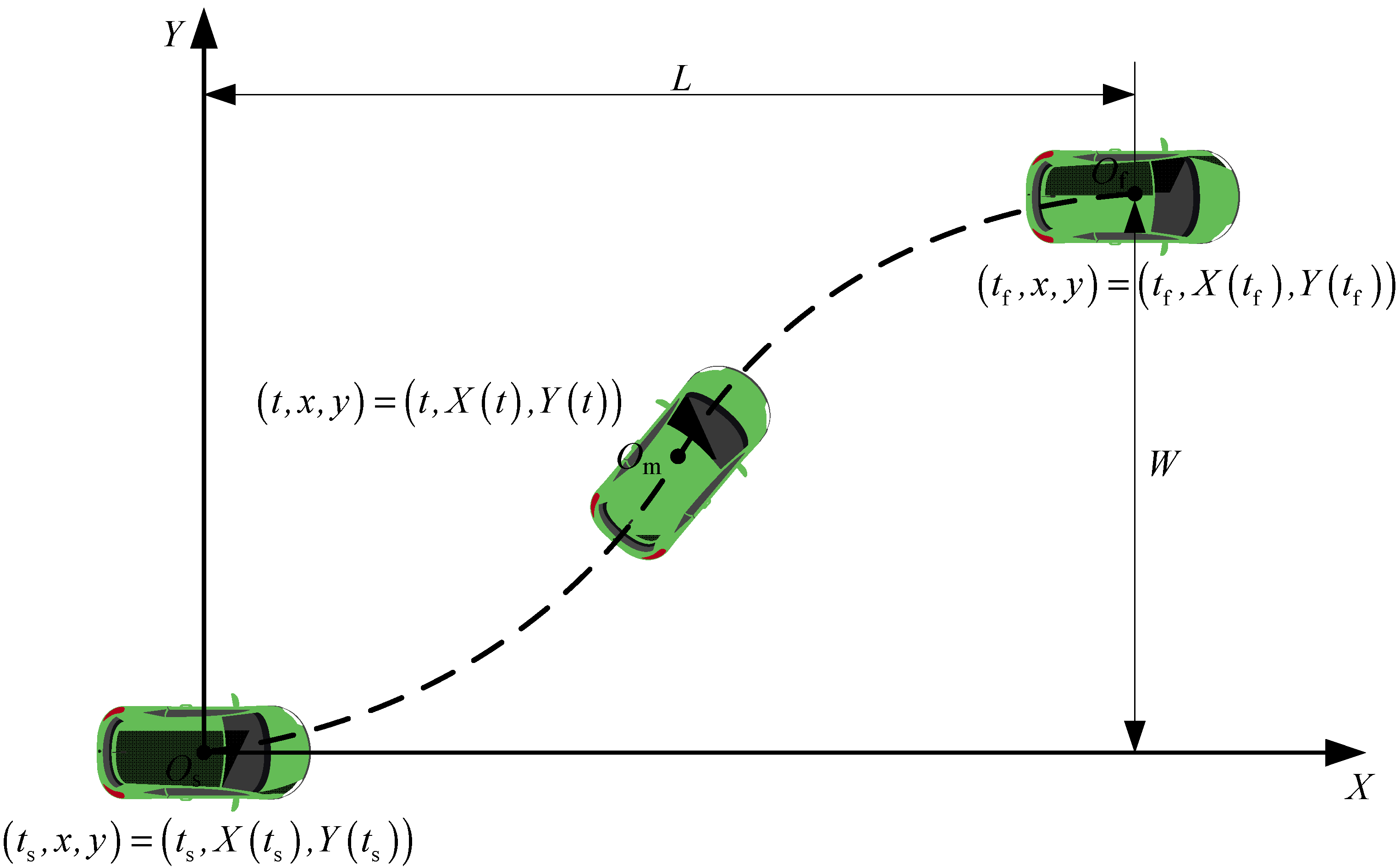
2.2. Vehicle Trajectory Planning Based on Quintic Polynomial Method
2.3. Tracking Error Model Based on Frenet Coordinate System
3. Controller Design
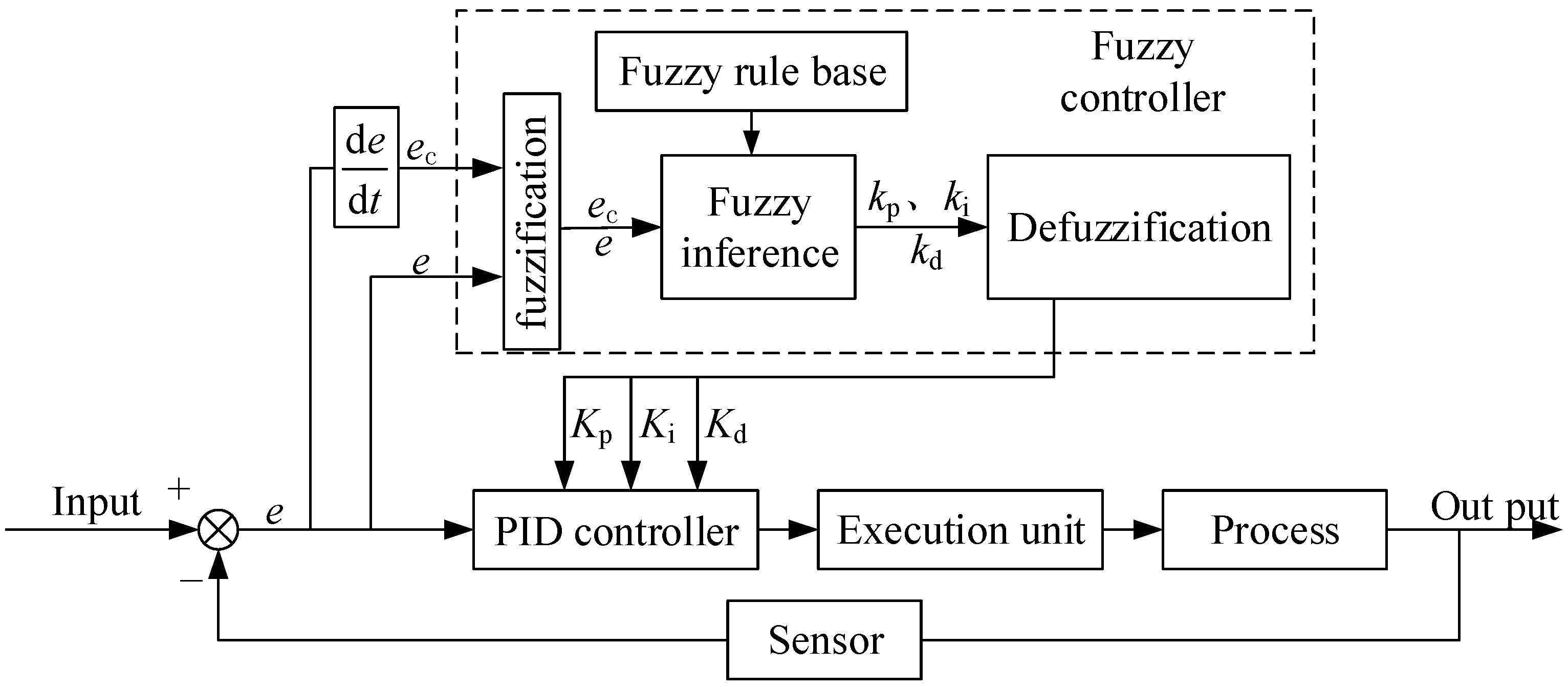
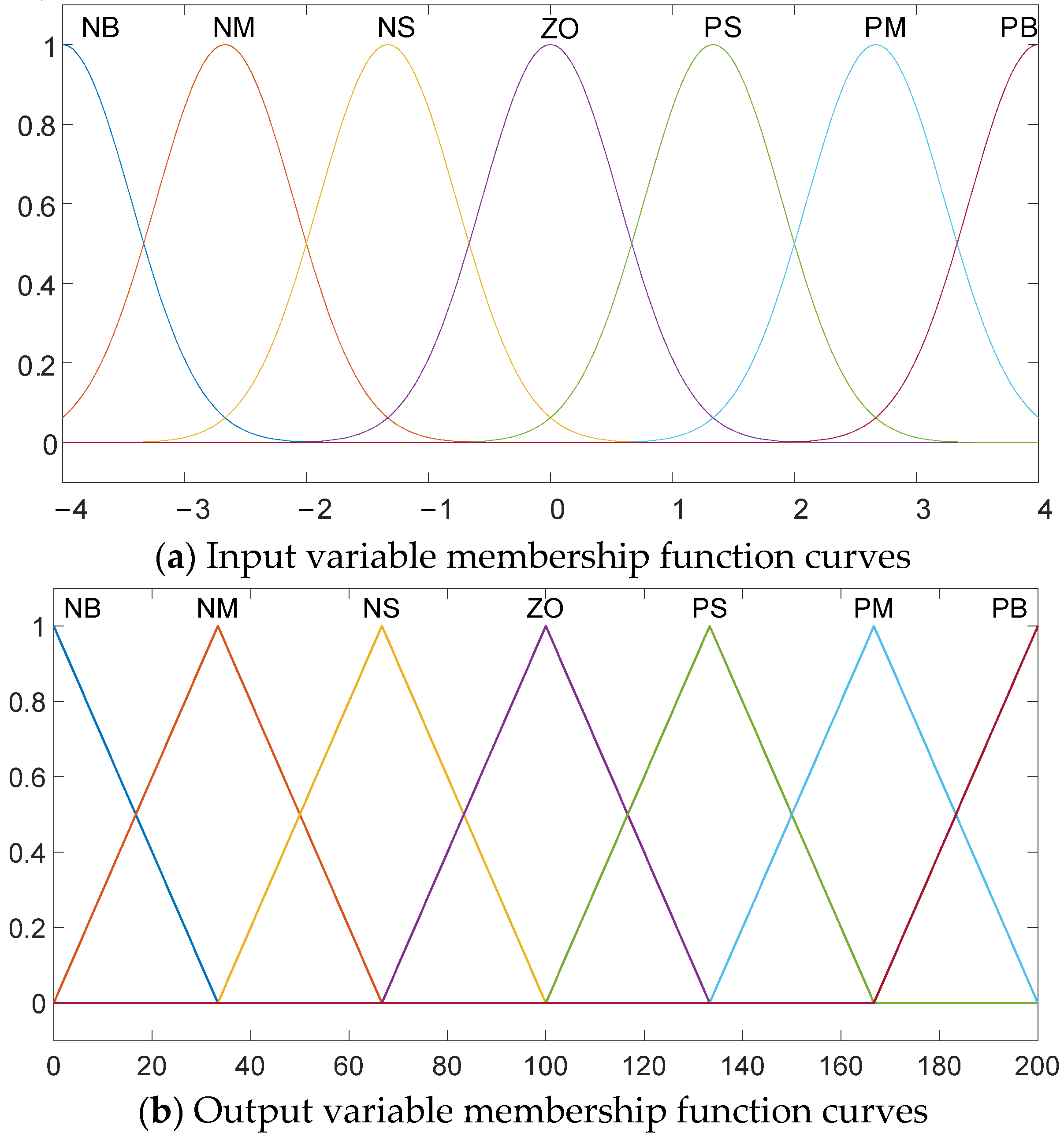
3.1. Lateral Fuzzy PID Controller Design
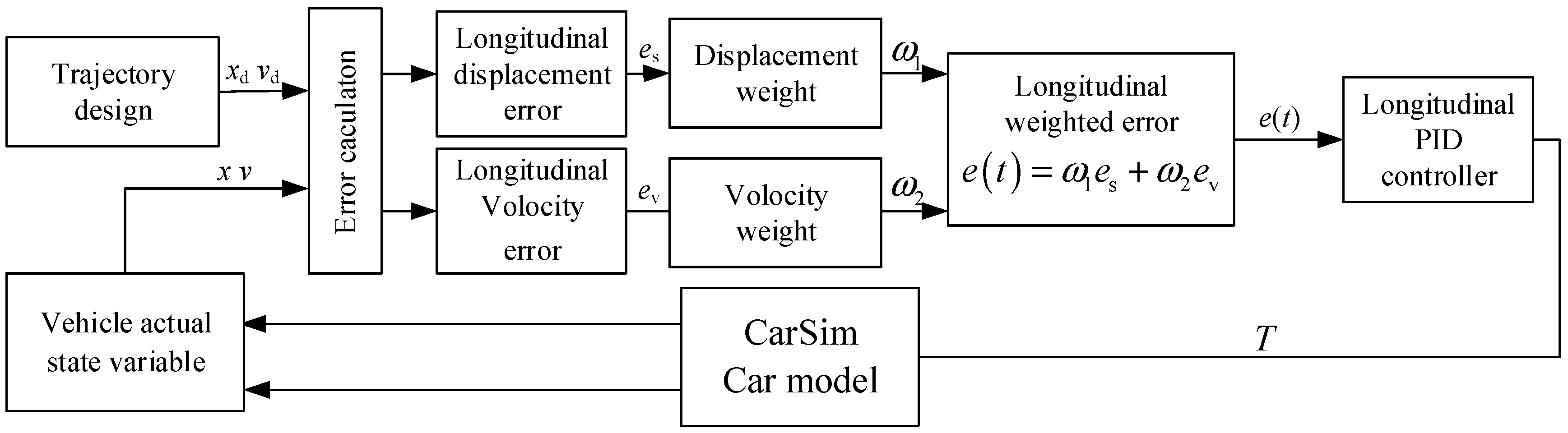
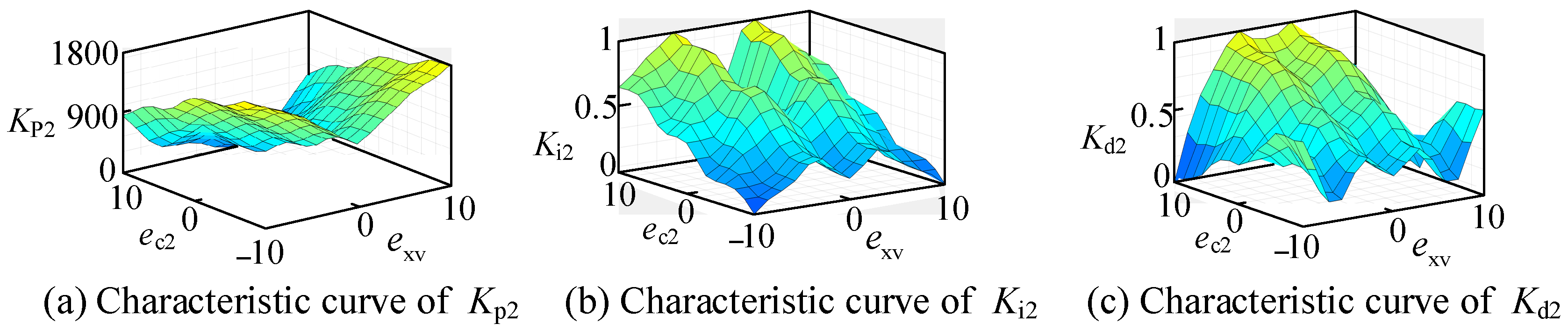
3.2. Vertical Fuzzy PID Controller Design
4. Experimental Validation
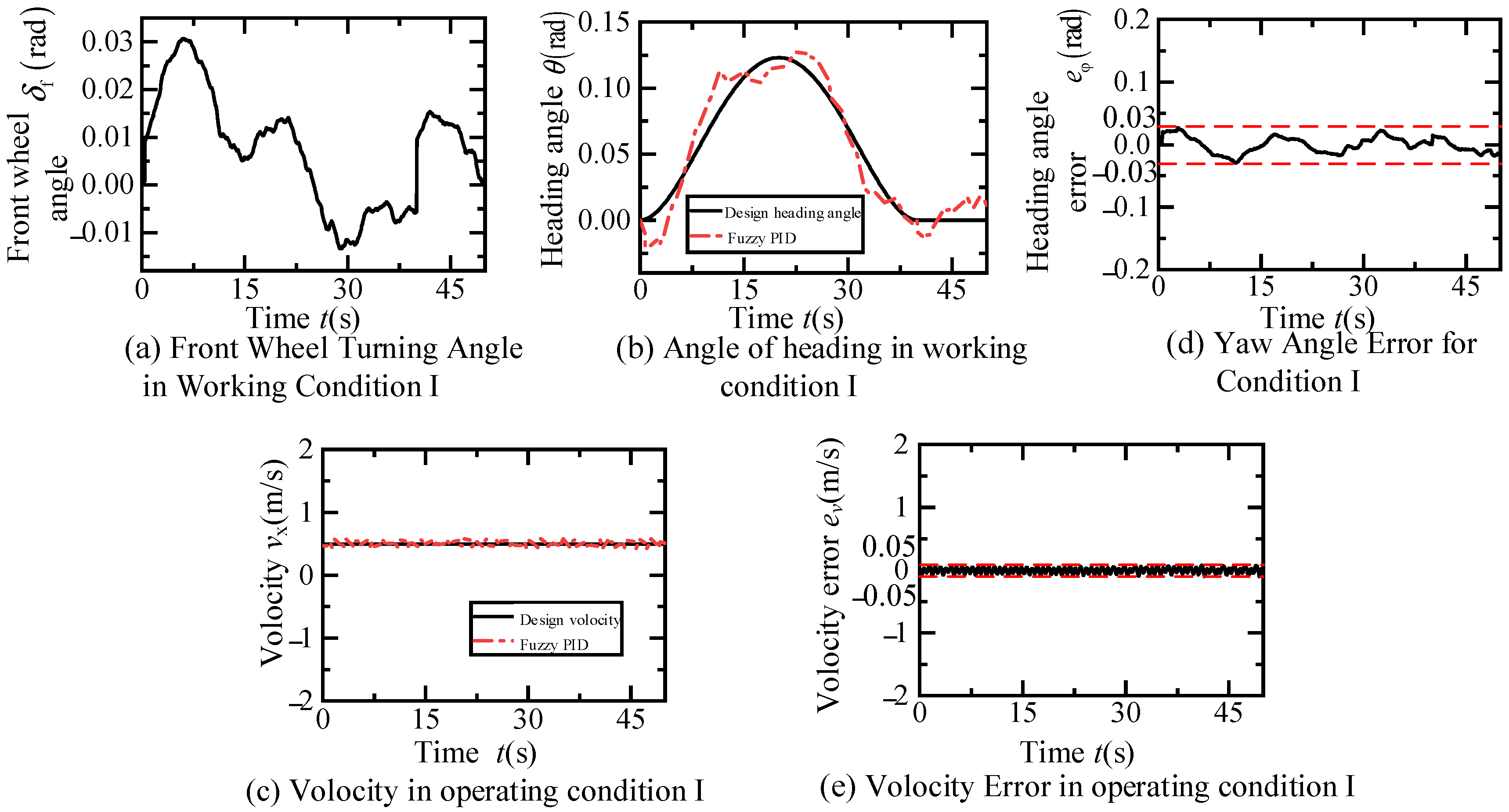
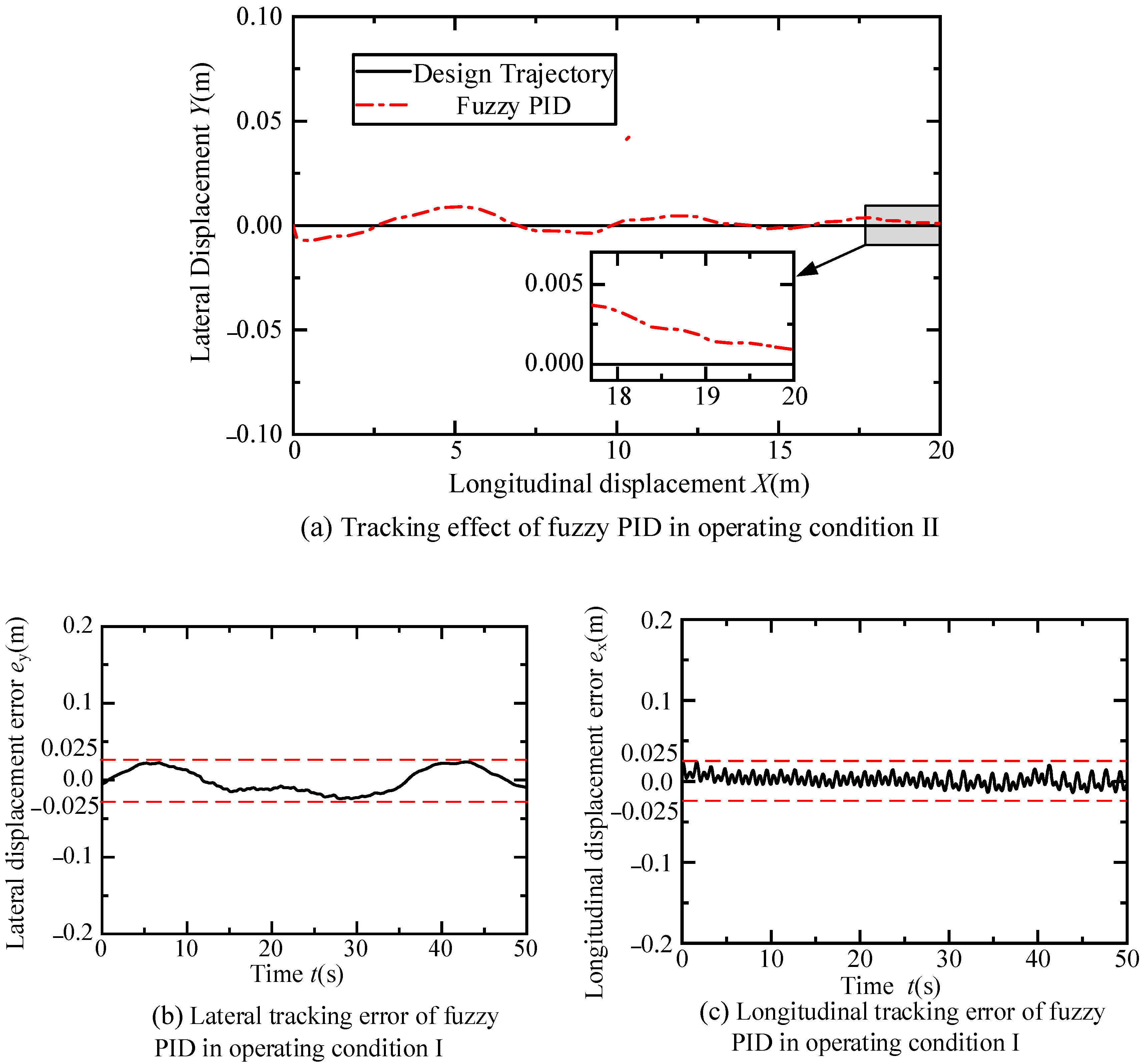
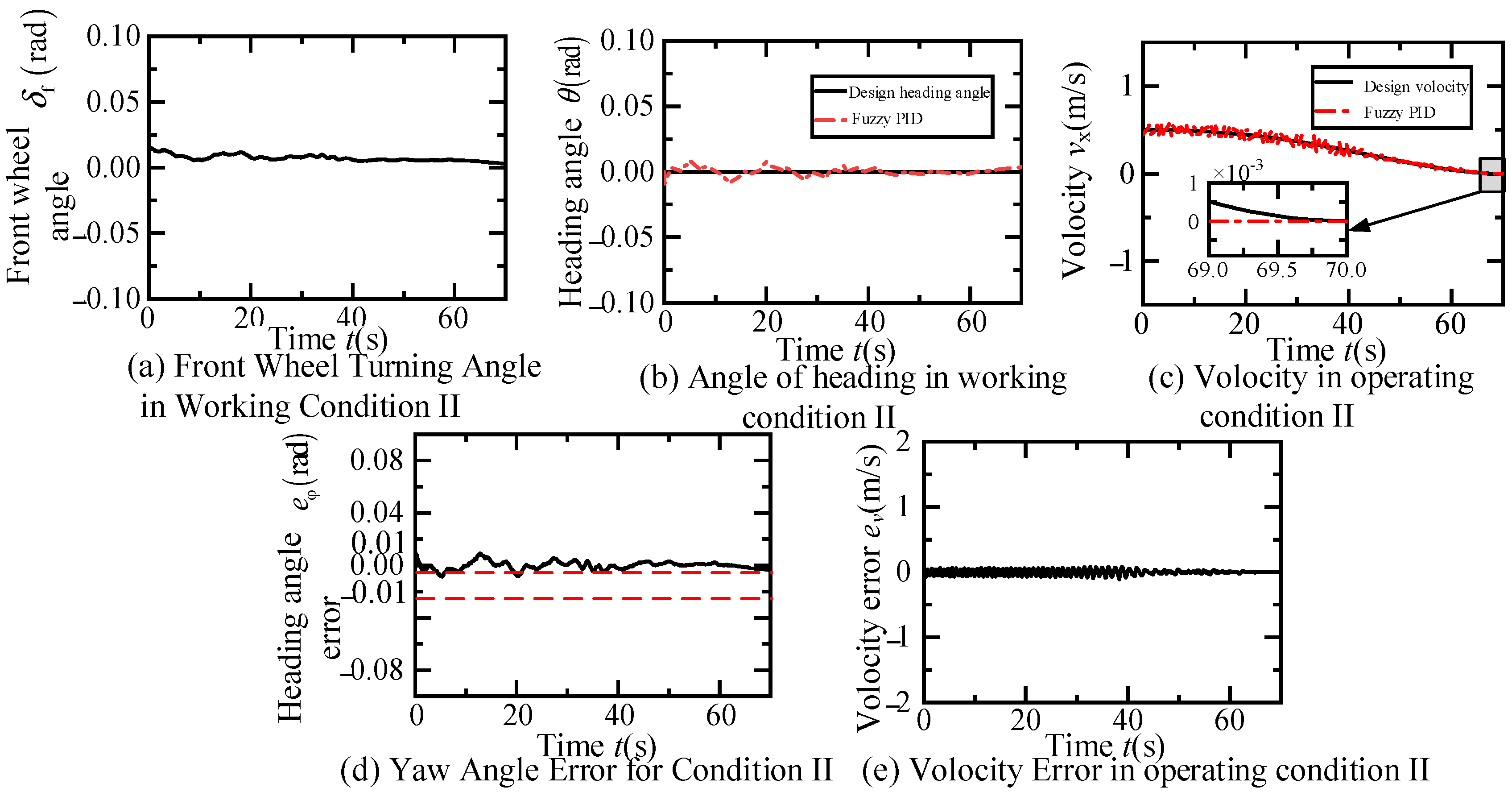
4.1. Operating Condition 1: Constant Speed Lane Changing and Straight Lane Driving
4.2. Scenario Two: Intersection Straight-Lane Parking
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Masuda, H.; Marai, O.E.; Tsukada, M.; Taleb, T.; Esaki, H. Feature-Based Vehicle Identification Framework for Optimization of Collective Perception Messages in Vehicular Networks. IEEE Trans. Veh. Technol. 2023, 72, 2120–2129. [Google Scholar] [CrossRef]
- Szántó, M.; Hidalgo, C.; González, L.; Rastelli, J.P.; Asua, E.; Vajta, L. Trajectory Planning of Automated Vehicles Using Real-Time Map Updates. IEEE Access 2023, 11, 67468–67481. [Google Scholar] [CrossRef]
- Lv, P.; Han, J.; Nie, J.; Zhang, Y.; Xu, J.; Cai, C.; Chen, Z. Cooperative Decision-Making of Connected and Autonomous Vehicles in an Emergency. IEEE Trans. Veh. Technol. 2023, 72, 1464–1477. [Google Scholar] [CrossRef]
- Wang, W.; Qie, T.; Yang, C.; Liu, W.; Xiang, C.; Huang, K. An Intelligent Lane-Changing Behavior Prediction and Decision-Making Strategy for an Autonomous Vehicle. IEEE Trans. Ind. Electron. 2022, 69, 2927–2937. [Google Scholar] [CrossRef]
- Hong, J.; Choi, J.; Woo, S.; Lee, J.; Lee, S.G.; Kim, J.; Cha, K. Automatic Lane Change System with Double Loop PID Algorithm. In Proceedings of the 2022 22nd International Conference on Control, Automation and Systems (ICCAS), Jeju, Republic of Korea, 27 November–1 December 2022; pp. 1977–1980. [Google Scholar]
- Li, Y.; Li, L.; Ni, D.; Wang, W. Automatic Lane-Changing Trajectory Planning: From Self-Optimum to Local-Optimum. IEEE Trans. Intell. Transp. Syst. 2022, 23, 21004–21014. [Google Scholar] [CrossRef]
- Zhao, N.; Wang, B.; Zhang, K.; Lu, Y.; Luo, R.; Su, R. LC-RSS: A Lane-Change Responsibility-Sensitive Safety Framework Based on Data-Driven Lane-Change Prediction. IEEE Trans. Intell. Veh. 2024, 9, 2531–2541. [Google Scholar] [CrossRef]
- He, J.; Qu, J.; Zhang, J.; He, Z. The Impact of a Single Discretionary Lane Change on Surrounding Traffic: An Analytic Investigation. IEEE Trans. Intell. Transp. Syst. 2023, 24, 554–563. [Google Scholar] [CrossRef]
- Griesbach, K.; Beggiato, M.; Hoffmann, K.H. Lane Change Prediction with an Echo State Network and Recurrent Neural Network in the Urban Area. IEEE Trans. Intell. Transp. Syst. 2022, 23, 6473–6479. [Google Scholar] [CrossRef]
- Yue, M.; Hou, X.; Zhao, X.; Wu, X. Robust Tube-Based Model Predictive Control for Lane Change Maneuver of Tractor-Trailer Vehicles Based on a Polynomial Trajectory. IEEE Trans. Syst. Man Cybern. Syst. 2020, 50, 5180–5188. [Google Scholar] [CrossRef]
- Singh, A.S.P.; Nishihara, O. Trajectory Tracking and Integrated Chassis Control for Obstacle Avoidance With Minimum Jerk. IEEE Trans. Intell. Transp. Syst. 2022, 23, 4625–4641. [Google Scholar] [CrossRef]
- Zhang, Q.; Langari, R.; Tseng, H.E.; Mohan, S.; Szwabowski, S.; Filev, D. Stackelberg Differential Lane Change Game Based on MPC and Inverse MPC. IEEE Trans. Intell. Transp. Syst. 2024, 25, 8473–8485. [Google Scholar] [CrossRef]
- Xu, W.-D.; Guo, X.-G.; Wang, J.-L.; Che, W.-W.; Wu, Z.-G. Nonlinear Disturbance Observer-Based Fault-Tolerant Sliding-Mode Control for 2-D Plane Vehicular Platoon with UTVFD and ANAS. IEEE Trans. Cybern. 2024, 54, 2050–2061. [Google Scholar] [CrossRef]
- Feng, C.; Shen, M.; Wang, Z.; Wu, H.; Liang, Z.; Liang, Z. Adaptive Terminal Sliding Mode Trajectory Tracking Control for Autonomous Vehicles Considering Completely Unknown Parameters and Unknown Perturbation Conditions. Machines 2024, 12, 237. [Google Scholar] [CrossRef]
- Chen, H.; Lv, C. Online Learning-Informed Feedforward-Feedback Controller Synthesis for Path Tracking of Autonomous Vehicles. IEEE Trans. Intell. Veh. 2023, 8, 2759–2769. [Google Scholar] [CrossRef]
- Wang, H.; Gelbal, S.Y.; Guvenc, L. Multi-Objective Digital PID Controller Design in Parameter Space and its Application to Automated Path Following. IEEE Access 2021, 9, 46874–46885. [Google Scholar] [CrossRef]
- Shi, Q.; Zhang, H. Road-Curvature-Range-Dependent Path Following Controller Design for Autonomous Ground Vehicles Subject to Stochastic Delays. IEEE Trans. Intell. Transp. Syst. 2022, 23, 17440–17450. [Google Scholar] [CrossRef]
- Feng, Z.; Yu, M.; Evangelou, S.A.; Jaimoukha, I.M.; Dini, D. Mu-Synthesis PID Control of Full-Car with Parallel Active Link Suspension Under Variable Payload. IEEE Trans. Veh. Technol. 2023, 72, 176–189. [Google Scholar] [CrossRef]
- Guo, G.; Yang, D.; Zhang, R. Distributed Trajectory Optimization and Platooning of Vehicles to Guarantee Smooth Traffic Flow. IEEE Trans. Intell. Veh. 2023, 8, 684–695. [Google Scholar] [CrossRef]
- Huang, Z.; Shen, S.; Ma, J. Decentralized iLQR for Cooperative Trajectory Planning of Connected Autonomous Vehicles via Dual Consensus ADMM. IEEE Trans. Intell. Transp. Syst. 2023, 24, 12754–12766. [Google Scholar] [CrossRef]
- Hu, Y.; Fu, J.; Wen, G. Safe Reinforcement Learning for Model-Reference Trajectory Tracking of Uncertain Autonomous Vehicles with Model-Based Acceleration. IEEE Trans. Intell. Veh. 2023, 8, 2332–2344. [Google Scholar] [CrossRef]
- Zheng, H.; Li, J.; Tian, Z.; Liu, C.; Wu, W. Hybrid Physics-Learning Model Based Predictive Control for Trajectory Tracking of Unmanned Surface Vehicles. IEEE Trans. Intell. Transp. Syst. 2024, 25, 11522–11533. [Google Scholar] [CrossRef]
- Kamezaki, M.; Kobayashi, A.; Kono, R.; Hirayama, M.; Sugano, S. Dynamic Waypoint Navigation: Model-Based Adaptive Trajectory Planner for Human-Symbiotic Mobile Robots. IEEE Access 2022, 10, 81546–81555. [Google Scholar] [CrossRef]
- Zhu, Y.; Lee, K.Y.; Wang, Y. Adaptive Elitist Genetic Algorithm with Improved Neighbor Routing Initialization for Electric Vehicle Routing Problems. IEEE Access 2021, 9, 16661–16671. [Google Scholar] [CrossRef]
- Leng, K.; Li, S. Distribution Path Optimization for Intelligent Logistics Vehicles of Urban Rail Transportation Using VRP Optimization Model. IEEE Trans. Intell. Transp. Syst. 2022, 23, 1661–1669. [Google Scholar] [CrossRef]
- Zhang, J.; Lu, Y.; Wu, Y.; Wang, C.; Zang, D.; Abusorrah, A.; Zhou, M. PSO-Based Sparse Source Location in Large-Scale Environments with a UAV Swarm. IEEE Trans. Intell. Transp. Syst. 2023, 24, 5249–5258. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Z.; Duan, J.; Liu, J.; Wong, P.K.; Zhao, J. Backup Pattern for traction system of FWIA electric vehicle to guarantee maneuverability and stability in presence of motor faults and failures. J. Frankl. Inst. 2024, 361, 106714. [Google Scholar] [CrossRef]
- Liang, Z.; Wang, Z.; Zhao, J.; Wong, P.K.; Yang, Z.; Ding, Z. Fixed-Time Prescribed Performance Path-Following Control for Autonomous Vehicle with Complete Unknown Parameters. IEEE Trans. Ind. Electron. 2023, 70, 8426–8436. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; Jiang, K.; Zhou, Z.; Nam, K.; Yin, C. Interactive Trajectory Prediction Using a Driving Risk Map-Integrated Deep Learning Method for Surrounding Vehicles on Highways. IEEE Trans. Intell. Transp. Syst. 2022, 23, 19076–19087. [Google Scholar] [CrossRef]
- Li, Y.; Ni, J.; Hu, J.; Pan, B. The Design of Driverless Vehicle Trajectory Tracking Control Strategy. IFAC-PapersOnLine 2018, 51, 738–745. [Google Scholar] [CrossRef]

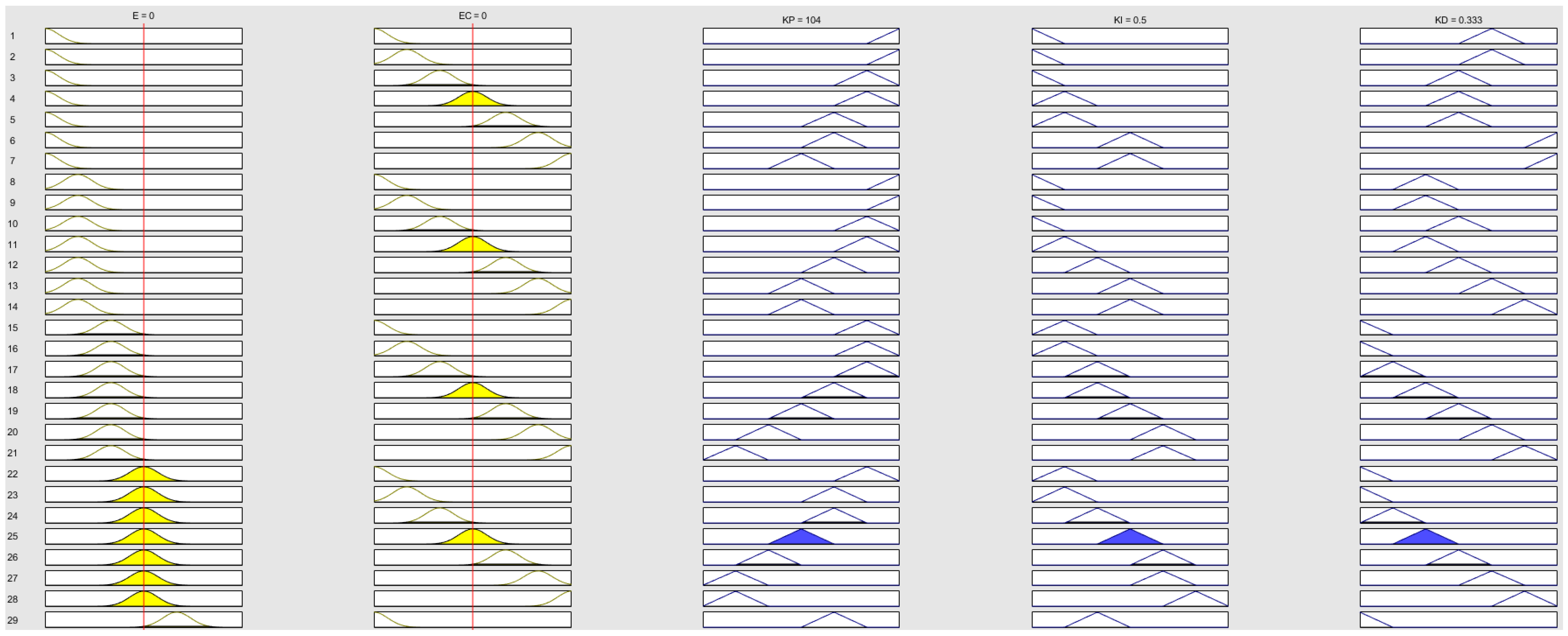




| eyφ/ec1 | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| Kp1, Ki1, Kd1 | |||||||
| NB | PB NB PS | PB NB PS | PM NB ZO | PM NM ZO | PS NM ZO | PS ZO PB | ZO ZO PB |
| NM | PB NB NS | PB NB NS | PM NB ZO | PM NM NS | PS NS ZO | ZO ZO PS | ZO ZO PM |
| NS | PM NM NB | PM NM NB | PM NS NM | PS NS NS | ZO ZO ZO | NS PS PS | NM PS PM |
| ZO | PM NM NB | PS NM NB | PS NS NM | ZO ZO NS | NS PS ZO | NM PS PS | NM PM PM |
| PS | PS NS NB | PS NS NM | ZO ZO NS | NS PS NS | NS PS ZO | NM PM PS | NM PM PS |
| PM | ZO ZO NM | ZO ZO NS | NS PS NS | NM PM NS | NM PM ZO | NM PB PS | NB PB PS |
| PB | ZO NB PS | NS NM ZO | NS NS ZO | NM ZO ZO | NM PS ZO | NB PM PB | NB PB PB |
| exv/ec2 | NB | NM | NS | ZO | PS | PM | PB |
|---|---|---|---|---|---|---|---|
| Kp2, Ki2, Kd2 | |||||||
| NB | PB NB PS | PB NM PS | PM NM ZO | PM NS ZS | PS NS NS | PS ZO NM | ZO ZO NB |
| NM | PM NM NM | PM NM NS | PS NS ZS | PS NS ZO | ZO ZO PS | NS ZO PS | NM PS PS |
| NS | PS NS ZO | PS NS ZO | ZO ZO PS | ZO PS PS | NS PS PM | NS PM PM | NM PM PB |
| ZO | ZO NM NS | ZO NM NS | NS NS ZO | NS NS ZO | NM NM PS | NM NM PS | NB NB PM |
| PS | PS NS ZO | PS NS ZO | ZO ZO PS | ZO PS PS | NS PS PM | NM PM PM | NB PM PB |
| PM | PM NM NM | PM NM NS | PS NS NS | PS NS ZO | ZO ZO PS | NS ZO PS | NM PS PS |
| PB | PB NB PS | PB NM PS | PM NM ZO | PM NS NB | PS NS NB | PS ZO NM | ZO ZO PS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jin, M.; Qu, M.; Gao, Q.; Huang, Z.; Su, T.; Liang, Z. Advanced Trajectory Planning and Control for Autonomous Vehicles with Quintic Polynomials. Sensors 2024, 24, 7928. https://doi.org/10.3390/s24247928
Jin M, Qu M, Gao Q, Huang Z, Su T, Liang Z. Advanced Trajectory Planning and Control for Autonomous Vehicles with Quintic Polynomials. Sensors. 2024; 24(24):7928. https://doi.org/10.3390/s24247928
Chicago/Turabian StyleJin, Ma, Mingcheng Qu, Qingyang Gao, Zhuo Huang, Tonghua Su, and Zhongchao Liang. 2024. "Advanced Trajectory Planning and Control for Autonomous Vehicles with Quintic Polynomials" Sensors 24, no. 24: 7928. https://doi.org/10.3390/s24247928
APA StyleJin, M., Qu, M., Gao, Q., Huang, Z., Su, T., & Liang, Z. (2024). Advanced Trajectory Planning and Control for Autonomous Vehicles with Quintic Polynomials. Sensors, 24(24), 7928. https://doi.org/10.3390/s24247928






