Simultaneous Temperature and Relative Humidity Measurement Using Machine Learning in Rayleigh-Based Optical Frequency Domain Reflectometry
Abstract
:1. Introduction
2. Materials and Methods
2.1. Experimental Setup
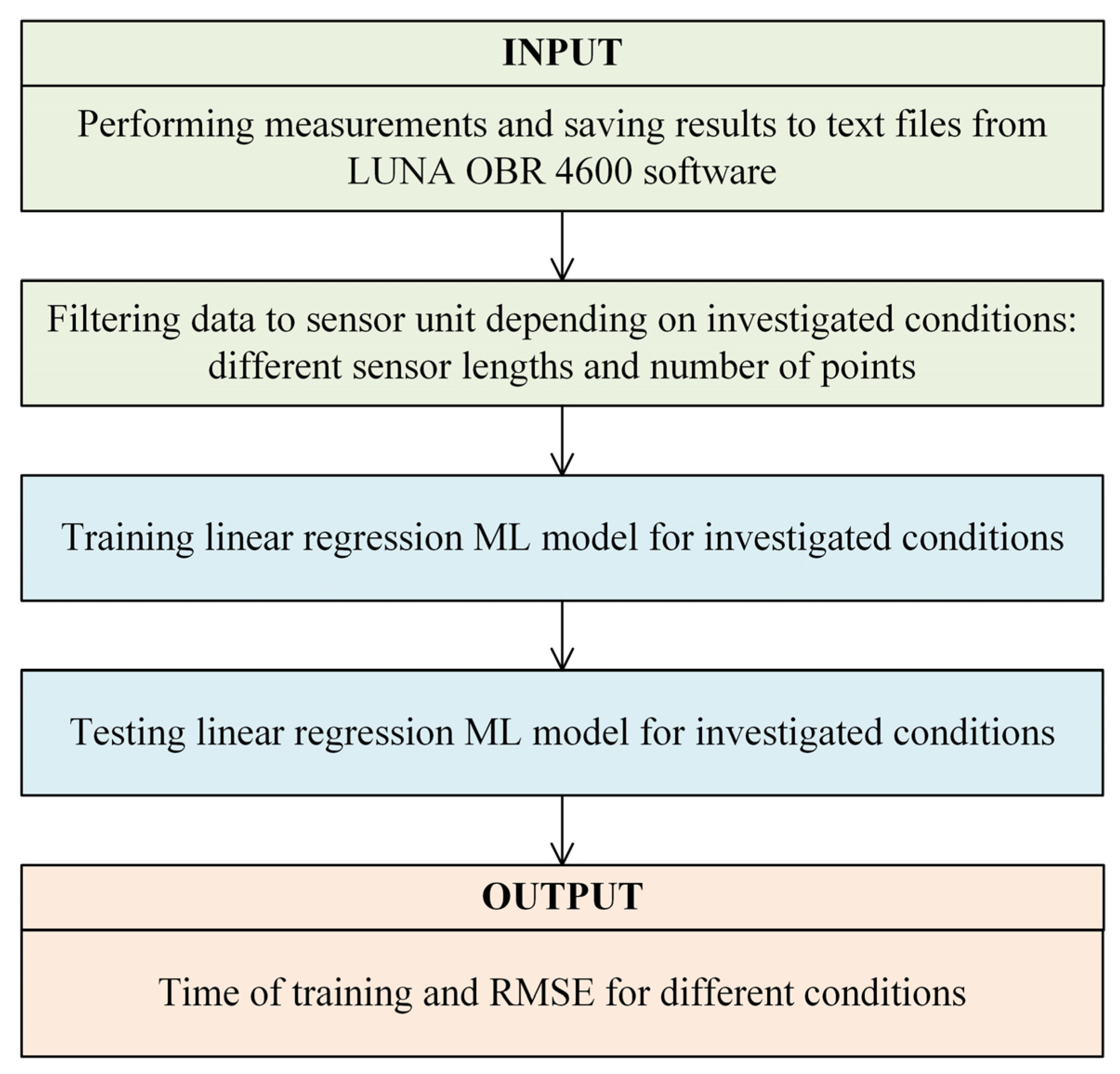
2.2. Machine Learning Approach
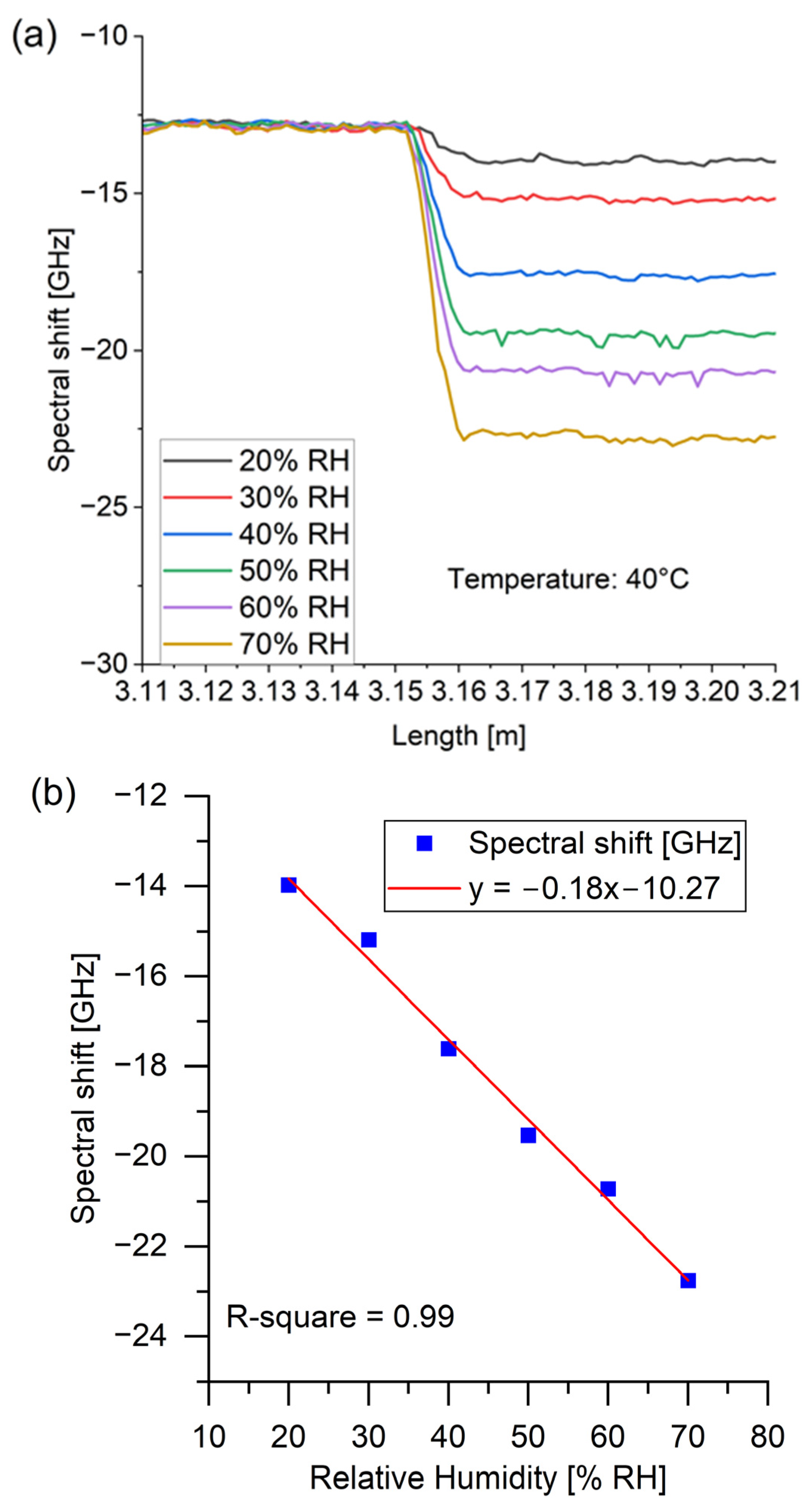
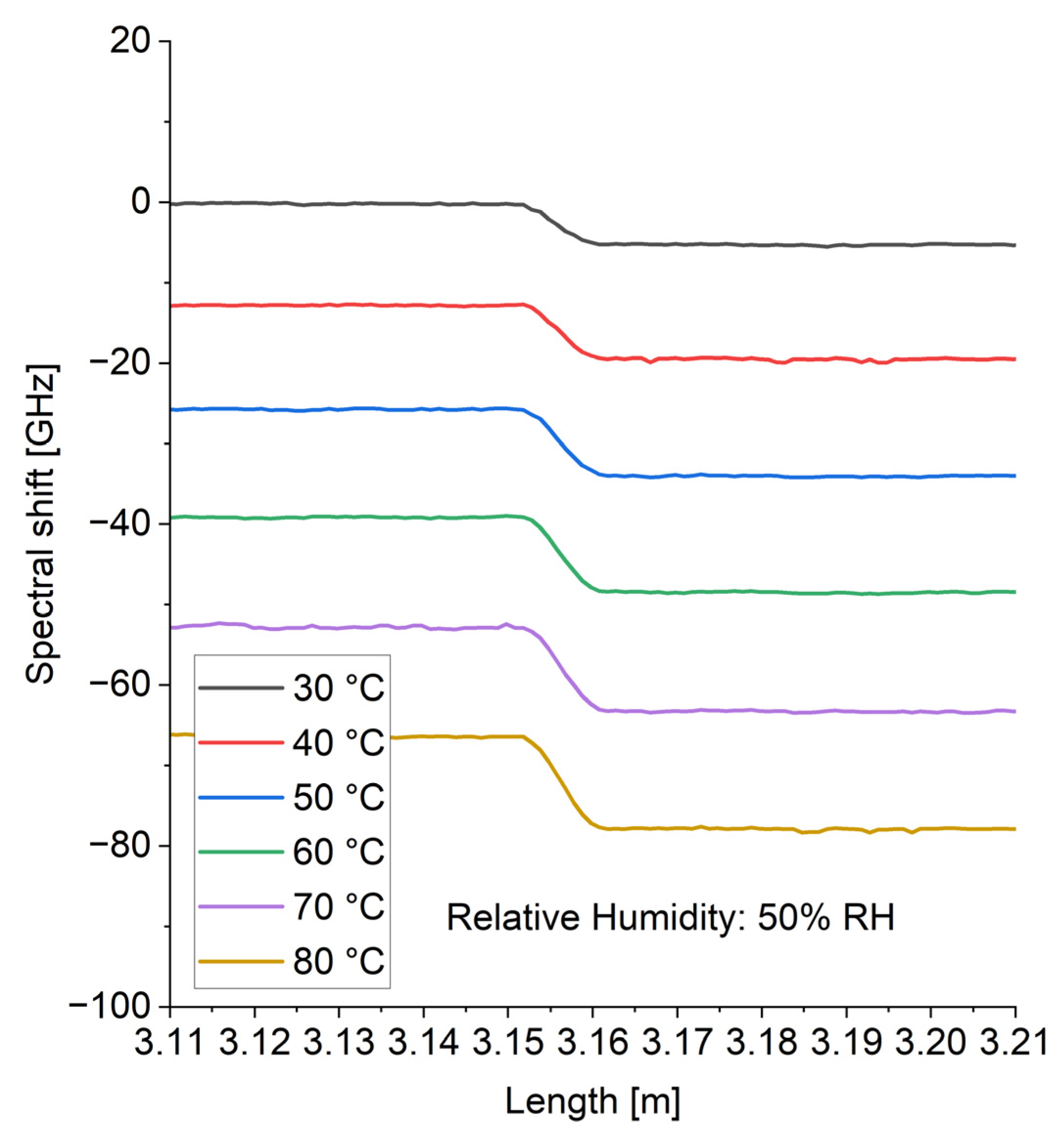
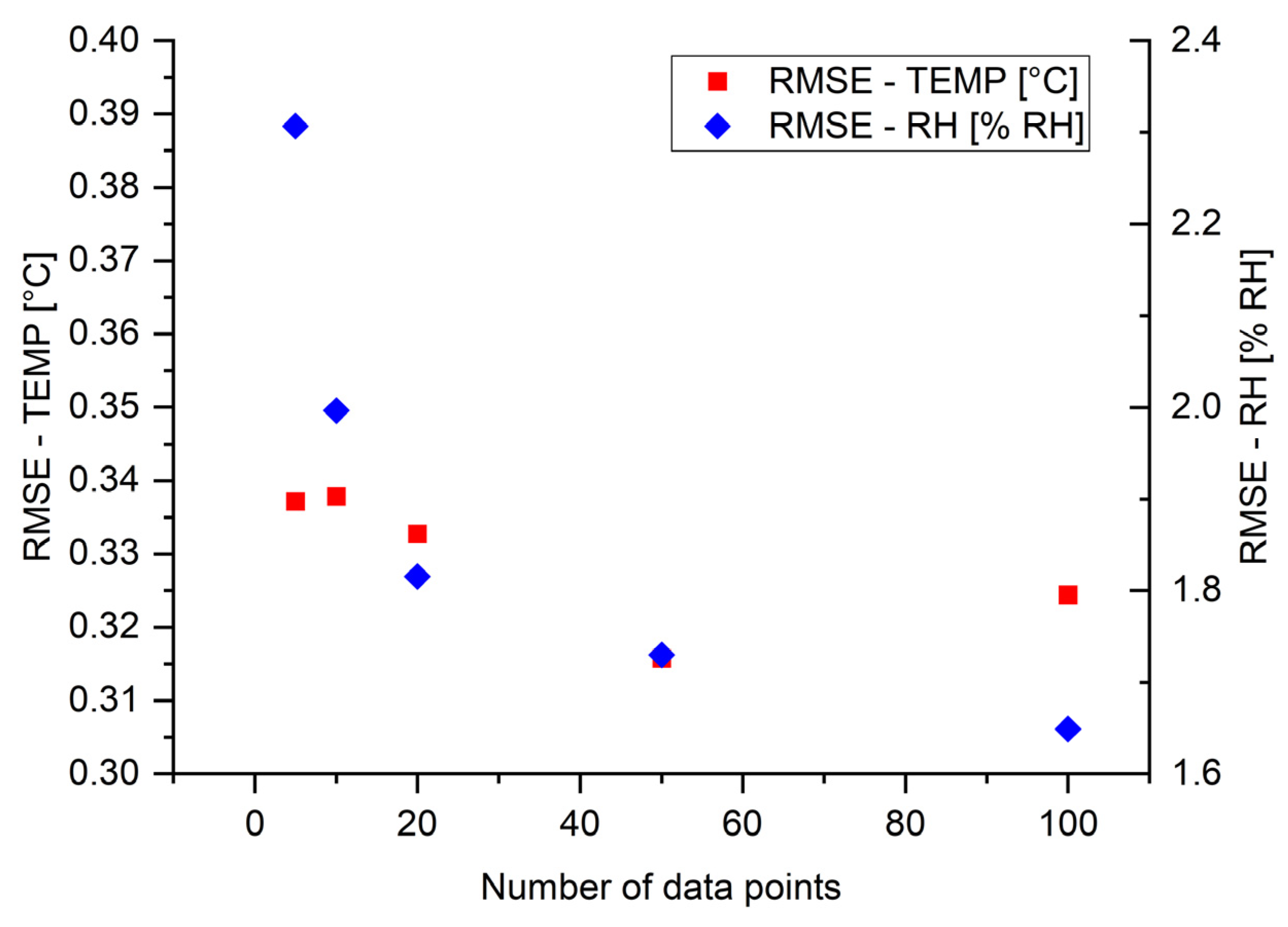
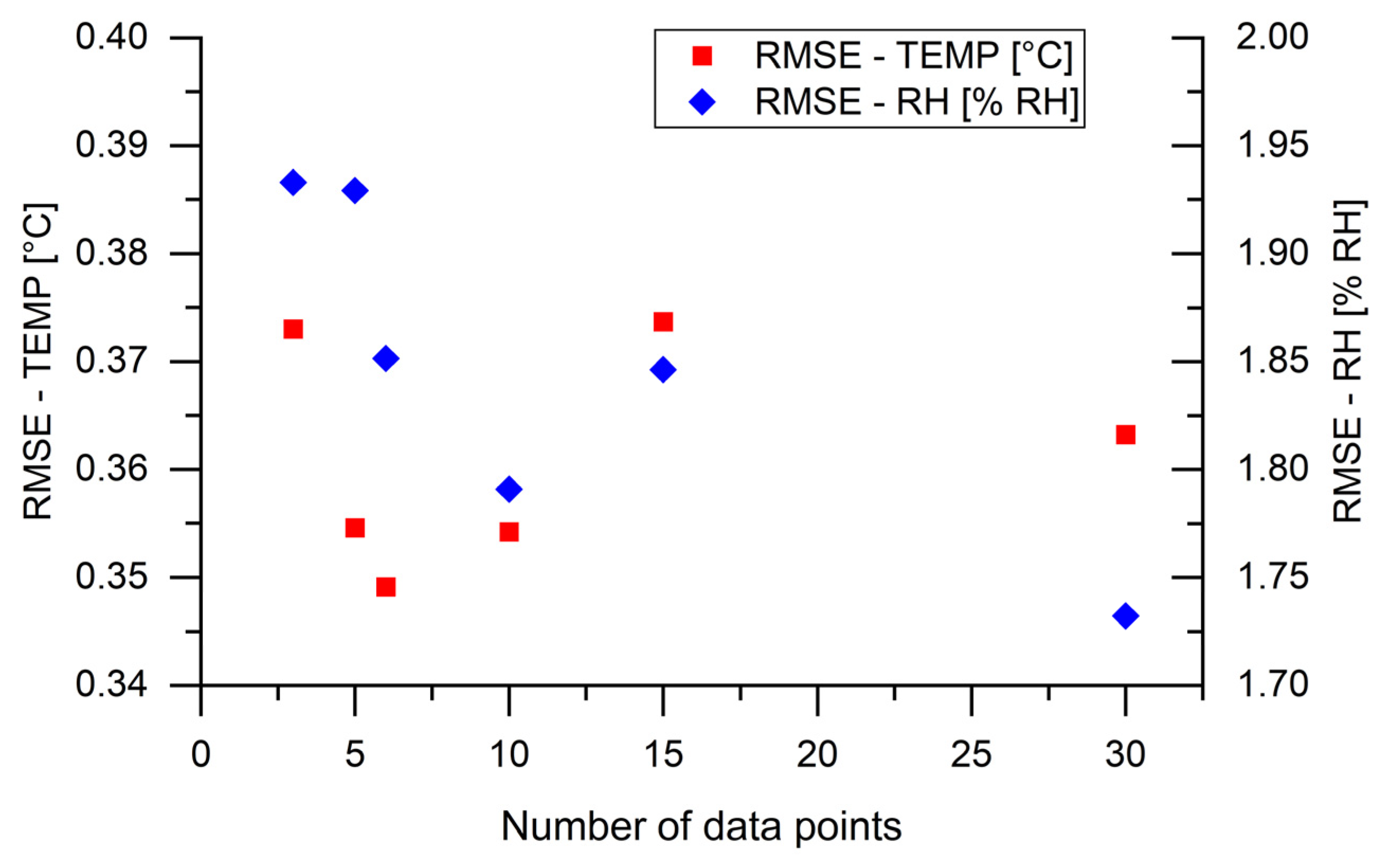
3. Results and Discussion
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lu, P.; Lalam, N.; Badar, M.; Liu, B.; Chorpening, B.T.; Buric, M.P.; Ohodnicki, P.R. Distributed optical fiber sensing: Review and perspective. Appl. Phys. Rev. 2019, 6, 041302. [Google Scholar] [CrossRef]
- Bado, M.F.; Casas, J.R. A review of recent distributed optical fiber sensors applications for civil engineering structural health monitoring. Sensors 2021, 21, 1818. [Google Scholar] [CrossRef]
- Barrias, A.; Casas, J.R.; Villalba, S. A review of distributed optical fiber sensors for civil engineering applications. Sensors 2016, 16, 748. [Google Scholar] [CrossRef]
- Qu, S.; Xu, Y.; Huang, S.; Sun, M.; Wang, C.; Shang, Y. Recent advancements in optical frequency-domain reflectometry: A review. IEEE Sens. J. 2022, 23, 1707–1723. [Google Scholar] [CrossRef]
- Alwis, L.; Sun, T.; Grattan, K.T.V. Optical fibre-based sensor technology for humidity and moisture measurement: Review of recent progress. Measurement 2013, 46, 4052–4074. [Google Scholar] [CrossRef]
- Thomas, P.J.; Hellevang, J.O. A fully distributed fibre optic sensor for relative humidity measurements. Sens. Actuators B Chem. 2017, 247, 284–289. [Google Scholar] [CrossRef]
- Thomas, P.J.; Hellevang, J.O. A high response polyimide fiber optic sensor for distributed humidity measurements. Sens. Actuators B Chem. 2018, 270, 417–423. [Google Scholar] [CrossRef]
- Stajanca, P.; Hicke, K.; Krebber, K. Distributed fiberoptic sensor for simultaneous humidity and temperature monitoring based on polyimide-coated optical fibers. Sensors 2019, 19, 5279. [Google Scholar] [CrossRef]
- Qin, Z.; Bao, X.; Li, Z. A fully distributed fiber optic sensor for simultaneous relative humidity and temperature measurement with polyimide-coated polarization maintaining fiber. Sensors Actuators B Chem. 2022, 373, 132699. [Google Scholar] [CrossRef]
- Li, S.; Li, H.; Yang, X.; Zhang, B.; Qu, S.; Xu, Y.; Liu, Z.; Qin, Z. Fully distributed multi-channel fiber-optic sensor for simultaneous relative humidity and temperature measurement with finer gauge length based on spatial-domain time-delayed multiplexing. J. Light. Technol. 2024, 42, 6133–6142. [Google Scholar] [CrossRef]
- Sarkar, S.; Tripathi, S.; Bhadra, S. Machine learning methods for discriminating strain and temperature effects on FBG-based sensors. IEEE Photon. Technol. Lett. 2021, 33, 876–879. [Google Scholar] [CrossRef]
- Dey, K.; Vangety, N.; Roy, S. Machine learning approach for simultaneous measurement of strain and temperature using FBG sensor. Sens. Actuators A Phys. 2022, 333, 113254. [Google Scholar] [CrossRef]
- Mei, Y.; Xia, T.; Cai, H.; Liu, Z. Deep learning improved spectral demodulation of interferometry vernier effect for pressure sensing. J. Light. Technol. 2024, 42, 430–440. [Google Scholar] [CrossRef]
- Zhu, C.; Alsalman, O.; Naku, W. Machine learning for a Vernier-effect-based optical fiber sensor. Opt. Lett. 2023, 48, 2488–2491. [Google Scholar] [CrossRef] [PubMed]
- Zhu, C.; Huang, J. Self-vernier effect-assisted optical fiber sensor based on microwave photonics and its machine learning analysis. J. Light. Technol. 2022, 41, 1890–1898. [Google Scholar] [CrossRef]
- Zhu, C.; Alsalman, O. Vernier effect-based optical fiber sensor for dynamic sensing using a coarsely resolved spectrometer. Opt. Express 2023, 31, 22250–22259. [Google Scholar] [CrossRef]
- Karapanagiotis, C.; Hicke, K.; Wosniok, A.; Krebber, K. Distributed humidity fiber-optic sensor based on BOFDA using a simple machine learning approach. Opt. Express 2022, 30, 12484–12494. [Google Scholar] [CrossRef]
- Karapanagiotis, C.; Hicke, K.; Krebber, K. Machine learning assisted BOFDA for simultaneous temperature and strain sensing in a standard optical fiber. Opt. Express 2023, 31, 5027–5041. [Google Scholar] [CrossRef]
- Karapanagiotis, C.; Krebber, K. Machine learning for strain, temperature and humidity discrimination in Brillouin optical frequency domain analysis. In Proceedings of the 28th International Conference on Optical Fiber Sensors, Hamamatsu, Japan, 20–24 November 2023. Technical Digest Series (Optica Publishing Group), paper Tu3.11. [Google Scholar]
- Karapanagiotis, C.; Krebber, K. Machine learning approaches in Brillouin distributed fiber optic sensors. Sensors 2023, 23, 6187. [Google Scholar] [CrossRef]
- Zhang, Z.; Peng, W.; Ma, L.; Zhu, C. Improvement of strain resolution by deep learning in an OFDR system. In Proceedings of the Frontiers in Optics + Laser Science 2023 (FiO, LS), Tacoma, WA, USA, 9–12 October 2023. Technical Digest Series (Optica Publishing Group), paper JM7A.111. [Google Scholar]
- Pedraza, A.; del Río, D.; Bautista-Juzgado, V.; Fernández-López, A.; Sanz-Andrés, Á. Study of the feasibility of decoupling temperature and strain from a ϕ-PA-OFDR over an SMF using neural networks. Sensors 2023, 23, 5515. [Google Scholar] [CrossRef]
- Gifford, D.; Soller, B.; Wolfe, M.; Froggatt, M. Distributed fiber-optic temperature sensing using Rayleigh backscatter. In Proceedings of the 31st European Conference on Optical Communication, ECOC 2005, Glasgow, UK, 25–29 September 2005; pp. 511–512. [Google Scholar]
- Ali-Alvarez, S.; Ferdinand, P.; Magne, S.; Nogueira, R. Optical fiber sensor for corrosion detection and evolution monitoring in reinforced concrete structures. In Proceedings of the 9th International Workshop on Structural Health Monitoring: A Roadmap to Intelligent Structures, IWSHM 2013, Stanford, CA, USA, 10–12 September 2013; pp. 1591–1596. [Google Scholar]
- Swanson, A.J.; Raymond, S.G.; Janssens, S.; Breukers, R.D.; Bhuiyan, M.D.H.; Lovell-Smith, J.W.; Waterland, M.R. Investigation of polyimide coated fibre Bragg gratings for relative humidity sensing. Meas. Sci. Technol. 2015, 26, 125101. [Google Scholar] [CrossRef]
- Kronenberg, P.; Rastogi, P.K.; Giaccari, P.; Limberger, H.G. Relative humidity sensor with optical fiber Bragg gratings. Opt. Lett. 2002, 27, 1385–1387. [Google Scholar] [CrossRef] [PubMed]
- Yeo, T.L.; Lee, H.K.; Tjin, S.C.; Tan, W.B. Polymer-coated fiber Bragg grating for relative humidity sensing. IEEE Sens. J. 2005, 5, 1082–1089. [Google Scholar] [CrossRef]
- Szczupak, B.; Olszewski, J.; Madry, M.; Pala, P.; Stefanska, K.; Statkiewicz-Barabach, G. The influence of germanium concentration in the fiber core on temperature sensitivity in Rayleigh scattering-based OFDR. IEEE Sens. J. 2021, 21, 20036–20044. [Google Scholar] [CrossRef]
- Tosi, D.; Molardi, C.; Sypabekova, M.; Blanc, W. Enhanced backscattering optical fiber distributed sensors: Tutorial and review. IEEE Sens. J. 2020, 21, 12667–12678. [Google Scholar] [CrossRef]
- Lee, T.; Beresna, M.; Masoudi, A.; Brambilla, G. Enhanced-backscattering and enhanced-backreflection fibers for distributed optical fiber sensors. J. Light. Technol. 2023, 41, 4051–4064. [Google Scholar] [CrossRef]
- Du, C.; Fu, C.; Li, P.; Meng, Y.; Zhong, H.; Du, B.; Guo, K.; Chen, L.; Wang, Y.; He, J. High-spatial-resolution strain sensor based on Rayleigh-scattering-enhanced SMF using direct UV exposure. J. Light. Technol. 2023, 41, 1566–1570. [Google Scholar] [CrossRef]
- Loranger, S.; Gagné, M.; Lambin-Iezzi, V.; Kashyap, R. Rayleigh scatter based order of magnitude increase in distributed temperature and strain sensing by simple UV exposure of optical fibre. Sci. Rep. 2015, 5, 11177. [Google Scholar] [CrossRef]
- Ayupova, T.; Shaimerdenova, M.; Korganbayev, S.; Sypabekova, M.; Bekmurzayeva, A.; Blanc, W.; Sales, S.; Guo, T.; Molardi, C.; Tosi, D. Fiber optic refractive index distributed multi-sensors by scattering-level multiplexing with MgO nanoparticle-doped fibers. IEEE Sens. J. 2019, 20, 2504–2510. [Google Scholar] [CrossRef]
- Beisenova, A.; Issatayeva, A.; Iordachita, I.; Blanc, W.; Molardi, C.; Tosi, D. Distributed fiber optics 3D shape sensing by means of high scattering NP-doped fibers simultaneous spatial multiplexing. Opt. Express 2019, 27, 22074–22087. [Google Scholar] [CrossRef]
- Bulot, P.; Bernard, R.; Cieslikiewicz-Bouet, M.; Laffont, G.; Douay, M. Performance study of a zirconia-doped fiber for distributed temperature sensing by OFDR at 800 °C. Sensors 2021, 21, 3788. [Google Scholar] [CrossRef] [PubMed]
- Fuertes, V.; Grégoire, N.; Labranche, P.; Gagnon, S.; Wang, R.; Ledemi, Y.; LaRochelle, S.; Messaddeq, Y. Engineering nanoparticle features to tune Rayleigh scattering in nanoparticles-doped optical fibers. Sci. Rep. 2021, 11, 9116. [Google Scholar] [CrossRef] [PubMed]
- Alwis, L.S.M.; Bustamante, H.; Roth, B.; Bremer, K.; Sun, T.; Grattan, K.T.V. Evaluation of the durability and performance of FBG-based sensors for monitoring moisture in an aggressive gaseous waste sewer environment. J. Light. Technol. 2017, 35, 3380–3386. [Google Scholar] [CrossRef]
- Zeng, H.; Geng, T.; Yang, W.; An, M.; Li, J.; Yang, F.; Yuan, L. Combining two types of gratings for simultaneous strain and temperature measurement. IEEE Photon-Technol. Lett. 2015, 28, 477–480. [Google Scholar] [CrossRef]
- Zhao, Y.; Li, H.; Li, J.; Zhou, A. Cascaded fiber MZIs for simultaneous measurement of pressure and temperature. Opt. Fiber Technol. 2021, 66, 102629. [Google Scholar] [CrossRef]
- Madry, M.; Alwis, L.; Binetti, L.; Pajewski, L.; Beres-Pawlik, E. Simultaneous Measurement of Temperature and Relative Humidity Using a Dual-Wavelength Erbium-Doped Fiber Ring Laser Sensor. IEEE Sens. J. 2019, 19, 9215–9220. [Google Scholar] [CrossRef]
- Urrutia Azcona, A.; Goicoechea Fernández, J.; Ricchiuti, A.L.; Barrera, D.; Arregui San Martín, F.J. Simultaneous measurement of humidity and temperature based on a partially coated optical fiber long period grating. Sens. Actuators B Chem. 2016, 227, 135–141. [Google Scholar] [CrossRef]
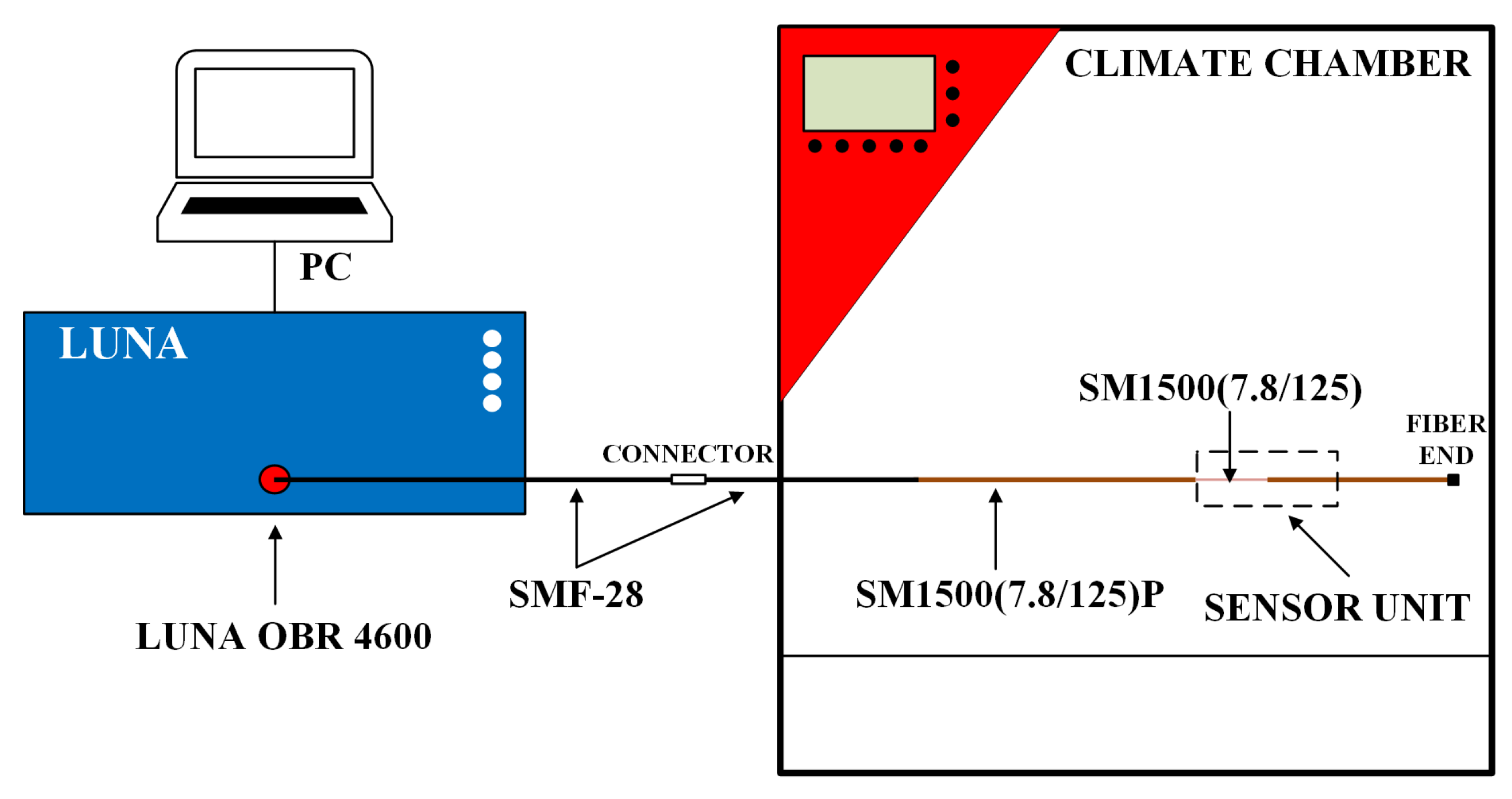

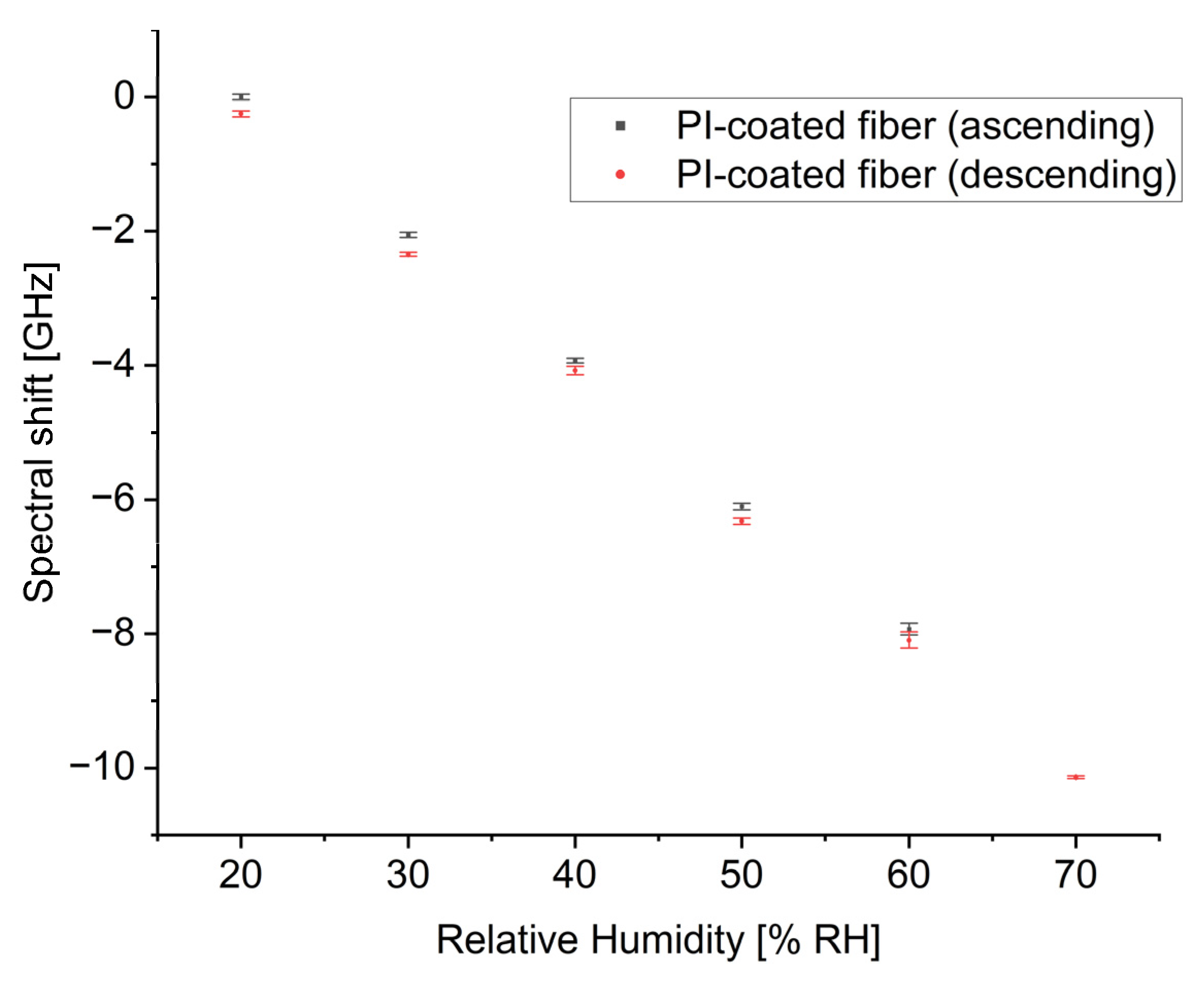
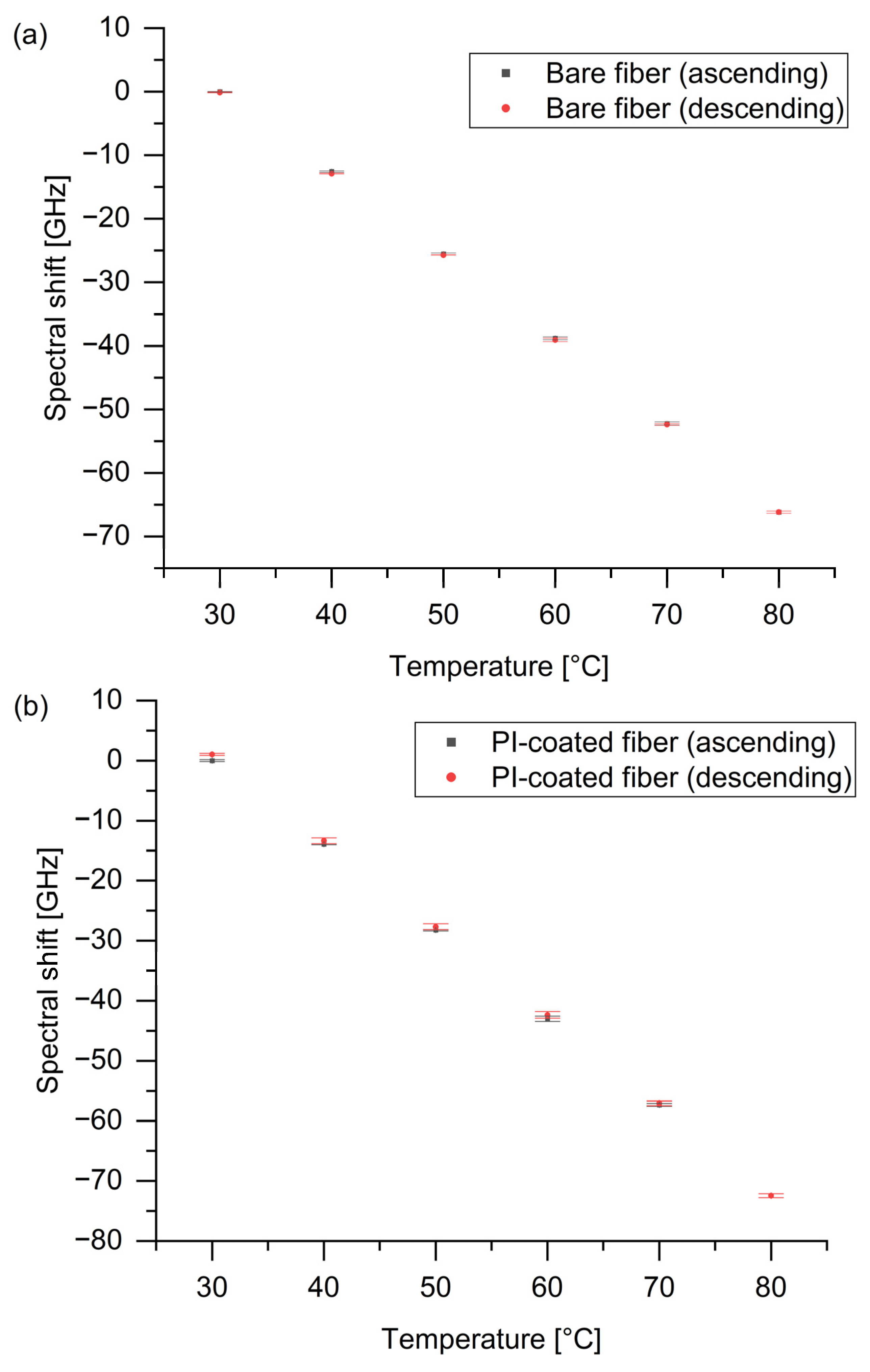
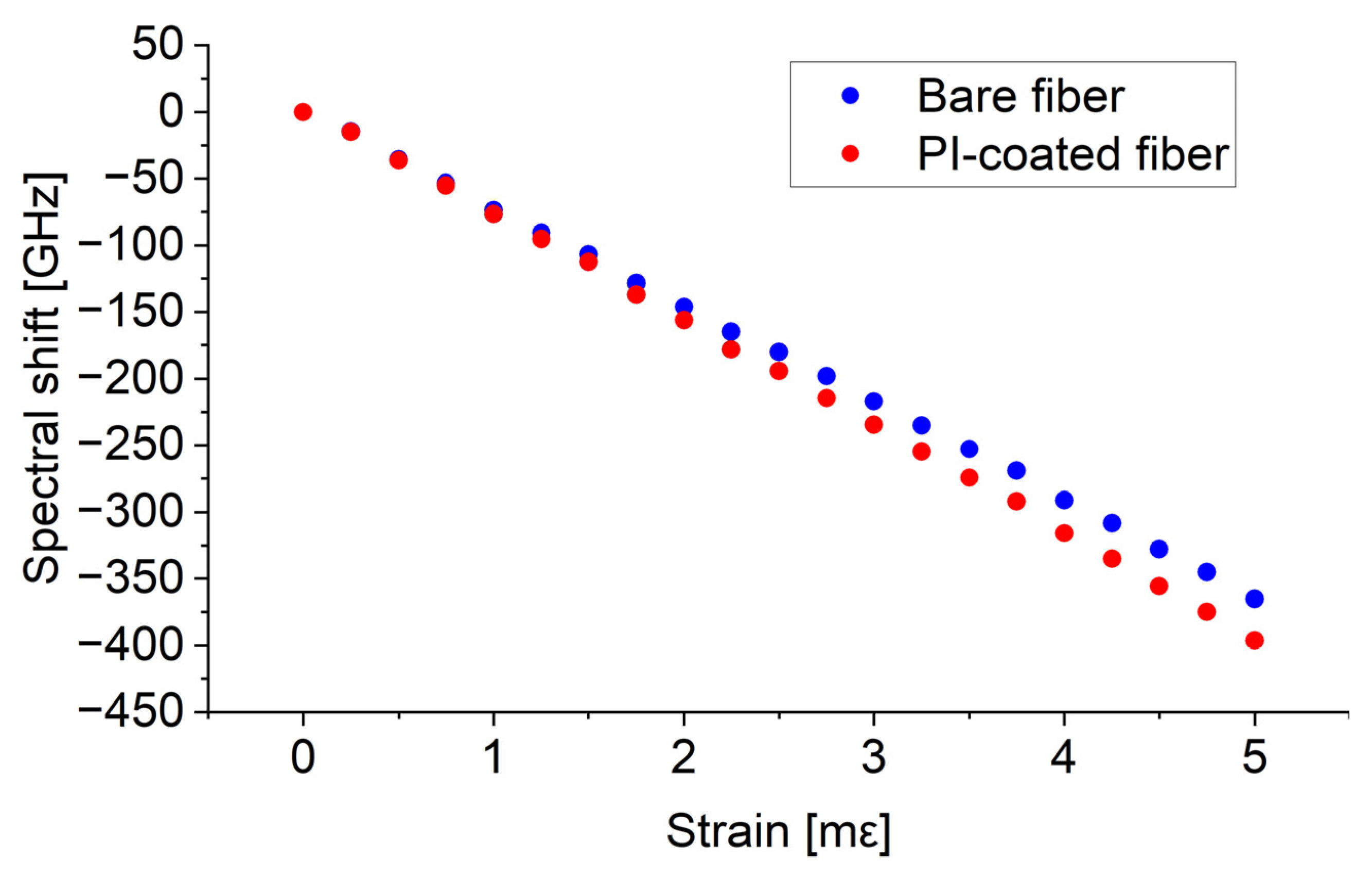
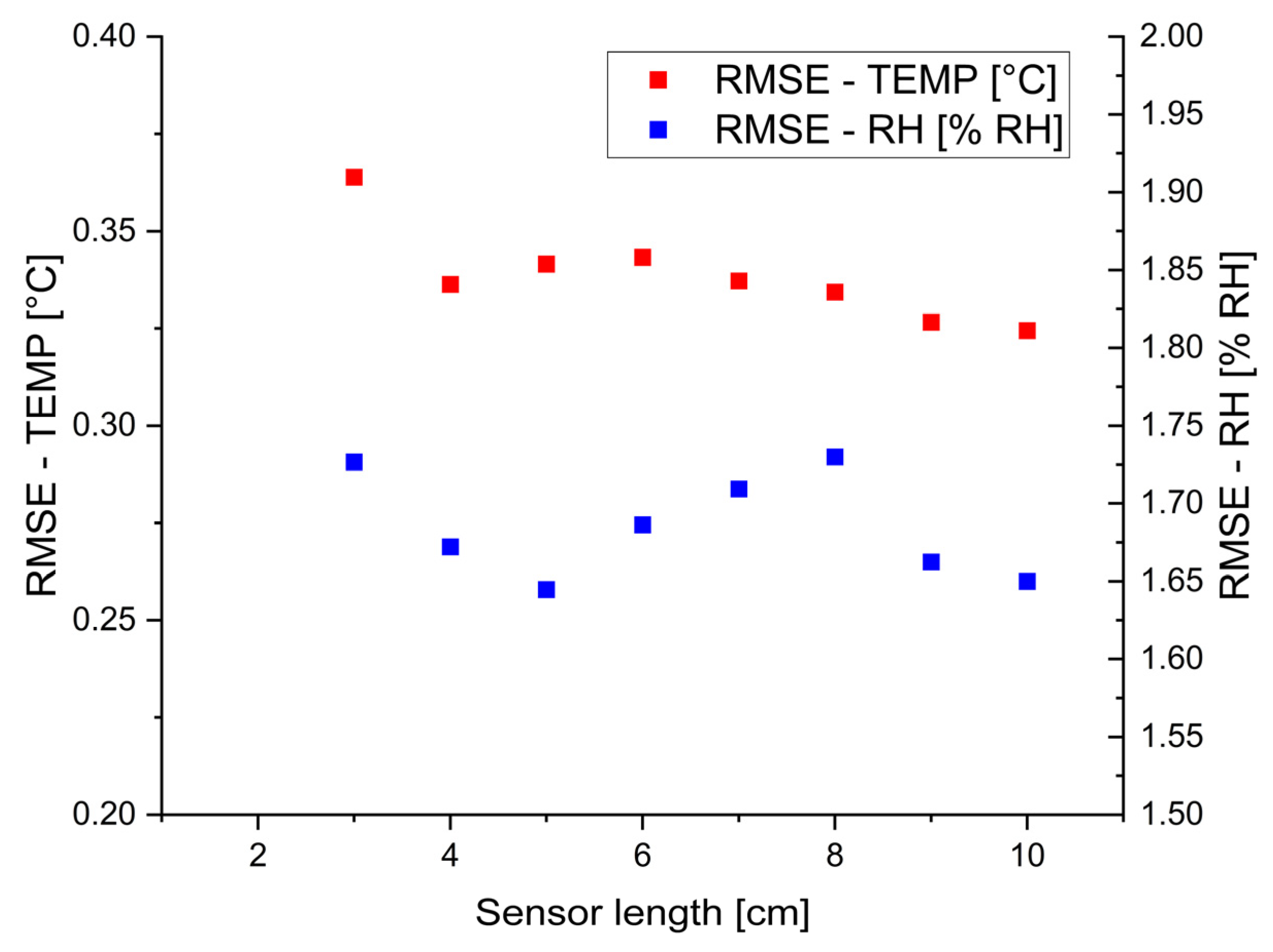
| Type of Fiber | SM1500(7.8/125)P |
|---|---|
| Core/cladding diameter [μm] | 7.8/125 |
| Operating wavelength [nm] | 1520–1650 |
| NA @1550 nm (catalog card) | 0.17 |
| Type of coating | Polyimide |
| Coating thickness [μm] | 15 |
| Ref | Configuration | Gauge Length | Machine Learning | Time of Data Processing | Prediction Errors |
|---|---|---|---|---|---|
| [8] | One fiber line (tandem) | 5 cm | No | Not given | ±5% RH, ±1 °C |
| [9] | One fiber line (PM fiber) | 5 cm | No | Not given | 2.75% RH, 0.54 °C |
| [10] | Two parallel fibers | 1 cm | No | Not given | 1.8% RH, 0.48 °C |
| This work | One fiber line (tandem) | 3 cm | Yes | 4 ms | 1.73% RH, 0.36 °C |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mądry, M.; Szczupak, B.; Śmigielski, M.; Matysiak, B. Simultaneous Temperature and Relative Humidity Measurement Using Machine Learning in Rayleigh-Based Optical Frequency Domain Reflectometry. Sensors 2024, 24, 7913. https://doi.org/10.3390/s24247913
Mądry M, Szczupak B, Śmigielski M, Matysiak B. Simultaneous Temperature and Relative Humidity Measurement Using Machine Learning in Rayleigh-Based Optical Frequency Domain Reflectometry. Sensors. 2024; 24(24):7913. https://doi.org/10.3390/s24247913
Chicago/Turabian StyleMądry, Mateusz, Bogusław Szczupak, Mateusz Śmigielski, and Bartosz Matysiak. 2024. "Simultaneous Temperature and Relative Humidity Measurement Using Machine Learning in Rayleigh-Based Optical Frequency Domain Reflectometry" Sensors 24, no. 24: 7913. https://doi.org/10.3390/s24247913
APA StyleMądry, M., Szczupak, B., Śmigielski, M., & Matysiak, B. (2024). Simultaneous Temperature and Relative Humidity Measurement Using Machine Learning in Rayleigh-Based Optical Frequency Domain Reflectometry. Sensors, 24(24), 7913. https://doi.org/10.3390/s24247913







