Robust Automatic Modulation Classification via a Lightweight Temporal Hybrid Neural Network
Abstract
1. Introduction
- The proposed TCN-GRU enables multiscale feature extraction and fusion, which allows our model to improve the classification accuracy of QAM and PSK, compared to other models;
- The proposed TCN-GRU is valid on RadioML2016.10a and RadioML2016.10b. Compared with some high-performing networks, our model demonstrates superior performance;
- The proposed TCN-GRU has fewer parameters than the existing high-precision model, and is structurally more efficient, making it highly practical.
2. Materials and Methods
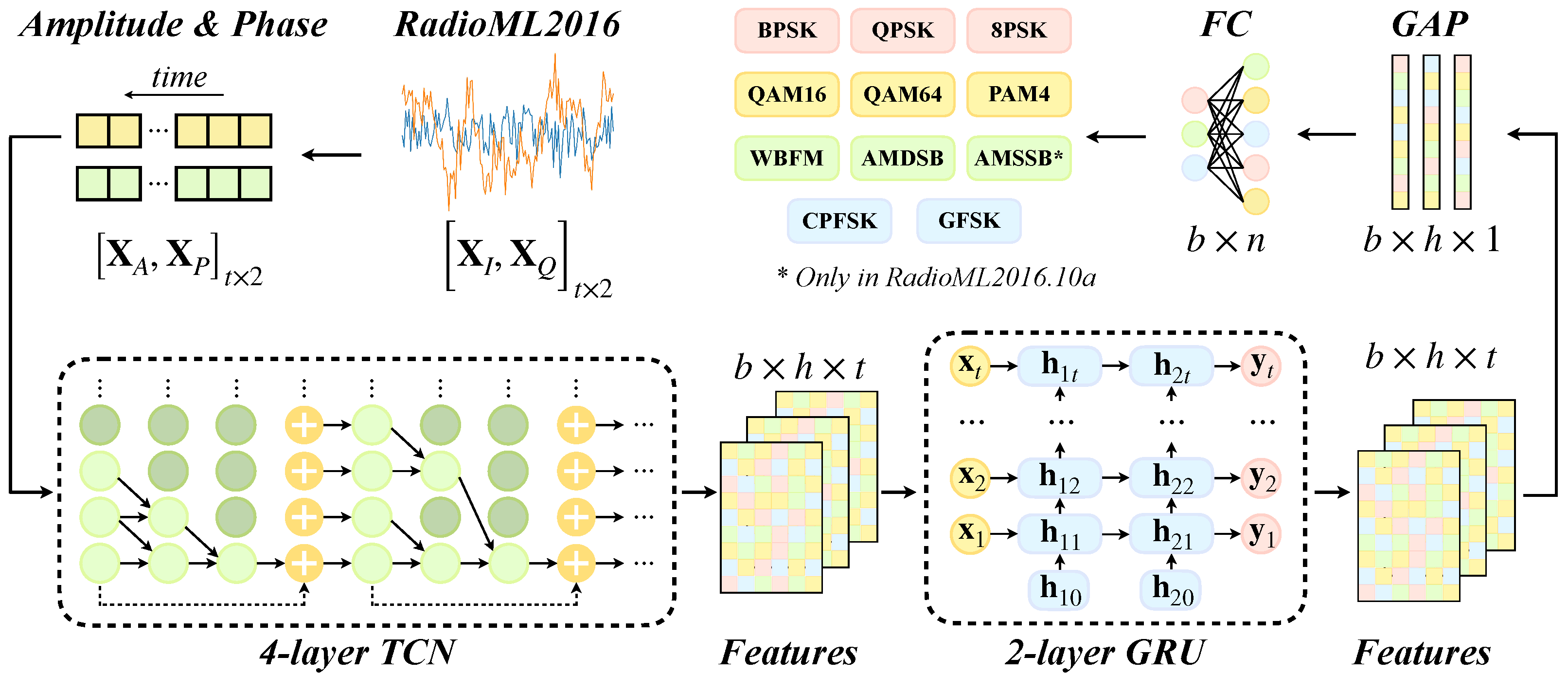
2.1. Modulation Signal Datasets
2.2. Deep Learining Networks
2.2.1. Temporal Convolutional Network
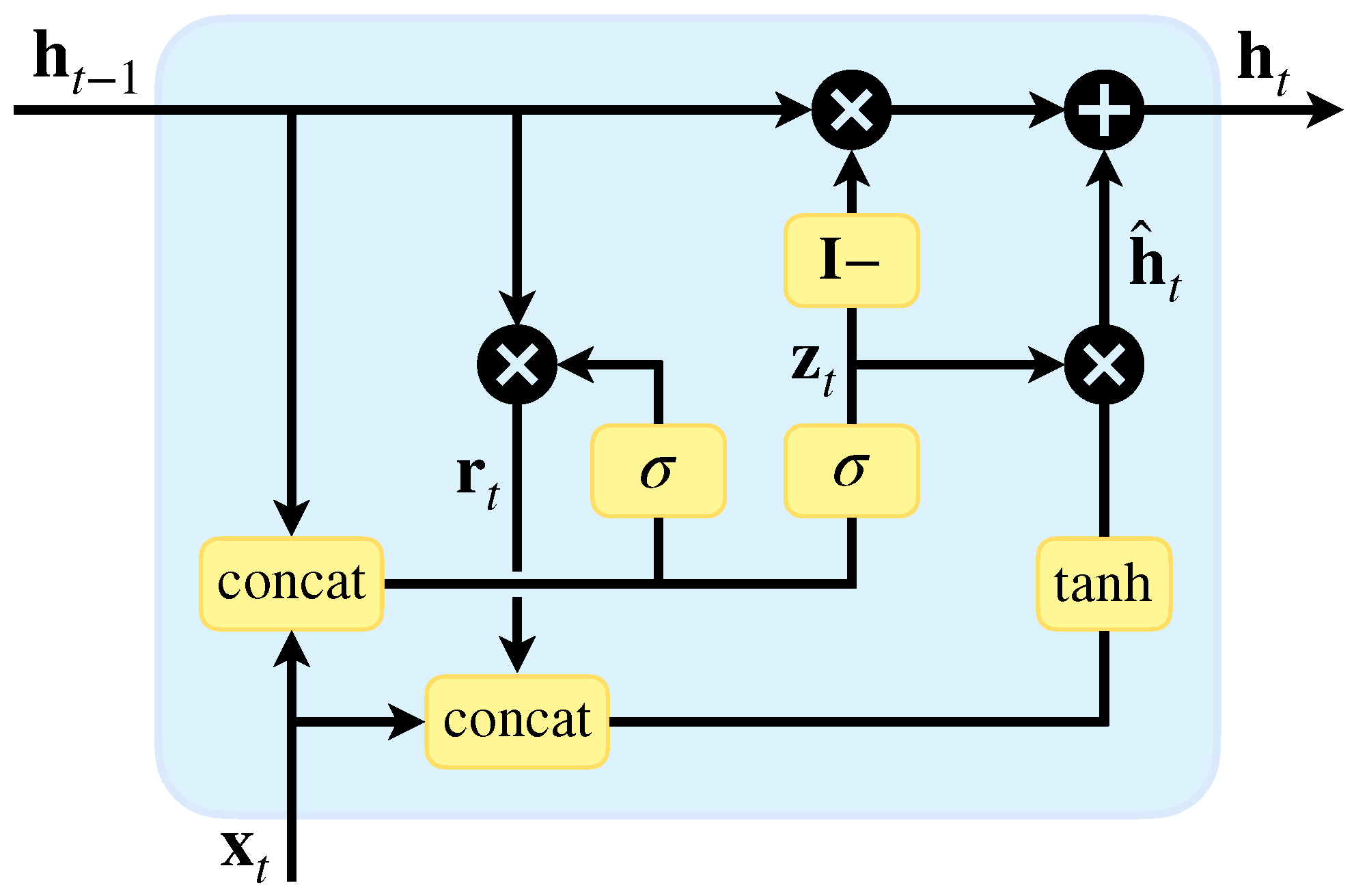
2.2.2. Gate Recurrent Unit
2.2.3. TCN-GRU
2.3. Performance Metrics
- True Positive (TP): Positive samples correctly predicted as positive;
- True Negative (TN): Negative samples correctly predicted as negative;
- False Positive (FP): Negative samples incorrectly predicted as positive;
- False Negative (FN): Positive samples incorrectly predicted as negative.
3. Experiments and Results
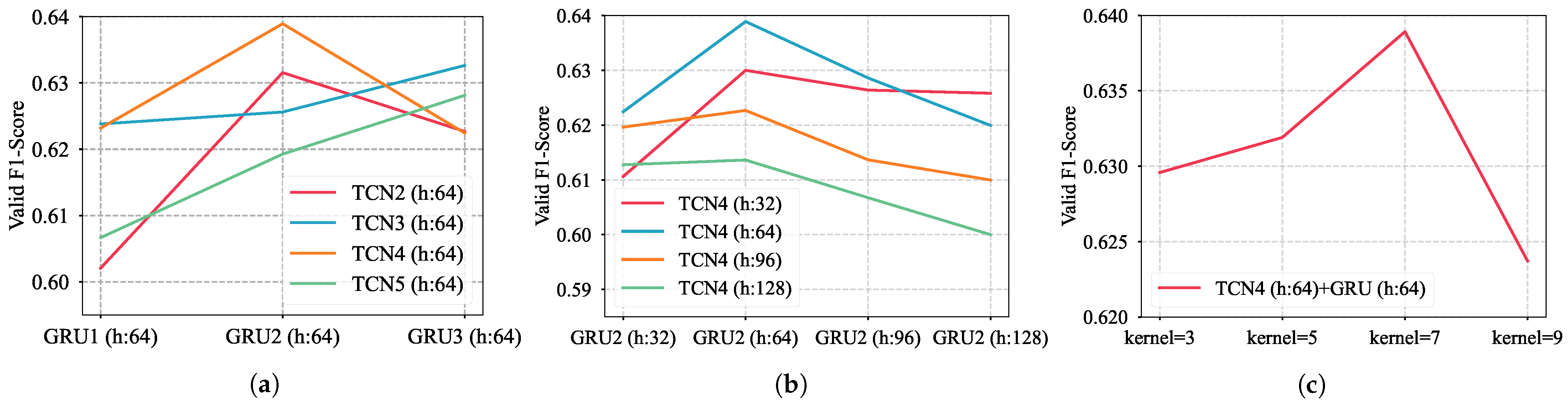
3.1. Determination of Network Structure
- Layer Optimization: We evaluated the valid F1-Score of networks with varying numbers of TCN and GRU layers, keeping hidden size and convolution kernel size constant. This determined the optimal layer count for both TCN and GRU.
- Hidden size Optimization: With the TCN and GRU layers fixed, we assessed the valid accuracy for different hidden sizes in TCN and GRU, maintaining a constant kernel size to identify the ideal count for each network.
- Convolution Kernel Size Optimization: Based on the optimal number of layers and hidden size, we evaluated the valid accuracy for networks with varying TCN convolution kernel sizes finalizing the network structure.
3.2. Comparison of Performance Between Models
- Performance metrics: Each model’s performance is compared using the metrics outlined in Section 2.3, aiming to reflect the classification capabilities of each model.
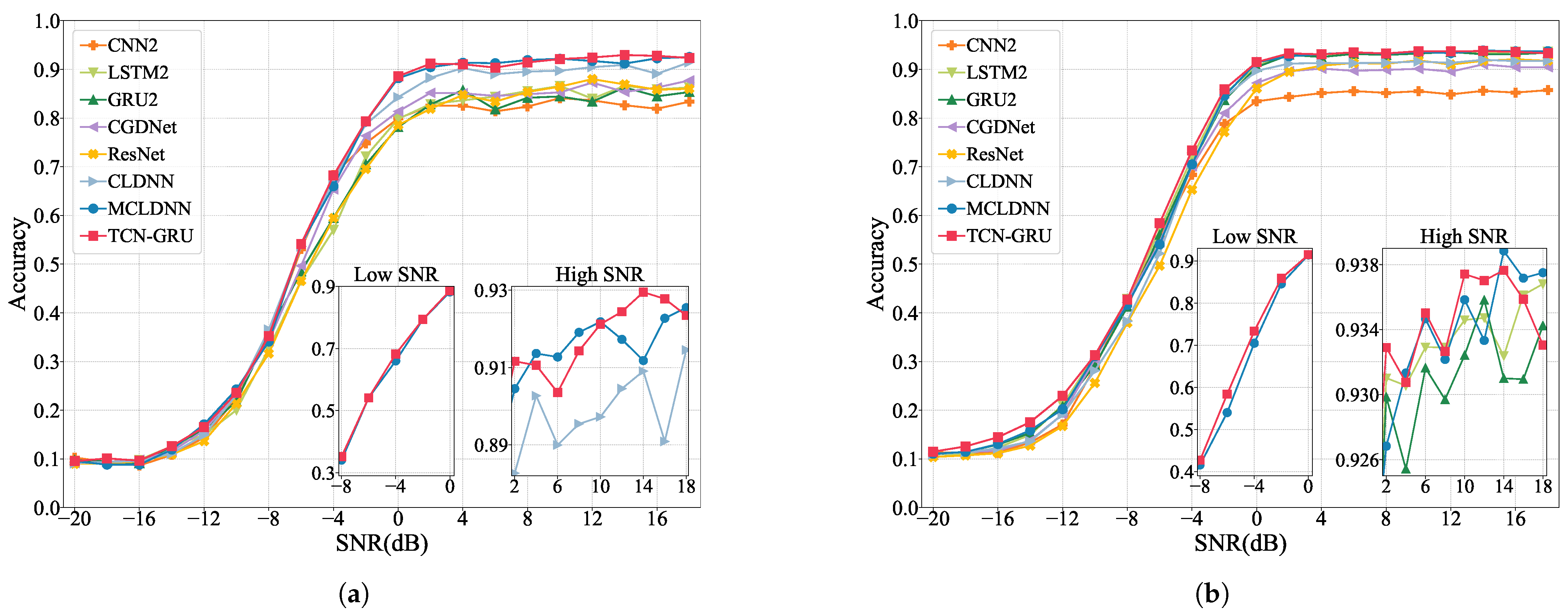
- Overall accuracy (OA) in different SNRs: We assess and compare the OA of all models across a spectrum of SNRs, measuring the model robustness in various noise powers.
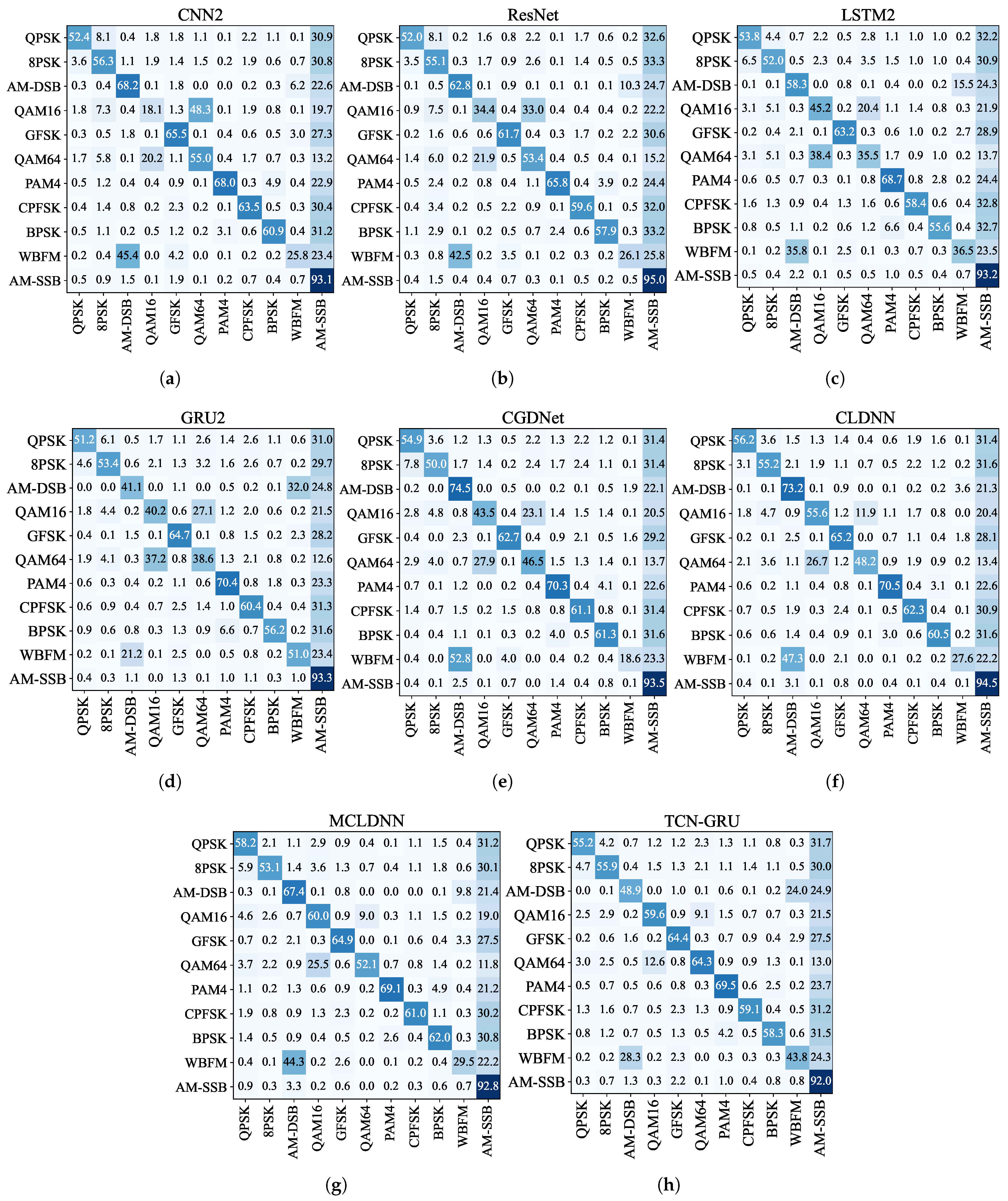
- Confusion matrices: We use confusion matrices to evaluate the model’s ability to recognize different modulated signals.
3.2.1. Comparison Between Model Performance Metrics
3.2.2. Comparison of OA with Different SNR Levels
3.2.3. Comparison of the Recognition Accuracy of Different Modulated Signals
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zhu, Z.; Nandi, A.K. Automatic Modulation Classification: Principles, Algorithms and Applications; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Zhang, Z.; Luo, H.; Wang, C.; Gan, C.; Xiang, Y. Automatic modulation classification using CNN-LSTM based dual-stream structure. IEEE Trans. Veh. Technol. 2020, 69, 13521–13531. [Google Scholar] [CrossRef]
- Peng, S.; Sun, S.; Yao, Y.D. A survey of modulation classification using deep learning: Signal representation and data preprocessing. IEEE Trans. Neural Netw. Learn. Syst. 2021, 33, 7020–7038. [Google Scholar] [CrossRef] [PubMed]
- Moser, E.; Moran, M.K.; Hillen, E.; Li, D.; Wu, Z. Automatic modulation classification via instantaneous features. In Proceedings of the 2015 National Aerospace and Electronics Conference (NAECON), Dayton, OH, USA, 15–19 June 2015; pp. 218–223. [Google Scholar]
- Simic, M.; Stanković, M.; Orlic, V.D. Automatic Modulation Classification of Real Signals in AWGN Channel Based on Sixth-Order Cumulants. Radioengineering 2021, 30, 204. [Google Scholar] [CrossRef]
- Wang, S.; Yue, J.; Lu, J.; Zheng, N.; Zhang, L.; Han, Y. Application of high-order cumulant based on the transient sequence in modulation recognition. In Proceedings of the 2023 5th International Conference on Frontiers Technology of Information and Computer (ICFTIC), Qingdao, China, 17–19 November 2023; pp. 268–273. [Google Scholar]
- Hazza, A.; Shoaib, M.; Alshebeili, S.A.; Fahad, A. An overview of feature-based methods for digital modulation classification. In Proceedings of the 2013 1st International Conference on Communications, Signal Processing, and Their Applications (ICCSPA), Sharjah, United Arab Emirates, 12–14 February 2013; pp. 1–6. [Google Scholar]
- Chen, W.; Jiang, Y.; Zhang, L.; Zhang, Y. A new modulation recognition method based on wavelet transform and high-order cumulants. J. Phys. Conf. Ser. 2021, 1738, 012025. [Google Scholar] [CrossRef]
- Mobasseri, B.G. Digital modulation classification using constellation shape. Signal Process. 2000, 80, 251–277. [Google Scholar] [CrossRef]
- Tekbıyık, K.; Akbunar, Ö.; Ekti, A.R.; Görçin, A.; Kurt, G.K. Multi–Dimensional Wireless Signal Identification Based on Support Vector Machines. IEEE Access 2019, 7, 138890–138903. [Google Scholar] [CrossRef]
- Sun, X.; Su, S.; Zuo, Z.; Guo, X.; Tan, X. Modulation Classification Using Compressed Sensing and Decision Tree–Support Vector Machine in Cognitive Radio System. Sensors 2020, 20, 1438. [Google Scholar] [CrossRef] [PubMed]
- Mao, Y.; Wang, Y.; Huang, W.; Qin, H.; Huang, D.; Guo, Y. Hidden-Markov-model-based calibration-attack recognition for continuous-variable quantum key distribution. Phys. Rev. A 2020, 101, 062320. [Google Scholar] [CrossRef]
- Ansari, S.; Alnajjar, K.A.; Abdallah, S.; Saad, M. Automatic Digital Modulation Recognition Based on Machine Learning Algorithms. In Proceedings of the 2020 International Conference on Communications, Computing, Cybersecurity, and Informatics (CCCI), Sharjah, United Arab Emirates, 3–5 November 2020; pp. 1–6. [Google Scholar]
- Wang, Y.; Wang, J.; Zhang, W.; Yang, J.; Gui, G. Deep learning-based cooperative automatic modulation classification method for MIMO systems. IEEE Trans. Veh. Technol. 2020, 69, 4575–4579. [Google Scholar] [CrossRef]
- Zhang, F.; Luo, C.; Xu, J.; Luo, Y.; Zheng, F.C. Deep learning based automatic modulation recognition: Models, datasets, and challenges. Digit. Signal Process. 2022, 129, 103650. [Google Scholar] [CrossRef]
- Szegedy, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- Graves, A.; Mohamed, A.r.; Hinton, G. Speech recognition with deep recurrent neural networks. In Proceedings of the 2013 IEEE International Conference on Acoustics, Speech and Signal Processing, Vancouver, BC, USA, 26–31 May 2013; pp. 6645–6649. [Google Scholar]
- O’Shea, T.J.; Corgan, J.; Clancy, T.C. Convolutional radio modulation recognition networks. In Proceedings of the Engineering Applications of Neural Networks: 17th International Conference, EANN 2016, Aberdeen, UK, 2–5 September 2016; Proceedings 17. Springer: Cham, Switzerland, 2016; pp. 213–226. [Google Scholar]
- Liu, X.; Yang, D.; El Gamal, A. Deep neural network architectures for modulation classification. In Proceedings of the 2017 51st Asilomar Conference on Signals, Systems, and Computers, Grove, CA, USA, 29 October–1 November 2017; pp. 915–919. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Las Vegas, NV, USA, 27–30 June 2016; pp. 770–778. [Google Scholar]
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef] [PubMed]
- Rajendran, S.; Meert, W.; Giustiniano, D.; Lenders, V.; Pollin, S. Deep learning models for wireless signal classification with distributed low-cost spectrum sensors. IEEE Trans. Cogn. Commun. Netw. 2018, 4, 433–445. [Google Scholar] [CrossRef]
- Xu, J.; Luo, C.; Parr, G.; Luo, Y. A spatiotemporal multi-channel learning framework for automatic modulation recognition. IEEE Wirel. Commun. Lett. 2020, 9, 1629–1632. [Google Scholar] [CrossRef]
- Cho, K.; Van Merriënboer, B.; Gulcehre, C.; Bahdanau, D.; Bougares, F.; Schwenk, H.; Bengio, Y. Learning phrase representations using RNN encoder-decoder for statistical machine translation. arXiv 2014, arXiv:1406.1078. [Google Scholar]
- Hong, D.; Zhang, Z.; Xu, X. Automatic modulation classification using recurrent neural networks. In Proceedings of the 2017 3rd IEEE International Conference on Computer and Communications (ICCC), Chengdu, China, 13–16 December 2017; pp. 695–700. [Google Scholar]
- West, N.E.; O’shea, T. Deep architectures for modulation recognition. In Proceedings of the 2017 IEEE International Symposium on Dynamic Spectrum Access Networks (DySPAN), Baltimore, MD, USA, 6–9 March 2017; pp. 1–6. [Google Scholar]
- Huang, G.; Liu, Z.; Van Der Maaten, L.; Weinberger, K.Q. Densely connected convolutional networks. In Proceedings of the Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 4700–4708. [Google Scholar]
- Wang, D.; Lin, M.; Zhang, X.; Huang, Y.; Zhu, Y. Automatic Modulation Classification Based on CNN-Transformer Graph Neural Network. Sensors 2023, 23, 7281. [Google Scholar] [CrossRef] [PubMed]
- O’shea, T.J.; West, N. Radio machine learning dataset generation with gnu radio. In Proceedings of the GNU Radio Conference, Boulder, CO, USA, 12–16 September 2016; Volume 1. [Google Scholar]
- Bai, S.; Kolter, J.Z.; Koltun, V. An empirical evaluation of generic convolutional and recurrent networks for sequence modeling. arXiv 2018, arXiv:1803.01271. [Google Scholar]
- Kalchbrenner, N.; Espeholt, L.; Simonyan, K.; Oord, A.v.d.; Graves, A.; Kavukcuoglu, K. Neural machine translation in linear time. arXiv 2016, arXiv:1610.10099. [Google Scholar]
- Yu, F.; Koltun, V. Multi-scale context aggregation by dilated convolutions. arXiv 2015, arXiv:1511.07122. [Google Scholar]
- Long, J.; Shelhamer, E.; Darrell, T. Fully convolutional networks for semantic segmentation. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, Boston, MA, USA, 7–12 June 2015; pp. 3431–3440. [Google Scholar]
- Kingma, D.P.; Ba, J. Adam: A method for stochastic optimization. arXiv 2014, arXiv:1412.6980. [Google Scholar]
- Njoku, J.N.; Morocho-Cayamcela, M.E.; Lim, W. CGDNet: Efficient hybrid deep learning model for robust automatic modulation recognition. IEEE Netw. Lett. 2021, 3, 47–51. [Google Scholar] [CrossRef]



| Dataset | Sample | SNR | Modulation Types |
|---|---|---|---|
| RadioML2016.10a | 220,000 | −20:2:18 dB | BPSK, QPSK, 8PSK, QAM16, QAM64, GFSK, CPFSK, PAM4, WBFM, AM-SSB, AM-DSB |
| RadioML2016.10b | 1,200,000 | −20:2:18 dB | BPSK, QPSK, 8PSK, QAM16, QAM64, GFSK, CPFSK, PAM4, WBFM, AM-DSB |
| Model | Structure |
|---|---|
| CNN2 [18] | I/Q-Input, Conv1(), Conv2(), FC1(128), FC2(N) |
| ResNet [19] | I/Q-Input, Conv1(), Conv2(), Concat(I/Q-Input, Conv3()), Conv4(), FC1(128), FC2(N) |
| LSTM2 [22] | A/P-Input, LSTM() × 2, FC(N) |
| GRU2 [25] | I/Q-Input, GRU() × 2, FC(N) |
| CGDNet [35] | I/Q-Input, Conv1(), MaxPool1(), Conv2(), MaxPool2(), Conv3(), MaxPool3(), Concat with MaxPool1, GRU(), FC1(256), FC2(N) |
| CLDNN [19] | I/Q-Input, Conv1(), Conv2(), Conv3() × 2, LSTM(), FC1(128), FC2(N) |
| MCLDNN [23] | Concat1(I-Input, Conv1(), Q-Input, Conv2()), I/Q-Input, Conv3(), Concat2(Concat1, Conv4()), Conv5(), LSTM(), FC1(128), FC2(128), Softmax(N) |
| GRU2-h64: wop | A/P-Input, GRU() × 2, FC(N) |
| GRU2-h64 | A/P-Input, GRU() × 2, GAP, FC(N) |
| TCN4: wop | A/P-Input, TCN ResBlock() × 4, FC(N) |
| TCN4 | A/P-Input, TCN ResBlock() × 4, GAP, FC(N) |
| TCN-GRU: wop | A/P-Input, TCN ResBlock() × 4, GRU() × 2, FC(N) |
| TCN-GRU | A/P-Input, TCN ResBlock() × 4, GRU() × 2, GAP, FC(N) |
| Model | Parameters | Valid Loss | Accuracy | F1-Score | Recall | Precision | Prediction Time (ms) |
|---|---|---|---|---|---|---|---|
| CNN2 | 1,592,383 | 1.1434 | 0.5698 | 0.5819 | 0.5698 | 0.6733 | 43.7356 |
| ResNet | 3,098,283 | 1.1809 | 0.5638 | 0.5861 | 0.5638 | 0.6891 | 61.7528 |
| LSTM2 | 201,099 | 1.1196 | 0.5849 | 0.6033 | 0.5849 | 0.6945 | 29.2208 |
| GRU2 | 151,179 | 1.1292 | 0.5692 | 0.5866 | 0.5692 | 0.6801 | 25.2324 |
| CGDNet | 124,933 | 1.1288 | 0.5789 | 0.5935 | 0.5789 | 0.7059 | 21.1059 |
| CLDNN | 517,643 | 1.1002 | 0.6056 | 0.6275 | 0.6056 | 0.7206 | 64.4990 |
| MCLDNN | 406,199 | 1.0824 | 0.6101 | 0.6344 | 0.6101 | 0.7321 | 128.4710 |
| GRU2-h64: wop | 38,731 | 1.1326 | 0.5708 | 0.5885 | 0.5708 | 0.6787 | 18.0023 |
| GRU2-h64 | 38,731 | 1.1074 | 0.5916 | 0.6077 | 0.5897 | 0.6834 | 17.4842 |
| TCN4: wop | 203,531 | 1.1285 | 0.5758 | 0.5945 | 0.5738 | 0.7031 | 113.3784 |
| TCN4 | 203,660 | 1.1174 | 0.5820 | 0.6034 | 0.5820 | 0.7018 | 116.3363 |
| TCN-GRU: wop | 253,451 | 1.0914 | 0.6143 | 0.6278 | 0.6085 | 0.7199 | 132.2325 |
| TCN-GRU | 253,451 | 1.0797 | 0.6156 | 0.6389 | 0.6156 | 0.7400 | 136.1084 |
| Model | Parameters | Valid Loss | Accuracy | F1-Score | Recall | Precision | Prediction Time (ms) |
|---|---|---|---|---|---|---|---|
| CNN2 | 1,592,126 | 0.9781 | 0.5944 | 0.5930 | 0.5944 | 0.6402 | 229.6624 |
| ResNet | 3,098,154 | 0.9631 | 0.6123 | 0.6259 | 0.6123 | 0.7001 | 325.3973 |
| LSTM2 | 200,970 | 0.8818 | 0.6442 | 0.6448 | 0.6442 | 0.6900 | 148.6904 |
| GRU2 | 151,050 | 0.8965 | 0.6393 | 0.6439 | 0.6393 | 0.7096 | 130.3700 |
| CGDNet | 124,676 | 0.9386 | 0.6217 | 0.6255 | 0.6217 | 0.6785 | 114.5280 |
| CLDNN | 517,514 | 0.9366 | 0.6269 | 0.6306 | 0.6269 | 0.7014 | 346.8208 |
| MCLDNN | 406,070 | 0.8864 | 0.6462 | 0.6444 | 0.6462 | 0.6761 | 705.3022 |
| GRU2-h64: wop | 38,666 | 0.8985 | 0.6402 | 0.6403 | 0.6386 | 0.6913 | 103.8465 |
| GRU2-h64 | 38,666 | 0.8936 | 0.6398 | 0.6447 | 0.6392 | 0.7172 | 106.9712 |
| TCN4: wop | 203,595 | 0.9239 | 0.6273 | 0.6282 | 0.6268 | 0.6801 | 630.0027 |
| TCN4 | 203,466 | 0.8842 | 0.6431 | 0.6477 | 0.6431 | 0.7066 | 635.1041 |
| TCN-GRU: wop | 253,386 | 0.8824 | 0.6445 | 0.6531 | 0.6439 | 0.7254 | 732.0409 |
| TCN-GRU | 253,386 | 0.8755 | 0.6466 | 0.6591 | 0.6466 | 0.7536 | 743.2286 |
| Model | QPSK | 8PSK | AM-DSB | WBFM | QAM16 | QAM64 | PAM4 | CPFSK | BPSK | GFSK | AM-SSB |
|---|---|---|---|---|---|---|---|---|---|---|---|
| CNN2 | 0.785 | 0.818 | 0.903 | 0.379 | 0.456 | 0.886 | 0.960 | 0.862 | 0.872 | 0.859 | 0.937 |
| ResNet | 0.796 | 0.822 | 0.942 | 0.457 | 0.592 | 0.770 | 0.971 | 0.926 | 0.924 | 0.960 | 0.950 |
| LSTM2 | 0.803 | 0.761 | 0.801 | 0.518 | 0.692 | 0.464 | 0.971 | 0.874 | 0.850 | 0.906 | 0.950 |
| GRU2 | 0.793 | 0.789 | 0.702 | 0.588 | 0.625 | 0.497 | 0.968 | 0.889 | 0.864 | 0.923 | 0.943 |
| CGDNet | 0.801 | 0.737 | 0.967 | 0.276 | 0.639 | 0.613 | 0.959 | 0.880 | 0.871 | 0.905 | 0.951 |
| CLDNN | 0.801 | 0.800 | 0.936 | 0.371 | 0.742 | 0.641 | 0.956 | 0.882 | 0.857 | 0.920 | 0.940 |
| MCLDNN | 0.851 | 0.786 | 0.896 | 0.436 | 0.856 | 0.744 | 0.976 | 0.883 | 0.901 | 0.941 | 0.936 |
| TCN-GRU | 0.859 | 0.828 | 0.718 | 0.617 | 0.877 | 0.901 | 0.979 | 0.879 | 0.884 | 0.924 | 0.932 |
| Model | QPSK | 8PSK | AM-DSB | WBFM | QAM16 | QAM64 | PAM4 | CPFSK | BPSK | GFSK |
|---|---|---|---|---|---|---|---|---|---|---|
| CNN2 | 0.817 | 0.866 | 0.972 | 0.362 | 0.553 | 0.710 | 0.969 | 0.929 | 0.894 | 0.947 |
| ResNet | 0.790 | 0.921 | 0.950 | 0.375 | 0.775 | 0.884 | 0.960 | 0.904 | 0.893 | 0.945 |
| LSTM2 | 0.839 | 0.823 | 0.944 | 0.413 | 0.864 | 0.960 | 0.974 | 0.933 | 0.882 | 0.946 |
| GRU2 | 0.858 | 0.789 | 0.958 | 0.388 | 0.881 | 0.936 | 0.973 | 0.931 | 0.885 | 0.943 |
| CGDNet | 0.798 | 0.818 | 0.953 | 0.371 | 0.789 | 0.774 | 0.971 | 0.923 | 0.892 | 0.927 |
| CLDNN | 0.809 | 0.822 | 0.949 | 0.354 | 0.835 | 0.810 | 0.957 | 0.915 | 0.885 | 0.937 |
| MCLDNN | 0.798 | 0.834 | 0.952 | 0.377 | 0.890 | 0.951 | 0.973 | 0.910 | 0.875 | 0.944 |
| TCN-GRU | 0.881 | 0.798 | 0.893 | 0.452 | 0.893 | 0.962 | 0.975 | 0.927 | 0.888 | 0.952 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, Z.; Zhang, W.; Zhao, Z.; Tang, P.; Zhang, Z. Robust Automatic Modulation Classification via a Lightweight Temporal Hybrid Neural Network. Sensors 2024, 24, 7908. https://doi.org/10.3390/s24247908
Wang Z, Zhang W, Zhao Z, Tang P, Zhang Z. Robust Automatic Modulation Classification via a Lightweight Temporal Hybrid Neural Network. Sensors. 2024; 24(24):7908. https://doi.org/10.3390/s24247908
Chicago/Turabian StyleWang, Zhao, Weixiong Zhang, Zhitao Zhao, Ping Tang, and Zheng Zhang. 2024. "Robust Automatic Modulation Classification via a Lightweight Temporal Hybrid Neural Network" Sensors 24, no. 24: 7908. https://doi.org/10.3390/s24247908
APA StyleWang, Z., Zhang, W., Zhao, Z., Tang, P., & Zhang, Z. (2024). Robust Automatic Modulation Classification via a Lightweight Temporal Hybrid Neural Network. Sensors, 24(24), 7908. https://doi.org/10.3390/s24247908







