An Improved STC-Based Full Coverage Path Planning Algorithm for Cleaning Tasks in Large-Scale Unstructured Social Environments
Abstract
1. Introduction
2. Related Works
3. Methodology
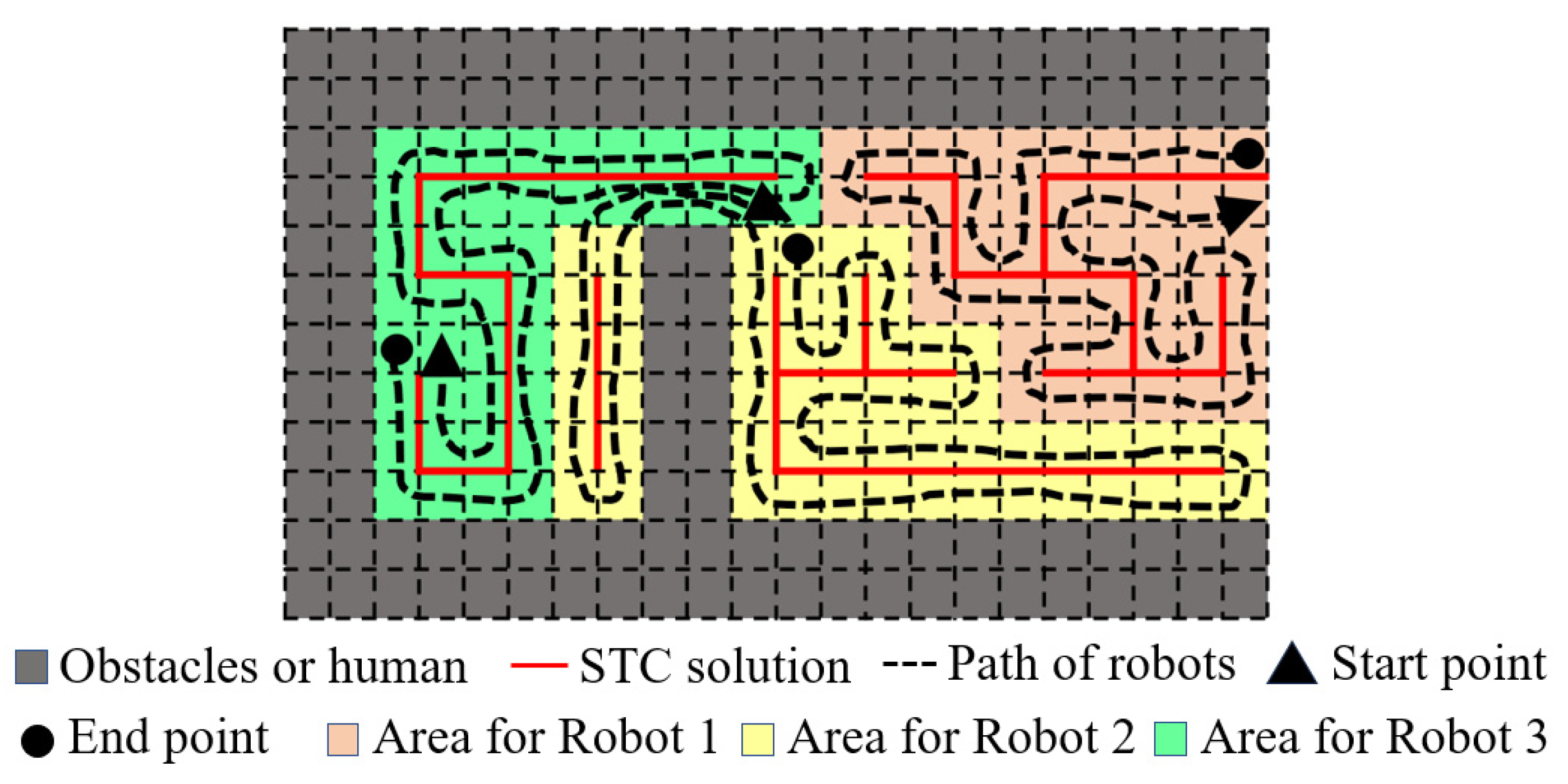
3.1. Problem Description
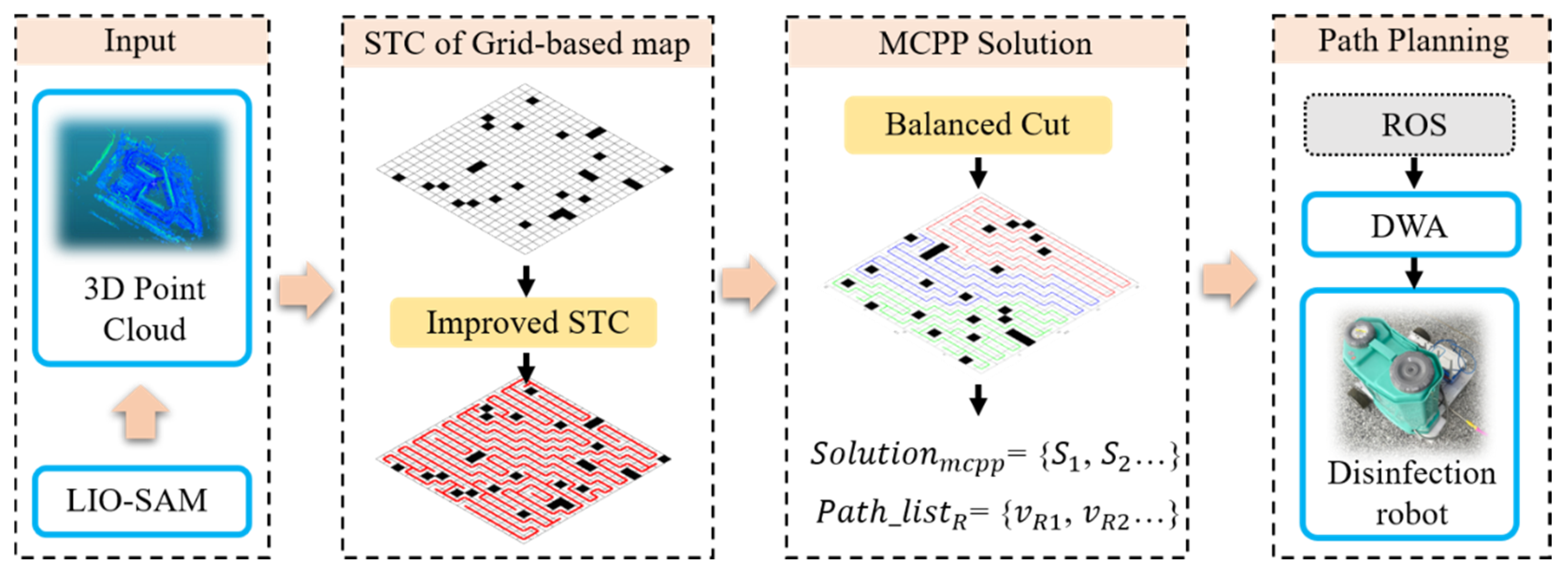
3.2. Proposed Solution Framework
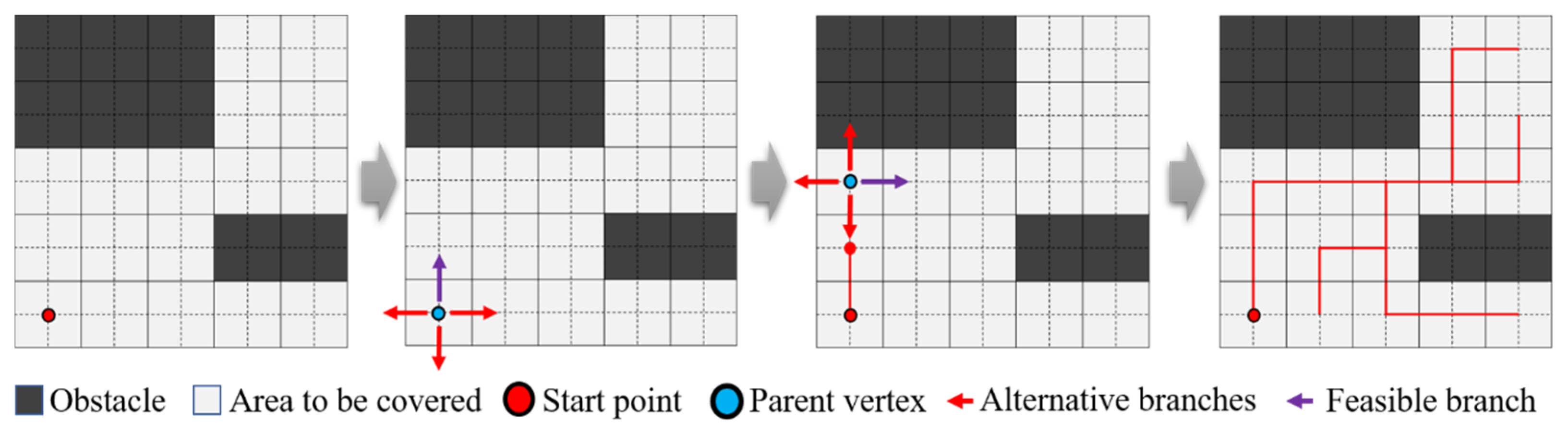
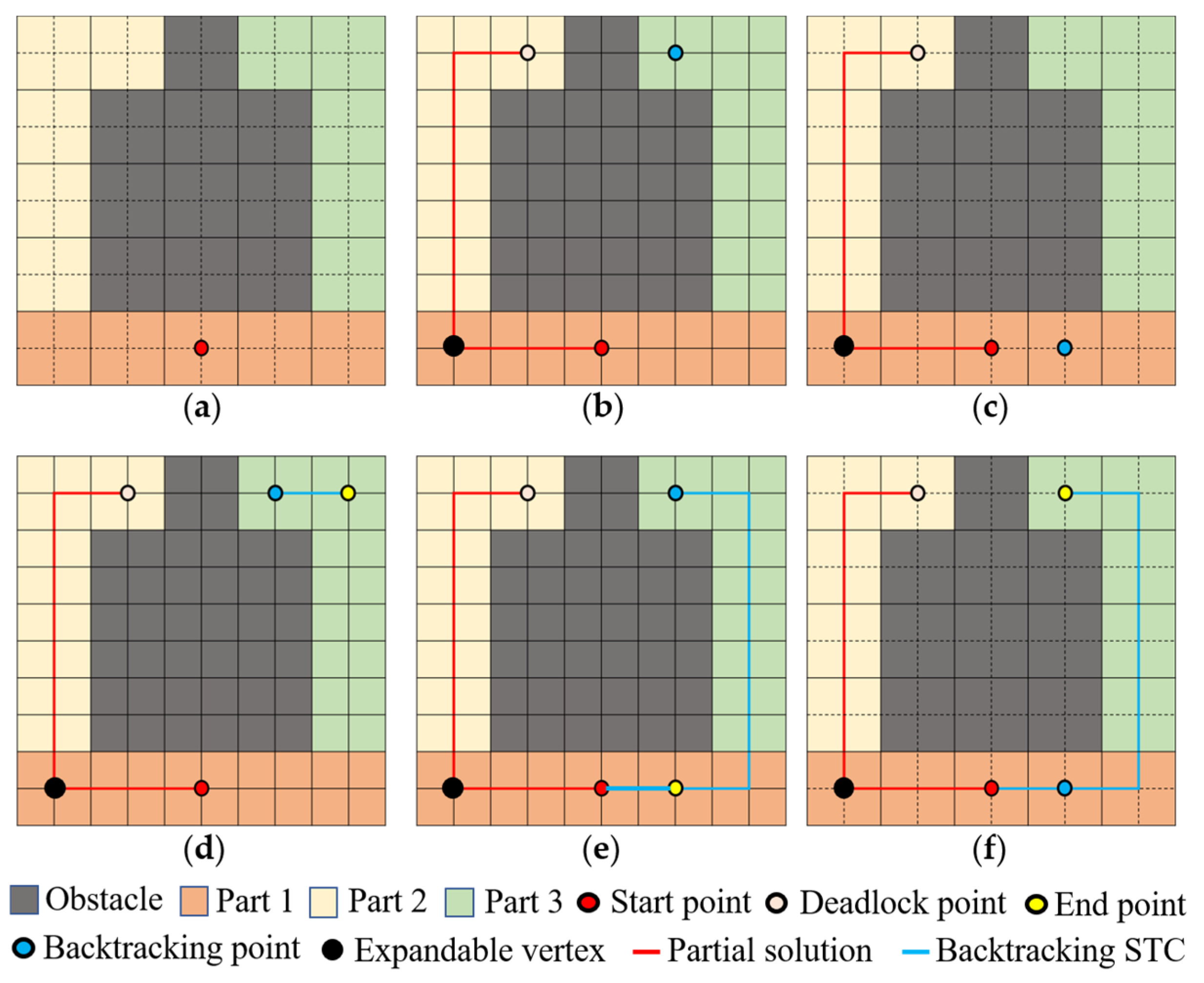
3.3. Improved STC Based on Optimized Backtracking Module
| Algorithm 1 Improved SCAN-STC to Cover the Area | ||||||||
| Input: Grid-based map Output: | ||||||||
| (UNOCCUPIED); | ||||||||
| ; | //Four points surrounding the current point | |||||||
| ; | //Initialize the superior backtracking list. | |||||||
| 1: | ; | //Load boundary points into the backtracking list. | ||||||
| 2: | For | |||||||
| 3: | ; | |||||||
| 4: | If is an obstacle or boundary | |||||||
| 5: | ; | |||||||
| 6: | For | |||||||
| 7: | If | |||||||
| 8: | If has not exceeded the boundary | |||||||
| 9: | Add the point to the end of the superior backtracking list; | |||||||
| 10: | End | |||||||
| 11: | End | |||||||
| 12: | End | |||||||
| 13: | End | |||||||
| 14: | End | |||||||
| 15: | to be covered as h; | |||||||
| 16: | ; | |||||||
| 17: | ; | |||||||
| 18: | ; | |||||||
| 19: | ; | |||||||
| 20: | While | |||||||
| 21: | ; | |||||||
| 22: | 0; | |||||||
| 23: | If UNOCCUPIED then | |||||||
| 24: | as parent vertex; | |||||||
| 25: | If | |||||||
| 26: | ; | |||||||
| 27: | ; | |||||||
| 28: | end | |||||||
| 29: | Else if UNOCCUPIED then | |||||||
| 30: | as parent vertex; | |||||||
| 31: | If | |||||||
| 32: | ; | |||||||
| 33: | ; | |||||||
| 34: | end | |||||||
| 35: | else if UNOCCUPIED then | |||||||
| 36: | as parent vertex; | |||||||
| 37: | If | |||||||
| 38: | ; | |||||||
| 39: | ; | |||||||
| 40: | end | |||||||
| 41: | else if UNOCCUPIED then | |||||||
| 42: | as parent vertex; | |||||||
| 43: | If | |||||||
| 44: | ; | |||||||
| 45: | ; | |||||||
| 46: | end | |||||||
| 47: | else | |||||||
| 48: | is the deadlock point; | |||||||
| 49: | end if | |||||||
| 50: | ; | |||||||
| 51: | ; | |||||||
| 52: | ; | |||||||
| 53: | ; | |||||||
| 54: | ; | |||||||
| 55: | End | |||||||
| 56: | ||||||||
| 57: | Return | |||||||
3.4. Balanced Cut of the Explicit Coverage Path for STC
| Algorithm 2 Balanced cut of the explicit coverage path | ||||||
| Input: Output: …} | ||||||
| (UNOCCUPIED); | ||||||
| ; | //Corresponding to the original grid map | |||||
| ; | //Corresponding to the STC sulotion | |||||
| ; | //Matrix containing virtual obstacles | |||||
| ; | //Four points surrounding the current point | |||||
| 1: | ; | //Vector matrix of each branch of the STC | ||||
| 2: | ; | |||||
| 3: | ; | |||||
| 4: | ; | |||||
| 5: | ; | |||||
| 6: | ; | |||||
| 7: | (UNOCCUPIED); | |||||
| 8: | ; | |||||
| 9: | For | |||||
| 10: | ; | |||||
| 11: | For | |||||
| 12: | If at a point or line segment | |||||
| 13: | Remove from ; | |||||
| 14: | End | |||||
| 15: | End | |||||
| 16: | End | |||||
| 17: | ; | |||||
| 18: | For | |||||
| 19: | For | |||||
| 20: | If at a point or line segment | |||||
| 21: | ; | |||||
| 22: | End | |||||
| 23: | End | |||||
| 24: | End | |||||
| 25: | ; | |||||
| 26: | ; | |||||
| 27: | ; | |||||
| 28: | While | |||||
| 29: | ; | |||||
| 30: | 0; | |||||
| 31: | If then | |||||
| 32: | If | |||||
| 33: | ; | |||||
| 34: | ; | |||||
| 35: | end | |||||
| 36: | Else if then | |||||
| 37: | If | |||||
| 38: | ; | |||||
| 39: | ; | |||||
| 40: | end | |||||
| 41: | else if then | |||||
| 42: | If | |||||
| 43: | ; | |||||
| 44: | ; | |||||
| 45: | end | |||||
| 46: | else if then | |||||
| 47: | If | |||||
| 48: | ; | |||||
| 49: | ; | |||||
| 50: | end | |||||
| 51: | else | |||||
| 52: | is the end point of the path; | |||||
| 53: | end if | |||||
| 54: | ; | |||||
| 55: | ; | |||||
| 56: | End | |||||
| 57: | ; | |||||
| 58: | ; | |||||
| 59: | ; | |||||
| 60: | ; | |||||
| 61: | For | |||||
| 62: | For | |||||
| 63: | If at matching positions | |||||
| 64: | ; | |||||
| 65: | End | |||||
| 66: | End | |||||
| 67: | End | |||||
| 68: | ; | |||||
| 69: | ; | |||||
| 70: | ||||||
| 71: | …}; | |||||
| 72: | Return …} | |||||
3.5. ROS Based Framework for MCPP
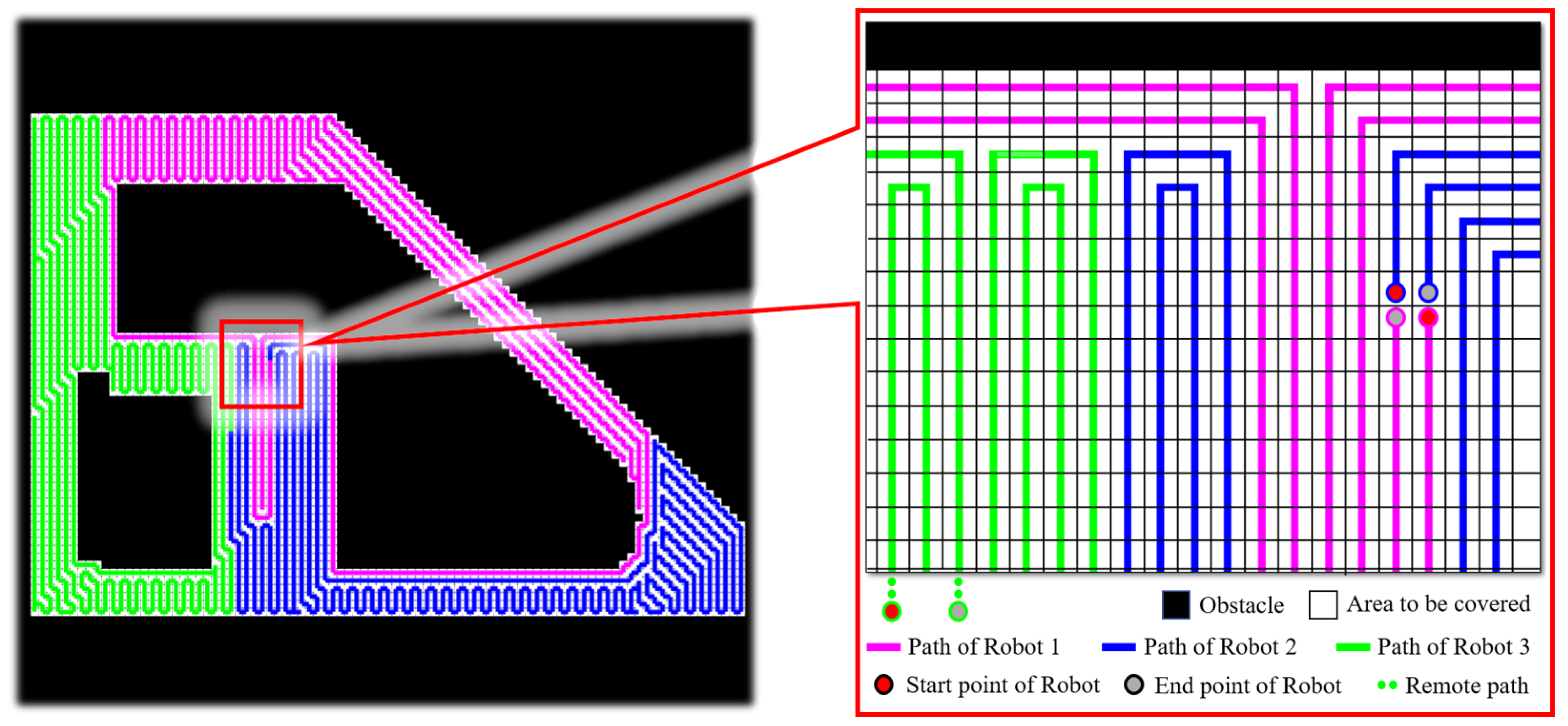
4. Experiment and Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Chen, Y.; Luo, Y.; Ozkan Yerebakan, M.; Hu, B. Human Acceptance of the Cleaning Robot in Grocery Environments During the COVID-19 Pandemic. In Proceedings of the Human Factors and Ergonomics Society Annual Meeting; SAGE Publications: Los Angeles, CA, USA, 2022; Volume 66, pp. 177–181. [Google Scholar]
- Mavrogiannis, C.; Baldini, F.; Wang, A.; Zhao, D.; Trautman, P.; Steinfeld, A.; Oh, J. Core challenges of social robot navigation: A survey. ACM Trans. Hum.-Robot. Interact. 2023, 12, 1–39. [Google Scholar] [CrossRef]
- Aldinhas Ferreira, M.I.; Sequeira, J.S. Robots in Ageing Societies. In A World with Robots. Intelligent Systems, Control and Automation: Science and Engineering; Aldinhas Ferreira, M., Silva Sequeira, J., Tokhi, M., E. Kadar, E., Virk, G., Eds.; Springer: Cham, Switzerland, 2017; Volume 84. [Google Scholar] [CrossRef]
- Garcia-Haro, J.M.; Oña, E.D.; Hernandez-Vicen, J.; Martinez, S.; Balaguer, C. Service robots in catering applications: A review and future challenges. Electronics 2020, 10, 47. [Google Scholar] [CrossRef]
- Shin, H.; Kang, J. Reducing perceived health risk to attract hotel customers in the COVID-19 pandemic era: Focused on technology innovation for social distancing and cleanliness. Int. J. Hosp. Manag. 2020, 91, 102664. [Google Scholar] [CrossRef]
- Dogru, S.; Marques, L. ECO-CPP: Energy constrained online coverage path planning. Robot. Auton. Syst. 2022, 157, 104242. [Google Scholar] [CrossRef]
- Bradner, K.M. Path Planning for Variable Scrutiny Multi-Robot Coverage. Master’s Thesis, Case Western Reserve University, Cleveland, OH, USA, 2020. [Google Scholar]
- Tang, J.; Ma, H. Mixed Integer Programming for Time-Optimal Multi-Robot Coverage Path Planning with Heuristics. IEEE Robot. Autom. Lett. 2023, 8, 6491–6498. [Google Scholar] [CrossRef]
- Lin, Q. Design Characteristics of Culturally-Themed Luxury Hotel Lobbies in Las Vegas: Perceptual, Sensorial, and Emotional Impacts of Fantasy Environments. Master’s Thesis, Iowa State University, Ames, IA, USA, 2020. [Google Scholar]
- Liu, L.; Wang, X.; Yang, X.; Liu, H.; Li, J.; Wang, P. Path planning techniques for mobile robots: Review and prospect. Expert Syst. Appl. 2023, 227, 120254. [Google Scholar] [CrossRef]
- Wang, N.; Yang, X.; Wang, T.; Xiao, J.; Zhang, M.; Wang, H.; Li, H. Collaborative path planning and task allocation for multiple agricultural machines. Comput. Electron. Agric. 2023, 213, 108218. [Google Scholar] [CrossRef]
- Abdulsaheb, J.A.; Kadhim, D.J. Classical and heuristic approaches for mobile robot path planning: A survey. Robotics 2023, 12, 93. [Google Scholar] [CrossRef]
- Tonola, C.; Faroni, M.; Pedrocchi, N.; Beschi, M. Anytime informed path re-planning and optimization for human-robot collaboration. In Proceedings of the 2021 30th IEEE International Conference on Robot & Human Interactive Communication (RO-MAN), Vancouver, BC, Canada, 8–12 August 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 997–1002. [Google Scholar]
- Pedergnana, A.; Calandra, I.; Bob, K.; Gneisinger, W.; Paixao, E.; Schunk, L.; Hildebrandt, A.; Marreiros, J. Evaluating the microscopic effect of brushing stone tools as a cleaning procedure. Quat. Int. 2020, 569, 263–276. [Google Scholar] [CrossRef]
- Karwowski, J.; Szynkiewicz, W. Quantitative metrics for benchmarking human-aware robot navigation. IEEE Access 2023, 11, 79941–79953. [Google Scholar] [CrossRef]
- Kumar, K.; Kumar, N. Region coverage-aware path planning for unmanned aerial vehicles: A systematic review. Phys. Commun. 2023, 59, 102073. [Google Scholar] [CrossRef]
- Glorieux, E.; Franciosa, P.; Ceglarek, D. Coverage path planning with targetted viewpoint sampling for robotic free-form surface inspection. Robot. Comput. Integr. Manuf. 2020, 61, 101843. [Google Scholar] [CrossRef]
- Prassler, E.; Munich, M.E.; Pirjanian, P.; Kosuge, K. Domestic robotics. In Springer Handbook of Robotics; Springer: Berlin/Heidelberg, Germany, 2016; pp. 1729–1758. [Google Scholar]
- Gabriely, Y.; Rimon, E. Spanning-tree based coverage of continuous areas by a mobile robot. Ann. Math. Artif. Intell. 2001, 31, 77–98. [Google Scholar] [CrossRef]
- Viet, H.H.; Dang, V.H.; Laskar, M.N.; Chung, T. BA*: An online complete coverage algorithm for cleaning robots. Appl. Intell. 2013, 39, 217–235. [Google Scholar] [CrossRef]
- Acar, E.U.; Choset, H. Sensor-based coverage of unknown environments: Incremental construction of morse decompositions. Int. J. Robot. Res. 2002, 21, 345–366. [Google Scholar] [CrossRef]
- Liu, H.; Dong, W.; Zhang, Z.; Wang, C.; Li, R.; Gao, Y. Optimization-based local planner for a nonholonomic autonomous mobile robot in semi-structured environments. Robot. Auton. Syst. 2024, 171, 104565. [Google Scholar] [CrossRef]
- Zhang, B.; Liu, Y.; Lu, Q.; Wang, J. A path planning strategy for searching the most reliable path in uncertain environments. Int. J. Adv. Robot. Syst. 2016, 13, 1729881416657751. [Google Scholar] [CrossRef]
- Tolstaya, E.; Paulos, J.; Kumar, V.; Ribeiro, A. Multi-robot coverage and exploration using spatial graph neural networks. In Proceedings of the 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS), Prague, Czech Republic, 27 Setember–1 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 8944–8950. [Google Scholar]
- Amorim, D.; Ventura, R. A physics-based optimization approach for path planning on rough terrains. In Proceedings of the 2015 12th International Conference on Informatics in Control, Automation and Robotics (ICINCO), Colmar, France, 21–23 July 2015; IEEE: Piscataway, NJ, USA, 2015; Volume 2, pp. 259–266. [Google Scholar]
- Zhong, Y.; Shirinzadeh, B.; Yuan, X. Optimal robot path planning with cellular neural network. Int. J. Intell. Mechatron. Robot. (IJIMR) 2011, 1, 20–39. [Google Scholar] [CrossRef]
- Zhou, Q.; Gao, S.; Qu, B.; Gao, X.; Zhong, Y. Crossover recombination-based global-best brain storm optimization algorithm for uav path planning. Proc. Rom. Acad. Ser. A-Math. Phys. Tech. Sci. Inf. Sci. 2022, 23, 207–216. [Google Scholar]
- Bahwini, T.; Zhong, Y.; Gu, C. Path planning in the presence of soft tissue deformation. Int. J. Interact. Des. Manuf. (IJIDeM) 2019, 13, 1603–1616. [Google Scholar] [CrossRef]
- Hills, J.; Zhong, Y. Cellular neural network-based thermal modelling for real-time robotic path planning. Int. J. Agil. Syst. Manag. 20 2014, 7, 261–281. [Google Scholar] [CrossRef]
- Zhong, Y.; Shirinzadeh, B.; Tian, Y. A new neural network for robot path planning. In Proceedings of the2008 IEEE/ASME International Conference on Advanced Intelligent Mechatronics, Xi’an, China, 2–5 July 2008; IEEE: Piscataway, NJ, USA, 2008; pp. 1361–1366. [Google Scholar]
- Choset, H.; Pignon, P. Coverage path planning: The boustrophedon cellular decomposition. In Field and Service Robotics; Springer: London, UK, 1998; pp. 203–209. [Google Scholar]
- Zhang, B.; Hong, T.; Xiong, R.; Chepinskiy, S.A. A terrain segmentation method based on pyramid scene parsing-mobile network for outdoor robots. Int. J. Adv. Robot. Syst. 2021, 18, 17298814211048633. [Google Scholar] [CrossRef]
- Tang, J.; Sun, C.; Zhang, X. MSTC∗: Multi-robot coverage path planning under physical constrain. In Proceedings of the 2021 IEEE International Conference on Robotics and Automation (ICRA), Xi’an, China, 30 May 2021–5 June 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 2518–2524. [Google Scholar]
- Lu, J.; Zeng, B.; Tang, J.; Lam, T.L. Tmstc*: A turn-minimizing algorithm for multi-robot coverage path planning. arXiv 2022, arXiv:2212.02231. [Google Scholar] [CrossRef]
- Yang, Y.; He, D.; Mao, H.; Chen, H.; Wu, H.; Liu, Z.W. RP-MSTC*: Multi-Agent Coverage Path Planning Algorithm Emphasizing Local Area Updates. In Proceedings of the 2023 International Conference on Neuromorphic Computing (ICNC), Wuhan, China, 15–17 December 2023; IEEE: Piscataway, NJ, USA, 2023; pp. 532–537. [Google Scholar]
- Vandermeulen, I.; Groß, R.; Kolling, A. Turn-minimizing multirobot coverage. In Proceedings of the 2019 International Conference on Robotics and Automation (ICRA), Montreal, QC, Canada, 20–24 May 2018; IEEE: Piscataway, NJ, USA, 2019; pp. 1014–1020. [Google Scholar]
- Nair, V.G.; Guruprasad, K.R. Geodesic-VPC: Spatial partitioning for multi-robot coverage problem. Int. J. Robot. Autom. 2020, 33, 189–198. [Google Scholar] [CrossRef]
- Gabriely, Y.; Rimon, E. Spiral-STC: An on-line coverage algorithm of grid environments by a mobile robot. In Proceedings of the 2002 IEEE International Conference on Robotics and Automation (Cat. No. 02CH37292), Washington, DC, USA, 11–15 May 2022; IEEE: Piscataway, NJ, USA, 2002; Volume 1, pp. 954–960. [Google Scholar]
- Guruprasad, K.R. X-stc: An extended spanning tree-based coverage algorithm for mobile robots. In Proceedings of the 2019 4th International Conference on Advances in Robotics, Chennai, India, 2–6 July 2019; pp. 1–6. [Google Scholar]
- Gao, G.Q.; Xin, B. A-STC: Auction-based spanning tree coverage algorithm for motion planning of cooperative robots. Front. Inf. Technol. Electron. Eng. 2019, 20, 18–31. [Google Scholar] [CrossRef]
- Tang, J.; Ma, H. Large-Scale Multi-Robot Coverage Path Planning via Local Search. Proc. AAAI Conf. Artif. Intell. 2024, 38, 17567–17574. [Google Scholar] [CrossRef]
- Gabriely, Y.; Rimon, E. Competitive on-line coverage of grid environments by a mobile robot. Comput. Geom. 2003, 24, 197–224. [Google Scholar] [CrossRef]
- Thiayagarajan, K.; Balaji, C.G. Traversal algorithm for complete coverage. J. Comput. Sci. 2012, 8, 2032. [Google Scholar] [CrossRef]
- Hazem, Z.B.; Ince, R.; Dilibal, S. Joint Control Implementation of 4-DOF Robotic Arm Using Robot Operating System. In Proceedings of the 2022 International Conference on Theoretical and Applied Computer Science and Engineering (ICTASCE), Ankara, Turkey, 29 September–1 October 2022; Available online: https://ieeexplore.ieee.org/abstract/document/10009733 (accessed on 16 November 2024).
- Available online: https://en.wikipedia.org/wiki/Universal_Studios_Beijing (accessed on 18 November 2024).
- Tan, C.S.; Mohd-Mokhtar, R.; Arshad, M.R. A comprehensive review of coverage path planning in robotics using classical and heuristic algorithms. IEEE Access 2021, 9, 119310–119342. [Google Scholar] [CrossRef]
- Kapoutsis, A.C.; Chatzichristofis, S.A.; Kosmatopoulos, E.B. DARP: Divide Areas Algorithm for Optimal Multi-Robot Coverage Path Planning. J. Intell. Robot Syst. 2017, 86, 663–680. [Google Scholar] [CrossRef]
- Guastella, D.C.; Cantelli, L.; Giammello, G.; Melita, C.D.; Spatino, G.; Muscato, G. Complete coverage path planning for aerial vehicle flocks deployed in outdoor environments. Comput. Electr. Eng. 2019, 75, 189–201. [Google Scholar] [CrossRef]
- Chen, G.; Shen, Y.; Zhang, Y.; Zhang, W.; Wang, D.; He, B. 2D multi-area coverage path planning using L-SHADE in simulated ocean survey. Appl. Soft Comput. 2021, 112, 107754. [Google Scholar] [CrossRef]







| Parameters | Settings |
|---|---|
| r | Set of robots’ labels for CPP task, indexed by r |
| R | Set of robot number for CPP task |
| The number of iterations in the algorithm for STC | |
| The area that robot number 1 needs to cover | |
| The area that all robots in the system need to cover | |
| The grid-map corresponding to the CPP problem | |
| Points on the coverage path of robot numbered r | |
| Total workload of robot numbered r | |
| Maximum threshold of the intersection of the covered areas | |
| The difference between obtained solution and optimal solution | |
| C | denotes matrix numbered as 1 |
| The width of the environment under study | |
| The length of the environment under study | |
| The number of cells occupied by obstacles in grid map | |
| The real-time STC solution queue | |
| The real-time updated superior backtracking point list | |
| The obstacle-adjacent point list | |
| The cells list which around the vertex | |
| The current point used in the loop instruction of the algorithm | |
| The Adjacent point used in the instructions of the algorithm | |
| One end of the vector or line segment | |
| Virtual grid map required for balance cut Algorithm | |
| The STC solution map for Algorithm | |
| Matrix corresponding to the original grid map | |
| Matrix corresponding to the STC grid map | |
| Vector matrix of each branch of the STC solution | |
| The points with STC solution explicitization path | |
| The coverage path assigned to the robot, indexed by r | |
| Global Navigation Path Error Value | |
| Local Planning Path Error Value | |
| Permissible Error for Global Navigation Planning | |
| Permissible Error for Local Navigation Planning | |
| Global Target Point coordinate value in the X Direction | |
| Global Target Point coordinate value in the Y Direction | |
| X Coordinate Value of the Robot in Global Coordinates | |
| Y Coordinate Value of the Robot in Global Coordinates | |
| Total grid number to be covered for comparison | |
| Solution time of the relatively advanced STC method | |
| Solution time of our STC method | |
| The solution time reduction percentage |
| Size of Case | (s) | (s) | (%) | Size of Case | (s) | (s) | (%) | ||
|---|---|---|---|---|---|---|---|---|---|
| 40 × 40 | 1500 | 1.1186 | 0.2216 | 80.19 | 200 × 200 | 23,764 | 772.9788 | 209.1804 | 72.94 |
| 1508 | 1.1669 | 0.2372 | 79.67 | 24,176 | 597.5242 | 241.9513 | 59.51 | ||
| 1532 | 1.3108 | 0.3088 | 76.44 | 23,848 | 504.8885 | 214.2867 | 57.56 | ||
| 1536 | 1.2728 | 0.2697 | 78.81 | 22,628 | 646.2358 | 239.2903 | 62.97 | ||
| 1524 | 1.3639 | 0.2390 | 82.47 | 24,828 | 759.1654 | 203.2268 | 73.23 | ||
| 80 × 80 | 6056 | 8.2671 | 2.2079 | 73.29 | 250 × 250 | 38,972 | 2020.1102 | 680.0454 | 66.34 |
| 6120 | 5.3840 | 1.5339 | 71.51 | 37,360 | 1570.5011 | 656.2255 | 58.18 | ||
| 6104 | 6.3608 | 2.0117 | 68.37 | 37,180 | 1691.3564 | 746.5494 | 55.86 | ||
| 6104 | 5.6826 | 1.7120 | 69.87 | 38,448 | 1433.5215 | 598.2217 | 58.27 | ||
| 6104 | 6.5864 | 2.2201 | 66.29 | 39,012 | 1717.2946 | 741.4400 | 56.84 | ||
| 120 × 120 | 13,632 | 29.6055 | 12.7036 | 57.09 | 350 × 350 | 75,428 | 3103.9135 | 1623.3156 | 47.69 |
| 13,712 | 20.1042 | 7.0489 | 64.94 | 72,072 | 4022.1956 | 1693.3251 | 57.91 | ||
| 13,736 | 29.3870 | 12.2862 | 58.19 | 76,792 | 3552.5219 | 1680.9143 | 52.70 | ||
| 13,684 | 22.0293 | 8.8440 | 59.85 | 76,156 | 4498.8956 | 1708.1125 | 62.03 | ||
| 13,668 | 25.0810 | 8.9820 | 64.18 | 73,840 | 3049.8012 | 1417.4019 | 53.55 | ||
| 160 × 160 | 24,252 | 87.2286 | 34.9469 | 59.93 | 400 × 400 | 97,760 | 15,051.1254 | 4435.7156 | 70.53 |
| 24,340 | 86.7675 | 32.2355 | 62.84 | 96,436 | 14,480.5340 | 4740.9543 | 67.26 | ||
| 24,440 | 77.7163 | 33.8955 | 56.38 | 97,724 | 14,406.0011 | 4376.3659 | 69.62 | ||
| 24,276 | 74.8750 | 28.2694 | 59.84 | 97,576 | 9805.2450 | 4612.1524 | 52.96 | ||
| 24,404 | 75.9683 | 34.1139 | 55.09 | 98,168 | 9842.7152 | 4616.5214 | 53.11 |
| Case Label | Quantitative Comparison Items | RW | DFS | DARP | Ours |
|---|---|---|---|---|---|
| 1 | Coverage rate | 90.62% | 93.98% | 100% | 100% |
| Secondary coverage | 315.21% | 17.18% | 0% | 0% | |
| Total path length | 6283 | 1774 | 1514 | 1514 | |
| Update frequency | 8.33 Hz | 5.52 Hz | 0.03 Hz | 0.40 Hz | |
| 2 | Coverage rate | 92.49% | 92.45% | 100% | 100% |
| Secondary coverage | 152.21% | 21.51% | 0% | 0% | |
| Total path length | 0.09 s | 1859 | 1530 | 1530 | |
| Update frequency | 11.11 Hz | 4.21 Hz | 0.05 Hz | 0.53 Hz | |
| 3 | Coverage rate | 91.11% | 91.12% | 100% | 100% |
| Secondary coverage | 255.21% | 32.48% | 0% | 0% | |
| Total path length | 5630 | 2093 | 1586 | 1586 | |
| Update frequency | 11.11 Hz | 5.15 Hz | 0.19 Hz | 0.42 Hz | |
| 4 | Coverage rate | 93.10% | 94.49% | 100% | 100% |
| Secondary coverage | 145.21% | 42.12% | 0% | 0% | |
| Total path length | 3848 | 2230 | 1571 | 1571 | |
| Update frequency | 10.00 Hz | 2.18 Hz | 0.14 Hz | 0.52 Hz | |
| 5 | Coverage rate | 90.98% | 93.01% | 100% | 100% |
| Secondary coverage | 385.21% | 35.24% | 0% | 0% | |
| Total path length | 7478 | 2081 | 1542 | 1542 | |
| Update frequency | 9.09 Hz | 3.15 Hz | 0.03 Hz | 0.51 Hz | |
| 6 | Coverage rate | 88.34% | 90.11% | 100% | 100% |
| Secondary coverage | 485.21% | 25.69% | 0% | 0% | |
| Total path length | 8769 | 1873 | 1499 | 1499 | |
| Update frequency | 11.11 Hz | 6.01 Hz | 0.05 Hz | 0.52 Hz | |
| 7 | Coverage rate | 91.28% | 92.52% | 100% | 100% |
| Secondary coverage | 354.21% | 46.11% | 0% | 0% | |
| Total path length | 6819 | 2177 | 1502 | 1502 | |
| Update frequency | 10.00 Hz | 3.11 Hz | 0.05 Hz | 0.49 Hz | |
| 8 | Coverage rate | 89.05% | 88.98% | 100% | 100% |
| Secondary coverage | 264.21% | 19.77% | 0% | 0% | |
| Total path length | 5179 | 1693 | 1423 | 1423 | |
| Update frequency | 7.69 Hz | 2.45 Hz | 0.05 Hz | 0.41 Hz | |
| 9 | Coverage rate | 93.31% | 95.09% | 100% | 100% |
| Secondary coverage | 157.21% | 45.29% | 0% | 0% | |
| Total path length | 3957 | 2233 | 1540 | 1540 | |
| Update frequency | 7.14 Hz | 2.00 Hz | 0.16 Hz | 0.81 Hz | |
| 10 | Coverage rate | 91.22% | 91.74% | 100% | 100% |
| Secondary coverage | 246.21% | 46.15% | 0% | 0% | |
| Total path length | 4927 | 2079 | 1424 | 1424 | |
| Update frequency | 12.5 Hz | 4.98 Hz | 0.09 Hz | 0.79 Hz |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Dong, W.; Li, R.; Dong, H.; Liu, H.; Gao, Y. An Improved STC-Based Full Coverage Path Planning Algorithm for Cleaning Tasks in Large-Scale Unstructured Social Environments. Sensors 2024, 24, 7885. https://doi.org/10.3390/s24247885
Wang C, Dong W, Li R, Dong H, Liu H, Gao Y. An Improved STC-Based Full Coverage Path Planning Algorithm for Cleaning Tasks in Large-Scale Unstructured Social Environments. Sensors. 2024; 24(24):7885. https://doi.org/10.3390/s24247885
Chicago/Turabian StyleWang, Chao, Wei Dong, Renjie Li, Hui Dong, Huajian Liu, and Yongzhuo Gao. 2024. "An Improved STC-Based Full Coverage Path Planning Algorithm for Cleaning Tasks in Large-Scale Unstructured Social Environments" Sensors 24, no. 24: 7885. https://doi.org/10.3390/s24247885
APA StyleWang, C., Dong, W., Li, R., Dong, H., Liu, H., & Gao, Y. (2024). An Improved STC-Based Full Coverage Path Planning Algorithm for Cleaning Tasks in Large-Scale Unstructured Social Environments. Sensors, 24(24), 7885. https://doi.org/10.3390/s24247885





