A Novel Multi-Objective Trajectory Planning Method for Robots Based on the Multi-Objective Particle Swarm Optimization Algorithm
Abstract
1. Introduction
2. Kinematics and Dynamics Analysis
2.1. Kinematics Analysis
2.1.1. Forward Kinematics Analysis
2.1.2. Inverse Kinematics Analysis
2.2. Dynamics Analysis
3. Multi-Objective Trajectory Planning
3.1. Construction of Joint Space Trajectory
3.2. Establishing the Multi-Objective Optimization Model
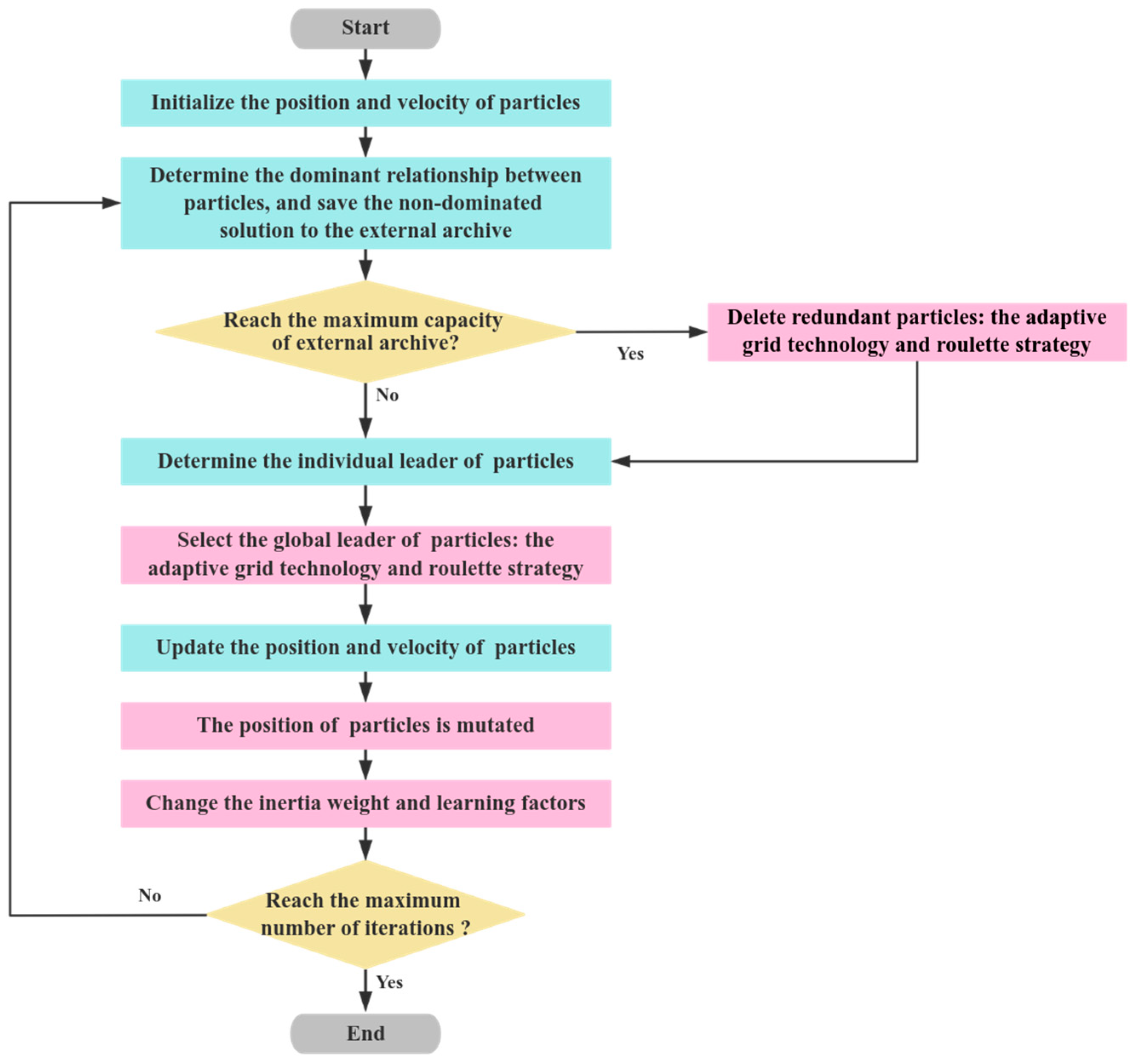
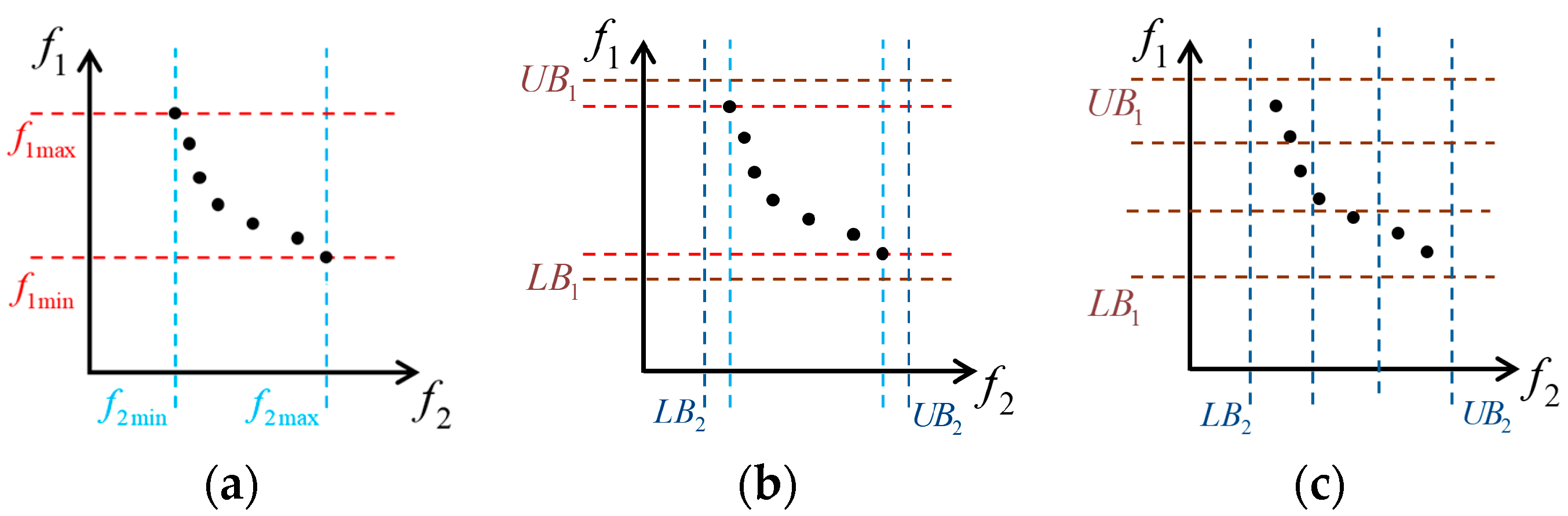
3.3. Solving the Multi-Objective Optimization Model
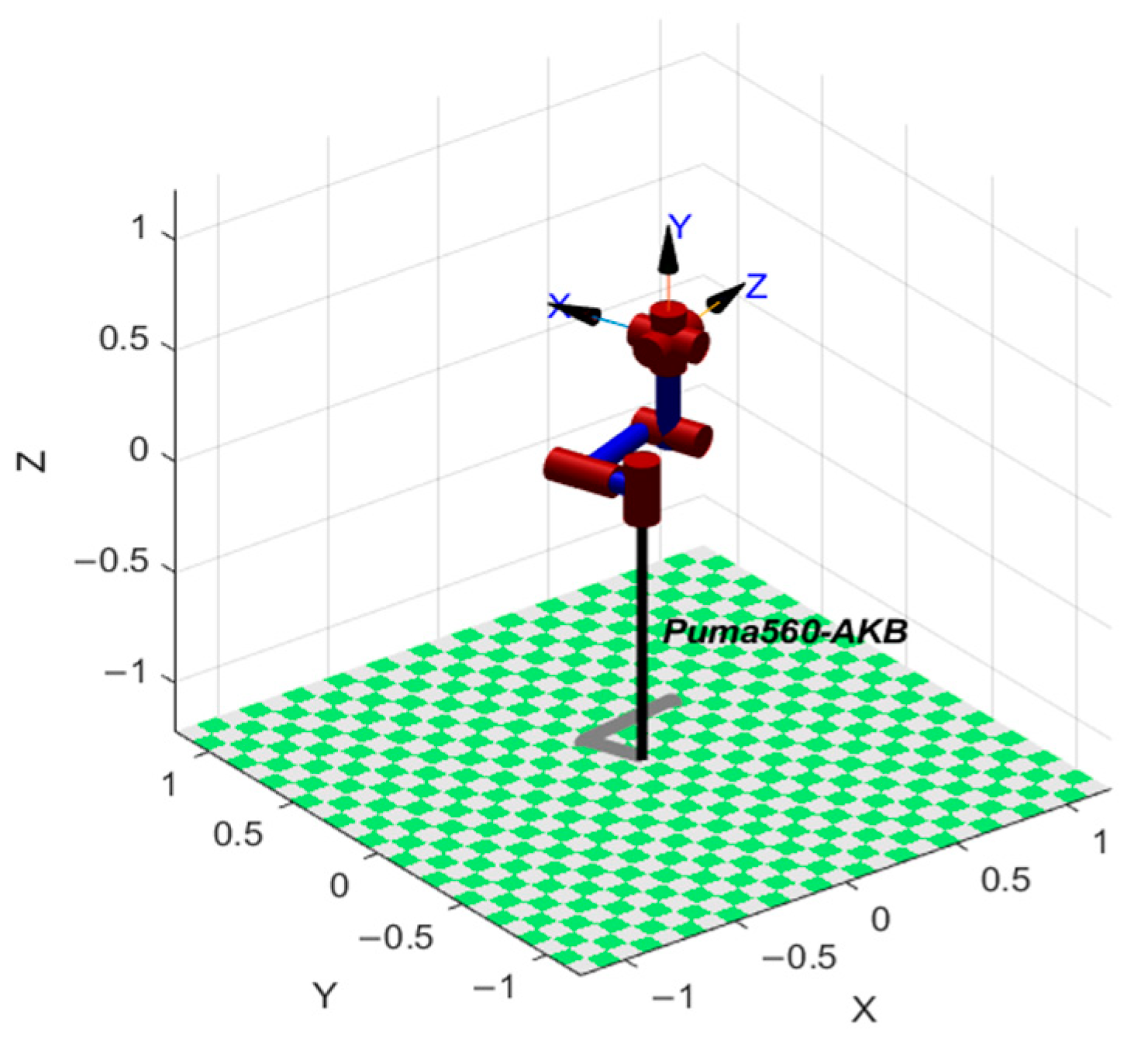
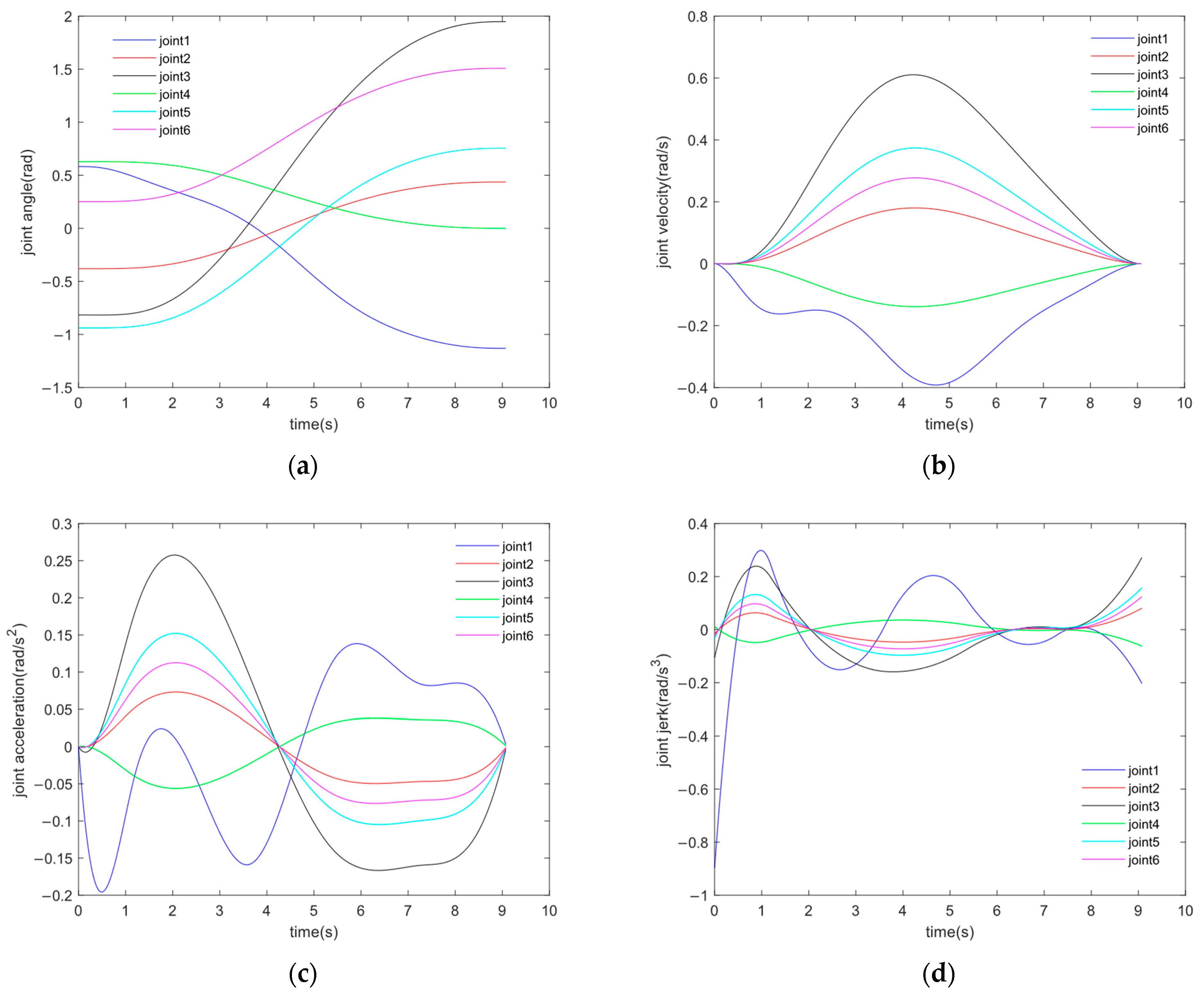
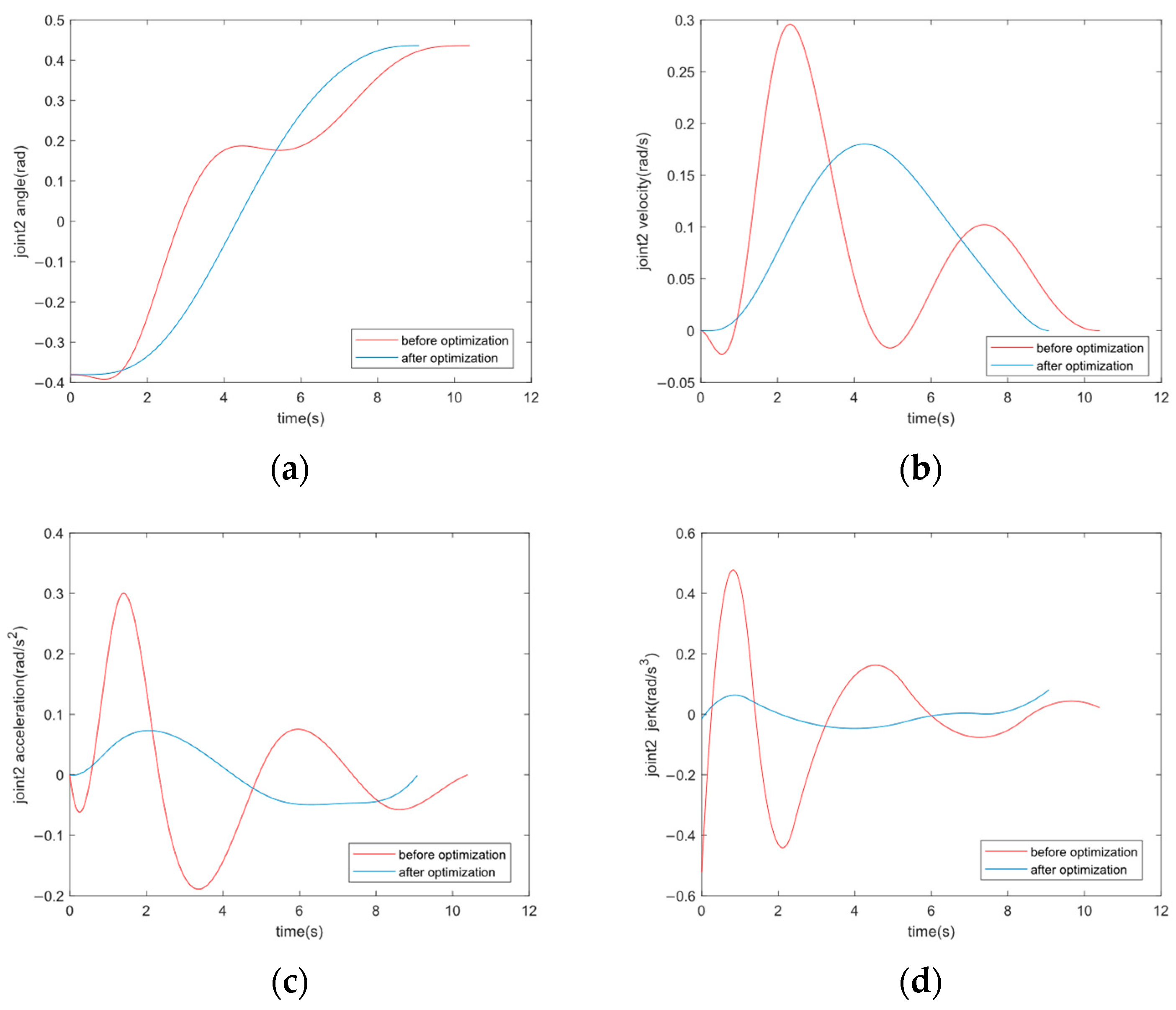
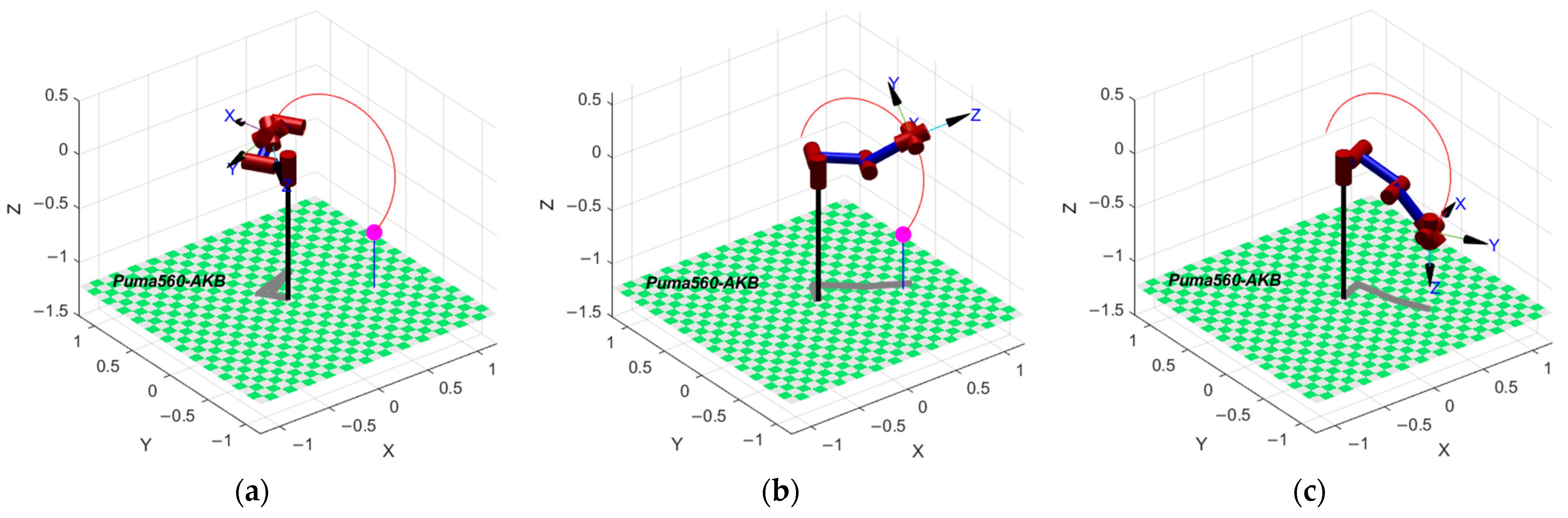
4. Simulation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Lan, J.; Xie, Y.; Liu, G.; Cao, M. A Multi-Objective Trajectory Planning Method for Collaborative Robot. Electronics 2020, 9, 859. [Google Scholar] [CrossRef]
- Bailon, W.P.; Cardiel, E.B.; Campos, I.J.; Paz, A.R. Mechanical energy optimization in trajectory planning for six DOF robot manipulators based on eighth-degree polynomial functions and a genetic algorithm. In Proceedings of the 7th International Conference on Electrical Engineering Computing Science and Automatic Control, Tuxtla Gutierrez, Mexico, 8–10 September 2010; pp. 446–451. [Google Scholar]
- Liu, J.; Wang, H.; Li, X.; Chen, K.; Li, C. Robotic arm trajectory optimization based on multiverse algorithm. Math. Biosci. Eng. 2023, 20, 2776–2792. [Google Scholar] [CrossRef] [PubMed]
- Machmudah, A.; Parman, S.; Zainuddin, A.; Chacko, S. Polynomial joint angle arm robot motion planning in complex geometrical obstacles. Appl. Soft Comput. 2013, 13, 1099–1109. [Google Scholar] [CrossRef]
- Porawagama, C.D.; Munasinghe, S.R. Reduced jerk joint space trajectory planning method using 5-3-5 spline for robot manipulators. In Proceedings of the 7th International Conference on Information and Automation for Sustainability, Colombo, Sri Lanka, 22–24 December 2014; pp. 1–6. [Google Scholar]
- Kim, K.W.; Kim, H.S.; Choi, Y.K.; Park, J.H. Optimization of cubic polynomial joint trajectories and sliding mode controllers for robots using evolution strategy. In Proceedings of the IECON’97 23rd International Conference on Industrial Electronics, Control, and Instrumentation, New Orleans, LA, USA, 14 November 1997; pp. 1444–1447. [Google Scholar]
- Lu, S.; Ding, B.; Li, Y. Minimum-jerk trajectory planning pertaining to a translational 3-degree-of-freedom parallel manipulator through piecewise quintic polynomials interpolation. Adv. Mech. Eng. 2020, 12, 1687814020913667. [Google Scholar] [CrossRef]
- Boryga, M.; Grabo, A. Planning of manipulator motion trajectory with higher-degree polynomials use. Mech. Mach. Theory 2009, 44, 1400–1419. [Google Scholar] [CrossRef]
- Chen, D.; Li, S.; Wang, J.; Feng, Y.; Liu, Y. A multi-objective trajectory planning method based on the improved immune clonal selection algorithm. Robot. Comput. Integr. Manuf. 2019, 59, 431–442. [Google Scholar] [CrossRef]
- Gasparetto, A.; Zanotto, V. Optimal trajectory planning for industrial robots. Adv. Eng. Softw. 2010, 41, 548–556. [Google Scholar] [CrossRef]
- Wang, Z.; Li, Y.; Sun, P.; Luo, Y.; Chen, B.; Zhu, W. A multi-objective approach for the trajectory planning of a 7-DOF serial-parallel hybrid humanoid arm. Mech. Mach. Theory 2021, 165, 104423. [Google Scholar] [CrossRef]
- Gao, Y.; Xie, W.; Li, Q.; Li, X.; Hu, M.; Zhao, L. Time-Jerk Optimal Trajectory Planning of Industrial Robot based on Hybrid Particle Swarm Optimization Algorithm. In Proceedings of the 2021 China Automation Congress (CAC), Beijing, China, 22–24 October 2021; pp. 6327–6331. [Google Scholar]
- Hansen, C.; Öltjen, J.; Meike, D.; Ortmaier, T. Enhanced approach for energy-efficient trajectory generation of industrial robots. In Proceedings of the IEEE International Conference on Automation Science and Engineering (CASE), Seoul, Republic of Korea, 20–24 August 2012; pp. 1–7. [Google Scholar]
- Shi, B.; Zeng, H. Time-Optimal Trajectory Planning for Industrial Robot based on Improved Hybrid-PSO. In Proceedings of the 40th Chinese Control Conference (CCC), Shanghai, China, 26–28 July 2021; pp. 3888–3893. [Google Scholar]
- Gasparetto, A.; Zanotto, V. A new method for smooth trajectory planning of robot manipulators. Mech. Mach. Theory 2007, 42, 455–471. [Google Scholar] [CrossRef]
- Yao, J.; Sun, C.; Zhang, L.; Xiao, C.; Yang, M.; Zhang, S. Time optimal trajectory planning based on simulated annealing algorithm for a train uncoupling robot. In Proceedings of the 29th Chinese Control and Decision Conference (CCDC), Chongqing, China, 28–30 May 2017; pp. 5781–5785. [Google Scholar]
- Bianco, C.G.L.; Piazzi, A. A genetic/interval approach to optimal trajectory planning of industrial robots under torque constraints. In Proceedings of the 1999 European Control Conference (ECC), Karlsruhe, Germany, 31 August–3 September 1999; pp. 942–947. [Google Scholar]
- Mora, P.R. On the Time-optimal Trajectory Planning along Predetermined Geometric Paths and Optimal Control Synthesis for Trajectory Tracking of Robot Manipulators. Ph.D. Thesis, University of California, Berkeley, CA, USA, 2013. [Google Scholar]
- Abu-Dakka, F.J.; Assad, I.F.; Alkhdour, R.M. Statistical evaluation of an evolutionary algorithm for minimum time trajectory planning problem for industrial robots. Int. J. Adv. Manuf. Technol. 2017, 89, 389–406. [Google Scholar] [CrossRef]
- Zhang, W.; Fu, S. Time-optimal Trajectory Planning of Dulcimer Music Robot Based on PSO Algorithm. In Proceedings of the 2020 Chinese Control and Decision Conference (CCDC), Hefei, China, 22–24 August 2020; pp. 4769–4774. [Google Scholar]
- Lin, H.I. A fast and unified method to find a minimum-jerk robot joint trajectory using particle swarm optimization. J. Intell. Robot. Syst. Theory Appl. 2014, 75, 379–392. [Google Scholar] [CrossRef]
- Zhou, Y.; Han, G.; Wei, Z.; Huang, Z.; Chen, X.; Wu, J. Optimal trajectory planning of robot energy consumption based on improved sparrow search algorithm. Meas. Control 2024, 57, 1014–1021. [Google Scholar] [CrossRef]
- Yokose, Y. Energy-saving trajectory planning for robots using the genetic algorithm with assistant chromosomes. Artif. Life Robot. 2020, 25, 89–93. [Google Scholar] [CrossRef]
- Luo, L.-P.; Yuan, C.; Yan, R.-J.; Yuan, Q.; Wu, J.; Shin, K.-S.; Han, C.-S. Trajectory planning for energy minimization of industry robotic manipulators using the Lagrange interpolation method. Int. J. Precis. Eng. Manuf. 2015, 16, 911–917. [Google Scholar] [CrossRef]
- Mohammed, A.; Schmidt, B.; Wang, L.; Gao, L. Minimizing Energy Consumption for Robot Arm Movement. Procedia CIRP 2014, 25, 400–405. [Google Scholar] [CrossRef]
- Paes, K.; Dewulf, W.; Elst, K.V. Energy efficient trajectories for an industrial ABB robot. Procedia CIRP 2014, 15, 105–110. [Google Scholar] [CrossRef]
- Ye, J.; Hao, L.; Cheng, H. Multi-objective optimal trajectory planning for robot manipulator attention to end-effector path limitation. Robotica 2024, 42, 1761–1780. [Google Scholar] [CrossRef]
- Chen, W.; Wang, H.; Liu, Z.; Jiang, K. Time-energy-jerk optimal trajectory planning for high-speed parallel manipulator based on quantum-behaved particle swarm optimization algorithm and quintic B-spline. Eng. Appl. Artif. Intell. 2023, 126, 107223. [Google Scholar] [CrossRef]
- Cao, X.; Yan, H.; Huang, Z.; Ai, S.; Xu, Y.; Fu, R.; Zou, X. A Multi-Objective Particle Swarm Optimization for Trajectory Planning of Fruit Picking Manipulator. Agronomy 2021, 11, 2286. [Google Scholar] [CrossRef]
- Saravanan, R.; Ramabalan, S. Evolutionary Minimum Cost Trajectory Planning for Industrial Robots. J. Intell. Robot. Syst. 2008, 52, 45–77. [Google Scholar] [CrossRef]
- Shi, X.; Fang, H.; Guo, L. Multi-objective optimal trajectory planning of manipulators based on quintic NURBS. In Proceedings of the 2016 IEEE International Conference on Mechatronics and Automation, Harbin, China, 7–10 August 2016. [Google Scholar]
- Craig, J.J. Introduction to Robotics: Mechanics and Control, 3rd ed.; Pearson Education, Inc.: London, UK, 2005; pp. 73–76. [Google Scholar]
- Pieper, D.L. The Kinematics of Manipulators Under Computer Control. Ph.D. Thesis, Stanford University, Stanford, CA, USA, 1968. [Google Scholar]
- Luh, J.Y.S.; Walker, M.W.; Paul, R.P.C. On-Line Computational Scheme for Mechanical Manipulators. ASME J. Dyn. Sys. Meas. Control 1980, 102, 69–76. [Google Scholar] [CrossRef]
- Piegl, L.; Tiller, W. The Nurbs Book, 2nd ed.; Springer: Berlin/Heidelberg, Germany, 1997; pp. 81–100. [Google Scholar]
- Sathiya, V.; Chinnadurai, M. Evolutionary Algorithms-Based Multi-Objective Optimal Mobile Robot Trajectory Planning. Robotica 2019, 37, 1363–1382. [Google Scholar] [CrossRef]
- Coello, C.A.C.; Lechuga, M.S. MOPSO: A proposal for multiple objective particle swarm optimization. In Proceedings of the 2002 Congress on Evolutionary Computation, Honolulu, HI, USA, 12–17 May 2002. [Google Scholar]
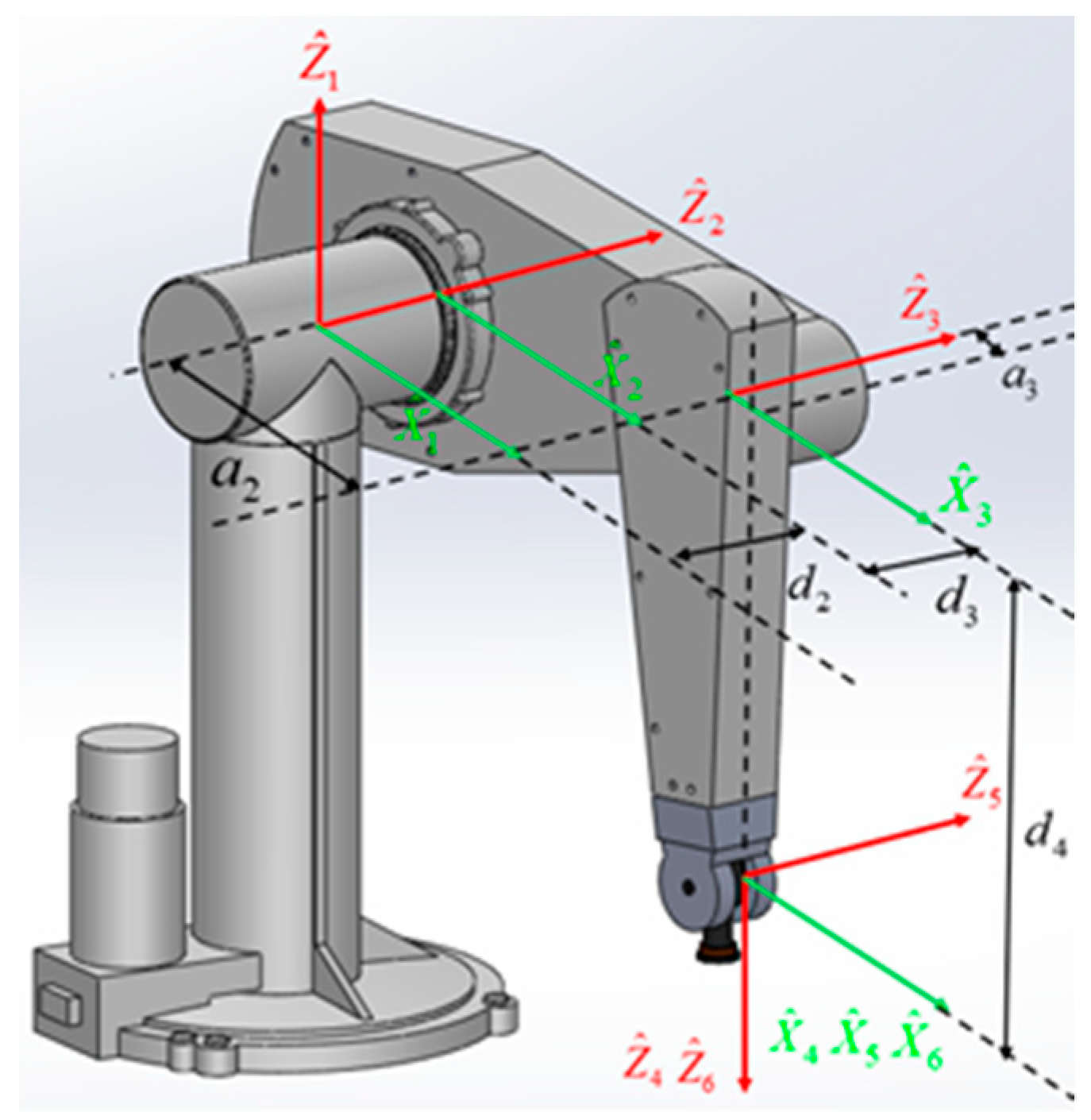

| Link i | (rad) | (m) | (m) | (rad) |
|---|---|---|---|---|
| 1 | 0 | 0 | 0 | |
| 2 | −1.5708 | 0 | 0.2435 | |
| 3 | 0 | 0.4318 | −0.0934 | |
| 4 | 1.5708 | −0.0203 | 0.4331 | |
| 5 | −1.5708 | 0 | 0 | |
| 6 | 1.5708 | 0 | 0 |
| Constraints | Joint 1 | Joint 2 | Joint 3 | Joint 4 | Joint 5 | Joint 6 |
|---|---|---|---|---|---|---|
| Angle/(rad) | 3.100 | 3.100 | 3.100 | 3.100 | 3.100 | 3.100 |
| ) | 0.876 | 0.876 | 1.598 | 0.876 | 0.926 | 0.926 |
| ) | 0.725 | 0.725 | 2.378 | 0.725 | 1.450 | 1.450 |
| ) | 44.940 | 44.940 | 8.866 | 44.940 | 0.050 | 0.050 |
| Node | Joint 1/(rad) | Joint 2/(rad) | Joint 3/(rad) | Joint 4/(rad) | Joint 5/(rad) | Joint 6/(rad) |
|---|---|---|---|---|---|---|
| 1 | 0.5821 | −0.3805 | −0.8168 | 0.6283 | −0.9390 | 0.2531 |
| 2 | 0.4829 | −0.3735 | −0.7981 | 0.6299 | −0.9245 | 0.2621 |
| 3 | 0.0383 | −0.1212 | 0.0608 | 0.4289 | −0.4005 | 0.6502 |
| 4 | −0.5872 | 0.1770 | 1.0702 | 0.1995 | 0.2189 | 1.1091 |
| 5 | −1.0317 | 0.3890 | 1.7877 | 0.0364 | 0.6592 | 1.4352 |
| 6 | −1.1310 | 0.4363 | 1.9478 | 0 | 0.7547 | 1.5080 |
| Solution | Travel Time/() | ) | ) |
|---|---|---|---|
| A | 3.7566 | 3.2251 | 8.2585 |
| B | 4.8760 | 1.6688 | 3.0157 |
| C | 9.0883 | 0.4932 | 0.4656 |
| D | 39.5825 | 0.0286 | 0.0069 |
| Solution | Travel Time/() | ) | |
|---|---|---|---|
| C | 9.0883 | 0.4932 | 0.4656 |
| E | 10.4000 | 1.1457 | 1.8733 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, J.; Zhang, Y.; Zhu, S.; Wang, J. A Novel Multi-Objective Trajectory Planning Method for Robots Based on the Multi-Objective Particle Swarm Optimization Algorithm. Sensors 2024, 24, 7663. https://doi.org/10.3390/s24237663
Wang J, Zhang Y, Zhu S, Wang J. A Novel Multi-Objective Trajectory Planning Method for Robots Based on the Multi-Objective Particle Swarm Optimization Algorithm. Sensors. 2024; 24(23):7663. https://doi.org/10.3390/s24237663
Chicago/Turabian StyleWang, Jiahui, Yongbo Zhang, Shihao Zhu, and Junling Wang. 2024. "A Novel Multi-Objective Trajectory Planning Method for Robots Based on the Multi-Objective Particle Swarm Optimization Algorithm" Sensors 24, no. 23: 7663. https://doi.org/10.3390/s24237663
APA StyleWang, J., Zhang, Y., Zhu, S., & Wang, J. (2024). A Novel Multi-Objective Trajectory Planning Method for Robots Based on the Multi-Objective Particle Swarm Optimization Algorithm. Sensors, 24(23), 7663. https://doi.org/10.3390/s24237663






