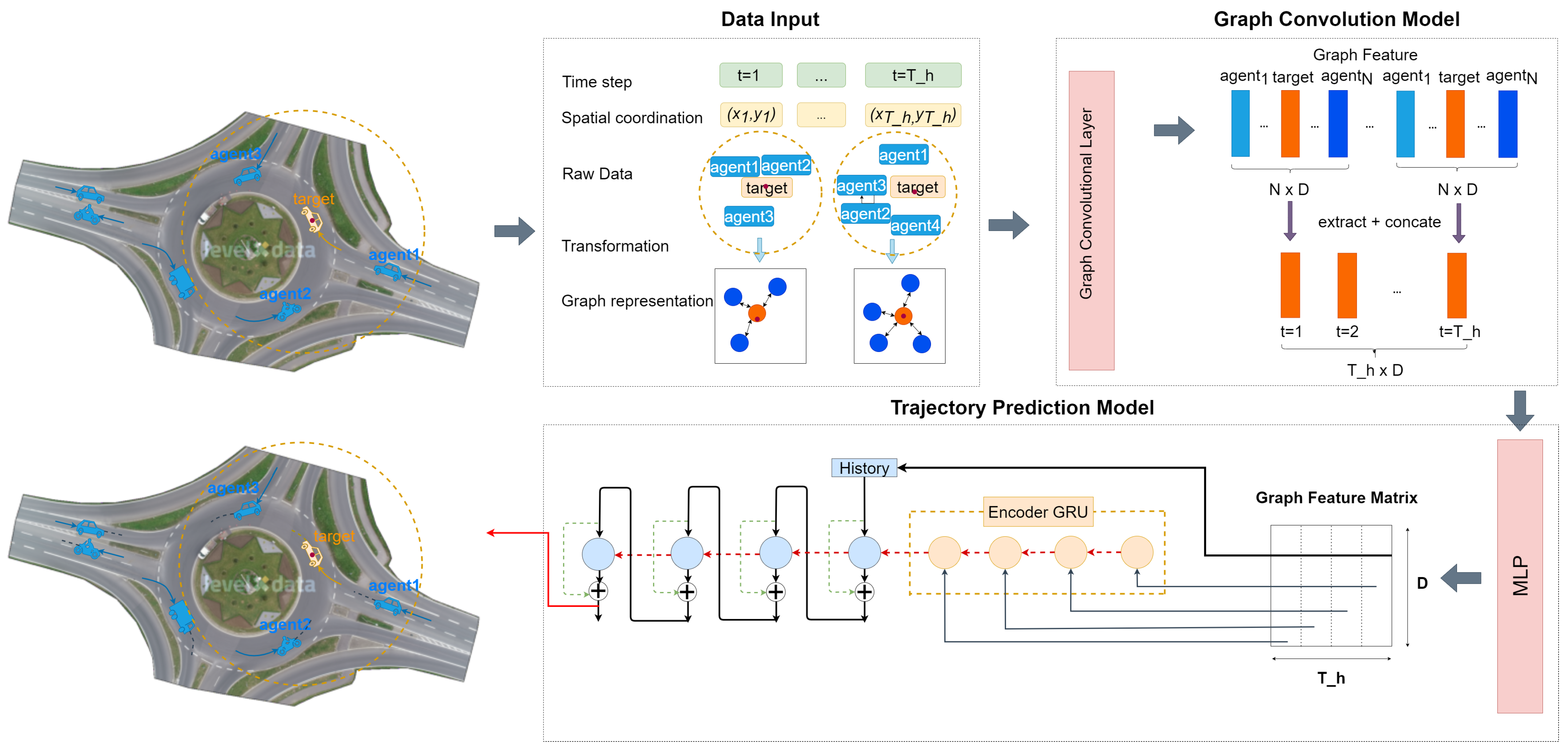
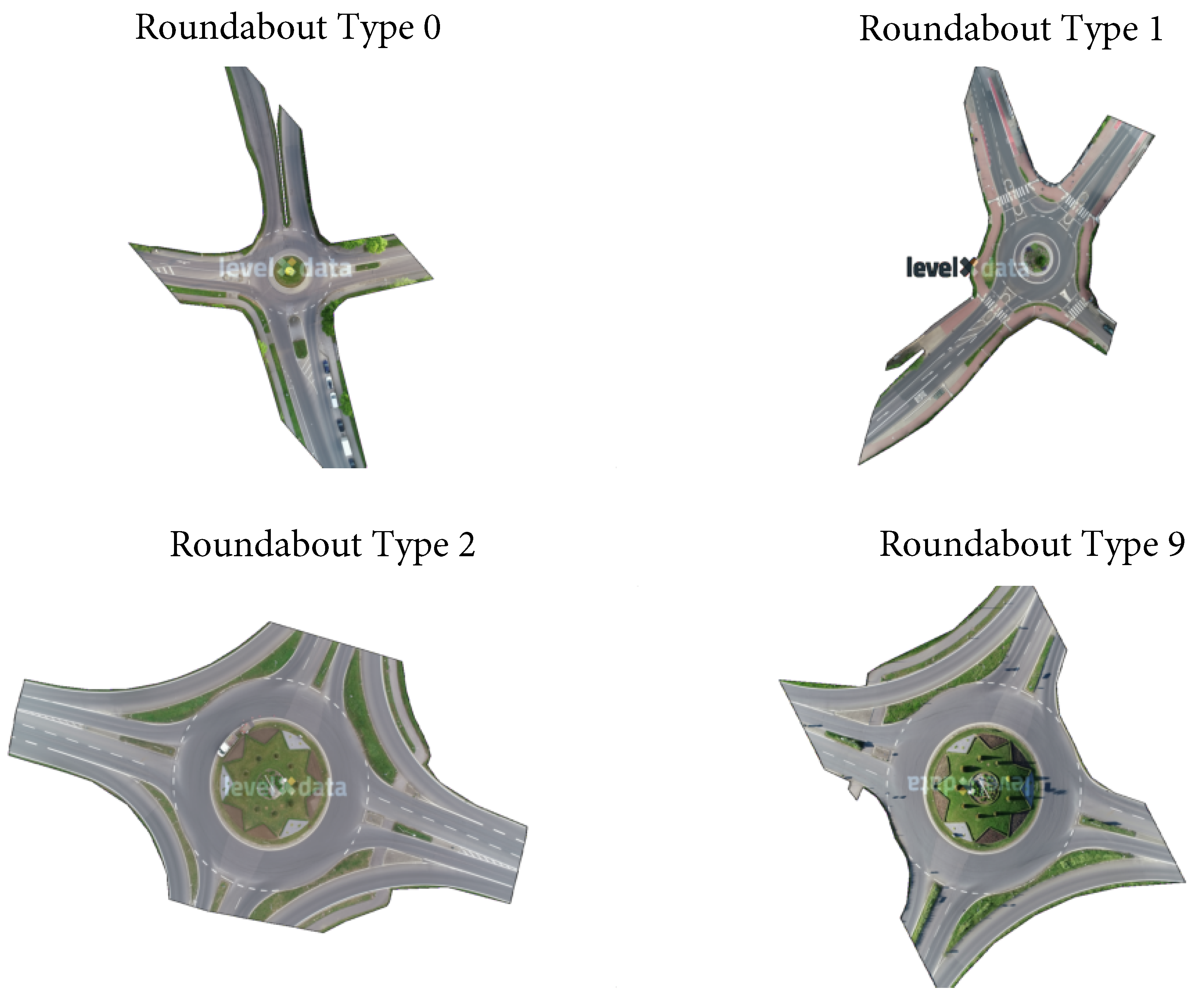
Figure 1.
All four roundabout types in the rounD dataset. Here, roundabout type 0 is denoted as the background image from recording file 0 and so are roundabout types 1, 2 and 9.
Figure 1.
All four roundabout types in the rounD dataset. Here, roundabout type 0 is denoted as the background image from recording file 0 and so are roundabout types 1, 2 and 9.
Figure 2.
Class distribution of agents, categorized into ‘Majority’ (car), ‘Medium’ (truck, van, trailer), and ‘Minority’ (motorcycle, bicycle, bus, pedestrian).
Figure 2.
Class distribution of agents, categorized into ‘Majority’ (car), ‘Medium’ (truck, van, trailer), and ‘Minority’ (motorcycle, bicycle, bus, pedestrian).
Figure 3.
Time distribution of recordings, divided into morning, noon, and afternoon categories, highlighting variations in driving behaviors.
Figure 3.
Time distribution of recordings, divided into morning, noon, and afternoon categories, highlighting variations in driving behaviors.
Figure 4.
Comparison of morning and afternoon driving behaviors: wider velocity and acceleration ranges are observed in the morning, indicating more aggressive, stop-and-go driving. Noon and afternoon driving shows higher velocities but more consistent, relaxed acceleration patterns.
Figure 4.
Comparison of morning and afternoon driving behaviors: wider velocity and acceleration ranges are observed in the morning, indicating more aggressive, stop-and-go driving. Noon and afternoon driving shows higher velocities but more consistent, relaxed acceleration patterns.
Figure 5.
Velocity and acceleration comparison of road agents and VRUs: road agents (e.g., car, truck, van, motorcycle, bus) exhibit a much wider range than VRUs. Both velocity and acceleration show similar trends, indicating their comparable impact in motion forecasting.
Figure 5.
Velocity and acceleration comparison of road agents and VRUs: road agents (e.g., car, truck, van, motorcycle, bus) exhibit a much wider range than VRUs. Both velocity and acceleration show similar trends, indicating their comparable impact in motion forecasting.
Figure 6.
Correlation matrix heatmap: darker colors and lighter colors indicate larger positive and smaller negative correlations between indicators. Notable relationships include connections between xCenter, yCenter, xVelocity, and yVelocity, as well as between velocity and acceleration (noted in red rectangles). These findings suggest potential redundancy and highlight areas for feature extraction or dimensional reduction.
Figure 6.
Correlation matrix heatmap: darker colors and lighter colors indicate larger positive and smaller negative correlations between indicators. Notable relationships include connections between xCenter, yCenter, xVelocity, and yVelocity, as well as between velocity and acceleration (noted in red rectangles). These findings suggest potential redundancy and highlight areas for feature extraction or dimensional reduction.
Figure 7.
Pie chart analysis: cars dominate across all scenarios (over 75%) according to all recordings. Missing classes (some classes cannot be observed in a certain roundabout type) and VRUs, like trailers, bicycles, and pedestrians, are present in low percentages.
Figure 7.
Pie chart analysis: cars dominate across all scenarios (over 75%) according to all recordings. Missing classes (some classes cannot be observed in a certain roundabout type) and VRUs, like trailers, bicycles, and pedestrians, are present in low percentages.
Figure 8.
Acceleration and deceleration frequencies vary across recordings in the roundabout scenario, with deceleration generally being more common. Different trends are observed (marked in red), such as roundabout type 2’s unique pattern, roundabout type 1’s emphasis on specific acceleration ranges, and roundabout type 9’s tendency for constant speed.
Figure 8.
Acceleration and deceleration frequencies vary across recordings in the roundabout scenario, with deceleration generally being more common. Different trends are observed (marked in red), such as roundabout type 2’s unique pattern, roundabout type 1’s emphasis on specific acceleration ranges, and roundabout type 9’s tendency for constant speed.
Figure 12.
Illustration of the transformation from a global coordinate system to a localized coordinate system.
Figure 12.
Illustration of the transformation from a global coordinate system to a localized coordinate system.
Figure 13.
Visualized Prediction Results: (target, neighboring agents). … and … are the trajectory history and labels of all road agents. ▽ are the predicted trajectories of the targets in model 0. × represents model 1, and + and ★ represent model 2 and model 9, respectively.
Figure 13.
Visualized Prediction Results: (target, neighboring agents). … and … are the trajectory history and labels of all road agents. ▽ are the predicted trajectories of the targets in model 0. × represents model 1, and + and ★ represent model 2 and model 9, respectively.
Table 1.
This table contains metadata for each recording. The metadata provide a general overview, e.g., of the time of recording, the road section considered, and the total number of objects tracked.
Table 1.
This table contains metadata for each recording. The metadata provide a general overview, e.g., of the time of recording, the road section considered, and the total number of objects tracked.
| Name | Description | Unit |
|---|
| recordingId | Unique identifier for the recording. | [-] |
| locationId | Unique identifier for the recording location. | [-] |
| frameRate | Video frame rate used during recording. | [hz] |
| speedLimit | Speed limit of the lanes in the recording. | [m/s] |
| weekday | Day of the week when the recording occurred. | [-] |
| startTime | Starting hour of the recording. | [hh] |
| duration | Total time of the recording. | [s] |
| numTracks | Number of tracked objects. | [-] |
| numVehicles | Number of tracked vehicles (cars, trucks, vans, trailers). | [-] |
| numVRUs | Number of tracked vulnerable road users (pedestrians, bicycles, motorcycles). | [-] |
| latLocation | Approximate latitude of the recording. | [deg] |
| lonLocation | Approximate longitude of the recording. | [deg] |
| xUtmOrigin | UTM X coordinate origin for the recording location. | [m] |
| yUtmOrigin | UTM Y coordinate origin for the recording location. | [m] |
| orthoPxToMeter | Conversion factor from ortho pixels to UTM meters. | [m/px] |
Table 2.
This table contains all the information of each agent, such as current position, velocity and acceleration.
Table 2.
This table contains all the information of each agent, such as current position, velocity and acceleration.
| Name | Description | Unit |
|---|
| recordingId | Unique recording identifier. | [-] |
| trackId | Unique track identifier for each recording. | [-] |
| frame | Frame number for the data. | [-] |
| trackLifetime | Age of the track at the current frame. | [-] |
| xCenter | X coordinate of the object’s centroid. | [m] |
| yCenter | Y coordinate of the object’s centroid. | [m] |
| heading | Object’s heading angle. | [deg] |
| width | Object’s width. | [m] |
| length | Object’s length. | [m] |
| xVelocity | Velocity along the x-axis. | [m/s] |
| yVelocity | Velocity along the y-axis. | [m/s] |
| xAcceleration | Acceleration along the x-axis. | [m/s2] |
| yAcceleration | Acceleration along the y-axis. | [m/s2] |
| lonVelocity | Longitudinal velocity. | [m/s] |
| latVelocity | Lateral velocity. | [m/s] |
| lonAcceleration | Longitudinal acceleration. | [m/s2] |
| latAcceleration | Lateral acceleration. | [m/s2] |
| initialFrame | Start frame of the track. | [-] |
| finalFrame | End frame of the track. | [-] |
| numFrames | Total lifetime of the track in frames. | [-] |
| class | Object class (e.g., Car, Pedestrian, Bicycle). | [-] |
Table 3.
Data volume for different roundabout types.
Table 3.
Data volume for different roundabout types.
| Roundabout Type | Index | Number of Records (Million) |
|---|
| 0 | 0 | 0.3 |
| 1 | 1 | 0.1 |
| 2 | 2–8 | 0.2, 0.3, 0.2, 0.2, 0.3, 0.3, 0.2 |
| 9 | 9–23 | 0.3, 0.3, 0.2, 0.2, 0.2, 0.3, 0.9, 0.1, 0.3, 0.3, 0.2, 0.3, 0.3, 0.2, 0.2 |
Table 4.
Result comparison of models trained on one particular domain (i.e., recording type 0) and tested on both in-distribution and out-distribution domains.
Table 4.
Result comparison of models trained on one particular domain (i.e., recording type 0) and tested on both in-distribution and out-distribution domains.
| ADE\FDE | Roundabout Type 0 |
|---|
| Train | 0 |
| Test | 0 | 1 | 2 | 9 |
| GCN | 2.33\5.42 | 2.87\4.28 | 3.21\5.44 | 3.02\5.32 |
| LSTM | 0.95\1.12 | 1.05\1.33 | 1.12\1.27 | 1.15\1.58 |
| Ours | 0.81\1.06 | 0.88\1.14 | 0.99\1.05 | 1.09\1.34 |
Table 5.
Result comparison of models trained on one particular domain (i.e.,Recording Type 1) and tested on both in-distribution and out-distribution domains.
Table 5.
Result comparison of models trained on one particular domain (i.e.,Recording Type 1) and tested on both in-distribution and out-distribution domains.
| ADE\FDE | Roundabout Type 1 |
|---|
| Train | 1 |
| Test | 0 | 1 | 2 | 9 |
| GCN | 3.02\3.82 | 2.45\4.19 | 3.67\5.67 | 4.28\5.12 |
| LSTM | 1.12\1.38 | 0.91\1.29 | 1.44\1.76 | 1.52\2.02 |
| Ours | 1.08\1.24 | 0.87\1.34 | 1.29\1.96 | 1.46\1.78 |
Table 6.
Result comparison of models trained on one particular domain (i.e., recording type 2) and tested on both in-distribution and out-distribution domains.
Table 6.
Result comparison of models trained on one particular domain (i.e., recording type 2) and tested on both in-distribution and out-distribution domains.
| ADE\FDE | Roundabout Type 2 |
|---|
| Train | 2 |
| Test | 0 | 1 | 2 | 9 |
| GCN | 4.35\5.18 | 3.53\4.44 | 2.89\3.69 | 3.17\4.21 |
| LSTM | 1.35\1.73 | 1.45\1.39 | 0.34\0.77 | 0.95\0.97 |
| Ours | 1.34\1.69 | 1.23\1.43 | 0.28\0.49 | 0.79\0.82 |
Table 7.
Result comparison of models trained on one particular domain (i.e., recording type 9) and tested on both in-distribution and out-distribution domains.
Table 7.
Result comparison of models trained on one particular domain (i.e., recording type 9) and tested on both in-distribution and out-distribution domains.
| ADE\FDE | Roundabout Type 9 |
|---|
| Train | 9 |
| Test | 0 | 1 | 2 | 9 |
| GCN | 3.57\4.01 | 2.99\4.05 | 2.91\4.06 | 2.53\1.99 |
| LSTM | 1.34\1.68 | 1.22\1.45 | 0.95\1.39 | 0.63\0.41 |
| Ours | 1.12\1.42 | 0.93\1.43 | 0.57\0.62 | 0.16\0.31 |