Numerical Simulation of Electromagnetic Nondestructive Testing Technology for Elasto–Plastic Deformation of Ferromagnetic Materials Based on Magneto–Mechanical Coupling Effect
Abstract
1. Introduction
2. Theoretical Analysis
2.1. Mechanical Analysis
2.2. Electromagnetic Field Finite Element–Infinite Element Coupling Analysis
2.3. Magneto–Mechanical Coupling Theory
Magneto–Plastic Coupling Model
3. Validation of the Numerical Method and the Proposed Model
3.1. Finite Element–Infinite Element Coupling
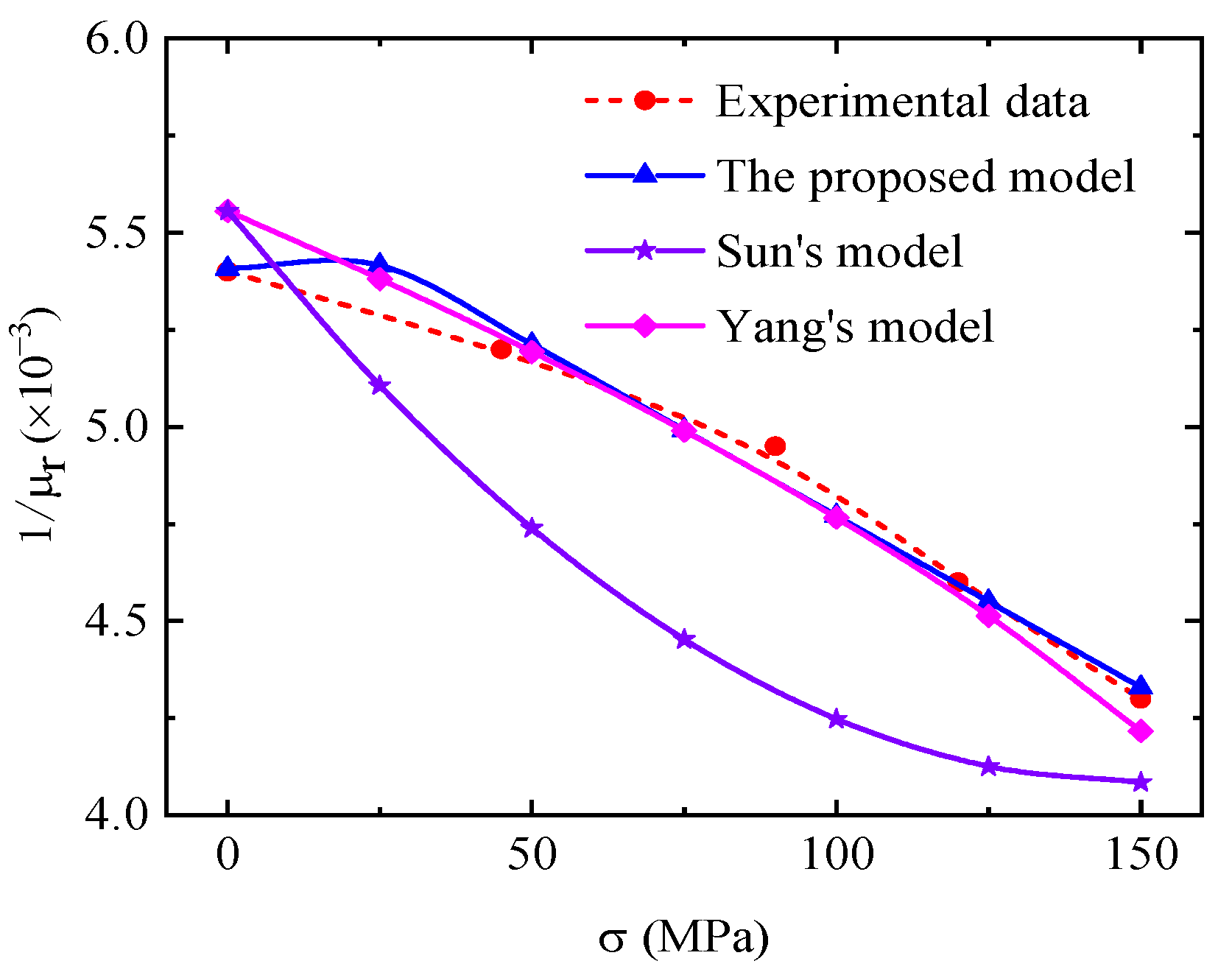
3.2. Magneto–Elastic Coupling Model
3.3. Magneto–Plastic Coupling Model
4. The Effect of Elasto–Plastic Deformation on Transient Magnetic Flux Signal
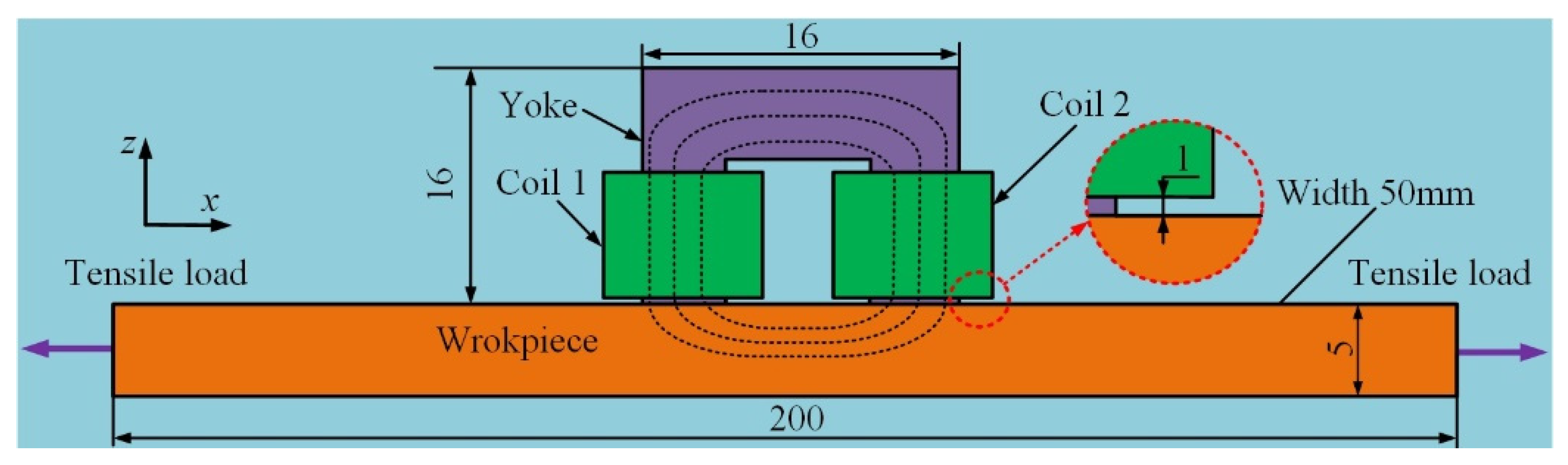
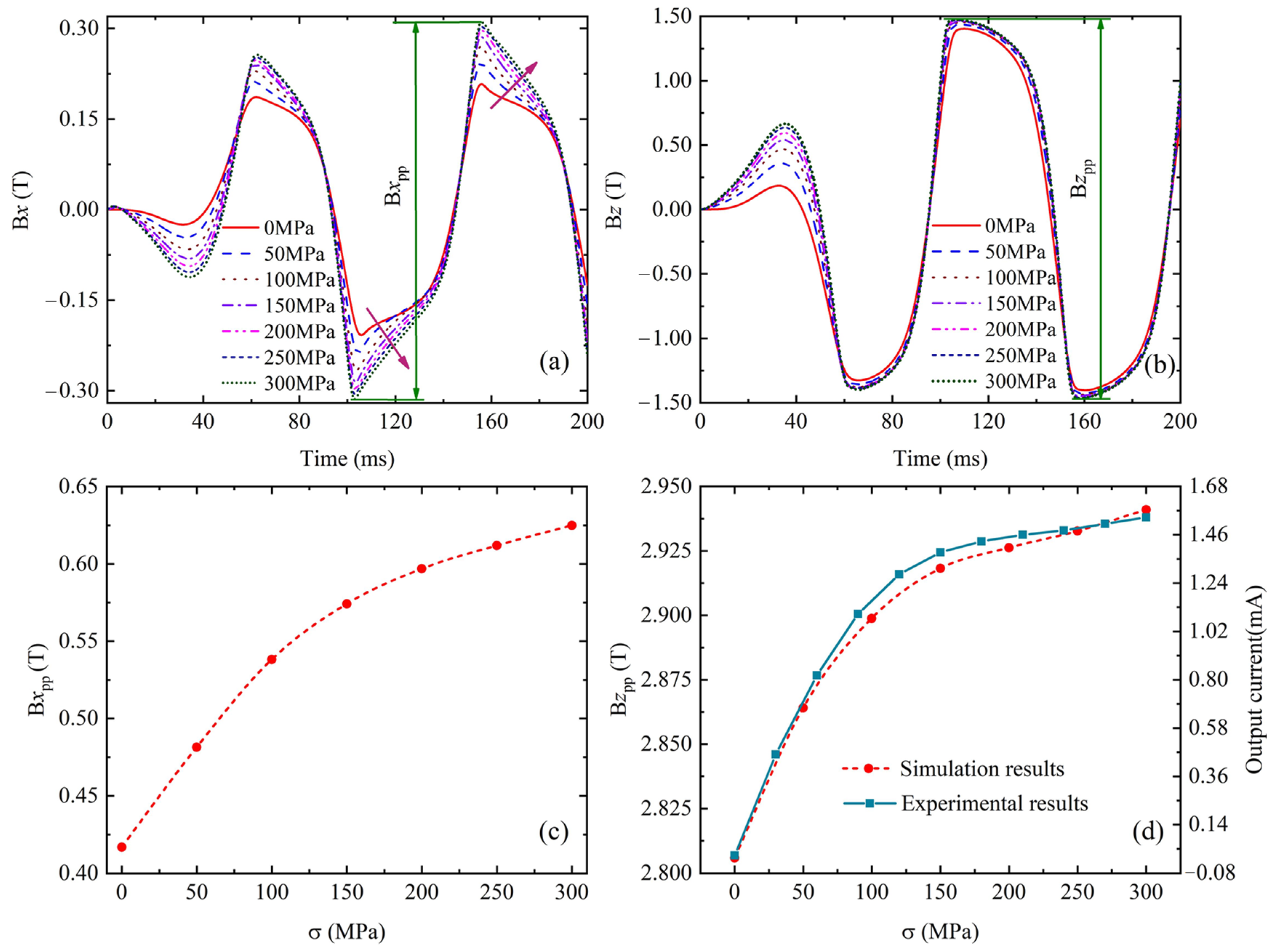
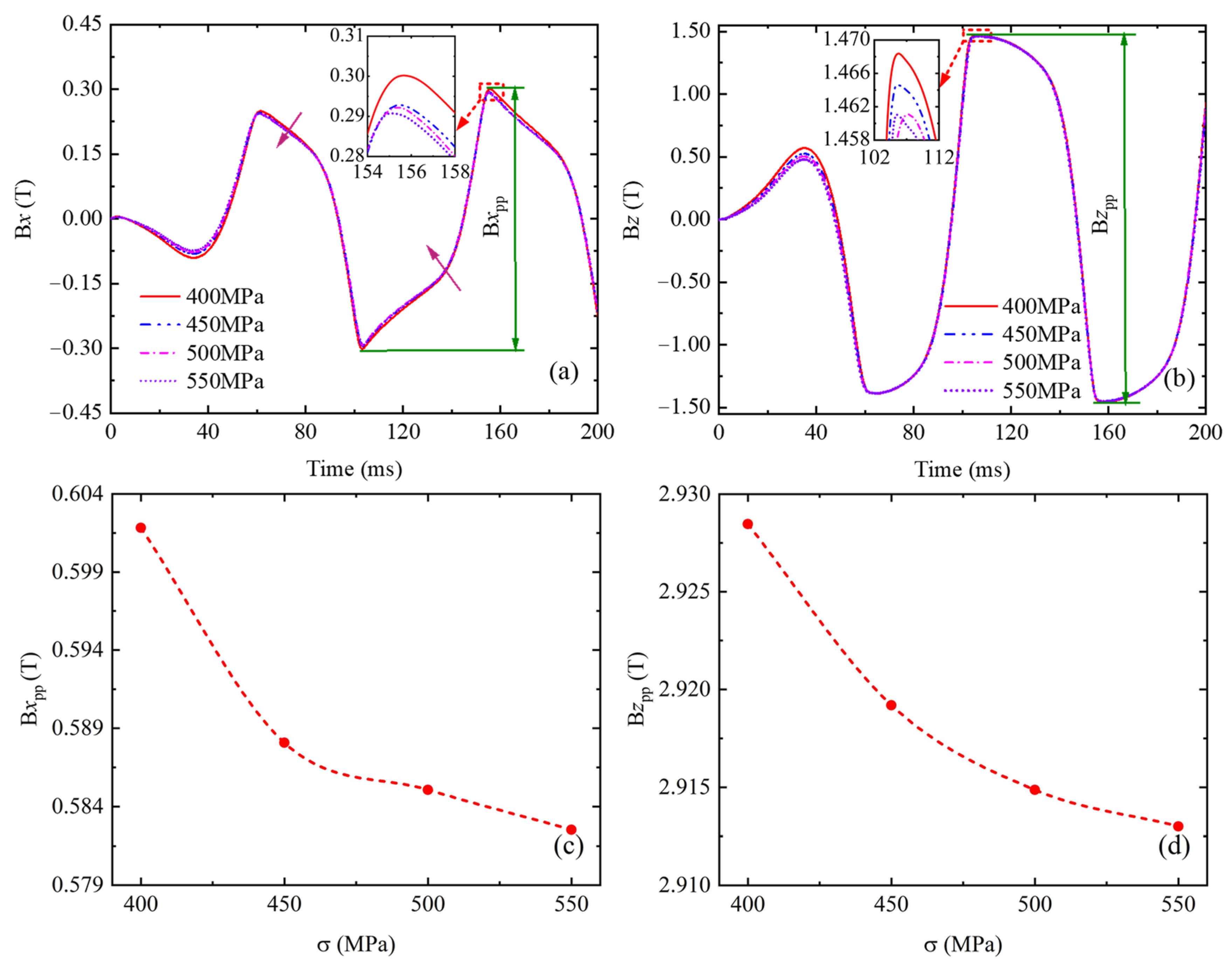
4.1. Simulation of Transient Magnetic Flux Signal Under Elastic Deformation
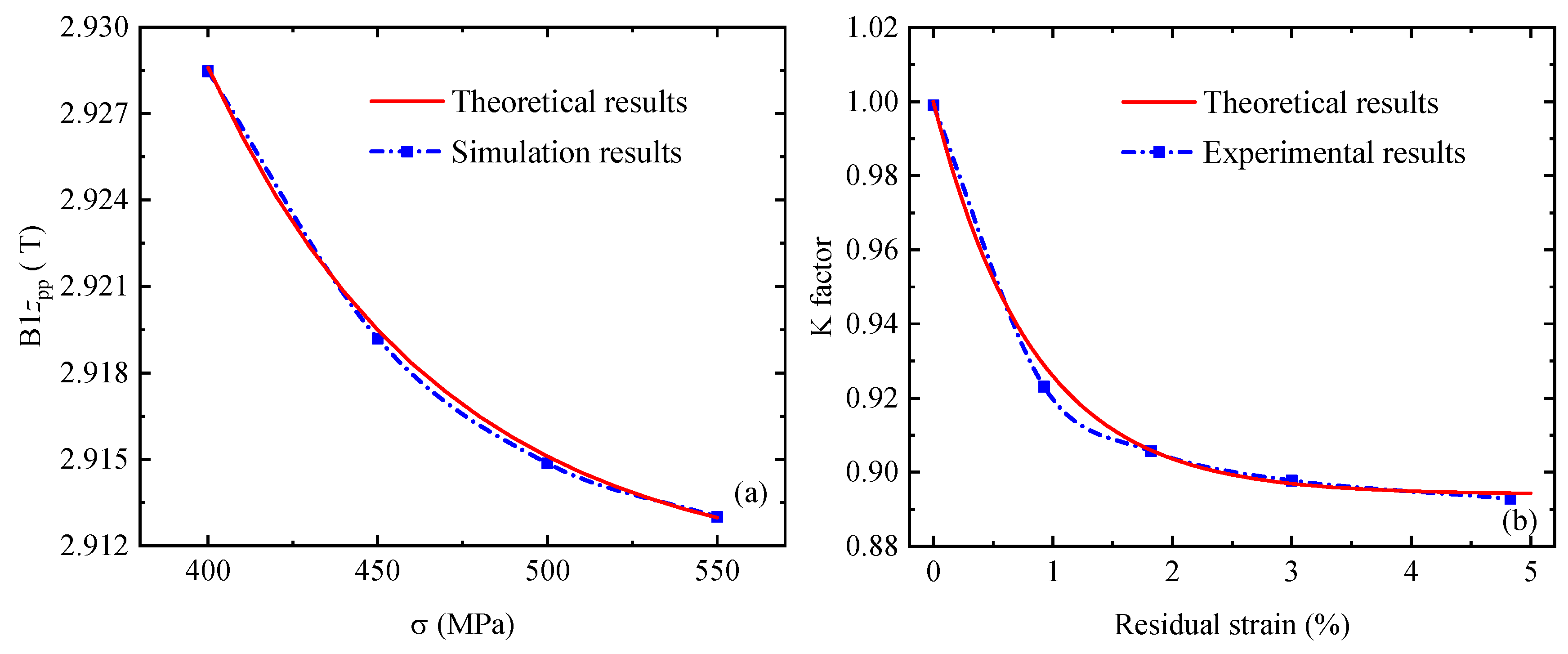
4.2. Simulation of Transient Magnetic Signals Under Plastic Deformation
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix A.1. Finite Element Method
Appendix A.2. Infinite Element Method

Appendix A.3. Finite Element–Infinite Element Coupling
Appendix B
Appendix B.1. The Magneto–Mechanical Coupling Model
References
- Yuan, X.; Li, W.; Chen, G.; Yin, X.; Jiang, W.; Zhao, J.; Ge, J. Inspection of both inner and outer cracks in aluminum tubes using double frequency circumferential current field testing method. Mech. Syst. Signal Process. 2019, 127, 16–34. [Google Scholar] [CrossRef]
- Shi, P. Quantitative Study of Micro-Magnetic Nondestructive Testing for Stress and Defect in Ferromagnetic Materials. Doctoral Dissertation, Xidian University, Xi’an, China, 2017. [Google Scholar]
- Hu, X.; Bu, Y.; Zhang, J. A nonlinear magneto-elastoplastic coupling model based on Jiles-Atherton theory of ferromagnetic materials. J. Phys. D Appl. Phys. 2022, 55, 165005. [Google Scholar] [CrossRef]
- Hu, X.; Fu, Z.; Wang, Z.; Zhang, J. Research on a theoretical model of magnetic nondestructive testing for ferromagnetic materials based on the magneto-mechanical coupling effect. J. Phys. D Appl. Phys. 2021, 54, 415002. [Google Scholar] [CrossRef]
- Liu, X.; Zheng, X. A nonlinear constitutive model for magnetostrictive materials. Acta Mech. Sin. 2005, 21, 278–285. [Google Scholar] [CrossRef]
- Shi, P. One-dimensional magneto-mechanical model for anhysteretic magnetization and magnetostriction in ferromagnetic materials. J. Magn. Magn. Mater. 2021, 537, 168212. [Google Scholar] [CrossRef]
- Sun, L.; Liu, X.; Dong, J.; Liu, H. Three-dimensional stress-induced magnetic anisotropic constitutive model for ferromagnetic material in low intensity magnetic field. AIP Adv. 2016, 6, 095226. [Google Scholar] [CrossRef]
- Wang, S.; Wang, W.; Su, S.; Zhang, S. A magneto-mechanical model on differential permeability and stress of ferromagnetic material. J. Xi’an Univ. Sci. Technol. 2005, 25, 288–291. [Google Scholar]
- Shi, P.; Jin, K.; Zheng, X. A magnetomechanical model for the magnetic memory method. Int. J. Mech. Sci. 2017, 124, 229–241. [Google Scholar] [CrossRef]
- Wang, Z.; Deng, B.; Yao, K. Physical model of plastic deformation on magnetization in ferromagnetic materials. J. Appl. Phys. 2011, 109, 083928. [Google Scholar] [CrossRef]
- Shi, P. Magneto-elastoplastic coupling model of ferromagnetic material with plastic deformation under applied stress and magnetic fields. J. Magn. Magn. Mater. 2020, 512, 166980. [Google Scholar] [CrossRef]
- Yao, K.; Deng, B.; Wang, Z. Numerical studies to signal characteristics with the metal magnetic memory-effect in plastically deformed samples. NDT E Int. 2012, 47, 7–17. [Google Scholar] [CrossRef]
- Yao, K.; Shen, K.; Wang, Z.; Wang, Y. Three-dimensional finite element analysis of residual magnetic field for ferromagnets under early damage. J. Magn. Magn. Mater. 2014, 354, 112–118. [Google Scholar] [CrossRef]
- Usarek, Z.; Augustyniak, B.; Augustyniak, M. Separation of the effects of notch and macroresidual stress on the MFL signal characteristics. IEEE Trans. Magn. 2014, 50, 6201204. [Google Scholar] [CrossRef]
- Wang, Z.; Yao, K.; Deng, B.; Ding, K. Quantitative study of metal magnetic memory signal versus local stress concentration. NDTE Int. 2010, 43, 513–518. [Google Scholar] [CrossRef]
- Sun, L.; Liu, X.; Niu, H. A method for identifying geometrical defects and stress concentration zones in MMM technique. NDTE Int. 2019, 107, 102133. [Google Scholar] [CrossRef]
- Han, G.; Huang, H. A dual-dipole model for stress concentration evaluation based on magnetic scalar potential analysis. NDT E Int. 2021, 118, 102394. [Google Scholar] [CrossRef]
- Astley, R.; Macaulay, G.; Coyette, J. Mapped wave envelope elements for acoustical radiation and scattering. J. Sound Vib. 1994, 170, 97–118. [Google Scholar] [CrossRef]
- Xie, J.; Cui, Y.; Zhang, L.; Ma, C.; Yang, B.; Chen, X.; Liu, J. 3D forward modeling of seepage self-potential using finite-infinite element coupling method. J. Environ. Eng. Geophys. 2020, 25, 381–390. [Google Scholar] [CrossRef]
- He, M.; Shi, P.; Xie, S.; Chen, Z.; Uchimoto, T.; Takagi, T. A numerical simulation method of nonlinear magnetic flux leakage testing signals for nondestructive evaluation of plastic deformation in a ferromagnetic material. Mech. Syst. Signal Process. 2021, 155, 107670. [Google Scholar] [CrossRef]
- Lobry, J. A FEM-Green approach for magnetic field problems with open boundaries. Mathematics 2021, 9, 1662. [Google Scholar] [CrossRef]
- Tang, J.; Gong, J. 3D DC resistivity forward modeling by finite-infinite element coupling method. Chin. J. Geophys. 2010, 53, 717–728. (In Chinese) [Google Scholar]
- Jiles, D. Theory of the magneto-mechanical effect. J. Phys. D Appl. Phys. 1995, 28, 1537–1546. [Google Scholar] [CrossRef]
- Luo, X.; Zhu, H.; Ding, Y. A modified model of magneto-mechanical effect on magnetization in ferromagnetic materials. Acta Phys. Sin. 2019, 68, 187501. [Google Scholar] [CrossRef]
- Kim, S.; Yun, K.; Kim, K.; Won, C.; Ji, K. A general nonlinear magneto-elastic coupled constitutive model for soft ferromagnetic materials. J. Magn. Magn. Mater. 2020, 500, 166406. [Google Scholar] [CrossRef]
- Shi, P. Magneto-mechanical model of ferromagnetic material under a constant weak magnetic field via analytical anhysteresis solution. J. Appl. Phys. 2020, 128, 115102. [Google Scholar] [CrossRef]
- Jiles, D.; Atherton, D. Theory of ferromagnetic hysteresis. J. Magn. Magn. Mater. 1986, 61, 48–60. [Google Scholar] [CrossRef]
- Iordache, V.; Hug, E.; Buiron, N. Magnetic behaviour versus tensile deformation mechanisms in a non-oriented Fe-(3wt.%)Si steel. Mater. Sci. Eng. A 2003, 359, 62–74. [Google Scholar] [CrossRef]
- Ma, X.; Su, S.; Wang, W.; Yang, Y.; Yi, S.; Zhao, X. Damage location and numerical simulation for steel wire under torsion based on magnetic memory method. Int. J. Appl. Electromagn. Mech. 2019, 60, 223–246. [Google Scholar] [CrossRef]
- Fujiwara, K.; Nakata, T. Results for benchmark problem 7 (Asymmetrical conductor with a hole). COMPEL-Int. J. Comput. Math. Electr. Electron. Eng. 1990, 9, 137–154. [Google Scholar] [CrossRef]
- Yang, X.; He, C.; Pu, H.; Chen, L. An extended magnetic-stress coupling model of ferromagnetic materials based on energy conservation law and its application in metal magnetic memory technique. J. Magn. Magn. Mater. 2022, 544, 168653. [Google Scholar] [CrossRef]
- Fu, M.; Bao, S.; Bai, S.; Gu, Y.; Hu, S. Influence of tensile stress on magnetic memory signal in Q345 steel with different thicknesses. J. Harbin Inst. Technol. 2017, 49, 178–182. [Google Scholar]
- Bao, S.; Lou, H.; Fu, M.; Gu, Y. Correlation of stress concentration degree with residual magnetic field of ferromagnetic steel subjected to tensile stress. Nondestruct. Test. Eval. 2017, 32, 255–268. [Google Scholar] [CrossRef]
- Dong, L.; Xu, B.; Dong, S.; Li, S.; Chen, Q.; Wang, D. Stress dependence of the spontaneous stray field signals of ferromagnetic steel. NDT E Int. 2009, 42, 323–327. [Google Scholar] [CrossRef]
- Bastos, J.; Sadowski, N. Magnetic Materials and 3D Finite Element Modeling; CRC Press: Boca Raton, FL, USA, 2014. [Google Scholar] [CrossRef]
- Langman, R. Measurement of the mechanical stress in mild steel by means of rotation of magnetic field strength—Part 2: Biaxial stress. NDTE Int. 1982, 15, 91–97. [Google Scholar] [CrossRef]
- Kenji, K.; Hiroshi, S. Linearization method of output vs. stress in stress measurement using magnetic anisotropy sensor. J. Jpn. Soc. Non-Destr. Insp. 2004, 53, 93–97. [Google Scholar] [CrossRef]
- Dhar, A.; Clapham, L.; Atherton, D.L. Influence of uniaxial plastic deformation on magnetic Barkhausen noise in steel. NDT E Int. 2001, 34, 507–514. [Google Scholar] [CrossRef]
- Li, J.; Xu, M. Influence of uniaxial plastic deformation on surface magnetic field in steel. Meccanica 2012, 47, 135–139. [Google Scholar] [CrossRef]
- Hu, B.; Liu, Y.; Yu, R.Q. Numerical simulation on magnetic–mechanical behaviors of 304 austenite stainless steel. Measurement 2020, 151, 107815. [Google Scholar] [CrossRef]

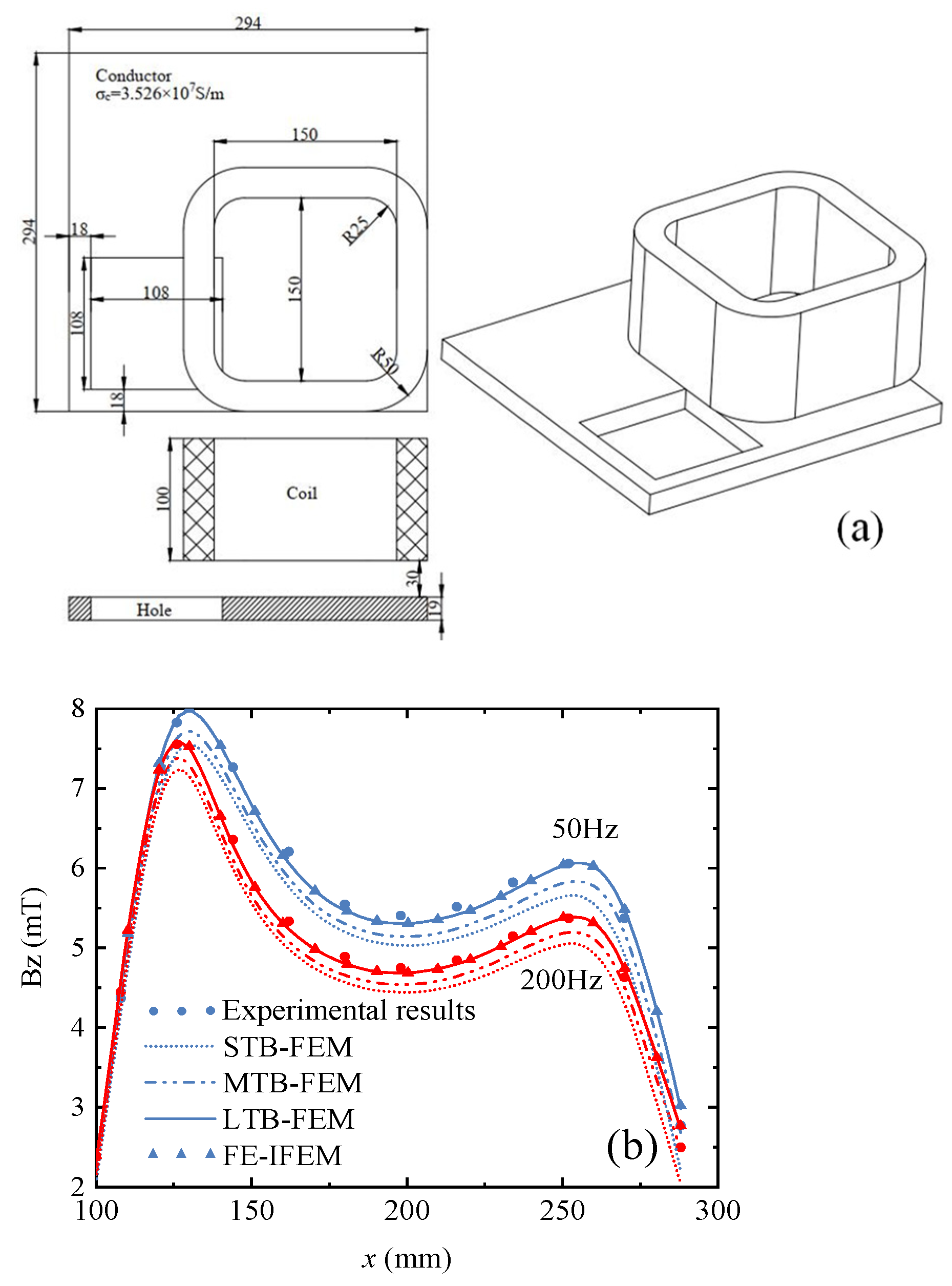





| NMSE | FE-IFEM | LTB-FEM | MTB-FEM | STB-FEM |
|---|---|---|---|---|
| 50 Hz | 0.035 | 0.038 | 0.093 | 0.438 |
| 200 Hz | 0.035 | 0.042 | 0.083 | 1.529 |
| Model | The Proposed Model | Sun’s Model [7] | Yang’s Model [31] |
|---|---|---|---|
| Hx | 7.96% | 14.07% | 9.61% |
| Hz | 40.26% | 49.16% | 48.15% |
| Parameter | Values on the Diagonal |
|---|---|
| Saturation magnetization | 1.31 × 106 A/m, 1.33 × 106 A/m, 1.31 × 106 A/m |
| Domain wall density | 233.78 A/m, 177.856 A/m, 233.78 A/m |
| Pinning loss | 374.975 A/m, 232.652 A/m, 374.975 A/m |
| Magnetization reversibility | 0.736, 0.652, 0.736 |
| Inter-domain coupling | 5.62 × 10−4, 4.17 × 10−4, 5.62 × 10−4 |
| Signal | Figure Number | Range | ||||
|---|---|---|---|---|---|---|
| Driving voltage | Figure 8a | A–B | B–C | C–D | D–E | E–F |
| Hysteresis loop | Figure 8b | a–b | b–c | c–d | d–e | e–f |
| Bx | Figure 8c | a1–b1 | b1–c1 | c1–d1 | d1–e1 | e1–f1 |
| B1x | Figure 8c | a11–b11 | b11–c11 | c11–d11 | d11–e11 | e11–f11 |
| Bz | Figure 8d | a2–b2 | b2–c2 | c2–d2 | d2–e2 | e2–f2 |
| B1z | Figure 8d | a21–b21 | b21–c21 | c21–d21 | d21–e21 | e21–f21 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hu, X.; Wang, X.; Cai, H.; Yang, X.; Pan, S.; Yang, Y.; Tan, H.; Zhang, J. Numerical Simulation of Electromagnetic Nondestructive Testing Technology for Elasto–Plastic Deformation of Ferromagnetic Materials Based on Magneto–Mechanical Coupling Effect. Sensors 2024, 24, 7103. https://doi.org/10.3390/s24227103
Hu X, Wang X, Cai H, Yang X, Pan S, Yang Y, Tan H, Zhang J. Numerical Simulation of Electromagnetic Nondestructive Testing Technology for Elasto–Plastic Deformation of Ferromagnetic Materials Based on Magneto–Mechanical Coupling Effect. Sensors. 2024; 24(22):7103. https://doi.org/10.3390/s24227103
Chicago/Turabian StyleHu, Xiangyi, Xiaoqiang Wang, Haichao Cai, Xiaokang Yang, Sanfei Pan, Yafeng Yang, Hao Tan, and Jianhua Zhang. 2024. "Numerical Simulation of Electromagnetic Nondestructive Testing Technology for Elasto–Plastic Deformation of Ferromagnetic Materials Based on Magneto–Mechanical Coupling Effect" Sensors 24, no. 22: 7103. https://doi.org/10.3390/s24227103
APA StyleHu, X., Wang, X., Cai, H., Yang, X., Pan, S., Yang, Y., Tan, H., & Zhang, J. (2024). Numerical Simulation of Electromagnetic Nondestructive Testing Technology for Elasto–Plastic Deformation of Ferromagnetic Materials Based on Magneto–Mechanical Coupling Effect. Sensors, 24(22), 7103. https://doi.org/10.3390/s24227103






