Adaptive Feature Extraction Using Sparrow Search Algorithm-Variational Mode Decomposition for Low-Speed Bearing Fault Diagnosis
Abstract
1. Introduction
- (i)
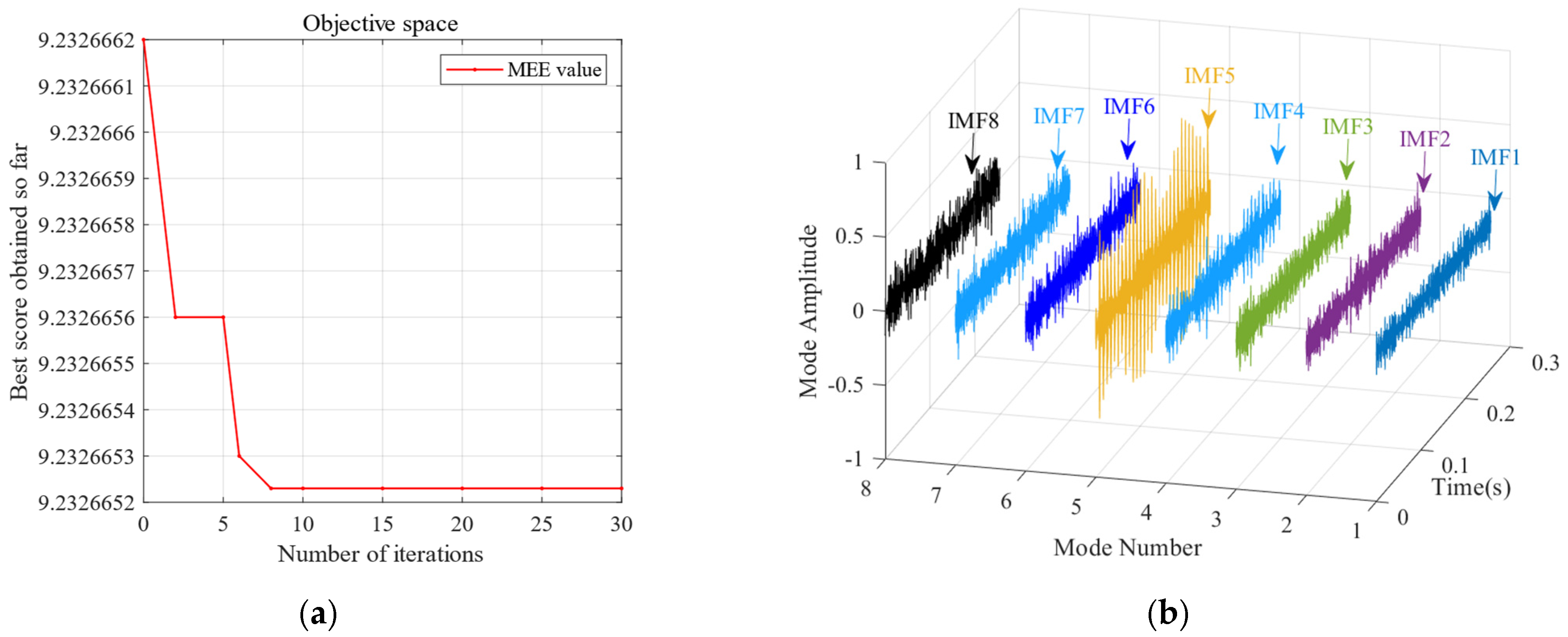
- The proposed method addresses the limitations of manually selecting VMD parameters through empirical methods and trial-and-error, which are commonly used in VMD. By integrating the SSA into the VMD decomposition and utilising the MEE as the adaptive function for the SSA to select the optimal VMD parameters, the efficiency of VMD decomposition is significantly improved.
- (ii)
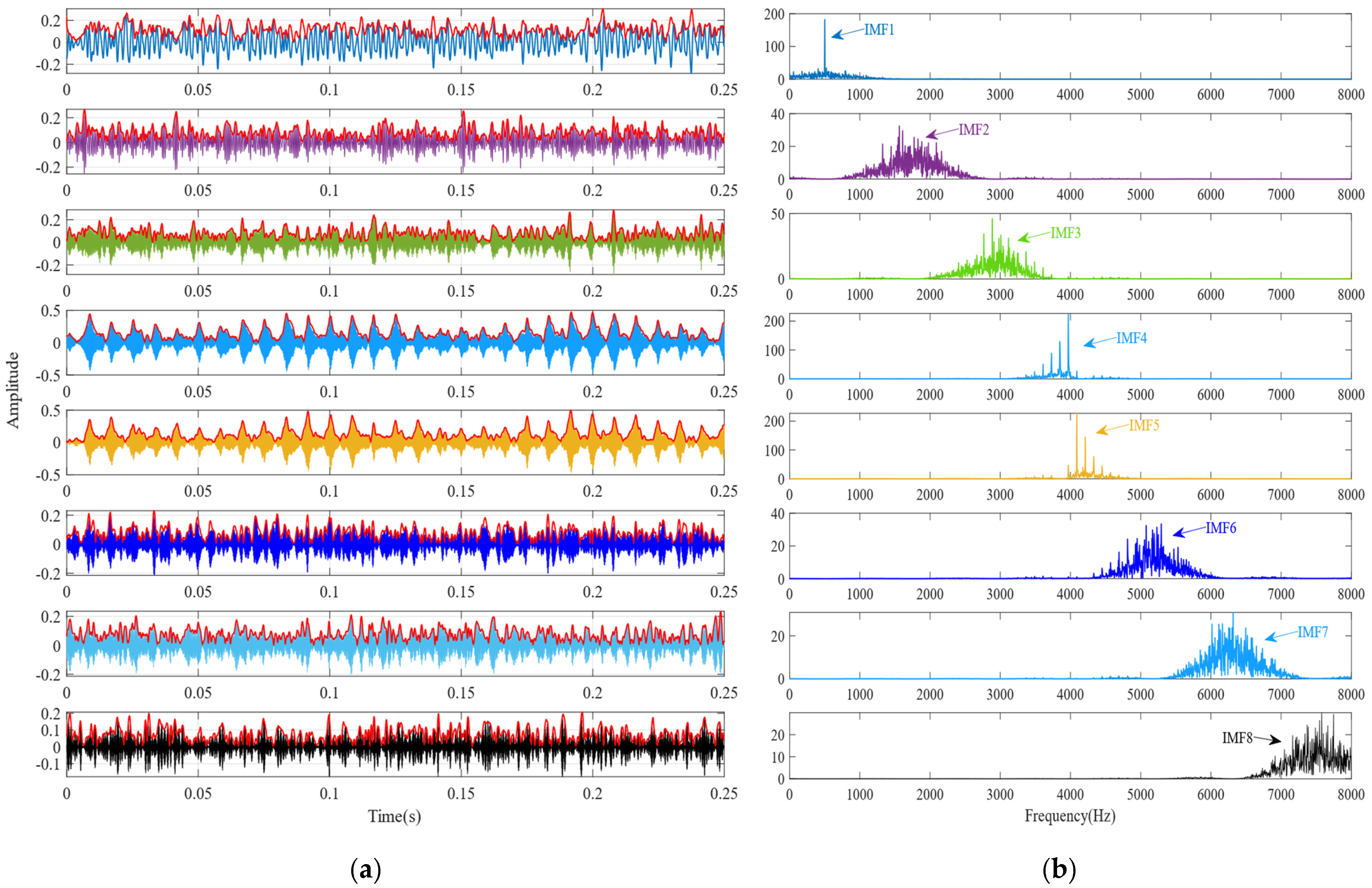
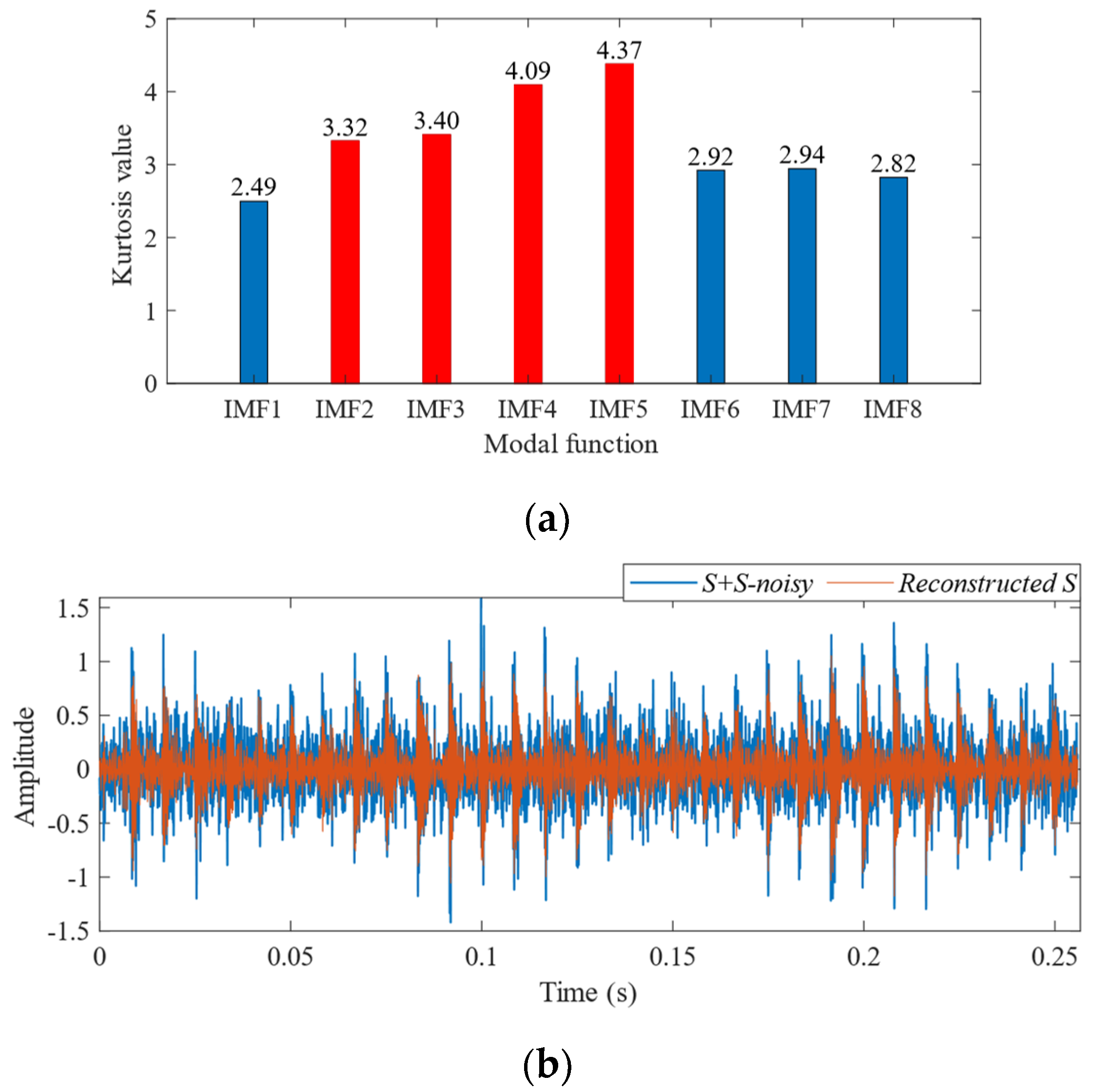
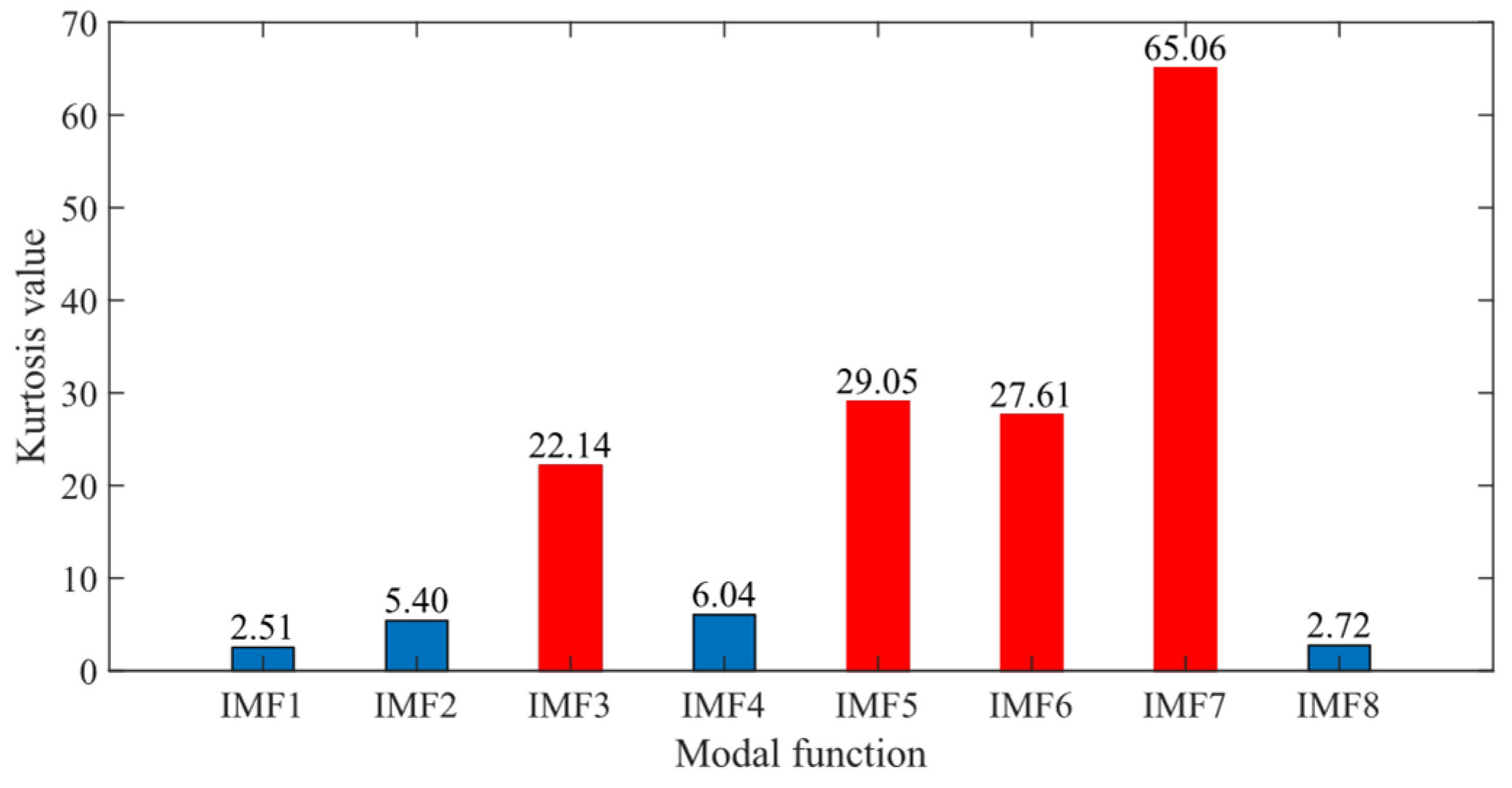
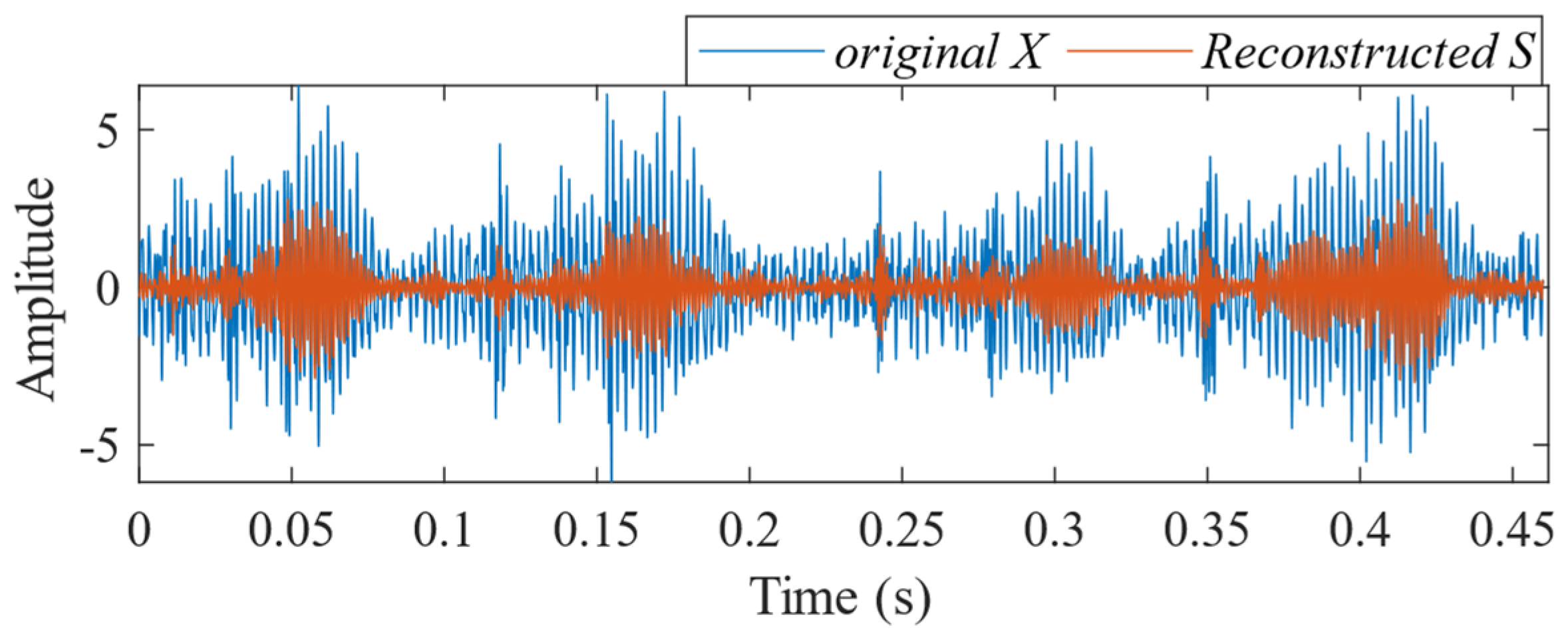
- To mitigate interference from noise components, IMF components from VMD decomposition are classified into useful and noise components using the kurtosis criterion. The useful IMF components are then reconstructed to obtain a denoised signal.
- (iii)
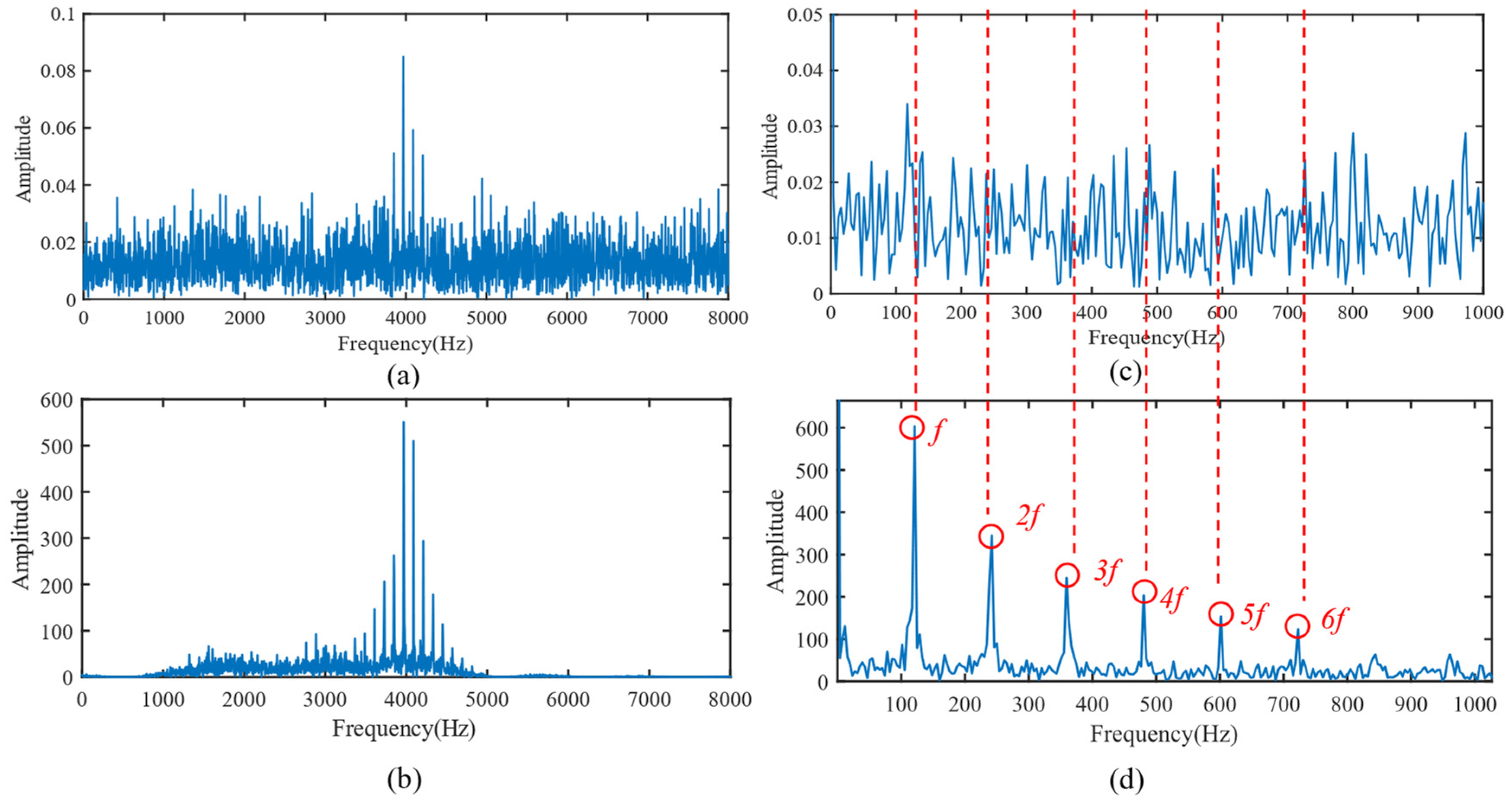
- The proposed SSA-VMD method addresses the challenge of extracting fault characteristics from low-speed bearings, even in the presence of strong environmental noise.
2. Basic Theory
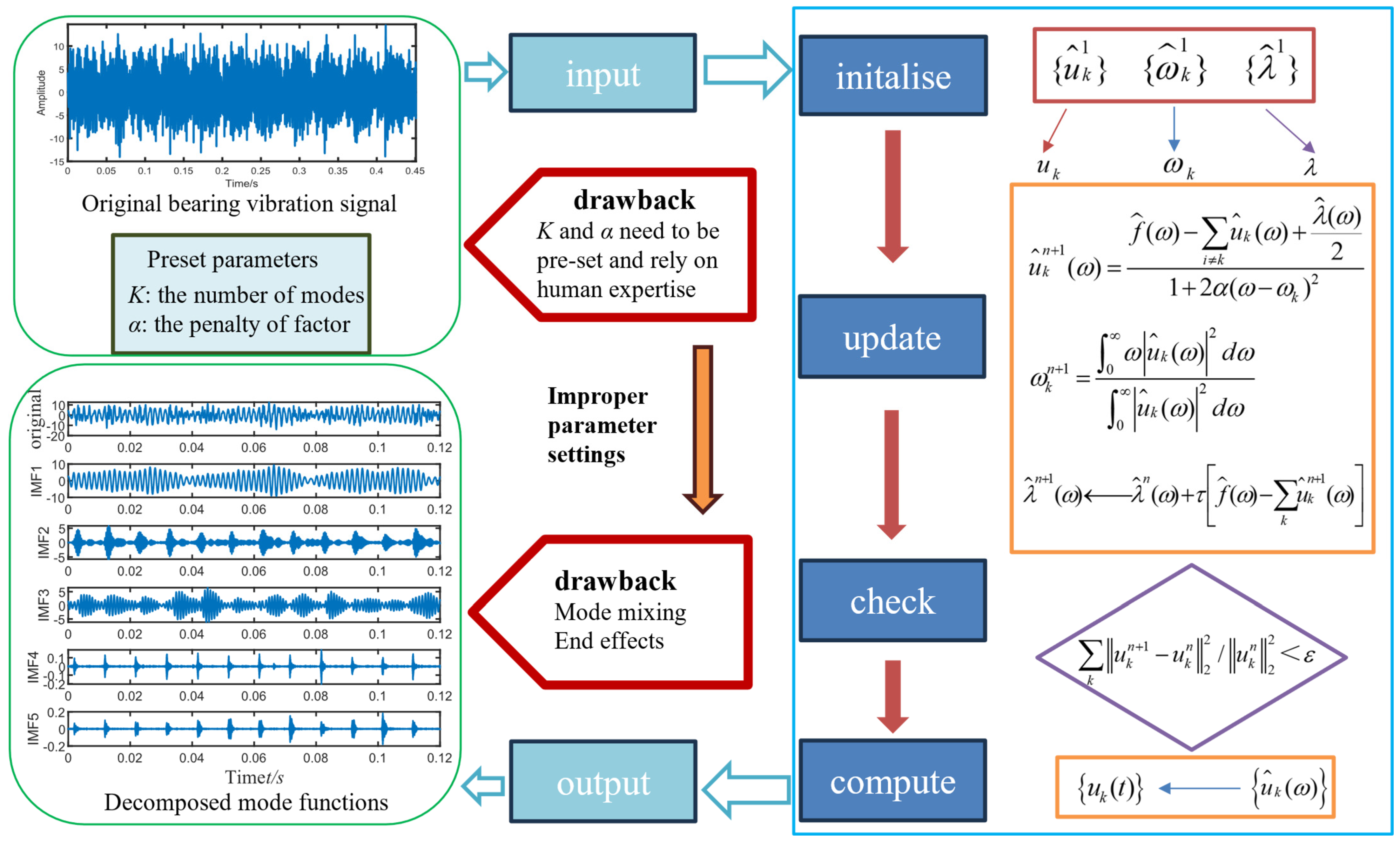
2.1. Variational Mode Decomposition
2.2. Sparrow Search Algorithm
| Algorithm 1: Framework of the SSA | |
| |
| |
| while (t < Tmax) | |
 | Rank the fitness values and find the current best individual and the current worst individual. R2 = rand (1) # Update the alarm value randomly |
| for Using Equation (8), update the sparrow’s location end | |
| for Using Equation (9), update the sparrow’s location end | |
| for Using Equation (10), update the sparrow’s location end for | |
| Get the current new location If the new location is better than before, update it t = t + 1 | |
| end while | |
| Return Xbest, fg | |
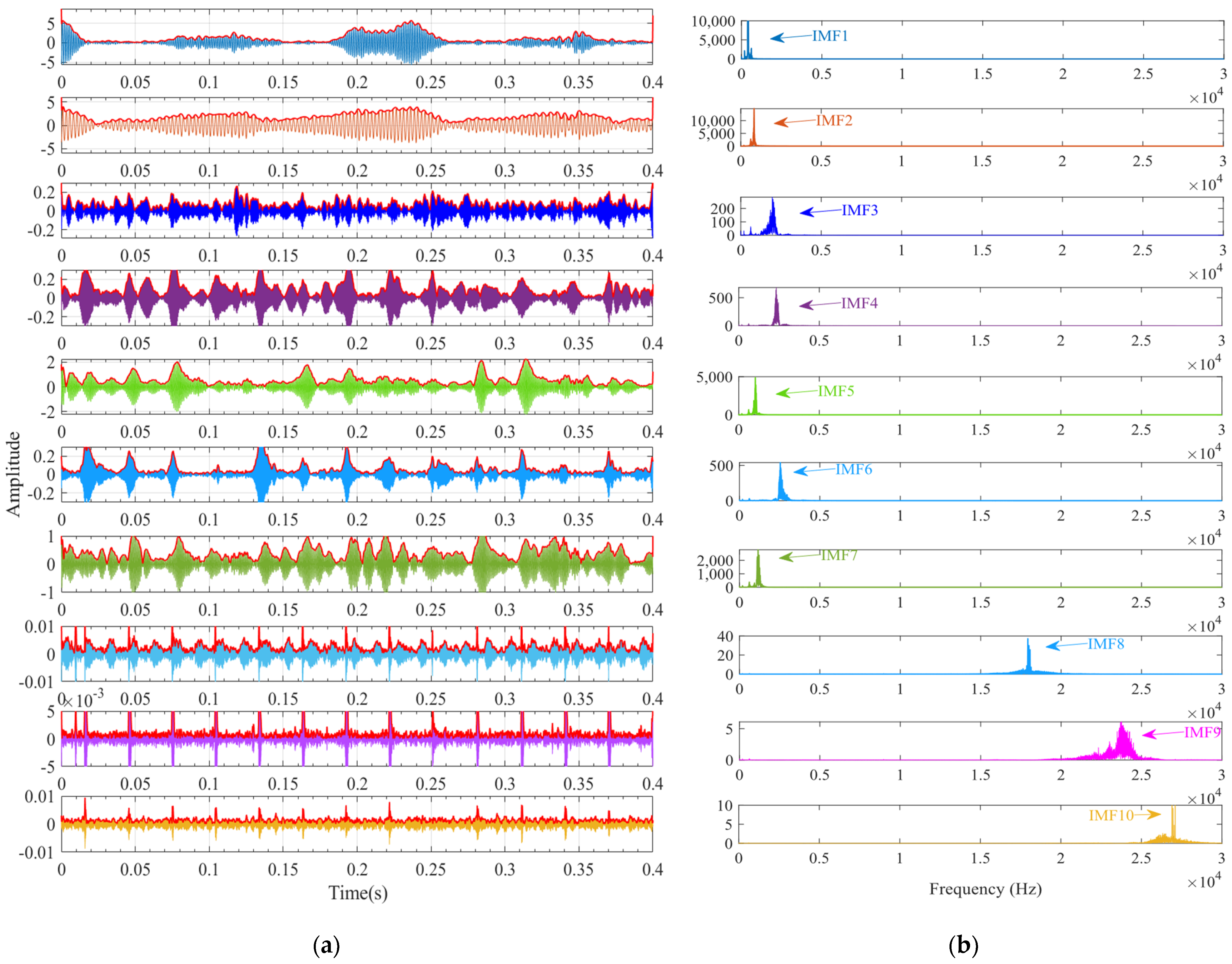
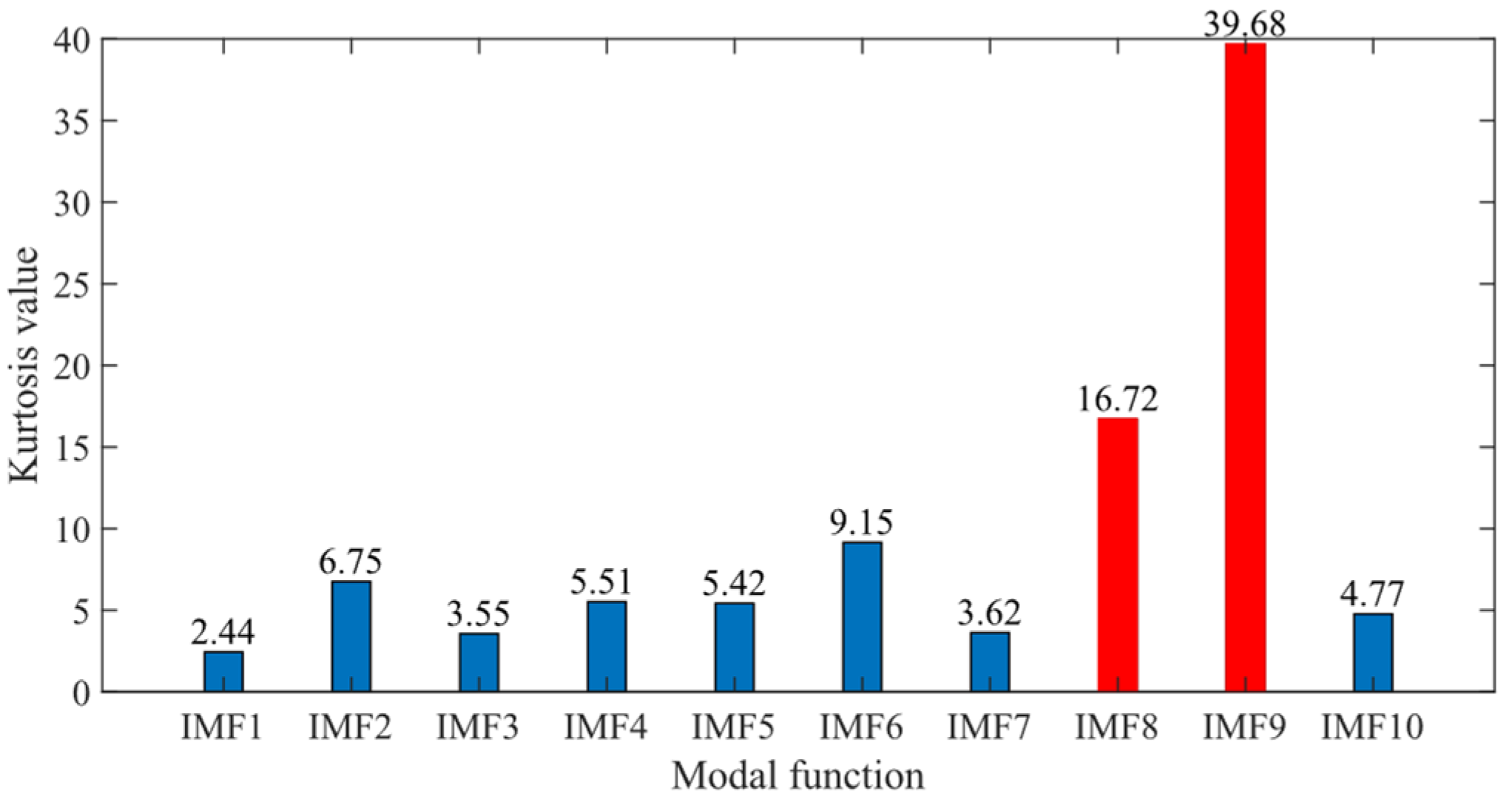
2.3. Kurtosis Criterion
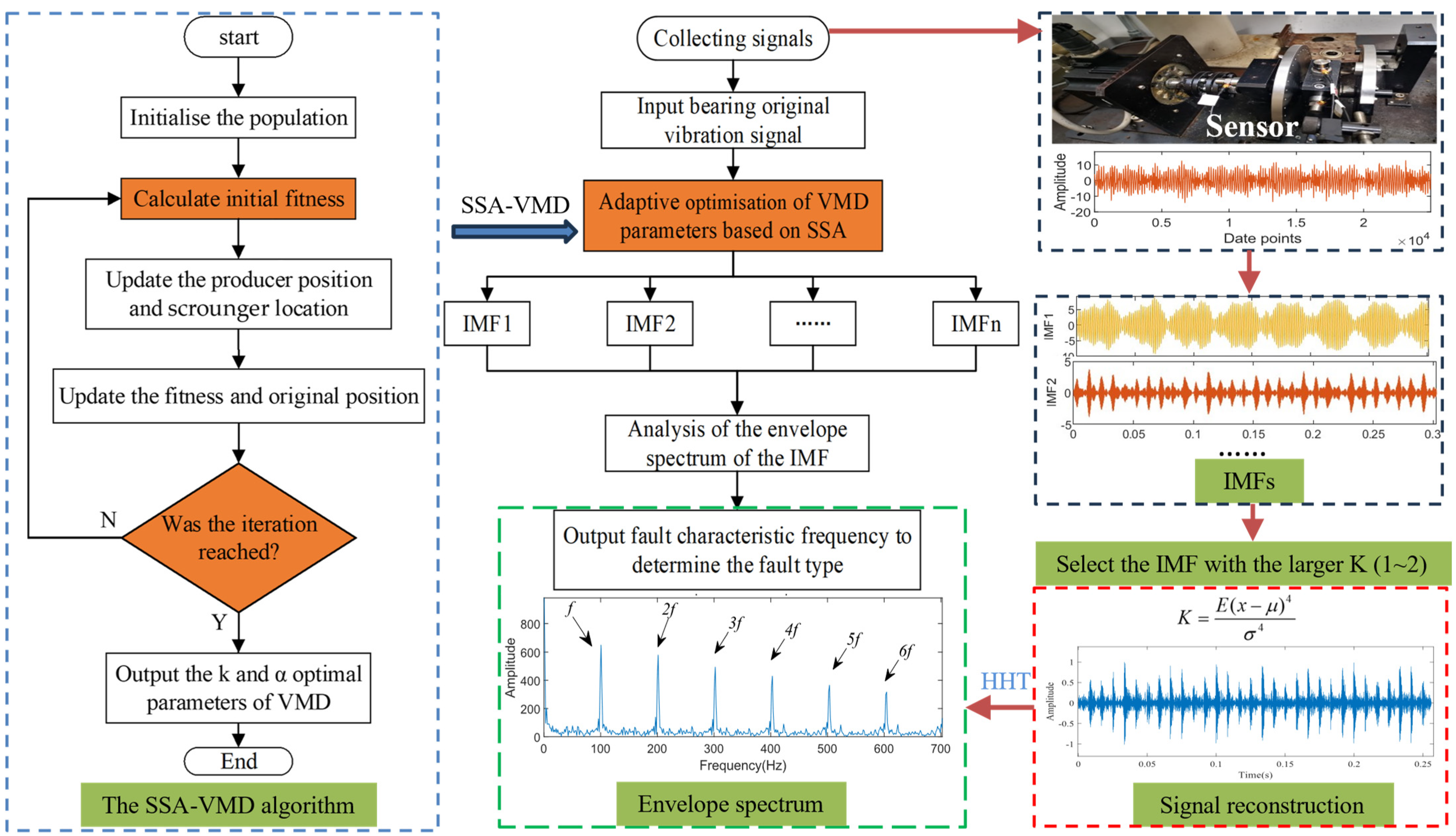
3. Proposed Method for Low-Speed Bearing Fault Diagnosis Based on SSA-VMD
| Algorithm 2: Steps of the implementation of the improved SSA-VMD model | |
| Input: raw signal | |
| Output: | |
| /* Adaptive optimisation of VMD parameters based on the SSA*/ | |
| Initialise Imax, R2, PD, SD | |
| Calculate the initial MEE | |
| Obtain | |
| while () | |
 | Update the sparrow’s location through Algorithm 1 |
| Calculate min | |
| If , | |
| end while | |
| obtain () | |
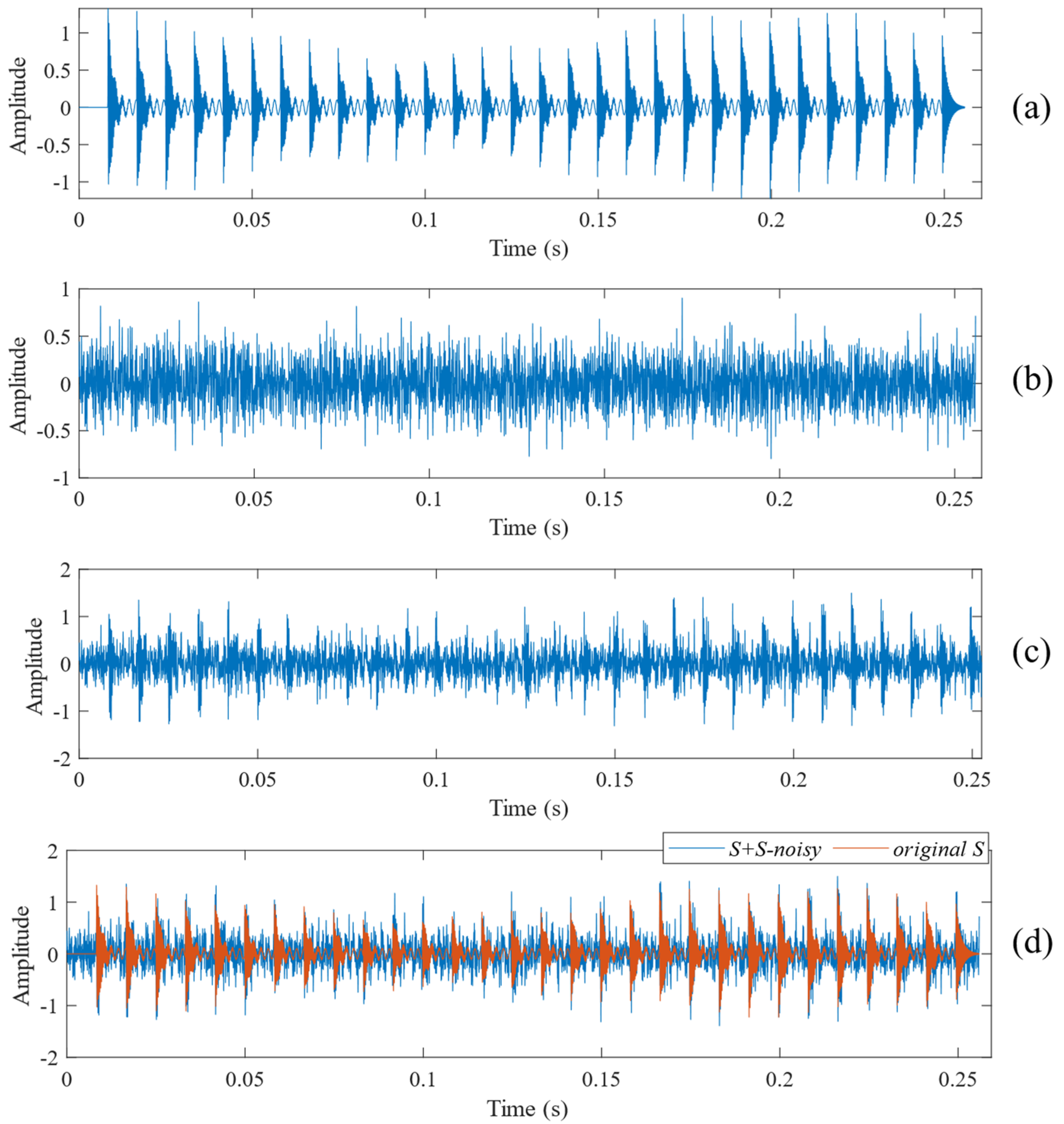
4. Simulation Signal Analysis and the Performance Testing of Algorithms
4.1. Simulation Experiment Based on Low-Speed Bearings
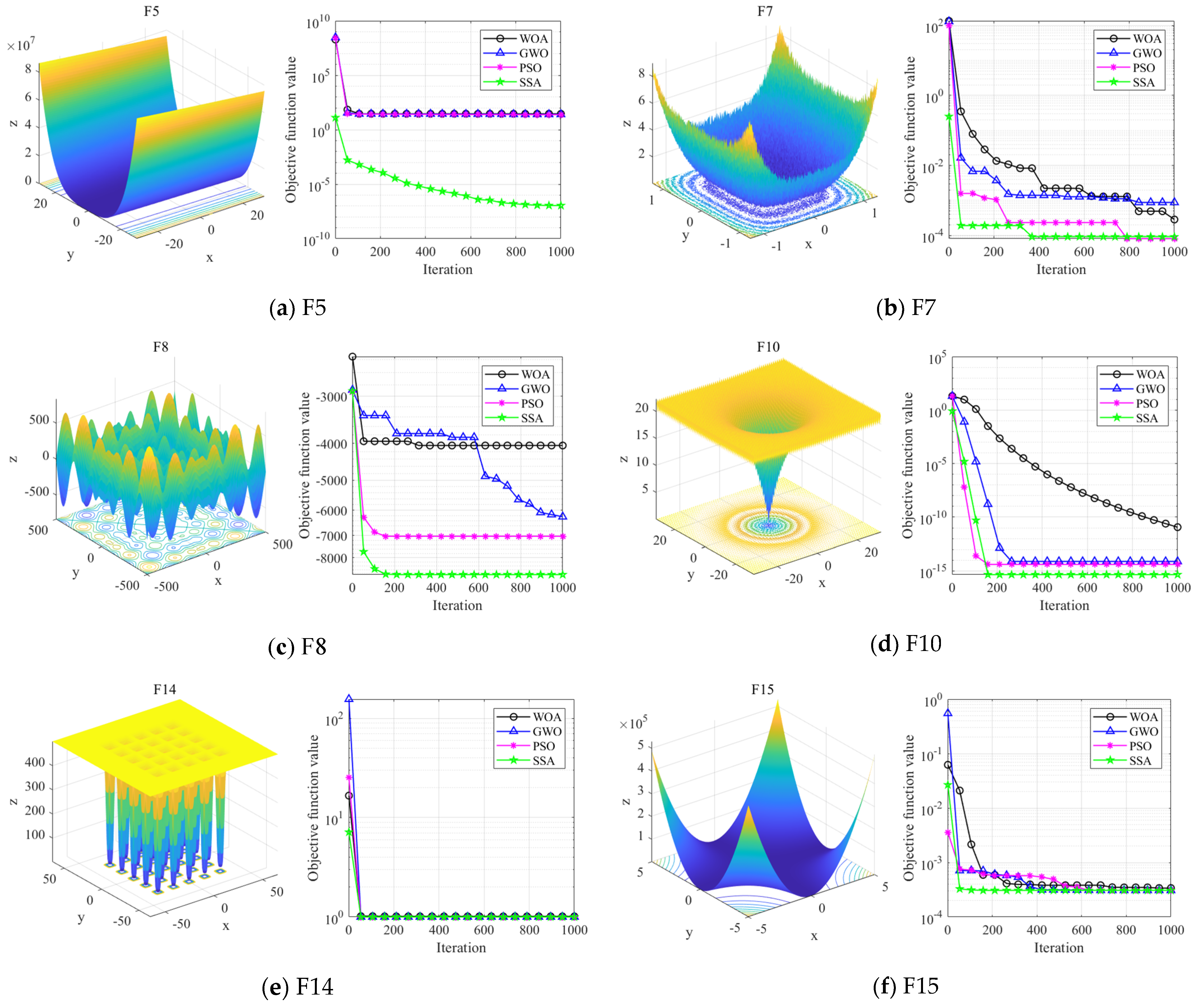
4.2. Performance Test of the SSA
- (i)
- Optimisation comparison on unimodal testing functions
- (ii)
- Optimisation comparison of multimodal testing functions
- (iii)
- Comparison of fixed-dimensional test functions
5. Experimental Analysis
5.1. Experimental Equipment
5.2. Single Fault Type Analysis
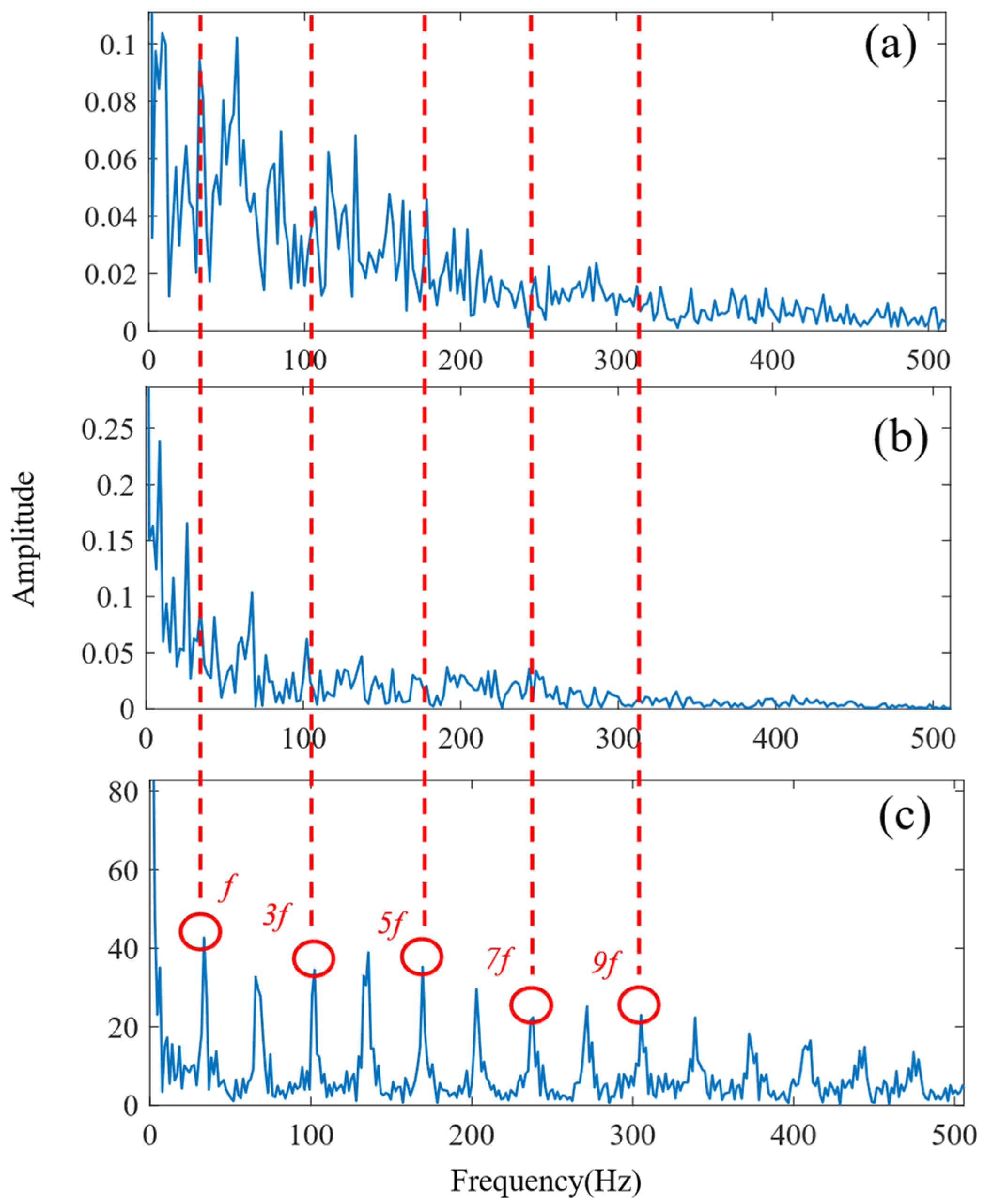
5.2.1. Outer Ring Fault
5.2.2. Inner Ring Fault
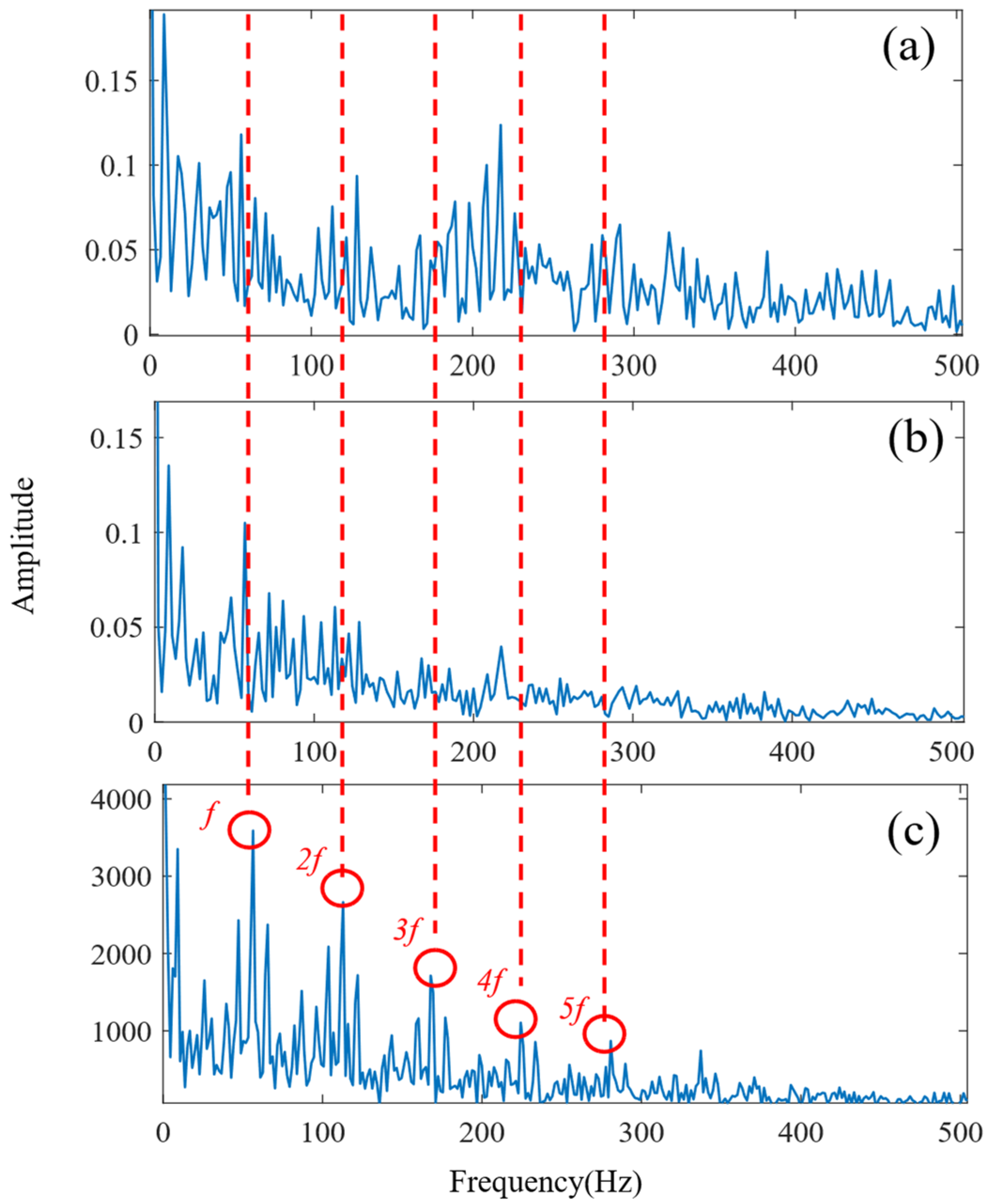
5.3. Compound Fault
6. Conclusions
- (i)
- The minimum mean envelope entropy is used as the fitness function. This enables the effective capture of weak signal information under low-speed conditions and the establishment of a robust link between the raw signal, VMD, and the SSA.
- (ii)
- The incorporation of the kurtosis criterion further enhances the method by providing a strategy for selecting the optimal IMFs for signal reconstruction, thereby reducing noise interference.
- (iii)
- The proposed method can be applied to both simulated signals and experimental signals of bearings with outer ring faults, inner ring faults, and compound faults.
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Tang, H.; Liao, Z.; Chen, P.; Zuo, D.; Yi, S. A Robust Deep Learning Network for Low-Speed Machinery Fault Diagnosis Based on Multikernel and RPCA. IEEE/ASME Trans. Mechatron. 2022, 27, 1522–1532. [Google Scholar] [CrossRef]
- Tang, H.; Liao, Z.; Chen, P.; Zuo, D.; Yi, S. A Novel Convolutional Neural Network for Low-Speed Structural Fault Diagnosis Under Different Operating Condition and Its Understanding via Visualization. IEEE Trans. Instrum. Meas. 2021, 70, 3501611. [Google Scholar] [CrossRef]
- Zhang, Z.W.; Huang, W.G.; Liao, Y.; Song, Z.S.; Shi, J.J.; Jiang, X.X.; Shen, C.Q.; Zhu, Z.K. Bearing fault diagnosis via generalized logarithm sparse regularization. Mech. Syst. Signal Proc. 2022, 167, 16. [Google Scholar] [CrossRef]
- Matania, O.; Bachar, L.; Bechhoefer, E.; Bortman, J. Signal Processing for the Condition-Based Maintenance of Rotating Machines via Vibration Analysis: A Tutorial. Sensors 2024, 24, 454. [Google Scholar] [CrossRef] [PubMed]
- Tang, H.H.; Tang, Y.M.; Su, Y.X.; Feng, W.W.; Wang, B.; Chen, P.; Zuo, D.W. Feature extraction of multi-sensors for early bearing fault diagnosis using deep learning based on minimum unscented kalman filter. Eng. Appl. Artif. Intell. 2024, 127, 14. [Google Scholar] [CrossRef]
- Giordano, D.; Giobergia, F.; Pastor, E.; La Macchia, A.; Cerquitelli, T.; Baralis, E.; Mellia, M.; Tricarico, D. Data-driven strategies for predictive maintenance: Lesson learned from an automotive use case. Comput. Ind. 2022, 134, 18. [Google Scholar] [CrossRef]
- Liu, C.; Tong, J.Y.; Zheng, J.D.; Pan, H.Y.; Bao, J.H. Rolling bearing fault diagnosis method based on multi-sensor two-stage fusion. Meas. Sci. Technol. 2022, 33, 14. [Google Scholar] [CrossRef]
- Campello, J.; Santos, D.; Pinto, M. Adaptive filtering for microelectromechanical inertial sensors using empirical mode decomposition, Hausdorff distance and fractional Gaussian noise modeling. Digit. Signal Process. 2024, 153, 104610. [Google Scholar] [CrossRef]
- Zhuo, R.J.; Deng, Z.H.; Li, Y.W.; Liu, T.; Ge, J.M.; Lv, L.S.; Liu, W. An online chatter detection and recognition method for camshaft non-circular contour high-speed grinding based on improved LMD and GAPSO-ABC-SVM. Mech. Syst. Signal Proc. 2024, 216, 111487. [Google Scholar] [CrossRef]
- Du, Y.Z.; Cao, Y.; Wang, H.C.; Li, G.H. Performance degradation assessment of rolling bearings based on the comprehensive characteristic index and improved SVDD. Meas. Sci. Technol. 2024, 35, 21. [Google Scholar] [CrossRef]
- Zhou, Z.Y.; Chen, W.H.; Yang, C. Adaptive range selection for parameter optimization of VMD algorithm in rolling bearing fault diagnosis under strong background noise. J. Mech. Sci. Technol. 2023, 37, 5759–5773. [Google Scholar] [CrossRef]
- Du, H.R.; Wang, J.X.; Qian, W.J.; Zhang, X.A.; Wang, Q. Rotating machinery fault diagnosis based on parameter-optimized variational mode decomposition. Digit. Signal Prog. 2024, 153, 20. [Google Scholar] [CrossRef]
- He, D.Q.; He, C.F.; Jin, Z.Z.; Lao, Z.P.; Yan, F.; Shan, S. A new weak fault diagnosis approach for train bearings based on improved grey wolf optimizer and adaptive variational mode decomposition. Meas. Sci. Technol. 2023, 34, 20. [Google Scholar] [CrossRef]
- Li, Z.P.; Chen, J.L.; Zi, Y.Y.; Pan, J. Independence-oriented VMD to identify fault feature for wheel set bearing fault diagnosis of high speed locomotive. Mech. Syst. Signal Proc. 2017, 85, 512–529. [Google Scholar] [CrossRef]
- Li, L.; Meng, W.L.; Liu, X.D.; Fei, J.Y. Research on Rolling Bearing Fault Diagnosis Based on Variational Modal Decomposition Parameter Optimization and an Improved Support Vector Machine. Electronics 2023, 12, 1290. [Google Scholar] [CrossRef]
- Yan, X.A.; Hua, X.; Jiang, D.; Xiang, L. A novel robust intelligent fault diagnosis method for rolling bearings based on SPAVMD and WOA-LSSVM under noisy conditions. Meas. Sci. Technol. 2024, 35, 24. [Google Scholar] [CrossRef]
- Wang, B.; Guo, Y.B.; Zhang, Z.; Wang, D.G.; Wang, J.Q.; Zhang, Y.S. Developing and applying OEGOA-VMD algorithm for feature extraction for early fault detection in cryogenic rolling bearing. Measurement 2023, 216, 14. [Google Scholar] [CrossRef]
- Wang, Y.P.; Zhang, Q.S.; Zhang, S.; Li, S.B.; Fan, Y.Q. A rotor bearing system fault diagnosis method based on FSASCA-VMD and GraphSAGE-SA. Meas. Sci. Technol. 2024, 35, 34. [Google Scholar] [CrossRef]
- Wu, C.Y.; Duan, Y.Y.; Wang, H. Signal Denoising of Traffic Speed Deflectometer Measurement Based on Partial Swarm Optimization-Variational Mode Decomposition Method. Sensors 2024, 24, 3708. [Google Scholar] [CrossRef]
- Lee, S.; Kim, S.; Kim, S.J.; Lee, J.; Yoon, H.; Youn, B.D. Revolution and peak discrepancy-based domain alignment method for bearing fault diagnosis under very low-speed conditions. Expert Syst. Appl. 2024, 251, 20. [Google Scholar] [CrossRef]
- Wei, W.; He, G.C.; Yang, J.Y.; Li, G.X.; Ding, S.L. Tool Wear Monitoring Based on the Gray Wolf Optimized Variational Mode Decomposition Algorithm and Hilbert-Huang Transformation in Machining Stainless Steel. Machines 2023, 11, 806. [Google Scholar] [CrossRef]
- Li, Z.; Yao, X.T.; Zhang, C.; Qian, Y.M.; Zhang, Y. Vibration Signal Noise-Reduction Method of Slewing Bearings Based on the Hybrid Reinforcement Chameleon Swarm Algorithm, Variate Mode Decomposition, and Wavelet Threshold (HRCSA-VMD-WT) Integrated Model. Sensors 2024, 24, 21. [Google Scholar] [CrossRef] [PubMed]
- Wumaier, T.; Xu, C.; Guo, H.Y.; Jin, Z.J.; Zhou, H.J. Fault Diagnosis of Wind Turbines Based on a Support Vector Machine Optimized by the Sparrow Search Algorithm. IEEE Access 2021, 9, 69307–69315. [Google Scholar]
- Liu, G.Y.; Shu, C.; Liang, Z.W.; Peng, B.H.; Cheng, L.F. A Modified Sparrow Search Algorithm with Application in 3d Route Planning for UAV. Sensors 2021, 21, 1224. [Google Scholar] [CrossRef]
- Zhang, M.; Xing, X.; Wang, W.L. Smart Sensor-Based Monitoring Technology for Machinery Fault Detection. Sensors 2024, 24, 2470. [Google Scholar] [CrossRef]
- Yuan, R.; Lv, Y.; Lu, Z.W.; Li, S.; Li, H.W.X. Robust fault diagnosis of rolling bearing via phase space reconstruction of intrinsic mode functions and neural network under various operating conditions. Struct. Health Monit. 2023, 22, 846–864. [Google Scholar] [CrossRef]
- Li, H.; Liu, T.; Wu, X.; Chen, Q. An optimized VMD method and its applications in bearing fault diagnosis. Measurement 2020, 166, 8. [Google Scholar] [CrossRef]
- Liu, H.; Tong, Z.M.; Shang, B.Y.; Tong, S.G. Cavitation Diagnostics Based on Self-Tuning VMD for Fluid Machinery with Low-SNR Conditions. Chin. J. Mech. Eng. 2023, 36, 15. [Google Scholar] [CrossRef]
- Han, C.K.; Lu, W.; Wang, H.Q.; Song, L.Y.; Cui, L.L. Multistate fault diagnosis strategy for bearings based on an improved convolutional sparse coding with priori periodic filter group. Mech. Syst. Signal Proc. 2023, 188, 20. [Google Scholar] [CrossRef]
- Niu, J.L.; Pan, J.F.; Qin, Z.H.; Huang, F.G.; Qin, H.H. Small-Sample Bearings Fault Diagnosis Based on ResNet18 with Pre-Trained and Fine-Tuned Method. Appl. Sci. 2024, 14, 5360. [Google Scholar] [CrossRef]
- Sha, Y.D.; Zhao, J.H.; Luan, X.C.; Liu, X.H. Fault feature signal extraction method for rolling bearings in gas turbine engines based on threshold parameter decision screening. Measurement 2024, 231, 13. [Google Scholar] [CrossRef]
- Xiong, X.; Sun, Z.R.; Wang, A.K.; Zhang, J.C.; Zhang, J.; Wang, C.W.; He, J.F. Research on Ocular Artifacts Removal from Single-Channel Electroencephalogram Signals in Obstructive Sleep Apnea Patients Based on Support Vector Machine, Improved Variational Mode Decomposition, and Second-Order Blind Identification. Sensors 2024, 24, 1642. [Google Scholar] [CrossRef] [PubMed]
- Zhang, M.; Guo, Y.B.; Zhang, Z.; He, R.B.; Wang, D.G.; Chen, J.Z.; Yin, T. Extraction of pipeline defect feature based on variational mode and optimal singular value decomposition. Pet. Sci. 2023, 20, 1200–1216. [Google Scholar] [CrossRef]
- Wang, D.; Zhong, J.J.; Shen, C.Q.; Pan, E.S.; Peng, Z.K.; Li, C. Correlation dimension and approximate entropy for machine condition monitoring: Revisited. Mech. Syst. Signal Proc. 2021, 152, 8. [Google Scholar] [CrossRef]
- Kumar, A.; Gandhi, C.P.; Vashishtha, G.; Kundu, P.; Tang, H.S.; Glowacz, A.; Shukla, R.K.; Xiang, J.W. VMD based trigonometric entropy measure: A simple and effective tool for dynamic degradation monitoring of rolling element bearing. Meas. Sci. Technol. 2022, 33, 18. [Google Scholar] [CrossRef]
- Ji, H.X.; Huang, K.; Mo, C.Q. Research on the Application of Variational Mode Decomposition Optimized by Snake Optimization Algorithm in Rolling Bearing Fault Diagnosis. Shock Vib. 2024, 2024, 21. [Google Scholar] [CrossRef]
- Tang, L.J.; Wu, X.; Wang, D.X.; Liu, X.Q. A Comparative Experimental Study of Vibration and Acoustic Emission on Fault Diagnosis of Low-Speed Bearing. IEEE Trans. Instrum. Meas. 2023, 72, 11. [Google Scholar] [CrossRef]
- Xue, J.; Shen, B. A novel swarm intelligence optimization approach: Sparrow search algorithm. Syst. Sci. Control. Eng. 2020, 8, 22–34. [Google Scholar] [CrossRef]







| Function | Range | Fmin | Dim | Type |
|---|---|---|---|---|
| x ∈ [−30, 30] | 0 | 30 | unimodal | |
| x ∈ [−1.28, 1.28] | 0 | 30 | ||
| x ∈ [−500, 500] | −418.9829n | 30 | multimodal | |
| x ∈ [−32, 32] | 0 | 30 | ||
| x ∈ [0, 14] | 0 | 2 | fixed dimensional | |
| x ∈ [−10, 10] | −1.0 | 2 |
| Function | Algorithm | Best | Average | STD |
|---|---|---|---|---|
| F5 | WOA | 26.8864 | 27.86558 | 0.763626 |
| GWO | 25.1280 | 26.0690 | 0.7228 | |
| PSO | 8.1702 | 46.5122 | 35.9017 | |
| SSA | ||||
| F7 | WOA | 0.001425 | 0.001149 | |
| GWO | ||||
| PSO | ||||
| SSA | ||||
| F8 | WOA | −7056.7 | −5080.76 | 695.7968 |
| GWO | −7570.5 | −6347.9 | 615.6736 | |
| PSO | −8700.4 | −6960.8 | 838.1568 | |
| SSA | −9013.0 | −7726.67 | 698.7294 | |
| F10 | WOA | 7.4043 | 9.897572 | |
| GWO | ||||
| PSO | 0.3429 | 0.6375 | ||
| SSA | 0.0 | |||
| F14 | WOA | 0.9980038 | 2.111973 | 2.498594 |
| GWO | 1.7593 | 0.5920 | ||
| PSO | 1.9333 | 0.3651 | ||
| SSA | ||||
| F15 | WOA | 0.0003076 | 0.000572 | 0.000324 |
| GWO | −1.0 | −0.0336 | 0.1825 | |
| PSO | −1.0 | −0.5732 | 0.3936 | |
| SSA | −1.0 | −1.0 | 0.0 |
| Parameter | Value |
|---|---|
| Bearing specs | NU204 |
| Contact angle (rad) Defect on outer (mm) | 0 0.7 × 0.25 (width × depth) |
| Defect on inner (mm) | 0.7 × 0.25 (width × depth) |
| Defect on compound outer (mm) | 0.3 × 0.05 (width × depth) |
| Defect on compound roller (mm) | 0.3 × 0.05 (width × depth) |
| Speed | fo | fi |
|---|---|---|
| 500 RPM | 36.5956 Hz | 55.0711 Hz |
| Speed | k | α |
|---|---|---|
| 500 RPM | 10 | 11,464 |
| Speed | k | α |
|---|---|---|
| 500 RPM | 8 | 17,553 |
| Speed | k | α |
|---|---|---|
| 300 RPM | 6 | 49,768 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, B.; Tang, H.; Zu, X.; Chen, P. Adaptive Feature Extraction Using Sparrow Search Algorithm-Variational Mode Decomposition for Low-Speed Bearing Fault Diagnosis. Sensors 2024, 24, 6801. https://doi.org/10.3390/s24216801
Wang B, Tang H, Zu X, Chen P. Adaptive Feature Extraction Using Sparrow Search Algorithm-Variational Mode Decomposition for Low-Speed Bearing Fault Diagnosis. Sensors. 2024; 24(21):6801. https://doi.org/10.3390/s24216801
Chicago/Turabian StyleWang, Bing, Haihong Tang, Xiaojia Zu, and Peng Chen. 2024. "Adaptive Feature Extraction Using Sparrow Search Algorithm-Variational Mode Decomposition for Low-Speed Bearing Fault Diagnosis" Sensors 24, no. 21: 6801. https://doi.org/10.3390/s24216801
APA StyleWang, B., Tang, H., Zu, X., & Chen, P. (2024). Adaptive Feature Extraction Using Sparrow Search Algorithm-Variational Mode Decomposition for Low-Speed Bearing Fault Diagnosis. Sensors, 24(21), 6801. https://doi.org/10.3390/s24216801






