i-PHAOS: An Overview with an Open-Source Collaborative Database on Miniaturized Integrated Spectrometers
Abstract
1. Introduction
2. Spectrometers: Definitions and Performance Metrics
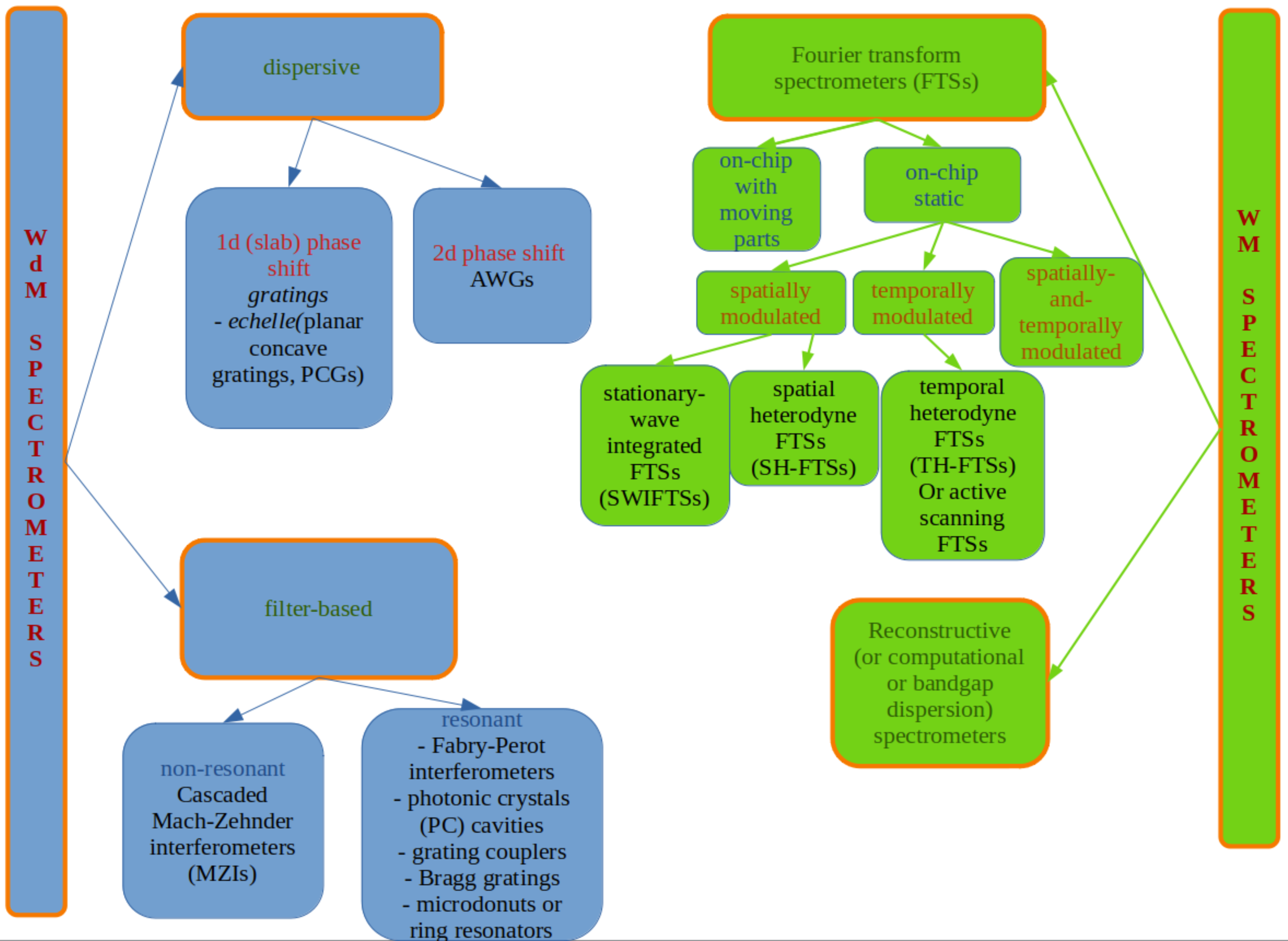
3. Mechanism-Based Classification of Spectrometers
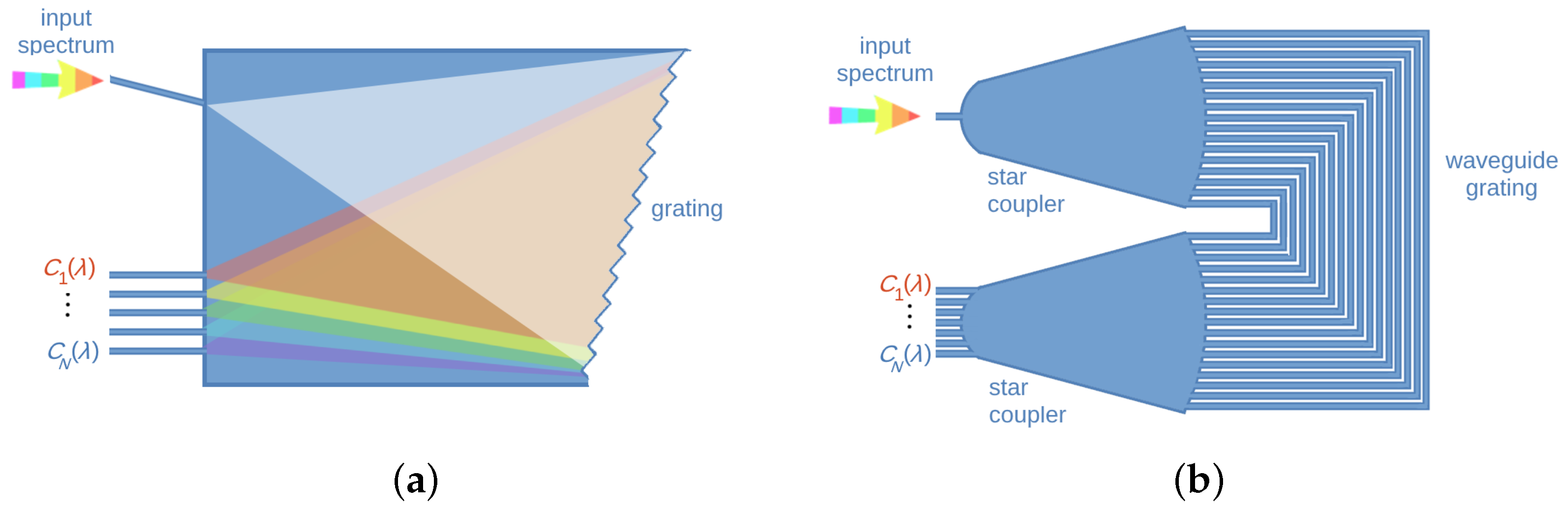
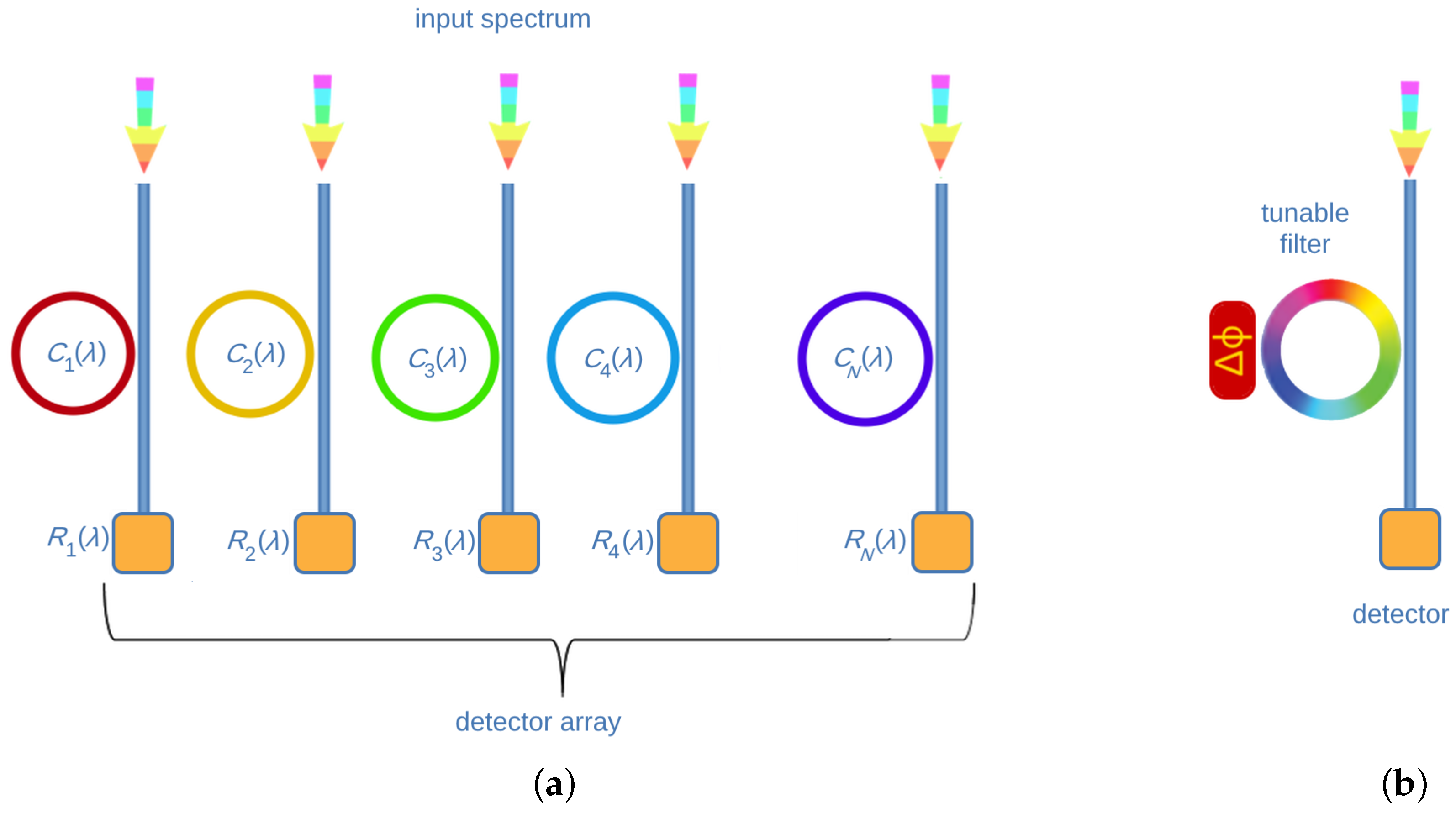
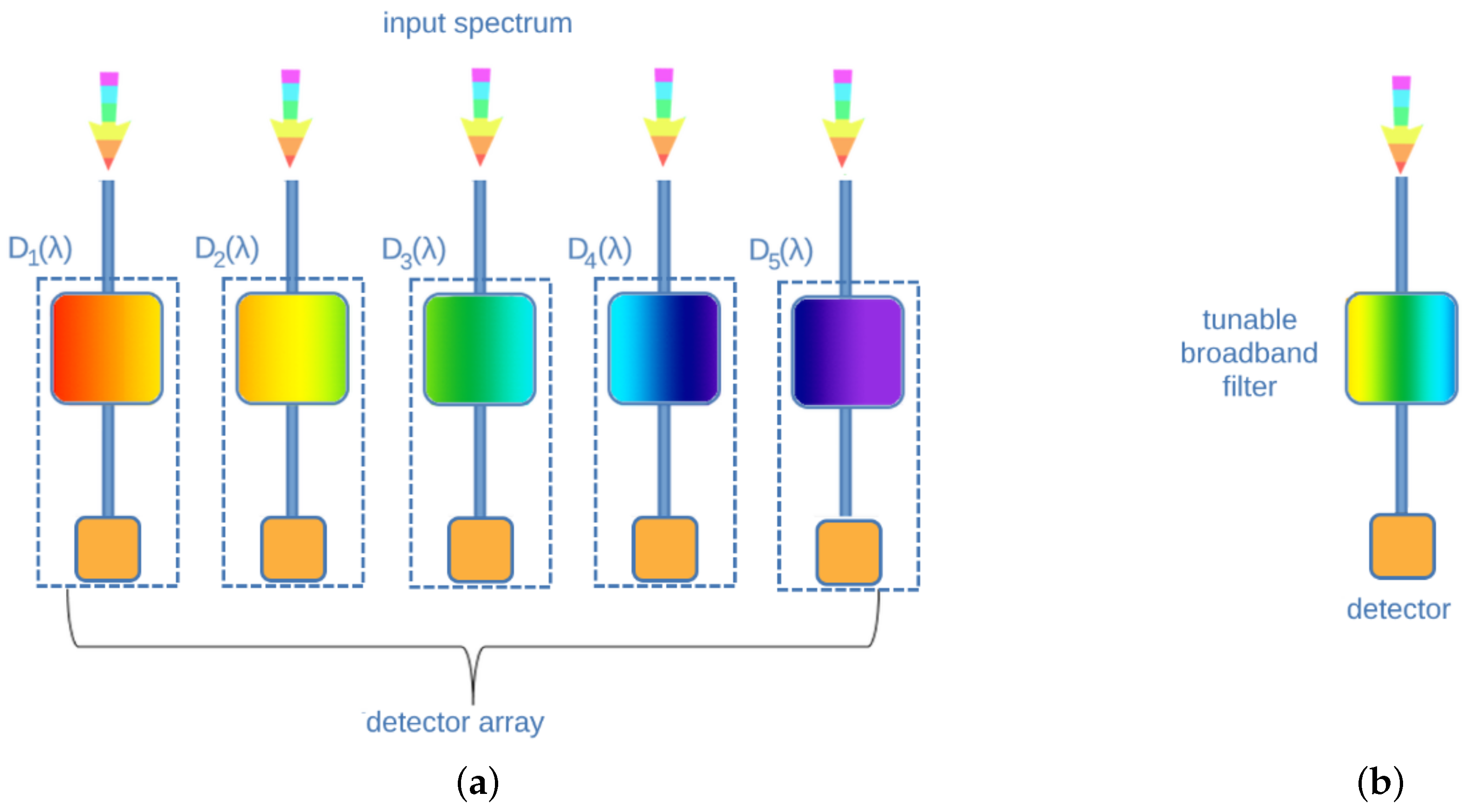
3.1. Wavelength Demultiplexing Spectrometers
3.2. Wavelength Multiplexing Spectrometers
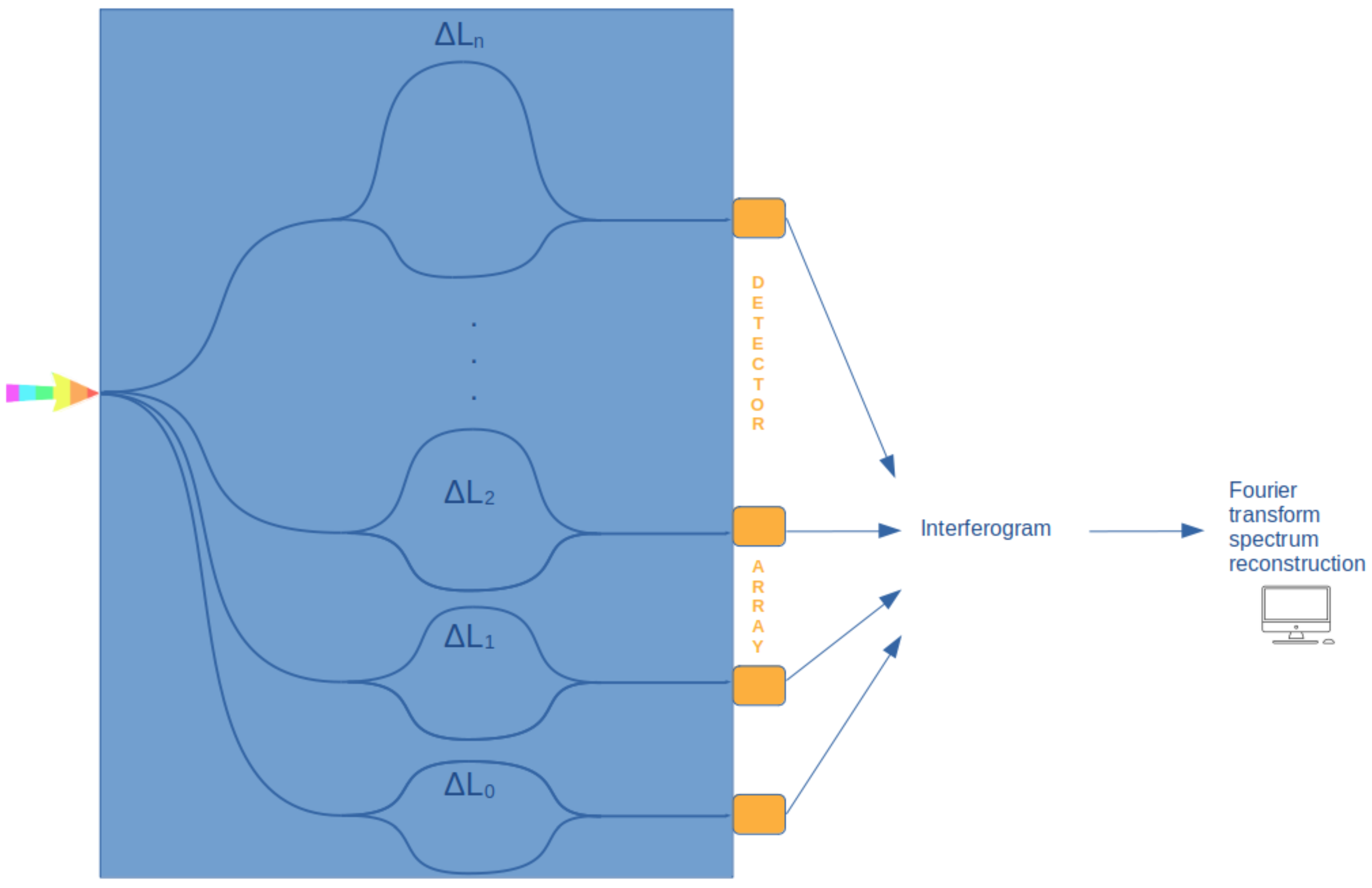
3.2.1. Fourier Transform Spectrometers (FTSs)
3.2.2. Reconstructive Spectrometers (or Computational Spectrometers) (RSs)
4. Spectrometer Classification Based on Material Type: Inorganic, Organic and Metamaterials
4.1. Inorganic Material-Based Spectrometers
4.2. Organic Material-Based Spectrometers
4.3. Metamaterial-Based Spectrometers
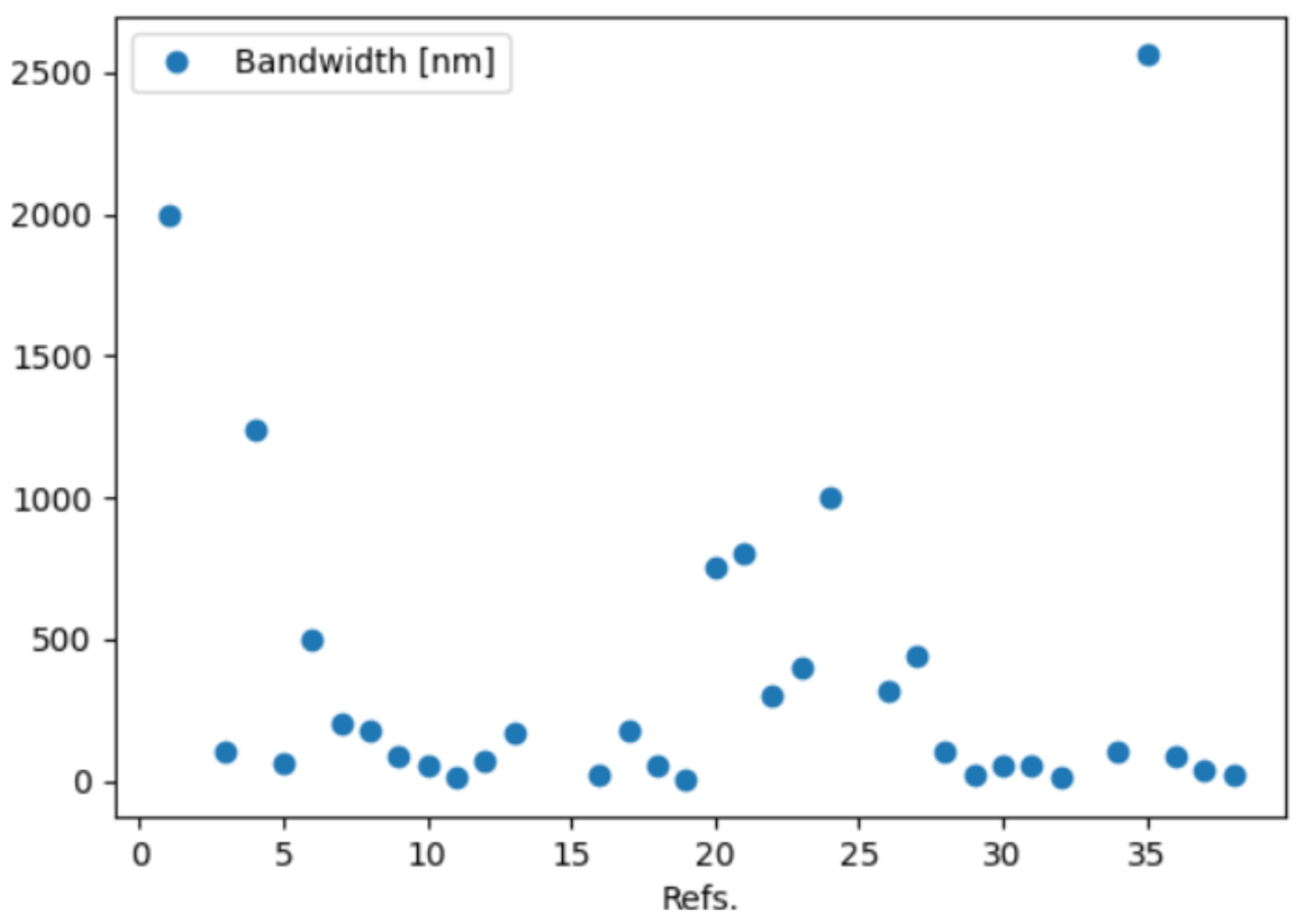
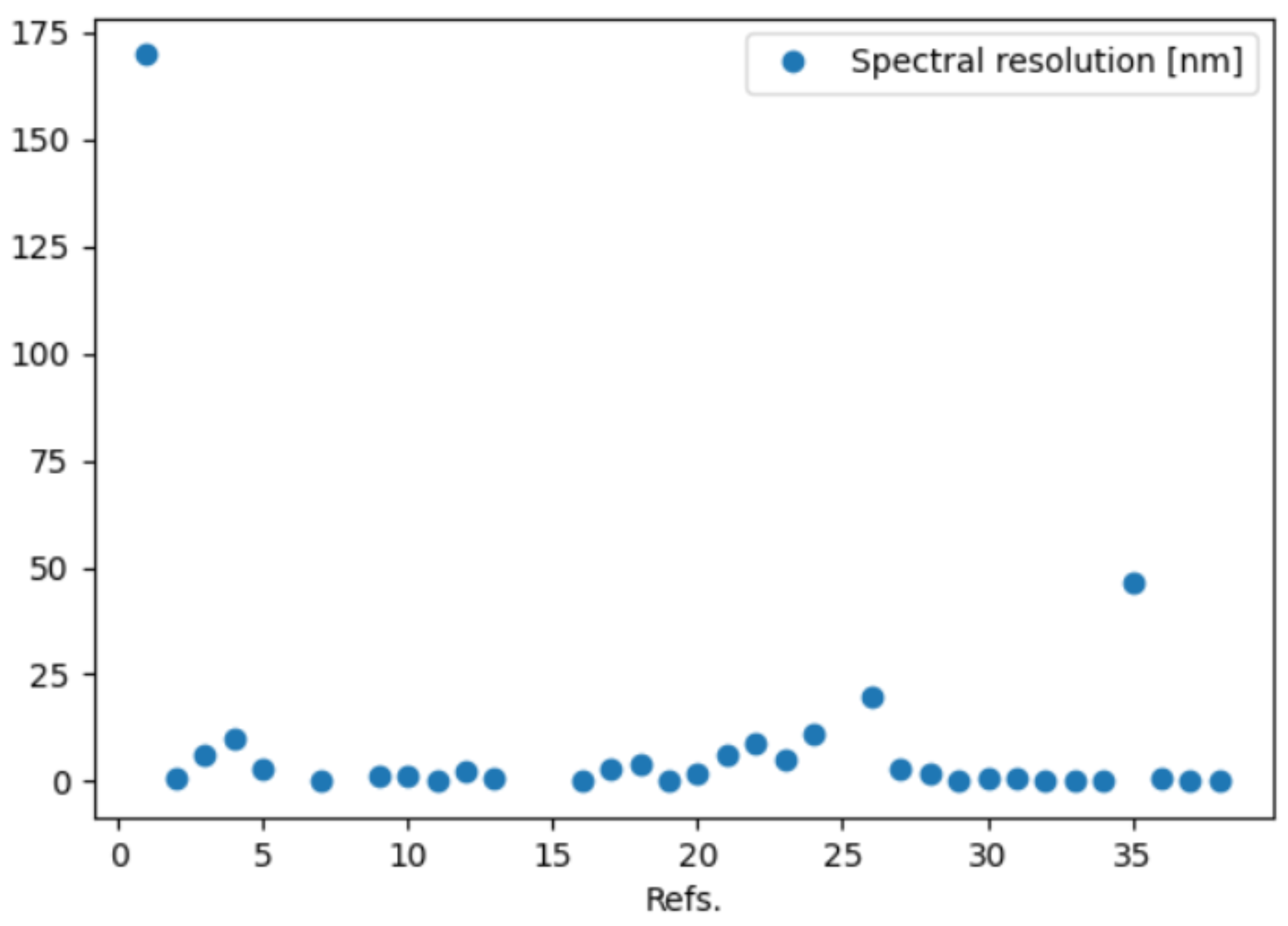
5. Open-Source Spectrometer Database
- 1.
- Type of spectrometer: it is possible to choose the entry as dispersive (gratings) spectrometer, filter-based spectrometer, Fourier transform spectrometer or reconstructive (computational) spectrometer.
- 2.
- Materials/integrated platform.
- 3.
- Spectral range: this is sub-categorized as spectral range (min value), spectral range (max value), bandwidth and target peak. All data are provided in nm.
- 4.
- Spectral resolution [nm].
- 5.
- Bandwidth-to-resolution ratio.
- 6.
- Dynamic range.
- 7.
- Footprint, area [mm].
- 8.
- Footprint, volume [mm].
- 9.
- Measuring speed [s].
- 10.
- CMOS compatibility.
- 11.
- Year.
- 12.
- Ref.
- 1.
- Material.
- 2.
- Spectral range: this is sub-categorized as spectral range (min value), spectral range (max value) and target peak. All data are provided in nm.
- 3.
- Spectral resolution [nm].
- 4.
- FWHM [nm].
- 5.
- D* [Jones].
- 6.
- EQE.
- 7.
- R [A W].
- 8.
- Bias [V].
- 9.
- LDR [dB].
- 10.
- f [kHz].
- 11.
- Footprint, area [mm].
- 12.
- Footprint, volume [mm].
- 13.
- CMOS compatible.
- 14.
- Year.
- 15.
- Ref.

6. Conclusions
Funding
Data Availability Statement
Conflicts of Interest
References
- Kulakowski, J.; d’Humières, B. Chip-size spectrometers drive spectroscopy towards consumer and medical applications. In Proceedings of the Photonic Instrumentation Engineering VIII, Online, 6–12 March 2021; p. 116931A. [Google Scholar] [CrossRef]
- Wolffenbuttel, R. State-of-the-art in integrated optical microspectrometers. IEEE Trans. Instrum. Meas. 2004, 53, 197–202. [Google Scholar] [CrossRef]
- Goldman, D.; White, P.; Anheier, N. Miniaturized spectrometer employing planar waveguides and grating couplers for chemical analysis. Appl. Opt. 1990, 29, 4583–4589. [Google Scholar] [CrossRef] [PubMed]
- Yang, Z.; Albrow-Owen, T.; Cai, W.; Hasan, T. Miniaturization of optical spectrometers. Science 2021, 371, eabe0722. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Yao, C.; Xia, J.; Wang, H.; Cheng, Q.; Penty, R.; Fainman, Y.; Pan, S. Advances in cost-effective integrated spectrometers. Light Sci. Appl. 2022, 11, 174. [Google Scholar] [CrossRef]
- Qiu, Y.; Zhou, X.; Tang, X.; Hao, Q.; Chen, M. Micro spectrometers based on materials nanoarchitectonics. Materials 2023, 16, 2253. [Google Scholar] [CrossRef]
- Wang, J.; Zheng, B.; Wang, X. Strategies for high performance and scalable on-chip spectrometers. J. Phys. Photonics 2020, 3, 012006. [Google Scholar] [CrossRef]
- Jones, R. Phenomenological description of the response and detecting ability of radiation detectors. Proc. IRE 1959, 47, 1495–1502. [Google Scholar] [CrossRef]
- Liu, J. Photonic Devices; Cambridge University Press: Cambridge, UK, 2005. [Google Scholar]
- Czerny, M.; Turner, A. Über den Astigmatismus bei Spiegelspektrometern. Z. Für Phys. 1930, 61, 792–797. [Google Scholar] [CrossRef]
- Ebert, H. Zwei Formen von Spectrographen. Ann. Der Phys. 1889, 274, 489–493. [Google Scholar] [CrossRef]
- Fastie, W. A Small Plane Grating Monochromator. J. Opt. Soc. Am. 1952, 42, 641–647. [Google Scholar] [CrossRef]
- Rowland, H. On concave gratings for optical purposes. Philos. Mag. Ser. 5 1883, 16, 197–210. [Google Scholar] [CrossRef]
- Namioka, T. Diffraction gratings. In Vacuum Ultraviolet Spectroscopy; Academic Press: Cambridge, MA, USA, 2000; pp. 347–377. [Google Scholar]
- Katsunari, O.; Kenzo, I. Fabrication of silicon reflection-type arrayed-waveguide gratings with distributed Bragg reflectors. Opt. Lett. 2013, 38, 3530–3533. [Google Scholar]
- Pathak, S.; Dumon, P.; Van Thourhout, D.; Bogaerts, W. Comparison of AWGs and Echelle Gratings for Wavelength Division Multiplexing on Silicon-on-Insulator. IEEE Photonics J. 2014, 6, 4900109. [Google Scholar] [CrossRef]
- Carmo, J.; Rocha, R.; Bartek, M.; de Graaf, G.; Wolffenbuttel, R.; Correia, J. A review of visible-range Fabry-Perot microspectrometers in silicon for the industry. Opt. Laser Technol. 2012, 44, 2312–2320. [Google Scholar] [CrossRef]
- Emadi, A.; Wu, H.; de Graaf, G.; Wolffenbuttel, R. Design and implementation of a sub-nm resolution microspectrometer based on a Linear-Variable Optical Filter. Opt. Express 2012, 20, 489–507. [Google Scholar] [CrossRef] [PubMed]
- Liapis, A.; Gao, B.; Siddiqui, M.; Shi, Z.; Boyd, R. On-chip spectroscopy with thermally tuned high-Q photonic crystal cavities. Appl. Phys. Lett. 2016, 108, 021105. [Google Scholar] [CrossRef]
- Sharma, N.; Kumar, G.; Rakesh, V.; Mote, G.; Gupta, S. Reconstructive spectrometer using a photonic crystal cavity. Opt. Express 2021, 29, 26645–26657. [Google Scholar] [CrossRef]
- Zheng, S.; Cai, H.; Gu, Y.; Chin, L.; Liu, A. High-resolution On-chip Spectrometer with a Tunable Micro-ring Resonator Filter. In Proceedings of the Conference on Lasers and Electro-Optics, OSA Technical Digest (Online), San Jose, CA, USA, 5–10 June 2016; Optica Publishing Group: Washington, DC, USA, 2016. [Google Scholar] [CrossRef]
- Zheng, S.; Cai, H.; Song, J.; Zou, J.; Liu, P.; Lin, Z.; Kwong, D.; Liu, A. A Single-Chip Integrated Spectrometer via Tunable Microring Resonator Array. IEEE Photonics J. 2019, 11, 6602809. [Google Scholar] [CrossRef]
- Chen, X.; Gan, X.; Zhu, Y.; Zhang, J. On-chip micro-ring resonator array spectrum detection system based on convex optimization algorithm. Nanophotonics 2023, 12, 715–724. [Google Scholar] [CrossRef]
- Zhu, H.; Zheng, S.; Zou, J.; Cai, H.; Li, Z.; Liu, A. A High-resolution Integrated Spectrometer based on cascaded a ring resonator and an AWG. In Proceedings of the Conference on Lasers and Electro-Optics, OSA Technical Digest (Online), San Jose, CA, USA, 10–15 May 2020; Optica Publishing Group: Washington, DC, USA, 2020. [Google Scholar] [CrossRef]
- Zhang, Z.; Wang, Y.; Wang, J.; Yi, D.; Chan, D.; Yuan, W.; Tsang, H. Integrated scanning spectrometer with a tunable micro-ring resonator and an arrayed waveguide grating. Photonics Res. 2022, 10, A74–A81. [Google Scholar] [CrossRef]
- Horie, Y.; Arbabi, A.; Han, S.; Faraon, A. High resolution on-chip optical filter array based on double subwavelength grating reflectors. Opt. Express 2015, 23, 29848–29854. [Google Scholar] [CrossRef] [PubMed]
- Alshamrani, N.; Grieco, A.; Hong, B.; Fainman, Y. Miniaturized integrated spectrometer using a silicon ring-grating design. Opt. Express 2021, 29, 15279–15287. [Google Scholar] [CrossRef] [PubMed]
- Bogaerts, W.; Pathak, S.; Ruocco, A.; Dwivedi, S. Silicon photonics non-resonant wavelength filters: Comparison between AWGs, echelle gratings, and cascaded Mach-Zehnder filters. In Proceedings of the Integrated Optics: Devices, Materials, and Technologies XIX, San Francisco, CA, USA, 7–12 February 2015; Volume 9365. [Google Scholar] [CrossRef]
- Bates, J. Fourier transform spectroscopy. Comput. Math. Appl. 1978, 4, 73–84. [Google Scholar] [CrossRef]
- Fellgett, P. Theory of Infrared Sensitivities and Its Application to Investigations of Stellar Radiation in the Near Infrared. Ph.D. Thesis, Cambridge University, Cambridge, UK, 1951. [Google Scholar]
- Connes, J.; Connes, P. Near-Infrared Planetary Spectra by Fourier Spectroscopy. I. Instruments and Results. J. Opt. Soc. Am. 1966, 56, 896–910. [Google Scholar] [CrossRef]
- Zhang, L.; Chen, J.; Ma, C.; Li, W.; Qi, Z.; Xue, N. Research Progress on On-Chip Fourier Transform Spectrometer. Laser Photonics Rev. 2021, 15, 2100016. [Google Scholar] [CrossRef]
- le Coarer, E.; Blaize, S.; Benech, P.; Stefanon, I.; Morand, A.; Lérondel, G.; Leblond, G.; Kern, P.; Fedeli, J.; Royer, P. Wavelength-scale stationary-wave integrated Fourier-transform spectrometry. Nat. Photon 2007, 1, 473–478. [Google Scholar] [CrossRef]
- le Coarer, E.; Venancio, L.; Kern, P.; Ferrand, J.; Puget, P.; Ayraud, M.; Bonneville, C.; Demonte, B.; Morand, A.; Boussey, J.; et al. SWIFTS: On-chip very high spectral resolution spectrometer. In Proceedings of the International Conference on Space Optics—ICSO 2010, Rhodes Island, Greece, 4–8 October 2010; Volume 10565. [Google Scholar] [CrossRef]
- Cavalier, P.; Villégier, J.; Feautrier, P.; Constancias, C.; Morand, A. Light interference detection on-chip by integrated SNSPD counters. AIP Adv. 2011, 1, 042120. [Google Scholar] [CrossRef]
- Pohl, D.; Reig Escalé, M.; Madi, M.; Kaufmann, F.; Brotzer, P.; Sergeyev, A.; Guldimann, B.; Giaccari, P.; Alberti, E.; Meier, U.; et al. An integrated broadband spectrometer on thin-film lithium niobate. Nat. Photonics 2019, 14, 24–29. [Google Scholar] [CrossRef]
- Heidari, E.; Xu, X.; Chung, C.; Chen, R. On-chip Fourier transform spectrometer on silicon-on-sapphire. Opt. Lett. 2019, 44, 2883–2886. [Google Scholar] [CrossRef]
- Zheng, S.; Zou, J.; Cai, H.; Song, J.; Chin, L.; Liu, P.; Lin, Z.; Kwong, D.; Liu, A. Microring resonator-assisted Fourier transform spectrometer with enhanced resolution and large bandwidth in single chip solution. Nat. Commun. 2019, 10, 2349. [Google Scholar] [CrossRef]
- Xu, H.; Qin, Y.; Hu, G.; Tsang, H.K. Scalable integrated two-dimensional Fourier-transform spectrometry. Nat. Commun. 2024, 15, 436. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Wu, Y.; Wang, C.; Bao, F.; Yang, Z.; Pan, S. An inversely designed integrated spectrometer with reconfigurable performance and ultra-low power consumption. Opto-Electron. Adv. 2024, 7, 240099-1. [Google Scholar] [CrossRef]
- Wang, Z.; Yu, Z. Spectral analysis based on compressive sensing in nanophotonic structures. Opt. Express 2014, 22, 25608–25614. [Google Scholar] [CrossRef] [PubMed]
- Cao, H. Perspective on speckle spectrometers. J. Opt. 2017, 19, 060402. [Google Scholar] [CrossRef]
- Wan, Y.; Fan, X.; He, Z. Review on Speckle-Based Spectrum Analyzer. Photonic Sens. 2021, 11, 187–202. [Google Scholar] [CrossRef]
- Cao, H.; Eliezer, Y. Harnessing disorder for photonic device applications. Appl. Phys. Rev. 2022, 9, 011309. [Google Scholar] [CrossRef]
- Boschetti, A.; Pattelli, L.; Torre, R.; Wiersma, D. Perspectives and recent advances in super-resolution spectroscopy: Stochastic and disordered-based approaches. Appl. Phys. Lett. 2022, 120, 250502. [Google Scholar] [CrossRef]
- Bao, J.; Bawendi, M. A colloidal quantum dot spectrometer. Nature 2015, 523, 67–70. [Google Scholar] [CrossRef]
- Wang, Z.; Yi, S.; Chen, A.; Zhou, M.; Luk, T.S.; James, A.; Nogan, J.; Ross, W.; Joe, G.; Shahsafi, A.; et al. Single-shot on-chip spectral sensors based on photonic crystal slabs. Nat. Commun. 2019, 10, 1020. [Google Scholar] [CrossRef]
- Liu, Q.; Xuan, Z.; Wang, Z.; Zhao, X.; Yin, Z.; Li, C.; Chen, G.; Wang, S.; Lu, W. Low-cost micro-spectrometer based on a nano-imprint and spectral-feature reconstruction algorithm. Opt. Lett. 2022, 47, 2923–2926. [Google Scholar] [CrossRef]
- Sun, C.; Chen, Z.; Ye, Y.; Weng, Y.; Lei, K.; Ma, H.; Wei, M.; Zhong, C.; Lin, H.; Li, L. Integrated Microring Spectrometer with In-Hardware Compressed Sensing to Break the Resolution-Bandwidth Limit for General Continuous Spectrum Analysis. Laser Photonics Rev. 2023, 17, 2300291. [Google Scholar] [CrossRef]
- Kabanikhin, S. Definitions and examples of inverse and ill-posed problems. J. Inverse Ill-Posed Probl. 2008, 16, 317–357. [Google Scholar] [CrossRef]
- Brady, D.; Gehm, M.; Pitsianis, N.; Sun, X. Compressive sampling strategies for integrated microspectrometers. In Proceedings of the SPIE Proceedings, Orlando, FL, USA, 17–21 April 2006. [Google Scholar] [CrossRef]
- Zhao, J.; Lakatos-Tóth, M.; Westerham, M.; Zhang, Z.; Moskoff, A.; Ren, F. OpenICS: Open image compressive sensing toolbox and benchmark. Softw. Impacts 2021, 9, 100081. [Google Scholar] [CrossRef]
- Candès, E.; Romberg, J. Sparsity and incoherence in compressive sampling. Inverse Probl. 2007, 23, 969. [Google Scholar] [CrossRef]
- Mondal, A.; Debnath, K. Design of Resolution-Tunable Neural Network-Based Integrated Reconstructive Spectrometer. Sens. J. 2022, 22, 2630–2636. [Google Scholar] [CrossRef]
- Redding, B.; Cao, H. Using a multimode fiber as a high-resolution, low-loss spectrometer. Opt. Lett. 2012, 37, 3384–3386. [Google Scholar] [CrossRef]
- Meng, J.; Cadusch, J.; Crozier, K. Detector-Only Spectrometer Based on Structurally Colored Silicon Nanowires and a Reconstruction Algorithm. Nano Lett. 2019, 20, 320–328. [Google Scholar] [CrossRef]
- Yang, Z.; Albrow-Owen, T.; Cui, H.; Alexander-Webber, J.; Gu, F.; Wang, X.; Wu, T.; Zhuge, M.; Williams, C.; Wang, P.; et al. Single-nanowire spectrometers. Science 2019, 365, 1017–1020. [Google Scholar] [CrossRef]
- Yuan, S.; Naveh, D.; Watanabe, K.; Taniguchi, T.; Xia, F. A wavelength-scale black phosphorus spectrometer. Nat. Photonics 2021, 15, 601–607. [Google Scholar] [CrossRef]
- Guo, L.; Sun, H.; Wang, M.; Wang, M.; Min, L.; Cao, F.; Tian, W.; Li, L. A Single-Dot Perovskite Spectrometer. Adv. Mater. 2022, 34, 2200221. [Google Scholar] [CrossRef]
- Kong, L.; Zhao, Q.; Wang, H.; Guo, J.; Lu, H.; Hao, H.; Guo, S.; Tu, X.; Zhang, L.; Jia, X.; et al. Single-Detector Spectrometer Using a Superconducting Nanowire. Nano Lett. 2021, 21, 9625–9632. [Google Scholar] [CrossRef] [PubMed]
- Zhang, Z.; Huang, B.; Zhang, Z.; Chen, H. On-Chip Reconstructive Spectrometer Based on Parallel Cascaded Micro-Ring Resonators. Appl. Sci. 2024, 14, 4886. [Google Scholar] [CrossRef]
- Yoon, H.; Fernandez, H.; Nigmatulin, F.; Cai, W.; Yang, Z.; Cui, H.; Ahmed, F.; Cui, X.; Uddin, M.G.; Minot, E.D.; et al. Miniaturized spectrometers with a tunable van der Waals junction. Science 2022, 378, 296–299. [Google Scholar] [CrossRef] [PubMed]
- Deng, D.; Zheng, Z.; Li, J.; Zhou, R.; Chen, X.; Zhang, D.; Lu, Y.; Wang, C.; You, C.; Li, S.; et al. Electrically tunable two-dimensional heterojunctions for miniaturized near-infrared spectrometers. Nat. Commun. 2022, 13, 4627. [Google Scholar] [CrossRef]
- Oliver, J.; Lee, W.; Park, S.; Lee, H. Improving resolution of miniature spectrometers by exploiting sparse nature of signals. Opt. Express 2012, 20, 2613–2625. [Google Scholar] [CrossRef] [PubMed]
- Oliver, J.; Lee, W.; Lee, H. Filters with random transmittance for improving resolution in filter-array-based spectrometers. Opt. Express 2013, 21, 3969–3989. [Google Scholar] [CrossRef]
- Zhang, Y.; Guo, X.; Albrow-Owen, T.; Zhao, Z.; Zhao, Y.; Hasan, T.; Yang, Z.; Su, Y. Miniaturized Computational Photonic Molecule Spectrometer. arXiv 2023, arXiv:2308.07764. [Google Scholar]
- Xu, H.; Qin, Y.; Hu, G.; Tsang, H.K. Breaking the resolution-bandwidth limit of chip-scale spectrometry by harnessing a dispersion-engineered photonic molecule. Light Sci. Appl. 2023, 12, 64. [Google Scholar] [CrossRef]
- Yao, C.; Chen, M.; Yan, T.; Ming, L.; Cheng, Q.; Penty, R. Broadband picometer-scale resolution on-chip spectrometer with reconfigurable photonics. Light Sci. Appl. 2023, 12, 156. [Google Scholar] [CrossRef]
- Yao, C.; Xu, K.; Zhang, W.; Chen, M.; Cheng, Q.; Penty, R. Integrated reconstructive spectrometer with programmable photonic circuits. Nat. Commun. 2023, 14, 6376. [Google Scholar] [CrossRef]
- Kwak, Y.; Park, S.; Ku, Z.; Urbas, A.; Kim, Y.L. A pearl spectrometer. Nano Lett. 2020, 21, 921–930. [Google Scholar] [CrossRef] [PubMed]
- Guan, Q.; Lim, Z.; Sun, H.; Chew, J.X.Y.; Zhou, G. Review of Miniaturized Computational Spectrometers. Sensors 2023, 23, 8768. [Google Scholar] [CrossRef] [PubMed]
- Li, A.; Fainman, Y. Integrated Silicon Fourier Transform Spectrometer with Broad Bandwidth and Ultra-High Resolution. Laser Photonics Rev. 2021, 15, 2000358. [Google Scholar] [CrossRef]
- Li, A.; Davis, J.; Grieco, A.; Alshamrani, N.; Fainman, Y. Fabrication-tolerant Fourier transform spectrometer on silicon with broad bandwidth and high resolution. Photonics Res. 2020, 8, 219. [Google Scholar] [CrossRef]
- Souza, M.; Grieco, A.; Frateschi, N.; Fainman, Y. Fourier transform spectrometer on silicon with thermo-optic non-linearity and dispersion correction. Nat. Commun. 2018, 9, 665. [Google Scholar] [CrossRef]
- Li, A.; Fainman, Y. On-chip spectrometers using stratified waveguide filters. Nat. Commun. 2021, 12, 2704. [Google Scholar] [CrossRef]
- Micó, G.; Gargallo, B.; Pastor, D.; Muñoz, P. Integrated Optic Sensing Spectrometer: Concept and Design. Sensors 2019, 19, 1018. [Google Scholar] [CrossRef]
- Soref, R.; De Leonardis, F.; Passaro, V.; Fainman, Y. On-Chip Digital Fourier-Transform Spectrometer Using a Thermo-Optical Michelson Grating Interferometer. J. Light. Technol. 2018, 36, 5160–5167. [Google Scholar] [CrossRef]
- Smit, M.; Leijtens, X.; Ambrosius, H.; Bente, E.; van der Tol, J.; Smalbrugge, B.; de Vries, T.; Geluk, E.J.; Bolk, J.; van Veldhoven, R.; et al. An introduction to InP-based generic integration technology. Semicond. Sci. Technol. 2014, 29, 083001. [Google Scholar] [CrossRef]
- Cheng, R.; Zou, C.; Guo, X.; Wang, S.; Han, X.; Tang, H.X. Broadband on-chip single-photon spectrometer. Nat. Commun. 2019, 10, 4104. [Google Scholar] [CrossRef]
- Rahim, A.; Ryckeboer, E.; Subramanian, A.Z.; Clemmen, S.; Kuyken, B.; Dhakal, A.; Raza, A.; Hermans, A.; Muneeb, M.; Dhoore, S.; et al. Expanding the Silicon Photonics Portfolio With Silicon Nitride Photonic Integrated Circuits. J. Light. Technol. 2017, 35, 639–649. [Google Scholar] [CrossRef]
- Ghorbani, H.; Tewari, R.; Rad, M.; Bernier, E.; Hall, T. Design and Simulation of a Si3N4 Sub-GHz Resolution Integrated Micro-Spectrometer. In Proceedings of the 2019 International Conference on Numerical Simulation of Optoelectronic Devices (NUSOD), Ottawa, ON, Canada, 8–12 July 2019. [Google Scholar] [CrossRef]
- Hasan, M.; Hasan, G.; Ghorbani, H.; Rad, M.; Liu, P.; Bernier, E.; Hall, T. Broadband high-resolution integrated spectrometer architecture & data processing method (Version 1). arXiv 2023, arXiv:2301.06653. [Google Scholar] [CrossRef]
- Nie, X.; Ryckeboer, E.; Roelkens, G.; Baets, R. CMOS-compatible broadband co-propagative stationary Fourier transform spectrometer integrated on a silicon nitride photonics platform. Opt. Express 2017, 25, A409–A418. [Google Scholar] [CrossRef] [PubMed]
- Subramanian, A.; Ryckeboer, E.; Dhakal, A.; Peyskens, F.; Malik, A.; Kuyken, B.; Zhao, H.; Pathak, S.; Ruocco, A.; De Groote, A.; et al. Silicon and silicon nitride photonic circuits for spectroscopic sensing on-a-chip. Photonics Res. 2015, 3, B47–B59. [Google Scholar] [CrossRef]
- Kaur, P.; Boes, A.; Ren, G.; Nguyen, T.; Roelkens, G.; Mitchell, A. Hybrid and heterogeneous photonic integration. APL Photonics 2021, 6, 061102. [Google Scholar] [CrossRef]
- Wang, R.; Vasiliev, A.; Muneeb, M.; Malik, A.; Sprengel, S.; Boehm, G.; Amann, M.C.; Simonyte, I.; Vizbaras, A.; Vizbaras, K.; et al. III-V-on-Silicon Photonic Integrated Circuits for Spectroscopic Sensing in the 2–4 μm Wavelength Range. Sensors 2017, 17, 1788. [Google Scholar] [CrossRef]
- Muneeb, M.; Vasiliev, A.; Ruocco, A.; Malik, A.; Chen, H.; Nedeljkovic, M.; Penades, J.; Cerutti, L.; Rodriguez, J.; Mashanovich, G.; et al. III-V-on-silicon integrated micro-spectrometer for the 3 μm wavelength range. Opt. Express 2016, 24, 9465. [Google Scholar] [CrossRef]
- Roelkens, G.; Dave, U.; Gassenq, A.; Hattasan, N.; Hu, C.; Kuyken, B.; Leo, F.; Malik, A.; Muneeb, M.; Ryckeboer, E.; et al. Mid-IR heterogeneous silicon photonics. In Proceedings of the SPIE Proceedings, San Francisco, CA, USA, 1–6 February 2014. [Google Scholar] [CrossRef]
- Mohr, J.; Anderer, B.; Ehrfeld, W. Fabrication of a planar grating spectrograph by deep-etch lithography with synchrotron radiation. Sens. Actuators A 1991, 25, 571–575. [Google Scholar] [CrossRef]
- Armin, A.; Jansen-van Vuuren, R.; Kopidakis, N.; Burn, P.; Meredith, P. Narrowband light detection via internal quantum efficiency manipulation of organic photodiodes. Nat. Commun. 2015, 6, 6343. [Google Scholar] [CrossRef]
- Xing, S.; Nikolis, V.; Kublitski, J.; Guo, E.; Jia, X.; Wang, Y.; Spoltore, D.; Vandewal, K.; Kleemann, H.; Benduhn, J.; et al. Miniaturized VIS-NIR Spectrometers Based on Narrowband and Tunable Transmission Cavity Organic Photodetectors with Ultrahigh Specific Detectivity above 1014 Jones. Adv. Mater. 2021, 33, 2102967. [Google Scholar] [CrossRef]
- Wang, Y.; Kublitski, J.; Xing, S.; Dollinger, F.; Spoltore, D.; Benduhn, J.; Leo, K. Narrowband organic photodetectors–towards miniaturized, spectroscopic sensing. Mater. Horizons 2022, 9, 220–251. [Google Scholar] [CrossRef] [PubMed]
- Li, T.; Hu, G.; Tao, L.; Jiang, J.; Xin, J.; Li, Y.; Ma, W.; Shen, L.; Fang, Y.; Lin, Y. Sensitive photodetection below silicon bandgap using quinoid-capped organic semiconductors. Sci. Adv. 2023, 9, eadf6152. [Google Scholar] [CrossRef]
- Fan, K.; Averitt, R.; Padilla, W. Active and tunable nanophotonic metamaterials. Nanophotonics 2022, 11, 3769–3803. [Google Scholar] [CrossRef]
- Li, Y.; Jiang, X.; Chen, Y.; Wang, Y.; Wu, Y.; Yu, D.; Wang, K.; Bai, S.; Xiao, S.; Song, Q. A platform for integrated spectrometers based on solution-processable semiconductors. Light Sci. Appl. 2023, 12, 184. [Google Scholar] [CrossRef] [PubMed]
- Khan, S.; Khan, A.; Azadmanjiri, J.; Kumar, R.; Děkanovský, L.; Sofer, Z.; Numan, A. 2D Heterostructures for Highly Efficient Photodetectors: From Advanced Synthesis to Characterizations, Mechanisms, and Device Applications. Adv. Photonics Res. 2022, 3, 2100342. [Google Scholar] [CrossRef]
- Chaves, A.; Azadani, J.; Alsalman, H.; da Costa, D.R.; Frisenda, R.; Chaves, A.J.; Song, S.H.; Kim, Y.D.; He, D.; Zhou, J.; et al. Bandgap engineering of two-dimensional semiconductor materials. NPJ 2D Mater. Appl. 2020, 4, 29. [Google Scholar] [CrossRef]
- Shabbir, H.; Wojnicki, M. Recent Progress of Non-Cadmium and Organic Quantum Dots for Optoelectronic Applications with a Focus on Photodetector Devices. Electronics 2023, 12, 1327. [Google Scholar] [CrossRef]
- Liu, H.; Gao, M.; McCaffrey, J.; Wasilewski, Z.; Fafard, S. Quantum dot infrared photodetectors. Appl. Phys. Lett. 2001, 78, 79–81. [Google Scholar] [CrossRef]
- Keuleyan, S.; Lhuillier, E.; Brajuskovic, V.; Guyot-Sionnest, P. Mid-infrared HgTe colloidal quantum dot photodetectors. Nat. Photonics 2011, 5, 489–493. [Google Scholar] [CrossRef]
- Grotevent, M.; Yakunin, S.; Bachmann, D.; Romero, C.; Vázquez de Aldana, J.; Madi, M.; Calame, M.; Kovalenko, M.; Shorubalko, I. Integrated photodetectors for compact Fourier-transform waveguide spectrometers. Nat. Photonics 2023, 17, 59–64. [Google Scholar] [CrossRef]
- Li, H.; Bian, L.; Gu, K.; Fu, H.; Yang, G.; Zhong, H.; Zhang, J. A Near-Infrared Miniature Quantum Dot Spectrometer. Adv. Opt. Mater. 2021, 9, 2100376. [Google Scholar] [CrossRef]
- Wen, C.; Zhao, X.; Mu, G.; Chen, M.; Tang, X. Simulation and Design of HgSe Colloidal Quantum-Dot Microspectrometers. Coatings 2022, 12, 888. [Google Scholar] [CrossRef]
- Shrestha, V.; Craig, B.; Meng, J.; Bullock, J.; Javey, A.; Crozier, K.B. Mid- to long-wave infrared computational spectroscopy with a graphene metasurface modulator. Sci. Rep. 2020, 10, 5377. [Google Scholar] [CrossRef] [PubMed]
- Pham, P.; Mai, T.; Do, H.; Ponnusamy, V.; Chuang, F. Integrated Graphene Heterostructures in Optical Sensing. Micromachines 2023, 14, 1060. [Google Scholar] [CrossRef]
- Bhimanapati, G.; Lin, Z.; Meunier, V.; Jung, Y.; Cha, J.; Das, S.; Xiao, D.; Son, Y.; Strano, M.; Cooper, V.; et al. Recent Advances in Two-Dimensional Materials beyond Graphene. ACS Nano 2015, 9, 11509–11539. [Google Scholar] [CrossRef]
- Luque-González, J.; Sánchez-Postigo, A.; Hadij-ElHouati, A.; Ortega-Moñux, A.; Wangüemert-Pérez, J.; Schmid, J.; Cheben, P.; Molina-Fernández, I.; Halir, R. A review of silicon subwavelength gratings: Building break-through devices with anisotropic metamaterials. Nanophotonics 2021, 10, 2765–2797. [Google Scholar] [CrossRef]
- Park, Y.; Kim, U.; Lee, S.; Kim, H.; Kim, J.; Ma, H.; Son, H.; Yoon, Y.Z.; Lee, J.-S.; Park, M.; et al. On-chip Raman spectrometers using narrow band filter array combined with CMOS image sensors. Sens. Actuators B Chem. 2023, 381, 133442. [Google Scholar] [CrossRef]
- Chang, C.; Lee, H. On the estimation of target spectrum for filter-array based spectrometers. Opt. Express 2008, 16, 1056. [Google Scholar] [CrossRef]
- Keuleyan, S.; Lhuillier, E.; Guyot-Sionnest, P. Synthesis of Colloidal HgTe Quantum Dots for Narrow Mid-IR Emission and Detection. J. Am. Chem. Soc. 2011, 133, 16422–16424. [Google Scholar] [CrossRef]
- Gong, X.; Tong, M.; Xia, Y.; Cai, W.; Moon, J.; Cao, Y.; Yu, G.; Shieh, C.; Nilsson, B.; Heeger, A. High-Detectivity Polymer Photodetectors with Spectral Response from 300 nm to 1450 nm. Science 2009, 325, 1665–1667. [Google Scholar] [CrossRef]
- Saracco, E.; Bouthinon, B.; Verilhac, J.; Celle, C.; Chevalier, N.; Mariolle, D.; Dhez, O.; Simonato, J. Work Function Tuning for High-Performance Solution-Processed Organic Photodetectors with Inverted Structure. Adv. Mater. 2013, 25, 6534–6538. [Google Scholar] [CrossRef] [PubMed]
- Guo, F.; Xiao, Z.; Huang, J. Fullerene Photodetectors with a Linear Dynamic Range of 90 dB Enabled by a Cross-Linkable Buffer Layer. Adv. Opt. Mater. 2013, 1, 289–294. [Google Scholar] [CrossRef]
- Armin, A.; Hambsch, M.; Kim, I.; Burn, P.; Meredith, P.; Namdas, E. Thick junction broadband organic photodiodes. Laser Photonics Rev. 2014, 8, 924–932. [Google Scholar] [CrossRef]
- Pierre, A.; Deckman, I.; Lechêne, P.; Arias, A. High Detectivity All-Printed Organic Photodiodes. Adv. Mater. 2015, 27, 6411–6417. [Google Scholar] [CrossRef]
- Zhou, X.; Yang, D.; Ma, D. Extremely Low Dark Current, High Responsivity, All-Polymer Photodetectors with Spectral Response from 300 nm to 1000 nm. Adv. Opt. Mater. 2015, 3, 1570–1576. [Google Scholar] [CrossRef]
- Zhang, H.; Jenatsch, S.; De Jonghe, J.; Nüesch, F.; Steim, R.; Véron, A.; Hany, R. Transparent Organic Photodetector using a Near-Infrared Absorbing Cyanine Dye. Sci. Rep. 2015, 5, 1. [Google Scholar] [CrossRef]
- Kielar, M.; Dhez, O.; Pecastaings, G.; Curutchet, A.; Hirsch, L. Long-Term Stable Organic Photodetectors with Ultra Low Dark Currents for High Detectivity Applications. Sci. Rep. 2016, 6, 1. [Google Scholar] [CrossRef]
- Shen, L.; Fang, Y.; Wei, H.; Yuan, Y.; Huang, J. A Highly Sensitive Narrowband Nanocomposite Photodetector with Gain. Adv. Mater. 2016, 28, 2043–2048. [Google Scholar] [CrossRef]
- Wang, W.; Zhang, F.; Du, M.; Li, L.; Zhang, M.; Wang, K.; Wang, Y.; Hu, B.; Fang, Y.; Huang, J. Highly Narrowband Photomultiplication Type Organic Photodetectors. Nano Lett. 2017, 17, 1995–2002. [Google Scholar] [CrossRef]
- Tang, Z.; Ma, Z.; Sánchez-Díaz, A.; Ullbrich, S.; Liu, Y.; Siegmund, B.; Mischok, A.; Leo, K.; Campoy-Quiles, M.; Li, W.; et al. Polymer:Fullerene Bimolecular Crystals for Near-Infrared Spectroscopic Photodetectors. Adv. Mater. 2017, 29, 1702184. [Google Scholar] [CrossRef]
- Siegmund, B.; Mischok, A.; Benduhn, J.; Zeika, O.; Ullbrich, S.; Nehm, F.; Böhm, M.; Spoltore, D.; Fröb, H.; Körner, C.; et al. Organic narrowband near-infrared photodetectors based on intermolecular charge-transfer absorption. Nat. Commun. 2017, 8, 15421. [Google Scholar] [CrossRef] [PubMed]
- Wei, Y.; Ren, Z.; Zhang, A.; Mao, P.; Li, H.; Zhong, X.; Li, W.; Yang, S.; Wang, J. Hybrid Organic/PbS Quantum Dot Bilayer Photodetector with Low Dark Current and High Detectivity. Adv. Funct. Mater. 2018, 28, 1706690. [Google Scholar] [CrossRef]
- Xiao, L.; Chen, S.; Chen, X.; Peng, X.; Cao, Y.; Zhu, X. High-detectivity panchromatic photodetectors for the near infrared region based on a dimeric porphyrin small molecule. J. Mater. Chem. C 2018, 6, 3341–3345. [Google Scholar] [CrossRef]
- Wang, W.; Du, M.; Zhang, M.; Miao, J.; Fang, Y.; Zhang, F. Organic Photodetectors with Gain and Broadband/Narrowband Response under Top/Bottom Illumination Conditions. Adv. Opt. Mater. 2018, 6, 1800249. [Google Scholar] [CrossRef]
- Zhang, X.; Zheng, E.; Esopi, M.; Cai, C.; Yu, Q. Flexible Narrowband Ultraviolet Photodetectors with Photomultiplication Based on Wide Band Gap Conjugated Polymer and Inorganic Nanoparticles. ACS Appl. Mater. Interfaces 2018, 10, 24064–24074. [Google Scholar] [CrossRef] [PubMed]
- Zhong, Z.; Li, K.; Zhang, J.; Ying, L.; Xie, R.; Yu, G.; Huang, F.; Cao, Y. High-Performance All-Polymer Photodetectors via a Thick Photoactive Layer Strategy. ACS Appl. Mater. Interfaces 2019, 11, 14208–14214. [Google Scholar] [CrossRef]
- Liess, A.; Arjona-Esteban, A.; Kudzus, A.; Albert, J.; Krause, A.; Lv, A.; Stolte, M.; Meerholz, K.; Würthner, F. Ultranarrow Bandwidth Organic Photodiodes by Exchange Narrowing in Merocyanine H- and J-Aggregate Excitonic Systems. Adv. Funct. Mater. 2018, 29, 1805058. [Google Scholar] [CrossRef]
- Wang, J.; Ullbrich, S.; Hou, J.; Spoltore, D.; Wang, Q.; Ma, Z.; Tang, Z.; Vandewal, K. Organic Cavity Photodetectors Based on Nanometer-Thick Active Layers for Tunable Monochromatic Spectral Response. ACS Photonics 2019, 6, 1393–1399. [Google Scholar] [CrossRef]
- Kaiser, C.; Schellhammer, K.; Benduhn, J.; Siegmund, B.; Tropiano, M.; Kublitski, J.; Spoltore, D.; Panhans, M.; Zeika, O.; Ortmann, F.; et al. Manipulating the Charge Transfer Absorption for Narrowband Light Detection in the Near-Infrared. Chem. Mater. 2019, 31, 9325–9330. [Google Scholar] [CrossRef]
- Lee, C.; Estrada, R.; Li, Y.; Biring, S.; Amin, N.; Li, M.; Liu, S.; Wong, K. Vacuum-Processed Small Molecule Organic Photodetectors with Low Dark Current Density and Strong Response to Near-Infrared Wavelength. Adv. Opt. Mater. 2020, 8, 2000519. [Google Scholar] [CrossRef]
- Xing, S.; Wang, X.; Guo, E.; Kleemann, H.; Leo, K. Organic Thin-Film Red-Light Photodiodes with Tunable Spectral Response Via Selective Exciton Activation. ACS Appl. Mater. Interfaces 2020, 12, 13061–13067. [Google Scholar] [CrossRef] [PubMed]
- Xie, B.; Xie, R.; Zhang, K.; Yin, Q.; Hu, Z.; Yu, G.; Huang, F.; Cao, Y. Self-filtering narrowband high performance organic photodetectors enabled by manipulating localized Frenkel exciton dissociation. Nat. Commun. 2020, 11, 2871. [Google Scholar] [CrossRef] [PubMed]
- Lan, Z.; Lau, Y.; Wang, Y.; Xiao, Z.; Ding, L.; Luo, D.; Zhu, F. Filter-Free Band-Selective Organic Photodetectors. Adv. Opt. Mater. 2020, 8, 2001388. [Google Scholar] [CrossRef]
- Wang, Y.; Siegmund, B.; Tang, Z.; Ma, Z.; Kublitski, J.; Xing, S.; Nikolis, V.; Ullbrich, S.; Li, Y.; Benduhn, J.; et al. Stacked Dual-Wavelength Near-Infrared Organic Photodetectors. Adv. Opt. Mater. 2020, 9, 2001784. [Google Scholar] [CrossRef]
- Huang, Z.; Zhong, Z.; Peng, F.; Ying, L.; Yu, G.; Huang, F.; Cao, Y. Copper Thiocyanate as an Anode Interfacial Layer for Efficient Near-Infrared Organic Photodetector. ACS Appl. Mater. Interfaces 2020, 13, 1027–1034. [Google Scholar] [CrossRef]
- Liu, M.; Wang, J.; Zhao, Z.; Yang, K.; Durand, P.; Ceugniet, F.; Ulrich, G.; Niu, L.; Ma, Y.; Leclerc, N.; et al. Ultra-Narrow-Band NIR Photomultiplication Organic Photodetectors Based on Charge Injection Narrowing. J. Phys. Chem. Lett. 2021, 12, 2937–2943. [Google Scholar] [CrossRef]
- Yang, J.; Huang, J.; Li, R.; Li, H.; Sun, B.; Lin, Q.; Wang, M.; Ma, Z.; Vandewal, K.; Tang, Z. Cavity-Enhanced Near-Infrared Organic Photodetectors Based on a Conjugated Polymer Containing [1,2,5]Selenadiazolo[3,4-c]Pyridine. Chem. Mater. 2021, 33, 5147–5155. [Google Scholar] [CrossRef]
- Kublitski, J.; Fischer, A.; Xing, S.; Baisinger, L.; Bittrich, E.; Spoltore, D.; Benduhn, J.; Vandewal, K.; Leo, K. Enhancing sub-bandgap external quantum efficiency by photomultiplication for narrowband organic near-infrared photodetectors. Nat. Commun. 2021, 12, 4259. [Google Scholar] [CrossRef]
- Deng, Z.; Jeong, K.; Guyot-Sionnest, P. Colloidal Quantum Dots Intraband Photodetectors. ACS Nano 2014, 8, 11707–11714. [Google Scholar] [CrossRef]
- Kim, J.; Kwon, S.; Kang, Y.; Kim, Y.; Lee, M.; Han, K.; Facchetti, A.; Kim, M.; Park, S. A skin-like two-dimensionally pixelized full-color quantum dot photodetector. Sci. Adv. 2019, 5, eaax8801. [Google Scholar] [CrossRef]
- Ramiro, I.; Özdemir, O.; Christodoulou, S.; Gupta, S.; Dalmases, M.; Torre, I.; Konstantatos, G. Mid- and Long-Wave Infrared Optoelectronics via Intraband Transitions in PbS Colloidal Quantum Dots. Nano Lett. 2020, 20, 1003–1008. [Google Scholar] [CrossRef] [PubMed]
- Jimenez, J.; Fonseca, L.; Brady, D.; Leburton, J.; Wohlert, D.; Cheng, K. The quantum dot spectrometer. Appl. Phys. Lett. 1997, 71, 3558–3560. [Google Scholar] [CrossRef]
- Zhu, X.; Bian, L.; Fu, H.; Wang, L.; Zou, B.; Dai, Q.; Zhang, J.; Zhong, H. Broadband perovskite quantum dot spectrometer beyond human visual resolution. Light. Sci. Appl. 2020, 9, 73. [Google Scholar] [CrossRef] [PubMed]
- Zheng, B.; Wang, J.; Huang, T.; Su, X.; Shi, Y.; Wang, X. Single-detector black phosphorus monolithic spectrometer with high spectral and temporal resolution. Appl. Phys. Lett. 2022, 120, 251102. [Google Scholar] [CrossRef]
- Zheng, J.; Xiao, Y.; Hu, M.; Zhao, Y.; Li, H.; You, L.; Feng, X.; Liu, F.; Cui, K.; Huang, Y.; et al. Photon counting reconstructive spectrometer combining metasurfaces and superconducting nanowire single-photon detectors. Photonics Res. 2023, 11, 234–244. [Google Scholar] [CrossRef]
- Cheben, P.; Schmid, J.; Delâge, A.; Densmore, A.; Janz, S.; Lamontagne, B.; Lapointe, J.; Post, E.; Waldron, P.; Xu, D. A high-resolution silicon-on-insulator arrayed waveguide grating microspectrometer with sub-micrometer aperture waveguides. Opt. Express 2007, 15, 2299–2306. [Google Scholar] [CrossRef]
- Xia, Z.; Asghar Eftekhar, A.; Soltani, M.; Momeni, B.; Li, Q.; Chamanzar, M.; Yegnanarayanan, S.; Adibi, A. High resolution on-chip spectroscopy based on miniaturized microdonut resonators. Opt. Express 2011, 19, 12356–12364. [Google Scholar] [CrossRef]
- Zhang, L.; Zhang, M.; Chen, T.; Liu, D.; Hong, S.; Dai, D. Ultrahigh-resolution on-chip spectrometer with silicon photonic resonators. Opto-Electron. Adv. 2022, 5, 210100. [Google Scholar] [CrossRef]
- Velasco, A.; Cheben, B.; Bock, P.; Delâge, A.; Schmid, J.; Lapointe, J.; Janz, S.; Calvo, M.; Xu, D.; Florjańczyk, M.; et al. High-resolution Fourier-transform spectrometer chip with microphotonic silicon spiral waveguides. Opt. Lett. 2013, 38, 706–708. [Google Scholar] [CrossRef]
- Loridat, J.; Heidmann, S.; Thomas, F.; Ulliac, G.; Courjal, N.; Morand, A.; Martin, G. All Integrated Lithium Niobate Standing Wave Fourier Transform Electro-Optic Spectrometer. J. Light. Technol. 2018, 36, 4900–4907. [Google Scholar] [CrossRef]
- Kang, X.; Li, J.; Yang, S.; Chen, H.; Chen, M. High-performance on-chip spectrometer based on micro-rings resonator. In Proceedings of the Optics Frontiers Online 2020: Micro and Nanophotonics (OFO-4 2020), Online, 25–27 September 2020; Volume 11608, p. 1160808. [Google Scholar]
- Kita, D.; Miranda, B.; Favela, D.; Bono, D.; Michon, J.; Lin, H.; Gu, T.; Hu, J. High-performance and scalable on-chip digital Fourier transform spectroscopy. Nat. Commun. 2018, 9, 4405. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Z.; Zhu, S.; Chen, Y.; Chen, H.; Chen, J. Towards integrated mode-division demultiplexing spectrometer by deep learning. Opto-Electron. Sci. 2022, 1, 220012. [Google Scholar] [CrossRef]
- Chen, C.; Li, X.; Yang, G.; Chen, X.; Liu, S.; Guo, Y.; Li, H. Computational hyperspectral devices based on quasi-random metasurface supercells. Nanoscale 2023, 15, 8854–8862. [Google Scholar] [CrossRef] [PubMed]
- Brouckaert, J.; Bogaerts, W.; Dumon, P.; Van Thourhout, D.; Baets, R. Planar Concave Grating Demultiplexer Fabricated on a Nanophotonic Silicon-on-Insulator Platform. J. Light. Technol. 2007, 25, 1269–1275. [Google Scholar] [CrossRef]
- Pottier, P.; Strain, M.; Packirisamy, M. Integrated Microspectrometer with Elliptical Bragg Mirror Enhanced Diffraction Grating on Silicon on Insulator. ACS Photonics 2014, 1, 430–436. [Google Scholar] [CrossRef]
- Momeni, B.; Askari, M.; Hosseini, E.S.; Atabaki, A.; Adibi, A. An on-chip silicon grating spectrometer using a photonic crystal reflector. J. Opt. 2010, 12, 035501. [Google Scholar] [CrossRef]
- Muneeb, M.; Chen, X.; Verheyen, P.; Lepage, G.; Pathak, S.; Ryckeboer, E.; Malik, A.; Kuyken, B.; Nedeljkovic, M.; Van Campenhout, J.; et al. Demonstration of Silicon-on-insulator mid-infrared spectrometers operating at 3.8 μm. Opt. Express 2013, 21, 11659–11669. [Google Scholar] [CrossRef]
- Brouckaert, J.; Bogaerts, W.; Selvaraja, S.; Dumon, P.; Baets, R.; Van Thourhout, D. Planar Concave Grating Demultiplexer with High Reflective Bragg Reflector Facets. IEEE Photonics Technol. Lett. 2008, 20, 309–311. [Google Scholar] [CrossRef]
- Tian, M.; Liu, B.; Lu, Z.; Wang, Y.; Zheng, Z.; Song, J.; Zhong, X.; Wang, F. Miniaturized on-chip spectrometer enabled by electrochromic modulation. Light. Sci. Appl. 2024, 13, 278. [Google Scholar] [CrossRef]




| WdM/WM | Spectrometer Type | Subtype | Pros | Cons |
|---|---|---|---|---|
| WdM | Dispersive | 1D (slab) phase shift | + Simple design + High measuring speed | - Limited spectral range - Low resolution |
| 2D phase shift | + High measuring speed | - More complex fabrication - Low resolution - Larger footprint | ||
| Filter-based | Non-resonant | + Wide spectral range + High resolution + Tunable options | - Lower spectral resolution - Larger footprint - Power hungry | |
| Resonant | + High spectral selectivity + Compact and integrable design | - Sensitive to temperature variations - Fabrication complexity | ||
| WM | Fourier transform spectrometers | Spatially modulated | + High spectral resolution + High throughput (Jacquinot advantage) | - Requires precise alignment - Potentially complex readout |
| Temporally modulated | + Very high spectral resolution (depending on delay range) | - Complex for broadband spectrometers - Requires sophisticated processing |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Coppola, C.M.; De Carlo, M.; De Leonardis, F.; Passaro, V.M.N. i-PHAOS: An Overview with an Open-Source Collaborative Database on Miniaturized Integrated Spectrometers. Sensors 2024, 24, 6715. https://doi.org/10.3390/s24206715
Coppola CM, De Carlo M, De Leonardis F, Passaro VMN. i-PHAOS: An Overview with an Open-Source Collaborative Database on Miniaturized Integrated Spectrometers. Sensors. 2024; 24(20):6715. https://doi.org/10.3390/s24206715
Chicago/Turabian StyleCoppola, Carla Maria, Martino De Carlo, Francesco De Leonardis, and Vittorio M. N. Passaro. 2024. "i-PHAOS: An Overview with an Open-Source Collaborative Database on Miniaturized Integrated Spectrometers" Sensors 24, no. 20: 6715. https://doi.org/10.3390/s24206715
APA StyleCoppola, C. M., De Carlo, M., De Leonardis, F., & Passaro, V. M. N. (2024). i-PHAOS: An Overview with an Open-Source Collaborative Database on Miniaturized Integrated Spectrometers. Sensors, 24(20), 6715. https://doi.org/10.3390/s24206715








