Noncircular Distributed Source DOA Estimation with Nested Arrays via Reduced-Dimension MUSIC
Abstract
1. Introduction
1.1. Prior Art
1.2. Motivations and Contributions
- We analyze the similarity among the sources in a certain parameter and degrade the CD sources into point sources based on this nature. Then, a rank-restoring method like a spatial smoothing technique could be applied to form a full-rank signal matrix.
- The feature of noncircular signals is taken advantage of by a nested array to form a DCA and two SCAs, which are well used to construct a longer virtual ULA. More DOFs are obtained compared with other algorithms [11,13,24,27]. The outstanding performance of the proposed algorithm is verified in simulations.
- Based on the idea of RD-MUSIC, we develop the MSD-RD-MUSIC to estimate the DOA parameter through a one-dimensional peak-searching procedure, which significantly lowers the computational complexity.
1.3. Organization and Notations
2. Mathematical Model
2.1. Coherently Distributed Source
2.2. Noncircular Signals
2.3. Nested Array and Sum-and-Difference Co-Array
3. Proposed Algorithm
3.1. Virtual Array Construction
3.2. MSD-RD-MUSIC Algorithm
4. Performance Analysis of Proposed Algorithm
4.1. Degrees of Freedom
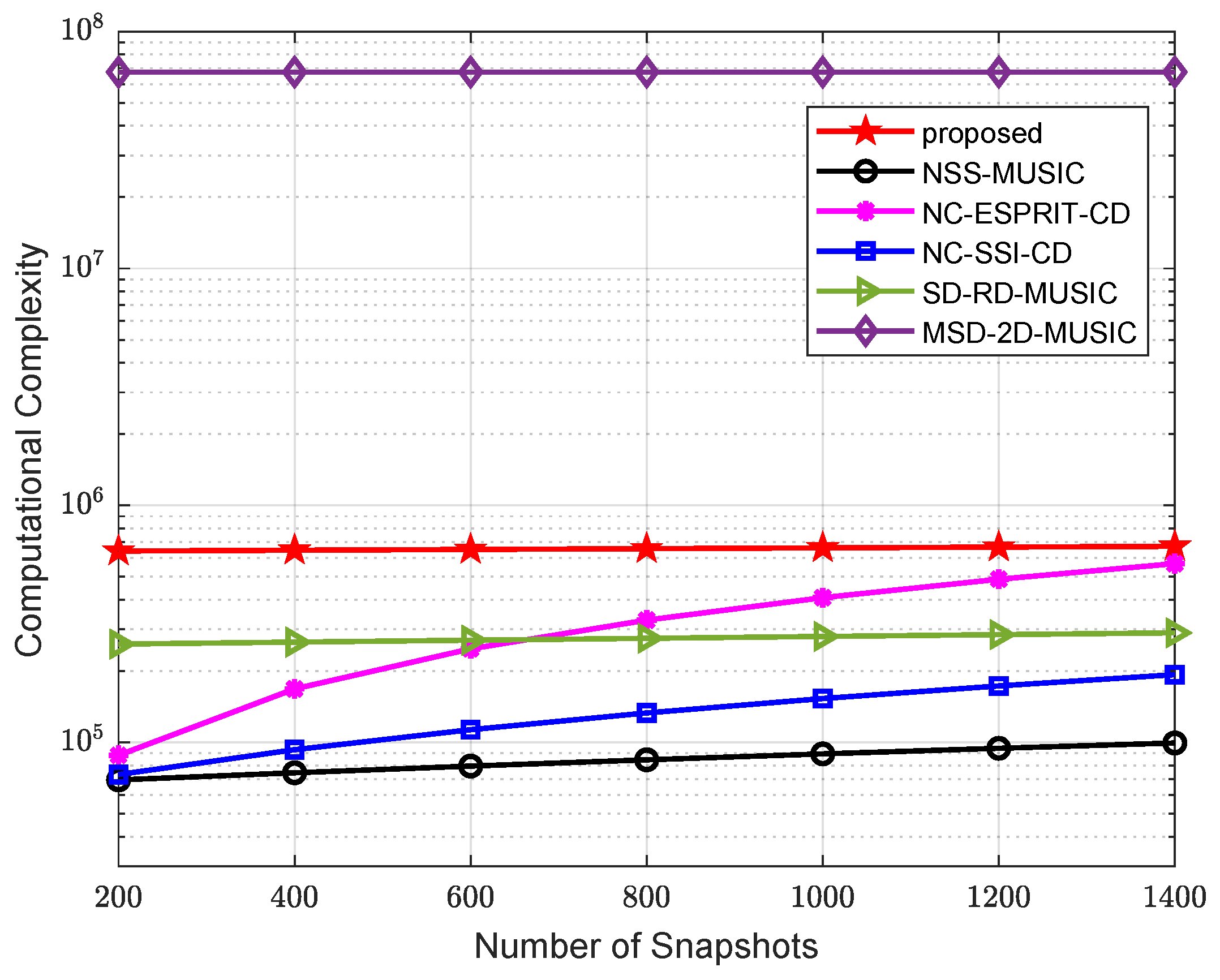
4.2. Computational Complexity
4.3. Advantages of the Proposed Algorithm
- Comparing MSD-2D-MUSIC with the cost function introduced in (53), our algorithm maintains the same DOFs while reducing complexity remarkably, which strikes a balance between the performance and complexity.
- Compared with SD-RD-MUSIC [24], it makes use of all three co-arrays. The extra positive SCA can provide additional DOFs, which improves the estimation accuracy.
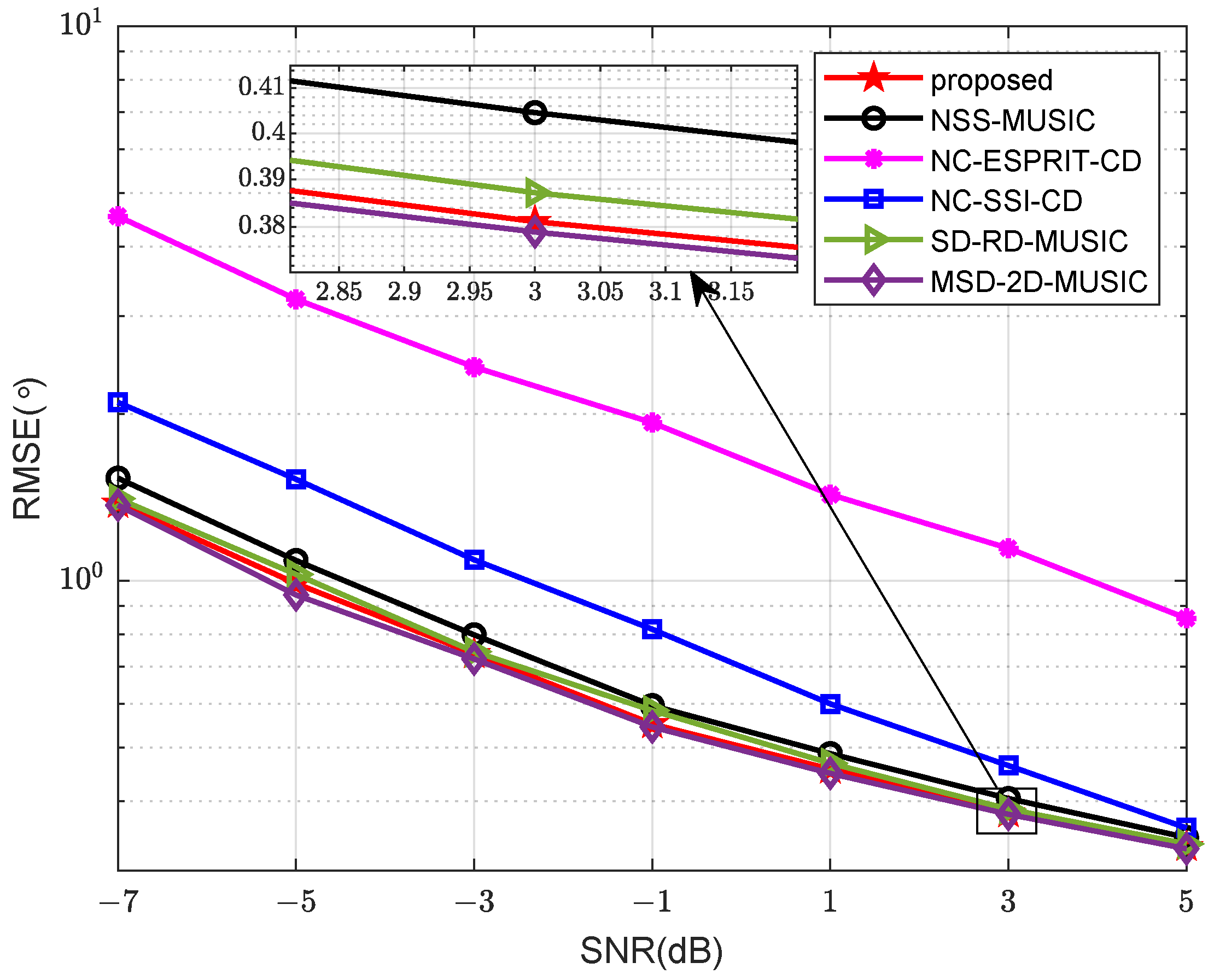
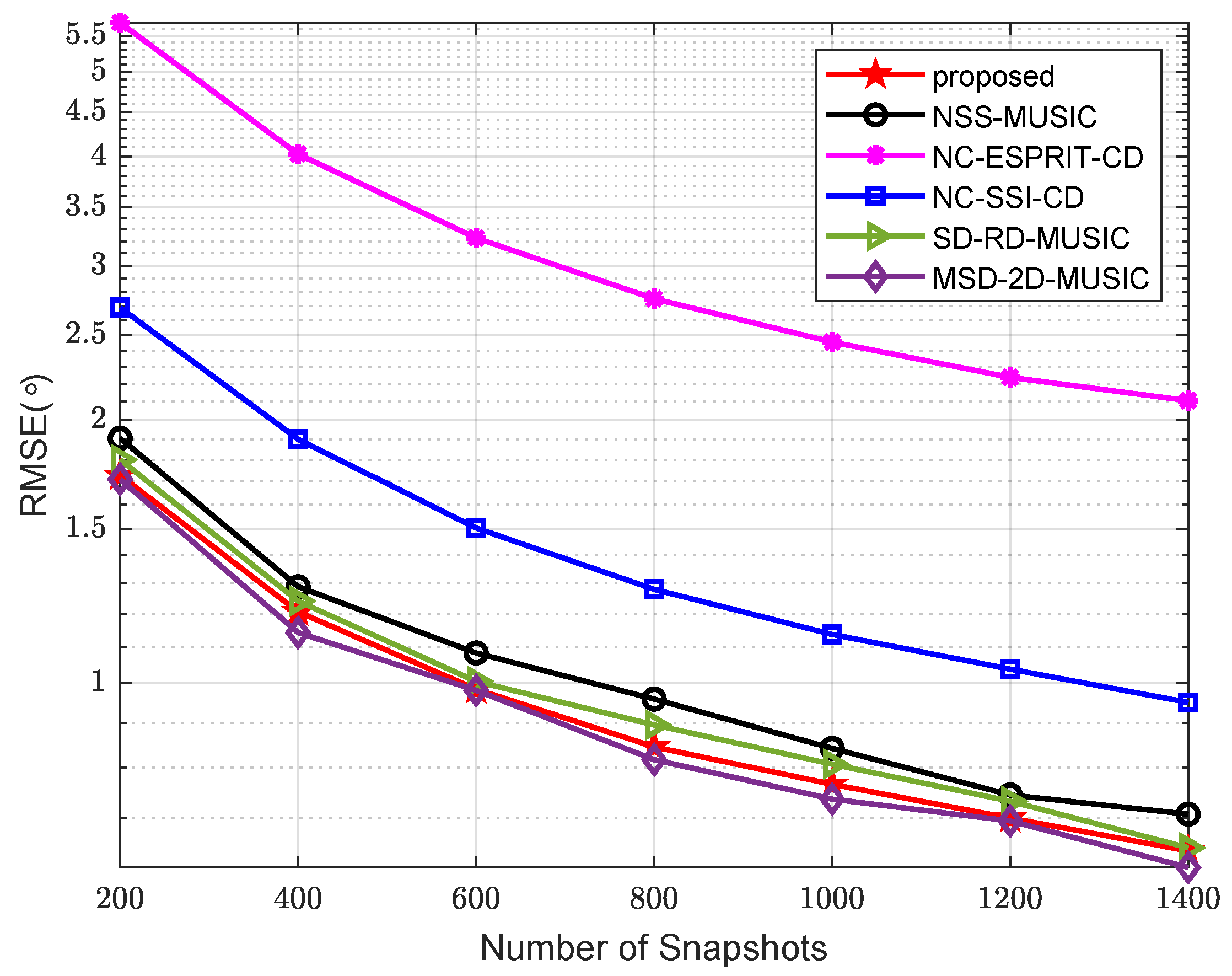
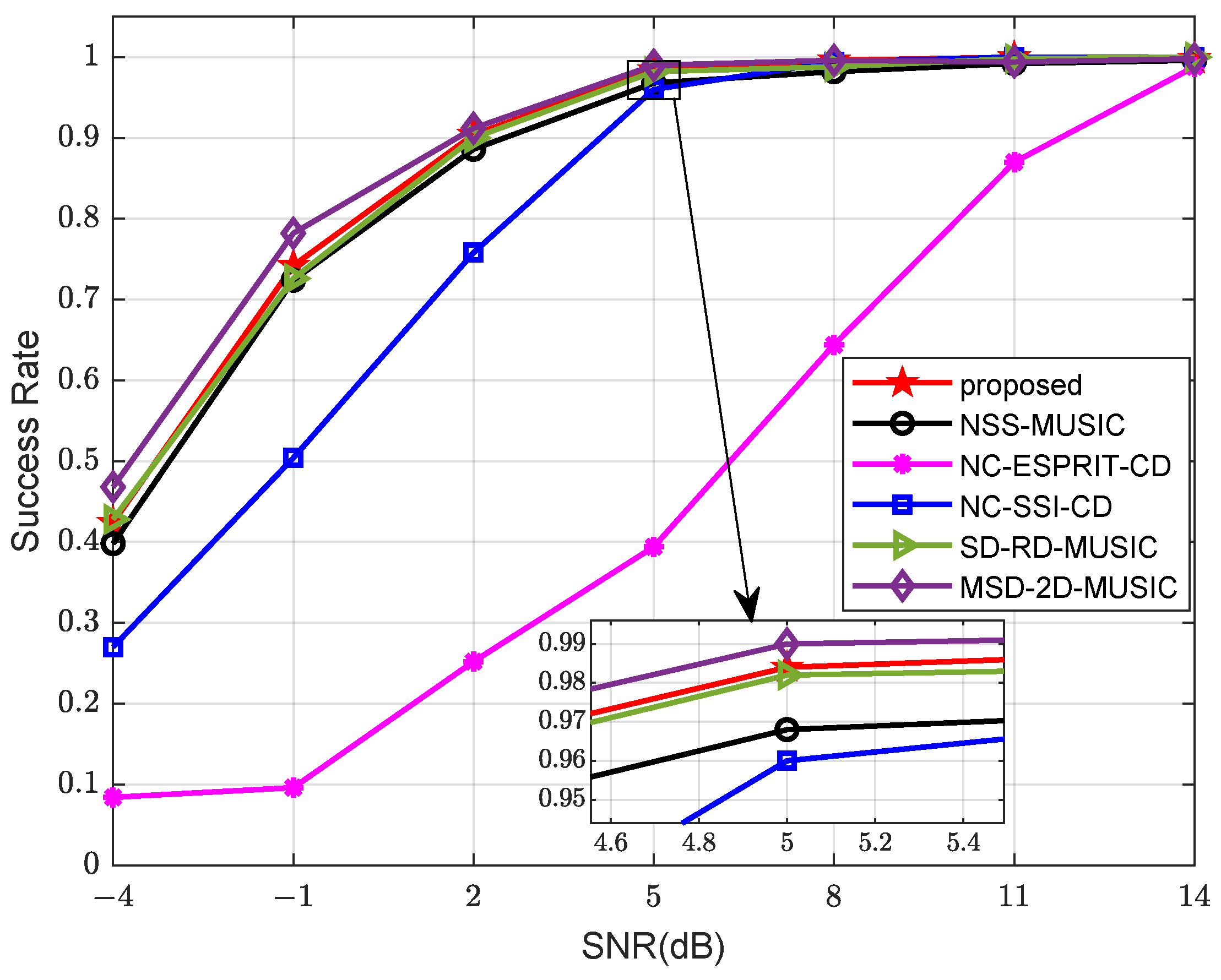
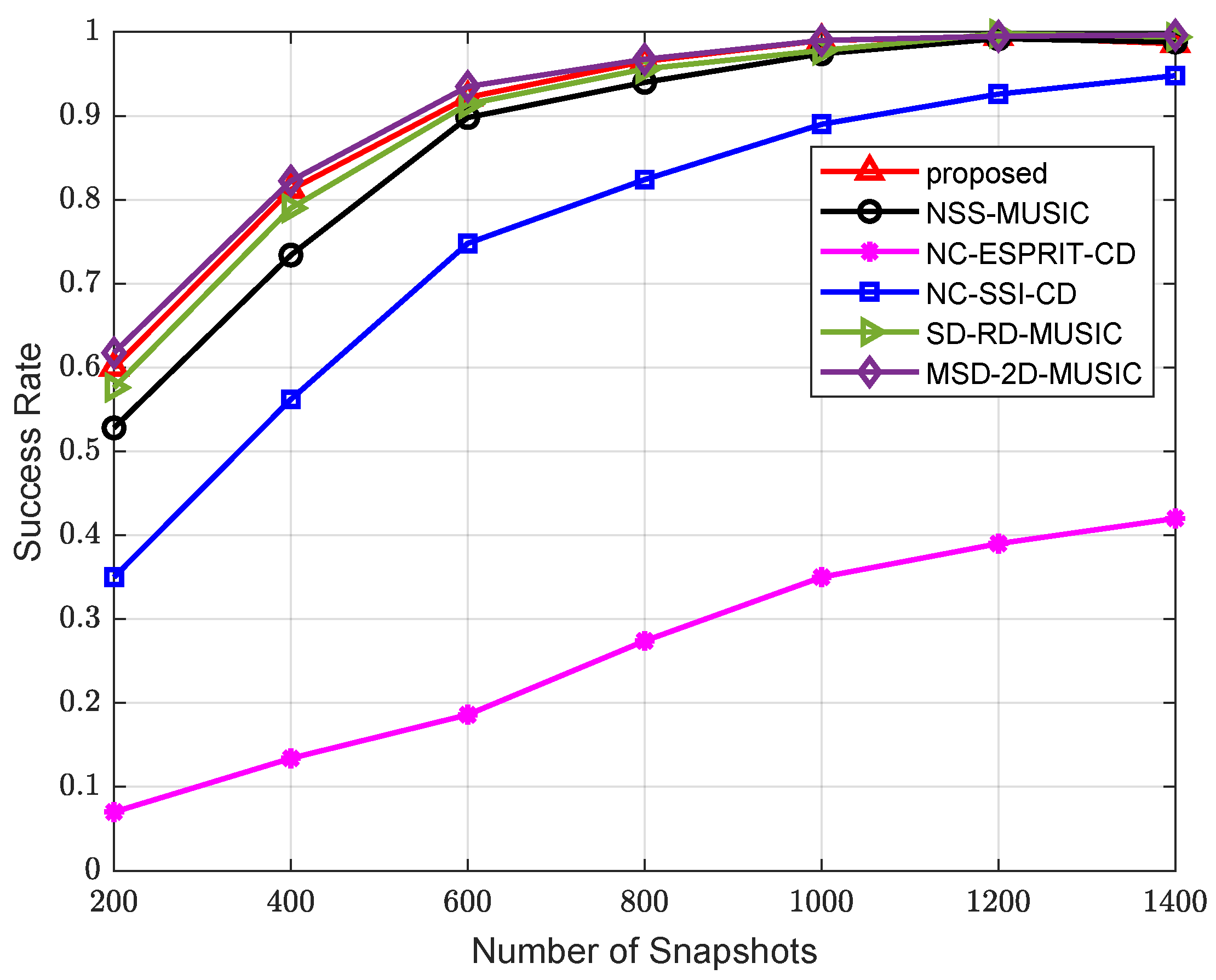
5. Numerical Simulation Results
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Li, J.; Jiang, D.; Zhang, X. DOA Estimation Based on Combined Unitary ESPRIT for Coprime MIMO Radar. IEEE Commun. Lett. 2017, 21, 96–99. [Google Scholar] [CrossRef]
- Dai, Z.; Zhang, L.; Han, X.; Yin, J. An Off-grid DOA Estimation Method for Passive Sonar Detection Based on Iterative Proximal Projection. J. Mar. Sci. Appl. 2024, 23, 417–424. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech, Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Wu, Y.W.; Rhodes, S.; Satorius, E. Direction of arrival estimation via extended phase interferometry. IEEE Trans. Aerosp. Electron. Syst. 1995, 31, 375–381. [Google Scholar] [CrossRef]
- Florio, A.; Avitabile, G.; Talarico, C.; Coviello, G. A Reconfigurable Full-Digital Architecture for Angle of Arrival Estimation. IEEE Trans. Circuits Syst. I Regul. Pap. 2024, 71, 1443–1455. [Google Scholar] [CrossRef]
- Guo, M.; Zhang, Y.D.; Chen, T. DOA Estimation Using Compressed Sparse Array. IEEE Trans. Signal Process. 2018, 66, 4133–4146. [Google Scholar] [CrossRef]
- Qin, G.; Amin, M.G.; Zhang, Y.D. DOA Estimation Exploiting Sparse Array Motions. IEEE Trans. Signal Process. 2019, 67, 3013–3027. [Google Scholar] [CrossRef]
- Jantti, T.P. The influence of extended sources on the theoretical performance of the MUSIC and ESPRIT methods: Narrow-band sources. In Proceedings of the ICASSP-92: 1992 IEEE International Conference on Acoustics, Speech, and Signal Processing, San Francisco, CA, USA, 23–26 March 1992; Volume 2, pp. 429–432. [Google Scholar] [CrossRef]
- Valaee, S.; Champagne, B.; Kabal, P. Parametric localization of distributed sources. IEEE Trans. Signal Process. 1995, 43, 2144–2153. [Google Scholar] [CrossRef]
- Shahbazpanahi, S.; Valaee, S.; Bastani, M. Distributed source localization using ESPRIT algorithm. IEEE Trans. Signal Process. 2001, 49, 2169–2178. [Google Scholar] [CrossRef]
- Cao, R.; Zhang, X.; Gao, F. Propagator-based algorithm for localization of coherently distributed sources. In Proceedings of the 2016 8th International Conference on Wireless Communications & Signal Processing (WCSP), Yangzhou, China, 13–15 October 2016; pp. 1–5. [Google Scholar] [CrossRef]
- Bae, E.; Kim, J.; Choi, B.; Lee, K. Decoupled parameter estimation of multiple distributed sources for uniform linear array with low complexity. Electron. Lett. 2008, 44, 649–651. [Google Scholar] [CrossRef]
- Vaidyanathan, P.P.; Pal, P. Sparse Sensing With Co-Prime Samplers and Arrays. IEEE Trans. Signal Process. 2011, 59, 573–586. [Google Scholar] [CrossRef]
- Qin, S.; Zhang, Y.D.; Amin, M.G. Generalized coprime array configurations. In Proceedings of the 2014 IEEE 8th Sensor Array and Multichannel Signal Processing Workshop (SAM), A Coruna, Spain, 22–25 June 2014; pp. 529–532. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested Arrays: A Novel Approach to Array Processing with Enhanced Degrees of Freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Zhou, C.; Shi, Z.; Gu, Y.; Shen, X. DECOM: DOA estimation with combined MUSIC for coprime array. In Proceedings of the 2013 International Conference on Wireless Communications and Signal Processing, Hangzhou, China, 24–26 October 2013; pp. 1–5. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Coprime sampling and the MUSIC algorithm. In Proceedings of the 2011 Digital Signal Processing and Signal Processing Education Meeting (DSP/SPE), Sedona, AZ, USA, 4–7 January 2011; pp. 289–294. [Google Scholar] [CrossRef]
- Zhou, C.; Gu, Y.; Fan, X.; Shi, Z.; Mao, G.; Zhang, Y.D. Direction-of-Arrival Estimation for Coprime Array via Virtual Array Interpolation. IEEE Trans. Signal Process. 2018, 66, 5956–5971. [Google Scholar] [CrossRef]
- Pan, J.; Sun, M.; Wang, Y.; Zhang, X. An Enhanced Spatial Smoothing Technique With ESPRIT Algorithm for Direction of Arrival Estimation in Coherent Scenarios. IEEE Trans. Signal Process. 2020, 68, 3635–3643. [Google Scholar] [CrossRef]
- Ollila, E. On the Circularity of a Complex Random Variable. IEEE Signal Process. Lett. 2008, 15, 841–844. [Google Scholar] [CrossRef]
- Abeida, H.; Delmas, J.P. MUSIC-like estimation of direction of arrival for noncircular sources. IEEE Trans. Signal Process. 2006, 54, 2678–2690. [Google Scholar] [CrossRef]
- Zoubir, A.; Chargé, P.; Wang, Y. Non circular sources localization with ESPRIT. In Proceedings of the European Conference on Wireless Technology (ECWT 2003), Munich, Germany, 6–10 October 2003. [Google Scholar]
- Yunfei, W.; Jinqing, S.; Xiaofei, Z.; Yi, H.; Xiangrui, D. Non-circular signals for nested array: Sum–difference co-array and direction of arrival estimation algorithm. IET Radar Sonar Navig. 2020, 14, 27–35. [Google Scholar] [CrossRef]
- Dong, X.; Zhao, J.; Sun, M.; Zhang, X. Non-Circular Signal DOA Estimation with Nested Array via Off-Grid Sparse Bayesian Learning. Sensors 2023, 23, 8907. [Google Scholar] [CrossRef]
- Zhang, X.; Xu, L.; Xu, L.; Xu, D. Direction of Departure (DOD) and Direction of Arrival (DOA) Estimation in MIMO Radar with Reduced-Dimension MUSIC. IEEE Commun. Lett. 2010, 14, 1161–1163. [Google Scholar] [CrossRef]
- Han, K.; Nehorai, A. Nested Array Processing for Distributed Sources. IEEE Signal Process. Lett. 2014, 21, 1111–1114. [Google Scholar] [CrossRef]
- Lee, Y.U.; Choi, J.; Song, I.; Lee, S.R. Distributed Source Modeling and Direction-of-Arrival Estimation Techniques. IEEE Trans. Signal Process. 1997, 45, 960–969. [Google Scholar] [CrossRef]
- Han, Y.; Wang, J.; Zhao, Q.; Wang, B. A new approach to parameter estimation for coherently distributed source. In Proceedings of the 2009 ISECS International Colloquium on Computing, Communication, Control, and Management, Sanya, China, 8–9 August 2009; Volume 4, pp. 507–510. [Google Scholar] [CrossRef]
- Gradshteyn, I.S.; Ryzhik, I.M. Table of Integrals, Series, and Products; Academic Press: Cambridge, MA, USA, 2014. [Google Scholar]
- Steinwandt, J.; Roemer, F.; Haardt, M. ESPRIT-type algorithms for a received mixture of circular and strictly non-circular signals. In Proceedings of the 2015 IEEE International Conference on Acoustics, Speech and Signal Processing (ICASSP), Brisbane, Australia, 19–24 April 2015; pp. 2809–2813. [Google Scholar] [CrossRef]
- Yang, M.; Zhang, Y.; Sun, Y.; Zhang, X. An Enhanced Spatial Smoothing Technique of Coherent DOA Estimation with Moving Coprime Array. Sensors 2023, 23, 8048. [Google Scholar] [CrossRef] [PubMed]
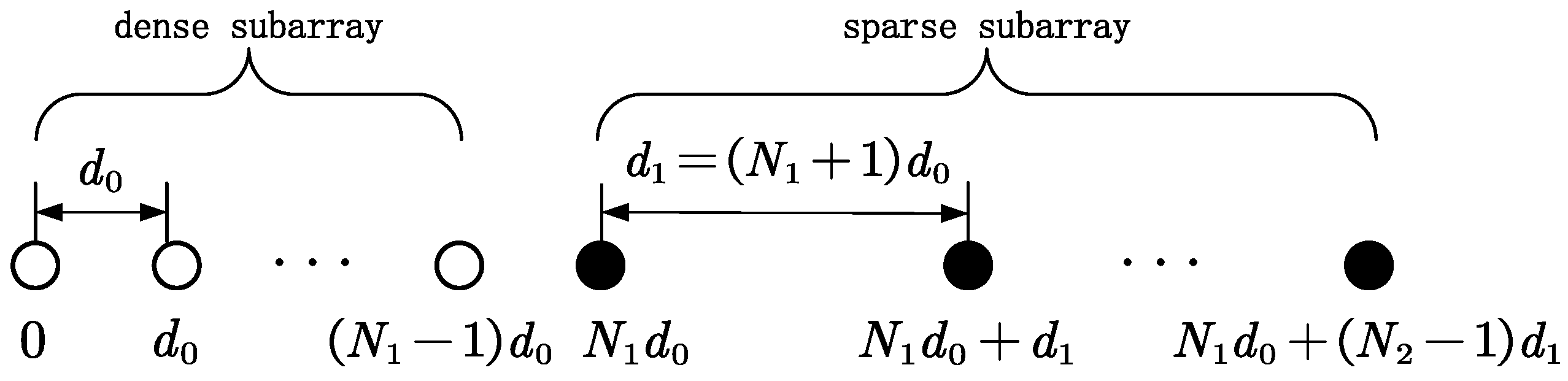



Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Chen, K.; Chen, W.; Li, J. Noncircular Distributed Source DOA Estimation with Nested Arrays via Reduced-Dimension MUSIC. Sensors 2024, 24, 6653. https://doi.org/10.3390/s24206653
Chen K, Chen W, Li J. Noncircular Distributed Source DOA Estimation with Nested Arrays via Reduced-Dimension MUSIC. Sensors. 2024; 24(20):6653. https://doi.org/10.3390/s24206653
Chicago/Turabian StyleChen, Kaiyuan, Weiyang Chen, and Jiaqi Li. 2024. "Noncircular Distributed Source DOA Estimation with Nested Arrays via Reduced-Dimension MUSIC" Sensors 24, no. 20: 6653. https://doi.org/10.3390/s24206653
APA StyleChen, K., Chen, W., & Li, J. (2024). Noncircular Distributed Source DOA Estimation with Nested Arrays via Reduced-Dimension MUSIC. Sensors, 24(20), 6653. https://doi.org/10.3390/s24206653






