Study on the Robust Filter Method of SINS/DVL Integrated Navigation Systems in a Complex Underwater Environment
Abstract
1. Introduction
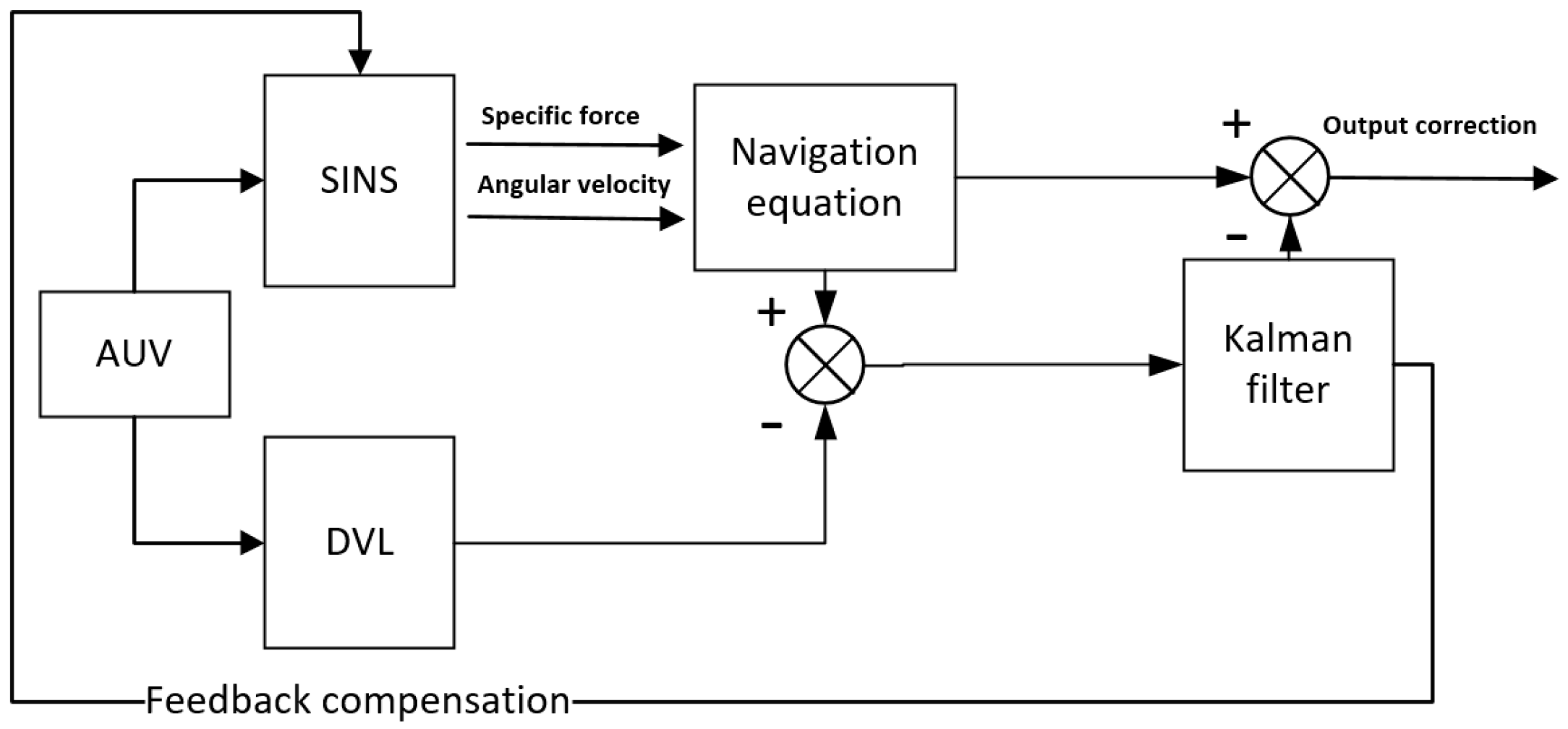
2. SINS/DVL Integrated Navigation System Model
2.1. Integrated Navigation Filtering Algorithm
2.2. Mathematical Model SINS Error
2.2.1. Error Model of Inertial Device
- (a)
- Gyroscope error model
- (b)
- Error model of accelerometer
2.2.2. Attitude Error Equation
2.2.3. Velocity Error Equation
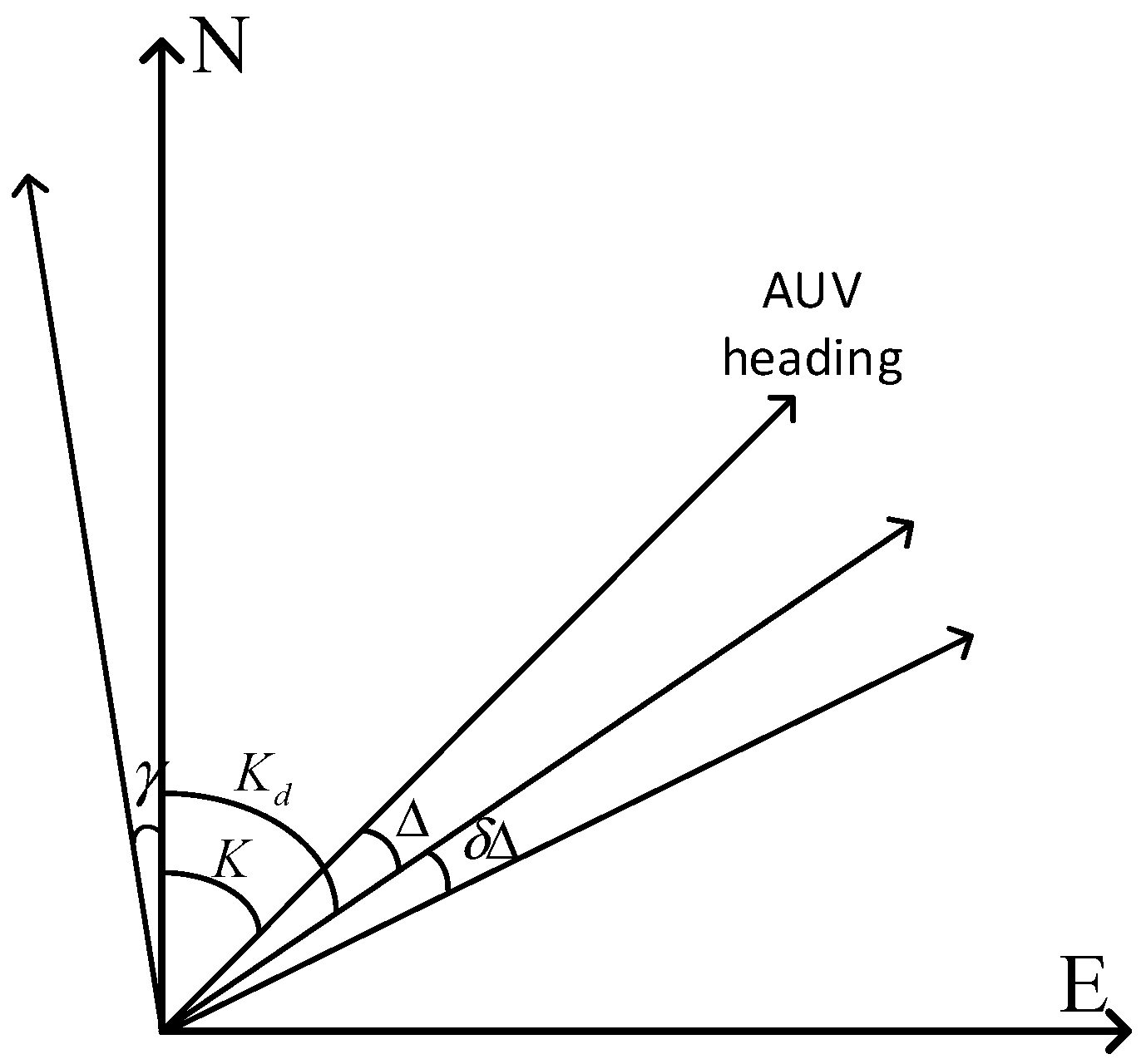
2.2.4. Selection of Correction Method
2.3. Mathematical Model of DVL Error
2.4. Mathematical Model of SINS/DVL Integrated Navigation System
- (1)
- Both system noise and measurement noise are Gaussian white noise sequences or zero-mean white noise sequences;
- (2)
- and are not correlated;
- (3)
- The statistical characteristics such as the mean and variance of the initial of the system are known;
- (4)
- Both and are independent of the initial state .
3. SINS/DVL Fault Detection and Beam Failure Processing
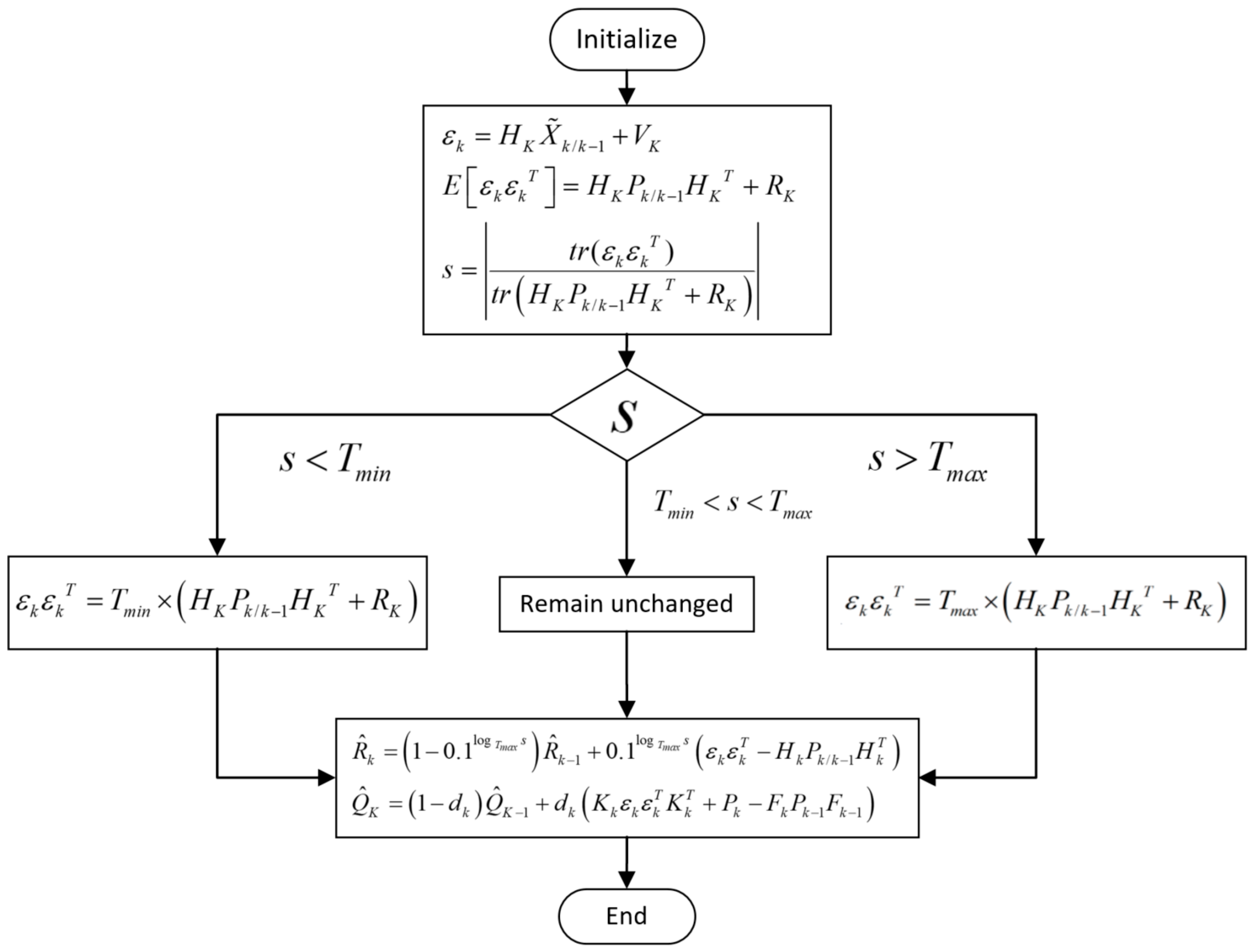
3.1. Beam Fault Detection Based on Innovation
3.2. Improved Adaptive Filtering Algorithm
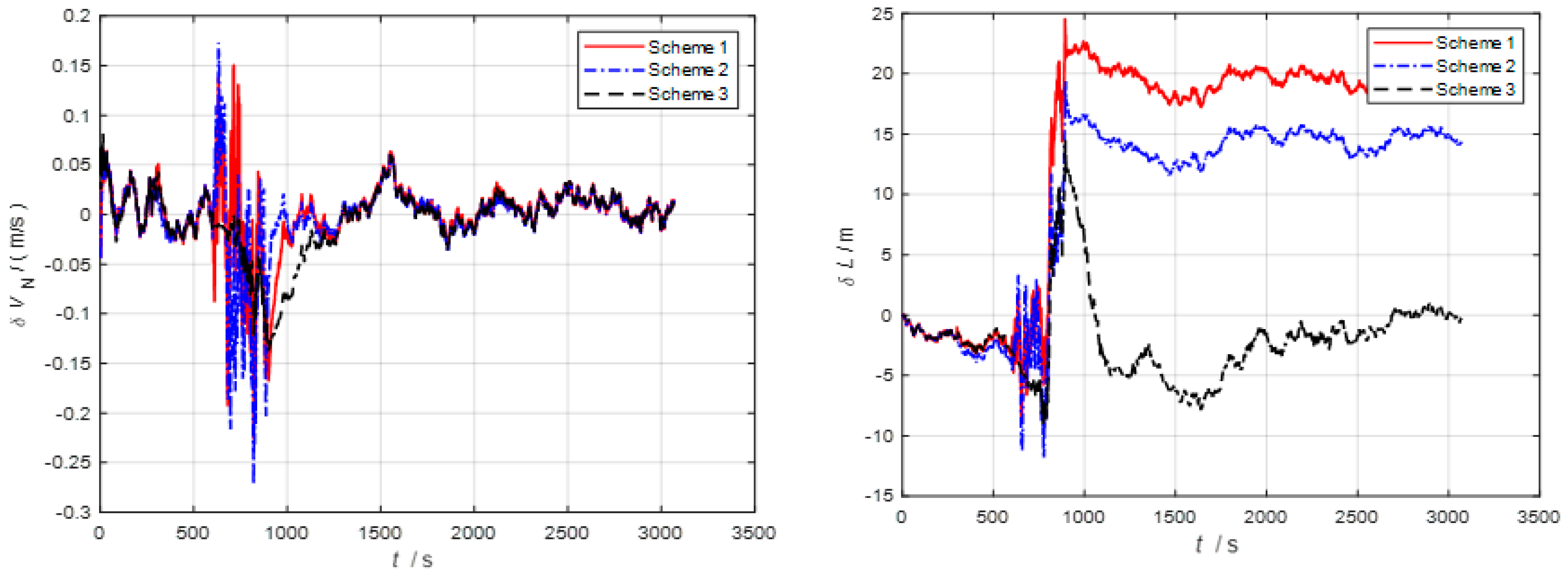
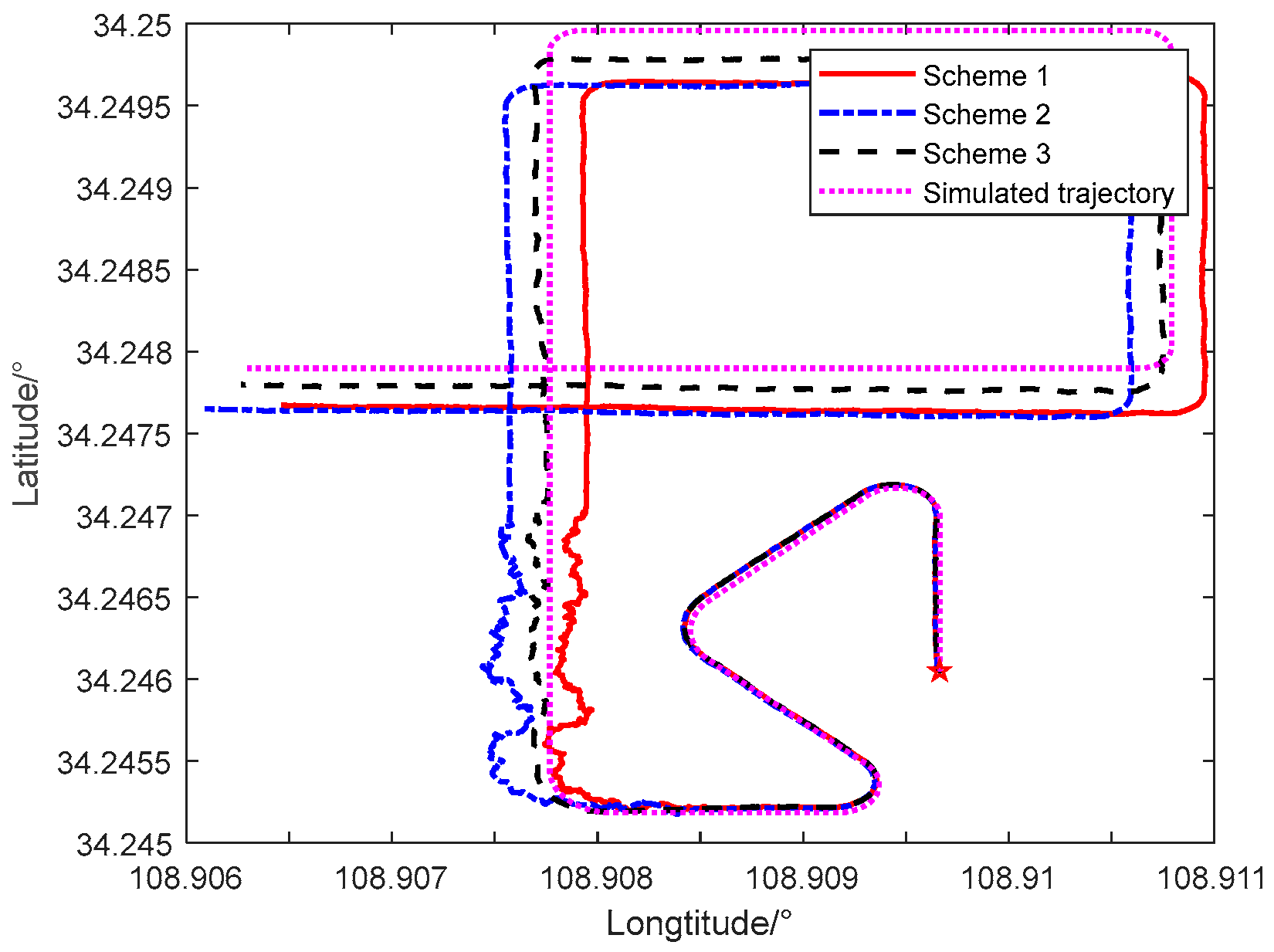
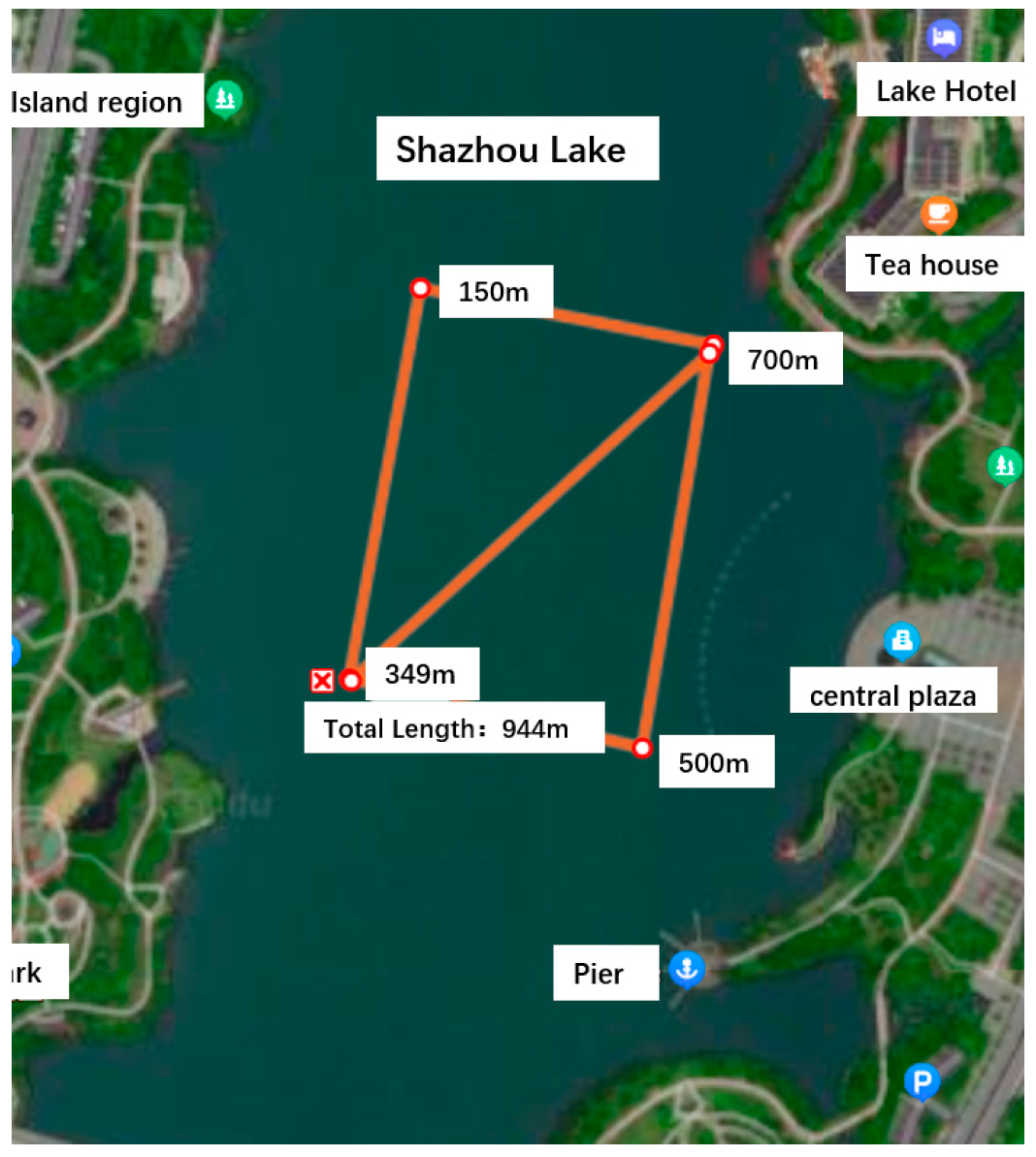
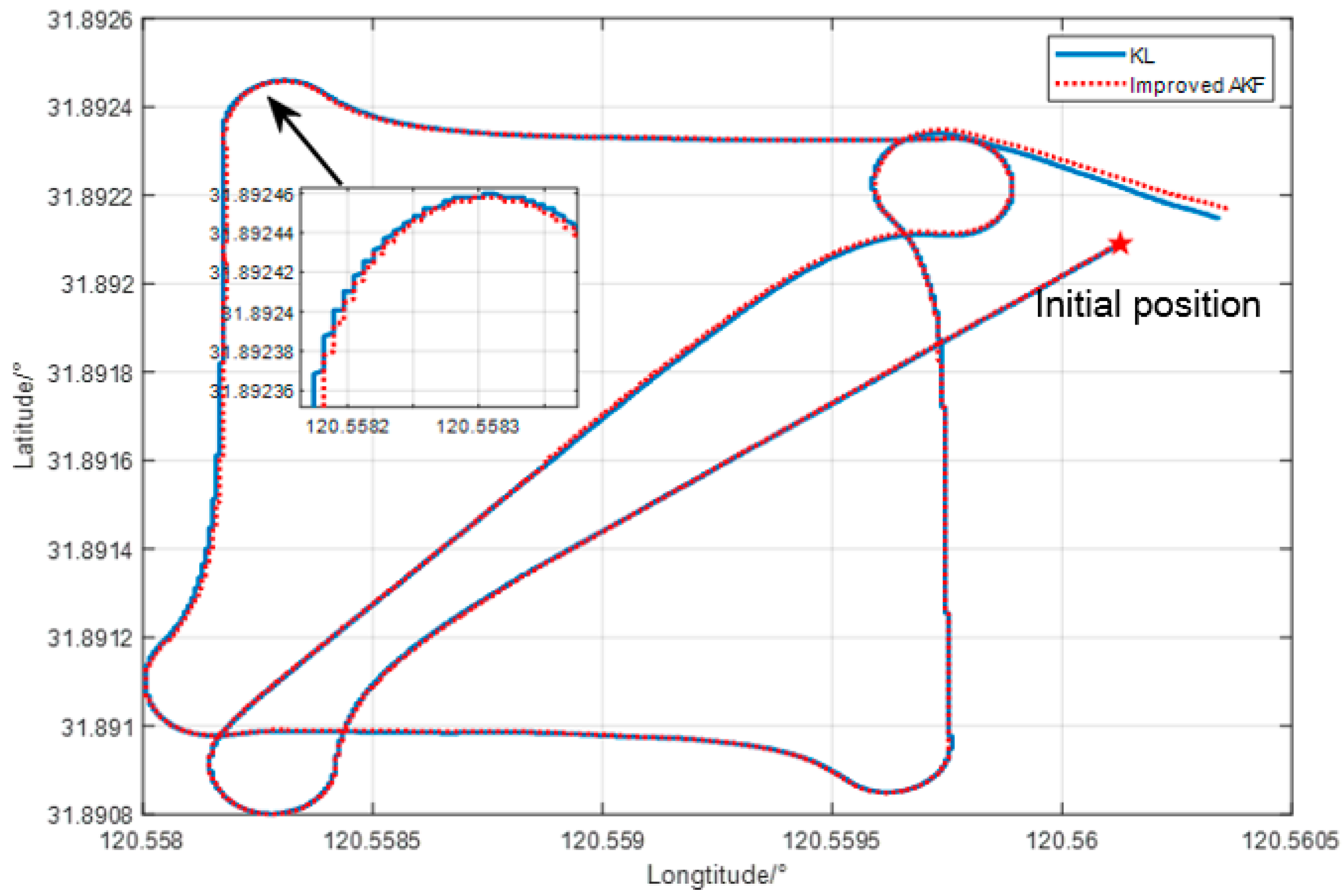
4. Experiment and Result Analysis
4.1. Simulation Experiment
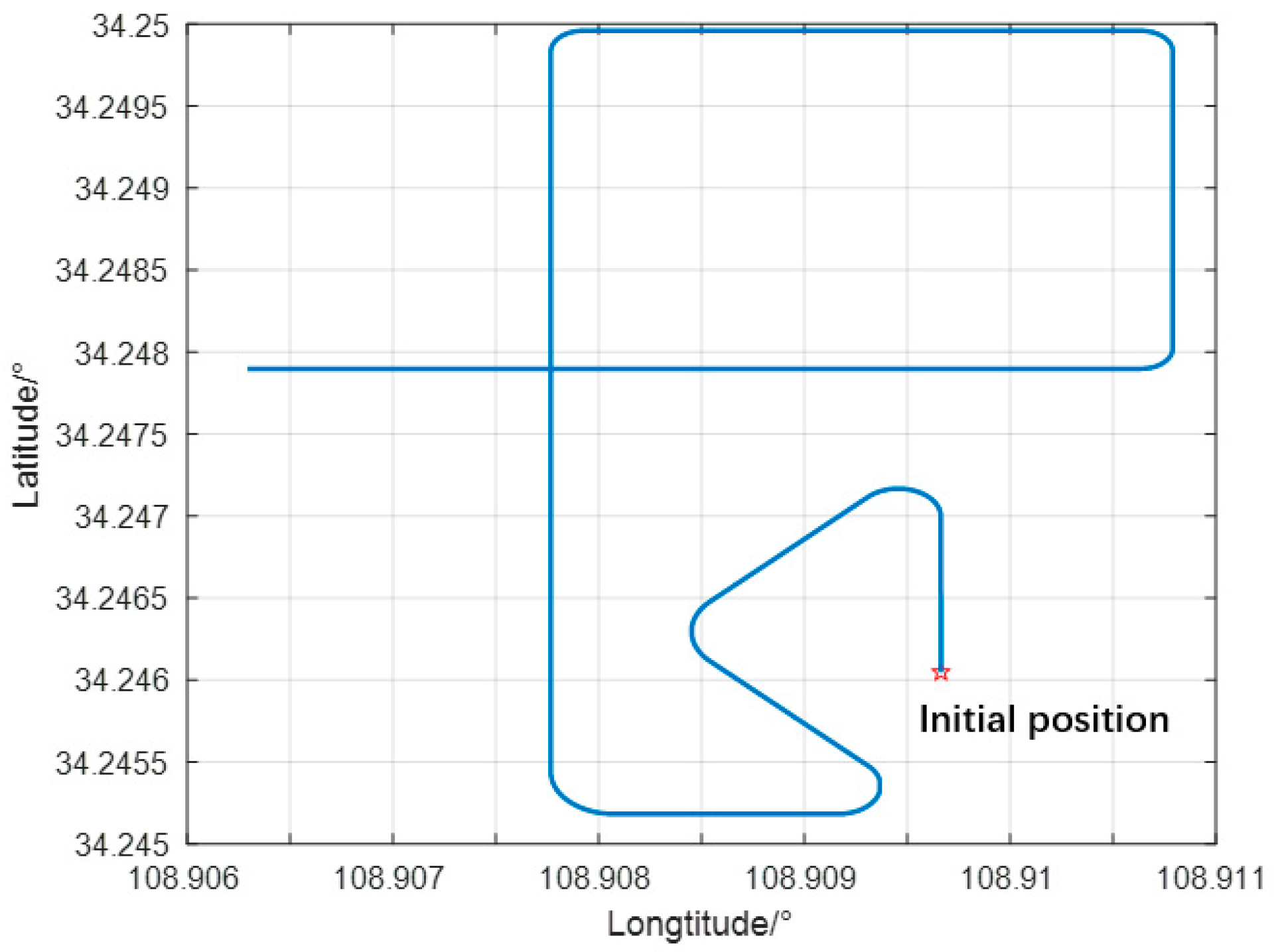
4.2. Lake Experiment
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Paull, L.; Saeedi, S.; Seto, M.; Li, H. AUV navigation and localization: A review. IEEE J. Ocean. Eng. 2013, 39, 131–149. [Google Scholar] [CrossRef]
- Sahoo, A.; Dwivedy, S.K.; Robi, P.S. Advancements in the field of autonomous underwater vehicle. Ocean. Eng. 2019, 181, 145–160. [Google Scholar] [CrossRef]
- Huang, Y.L.; Zhang, Y.G.; Zhao, Y.X. Review of autonomous undersea vehicle navigation methods. J. Unmanned Undersea Syst. 2019, 27, 232–253. [Google Scholar]
- Wang, Q.; Diao, M.; Gao, W.; Zhu, M.; Xiao, S. Integrated navigation method of a marine strapdown inertial navigation system using a star sensor. Meas. Sci. Technol. 2015, 26, 115101. [Google Scholar] [CrossRef]
- Noureldin, A.; Karamat, T.B.; Georgy, J. Fundamentals of Inertial Navigation, Satellite-Based Positioning and Their Integration; Springer Science & Business Media: Berlin, Germany, 2012. [Google Scholar]
- Zhang, Q.; Meng, X.; Zhang, S.; Wang, Y. Singular value decomposition-based robust cubature Kalman filtering for an integrated GPS/SINS navigation system. J. Navig. 2015, 68, 549–562. [Google Scholar] [CrossRef]
- Pan, X.; Wu, Y. Underwater Doppler navigation with self-calibration. J. Navig. 2016, 69, 295–312. [Google Scholar] [CrossRef]
- Taudien, J.Y.; Bilén, S.G. Quantifying long-term accuracy of sonar Doppler velocity logs. IEEE J. Ocean. Eng. 2017, 43, 764–776. [Google Scholar] [CrossRef]
- Xu, B.; Wang, L.; Li, S.; Zhang, J. A novel calibration method of SINS/DVL integration navigation system based on quaternion. IEEE Sens. J. 2020, 20, 9567–9580. [Google Scholar] [CrossRef]
- Wang, C.; Cheng, C.; Yang, D.; Pan, G.; Zhang, F. Underwater AUV Navigation Dataset in Natural Scenarios. Electronics 2023, 12, 3788. [Google Scholar] [CrossRef]
- Liu, X.; Liu, X.; Wang, L.; Huang, Y.; Wang, Z. SINS/DVL integrated system with current and misalignment estimation for midwater navigation. IEEE Access 2021, 9, 51332–51342. [Google Scholar] [CrossRef]
- Shi, W.; Xu, J.; He, H.; Li, D.; Tang, H.; Lin, E. Fault-tolerant SINS/HSB/DVL underwater integrated navigation system based on variational Bayesian robust adaptive Kalman filter and adaptive information sharing factor. Measurement 2022, 196, 111225. [Google Scholar] [CrossRef]
- Wang, D.; Xu, X.; Hou, L. An improved adaptive Kalman filter for underwater SINS/DVL system. Math. Probl. Eng. 2020, 2020, 5456961. [Google Scholar] [CrossRef]
- Klein, I.; Lipman, Y. Continuous INS/DVL fusion in situations of DVL outages. In Proceedings of the 2020 IEEE/OES Autonomous Underwater Vehicles Symposium (AUV), St. Johns, NL, Canada, 30 September–2 October 2020; pp. 1–6. [Google Scholar]
- Zhu, T.; Liu, Y.; Li, W.; Luo, j.; Zhu, X. The Integrated Navigation of SINS/DVLAn Based on Improved Sage-Husa Adaptive Filtering Algorithm. Fire Control Command Control 2023, 48, 38–43. [Google Scholar]
- Zhu, J.; Li, A.; Qin, F.; Chang, L.; Qian, L. A hybrid method for dealing with DVL faults of SINS/DVL integrated navigation system. IEEE Sens. J. 2022, 22, 15844–15854. [Google Scholar] [CrossRef]
- Xu, X.; Xu, X.; Zhang, T.; Li, Y.; Tong, J. A Kalman filter for SINS self-alignment based on vector observation. Sensors 2017, 17, 264. [Google Scholar] [CrossRef] [PubMed]
- Li, J.; Gu, M.; Zhu, T.; Wang, Z.; Zhang, Z.; Han, G. Research on error correction technology in underwater SINS/DVL integrated positioning and navigation. Sensors 2023, 23, 4700. [Google Scholar] [CrossRef]
- Ding, G.; Zhou, W.; Cuo, G. Study on error modeling methods of strap-down INS and their relations. In Proceedings of the 2009 Second International Conference on Information and Computing Science, Manchester, UK, 21–22 May 2009; Volume 3, pp. 341–344. [Google Scholar]
- Liu, R.; Liu, F.; Liu, C.; Zhang, P. Modified Sage-Husa Adaptive Kalman Filter-Based SINS/DVL Integrated Navigation System for AUV. J. Sens. 2021, 2021, 9992041. [Google Scholar] [CrossRef]
- Ghanipoor, F.; Alasty, A.; Salarieh, H.; Hashemi, M.; Shahbazi, M. Model identification of a Marine robot in presence of IMU-DVL misalignment using TUKF. Ocean. Eng. 2020, 206, 107344. [Google Scholar] [CrossRef]
- Tal, A.; Klein, I.; Katz, R. Inertial navigation system/Doppler velocity log (INS/DVL) fusion with partial DVL measurements. Sensors 2017, 17, 415. [Google Scholar] [CrossRef]
- Wang, Q.; Liu, K.; Cao, Z. System noise variance matrix adaptive Kalman filter method for AUV INS/DVL navigation system. Ocean. Eng. 2023, 267, 113269. [Google Scholar] [CrossRef]
- Xu, X.S.; Pan, Y.F.; Zou, H.J. SINS/DVL integrated navigation system based on adaptive filtering. J. Huazhong Univ. Sci. Technol. 2015, 43, 95–99. [Google Scholar]
- Du, X.; Hu, X.B.; Hu, J.S.; Sun, Z. An adaptive interactive multi-model navigation method based on UUV. Ocean Eng. 2023, 267, 113217. [Google Scholar] [CrossRef]
- Li, N.; Zhu, R.H.; Zhang, Y.G. Adaptive square CKF method for target tracking based on Sage-Husa algorithm. Syst. Eng. Electron. 2014, 36, 2. [Google Scholar]
- Xue, L.; Gao, S.S.; Hu, G.G. Adaptive Sage-Husa particle filtering and its application in integrated navigation. Zhongguo Guanxing Jishu Xuebao 2013, 21. [Google Scholar]






| Sensors | Parameter | Value |
|---|---|---|
| Gyroscope | Biases drift | 0.03°/h |
| Random walk noise | 0.01°/ | |
| Accelerometer | Biases drift | 100 μg |
| Random walk noise | 50 μg | |
| DVL | Scale factor error | 0.1% |
| Eastbound Position Error/m | Northbound Position Error/m | Relative Position Error/m | |
|---|---|---|---|
| Kalman filter | 50.7 | 20.0 | 52.1 |
| Sage–Husa filter | 16.9 | 22.7 | 10.5 |
| Improved adaptive filter | 16.6 | 17.3 | 6.2 |
| /(m/s) | /(m/s) | /(m/s) | /m | /m | /m | |
|---|---|---|---|---|---|---|
| Kalman filter | 0.0682 | 0.0654 | 0.0190 | 22.0380 | 37.6062 | 13.4920 |
| Sage–Husa filter | 0.0393 | 0.0641 | 0.0103 | 18.4179 | 15.8249 | 3.7923 |
| Improved adaptive filter | 0.0181 | 0.0256 | 0.0043 | 11.2491 | 4.9841 | 3.7745 |
| Laboratory Equipment | The Performance Parameters | Parameters |
|---|---|---|
| SINS | Accelerometer accuracy and maximum range | 5 × 10−5 G; ±15 g |
| Gyro accuracy and maximum range | 0.001°/h; ±200°/s | |
| DVL | Speed measuring precision | 0.2% of 1 mm/s± |
| Underground height survey | 0.3~110 m | |
| DGPS | Positioning accuracy | 0.1 m |
| Sound speed meter | Speed measuring precision | 0.1 m/s |
| Attitude measuring instrument | Three-axis rotary accuracy | 0.001° |
| Depth gauge | Accuracy of measurement | ±0.25% FS |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhu, T.; Li, J.; Duan, K.; Sun, S. Study on the Robust Filter Method of SINS/DVL Integrated Navigation Systems in a Complex Underwater Environment. Sensors 2024, 24, 6596. https://doi.org/10.3390/s24206596
Zhu T, Li J, Duan K, Sun S. Study on the Robust Filter Method of SINS/DVL Integrated Navigation Systems in a Complex Underwater Environment. Sensors. 2024; 24(20):6596. https://doi.org/10.3390/s24206596
Chicago/Turabian StyleZhu, Tianlong, Jian Li, Kun Duan, and Shouliang Sun. 2024. "Study on the Robust Filter Method of SINS/DVL Integrated Navigation Systems in a Complex Underwater Environment" Sensors 24, no. 20: 6596. https://doi.org/10.3390/s24206596
APA StyleZhu, T., Li, J., Duan, K., & Sun, S. (2024). Study on the Robust Filter Method of SINS/DVL Integrated Navigation Systems in a Complex Underwater Environment. Sensors, 24(20), 6596. https://doi.org/10.3390/s24206596





