Robust Cubature Kalman Filter for Moving-Target Tracking with Missing Measurements
Abstract
1. Introduction
- The RCKF was developed by integrating Huber’s M-estimation theory with the standard CKF to effectively handle nonlinear systems, with missing measurements characterized using random variables following the Bernoulli distribution.
- The RCKF exhibited superior performance compared to the EKF, EnKF, and CKF in terms of accuracy and reliability on two moving-target tracking models (UNGM and BOT) with missing measurements, indicating that the RCKF is the most effective approach for nonlinear systems with missing measurements.
2. Nonlinear System with Missing Measurements
- The initial state follows a Gaussian distribution, i.e., .
- The noise sequences and are independent Gaussian sequences with zero means, and the covariance matrix of is denoted as , while the covariance matrix of is denoted as .
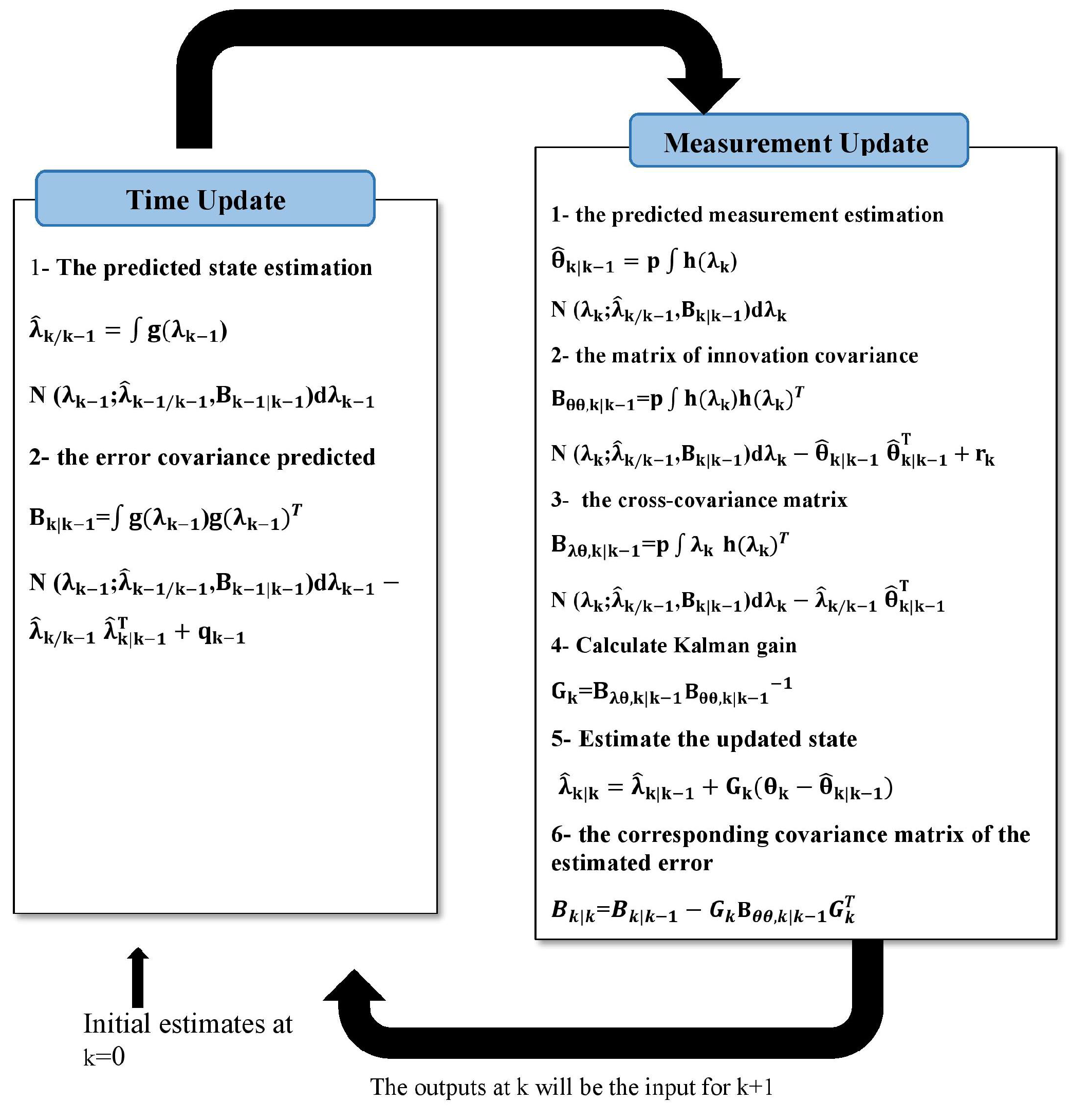
3. Cubature Kalman Filter with Missing Measurements
- The time prediction is as follows:
- I
- The posterior probability distribution of a given time isBy Cholesky decomposition, The expression denoting the error covariance at time , denoted as , is given bywhere denotes a diagonal time matrix.
- II
- Calculating the cubature points.where represents the system state of the t-th cubature point at time . The cubature points set is denoted as and can be defined aswhere is the number of cubature points or twice the state dimension; refers to a set of problems; and is the t-th point in .
- III
- Predicting state.The t-th cubature point’s predicted state from time to time k is defined as
- The measurement update is as follows, including the error covariance at time k:
- I
- Factorizing the CM of the error .
- II
- Calculating the cubature points.
- III
- Updating observation.The estimated observation of the t-th cubature point between epochs and k is denoted byFrom (24), we can obtain the predicted observation of the t-th cubature point from time to :and its covariance and cross-covariance matrices areand
- IV
- Calculating the Kalman gain.
- V
- State update.
- VI
- CM of the estimate error update.
4. Robust Cubature Kalman Filter with Missing Measurements
5. Metrics of Performance
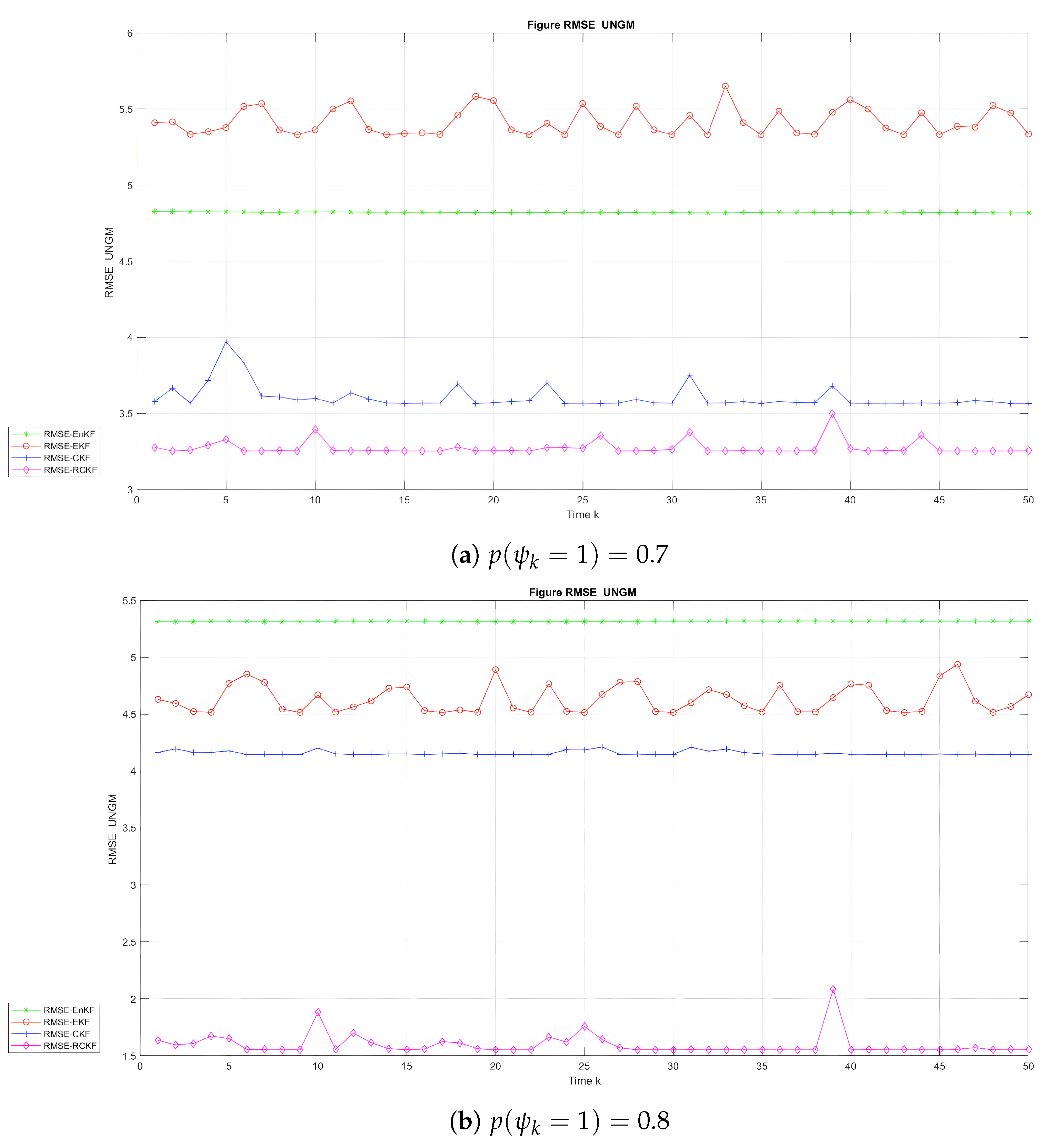
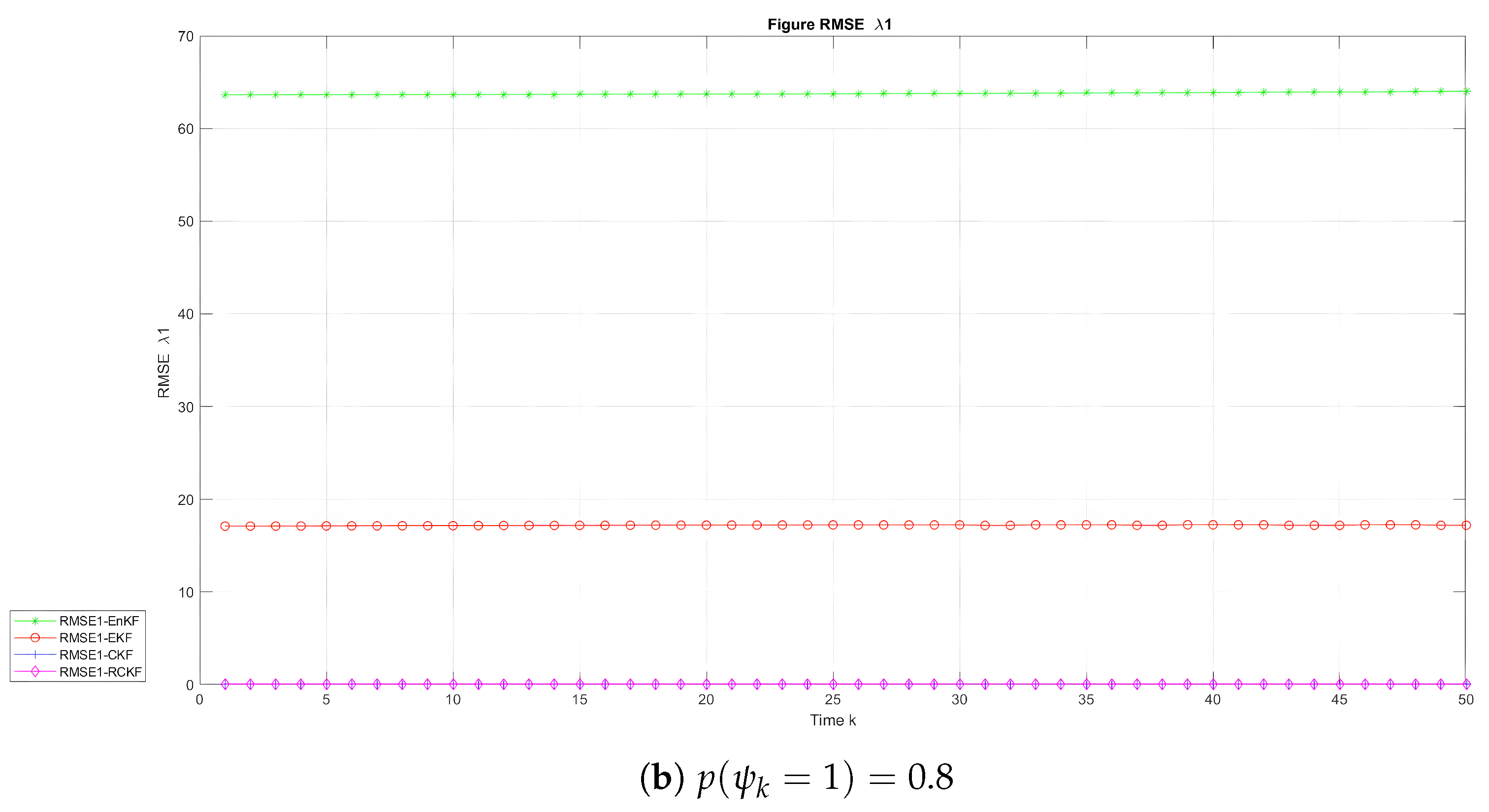
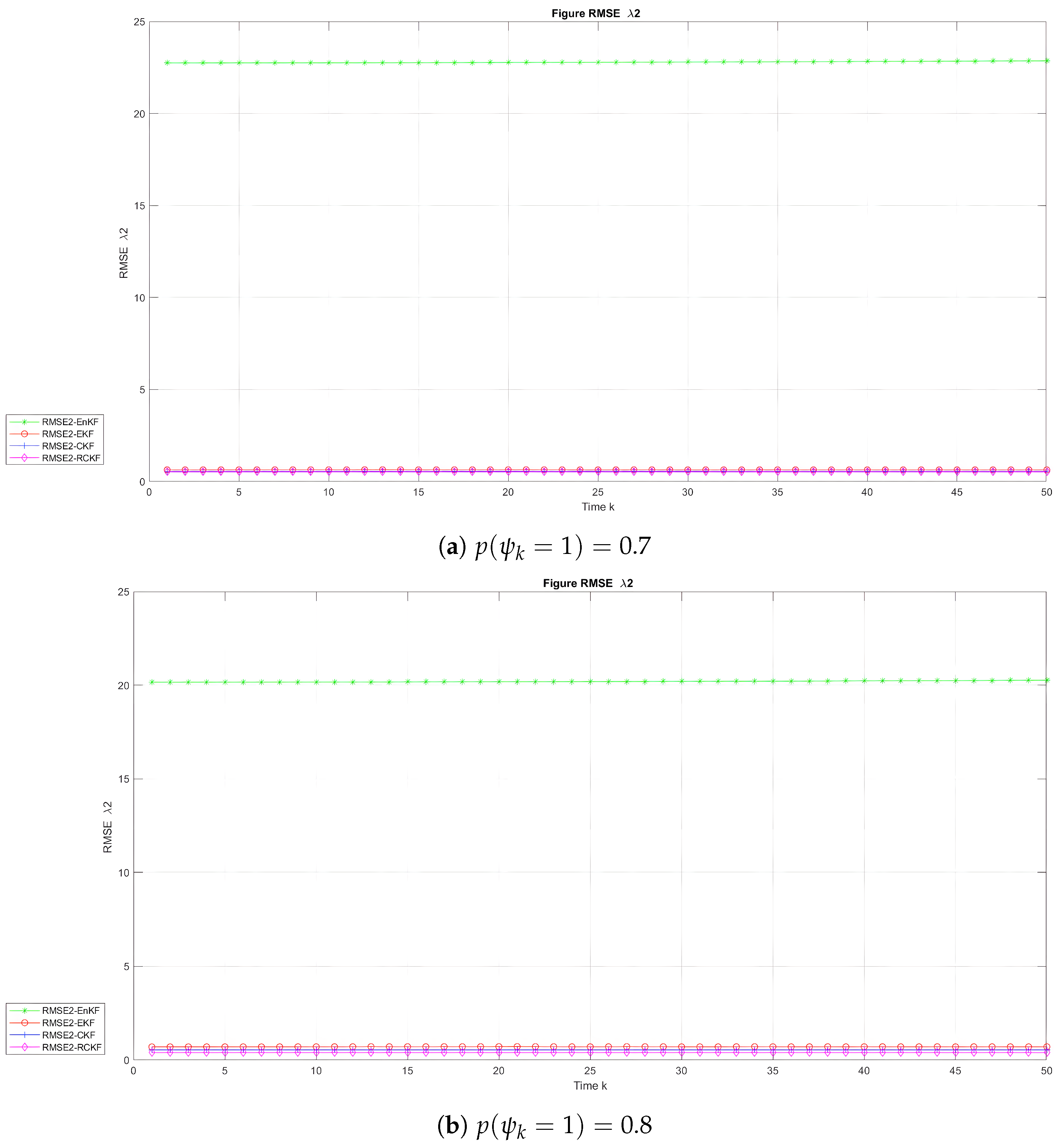
- Root mean square error (RMSE).The RMSE for the state estimate generated utilizing M Monte Carlo simulations at time instant k is as follows:where the estimate of at the t-th Monte Carlo simulation is .
- Non-credibility index.In order to calculate the NCI, we compared the estimator’s normalized squared estimation error, which is defined aswith the credible estimator’s normalized squared estimation error, expressed as [35]where is the mean square error (MSE) computed by . The NCI is described asThe NCI can measure the estimator’s credibility. That is, the estimator’s CM is close to the MSE . The lower the NCI score, the more reliable the estimator; therefore, an NCI score of zero indicates an entirely credible estimator.
6. Numerical Experiments
6.1. Model Specifications
- The UNGM.This model is described as follows:andwhere , , , probability , and .
- BOT.There are two states inside the bearing-only tracking (BOT) paradigm, with the state displaying a tracked target’s positioning in Cartesian coordinates. Its nonlinear model is as follows:where , , , and , .
6.2. Experiment and Analysis
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Abbreviations
| Abbreviations | ||
| RCKF | Robust cubature Kalman filter | |
| CKF | Cubature Kalman filter | |
| EKF | Extended Kalman filter | |
| UKF | Unscented Kalman filter | |
| EnKF | Ensemble Kalman filter | |
| CM | Covariance matrix | |
| MSE | Mean square error | |
| RMSE | Root mean square error | |
| NCI | Non-credibility index | |
| UNGM | Univariate Non-stationary Growth Model | |
| BOT | Bearing-only tracking | |
| Symbols | ||
| The state vector | ||
| The measurement vector | ||
| Nonlinear function of the state | ||
| Nonlinear function of the measurement | ||
| The process noise | ||
| The measurement noise | ||
| The covariance matrix of | ||
| The covariance matrix of | ||
| Factor of missing measurement | ||
| The predicted state estimation | ||
| The predicted measurement estimation | ||
| Predicted error covariance estimation | ||
| Estimated matrix of innovation covariance | ||
| Estimated cross-covariance matrix | ||
| Kalman gain | ||
| Estimated update state | ||
| The cubature point | ||
| Estimated matrix of innovation covariance using an absence of difference M-estimation approach | ||
| Residue vectors t-th | ||
| Residue vectors t-th | ||
| Mean variance of | ||
References
- Kalman, R. A New Approach to Liner Filtering and Prediction Problems, Transaction of ASME. J. Basic Eng. 1961, 83, 95–108. [Google Scholar] [CrossRef]
- Radhakrishnan, R.; Bhaumik, S.; Tomar, N.K. Continuous-discrete filters for bearings-only underwater target tracking problems. Asian J. Control 2019, 21, 1576–1586. [Google Scholar] [CrossRef]
- Haus, B.; Mercorelli, P. An extended Kalman filter for time delays inspired by a fractional order model. In Proceedings of the Conference on Non-integer Order Calculus and Its Applications, Lodz, Poland, 11–13 October 2017; Springer: Berlin/Heidelberg, Germany, 2017; pp. 151–163. [Google Scholar]
- Schimmack, M.; Haus, B.; Mercorelli, P. An extended Kalman filter as an observer in a control structure for health monitoring of a metal–polymer hybrid soft actuator. IEEE/ASME Trans. Mechatron. 2018, 23, 1477–1487. [Google Scholar] [CrossRef]
- Brossard, M.; Barrau, A.; Bonnabel, S. A code for unscented Kalman filtering on manifolds (UKF-M). In Proceedings of the 2020 IEEE International Conference on Robotics and Automation (ICRA), Paris, France, 31 May– 31 August 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 5701–5708. [Google Scholar]
- Gao, B.; Gao, S.; Hu, G.; Zhong, Y.; Gu, C. Maximum likelihood principle and moving horizon estimation based adaptive unscented Kalman filter. Aerosp. Sci. Technol. 2018, 73, 184–196. [Google Scholar] [CrossRef]
- Nilam, B.; Ram, S.T. Forecasting Geomagnetic activity (Dst Index) using the ensemble kalman filter. Mon. Not. R. Astron. Soc. 2022, 511, 723–731. [Google Scholar] [CrossRef]
- Gillijns, S.; Mendoza, O.B.; Chandrasekar, J.; De Moor, B.; Bernstein, D.; Ridley, A. What is the ensemble Kalman filter and how well does it work? In Proceedings of the 2006 American Control Conference, Minneapolis, MN, USA, 14–16 June 2006; IEEE: Piscataway, NJ, USA, 2006; p. 6. [Google Scholar]
- Katzfuss, M.; Stroud, J.R.; Wikle, C.K. Understanding the ensemble Kalman filter. Am. Stat. 2016, 70, 350–357. [Google Scholar] [CrossRef]
- Zhou, N.; Meng, D.; Huang, Z.; Welch, G. Dynamic state estimation of a synchronous machine using PMU data: A comparative study. IEEE Trans. Smart Grid 2014, 6, 450–460. [Google Scholar] [CrossRef]
- Arasaratnam, I.; Haykin, S. Cubature Kalman filters. IEEE Trans. Autom. Control 2009, 54, 1254–1269. [Google Scholar] [CrossRef]
- Mallick, M.; Tian, X.; Liu, J. Evaluation of measurement converted KF, EKF, UKF, CKF, and PF in GMTI filtering. In Proceedings of the 2021 International Conference on Control, Automation and Information Sciences (ICCAIS), Xi’an, China, 14–17 October 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 21–27. [Google Scholar]
- Liu, W.; Zhang, Q.; Zhao, Y. Performance Evaluation of Cubature Kalman Filtering and Extended Kalman Filtering Based Phase Unwrapping For Insar. In Proceedings of the IOP Conference Series: Earth and Environmental Science, Surakarta, Indonesia, 24–25 August 2021; IOP Publishing: Bristol, UK, 2021; Volume 693, p. 012047. [Google Scholar]
- Zhao, L.; Wang, R.; Wang, J.; Yu, T.; Su, A. Nonlinear state estimation with delayed measurements using data fusion technique and cubature Kalman filter for chemical processes. Chem. Eng. Res. Des. 2019, 141, 502–515. [Google Scholar] [CrossRef]
- Zhang, Y.; Wang, J.; Sun, Q.; Gao, W. Adaptive cubature Kalman filter based on the variance-covariance components estimation. J. Glob. Position. Syst. 2017, 15, 1–9. [Google Scholar] [CrossRef]
- Zhao, X.; Li, J.; Yan, X.; Ji, S. Robust adaptive cubature Kalman filter and its application to ultra-tightly coupled SINS/GPS navigation system. Sensors 2018, 18, 2352. [Google Scholar] [CrossRef] [PubMed]
- Zhang, C.; Zhi, R.; Li, T.; Corchado, J. Adaptive m-estimation for robust cubature kalman filtering. In Proceedings of the 2016 Sensor Signal Processing for Defence (SSPD), Edinburgh, UK, 22–23 September 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 1–5. [Google Scholar]
- Cui, B.; Chen, X.; Tang, X.; Huang, H.; Liu, X. Robust cubature Kalman filter for GNSS/INS with missing observations and colored measurement noise. ISA Trans. 2018, 72, 138–146. [Google Scholar] [CrossRef] [PubMed]
- Ye, X.; Wang, J.; Wu, D.; Zhang, Y.; Li, B. A Novel Adaptive Robust Cubature Kalman Filter for Maneuvering Target Tracking with Model Uncertainty and Abnormal Measurement Noises. Sensors 2023, 23, 6966. [Google Scholar] [CrossRef] [PubMed]
- Atitallah, M.; Davoodi, M.; Meskin, N. Event-triggered fault detection for networked control systems subject to packet dropout. Asian J. Control 2018, 20, 2195–2206. [Google Scholar] [CrossRef]
- Liu, W.Q.; Tao, G.L.; Fan, Y.J.; Zhang, G.Q. Robust fusion steady-state filtering for multisensor networked systems with one-step random delay, missing measurements, and uncertain-variance multiplicative and additive white noises. Int. J. Robust Nonlinear Control 2019, 29, 4716–4754. [Google Scholar] [CrossRef]
- Xu, L.; Ma, K.; Fan, H. Unscented Kalman filtering for nonlinear state estimation with correlated noises and missing measurements. Int. J. Control Autom. Syst. 2018, 16, 1011–1020. [Google Scholar] [CrossRef]
- Zhang, X.; Yan, Z.; Chen, Y. High-degree cubature Kalman filter for nonlinear state estimation with missing measurements. Asian J. Control 2022, 24, 1261–1272. [Google Scholar] [CrossRef]
- Fang, H.; Tian, N.; Wang, Y.; Zhou, M.; Haile, M.A. Nonlinear Bayesian estimation: From Kalman filtering to a broader horizon. IEEE/CAA J. Autom. Sin. 2018, 5, 401–417. [Google Scholar] [CrossRef]
- Meng, Q.; Leib, H.; Li, X. Cubature ensemble Kalman filter for highly dimensional strongly nonlinear systems. IEEE Access 2020, 8, 144892–144907. [Google Scholar] [CrossRef]
- Li, Y.; Li, J.; Qi, J.; Chen, L. Robust cubature Kalman filter for dynamic state estimation of synchronous machines under unknown measurement noise statistics. IEEE Access 2019, 7, 29139–29148. [Google Scholar] [CrossRef]
- Pu, Y.; Li, X.; Liu, Y.; Wang, Y.; Wu, S.; Qu, T.; Xi, J. Improved Strong Tracking Cubature Kalman Filter for UWB Positioning. Sensors 2023, 23, 7463. [Google Scholar] [CrossRef] [PubMed]
- Durovic, Z.M.; Kovacevic, B.D. Robust estimation with unknown noise statistics. IEEE Trans. Autom. Control 1999, 44, 1292–1296. [Google Scholar] [CrossRef]
- Gui, Q.; Zhang, J. Robust biased estimation and its applications in geodetic adjustments. J. Geod. 1998, 72, 430–435. [Google Scholar] [CrossRef]
- Huang, Y.; Wu, L.; Sun, F. Robust Cubature Kalman filter based on Huber M estimator. Control Decis. 2014, 29, 572–576. [Google Scholar]
- Li, K.; Hu, B.; Chang, L.; Li, Y. Robust square-root cubature Kalman filter based on Huber’s M-estimation methodology. Proc. Inst. Mech. Eng. Part G J. Aerosp. Eng. 2015, 229, 1236–1245. [Google Scholar] [CrossRef]
- Hodson, T.O. Root-mean-square error (RMSE) or mean absolute error (MAE): When to use them or not. Geosci. Model Dev. 2022, 15, 5481–5487. [Google Scholar] [CrossRef]
- Li, X.R.; Zhao, Z. Measuring estimator’s credibility: Noncredibility index. In Proceedings of the 2006 9th International Conference on Information Fusion, Florence, Italy, 10–13 July 2006; IEEE: Piscataway, NJ, USA, 2006; pp. 1–8. [Google Scholar]
- Rohr, D.; Lawrance, N.; Andersson, O.; Siegwart, R. Credible Online Dynamics Learning for Hybrid UAVs. In Proceedings of the 2023 IEEE International Conference on Robotics and Automation (ICRA), London, UK, 29 May–2 June 2023; pp. 1305–1311. [Google Scholar] [CrossRef]
- Bar-Shalom, Y.; Li, X.R.; Kirubarajan, T. Estimation with Applications to Tracking and Navigation: Theory Algorithms and Software; John Wiley & Sons: Hoboken, NJ, USA, 2004. [Google Scholar]
- Tong, Y.; Zheng, Z.; Fan, W.; Li, Q.; Liu, Z. An improved unscented Kalman filter for nonlinear systems with one-step randomly delayed measurement and unknown latency probability. Digit. Signal Process. 2022, 121, 103324. [Google Scholar] [CrossRef]
- Julier, S.J.; Uhlmann, J.K. New extension of the Kalman filter to nonlinear systems. In Proceedings of the Signal Processing, Sensor Fusion, and Target Recognition VI, Orlando, FL, USA, 21–24 April 1997; SPIE: Bellingham, WA, USA, 1997; Volume 3068, pp. 182–193. [Google Scholar]
- Kotecha, J.H.; Djuric, P.M. Gaussian sum particle filtering. IEEE Trans. Signal Process. 2003, 51, 2602–2612. [Google Scholar] [CrossRef]





| Authors | Method | Results |
|---|---|---|
| Tiancheng Li et al. [17] | Huber’s M-estimation-based robust CKF and robust square root CKF adapted to anomalous measurement noise using innovation covariance comparison. | Simulations demonstrated the superior performance in terms of accuracy, robustness, and reliability compared to standard methods for target tracking. |
| Zhao et al. [16] | Robust adaptive CKF to reduce kinematic model errors through covariance adjustment and dynamic disturbance processing. | The experiment confirmed the proposed strategy’s effectiveness in dynamic systems with high dynamics and weak signals. |
| Cui Bingbo et al. [18] | RCKF enhanced GNSS/INS accuracy in GNSS-denied environments by considering noise using missing observations. | Numerical experiments and field tests demonstrated the RCKF’s superior robustness compared to the CKF and EKF. |
| Xiangzhou Ye et al. [19] | Adaptive robust CKF (ARCKF) based on the H-infinity CKF by incorporating two adaptable algorithm components to address erroneous system models and noise statistics. | Simulations favored the recommended approach over the HCKF for handling model errors and aberrant observations. |
| Method | Average RMSE When | Average RMSE When |
|---|---|---|
| EKF | 5.41 | 4.63 |
| EnKF | 4.82 | 5.32 |
| CKF | 3.60 | 4.16 |
| RCKF | 3.27 | 1.60 |
| Method | Average RMSE When | Average RMSE When | Average RMSE | Average RMSE When |
|---|---|---|---|---|
| EKF | 17.50 | 17.19 | 0.64 | 0.71 |
| EnKF | 74.38 | 63.78 | 22.79 | 20.20 |
| CKF | 0.067 | 0.07 | 0.55 | 0.54 |
| RCKF | 0.057 | 0.07 | 0.53 | 0.40 |
| Method | Average NCI When | Average NCI When |
|---|---|---|
| EKF | 9.08 | 7.58 |
| EnKF | 9.44 | 11.07 |
| CKF | 5.23 | 7.46 |
| RCKF | 4.83 | 7.10 |
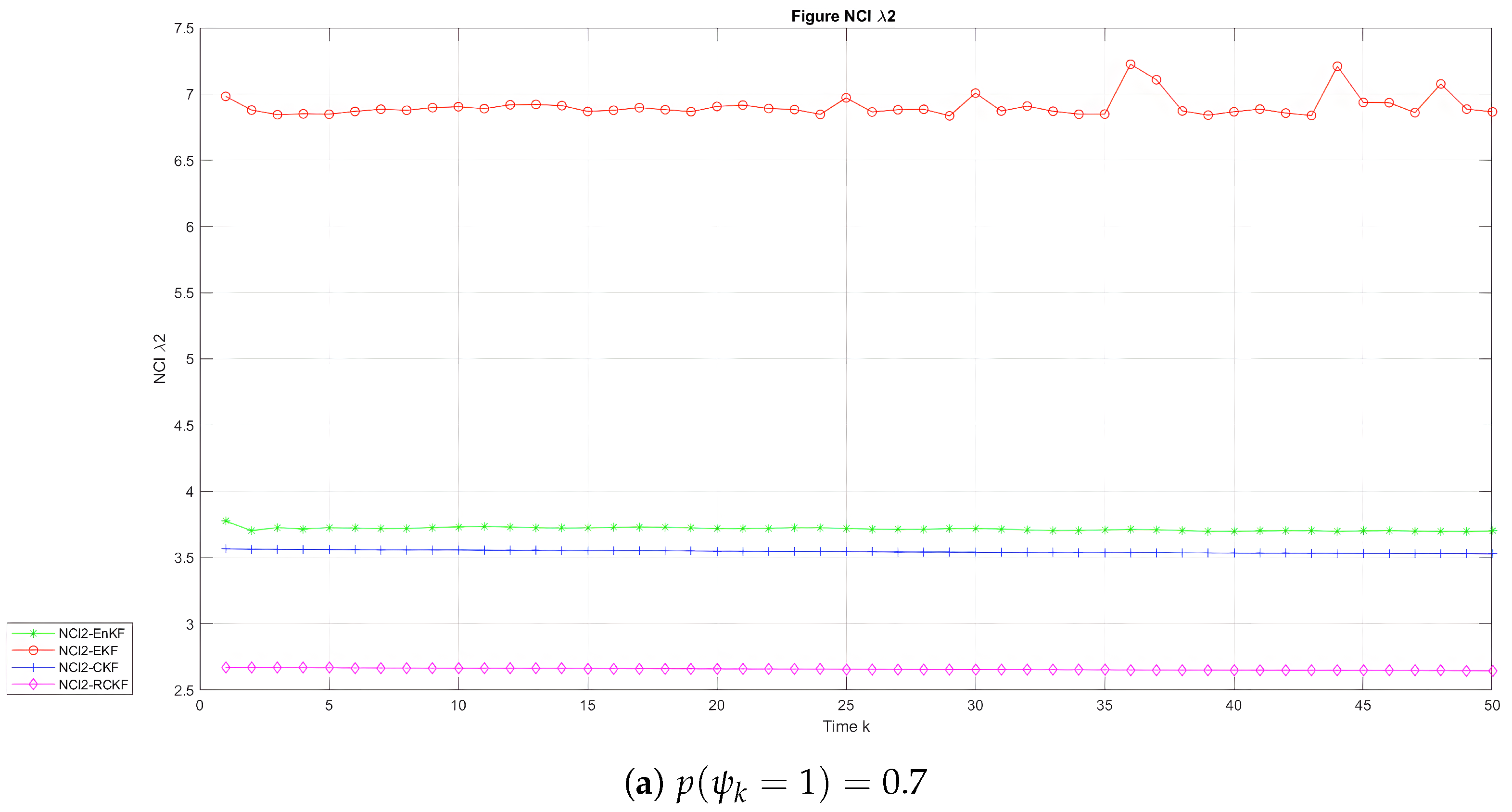
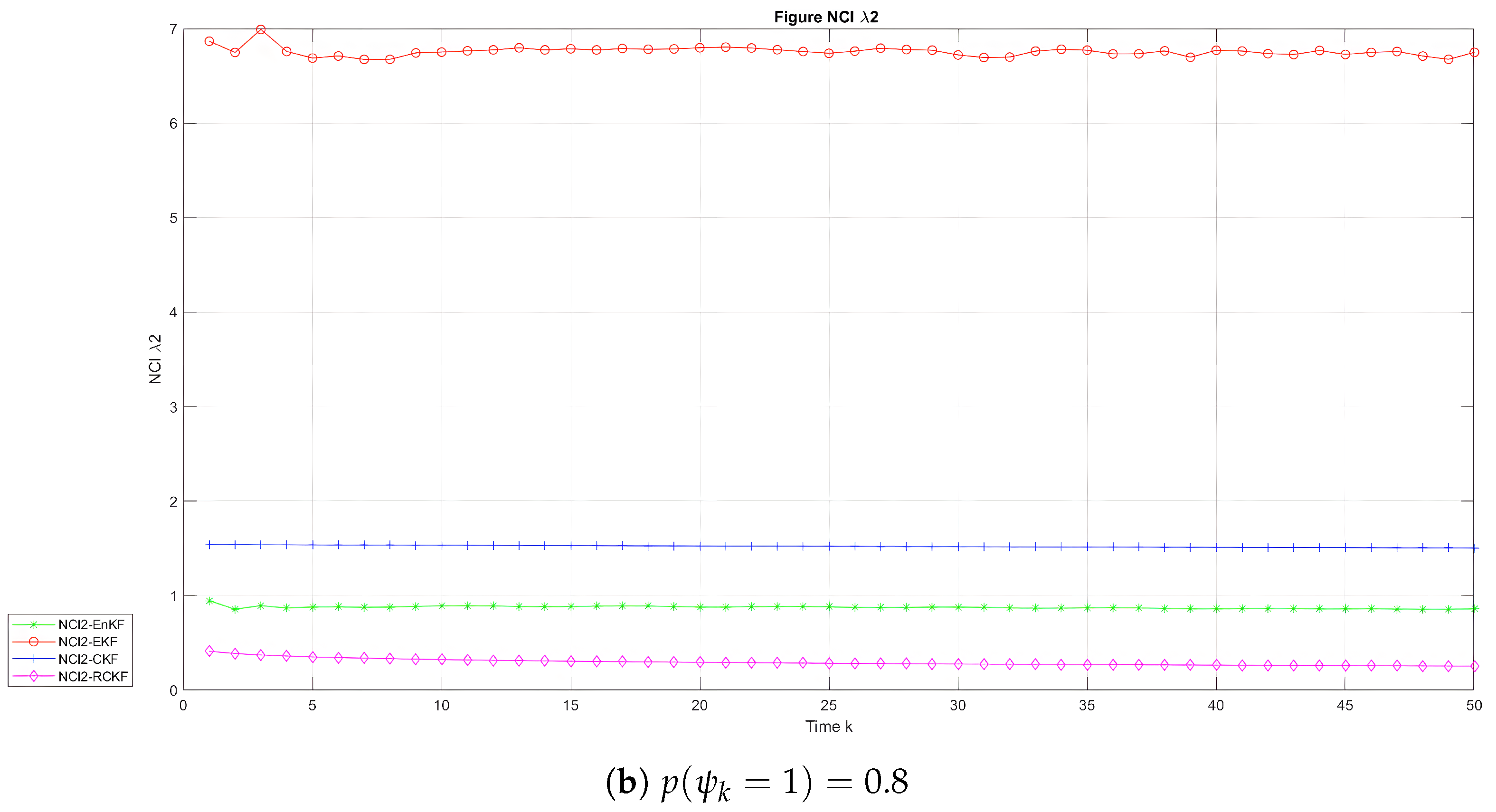
| Method | Average NCI When | Average NCI When | Average NCI When | Average NCI When |
|---|---|---|---|---|
| EKF | 3.91 | 0.69 | 6.91 | 6.76 |
| EnKF | 3.89 | 0.47 | 3.72 | 0.88 |
| CKF | 4.71 | 0.40 | 3.53 | 1.52 |
| RCKF | 3.75 | 0.18 | 2.65 | 0.29 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Sahl, S.; Song, E.; Niu, D. Robust Cubature Kalman Filter for Moving-Target Tracking with Missing Measurements. Sensors 2024, 24, 392. https://doi.org/10.3390/s24020392
Sahl S, Song E, Niu D. Robust Cubature Kalman Filter for Moving-Target Tracking with Missing Measurements. Sensors. 2024; 24(2):392. https://doi.org/10.3390/s24020392
Chicago/Turabian StyleSahl, Samer, Enbin Song, and Dunbiao Niu. 2024. "Robust Cubature Kalman Filter for Moving-Target Tracking with Missing Measurements" Sensors 24, no. 2: 392. https://doi.org/10.3390/s24020392
APA StyleSahl, S., Song, E., & Niu, D. (2024). Robust Cubature Kalman Filter for Moving-Target Tracking with Missing Measurements. Sensors, 24(2), 392. https://doi.org/10.3390/s24020392






