Raman Spectroscopy of Glass Beads in Ammonium Nitrate Solution and Compensation of Signal Losses
Abstract
1. Introduction
2. Materials and Methods
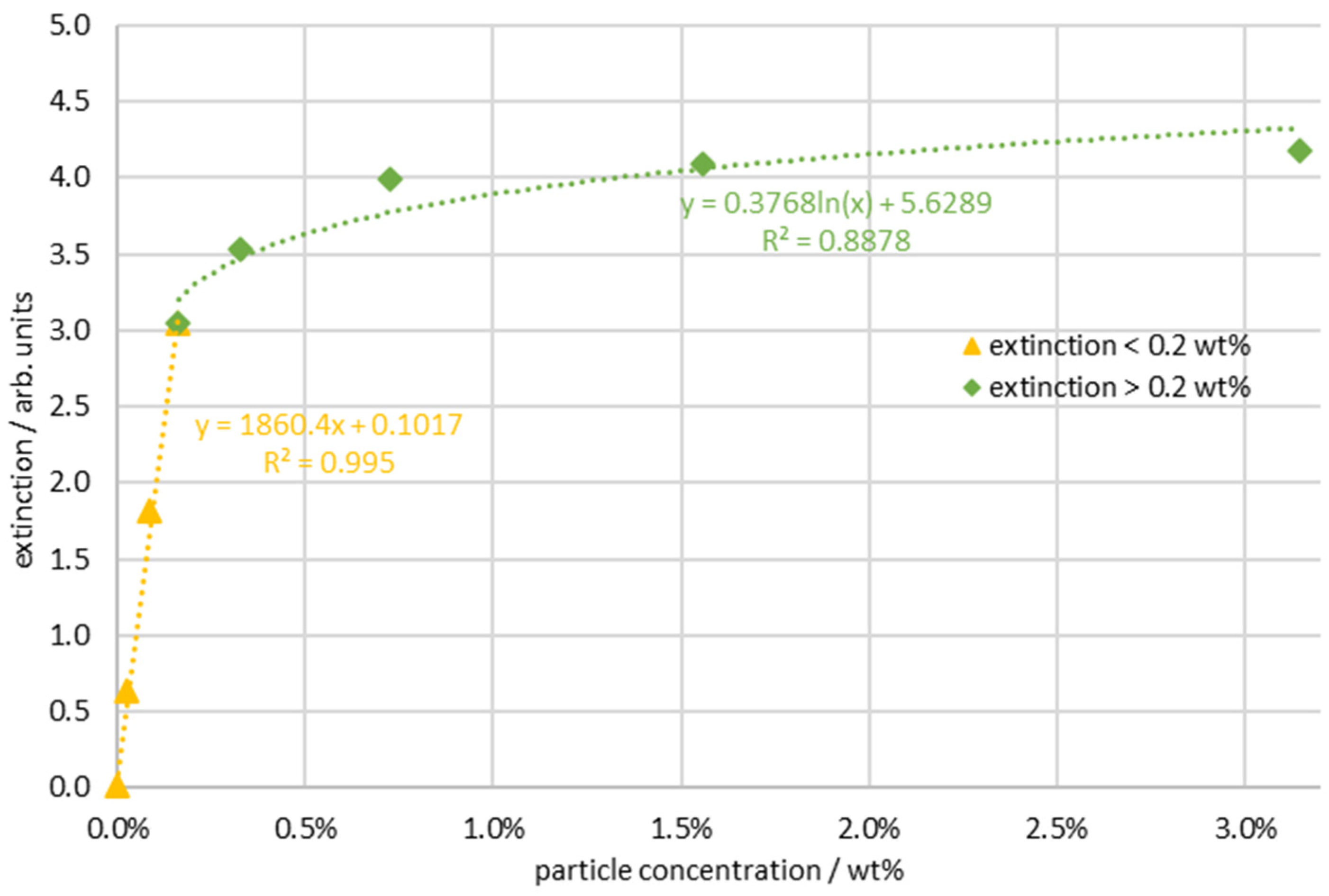
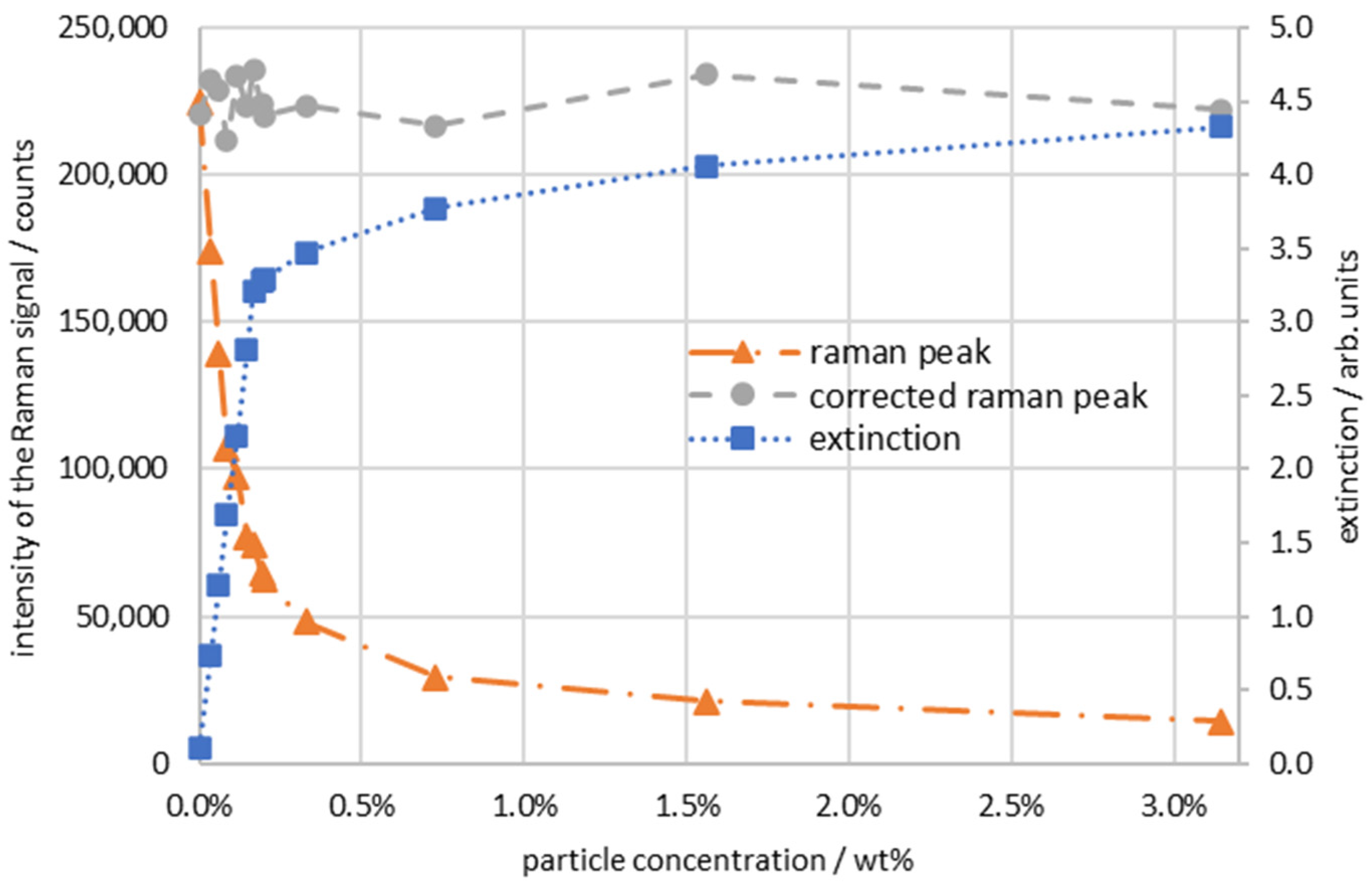
3. Results
4. Discussion and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Bakeev, K.A. Process Analytical Technology: Spectroscopic Tools and Implementation Strategies for the Chemical and Pharmaceutical Industries, 2nd ed.; Wiley: Chichester, UK, 2010; ISBN 978-0-470-72207-7. [Google Scholar]
- Kessler, R.W.; Kessler, W.; Zikulnig-Rusch, E. A Critical Summary of Spectroscopic Techniques and their Robustness in Industrial PAT Applications. Chem. Ing. Tech. 2016, 88, 710–721. [Google Scholar] [CrossRef]
- Simon, L.L.; Pataki, H.; Marosi, G.; Meemken, F.; Hungerbühler, K.; Baiker, A.; Tummala, S.; Glennon, B.; Kuentz, M.; Steele, G.; et al. Assessment of Recent Process Analytical Technology (PAT) Trends: A Multiauthor Review. Org. Process Res. Dev. 2015, 19, 3–62. [Google Scholar] [CrossRef]
- Parson, W.W.B.C. Modern Optical Spectroscopy: From fundamentals to Applications in Chemistry, Biochemistry and… Biophysics; Springer International pu: [S.l.]: Cham, Switzerland, 2023; ISBN 3-031-17221-3. [Google Scholar]
- Ritgen, U. Analytische Chemie I; 1. Edition 2019; Springer: Berlin/Heidelberg, Germany, 2020; ISBN 3662604949. [Google Scholar]
- Günzler, H. IR-Spektroskopie: Eine Einführung; 4. vollständig überarbeitete und aktualisierte Aufl (Online-Ausg.); Wiley-VCH GmbH & Co. KGaA: Weinheim, Germany, 2003; ISBN 978-3-527-30801-9. [Google Scholar]
- Vahur, S.; Knuutinen, U.; Leito, I. ATR-FT-IR spectroscopy in the region of 500–230 cm−1 for identification of inorganic red pigments. Spectrochim. Acta A Mol. Biomol. Spectrosc. 2009, 73, 764–771. [Google Scholar] [CrossRef] [PubMed]
- Shinde, G.; Godage, R.K.; Jadhav, R.S.; Manoj, B.; Aniket, B. A Review on Advances in UV Spectroscopy. Res. J. Sci. Technol. 2020, 12, 47. [Google Scholar] [CrossRef]
- Blanco, M.; Villarroya, I. NIR spectroscopy: A rapid-response analytical tool. TrAC Trends Anal. Chem. 2002, 21, 240–250. [Google Scholar] [CrossRef]
- Wang, H.-P.; Chen, P.; Dai, J.-W.; Liu, D.; Li, J.-Y.; Xu, Y.-P.; Chu, X.-L. Recent advances of chemometric calibration methods in modern spectroscopy: Algorithms, strategy, and related issues. TrAC Trends Anal. Chem. 2022, 153, 116648. [Google Scholar] [CrossRef]
- Pandiselvam, R.; Mahanti, N.K.; Manikantan, M.R.; Kothakota, A.; Chakraborty, S.K.; Ramesh, S.V.; Beegum, P.S. Rapid detection of adulteration in desiccated coconut powder: Vis-NIR spectroscopy and chemometric approach. Food Control 2022, 133, 108588. [Google Scholar] [CrossRef]
- Li, W.; Luo, Y.; Wang, X.; Gong, X.; Huang, W.; Wang, G.; Qu, H. Development and Validation of a Near-Infrared Spectroscopy Method for Multicomponent Quantification during the Second Alcohol Precipitation Process of Astragali radix. Separations 2022, 9, 310. [Google Scholar] [CrossRef]
- Quintero Balbas, D.; Lanterna, G.; Cirrincione, C.; Fontana, R.; Striova, J. Non-invasive identification of textile fibres using near-infrared fibre optics reflectance spectroscopy and multivariate classification techniques. Eur. Phys. J. Plus 2022, 137, 1–15. [Google Scholar] [CrossRef]
- Büning-Pfaue, H. Analysis of water in food by near infrared spectroscopy. Food Chem. 2003, 82, 107–115. [Google Scholar] [CrossRef]
- Shao, X.; Bian, X.; Liu, J.; Zhang, M.; Cai, W. Multivariate calibration methods in near infrared spectroscopic analysis. Anal. Methods 2010, 2, 1662. [Google Scholar] [CrossRef]
- Krishnan, R.S.; Shankar, R.K. Raman effect: History of the discovery. J. Raman Spectrosc. 1981, 10, 1–8. [Google Scholar] [CrossRef]
- Vaskova, H. A powerful tool for material identification: Raman spectroscopy. Int. J. Math. Models Methods Appl. Sci. 2011, 5, 1205–1212. [Google Scholar]
- Braun, F.; Schwolow, S.; Seltenreich, J.; Kockmann, N.; Röder, T.; Gretz, N.; Rädle, M. Highly Sensitive Raman Spectroscopy with Low Laser Power for Fast In-Line Reaction and Multiphase Flow Monitoring. Anal. Chem. 2016, 88, 9368–9374. [Google Scholar] [CrossRef] [PubMed]
- Ma, B.; Rodriguez, R.D.; Ruban, A.; Pavlov, S.; Sheremet, E. The correlation between electrical conductivity and second-order Raman modes of laser-reduced graphene oxide. Phys. Chem. Chem. Phys. 2019, 21, 10125–10134. [Google Scholar] [CrossRef]
- Makukha, O.; Lysenko, I.; Belarouci, A. Liquid-Modulated Photothermal Phenomena in Porous Silicon Nanostructures Studied by μ-Raman Spectroscopy. Nanomaterials 2023, 13, 310. [Google Scholar] [CrossRef]
- Gutiérrez, T.J. (Ed.) . Polymers for Agri-Food Applications, 1st ed.; Springer: Cham, Switzerland, 2019; ISBN 978-3-030-19415-4. [Google Scholar]
- Ohkouchi, T.; Tsuji, K. Basic Technology and Recent Trends in Agricultural Formulation and Application Technology. J. Pestic. Sci. 2022, 47, 155–171. [Google Scholar] [CrossRef]
- Bibette, J.; Calderon, F.L.; Poulin, P. Emulsions: Basic principles. Rep. Prog. Phys. 1999, 62, 969–1033. [Google Scholar] [CrossRef]
- Schramm, L.L. Emulsions, Foams, Suspensions, and Aerosols: Microscience and Applications, 2nd ed.; Wiley-VCH: Weinheim, Germany, 2014; ISBN 978-3-527-67949-2. [Google Scholar]
- Boudenne, A.; Ibos, L.; Candau, Y.; Thomas, S. (Eds.) . Handbook of Multiphase Polymer Systems; Wiley: Hoboken, NJ, USA, 2011; ISBN 9780470714201. [Google Scholar]
- Zhong, J.-F.; Chai, X.-S.; Fu, S.-Y.; Qin, X.-L. An improved sample preparation method for monomer conversion measurement using headspace gas chromatography in emulsion polymerization research. J. Appl. Polym. Sci. 2012, 124, 3525–3528. [Google Scholar] [CrossRef]
- Martínez, R.I.; Ramírez, A.O.; González, R.L.; León, R.D.d.; Cárdenas, L.V.; Martínez, E.T.; Elizondo, A.D.; Vielma, B.R. Polymerization Reactor Monitoring by In-line Raman Spectrometry. J. Mater. Sci. Eng. A 2017, 7, 303–310. [Google Scholar] [CrossRef][Green Version]
- Frauendorfer, E.; Hergeth, W.-D. Industrial application of Raman spectroscopy for control and optimization of vinyl acetate resin polymerization. Anal. Bioanal. Chem. 2017, 409, 631–636. [Google Scholar] [CrossRef] [PubMed]
- Chen, X.; Laughlin, K.; Sparks, J.R.; Linder, L.; Farozic, V.; Masser, H.; Petr, M. In Situ Monitoring of Emulsion Polymerization by Raman Spectroscopy: A Robust and Versatile Chemometric Analysis Method. Org. Process Res. Dev. 2015, 19, 995–1003. [Google Scholar] [CrossRef]
- Chang, C.; Feng, L.-F.; Gu, X.-P.; Zhang, C.-L.; Dai, L.-K.; Chen, X.; Hu, G.-H. In Situ Raman Spectroscopy Real-Time Monitoring of a Polyester Polymerization Process for Subsequent Process Optimization and Control. Ind. Eng. Chem. Res. 2022, 61, 17993–18003. [Google Scholar] [CrossRef]
- Hufnagel, T.; Rädle, M.; Karbstein, H.P. Influence of Refractive Index Differences on the Signal Strength for Raman-Spectroscopic Measurements of Double Emulsion Droplets. Appl. Sci. 2022, 12, 9056. [Google Scholar] [CrossRef]
- Kollhoff, R.T.; Kelemen, K.; Schuchmann, H.P. Local Multiphase Flow Characterization with Micro Particle Image Velocimetry Using Refractive Index Matching. Chem. Eng. Technol. 2015, 38, 1774–1782. [Google Scholar] [CrossRef]
- Schalk, R.; Braun, F.; Frank, R.; Rädle, M.; Gretz, N.; Methner, F.-J.; Beuermann, T. Non-contact Raman spectroscopy for in-line monitoring of glucose and ethanol during yeast fermentations. Bioprocess Biosyst. Eng. 2017, 40, 1519–1527. [Google Scholar] [CrossRef] [PubMed]
- van den Brink, M.; Pepers, M.; van Herk, A.M. Raman spectroscopy of polymer latexes. J. Raman Spectrosc. 2002, 33, 264–272. [Google Scholar] [CrossRef]
- Meyer, K.; Ruiken, J.-P.; Illner, M.; Paul, A.; Müller, D.; Esche, E.; Wozny, G.; Maiwald, M. Process spectroscopy in microemulsions—Setup and multi-spectral approach for reaction monitoring of a homogeneous hydroformylation process. Meas. Sci. Technol. 2017, 28, 35501. [Google Scholar] [CrossRef]
- Kortüm, G. Reflectance Spectroscopy: Principles, Methods, Applications; Softcover repr. of the Hardcover 1. ed.; Springer: New York, NY, USA, 2014; ISBN 978-3-642-88073-5. [Google Scholar]
- Carl Roth. Safety Data Sheet Ammonium Nitrate. Available online: https://www.carlroth.com/medias/SDB-X988-GB-EN.pdf?context=bWFzdGVyfHNlY3VyaXR5RGF0YXNoZWV0c3wyNjIxNTF8YXBwbGljYXRpb24vcGRmfHNlY3VyaXR5RGF0YXNoZWV0cy9oNjUvaDFiLzkwMTUzMDQyMjQ3OTgucGRmfDZjZGU1NDNjNTUyOGRlMDE3OGQzMGIzODE2ZWUwMTM1YTRlZTkxMzIzMDYxMDk5MjIzZjYyYzM3YWI3YjJiMjY (accessed on 2 November 2022).
- Schmitt, L.; Meyer, C.; Schorz, S.; Manser, S.; Scholl, S.; Rädle, A.M. Use of a Scattered Light Sensor for Monitoring the Dispersed Surface in Crystallization. Chem. Ing. Tech. 2022, 94, 1177–1184. [Google Scholar] [CrossRef]
- Mishra, Y.N. Droplet Size, Concentration, and Temperature Mapping in Sprays Using SLIPI-Based Techniques; Division of Combustion Physics, Department of Physics, Lund University: Lund, Sweden, 2018; ISBN 978-91-7753-468-6. [Google Scholar]
- Gillen, G.; Najarro, M.; Wight, S.; Walker, M.; Verkouteren, J.; Windsor, E.; Barr, T.; Staymates, M.; Urbas, A. Particle Fabrication Using Inkjet Printing onto Hydrophobic Surfaces for Optimization and Calibration of Trace Contraband Detection Sensors. Sensors 2015, 15, 29618–29634. [Google Scholar] [CrossRef]
- Henderson, G.S.; Neuville, D.R.; Cochain, B.; Cormier, L. The structure of GeO2–SiO2 glasses and melts: A Raman spectroscopy study. J. Non-Cryst. Solids 2009, 355, 468–474. [Google Scholar] [CrossRef]
- Chen, X.; Feng, W.; Zhang, G.; Gao, Y. Raman Spectra of Quartz and Pb4+-Doped SiO2 Crystals at Different Temperature and Pressure. Crystals 2019, 9, 569. [Google Scholar] [CrossRef]
- Guffart, J.; Bus, Y.; Nachtmann, M.; Lettau, M.; Schorz, S.; Nieder, H.; Repke, J.-U.; Rädle, M. Photometric Inline Monitoring of Pigment Concentration in Highly Filled Lacquers. Chem. Ing. Tech. 2020, 92, 729–735. [Google Scholar] [CrossRef]

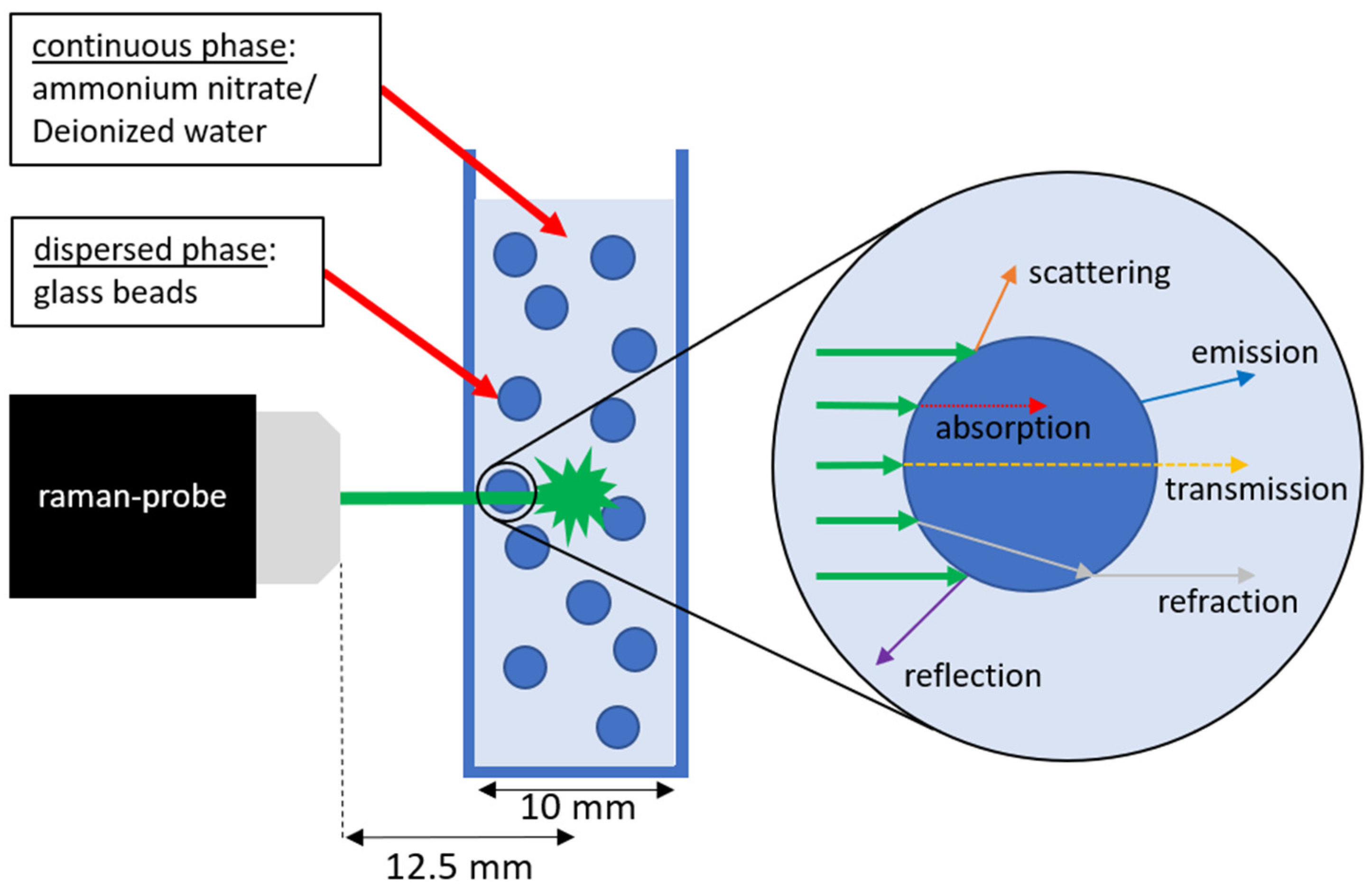
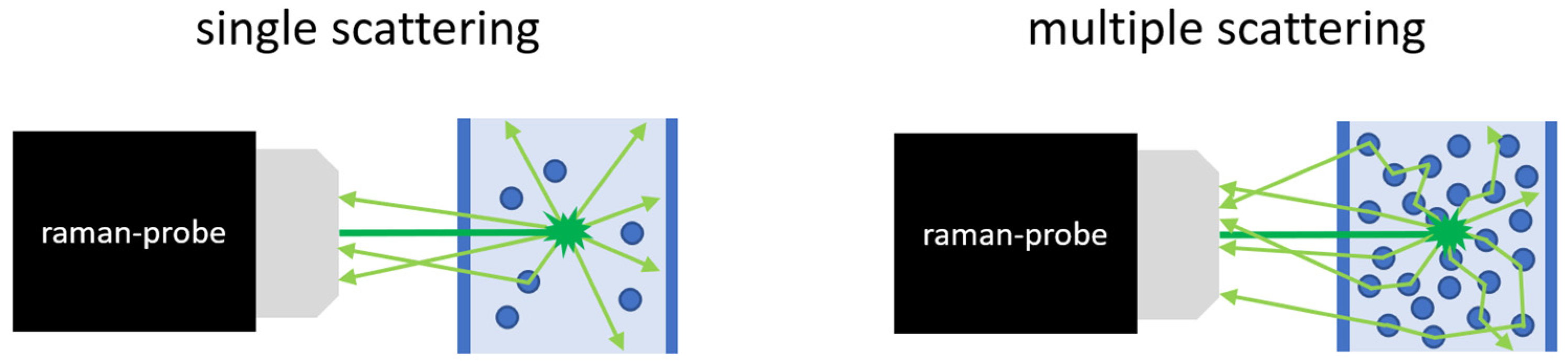

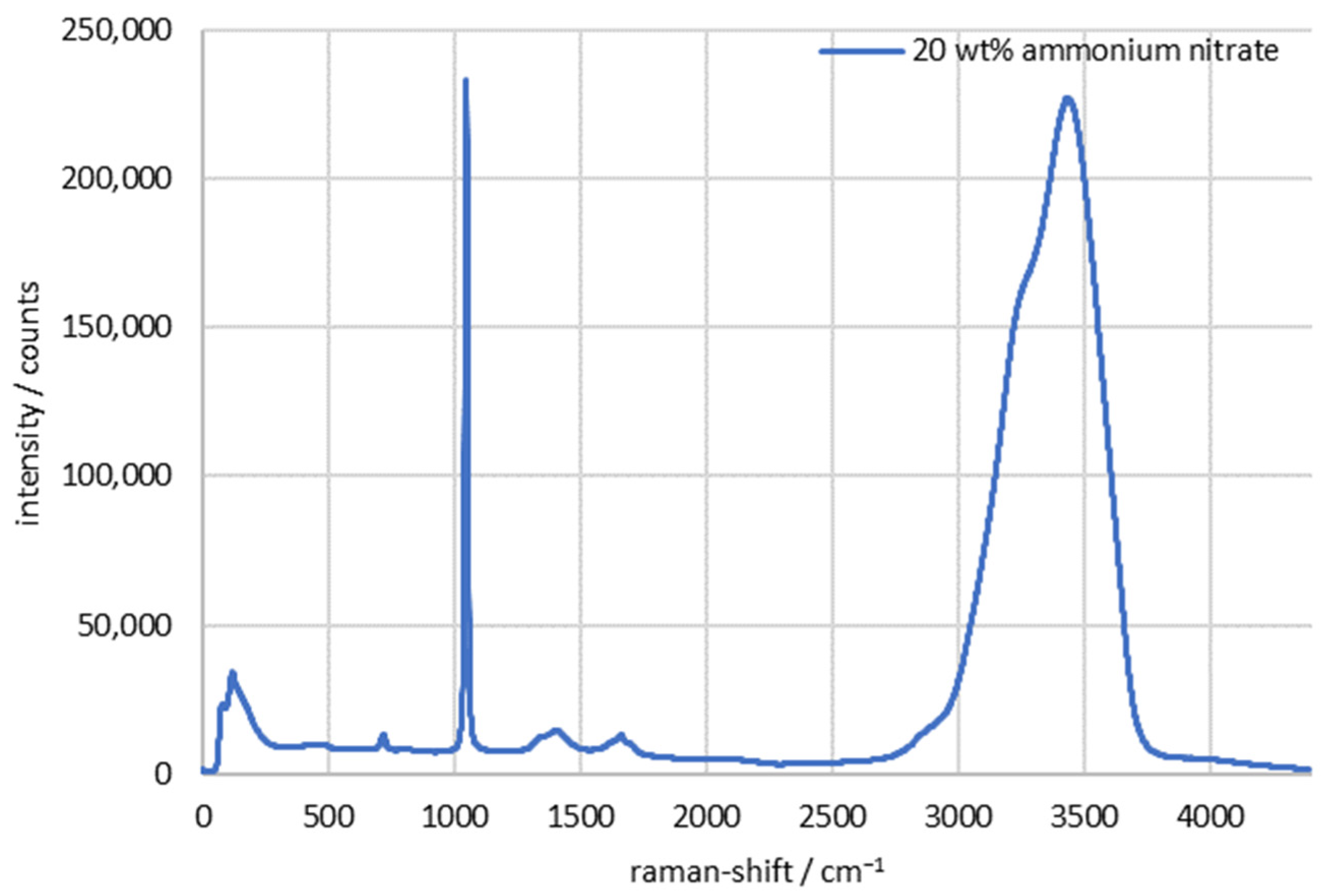
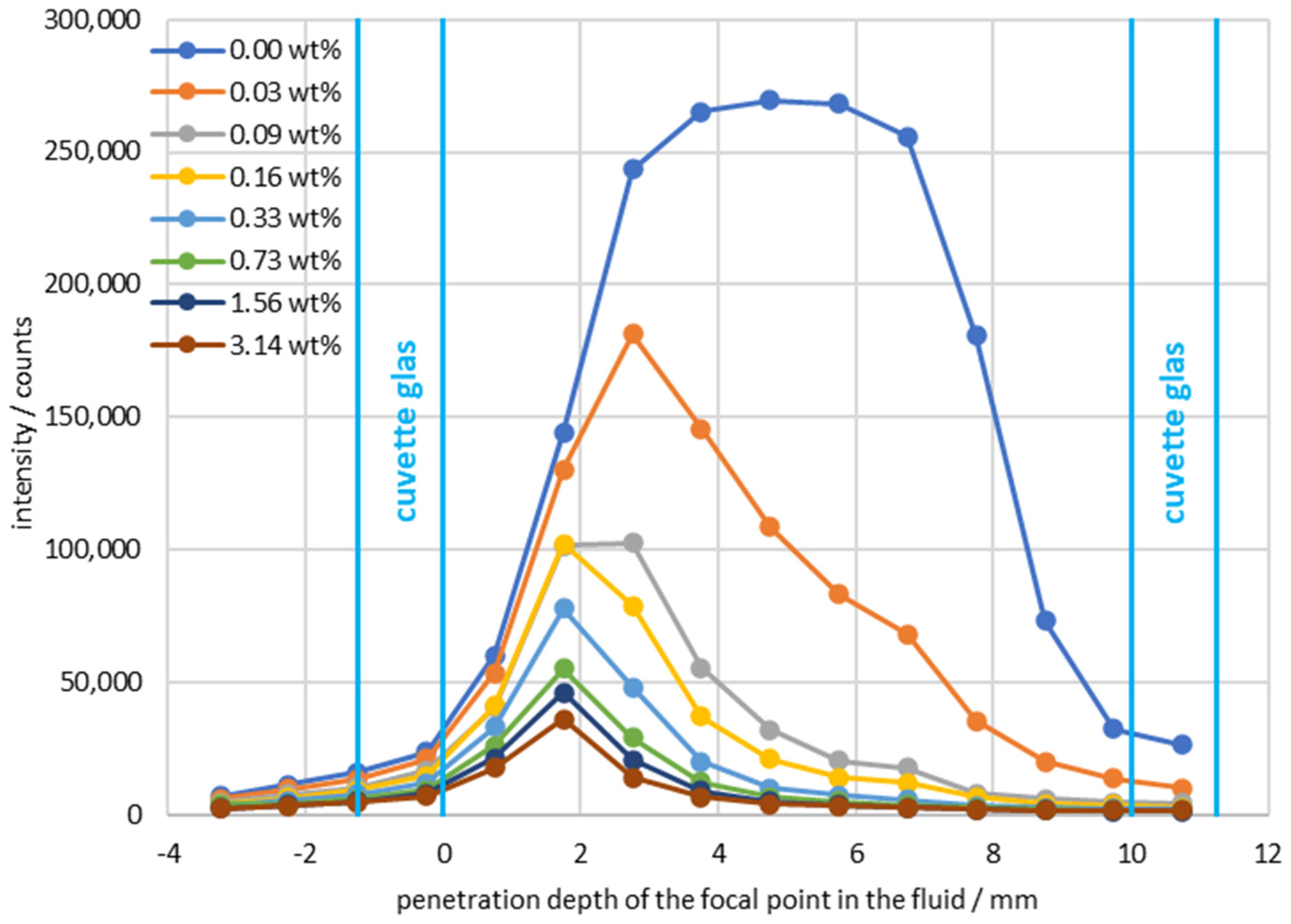


| Continuous Phase | Dispersed Phase | |
|---|---|---|
| Ammonium Nitrate/wt % | Deionized Water/wt % | Glass Beads/wt % |
| 20.00 | 80.00 | 0.00 |
| 19.99 | 79.97 | 0.03 |
| 19.99 | 79.95 | 0.06 |
| 19.98 | 79.93 | 0.09 |
| 19.98 | 79.91 | 0.11 |
| 19.97 | 79.88 | 0.15 |
| 19.97 | 79.87 | 0.17 |
| 19.96 | 79.85 | 0.19 |
| 19.96 | 79.84 | 0.20 |
| 19.96 | 79.71 | 0.33 |
| 19.88 | 79.39 | 0.73 |
| 19.72 | 78.72 | 1.56 |
| 19.40 | 77.46 | 3.14 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Spoor, E.; Rädle, M.; Repke, J.-U. Raman Spectroscopy of Glass Beads in Ammonium Nitrate Solution and Compensation of Signal Losses. Sensors 2024, 24, 314. https://doi.org/10.3390/s24020314
Spoor E, Rädle M, Repke J-U. Raman Spectroscopy of Glass Beads in Ammonium Nitrate Solution and Compensation of Signal Losses. Sensors. 2024; 24(2):314. https://doi.org/10.3390/s24020314
Chicago/Turabian StyleSpoor, Erik, Matthias Rädle, and Jens-Uwe Repke. 2024. "Raman Spectroscopy of Glass Beads in Ammonium Nitrate Solution and Compensation of Signal Losses" Sensors 24, no. 2: 314. https://doi.org/10.3390/s24020314
APA StyleSpoor, E., Rädle, M., & Repke, J.-U. (2024). Raman Spectroscopy of Glass Beads in Ammonium Nitrate Solution and Compensation of Signal Losses. Sensors, 24(2), 314. https://doi.org/10.3390/s24020314








