Phasor-Based Myoelectric Synergy Features: A Fast Hand-Crafted Feature Extraction Scheme for Boosting Performance in Gait Phase Recognition
Abstract
1. Introduction
2. Materials and Methods
2.1. Dataset Presentation and Pre-Processing
2.2. PHASOR-Based Features and State-of-the-Art Feature Sets
2.3. Feature Space Quality Metrics
2.4. Pattern Recognition Models and Testing
3. Results
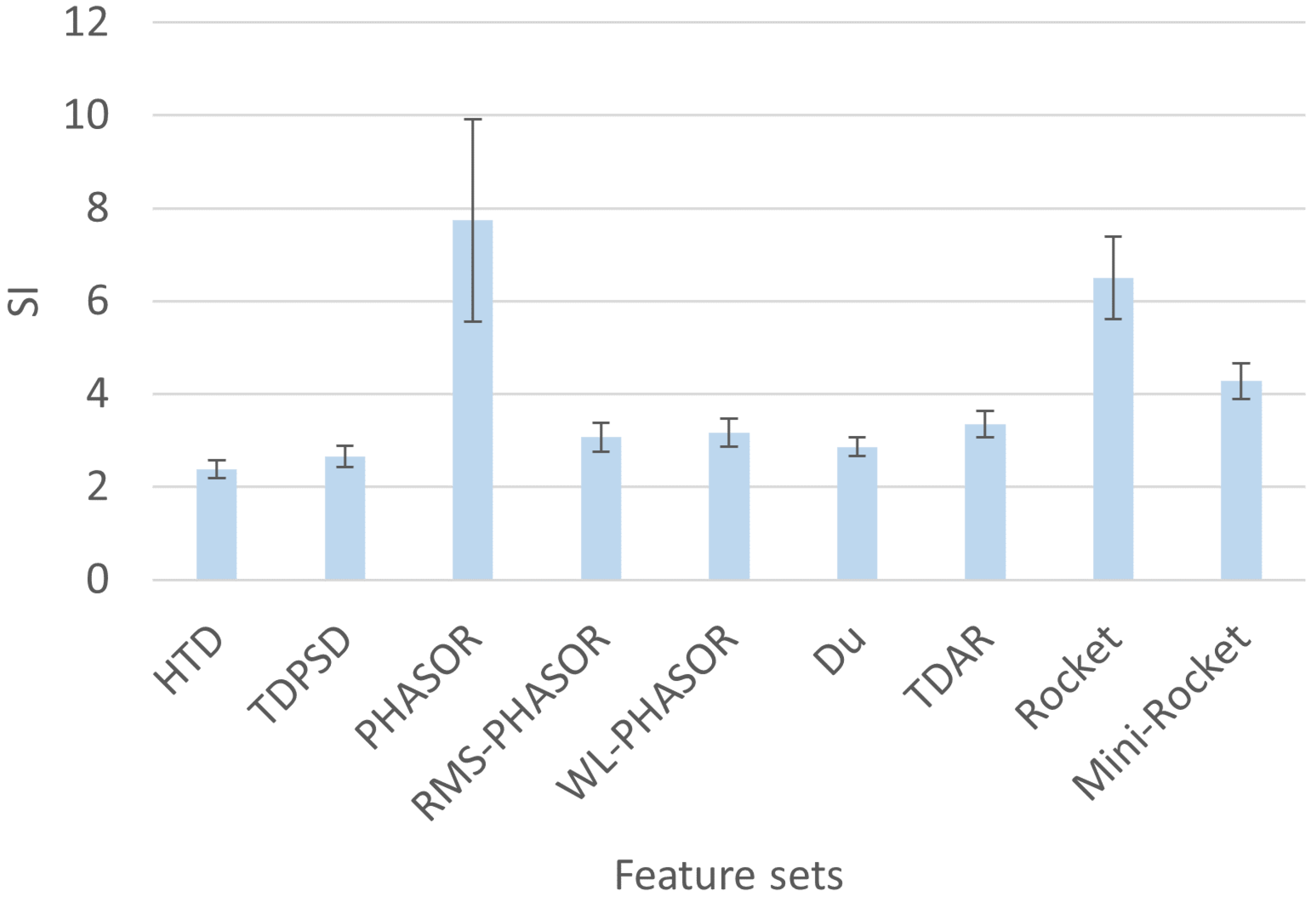
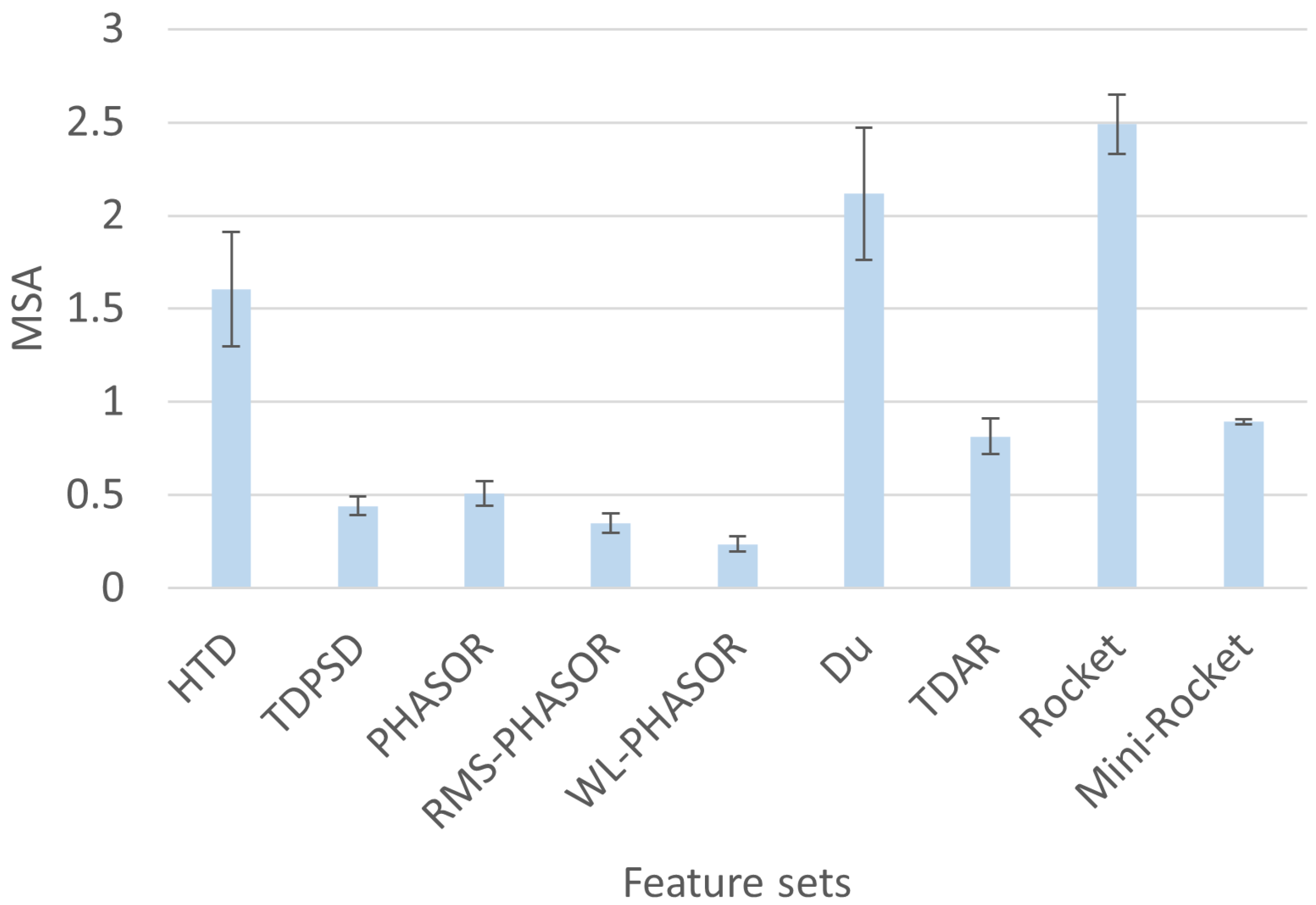
3.1. Feature Space Quality Metrics
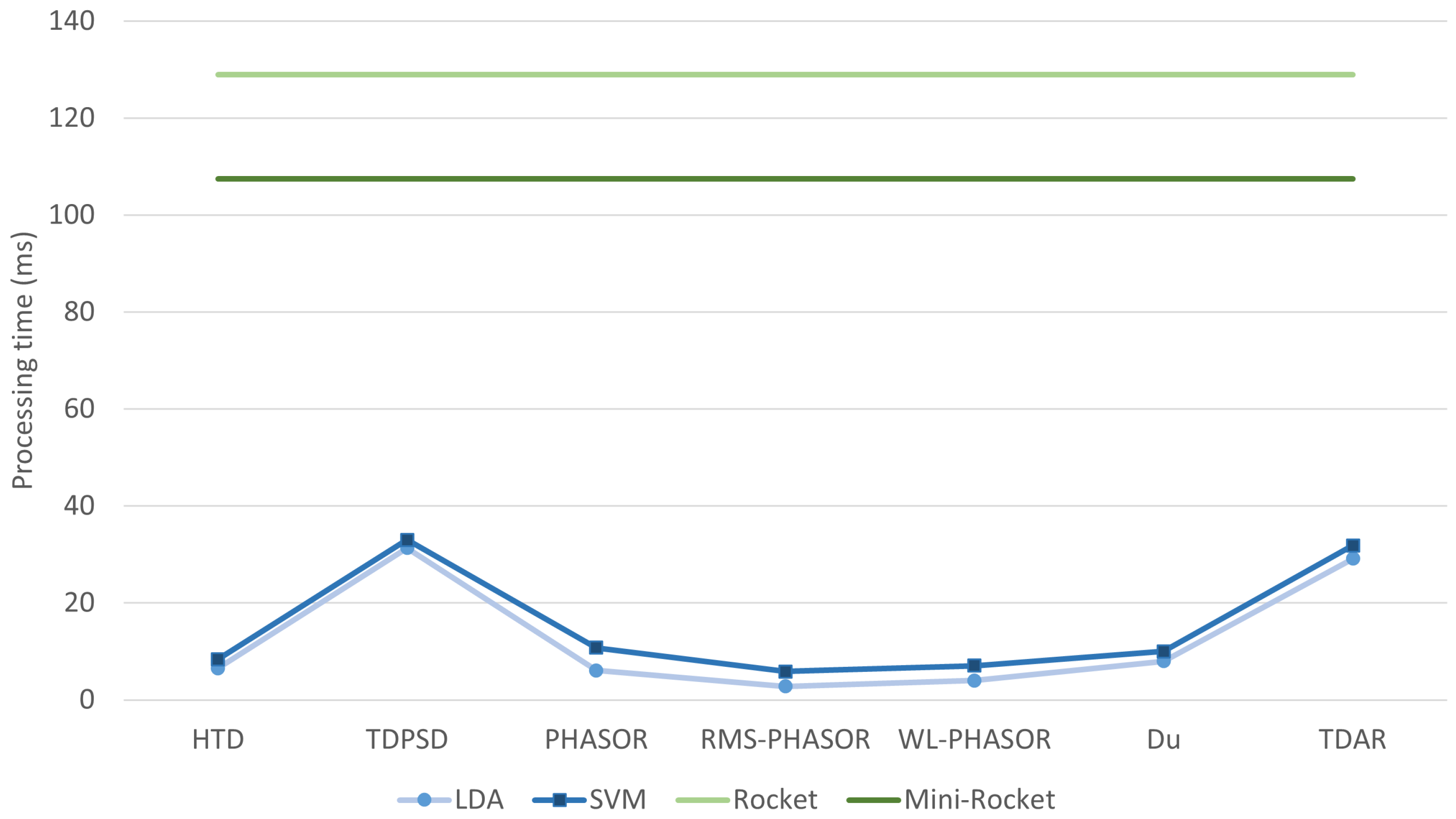
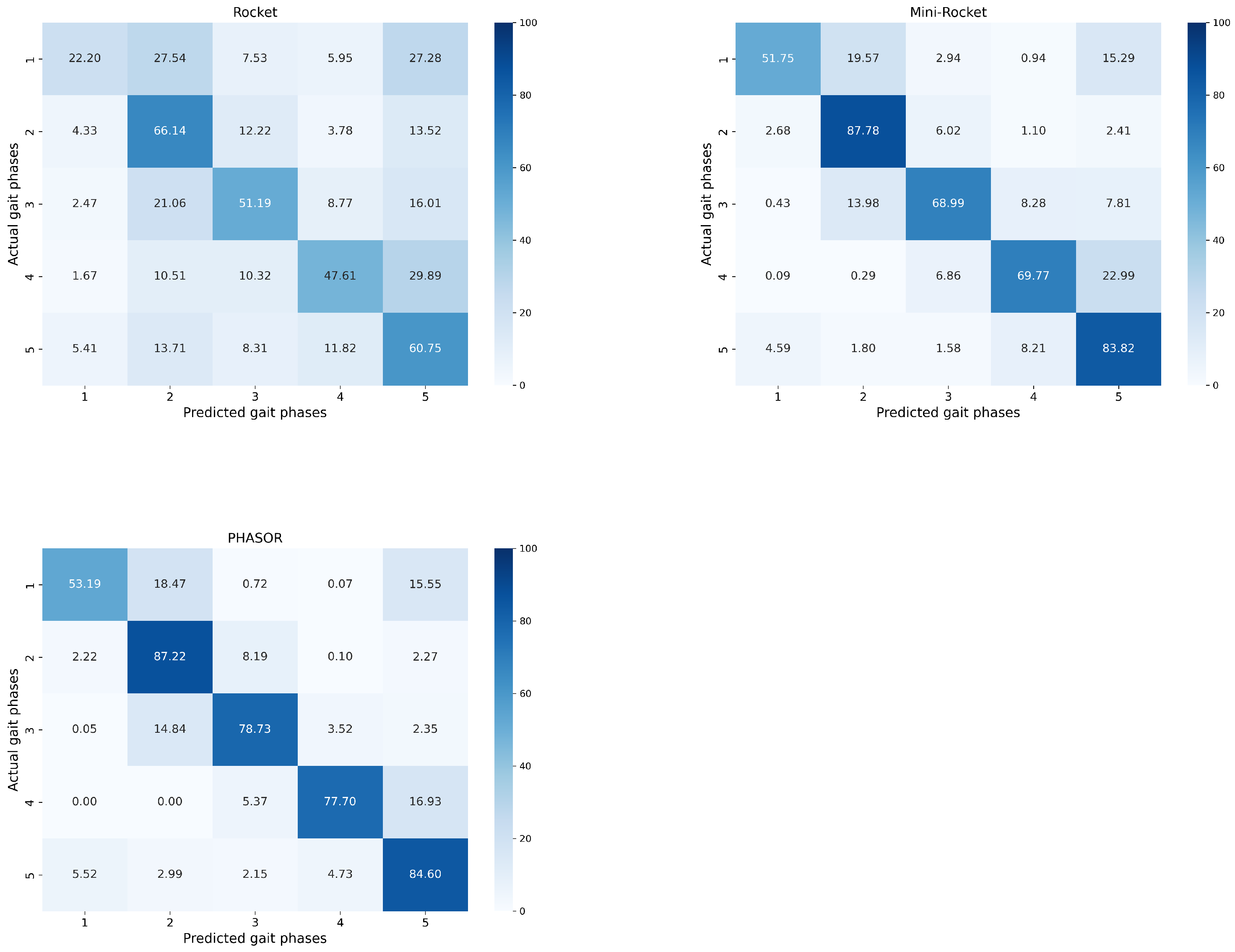
3.2. Performance Metrics and Computation Time
4. Discussion
5. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Zheng, M.; Crouch, M.S.; Eggleston, M.S. Surface electromyography as a natural human–machine interface: A review. IEEE Sens. J. 2022, 22, 9198–9214. [Google Scholar] [CrossRef]
- Tigrini, A.; Ranaldi, S.; Verdini, F.; Mobarak, R.; Scattolini, M.; Conforto, S.; Schmid, M.; Burattini, L.; Gambi, E.; Fioretti, S.; et al. Intelligent Human–Computer Interaction: Combined Wrist and Forearm Myoelectric Signals for Handwriting Recognition. Bioengineering 2024, 11, 458. [Google Scholar] [CrossRef] [PubMed]
- Just, F.; Ghinami, C.; Zbinden, J.; Ortiz-Catalan, M. Deployment of Machine Learning Algorithms on Resource-Constrained Hardware Platforms for Prosthetics. IEEE Access 2024, 12, 40439–40449. [Google Scholar] [CrossRef]
- Mobarak, R.; Tigrini, A.; Verdini, F.; Al-Timemy, A.H.; Fioretti, S.; Burattini, L.; Mengarelli, A. A Minimal and Multi-Source Recording Setup for Ankle Joint Kinematics Estimation During Walking using only Proximal Information from Lower Limb. IEEE Trans. Neural Syst. Rehabil. Eng. 2024, 32, 812–821. [Google Scholar] [CrossRef]
- Gonzales-Huisa, O.A.; Oshiro, G.; Abarca, V.E.; Chavez-Echajaya, J.G.; Elias, D.A. EMG and IMU Data Fusion for Locomotion Mode Classification in Transtibial Amputees. Prosthesis 2023, 5, 1232–1256. [Google Scholar] [CrossRef]
- Micera, S.; Carpaneto, J.; Raspopovic, S. Control of hand prostheses using peripheral information. IEEE Rev. Biomed. Eng. 2010, 3, 48–68. [Google Scholar] [CrossRef]
- Tigrini, A.; Verdini, F.; Fioretti, S.; Mengarelli, A. On the Decoding of Shoulder Joint Intent of Motion from Transient EMG: Feature Evaluation and Classification. IEEE Trans. Med. Robot. Bionics 2023, 5, 1037–1044. [Google Scholar] [CrossRef]
- Earley, E.J.; Chan, N.S.; Naber, A.; Mastinu, E.; Truong, M.T.; Ortiz-Catalan, M. Low-Cost, Wireless Bioelectric Signal Acquisition and Classification Platform. IEEE Access 2024, 12, 69350–69358. [Google Scholar] [CrossRef]
- Jiang, N.; Falla, D.; d’Avella, A.; Graimann, B.; Farina, D. Myoelectric control in neurorehabilitation. Crit. Rev. Biomed. Eng. 2010, 38, 381–391. [Google Scholar] [CrossRef]
- McDonald, C.G.; Sullivan, J.L.; Dennis, T.A.; O’Malley, M.K. A myoelectric control interface for upper-limb robotic rehabilitation following spinal cord injury. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 28, 978–987. [Google Scholar] [CrossRef]
- Ahkami, B.; Ahmed, K.; Thesleff, A.; Hargrove, L.; Ortiz-Catalan, M. Electromyography-based control of lower limb prostheses: A systematic review. IEEE Trans. Med. Robot. Bionics 2023, 5, 547–562. [Google Scholar] [CrossRef]
- Fleming, A.; Stafford, N.; Huang, S.; Hu, X.; Ferris, D.P.; Huang, H.H. Myoelectric control of robotic lower limb prostheses: A review of electromyography interfaces, control paradigms, challenges and future directions. J. Neural Eng. 2021, 18, 041004. [Google Scholar] [CrossRef] [PubMed]
- Nasr, A.; Laschowski, B.; McPhee, J. Myoelectric control of robotic leg prostheses and exoskeletons: A review. In Proceedings of the International Design Engineering Technical Conferences and Computers and Information in Engineering Conference, Virtual, 17–19 August 2021; American Society of Mechanical Engineers: New York, NY, USA, 2021; Volume 85444, p. V08AT08A043. [Google Scholar]
- Duraffourg, C.; Bonnet, X.; Dauriac, B.; Pillet, H. Real time estimation of the pose of a lower limb prosthesis from a single shank mounted IMU. Sensors 2019, 19, 2865. [Google Scholar] [CrossRef] [PubMed]
- Du, L.; Zhang, F.; He, H.; Huang, H. Improving the performance of a neural-machine interface for prosthetic legs using adaptive pattern classifiers. In Proceedings of the 2013 35th Annual International Conference of the IEEE Engineering in Medicine and Biology Society (EMBC), Osaka, Japan, 3–7 July 2013; IEEE: Piscataway, NJ, USA, 2013; pp. 1571–1574. [Google Scholar]
- Gehlhar, R.; Tucker, M.; Young, A.J.; Ames, A.D. A review of current state-of-the-art control methods for lower-limb powered prostheses. Annu. Rev. Control 2023, 55, 142–164. [Google Scholar] [CrossRef] [PubMed]
- Huang, H.; Zhang, F.; Hargrove, L.J.; Dou, Z.; Rogers, D.R.; Englehart, K.B. Continuous locomotion-mode identification for prosthetic legs based on neuromuscular–mechanical fusion. IEEE Trans. Biomed. Eng. 2011, 58, 2867–2875. [Google Scholar] [CrossRef]
- Hargrove, L.J.; Simon, A.M.; Lipschutz, R.; Finucane, S.B.; Kuiken, T.A. Non-weight-bearing neural control of a powered transfemoral prosthesis. J. Neuroeng. Rehabil. 2013, 10, 1–11. [Google Scholar] [CrossRef]
- Nazmi, N.; Rahman, M.A.A.; Yamamoto, S.I.; Ahmad, S.A. Walking gait event detection based on electromyography signals using artificial neural network. Biomed. Signal Process. Control 2019, 47, 334–343. [Google Scholar] [CrossRef]
- Taborri, J.; Palermo, E.; Rossi, S.; Cappa, P. Gait partitioning methods: A systematic review. Sensors 2016, 16, 66. [Google Scholar] [CrossRef]
- Wei, W.; Tan, F.; Zhang, H.; Mao, H.; Fu, M.; Samuel, O.W.; Li, G. Surface electromyogram, kinematic, and kinetic dataset of lower limb walking for movement intent recognition. Sci. Data 2023, 10, 358. [Google Scholar] [CrossRef]
- Li, Y.; Gao, F.; Chen, H.; Xu, M. Gait recognition based on EMG with different individuals and sample sizes. In Proceedings of the 2016 35th Chinese Control Conference (CCC), Chengdu, China, 27–29 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 4068–4072. [Google Scholar]
- Wei, P.n.; Xie, R.; Tang, R.; Li, C.; Kim, J.; Wu, M. sEMG based gait phase recognition for children with spastic cerebral palsy. Ann. Biomed. Eng. 2019, 47, 223–230. [Google Scholar] [CrossRef]
- Ovadia, D.; Segal, A.; Rabin, N. Classification of hand and wrist movements via surface electromyogram using the random convolutional kernels transform. Sci. Rep. 2024, 14, 4134. [Google Scholar] [CrossRef]
- Phinyomark, A.; Scheme, E. EMG pattern recognition in the era of big data and deep learning. Big Data Cogn. Comput. 2018, 2, 21. [Google Scholar] [CrossRef]
- Bao, T.; Xie, S.Q.; Yang, P.; Zhou, P.; Zhang, Z.Q. Toward robust, adaptiveand reliable upper-limb motion estimation using machine learning and deep learning—A survey in myoelectric control. IEEE J. Biomed. Health Inform. 2022, 26, 3822–3835. [Google Scholar] [CrossRef]
- Côté-Allard, U.; Campbell, E.; Phinyomark, A.; Laviolette, F.; Gosselin, B.; Scheme, E. Interpreting deep learning features for myoelectric control: A comparison with handcrafted features. Front. Bioeng. Biotechnol. 2020, 8, 158. [Google Scholar] [CrossRef] [PubMed]
- Josephs, D.; Drake, C.; Heroy, A.; Santerre, J. sEMG gesture recognition with a simple model of attention. In Proceedings of the Machine Learning for Health, PMLR, Virtual, 7–8 August 2020; pp. 126–138. [Google Scholar]
- Nasri, N.; Orts-Escolano, S.; Cazorla, M. An semg-controlled 3d game for rehabilitation therapies: Real-time time hand gesture recognition using deep learning techniques. Sensors 2020, 20, 6451. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Nazarpour, K. Decoding hd-emg signals for myoelectric control-how small can the analysis window size be? IEEE Robot. Autom. Lett. 2021, 6, 8569–8574. [Google Scholar] [CrossRef]
- Keleş, A.D.; Yucesoy, C.A. Development of a neural network based control algorithm for powered ankle prosthesis. J. Biomech. 2020, 113, 110087. [Google Scholar] [CrossRef] [PubMed]
- Keleş, A.D.; Türksoy, R.T.; Yucesoy, C.A. The use of nonnormalized surface EMG and feature inputs for LSTM-based powered ankle prosthesis control algorithm development. Front. Neurosci. 2023, 17, 1158280. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Kodagoda, S.; Takruri, M.; Dissanayake, G. Toward improved control of prosthetic fingers using surface electromyogram (EMG) signals. Expert Syst. Appl. 2012, 39, 10731–10738. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Takruri, M.; Miro, J.V.; Kodagoda, S. Towards limb position invariant myoelectric pattern recognition using time-dependent spectral features. Neural Netw. 2014, 55, 42–58. [Google Scholar] [CrossRef]
- Tresch, M.C.; Cheung, V.C.; d’Avella, A. Matrix factorization algorithms for the identification of muscle synergies: Evaluation on simulated and experimental data sets. J. Neurophysiol. 2006, 95, 2199–2212. [Google Scholar] [CrossRef]
- Soomro, M.H.; Conforto, S.; Giunta, G.; Ranaldi, S.; De Marchis, C. Comparison of initialization techniques for the accurate extraction of muscle synergies from myoelectric signals via nonnegative matrix factorization. Appl. Bionics Biomech. 2018, 2018, 3629347. [Google Scholar] [CrossRef]
- Ranaldi, S.; De Marchis, C.; Severini, G.; Conforto, S. An objective, information-based approach for selecting the number of muscle synergies to be extracted via non-negative matrix factorization. IEEE Trans. Neural Syst. Rehabil. Eng. 2021, 29, 2676–2683. [Google Scholar] [CrossRef] [PubMed]
- Zecca, M.; Micera, S.; Carrozza, M.C.; Dario, P. Control of multifunctional prosthetic hands by processing the electromyographic signal. Crit. Rev. Biomed. Eng. 2002, 30, 4–6. [Google Scholar] [CrossRef] [PubMed]
- Onay, F.; Mert, A. Phasor represented EMG feature extraction against varying contraction level of prosthetic control. Biomed. Signal Process. Control 2020, 59, 101881. [Google Scholar] [CrossRef]
- Dempster, A.; Petitjean, F.; Webb, G.I. ROCKET: Exceptionally fast and accurate time series classification using random convolutional kernels. Data Min. Knowl. Discov. 2020, 34, 1454–1495. [Google Scholar] [CrossRef]
- Dempster, A.; Schmidt, D.F.; Webb, G.I. Minirocket: A very fast (almost) deterministic transform for time series classification. In Proceedings of the 27th ACM SIGKDD Conference on Knowledge Discovery & Data Mining, Virtual, 14–18 August 2021; pp. 248–257. [Google Scholar]
- Khushaba, R.N.; Al-Timemy, A.H.; Samuel, O.W.; Scheme, E.J. Myoelectric control with fixed convolution-based time-domain feature extraction: Exploring the spatio–temporal interaction. IEEE Trans. Hum. Mach. Syst. 2022, 52, 1247–1257. [Google Scholar] [CrossRef]
- Tigrini, A.; Al-Timemy, A.H.; Verdini, F.; Fioretti, S.; Morettini, M.; Burattini, L.; Mengarelli, A. Decoding transient sEMG data for intent motion recognition in transhumeral amputees. Biomed. Signal Process. Control 2023, 85, 104936. [Google Scholar] [CrossRef]
- Al-Timemy, A.H.; Khushaba, R.N.; Bugmann, G.; Escudero, J. Improving the performance against force variation of EMG controlled multifunctional upper-limb prostheses for transradial amputees. IEEE Trans. Neural Syst. Rehabil. Eng. 2015, 24, 650–661. [Google Scholar] [CrossRef]
- Franzke, A.W.; Kristoffersen, M.B.; Jayaram, V.; van der Sluis, C.K.; Murgia, A.; Bongers, R.M. Exploring the relationship between EMG feature space characteristics and control performance in machine learning myoelectric control. IEEE Trans. Neural Syst. Rehabil. Eng. 2020, 29, 21–30. [Google Scholar] [CrossRef]
- Eddy, E.; Campbell, E.; Phinyomark, A.; Bateman, S.; Scheme, E. LibEMG: An Open Source Library to Facilitate the Exploration of Myoelectric Control. IEEE Access 2023, 11, 87380–87397. [Google Scholar] [CrossRef]
- Toledo-Pérez, D.C.; Rodríguez-Reséndiz, J.; Gómez-Loenzo, R.A.; Jauregui-Correa, J. Support vector machine-based EMG signal classification techniques: A review. Appl. Sci. 2019, 9, 4402. [Google Scholar] [CrossRef]
- Khushaba, R.N.; Scheme, E.; Al-Timemy, A.H.; Phinyomark, A.; Al-Taee, A.; Al-Jumaily, A. A long short-term recurrent spatial-temporal fusion for myoelectric pattern recognition. Expert Syst. Appl. 2021, 178, 114977. [Google Scholar] [CrossRef]
- Anselmino, E.; Mazzoni, A.; Micera, S. EMG-based prediction of step direction for a better control of lower limb wearable devices. Comput. Methods Programs Biomed. 2024, 254, 108305. [Google Scholar] [CrossRef] [PubMed]
- Wei, P.; Zhang, J.; Wang, B.; Hong, J. Surface electromyography and electroencephalogram-based gait phase recognition and correlations between cortical and locomotor muscle in the seven gait phases. Front. Neurosci. 2021, 15, 607905. [Google Scholar] [CrossRef] [PubMed]
- Mobarak, R.; Mengarelli, A.; Verdini, F.; Fioretti, S.; Burattini, L.; Tigrini, A. Enhanced Gait Phases Recognition by EMG and Kinematics Information Fusion and a Minimal Recording Setuping Setup. Al-Khwarizmi Eng. J. 2024, 20, 89–93. [Google Scholar] [CrossRef]
- Yeon, S.H.; Shu, T.; Rogers, E.A.; Song, H.; Hsieh, T.H.; Freed, L.E.; Herr, H.M. Flexible dry electrodes for emg acquisition within lower extremity prosthetic sockets. In Proceedings of the 2020 8th IEEE RAS/EMBS International Conference for Biomedical Robotics and Biomechatronics (BioRob), New York, NY, USA, 29 November–1 December 2020; IEEE: Piscataway, NJ, USA, 2020; pp. 1088–1095. [Google Scholar]
- Atzori, M.; Gijsberts, A.; Castellini, C.; Caputo, B.; Hager, A.G.M.; Elsig, S.; Giatsidis, G.; Bassetto, F.; Müller, H. Electromyography data for non-invasive naturally-controlled robotic hand prostheses. Sci. Data 2014, 1, 140053. [Google Scholar] [CrossRef] [PubMed]

| Classifier | HTD | TDPSD | PHASOR | RMS-PHASOR | WL-PHASOR | Du | TDAR |
|---|---|---|---|---|---|---|---|
| SVM | 0.74 ± 0.10 | 0.69 ± 0.12 | 0.77 ± 0.08 | 0.75 ± 0.10 | 0.74 ± 0.09 | 0.75 ± 0.10 | 0.71 ± 0.13 |
| LDA | 0.71 ± 0.11 | 0.69 ± 0.11 | 0.64 ± 0.13 | 0.70 ± 0.12 | 0.71 ± 0.11 | 0.71 ± 0.11 | 0.67 ± 0.12 |
| Rocket | 0.36 ± 0.14 | ||||||
| Mini-Rocket | 0.74 ± 0.10 | ||||||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Tigrini, A.; Mobarak, R.; Mengarelli, A.; Khushaba, R.N.; Al-Timemy, A.H.; Verdini, F.; Gambi, E.; Fioretti, S.; Burattini, L. Phasor-Based Myoelectric Synergy Features: A Fast Hand-Crafted Feature Extraction Scheme for Boosting Performance in Gait Phase Recognition. Sensors 2024, 24, 5828. https://doi.org/10.3390/s24175828
Tigrini A, Mobarak R, Mengarelli A, Khushaba RN, Al-Timemy AH, Verdini F, Gambi E, Fioretti S, Burattini L. Phasor-Based Myoelectric Synergy Features: A Fast Hand-Crafted Feature Extraction Scheme for Boosting Performance in Gait Phase Recognition. Sensors. 2024; 24(17):5828. https://doi.org/10.3390/s24175828
Chicago/Turabian StyleTigrini, Andrea, Rami Mobarak, Alessandro Mengarelli, Rami N. Khushaba, Ali H. Al-Timemy, Federica Verdini, Ennio Gambi, Sandro Fioretti, and Laura Burattini. 2024. "Phasor-Based Myoelectric Synergy Features: A Fast Hand-Crafted Feature Extraction Scheme for Boosting Performance in Gait Phase Recognition" Sensors 24, no. 17: 5828. https://doi.org/10.3390/s24175828
APA StyleTigrini, A., Mobarak, R., Mengarelli, A., Khushaba, R. N., Al-Timemy, A. H., Verdini, F., Gambi, E., Fioretti, S., & Burattini, L. (2024). Phasor-Based Myoelectric Synergy Features: A Fast Hand-Crafted Feature Extraction Scheme for Boosting Performance in Gait Phase Recognition. Sensors, 24(17), 5828. https://doi.org/10.3390/s24175828













