Spatial–Temporal Transformer Networks for Traffic Flow Forecasting Using a Pre-Trained Language Model
Abstract
1. Introduction
- (1)
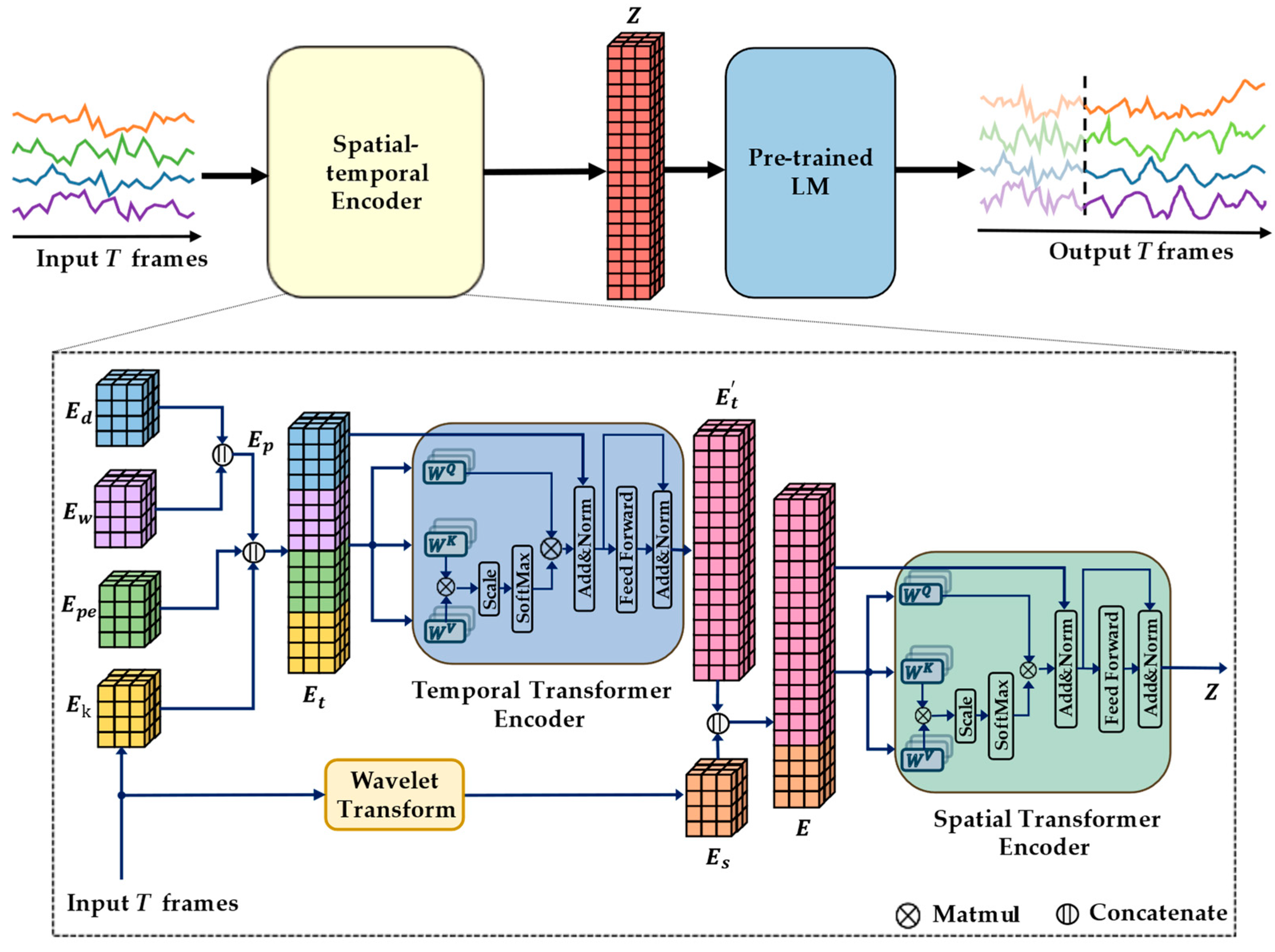
- We have developed a framework to extract spatial–temporal features from traffic data using the Transformer’s self-attention mechanism and the design of embeddings to extract spatial–temporal dependencies.
- (2)
- Our approach involves using the temporal Transformer (TT) first to extract the features related to temporal information separately. Then, these features are input into the spatial Transformer (ST) together with the unique embedding associated with spatial data. This method realizes the fusion of spatial–temporal information, avoids the confusion of spatial-temporal details during the initial self-attention process, and maximizes the role of embedding in the model.
- (3)
- Additionally, we utilized pre-trained language models to improve sequence prediction performance without the need for complex temporal and linguistic data alignment.
2. Related Work
2.1. TT and ST
2.2. Embedding
2.3. Pre-Trained LM
2.4. LLM Fine-Tuning
3. Method
3.1. Embedding Layer
- : To maintain the native information in the source sequences, we put through a fully connected layer of to obtain the feature embedding , .
- : Positional encoding is incorporated when using a Transformer as a language model [14]. . A study [18] introduced relative position coding and global position coding for the temporal continuity of traffic flow. Both methods use hard coding (e.g., predefined sine/cosine functions, and precomputed values). Temporal continuity encoding can be obtained through training and hard coding. We first assign a random value to and let it learn the time continuity of the traffic sequence during training.
- : Unlike natural language, time series contain periodicity and temporal continuity information. For instance, traffic flow, characterized simultaneously on different days, may be extremely similar, and the same embedding can be designed for data in the traffic sequence at the same moment. Similarly, the same day in different weeks can correspond to the same embedding [30]. denotes the embedding of the weekly cycle, and denotes the embedding of the daily cycle. The weights of the embedding layer are also randomly assigned first and then trained. , =, .
- : Time series from two traffic nodes that are physically close to each other may have a time difference even if their waveforms are similar. The embeddings mentioned above do not reflect this association. However, if the time domain waveforms are transformed into another transform domain, the effect of the time difference can be removed, showing a strong spatial node correlation. is viewed as an embedding generated based on the information in the transform domain to represent spatial information obtained based on DFT or wavelet transform. As a result, we use Harr wavelet to perform wavelet transform on the traffic series of each node. The coefficients l of the low-pass filter and coefficients h of the high-pass filter in the Harr wavelet transform are calculated as follows:
- The approximate coefficients and detail coefficients are calculated as follows:
- Then, the spatial embedding .
3.2. Network Structure
4. Experiment Details
4.1. Dataset
4.2. Implementation
4.3. Metrics
4.4. Baselines
5. Result and Discussion
5.1. Main Results
5.2. Ablation Study
- w/o : It removes temporal continuity embedding.
- w/o : It removes temporal periodicity embedding.
- w/o : It removes spatial embedding (See Table 5).
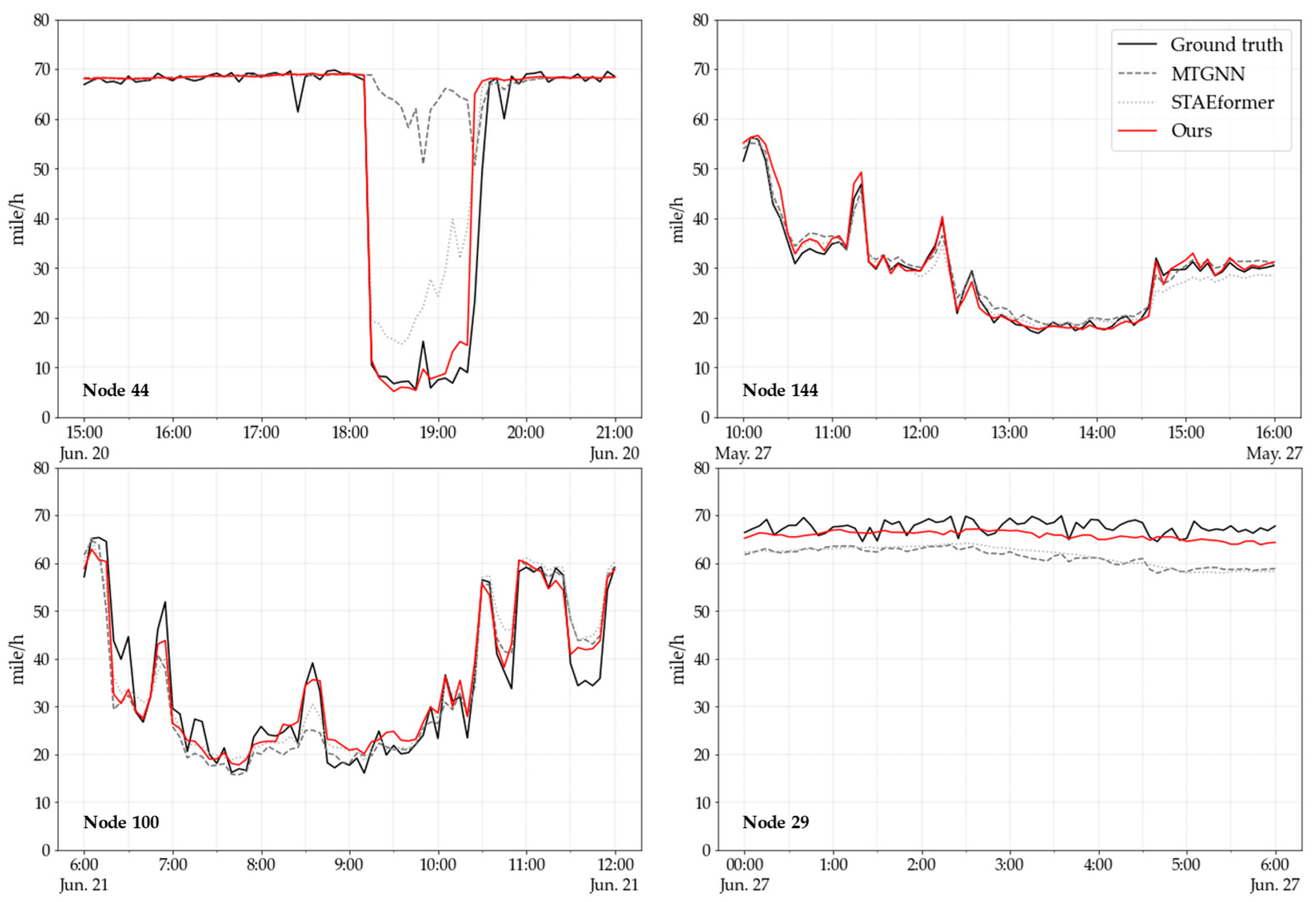
5.3. Case Study
5.4. Limitations
6. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Xia, Y.; Jian, X.; Yan, B.; Su, D. Infrastructure safety oriented traffic load monitoring using multi-sensor and single camera for short and medium span bridges. Remote Sens. 2019, 11, 2651. [Google Scholar] [CrossRef]
- Zhou, J.; Wu, W.; Caprani, C.C.; Tan, Z.; Wei, B.; Zhang, J. A hybrid virtual–real traffic simulation approach to reproducing the spatiotemporal distribution of bridge loads. Comput. Aided Civ. Infrastruct. Eng. 2024, 39, 1699–1723. [Google Scholar] [CrossRef]
- Zhao, Z.; Chen, W.; Yue, H.; Zhong, L. A novel short-term traffic forecast model based on travel distance estimation and ARIMA[C]. In Proceedings of the Chinese Control and Decision Conference (CCDC), Yinchuan, China, 28–30 May 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 6270–6275. [Google Scholar] [CrossRef]
- Yu, G.; Zhang, C. Switching ARIMA model based forecasting for traffic flow. In Proceedings of the 2004 IEEE International Conference on Acoustics, Speech, and Signal Processing, Montreal, QC, Canada, 17–21 May 2004; IEEE: Piscataway, NJ, USA, 2004; Volume 2, p. ii-429. [Google Scholar] [CrossRef]
- Chikkakrishna, N.K.; Hardik, C.; Deepika, K.; Sparsha, N. Short-term traffic prediction using sarima and FbPROPHET. In Proceedings of the 2019 IEEE 16th INDIA Council International Conference (INDICON), Rajkot, India, 13–15 December 2019; IEEE: Piscataway, NJ, USA, 2019; pp. 1–4. [Google Scholar] [CrossRef]
- Mingheng, Z.; Yaobao, Z.; Ganglong, H.; Gang, C. Accurate multisteps traffic flow prediction based on SVM. Math. Probl. Eng. 2013, 1, 418303. [Google Scholar] [CrossRef]
- Feng, X.; Ling, X.; Zheng, H.; Chen, Z.; Xu, Y. Adaptive multi-kernel SVM with spatial–temporal correlation for short-term traffic flow prediction. IEEE Trans. Intell. Transp. Syst. 2018, 20, 2001–2013. [Google Scholar] [CrossRef]
- Duan, M. Short-time prediction of traffic flow based on PSO optimized SVM. In Proceedings of the 2018 International Conference on Intelligent Transportation, Big Data & Smart City (ICITBS), Xiamen, China, 25–26 January 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 41–45. [Google Scholar] [CrossRef]
- Dong, X.; Lei, T.; Jin, S.; Hou, Z. Short-term traffic flow prediction based on XGBoost. In Proceedings of the 2018 IEEE 7th Data Driven Control and Learning Systems Conference (DDCLS), Enshi, China, 25–27 May 2018; IEEE: Piscataway, NJ, USA, 2018; pp. 854–859. [Google Scholar] [CrossRef]
- Zhou, T.; Han, G.; Xu, X.; Lin, Z.; Han, C.; Huang, Y.; Qin, J. δ-agree AdaBoost stacked autoencoder for short-term traffic flow forecasting. Neurocomputing 2017, 247, 31–38. [Google Scholar] [CrossRef]
- Leshem, G.; Ritov, Y.A. Traffic flow prediction using adaboost algorithm with random forests as a weak learner. Int. J. Math. Comput. Sci. 2007, 1, 1–6. [Google Scholar]
- Schuster, M.; Paliwal, K.K. Bidirectional recurrent neural networks. IEEE Trans. Signal Process. 1997, 45, 2673–2681. [Google Scholar] [CrossRef]
- Chung, J.; Gulcehre, C.; Cho, K.; Bengio, Y. Empirical evaluation of gated recurrent neural networks on sequence modeling. In Proceedings of the NIPS 2014 Workshop on Deep Learning, Montreal, QC, Canada, 13 December 2014; Available online: https://nyuscholars.nyu.edu/en/publications/empirical-evaluation-of-gated-recurrent-neural-networks-on-sequen (accessed on 22 August 2024).
- Hochreiter, S.; Schmidhuber, J. Long short-term memory. Neural Comput. 1997, 9, 1735–1780. [Google Scholar] [CrossRef]
- Hewage, P.; Behera, A.; Trovati, M.; Zambreno, J.; Xu, Y.; EI-Saddik, A. Temporal convolutional neural (TCN) network for an effective weather forecasting using time-series data from the local weather station. Soft Comput. 2020, 24, 16453–16482. [Google Scholar] [CrossRef]
- Vaswani, A.; Shazeer, N.; Parmar, N.; Uszkoreit, J.; Jones, L.; Gomez, A.N.; Kaiser, L.; Polosukhin, I. Attention is all you need. In Proceedings of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 12 June 2017; pp. 6000–6010. Available online: https://api.semanticscholar.org/CorpusID:13756489 (accessed on 22 August 2024).
- Sutskever, I.; Vinyals, O.; Le, Q.V. Sequence to sequence learning with neural networks. In Proceedings of the 27th Conference on Neural Information Processing Systems; MIT Press: Cambridge, MA, USA, 2014; Volume 2, pp. 3104–3112. [Google Scholar] [CrossRef]
- Cai, L.; Janowicz, K.; Mai, G.; Yan, B.; Zhu, R. Traffic transformer: Capturing the continuity and periodicity of time series for traffic forecasting. Trans. GIS 2020, 24, 736–755. [Google Scholar] [CrossRef]
- Scarselli, F.; Gori, M.; Tsoi, A.C.; Hagenbuchner, M.; Monfardini, G. The graph neural network model. IEEE Trans. Neural Netw. 2009, 20, 61–80. [Google Scholar] [CrossRef]
- Grover, A.; Leskovec, J. node2vec: Scalable Feature Learning for Networks. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (KDD), San Francisco, CA, USA, 13–17 August 2016; pp. 855–864. [Google Scholar] [CrossRef]
- Hamilton, W.L.; Ying, R.; Leskovec, J. Inductive representation learning on large graphs. In Proceeding of the 31st International Conference on Neural Information Processing Systems (NIPS), Long Beach, CA, USA, 4–9 December 2017; pp. 1025–1035. Available online: https://api.semanticscholar.org/CorpusID:4755450 (accessed on 22 August 2024).
- Kipf, T.N.; Welling, M. Semi-supervised classification with graph convolutional networks. In Proceedings of the 5th International Conference on Learning Representations (ICRL), Toulon, France, 24–26 April 2017; Available online: https://openreview.net/forum?id=SJU4ayYgl (accessed on 22 August 2024).
- Li, Y.; Yu, R.; Shahabi, C.; Liu, Y. Diffusion Convolutional Recurrent Neural Network: Data-Driven Traffic Forecasting. In Proceedings of the 5th International Conference on Learning Representations (ICLR), Vancouver, BC, Canada, 30 April–3 May 2018; Available online: https://www.khoury.northeastern.edu/published_research/diffusion-convolutional-recurrent-neural-network-data-driven-traffic-forecasting/ (accessed on 22 August 2024).
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Zhang, C. Graph wavenet for deep spatial-temporal graph modeling. In Proceedings of the 28th International Joint Conference on Artificial Intelligence (IJCAI), Macao, China, 10–16 August 2019; AAAI Press: Macao, China, 2019; pp. 1907–1913. Available online: https://dl.acm.org/doi/abs/10.5555/3367243.3367303 (accessed on 22 August 2024).
- Bai, L.; Yao, L.; Li, C.; Wang, X.; Wang, C. Adaptive Graph Convolutional Recurrent Network for Traffic Forecasting. In Proceedings of the 34th International Conference on Neural Information Processing Systems (NIPS), Vancouver, BC, Canada, 6–12 December 2020; pp. 17804–17815. Available online: https://dl.acm.org/doi/10.5555/3495724.3497218 (accessed on 22 August 2024).
- Wu, Z.; Pan, S.; Long, G.; Jiang, J.; Chang, X.; Zhang, C. Connecting the Dots: Multivariate Time Series Forecasting with Graph Neural Networks. In Proceedings of the 26th ACM SIGKDD International Conference on Knowledge Discovery & Data Mining (KDD), Virtual Event, 6–10 July 2020; pp. 753–763. Available online: https://dl.acm.org/doi/10.1145/3394486.3403118 (accessed on 22 August 2024).
- Lablack, M.; Shen, Y. Spatio-temporal graph mixformer for traffic forecasting. Expert Syst. Appl. 2023, 288, 120281. [Google Scholar] [CrossRef]
- Ruan, H.; Feng, X.; Zheng, H. Graph transformer attention networks for traffic flow prediction. In Proceedings of the 2021 7th International Conference on Computer and Communications (ICCC), Chengdu, China, 10–13 December 2021; IEEE: Piscataway, NJ, USA, 2021; pp. 1778–1782. [Google Scholar] [CrossRef]
- Ying, C.; Cai, T.; Luo, S.; Zheng, S.; Ke, G.; He, D.; Shen, Y.; Liu, T.-Y. Do Transformers Really Perform Bad for Graph Representation? Adv. Neural Inf. Process. Syst. 2021, 34, 28877–28888. [Google Scholar]
- Liu, H.; Dong, Z.; Jiang, R.; Deng, J.; Chen, Q.; Song, X. STAEformer: Spatio-Temporal Adaptive Embedding Makes Vanilla Transformers SOTA for Traffic Forecasting. In Proceedings of the 32nd ACM International Conference on Information and Knowledge Management (CIKM), Birmingham, UK, 21–25 October 2023; pp. 4125–4129. [Google Scholar] [CrossRef]
- Gao, H.; Jiang, R.; Dong, Z.; Deng, J.; Song, X. Spatio-Temporal-Decoupled Masked Pre-training for Traffic Forecasting. arXiv 2023, arXiv:2312.00516. [Google Scholar]
- Fang, S.; Ji, W.; Xiang, S.; Hua, W. PreSTNet: Pretrained Spatio-Temporal Network for traffic forecasting. Inf. Fusion 2024, 106, 102241. [Google Scholar] [CrossRef]
- Godahewa, R.; Bandara, K.; Webb, G.I.; Smyl, S.; Bergmeir, C. Ensembles of localised models for time series forecasting. Knowl. Based Syst. 2020, 233, 107518. [Google Scholar] [CrossRef]
- Zhou, T.; Niu, P.; Wang, X.; Sun, L.; Jin, R. One Fits All: Power General Time Series Analysis by Pretrained LM. In Proceedings of the Neural Information Processing Systems, New Orleans, LA, USA, 10–16 December 2023; Volume 36, pp. 43322–43355. Available online: https://www.semanticscholar.org/paper/One-Fits-All%3A-Power-General-Time-Series-Analysis-by-Zhou-Niu/5b7f5488c380cf5085a5dd93e993ad293b225eee (accessed on 22 August 2024).
- Chen, Y.; Wang, X.; Xu, G. Gatgpt: A pre-trained large language model with graph attention network for spatiotemporal imputation. arXiv 2023, arXiv:2311.14332. [Google Scholar] [CrossRef]
- Jin, M.; Wang, S.; Ma, L.; Chu, Z.; Zhang, J.Y.; Shi, X.L.; Chen, P.-Y.; Liang, Y.-F.; Pan, S.; Wen, Q. TimeLLM: Time Series Forecasting by Reprogramming Large Language Models. arXiv 2023, arXiv:2310.01728. [Google Scholar] [CrossRef]
- Liu, C.; Yang, S.; Xu, Q.; Li, Z.; Long, C.; Li, Z.; Zhao, R. Spatial-Temporal Large Language Model for Traffic Prediction. arXiv 2024, arXiv:2401.10134. [Google Scholar]
- Li, Z.; Xia, L.; Tang, J.; Xu, Y.; Shi, L.; Xia, L.; Yin, D.; Huang, C. Urbangpt: Spatio-temporal large language models. arXiv 2024, arXiv:2403.00813. [Google Scholar] [CrossRef]
- Chen, D.; O’Bray, L.; Borgwardt, K.M. Structure-Aware Transformer for Graph Representation Learning. In Proceedings of the International Conference on Machine Learning (ICML), Baltimore, MD, USA, 17–23 July 2022; Volume 162, pp. 3469–3489. Available online: https://proceedings.mlr.press/v162/chen22r.html (accessed on 22 August 2024).
- Jiang, J.; Han, C.; Zhao, W.X.; Wang, J. PDFormer: Propagation Delay-aware Dynamic Long-range Transformer for Traffic Flow Prediction. In Proceedings of the AAAI Conference on Artificial Intelligence (AAAI), Vancouver, BC, Canada, 20–27 February 2024; Volume 37, pp. 4365–4373. [Google Scholar] [CrossRef]
- Shao, Z.; Zhang, Z.; Wang, F.; Wei, W.; Xu, Y. Spatial-Temporal Identity: A Simple yet Effective Baseline for Multivariate Time Series Forecasting. In Proceedings of the 31st ACM International Conference on Information & Knowledge Management (CIKM), Atlanta, GA, USA, 17–21 October 2022; pp. 4454–4458. [Google Scholar] [CrossRef]
- Bahl, L.R.; Jelinek, F.; Mercer, R.L. A Maximum Likelihood Approach to Continuous Speech Recognition. IEEE Trans. Pattern Anal. Mach. Intell. 1983, PAMI-5, 179–190. [Google Scholar] [CrossRef] [PubMed]
- Chen, S.F.; Goodman, J. An empirical study of smoothing techniques for language modeling. Comput. Speech Lang. 1999, 13, 359–394. [Google Scholar] [CrossRef]
- Devlin, J.; Chang, M.; Lee, K.; Toutanova, K. BERT: Pre-training of deep bidirectional transformers for language understanding. In Proceedings of the 2019 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Minneapolis, MN, USA, 2–7 June 2019; pp. 4171–4186. [Google Scholar] [CrossRef]
- Liu, Z.; Lin, W.; Shi, Y.; Zhao, J. A robustly optimized BERT pre-training approach with post-training. In Proceedings of the China National Conference on Chinese Computational Linguistics, Hohhot, China, 13–15 August 2021; Springer International Publishing: Cham, Switzerland, 2021; pp. 471–484. [Google Scholar] [CrossRef]
- Radford, A.; Narasimhan, K.; Salimans, T.; Sutskever, I. Improving Language Understanding by Generative Pre-Training; OpenAI: San Francisco, CA, USA, 2018; Available online: https://cdn.openai.com/research-covers/language-unsupervised/language_understanding_paper.pdf (accessed on 22 August 2024).
- Jiang, A.Q.; Sablayrolles, A.; Mensch, A.; Bamford, C.; Chaplot, D.S.; Casas, D.D.L.; Sayed, W.E.; Lavril, T.; Wang, T.; Lacroix, T.; et al. Mistral 7B. arXiv 2023, arXiv:2310.06825v1. [Google Scholar] [CrossRef]
- Touvron, H.; Lavril, T.; Izacard, G.; Martine, X.; Lachaux, M.-A.; Lacroix, T.; Rozière, B.; Goyal, N.; Hambro, E.; Azhar, F.; et al. LLaMA: Open and Efficient Foundation Language Models. arXiv 2023, arXiv:2302.13971. [Google Scholar] [CrossRef]
- Church, K.W.; Chen, Z.; Ma, Y. Emerging trends: A gentle introduction to fine-tuning. Nat. Lang. Eng. 2021, 27, 763–778. [Google Scholar] [CrossRef]
- Huang, J.; Chang, K.C.C. Towards reasoning in large language models: A survey. In Proceedings of the Findings of the Association for Computational Linguistics: ACL 2023, Toronto, ON, Canada, 14 July 2023; pp. 1049–1065. [Google Scholar] [CrossRef]
- Ding, N.; Qin, Y.; Yang, G.; Wei, F.; Yang, Z.; Su, Y.; Liu, Y.; Tang, J.; Li, J.; Sun, M.; et al. Parameter-efficient fine-tuning of large-scale pre-trained language models. Nat. Mach. Intell. 2023, 5, 220–235. [Google Scholar] [CrossRef]
- Fu, Z.; Yang, H.; So, A.M.C.; Lam, W.; Bing, L.; Collier, N. On the effectiveness of parameter-efficient fine-tuning. Proc. AAAI Conf. Artif. Intell. 2023, 37, 12799–12807. [Google Scholar] [CrossRef]
- Lv, K.; Yang, Y.; Liu, T.; Gao, Q.; Guo, Q.; Qiu, X. Full parameter fine-tuning for large language models with limited resources. arXiv 2023, arXiv:2306.09782v2. [Google Scholar] [CrossRef]
- Hu, J.E.; Shen, Y.; Wallis, P.; Allen-Zhu, Z.; Li, Y.; Wang, S.; Chen, W. LoRA: Low-Rank Adaptation of Large Language Models. In Proceedings of the Tenth International Conference on Learning Representations (ICRL), Virtual Event, 25–29 April 2022; Available online: https://openreview.net/forum?id=nZeVKeeFYf9 (accessed on 22 August 2024).
- Liu, X.; Ji, K.; Fu, Y.; Tam, W.; Du, Z.; Yang, Z.; Tang, J. P-Tuning: Prompt Tuning Can Be Comparable to Fine-tuning Across Scales and Tasks. In Proceedings of the 60th Annual Meeting of the Association for Computational Linguistics, Dunlin, Lreland, 22–27 May 2022; Volume 2, (Short Papers). pp. 61–68. [Google Scholar] [CrossRef]
- Rubin, O.; Herzig, J.; Berant, J. Learning To Retrieve Prompts for In-Context Learning. In Proceedings of the 2022 Conference of the North American Chapter of the Association for Computational Linguistics: Human Language Technologies, Seattle, DC, USA; 2022; pp. 2655–2671. [Google Scholar] [CrossRef]
- Zhang, S.; Dong, L.; Li, X.; Zhang, S.; Sun, X.; Wang, S.; Li, J.; Hu, R.; Zhang, T.; Wang, G.; et al. Instruction tuning for large language models: A survey. arXiv 2023, arXiv:2308.10792. [Google Scholar] [CrossRef]
- Wei, J.; Wang, X.; Schuurmans, D.; Bosma, M.; Xia, F.; Chi, E.; Le, Q.V.; Zhou, D. Chain-of-thought prompting elicits reasoning in large language models. Adv. Neural Inf. Process. Syst. 2022, 35, 24824–24837. [Google Scholar] [CrossRef]
- Song, C.; Lin, Y.; Guo, S.; Wan, H. Spatial-Temporal Synchronous Graph Convolutional Networks: A New Framework for Spatial-Temporal Network Data Forecasting. Proc. AAAI Conf. Artif. Intell. 2020, 34, 914–921. [Google Scholar] [CrossRef]

| Dataset | Number of Sensors | Samples | Time Range |
|---|---|---|---|
| METR-LA | 207 | 34,272 | 1 March 2012–27 June 2012 |
| PEMS-Bay | 325 | 52,116 | 1 January 2017–30 June 2017 |
| PEMS04 | 307 | 16,992 | 1 January 2018–28 February 2018 |
| PEMS08 | 170 | 17,856 | 1 July 2016–31 August 2016 |
| Model | Total Params | Trainable Params | Params in Embedding Layers | Trainable Params in Pre-Trained LM |
|---|---|---|---|---|
| STTLM | 335,076,981 | 1,617,525 | 809,704 | 786,432 |
| STTLM_2L | 538,246,773 | 2,403,957 | 809,704 | 1,572,864 |
| Dataset | Metric | DCRNN | GWNet | AGCRN | MTGNN | STAEformer | ST_4L | ST_7L | STTLM | |
|---|---|---|---|---|---|---|---|---|---|---|
| METR-LA | 3 | MAE | 2.67 | 2.69 | 2.85 | 2.69 | 2.65 | 3.05 | 2.93 | 2.62 |
| RMSE | 5.16 | 5.15 | 5.53 | 5.16 | 5.11 | 6.22 | 5.88 | 5.05 | ||
| MAPE | 6.86% | 6.99% | 7.63% | 6.89% | 6.85% | 8.51% | 7.84% | 6.72% | ||
| 6 | MAE | 3.12 | 3.08 | 3.20 | 3.05 | 2.97 | 3.11 | 2.94 | 2.94 | |
| RMSE | 6.27 | 6.20 | 6.52 | 6.13 | 6.00 | 6.46 | 5.98 | 5.94 | ||
| MAPE | 8.42% | 8.47% | 9.00% | 8.16% | 8.13% | 8.84% | 8.03% | 7.98% | ||
| 12 | MAE | 3.54 | 3.51 | 3.59 | 3.47 | 3.34 | 3.74 | 3.64 | 3.31 | |
| RMSE | 7.47 | 7.28 | 7.45 | 7.21 | 7.02 | 7.87 | 7.64 | 6.88 | ||
| MAPE | 10.32% | 9.96% | 10.47% | 9.70% | 9.70% | 10.79% | 10.25% | 9.54% | ||
| PEMS-BAY | 3 | MAE | 1.31 | 1.30 | 1.35 | 1.33 | 1.31 | 1.64 | 1.60 | 1.29 |
| RMSE | 2.76 | 2.73 | 2.88 | 2.8 | 2.78 | 3.81 | 3.68 | 2.78 | ||
| MAPE | 2.73% | 2.71% | 2.91% | 2.81% | 2.76% | 3.72% | 3.62% | 2.74% | ||
| 6 | MAE | 1.65 | 1.63 | 1.67 | 1.66 | 1.62 | 1.62 | 1.59 | 1.58 | |
| RMSE | 3.75 | 3.73 | 3.82 | 3.77 | 3.68 | 3.77 | 3.66 | 3.63 | ||
| MAPE | 3.71% | 3.73% | 3.81% | 3.75% | 3.62% | 3.67% | 3.59% | 3.55% | ||
| 12 | MAE | 1.97 | 1.99 | 1.94 | 1.95 | 1.88 | 2.10 | 2.1 | 1.83 | |
| RMSE | 4.60 | 4.60 | 4.5 | 4.5 | 4.34 | 4.97 | 4.94 | 4.27 | ||
| MAPE | 4.68% | 4.71% | 4.55% | 4.62% | 4.41% | 4.82% | 4.81% | 4.30% | ||
| Dataset | Metric | DCRNN | GWNet | AGCRN | MTGNN | STAEformer | ST _4L | ST_7L | STTLM |
|---|---|---|---|---|---|---|---|---|---|
| PEMS04 | MAE | 19.63 | 18.53 | 19.38 | 19.17 | 18.22 | 21.36 | 21.35 | 17.73 |
| RMSE | 31.26 | 29.92 | 31.25 | 31.7 | 30.18 | 33.36 | 33.20 | 29.31 | |
| MAPE | 13.59% | 12.89% | 13.40% | 13.37% | 11.98% | 14.34% | 14.28% | 11.83% | |
| PEMS08 | MAE | 15.22 | 14.4 | 15.32 | 15.18 | 13.46 | 17.06 | 17.02 | 12.82 |
| RMSE | 24.17 | 23.39 | 24.41 | 24.24 | 23.25 | 26.86 | 26.78 | 22.36 | |
| MAPE | 10.21% | 9.21% | 10.03% | 10.20% | 8.88% | 10.91% | 10.91% | 8.46% |
| Dataset | Metric | w/o Eep | w/o Ep | w/o Es | STTLM | |
|---|---|---|---|---|---|---|
| METR-LA | 3 | MAE | 2.97 | 2.66 | 2.62 | 2.62 |
| RMSE | 5.84 | 5.06 | 5.06 | 5.05 | ||
| MAPE | 7.94% | 6.80% | 6.79% | 6.72% | ||
| 6 | MAE | 3.53 | 3.02 | 2.95 | 2.94 | |
| RMSE | 7.16 | 6.03 | 6.00 | 5.94 | ||
| MAPE | 10.12% | 8.15% | 8.10% | 7.98% | ||
| 12 | MAE | 4.34 | 3.42 | 3.32 | 3.31 | |
| RMSE | 8.77 | 6.97 | 6.96 | 6.88 | ||
| MAPE | 13.38% | 9.65% | 9.65% | 9.54% | ||
| PEMS-BAY | 3 | MAE | 1.39 | 1.33 | 1.32 | 1.29 |
| RMSE | 3.00 | 2.81 | 2.83 | 2.78 | ||
| MAPE | 2.92% | 2.91% | 2.92% | 2.74% | ||
| 6 | MAE | 1.81% | 1.63 | 1.60 | 1.58 | |
| RMSE | 4.15 | 3.72 | 3.71 | 3.63 | ||
| MAPE | 4.13% | 3.76% | 3.76% | 3.55% | ||
| 12 | MAE | 2.3 | 1.9 | 1.84 | 1.83 | |
| RMSE | 5.27 | 4.41 | 4.31 | 4.27 | ||
| MAPE | 5.66% | 4.56% | 4.46% | 4.30% | ||
| Dataset | Metric | STTLM_2L | STTLM | |
|---|---|---|---|---|
| METR-LA | 3 | MAE | 2.61 | 2.62 |
| RMSE | 5.01 | 5.05 | ||
| MAPE | 6.74% | 6.72% | ||
| 6 | MAE | 2.93 | 2.94 | |
| RMSE | 5.96 | 5.94 | ||
| MAPE | 8.03% | 7.98% | ||
| 12 | MAE | 3.30 | 3.31 | |
| RMSE | 6.93 | 6.88 | ||
| MAPE | 9.56% | 9.54% | ||
| PEMS-BAY | 3 | MAE | 1.32 | 1.29 |
| RMSE | 2.81 | 2.78 | ||
| MAPE | 2.88% | 2.74% | ||
| 6 | MAE | 1.60 | 1.58 | |
| RMSE | 3.67 | 3.63 | ||
| MAPE | 3.71% | 3.55% | ||
| 12 | MAE | 1.85 | 1.83 | |
| RMSE | 4.31 | 4.27 | ||
| MAPE | 4.44% | 4.30% | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ma, J.; Zhao, J.; Hou, Y. Spatial–Temporal Transformer Networks for Traffic Flow Forecasting Using a Pre-Trained Language Model. Sensors 2024, 24, 5502. https://doi.org/10.3390/s24175502
Ma J, Zhao J, Hou Y. Spatial–Temporal Transformer Networks for Traffic Flow Forecasting Using a Pre-Trained Language Model. Sensors. 2024; 24(17):5502. https://doi.org/10.3390/s24175502
Chicago/Turabian StyleMa, Ju, Juan Zhao, and Yao Hou. 2024. "Spatial–Temporal Transformer Networks for Traffic Flow Forecasting Using a Pre-Trained Language Model" Sensors 24, no. 17: 5502. https://doi.org/10.3390/s24175502
APA StyleMa, J., Zhao, J., & Hou, Y. (2024). Spatial–Temporal Transformer Networks for Traffic Flow Forecasting Using a Pre-Trained Language Model. Sensors, 24(17), 5502. https://doi.org/10.3390/s24175502






