Direction-of-Arrival Estimation for Unmanned Aerial Vehicles and Aircraft Transponders Using a Multi-Mode Multi-Port Antenna
Abstract
1. Introduction
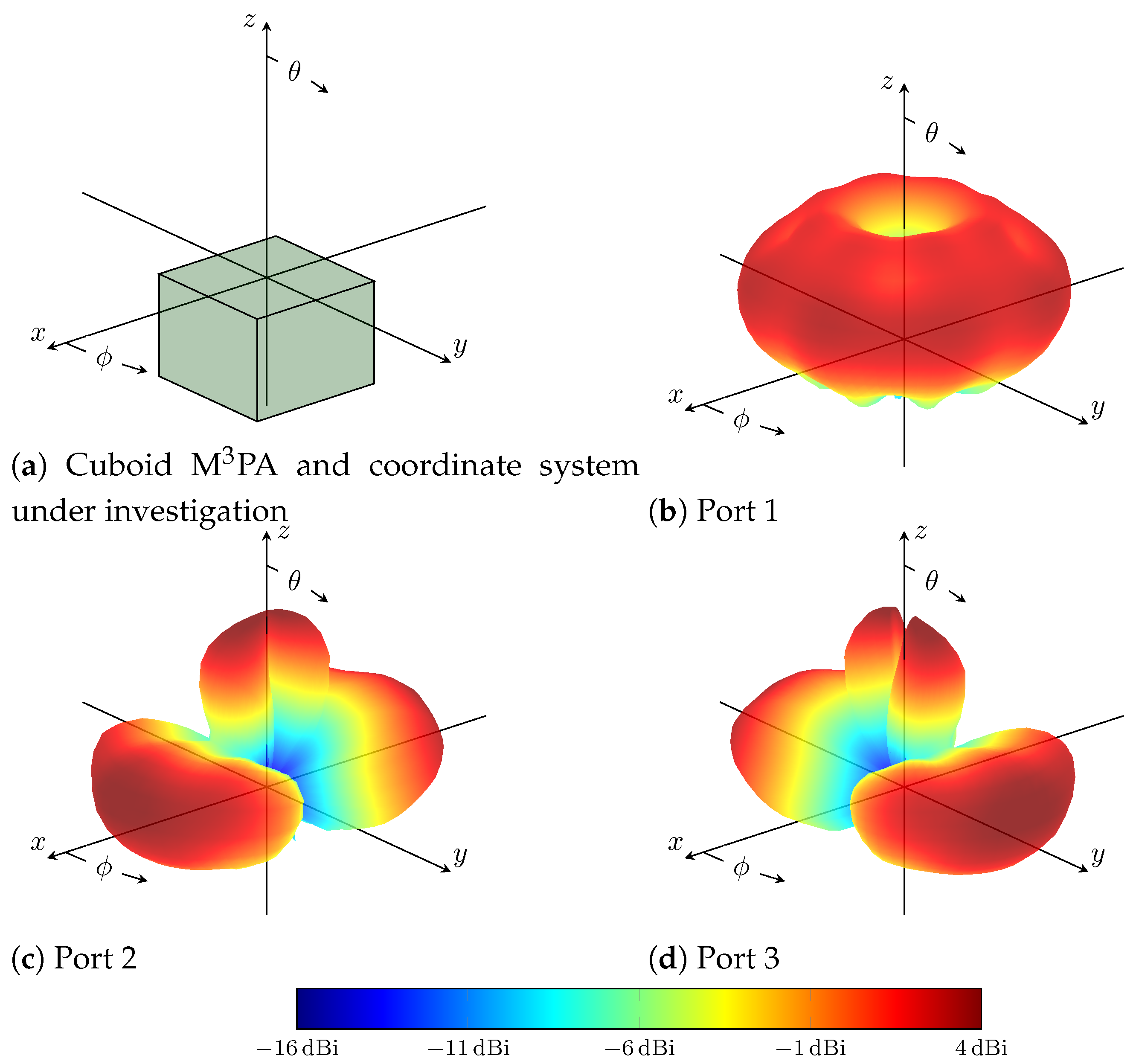
2. Cuboid Multi-Mode Multi-Port Antennas
3. System Description
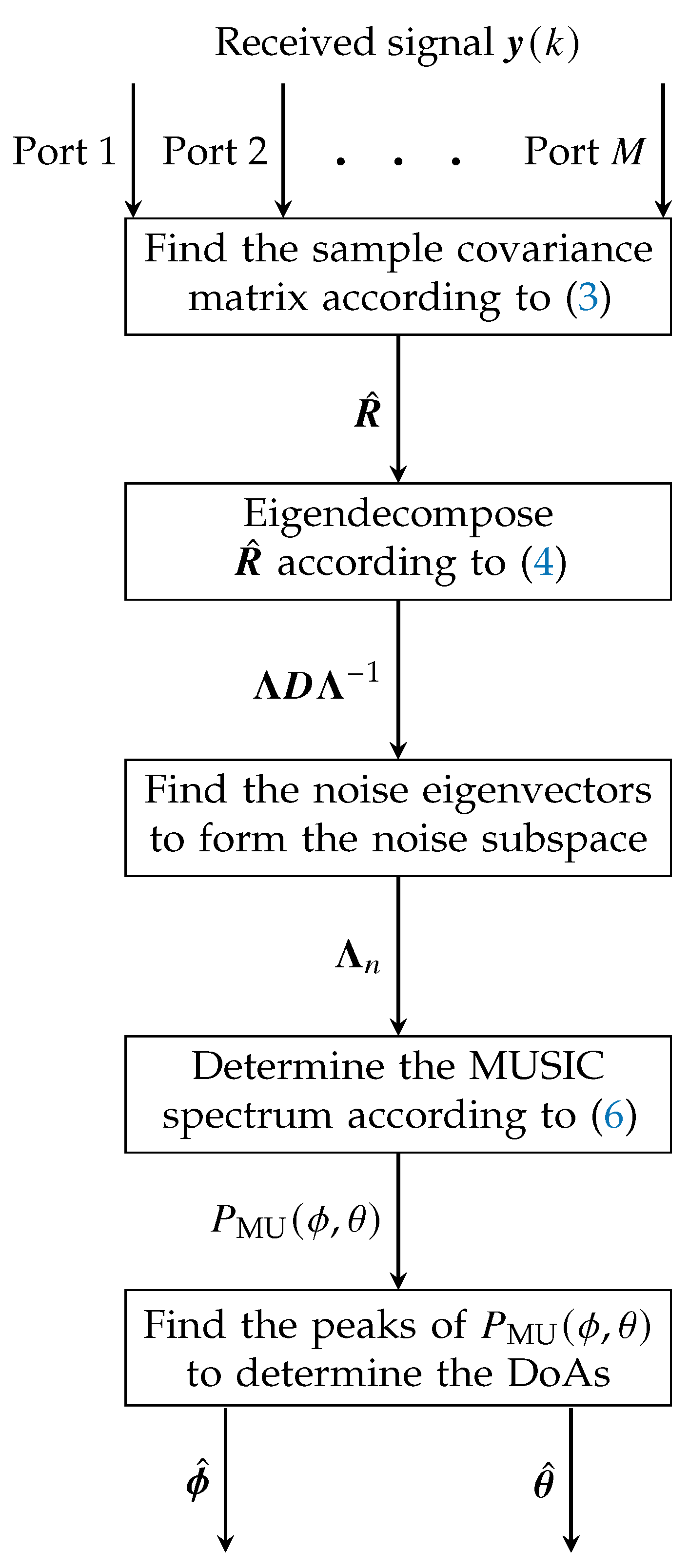
4. MUSIC-Based 3D DoA Estimation Adopted to Multi-Mode Multi-Port Antennas
| Algorithm 1 MUSIC-based 3D DoA estimation adopted to multi-mode multi-port antennas |
|
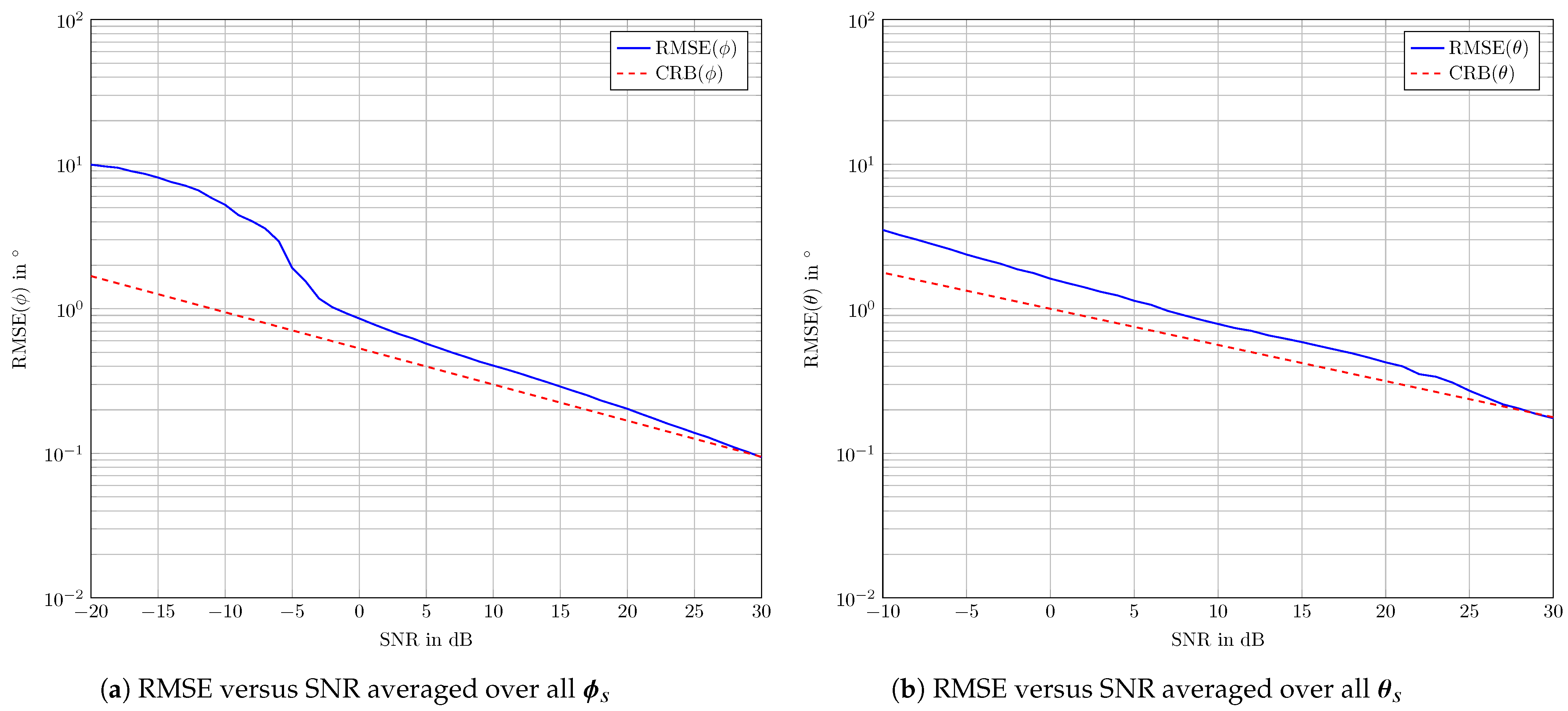
5. Numerical Results
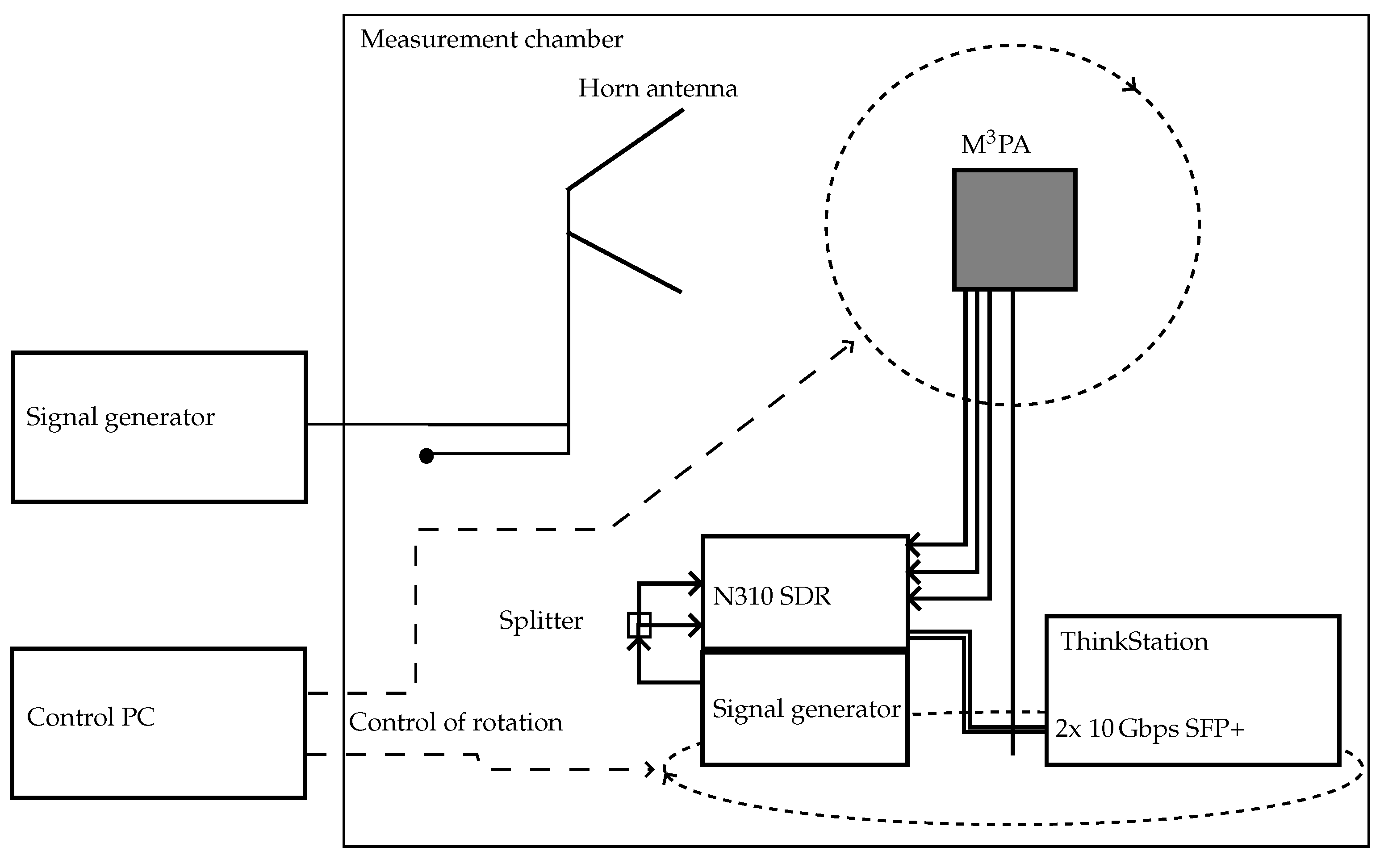
6. Measurement Setup
7. Experimental Results
8. Discussion
9. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Dalamagkidis, K.; Valavanis, K.P.; Piegl, L.A. On Unmanned Aircraft Systems Issues, Challenges and Operational Restrictions Preventing Integration into the National Airspace System. Prog. Aerosp. Sci. 2008, 44, 503–519. [Google Scholar] [CrossRef]
- Loh, R.; Bian, Y.; Roe, T. UAVs in Civil Airspace: Safety Requirements. IEEE Aerosp. Electron. Syst. Mag. 2009, 24, 5–17. [Google Scholar] [CrossRef]
- Balestrieri, E.; Daponte, P.; De Vito, L.; Picariello, F.; Tudosa, I. Sensors and Measurements for UAV Safety: An Overview. Sensors 2021, 21, 8253. [Google Scholar] [CrossRef]
- Wang, W.; Li, X.; Xie, L.; Lv, H.; Lv, Z. Unmanned Aircraft System Airspace Structure and Safety Measures Based on Spatial Digital Twins. IEEE Trans. Intell. Transp. Syst. 2022, 23, 2809–2818. [Google Scholar] [CrossRef]
- EUROCONTROL. ACAS Guide. 2022. Available online: https://www.eurocontrol.int/system/acas (accessed on 31 March 2024).
- Manfredi, G.; Jestin, Y. An Introduction to ACAS Xu and the Challenges Ahead. In Proceedings of the 2016 IEEE/AIAA 35th Digital Avionics Systems Conference (DASC), Sacramento, CA, USA, 25–29 September 2016; pp. 1–9. [Google Scholar] [CrossRef]
- Balestrieri, E.; Daponte, P.; De Vito, L.; Lamonaca, F. Sensors and Measurements for Unmanned Systems: An Overview. Sensors 2021, 21, 1518. [Google Scholar] [CrossRef]
- Corraro, F.; Corraro, G.; Cuciniello, G.; Garbarino, L. Unmanned Aircraft Collision Detection and Avoidance for Dealing with Multiple Hazards. Aerospace 2022, 9, 190. [Google Scholar] [CrossRef]
- Ray, P.P. A Review on 6G for Space-Air-Ground Integrated Network: Key Enablers, Open Challenges, and Future Direction. J. King Saud Univ.-Comput. Inf. Sci. 2022, 34, 6949–6976. [Google Scholar] [CrossRef]
- Jiang, X.; Sheng, M.; Zhao, N.; Xing, C.; Lu, W.; Wang, X. Green UAV Communications for 6G: A Survey. Chin. J. Aeronaut. 2022, 35, 19–34. [Google Scholar] [CrossRef]
- Cheng, N.; He, J.; Yin, Z.; Zhou, C.; Wu, H.; Feng, L.; Zhou, H.; Shen, X. 6G Service-Oriented Space-Air-Ground Integrated Network: A Survey. Chin. J. Aeronaut. 2022, 35, 1–18. [Google Scholar] [CrossRef]
- Dicandia, F.A.; Fonseca, N.J.; Bacco, M.; Mugnaini, S.; Genovesi, S. Space-Air-Ground Integrated 6G Wireless Communication Networks: A Review of Antenna Technologies and Application Scenarios. Sensors 2022, 22, 3136. [Google Scholar] [CrossRef]
- Mozaffari, M.; Lin, X.; Hayes, S. Toward 6G with Connected Sky: UAVs and Beyond. IEEE Commun. Mag. 2021, 59, 74–80. [Google Scholar] [CrossRef]
- Li, S.; Cheng, X.; Huang, X.; Otaibi, S.A.; Wang, H. Cooperative Conflict Detection and Resolution and Safety Assessment for 6G Enabled Unmanned Aerial Vehicles. IEEE Trans. Intell. Transp. Syst. 2023, 24, 2183–2198. [Google Scholar] [CrossRef]
- International Civil Aviation Organization. Airborne Collision Avoidance System Manual, 1st ed.; International Civil Aviation Organization: Montreal, QC, Canada, 2006. [Google Scholar]
- Tuncer, T.E.; Friedlander, F. Classical and Modern Direction-of-Arrival Estimation; Academic Press: Burlington, MA, USA, 2009. [Google Scholar]
- Manteuffel, D.; Lin, F.H.; Li, T.; Peitzmeier, N.; Chen, Z.N. Characteristic Mode-Inspired Advanced Multiple Antennas: Intuitive Insight Into Element-, Interelement-, and Array Levels of Compact Large Arrays and Metantennas. IEEE Antennas Propag. Mag. 2022, 64, 49–57. [Google Scholar] [CrossRef]
- Harrington, R.; Mautz, J. Theory of Characteristic Modes for Conducting Bodies. IEEE Trans. Antennas Propag. 1971, 19, 622–628. [Google Scholar] [CrossRef]
- Chen, Y.; Wang, C.F. Characteristic Modes: Theory and Applications in Antenna Engineering; John Wiley & Sons: Hoboken, NJ, USA, 2015. [Google Scholar]
- Lu, W.J.; Zhu, L. Multi-Mode Resonant Antennas: Theory, Design, and Applications; CRC Press: Boca Raton, FL, USA, 2022. [Google Scholar]
- Peitzmeier, N.; Manteuffel, D. Upper Bounds and Design Guidelines for Realizing Uncorrelated Ports on Multi-Mode Antennas Based on Symmetry Analysis of Characteristic Modes. IEEE Trans. Antennas Propag. 2019, 67, 3902–3914. [Google Scholar] [CrossRef]
- Peitzmeier, N.; Hahn, T.; Manteuffel, D. Systematic Design of Multimode Antennas for MIMO Applications by Leveraging Symmetry. IEEE Trans. Antennas Propag. 2022, 70, 145–155. [Google Scholar] [CrossRef]
- Manteuffel, D.; Martens, R. Compact Multimode Multielement Antenna for Indoor UWB Massive MIMO. IEEE Trans. Antennas Propag. 2016, 64, 2689–2697. [Google Scholar] [CrossRef]
- Hoeher, P.A.; Manteuffel, D.; Doose, N.; Peitzmeier, N. Ultra-Wideband Massive MIMO Communications Using Multi-mode Antennas. Frequenz 2017, 71, 429–448. [Google Scholar] [CrossRef]
- Hoeher, P.A.; Doose, N. A massive MIMO Terminal Concept Based on Small-Size Multi-Mode Antennas. Trans. Emerg. Telecommun. Technol. 2017, 28, e2934. [Google Scholar] [CrossRef]
- Johannsen, N.L.; Hoeher, P.A. Single-Element Beamforming Using Multi-Mode Antenna Patterns. IEEE Wirel. Commun. Lett. 2020, 9, 1120–1123. [Google Scholar] [CrossRef]
- Johannsen, N.L.; Peitzmeier, N.; Hoeher, P.A.; Manteuffel, D. On the Feasibility of Multi-Mode Antennas in UWB and IoT Applications Below 10 GHz. IEEE Commun. Mag. 2020, 58, 69–75. [Google Scholar] [CrossRef]
- Johannsen, N.L.; Hoeher, P.A.; Peitzmeier, N.; Manteuffel, D. M4: Multi-Mode Massive MIMO. In Wireless 100 Gbps and Beyond: Architectures, Approaches and Findings of German Research Foundation (DFG) Priority Programme SPP1655; IHP—Innovations for High Performance Microelectronics: Frankfurt, Germany, 2022; pp. 167–212. [Google Scholar] [CrossRef]
- Ojaroudi Parchin, N.; Jahanbakhsh Basherlou, H.; Abd-Alhameed, R.A. Design of Multi-Mode Antenna Array for Use in Next-Generation Mobile Handsets. Sensors 2020, 20, 2447. [Google Scholar] [CrossRef] [PubMed]
- Almasri, S.A.; Doose, N.; Hoeher, P.A. Parametric Direction-of-Arrival Estimation for Multi-Mode Antennas. In Proceedings of the 14th Workshop on Positioning, Navigation and Communications (WPNC), Bremen, Germany, 25–26 October 2017; pp. 1–5. [Google Scholar] [CrossRef]
- Pöhlmann, R.; Almasri, S.; Zhang, S.; Jost, T.; Dammann, A.; Hoeher, P. On the Potential of Multi-Mode Antennas for Direction-of-Arrival Estimation. IEEE Trans. Antennas Propag. 2019, 67, 3374–3386. [Google Scholar] [CrossRef]
- Almasri, S.A.; Pöhlmann, R.; Doose, N.; Hoeher, P.A.; Dammann, A. Modeling Aspects of Planar Multi-Mode Antennas for Direction-of-Arrival Estimation. IEEE Sens. J. 2019, 19, 4585–4597. [Google Scholar] [CrossRef]
- Johannsen, N.L.; Mietzner, J.; Hoeher, P.A. Joint Communication and Sensing Using Compressive Sensing and a Single Multi-Mode Multi-Port Antenna. IEEE Open J. Commun. Soc. 2024, 5, 71–82. [Google Scholar] [CrossRef]
- Johannsen, N.L.; Schurwanz, M.; Grundmann, L.; Mietzner, J.; Manteuffel, D.; Hoeher, P.A. Joint Communication, Sensing and Localization for Airborne Applications. arXiv 2022, arXiv:2209.10991. [Google Scholar]
- Johannsen, N.L.; Alkubti Almasri, S.; Hoeher, P.A. Geometry-Based UAV MIMO Channel Modeling and Pattern Optimization for Multimode Antennas. IEEE Trans. Antennas Propag. 2022, 70, 11024–11032. [Google Scholar] [CrossRef]
- EUROCAE. Minimum Operational Performance Standards For Airborne Collision Avoidance System XU (ACAS XU). ED 275 2020, 1, 176–177. [Google Scholar]
- Ma, R.; Behdad, N. Design of Platform-Based HF Direction-Finding Antennas Using the Characteristic Mode Theory. IEEE Trans. Antennas Propag. 2019, 67, 1417–1427. [Google Scholar] [CrossRef]
- Ren, K.; Ma, R.; Behdad, N. Performance-Enhancement of Platform-Based, HF Direction-Finding Systems Using Dynamic Mode Selection. IEEE Open J. Antennas Propag. 2021, 2, 793–806. [Google Scholar] [CrossRef]
- Ma, R.; Behdad, N. A Spatially Confined, Platform-Based HF Direction Finding Array. IEEE Trans. Antennas Propag. 2022, 70, 1298–1308. [Google Scholar] [CrossRef]
- Grundmann, L.; Manteuffel, D. Evaluation Method and Design Guidance for Direction-Finding Antenna Systems. IEEE Trans. Antennas Propag. 2023, 71, 7146–7157. [Google Scholar] [CrossRef]
- The European Organisation for Civil Aciation Equipment. Minimum Operational Performance Specification for Secondary Surveilance Radar Mode S Transponders. ED-73C 2008, 1, 28. [Google Scholar]
- Schmidt, R. Multiple Emitter Location and Signal Parameter Estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Doron, M.A.; Doron, E. Wavefield Modeling and Array Processing, I. Spatial Sampling. IEEE Trans. Signal Process. 1994, 42, 2549–2559. [Google Scholar] [CrossRef]
- Doron, M.A.; Doron, E. Wavefield Modeling and Array Processing, II. Algorithms. IEEE Trans. Signal Process. 1994, 42, 2560–2570. [Google Scholar] [CrossRef]
- Doron, M.A.; Doron, E. Wavefield Modeling and Array Processing, III. Resolution Capacity. IEEE Trans. Signal Process. 1994, 42, 2571–2580. [Google Scholar] [CrossRef]
- Kay, S.M. Fundamentals of Statistical Signal Processing—Estimation Theory; Prentice Hall: Hoboken, NJ, USA, 1993. [Google Scholar]
- Stoica, P.; Nehorai, A. MUSIC, Maximum Likelihood, and Cramer-Rao Bound. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 720–741. [Google Scholar] [CrossRef]
- Ettus. USRP N310 Datasheet. 2019. Available online: https://www.ettus.com/wp-content/uploads/2019/01/USRP_N310_Datasheet_v3.pdf (accessed on 22 May 2024).
- Marinho, D.; Arruela, R.; Varum, T.; Matos, J. Software-Defined Radio Beamforming System for 5G/Radar Applications. Appl. Sci. 2020, 10, 7187. [Google Scholar] [CrossRef]
- Jaffer, A. Maximum Likelihood Direction Finding of Stochastic Sources: A Separable Solution. In Proceedings of the ICASSP-88, International Conference on Acoustics, Speech, and Signal Processing, New York, NY, USA, 11–14 April 1988; pp. 2893–2896. [Google Scholar] [CrossRef]
- Zhang, J.A.; Liu, F.; Masouros, C.; Heath, R.W.; Feng, Z.; Zheng, L.; Petropulu, A. An Overview of Signal Processing Techniques for Joint Communication and Radar Sensing. IEEE J. Sel. Top. Signal Process. 2021, 15, 1295–1315. [Google Scholar] [CrossRef]
- Zhang, J.A.; Rahman, M.L.; Wu, K.; Huang, X.; Guo, Y.J.; Chen, S.; Yuan, J. Enabling Joint Communication and Radar Sensing in Mobile Networks— A Survey. IEEE Commun. Surv. Tutor. 2021, 24, 306–345. [Google Scholar] [CrossRef]
- Wild, T.; Braun, V.; Viswanathan, H. Joint Design of Communication and Sensing for Beyond 5G and 6G Systems. IEEE Access 2021, 9, 30845–30857. [Google Scholar] [CrossRef]


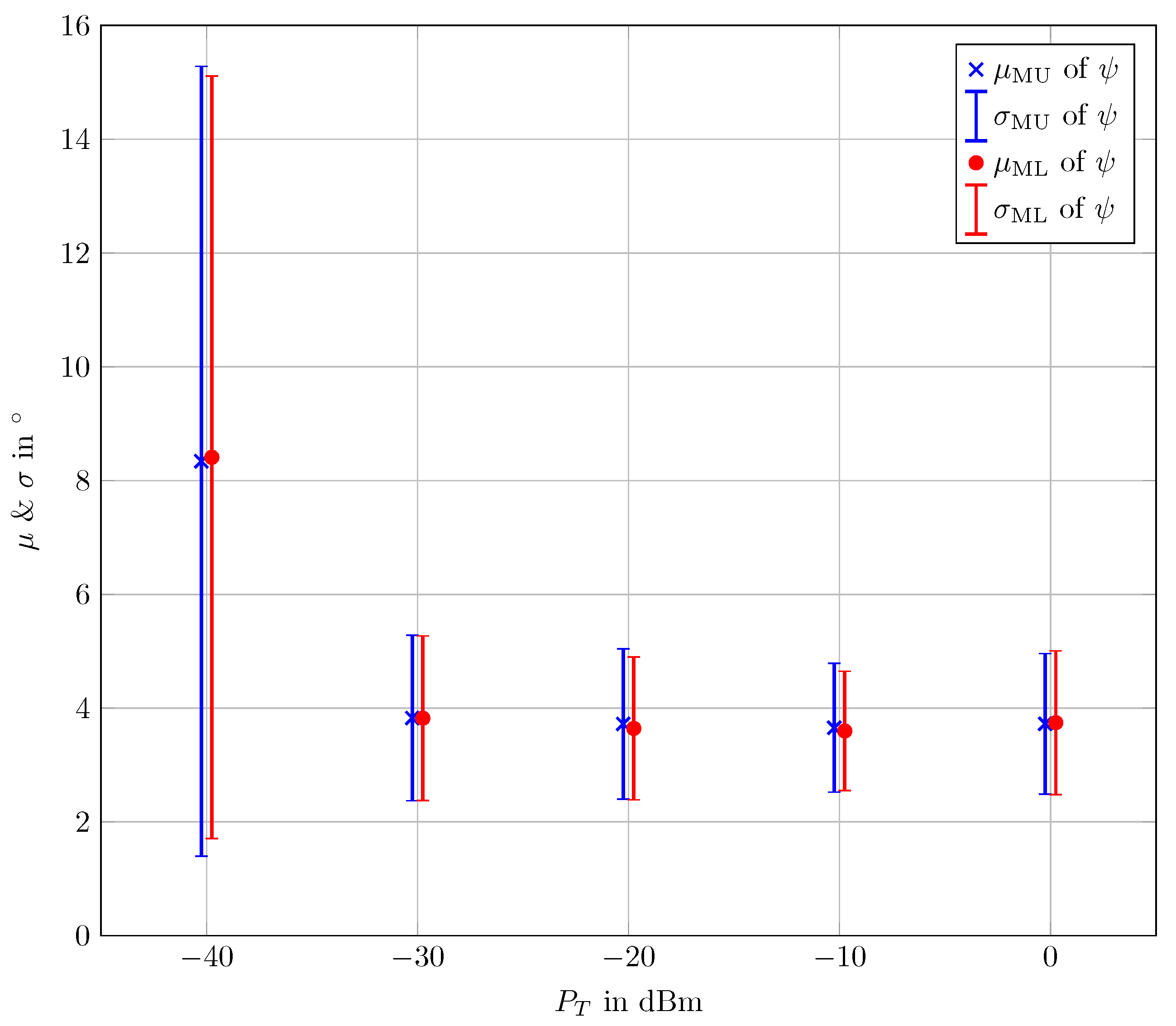
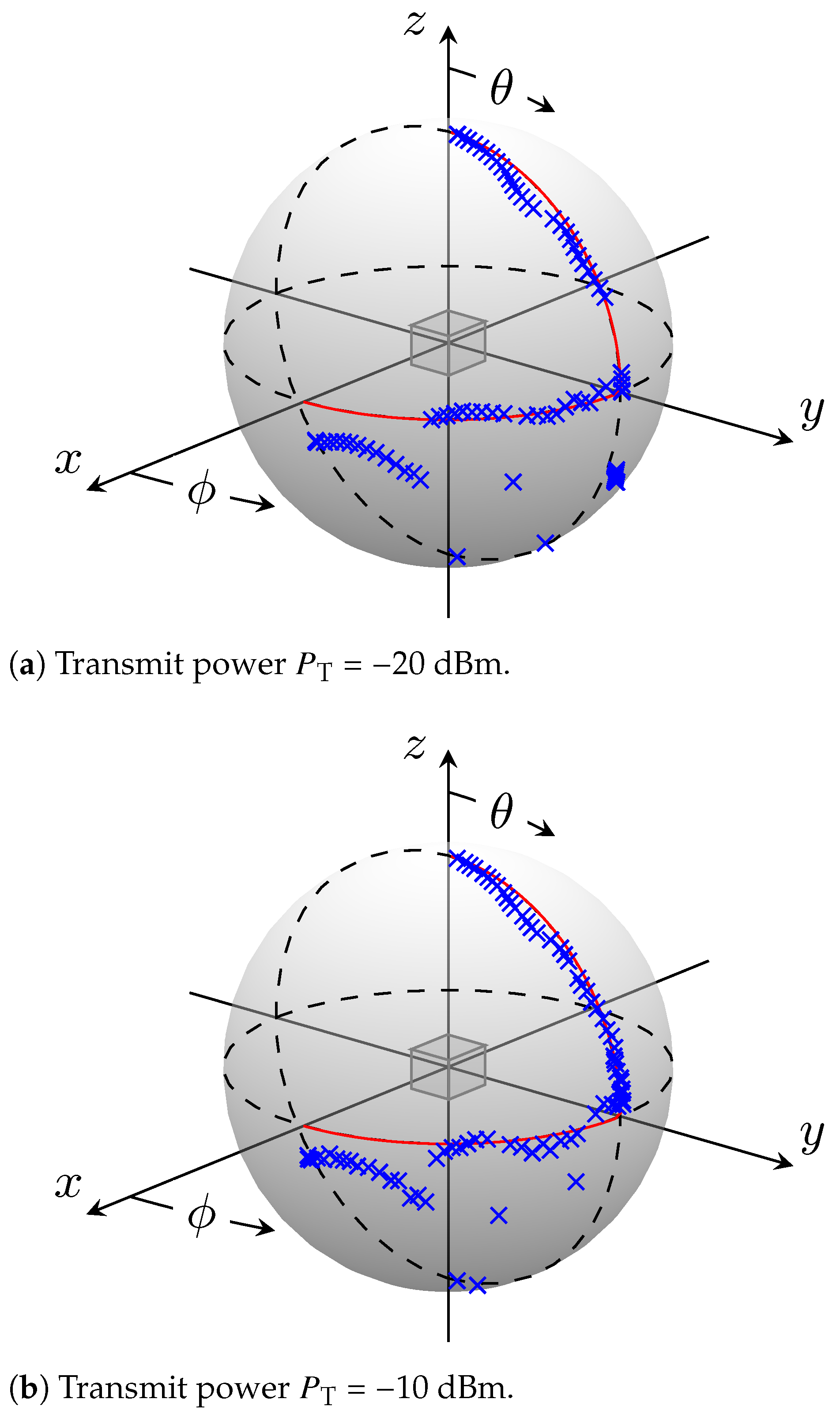
| (a) Transmit power = 0 dBm and = dBm. | ||||||
| = 0 dBm | = dBm | |||||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (b) Transmit power dBm and dBm. | ||||||
| = dBm | = dBm | |||||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (c) Transmit power dBm and dBm. | ||||||
| = dBm | = dBm | |||||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
| (, ) | (, ) | (, ) | (, ) | (, ) | ||
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Almasri, S.A.; Johannsen, N.L.; Hoeher, P.A. Direction-of-Arrival Estimation for Unmanned Aerial Vehicles and Aircraft Transponders Using a Multi-Mode Multi-Port Antenna. Sensors 2024, 24, 3452. https://doi.org/10.3390/s24113452
Almasri SA, Johannsen NL, Hoeher PA. Direction-of-Arrival Estimation for Unmanned Aerial Vehicles and Aircraft Transponders Using a Multi-Mode Multi-Port Antenna. Sensors. 2024; 24(11):3452. https://doi.org/10.3390/s24113452
Chicago/Turabian StyleAlmasri, Sami Alkubti, Nils L. Johannsen, and Peter A. Hoeher. 2024. "Direction-of-Arrival Estimation for Unmanned Aerial Vehicles and Aircraft Transponders Using a Multi-Mode Multi-Port Antenna" Sensors 24, no. 11: 3452. https://doi.org/10.3390/s24113452
APA StyleAlmasri, S. A., Johannsen, N. L., & Hoeher, P. A. (2024). Direction-of-Arrival Estimation for Unmanned Aerial Vehicles and Aircraft Transponders Using a Multi-Mode Multi-Port Antenna. Sensors, 24(11), 3452. https://doi.org/10.3390/s24113452









