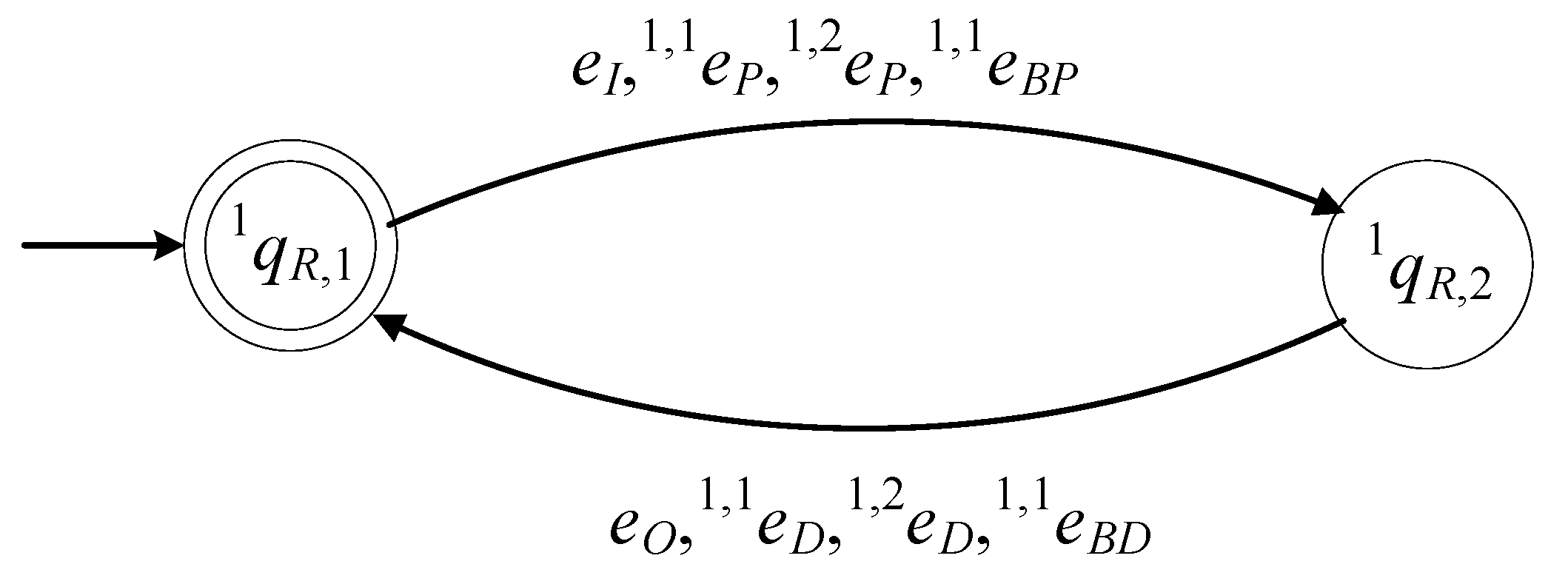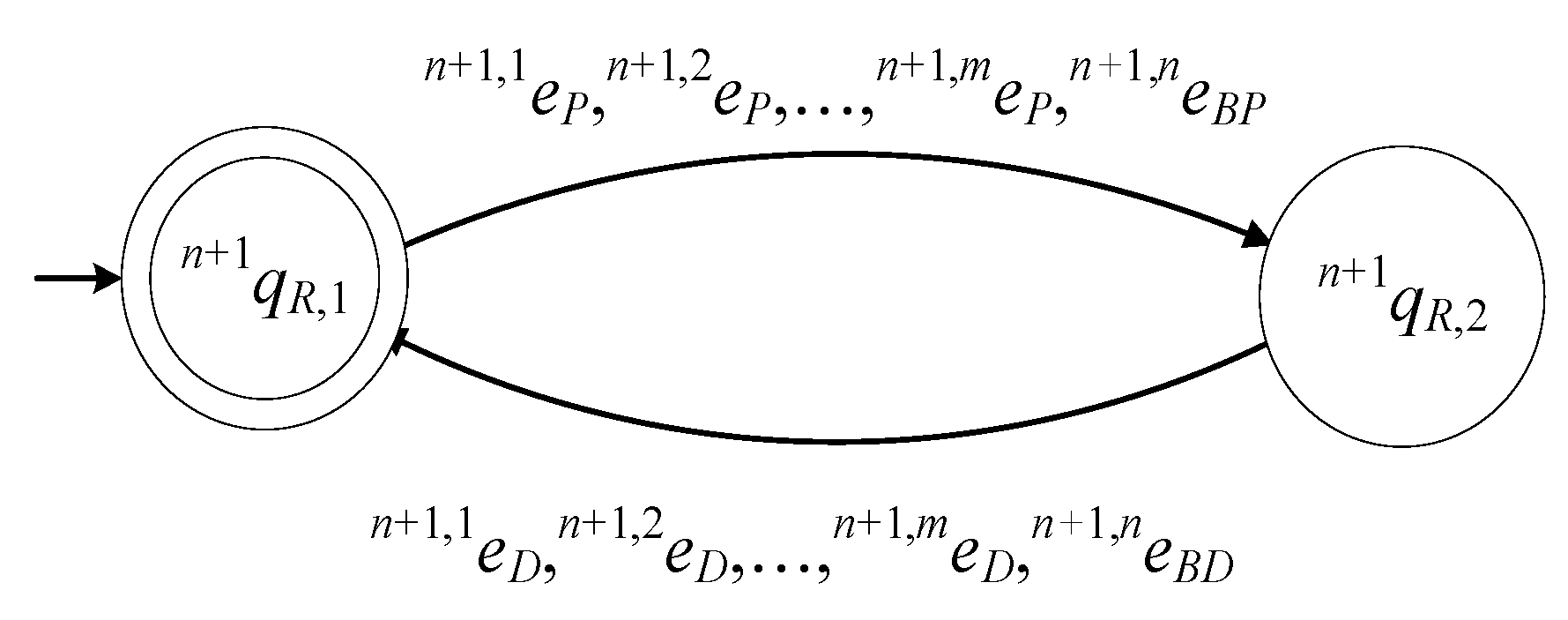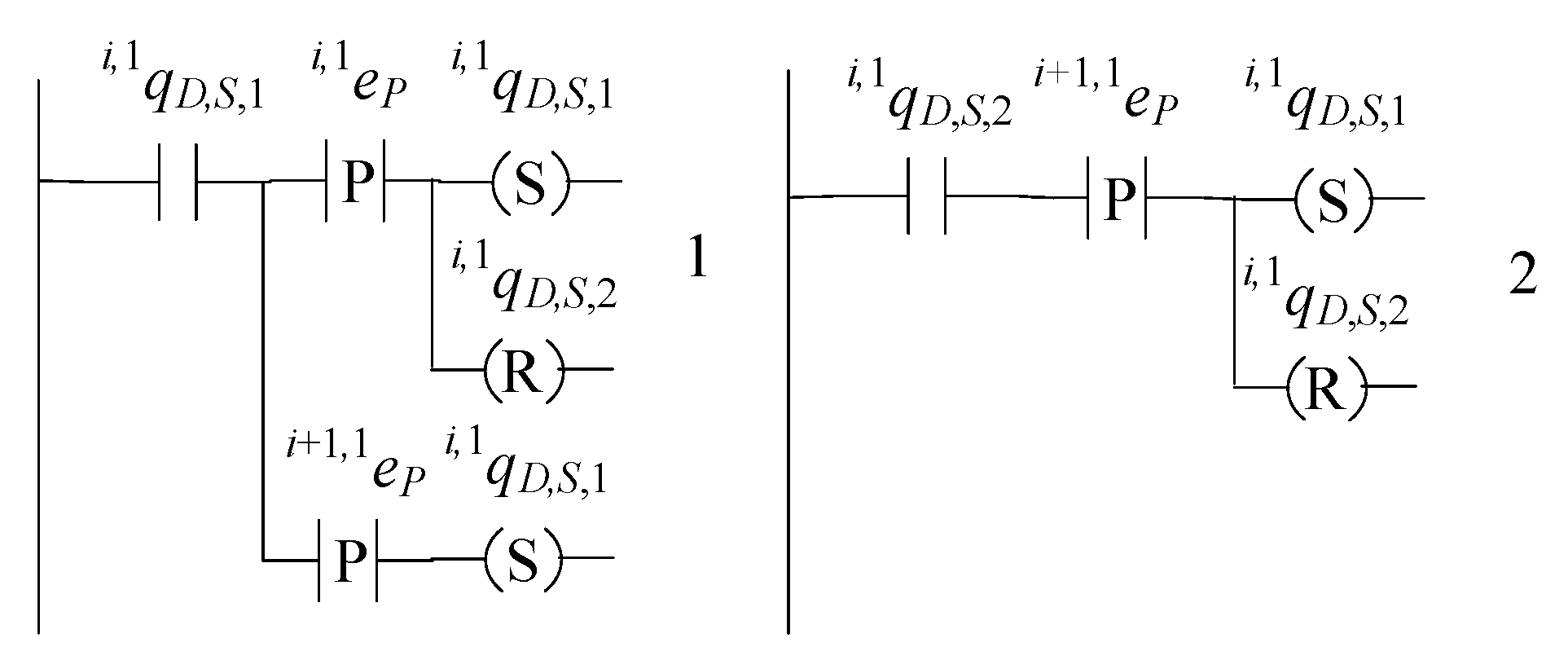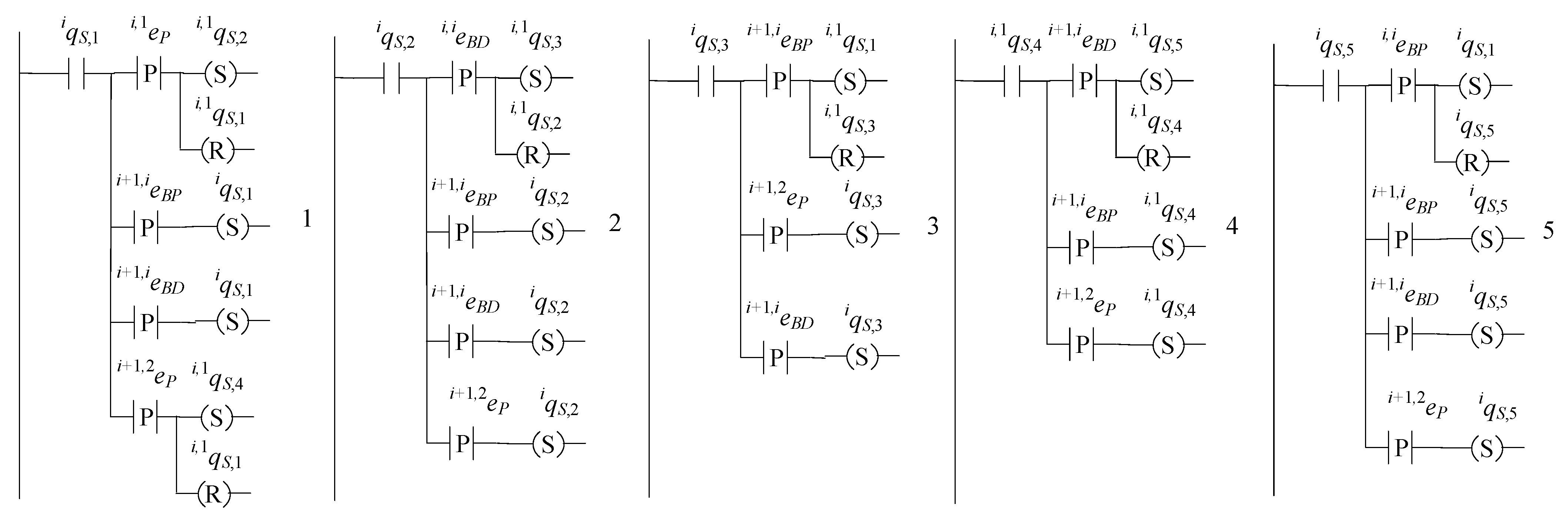1. Introduction
One of the main goals of Industry 4.0 is to improve existing systems and processes via the automatization of manufacturing processes and the interoperability of corresponding applications using cyber-physical systems and the Internet of Things (IoT). The adaptation of these tools in many systems’ processes, including installed robotic manipulators, and the direction for more flexible and easily expandable manufacturing systems increase the need for smarter and more efficient control systems. One of the manufacturing sectors into which these tools are introduced at many different stages of the manufacturing process is the semiconductor manufacturing industry [
1].
In semiconductor industry, wafer processing units have an important role. The wafer processing unit (see [
2,
3,
4,
5,
6,
7,
8,
9]) is a manufacturing unit consisting of a set of integrated production stations (process chambers), a set of one-slot buffers, one loading dock (input) of the raw products, one loading dock (output) of the manufactured products, and a set of robotic manipulators that transfer the products between the stations, the buffers, and the input and output docks. For every production station, there is one robotic manipulator dedicated to serve the production station. The production station and the robotic manipulator constitute an individual manufacturing unit, called a cluster tool. The first studies of wafer manufacturing units (see [
2,
3,
4,
5,
6,
7]) have been limited to single cluster tool systems up to four cluster tools systems. The systems that have more than one cluster tool are called multicluster tool systems. The current trend in the wafer industry is to increase the number of cluster tools participating in the process (see [
8,
9]), or/and to increase the number of production stations in each cluster tool (see [
10,
11]).
For the case of multicluster tool systems, with a parametric number of production stations in each cluster, the number of studies towards synchronization of the cluster tool and scheduling analysis of the manufacturing unit is increasing (indicatively, see [
10,
11,
12,
13,
14]). The goal of these studies is to increase the production speed and optimize the job scheduling of the manufacturing unit. According to [
10], multicluster tool systems can be viewed either from the point of view of the robots or from the point of view of the wafer product flow. In the first case, the production times are considered to be neglectable. Therefore, the study is focused on the supervision of the pick-and-place tasks of the robotic manipulators. In the second case, the processing time is considered to be non-neglectable, while the pick-and-place times are considered to be neglectable. Therefore, the study focuses on the flow of wafers and the processing timing of the wafers in the production sections. In the present paper, the study focuses on the supervision of the robotic manipulators, and the production time is considered to be zero.
The architecture of a cluster tool in the semiconductor industry has been presented in [
2], where linear wafer processing has been introduced. In [
2], the system’s analysis focuses on the time needed for the manufacturing of the wafers to be completed. In [
3,
4], a wafer processing unit, consisting of nine production stations, three buffers, and four robotic manipulators, is studied. In [
3], the wafer processing units are modelled using finite deterministic automata. The automaton of the stations and the buffers has a deadlock. In [
3], a set of local supervisors is proposed to avoid the deadlock and coordinate the transfer of the wafers from one production unit to another. In [
4], the models developed in [
3] have been used and a set of supervisors is proposed to avoid deadlock and coordinate the overall manufacturing unit. In [
5,
6], a wafer manufacturing unit with two production stations, one buffer, and two robotic manipulators is studied. Furthermore, a set of local supervisors is proposed for the coordination of the unit. In [
7], an extended version of the wafer manufacturing unit, consisting of eleven production stations, four buffers, and five robotic manipulators, is studied. In [
7], the models of the stations and the buffers are not used and the supervisor design is based on the models of the robotic manipulators. The models of the manipulators can be viewed as controlled versions of the models in [
3,
4]. In [
7], about 70 local supervisors are derived to prevent overflow of the stations and buffers as well as unnecessary use of manipulators. In [
8,
9], a wafer production line, with a parametric number of robots, is studied. Each robot serves two production stations, except for the last robot, which serves three production stations. The design specifications in [
8,
9] guarantee nonblocking through a distributed supervisory control scheme including a set of four two-state supervisors for each robotic manipulator and a global supervisor counting the wafers. In [
8,
9], the design of supervisors is based on abstractions of the automata models of the process in [
3]. Both works focus on the time needed for the completion of manufacturing.
In the present paper, a modular discrete event model of a wafer manufacturing unit, being parametric with respect to the number of production stations, the number of buffers, and the number of robotic manipulators, is developed using discrete event systems (DES) and especially the Ramadge–Wonham (RW) framework (see [
15,
16]). The configuration of the present wafer manufacturing unit consists of a chain of a parametric number of robots, where each robot serves two production stations, and two buffers. The last manipulator serves another parametric number of production stations. The model covers the models in [
8,
9] as special cases. This general model is the first contribution of the paper. The desired specification is expressed in the form of five rules. The specifications are translated and decomposed to appropriate sets of local regular languages, one per robotic manipulator. A set of parametric supervisors in the form of finite deterministic automata and in the RW framework is developed. Furthermore, a distributed supervisory control architecture is developed. For distributed supervisory control and its properties, see [
15]. The architecture consists of appropriate control units, one per robotic manipulator, monitoring appropriate event signals of the adjacent control units. The development of the present distributed supervisory control, with parametric supervisors, is the second contribution of the paper. The desired performance of the controlled total manufacturing system, the realizability of the control structure (for the notion of realizability see [
17]), and the nonblocking property (see [
15]) of the proposed architecture are guaranteed. Finally, implementation issues are tackled, and the complexity of the distributed architecture is determined in a parametric formula. The final contribution of the paper is the development of a clear and sufficient method to face possible extensions of the number of production stations and robotic manipulators in the wafer industry. The motivations of the present research were (a) the introduction of a generic modelling for wafer manufacturing in the semiconductor industry, and (b) the cover of the current industrial trends by the extension of the number of the production stations and the number of the serving robotic manipulators. An additional significant motivation was to provide a generic distributed supervisory control architecture, with respect to the system’s devices, that will be able to adopt a system’s specifications to any possible extensions of the system.
This study is structured as follows: In
Section 2, the DES models of the components of the parametric wafer manufacturing system are presented. In
Section 3, the desired behavior of the manufacturing process is expressed in the form of a set of desired regular languages. In
Section 4, the distributed supervisory control architecture is analyzed. In
Section 5, the supervisor automata realizing the desired regular languages are presented. In
Section 6, the required system properties of the controlled automaton of the wafer manufacturing system are investigated. In
Section 7, simulation results of the controlled automaton regarding a practical sequence of operating commands are presented. In
Section 8, the total complexity of the proposed distributed supervisory scheme is calculated. Finally, in
Section 9, implementation aspects of the proposed scheme are presented, and the implementation of the proposed supervisors in the ladder diagram (LD) framework are developed.
2. Modelling of the Manufacturing Process
2.1. Parametric Notation and Configuration of the Process
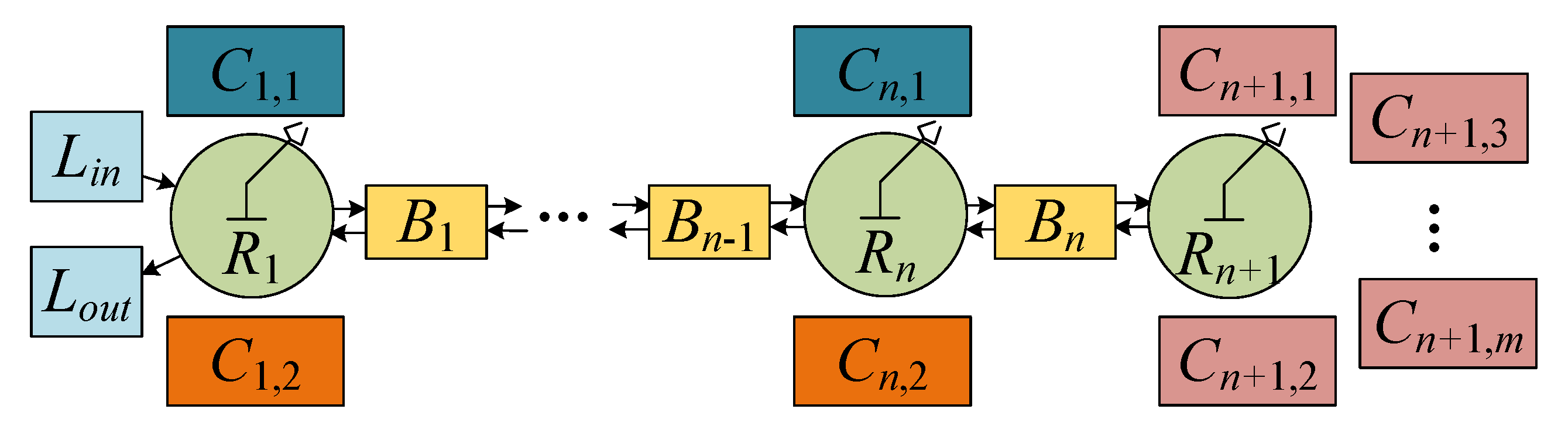
As already mentioned, the wafer manufacturing system consists of production stations, buffers, two loading docks (one for the raw product and one for the manufactured products), and a set of robotic manipulators dedicated to the product transfer between the stations and the two docks. Here, the process is considered in parametric form. The number of robotic manipulators is equal to
, where
and
comprise the set of positive integers. Each robotic manipulator is indexed by the integer
, where
The
-th robotic manipulator is denoted by
. It is important to mention that if
, then every
serves two production stations, configured as a couple in the production line, while if
, then
serves a parametric number of
production stations. The total number of production stations is equal to
. Furthermore, each production station is indexed by the integers
and
, where
According to (1b), the set
, namely the range of
, depends upon
. The index
is the index of the robot manipulator serving the
station. The index
is the index of the production station served by the
-th robot. So, each production station is denoted by
. The number of buffers is equal to
. Each buffer is indexed by the integer
, where
The symbol represents the -th buffer. The first loading dock is the input dock of the process and is represented by . The second loading dock is the output dock of the process and is represented by .
To illustrate the above integer definitions, an example is presented. Let and . Therefore it holds that , , , and . Thus, there are four robotic manipulators, denoted by , , , and , and three buffers, denoted by , , and . The number of production stations is equal to nine, and they are denoted by , , , , , , , , and .
In
Figure 1, a simplified drawing of the configuration of the components of the wafer production process is presented. The configuration of the array of the production stations as well as the array of the robotic manipulators and the array of the buffers allows appropriate transfer of products. In particular, this process enables the following:
- (i)
to transfer products from to , from and to , and from to ,
- (ii)
, where , to transfer products from and to and , and vice versa, i.e., from and to and ,
- (iii)
to transfer products from ,…, to and vice versa.
In the following subsections, the physical entities , , , , and , composing the production unit, will be modelled by mathematical entities in DES forms. In particular, the DES model of is denoted by , the DES model of is denoted by , the DES model of is denoted by , the DES model of is denoted by , and the DES model of is denoted by .
2.2. The Models of the Production Stations
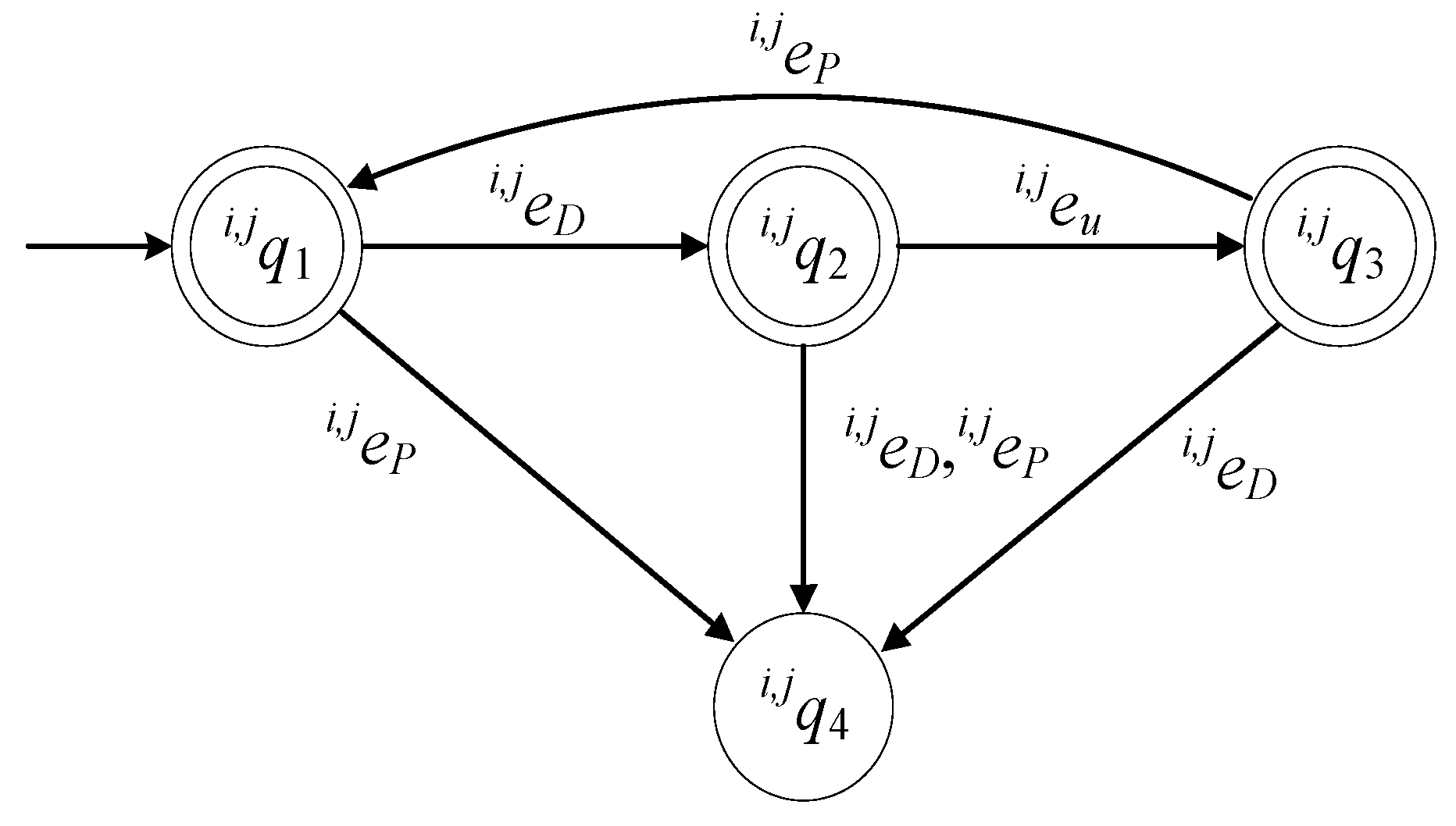
The model of the production station
is described by the 6-tuple
For the description of finite deterministic automata in the form of a 6-tuple, see [
17,
18,
19,
20,
21]. The set of the states of the automaton is
The state describes the case where there is no product at and the station is in idle mode (standby). The state describes the case where there is a product at the station, dropped by . The state describes the case where the processing of the product at the station has been completed and the processed product has not yet been picked up by . The state describes two malfunction cases. The first is the case where tried to pick a product when there was no processed product at the station. The second is the case where dropped a product to the station when there was a product at the station. Clearly, describes a functional faulty situation. The initial state is . The set of the marked states of the automaton is .
The alphabet of the automaton is
The event is the command to to pick a product from the station. The event is the command to to drop a product at the station. The event takes place when the processing of the product has been completed. The set of the controllable events of the automaton is . Hence, the set of the uncontrollable events is .
The values of the transition function of the automaton are:
The active event sets of the automaton are:
The closed behavior of the automaton is
and the marked behavior of the automaton is
where the symbol “
” denotes the Kleene star of a language. Regarding the Kleene star, see [
7,
16]. Regarding the definition and properties
and
, namely the closed and the marked behavior of the argument automaton, see [
7]. The automaton
in (2) is a blocking automaton, as
.
In
Figure 2, the state diagram of
is presented. The state diagram of
is the same as the state diagram of the model of the production station proposed in [
4].
2.3. The Models of the Buffers
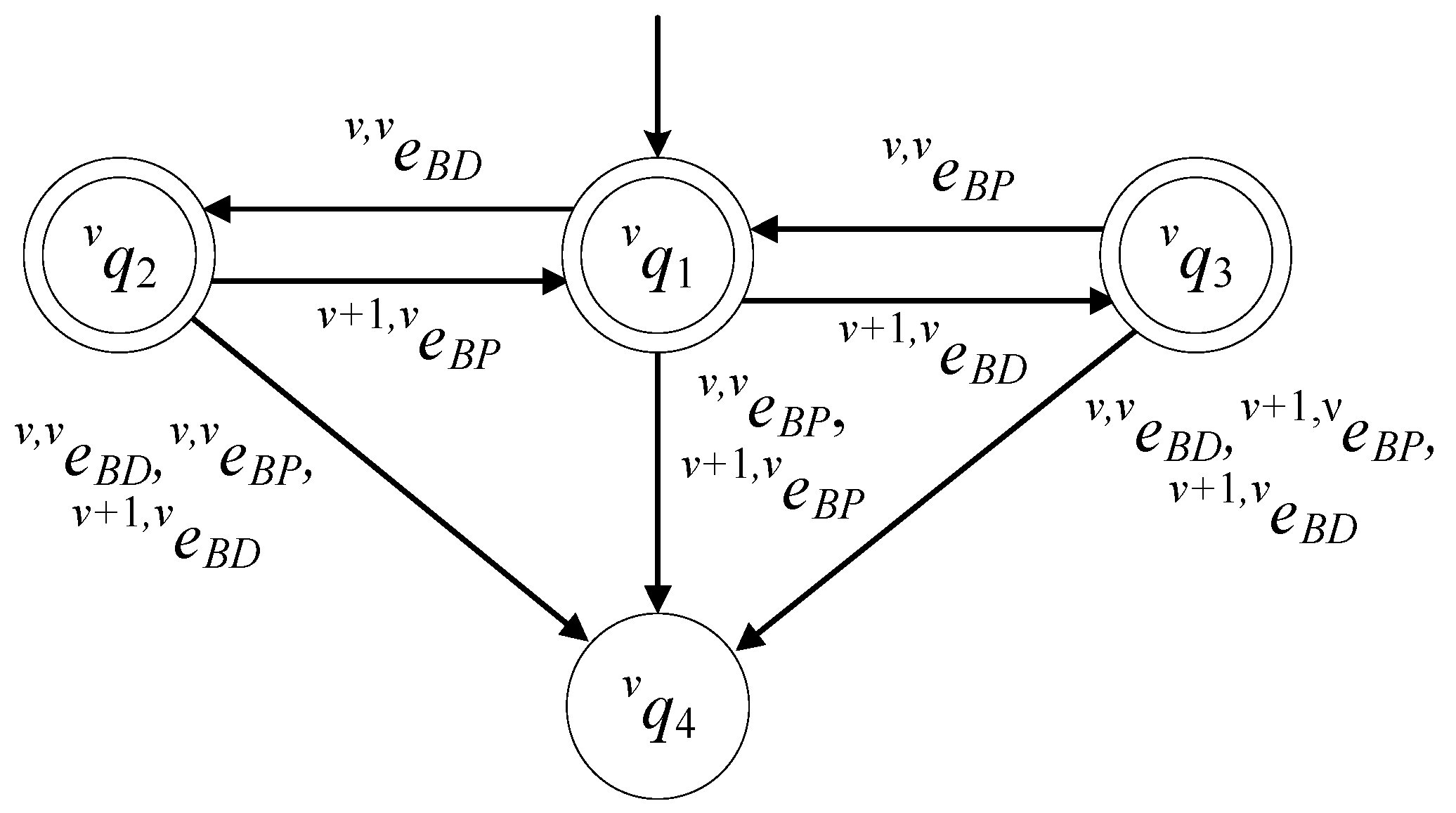
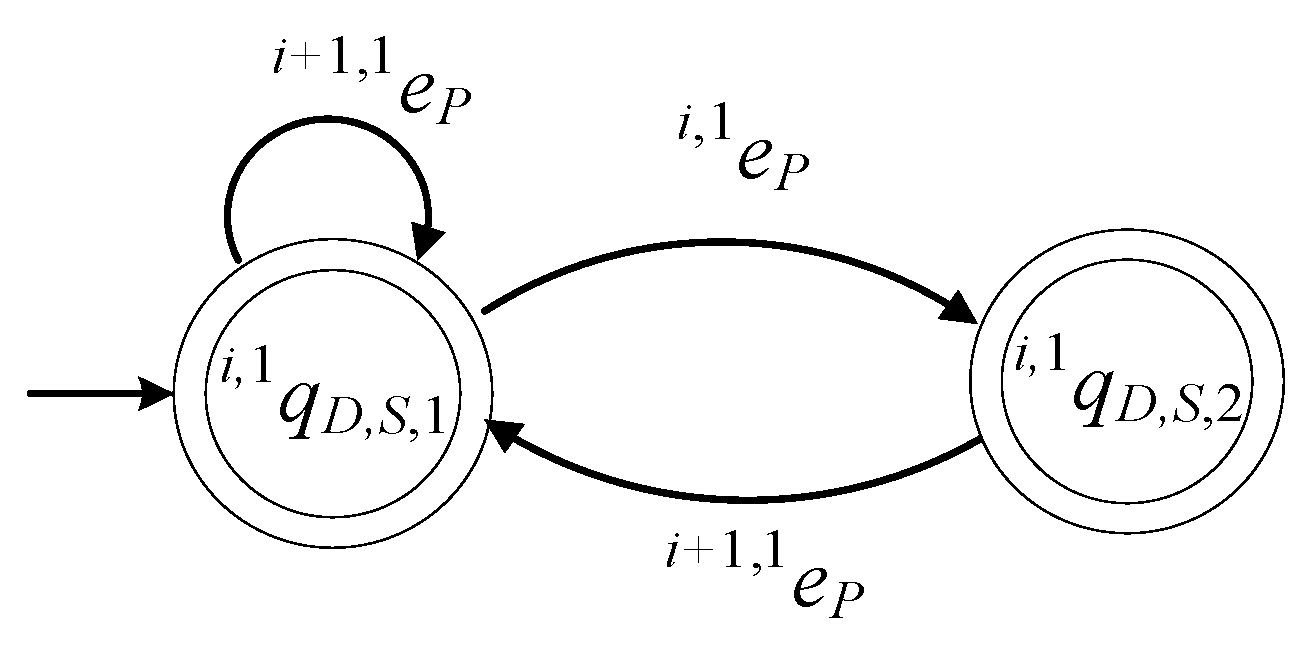
The model of
is described by the 6-tuple
The set of the states of the automaton is
The state describes the case where the buffer is empty. The state describes the case where there is a product at the buffer, dropped by . The state describes the case where there is a product at the buffer, dropped by . The state describes two faulty cases. The first is the case where (or ) tried to pick a product when the buffer was empty. The second is the case where (or ) dropped a product when the buffer was full. The initial state of the automaton is . The set of the marked states of the automaton is .
The alphabet of the automaton is
The event is the command to to pick a product from . The event is the command to to drop a product to . The event is the command to to pick a product from . The event is the command to to drop a product to . The set of the controllable events of the automaton is . Hence, the set of the uncontrollable events is .
The values of the transition functions of the automaton are:
The active event sets of the automaton are
The closed behavior of the automaton is
and the marked behavior of the automaton is
The automaton in (7) is a blocking automaton, as .
In
Figure 3, the state diagram of
is presented. The state diagram of
is the same as the model of the buffer proposed in [
4].
2.4. The Models of the Loading Docks
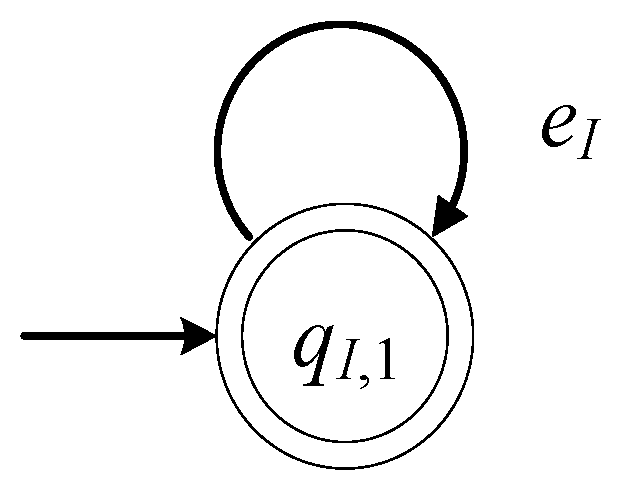
The model of
(input loading dock) is described by the 6-tuple
The set of the states of the automaton is . The state is the only state of the automaton. The initial state of the automaton is . The set of the marked states is .
The alphabet of the automaton is . The event is the command to to pick a product from . The set of the controllable events is . Hence, the set of the uncontrollable events is . The transition function is . The active event set is .
The closed behavior of the automaton is equal to the marked behavior of the automaton, i.e.,
. Thus,
in (12) is a nonblocking automaton. In
Figure 4, the state diagram of
is presented.
The model of
(output loading dock) is described by the 6-tuple
The set of the states of the automaton is . The state is the only state of the automaton. The initial state of the automaton is . The set of the marked states of the automaton is .
The alphabet of the automaton is . The event is the command to to drop a product to . The set of the controllable events is . Hence, the set of the uncontrollable events is . The transition function of the automaton is . The active events set is .
The closed behavior of the automaton is equal to the marked behavior of the automaton, i.e.,
. Thus,
in (13) is a nonblocking automaton. In
Figure 5, the state diagram of
is presented.
The state diagrams of each of the two loading docks, in
Figure 4 and
Figure 5, are the same with the respective models in [
4].
2.5. The Models of the Robotic Manipulators
The model of
is described by the 6-tuple
The set of the states of the automaton is . The state describes the case where the gripper of is empty. The state describes the case where a product is gripped by . The initial state of the automaton is . The set of the marked states is .
The alphabet of the automaton is
The events of the above alphabet have been defined in the previous subsections. It is important to mention that all events of in (15) are controllable.
The values of the transition function of the automaton are
The active event sets of the automaton are
The closed behavior of the automaton is
and the marked behavior of the automaton is
Thus, in (14) is a nonblocking automaton.
In
Figure 6, the state diagram of
is presented.
The model of
where
is described by the 6-tuple
The set of the states of the automaton is
The state describes the case where the gripper of is empty. The state describes the case where a product is gripped by . The initial state of the automaton is . The set of the marked states of the automaton is .
The alphabet of the automaton is
The events of the above alphabet have been defined in the previous subsections. It is important to mention that all events of in (20) are controllable.
The values of the transition function of the automaton are
The active event sets of the automaton are
The closed behavior of the automaton is
and the marked behavior of the automaton is
Hence, in (18) is a nonblocking automaton.
In
Figure 7, the state diagram of
is presented.
The model of
is described by the 6-tuple
The set of the states is . The state describes the case where the gripper of is empty. The state describes the case where a product is gripped by . The initial state of the automaton is . The set of the marked states of the automaton is .
The alphabet of the automaton is
The events of the above alphabet have been defined in the previous subsections. It is important to mention that all events of in (24) are controllable.
The values of the transition function of the automaton are
The active event sets of the automaton are
The closed behavior of the automaton is
and the marked behavior of the automaton is
Hence, in (23) is a nonblocking automaton.
In
Figure 8, the state diagram of
is presented.
For the case where
and
, the models of the robotic manipulators, presented in this subsection, are reduced to those presented by respective state diagrams in [
4].
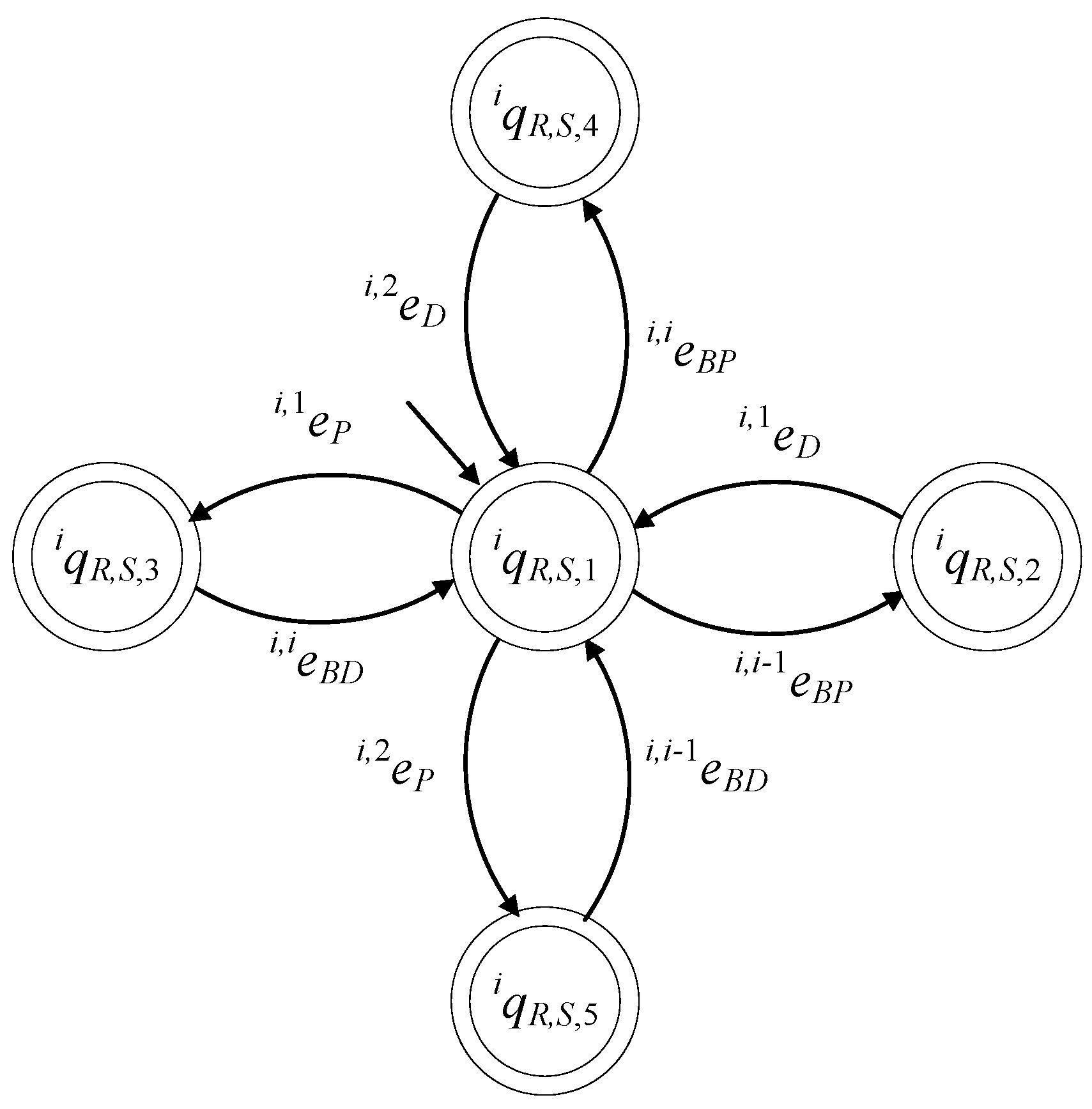
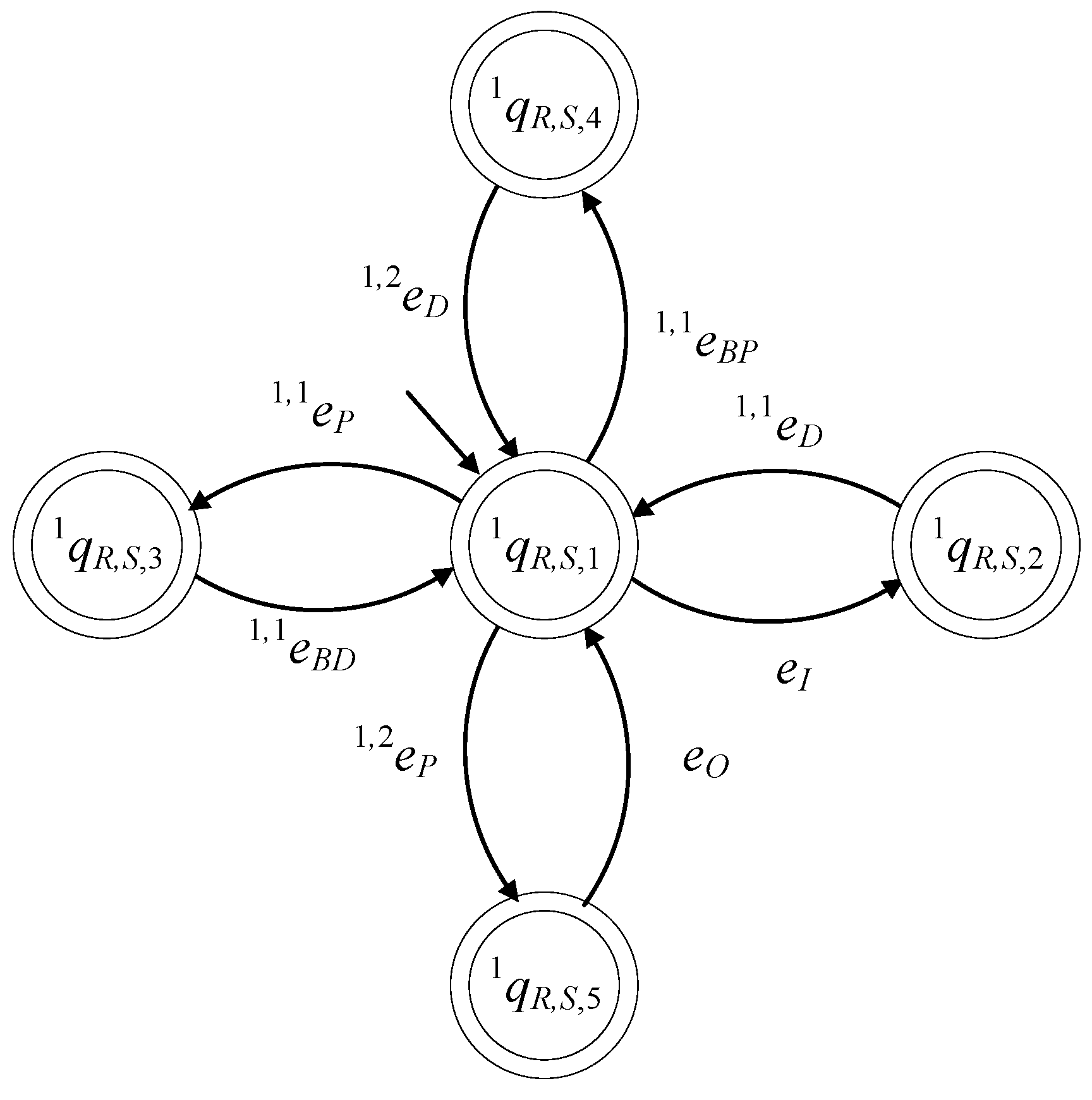
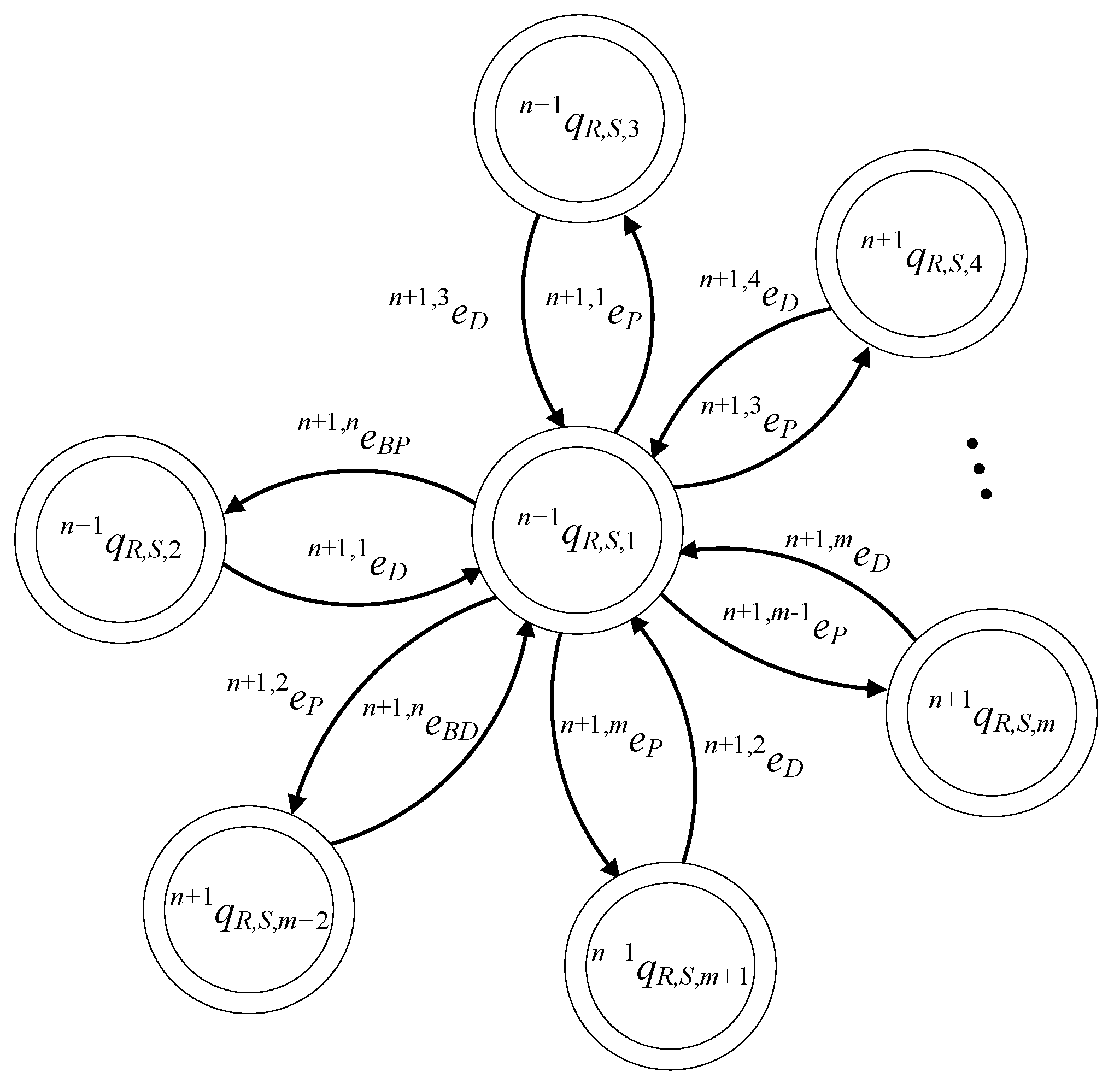
4. Distributed Supervisory Control Architecture
The control of the wafer manufacturing process will be implemented by local control units, e.g., programmable logic controllers (PLCs), remote terminal units (RTUs), and microcontrollers. Each local control unit is denoted as
, where
. Each
is dedicated to controlling the allowability of the influence of a particular set of controllable events. This event set is disjoint to the respective set of any other local control unit. This way, inspired by the respective decentralized architecture proposed in [
7] for
and
, a distributed control configuration is proposed. Details regarding distributed supervisory control can be found in [
15]. In
Section 5, the design specifications, defined by the regular languages presented in
Section 3.2, will be realized through appropriate supervisor automata implemented to the local control units
, where
.
Particularly, the supervisor automata implemented in , where , are the supervisors , , , , ,, and . The supervisors realize the languages , , , , , , and , respectively. Note that the languages and do not correspond to any rule of desired behavior and are introduced exclusively for uniformity reasons to be and .
The input signals of , where , are:
- (i)
The events of ;
- (ii)
the single uncontrollable event of , namely the event , where ;
- (iii)
The events , , , and , of ;
- (iv)
the events , , , and of , where .
Particularly, the supervisor automata implemented in are the supervisors ,…, , , , , , and . The supervisors realize the languages ,…,, , , , , and , respectively. Note that the languages and do not correspond to any rule of desired behavior and are introduced exclusively for uniformity reasons to be and .
The input signals of are:
- (i)
The events of ;
- (ii)
The uncontrollable events of , namely the events , where ;
- (iii)
The events , , , and of .
Clearly, the events of the categories (iii) and (iv) of
, where
, and the events of the category (iii) of
cannot be restricted by the control unit and serve only as monitoring events. The events
, where
and
, being uncontrollable events of the production stations, cannot be restricted by the control unit
. Furthermore, the events
,
,
,
, and the events
,
,
, and
, where
, are used by
exclusively for monitoring purposes and are not allowed to be restricted by the control unit
. Based on this interconnection, the alphabet of
will be augmented as compared to the alphabet of the automaton
. The augmented alphabet is the following:
where
, and
It is important to mention that the set of the events that can be restricted by
(controllable event set), where
, is
. Regarding these event sets, it holds that
Also, regarding the adjacent control units, it holds that
Before presenting the design requirements of the present supervisory control scheme, the alphabets of the desired languages will be presented. The alphabets of and are and , respectively. The alphabets of and are and , where , respectively. The alphabet of is , the alphabet of is , the alphabet of is , where , and the alphabet of is . The alphabet of is , where . The alphabet of is . The alphabet of is , where . The alphabet of is . The alphabet of is , where . The alphabet of is , where . The alphabet of is . Finally, the alphabet of is , where . The alphabet of is .
The design requirements of the supervisors of
, where
, are expressed in terms of a respective controlled automaton, denoted by
, being of the following structure:
where
denotes the synchronous product [
15] (or the parallel connection [
16]) of two automata, and where
. Clearly, for every automaton
it holds that
. It is important to mention that the final equality in (36) results from the structure of the automata of the loading docks, having only one state and being marked, and a self-transition activated by all events of the automaton’s alphabet. The closed and the marked behavior of the synchronous product in (36), where
, are in the following form:
where
is the projection of
to
;
and
are the projections of
to
and
, respectively;
and
are the projections of
to
and
, respectively;
and
are the projections of
to
and
, respectively;
is the projection of
to
; and
is the projection of
to
.
For
, the controlled automaton is required to be of the following structure:
Clearly, the closed and the marked behavior of the synchronous product in (38) are in the following form:
where
is the projection of
to
;
and
are the projections of
to
and
(
), respectively;
and
are the projections of
to
and
, respectively; and
is the projection of
to
.
In accordance with [
7,
16], the present supervisors are designed in a way that all supervisors’ states are marked. Thus, the closed and the marked behaviors of the supervisors for
and
are required to be
According to Equation (40a–f), the closed and marked behaviors of the respective supervisors are designed to be equal to the prefix closure of the desired languages. Furthermore, regarding Equation (40a–e), it is observed that since the languages
,
,
,
, and
are prefix-closed, then the equality between the closed and marked behaviors of the respective supervisors is derived. Here, it is important to recall that, according to Proposition 1, the language
is
-closed. For the definition and properties of prefixed-closed languages, see [
15,
16].
In addition to the above design requirements, the marked behavior of the controlled automaton
, for
, is required to be
For
, the marked behavior of the controlled automaton
is required to be
In addition, for all
, the marked behaviors of the controlled automata are required to satisfy the nonblocking requirement, i.e.,
Finally, it is required for the supervisors embedded in
, where
and
, to be physical realizable (PR) (see [
17]) with respect to the automata
,
,
, and
through the synchronous products in (36) and (38).
The satisfaction of the design requirements (36), (38) and (40)–(43) will be accomplished through the distributed control architecture proposed here, providing separate development and implementation of the control algorithm of each control unit
. Furthermore, the control algorithm of each
is analyzed for the conjunction of several supervisors providing modularity at the local control layer. The distributed- control architecture, designed for the present wafer system and being in accordance with the definition of distributed architectures presented in [
7], is analyzed for a set of local controllers, i.e., one controller per robotic manipulator and the respective served production stations. Each local controller is fed by the events of the respective controlling subsystem and a set of distinct events coming from the adjacent subsystems through a “transfer line” (shared resources). It is mentioned that in [
3,
4], a distributed control architecture is proposed for the case where
and
. To the best to our knowledge the presents control architecture is the first distributed control architecture for the general parametric model of wafer manufacturing systems.
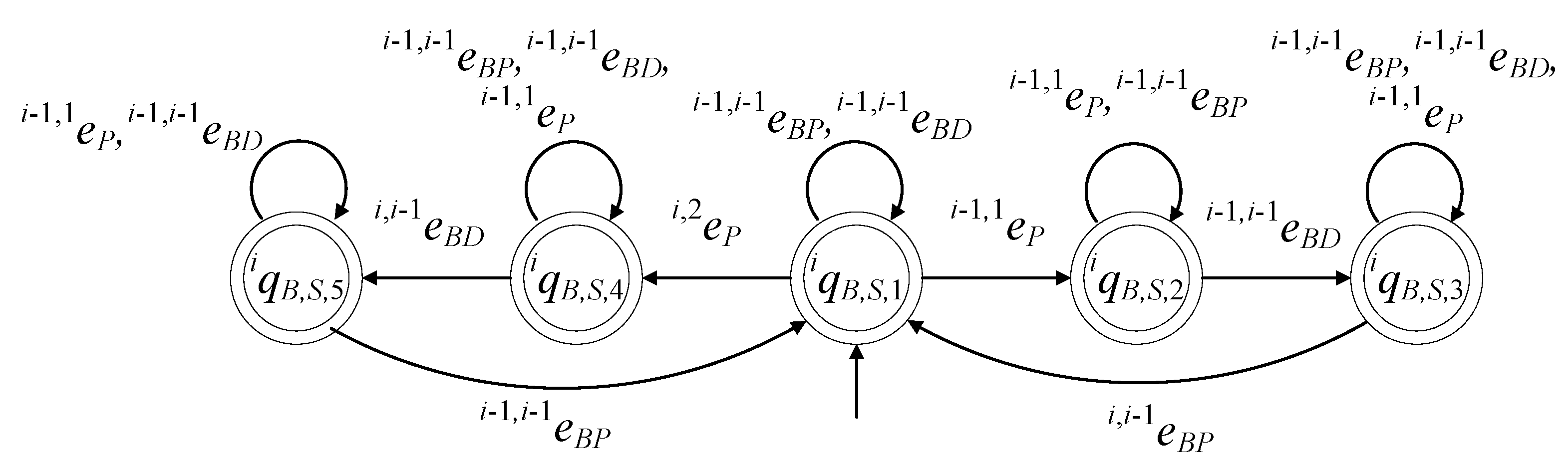
In
Figure 10, a simplified drawing of the configuration of the distributed control architecture is presented. Ιn each control unit, the respective supervisors to be implemented and the respective participating alphabets are depicted. Clearly, each of the supervisors
,
,
, and
, introduced for uniformity purposes, can be realized by an automaton with one state being marked and self-transitions for all the events of the corresponding alphabets. Nevertheless, the implementation of these supervisors is not necessary as they do not impose any additional desired performance. However, in the analysis in
Section 6, they will be used for uniformity reasons.
As already mentioned, in the special case where
and
, the resulting model of the system is similar to the one in [
7]. In
Section 3, differences and similarities of the proposed desired behavior, in comparison to the one in [
7], have been presented. The main difference is imposed by the combination of the second, fourth, and fifth specifications, regarding blocking avoidance. In the present paper, a more restrictive rule is proposed. Particularly, if a buffer or a manufacturing station (in any flow direction) is full, then the respective robotic manipulator is not allowed to pick a product from the respective station.
The present method can be effective in cases of station faults, i.e., if a fault takes place in a station, then the robotic manipulator is not allowed to pick or place products in this station. This way, the respective buffers are kept available to receive products from the reverse product flow.
The realization of the supervisors, depicted in
Figure 10 and satisfying the design requirements (40a–f), will be determined in
Section 5. In
Section 6, the design requirements (40)–(43) and the physical realizability of the distributed supervisor design scheme will be proven to be satisfied.
6. Establishment of the Satisfactory Performance of the Controlled Automaton
In the present section, two lemmas, five theorems and two remarks regarding the implementability of the control architecture proposed in
Section 4 will be established using the supervisor realizations derived in
Section 5. In particular, the controllability of the desired languages will be proven through the proof of the physical realizability (see [
17]) of the derived supervisors. Furthermore, the nonblocking property of the resulting controlled automaton will be proven. Finally, using these theorems and remarks, the satisfactory performance of the controlled automaton will be guaranteed. The satisfactory transition sequence of the controlled automaton will be determined in terms of the closed and the marked behavior of the controlled automaton. According to the distributed control architecture, proposed in
Section 4, the supervisors embedded in
, where
, are designed in order to satisfy the physical realizability of the supervisors with respect to the wafer manufacturing process, the nonblocking property of the resulting controlled automaton, and the satisfactory closed and marked behaviors of the controlled automaton.
Regarding the physical realizability, the investigation is limited to the physical realizability of the supervisors of with respect to the robotic manipulator , the production station , where , and the buffer , where , through the synchronous products in (36) and (38). The physical realizability of the supervisors of with respect to the loading docks is not investigated as all events in their alphabets are controllable.
Regarding nonblocking, the investigation will start with the nonblocking property of the automata in the synchronous products (36) and (38). Then the nonblocking property of the overall system will be investigated. Regarding the loading docks, it is observed that they cannot cause blocking to the controlled automaton, as they have only one state, being marked, and a single event self-transition.
As already mentioned, in the present section, two lemmas and five theorems will be presented. In the two lemmas, the exclusion of non-marked states in appropriate synchronous products, due to non-accessibility, will be proven. Regarding non-accessible states, see [
16]. In the first four theorems of the present section, the issues of physical realizability and nonblocking will be investigated with respect to the influence of the supervisors of
to the devices controlled by the respective control unit. Finally, in the fifth theorem, the nonblocking property of the overall controlled wafer manufacturing system is investigated through the synchronous product of the participating controlled automata.
In the first theorem, the physical realizability of the supervisors, embedded to , where , with respect to the automata of the production stations, the robot, and the buffer affected by the events of the control unit , through the synchronous product (36) will be proven. All automata affected by the control unit are composed as the synchronous product . In the second theorem, the physical realizability of the supervisors, embedded to , with respect to the automaton , through the synchronous product (38) will be proven. Furthermore, the first of the two remarks of the section will cover the physical realizability of the supervisors, embedded to .
Theorem 1. The synchronous product in (36), where , is physical realizable (PR), with respect to .
Proof of Theorem 1. Regarding the supervisors embedded in the control unit
, the several events of the automaton
are not allowed to be restricted by the supervisors. These events, being uncontrollable by
, are the uncontrollable events of the two production stations, i.e., the events
and
, and the monitoring events of the adjacent control units, i.e., the events
,
,
,
,
,
,
, and
. Here, it will be investigated if each supervisor of
is able to restrict these 10 events. To this end, first it is observed that all events in the alphabet of
are controllable. Thus,
does not restrict any of the 10 events. Second, it is observed that the uncontrollable events in the alphabet of
, being the events
,
, and
, satisfy the following properties:
The above relations reveal that the three uncontrollable events of
belong to the active even sets of all states of
. Thus,
does not restrict any of the 10 events. Third, it is observed that the uncontrollable events in the alphabet of
, being the events
,
, and
, satisfy the following properties
The above relations reveal that the three uncontrollable events of belong to the active even sets of all states of . Thus, does not restrict any of the 10 events.
Fourth, it is observed that there is only one uncontrollable event in the alphabet of
, being the event
, where
. The above relation reveals that the uncontrollable event of
belongs to the active even sets of all states of
. Thus,
does not restrict any of the 10 events. Fifth, it is observed that there is only one uncontrollable event in the alphabet of
, being the event
where
. The above relation reveals that the uncontrollable event of
belongs to the active even sets of all states of
. Thus,
does not restrict any of the 10 events. Sixth, it is observed that there is only one uncontrollable event in the alphabet of
, where
, being the event
where
. The above relation reveals that the uncontrollable event of
belongs to the active even sets of all states of
. Thus,
does not restrict any of the 10 events. Hence, according to Corollary 1 in [
17], all supervisors are PR with respect to
, through (36). □
Remark 1. The proof of the physical realizability for is similar to the one of , for , if the events of the loading docks are considered, i.e., if the events and are used instead of the events and in the proof of Theorem 1.
Theorem 2. The synchronous product in (38) is physically realizable (PR) with respect to .
Proof of Theorem 2. The uncontrollable events of the automaton
are the
uncontrollable events of the last
production stations, i.e., the events
where
and the monitoring events of the adjacent control units considered as uncontrollable events. The monitoring events are the events
,
,
, and
. Here, it will be investigated if each supervisor of
is able to restrict these
events. To this end, first, it is observed that all event of
are controllable. Thus,
does not restrict any of the
events. Second, it is observed that the uncontrollable events in the alphabet of
, being the events
,
and
, satisfy the following properties:
The above relations reveal that the three uncontrollable events of
belong to the active even sets of all states of
. Thus,
does not restrict any of the
events. Third, it is observed that there is only one uncontrollable event in the alphabet of
, being the event
where
. The above relation reveals that the uncontrollable event of
belongs to the active even sets of all states of
. Thus,
does not restrict any of the
events. Fourth, it is observed that there is only one uncontrollable event in the alphabet of
, being the event
where
. The above relation reveals that the uncontrollable event of
belongs to the active even sets of all states of
. Thus,
does not restrict any of the
events. Hence, according to Corollary 1 in [
17], all supervisors in (38) are PR with respect to
, through (38). Since the uncontrollable alphabets of all supervisors are disjoint sets, the conjunction of all supervisors is PR with respect to
, through (38). □
In the following two lemmas, a subautomaton of the synchronous product of the automaton of the production station and one of the proposed supervisors, as well as a subautomaton of the synchronous product of the automaton of the buffer and two of the proposed supervisors, are presented. All states of these two subautomata will be proven to be marked. Regarding subautomata, see [
15,
16].
Lemma 1. All states of the automaton , for and , are marked states.
Proof of Lemma 1. For the automaton
it holds that
where
is the transition function and
is the set of the active events of the automaton
. From the above it is observed that any pair of states, where the first element is
and the second is a state of
, is not a state of
, in the sense that this pair is non-accessible. The rest states of
, i.e., the states
,
, and
, are all marked. Furthermore, the states of
are all marked. Thus, the proof has been completed. □
Corollary 1. The automaton is a nonblocking automaton.
Before presenting the following lemma, it is important to mention that the alphabets of the buffers contain events of the adjacent control units, controlling the buffer. Thus, the controlled automaton of the buffer is a result of the joint action of the adjacent control units.
Lemma 2. All accessible states of the automaton , under the influence of the supervisors and , for , are marked states.
Proof of Lemma 2. First, the properties of the automaton
will be examined. Regarding
, it is observed that the arrival to the non-marked state
, having no transitions, can be accomplished only by transitions from
,
, and
. Regarding
, the respective transitions in
are
where
is the transition function of the automaton
. Regarding
, the respective transition in
is
. Regarding
, the respective transitions in
are
and
. At first, it is observed that
is a blocking automaton, where all events provoking a transition to the non-marked state
are events of
. Next, the properties of
will be examined. It is observed that the transitions to the non-marked state
, from the state
, are
where
is the transition function of the automaton
. The respective transitions from
are
The transition from is . Thus, the automaton is a blocking automaton, where all events provoking a transition to the non-marked state are events of . From the above it is concluded that the joint action of the control units and to restricts all transitions to . Since, is the only non-marked state of , it is concluded that , under the influence of the supervisors and , namely the resulting controlled automaton, has all its accessible states marked. Clearly, the controlled automaton is a nonblocking automaton. □
From Lemma 2 it is concluded that the non-marked state of the automaton of the buffer
is non-accessible, under the influence of the control actions imposed by
and
. Define the automaton
, being a subautomaton of
and derived by removing the single non-marked state
and the corresponding transitions of
. Clearly, the set of the states of
is the set
. Using the present definition, the following synchronous products, being subautomata of the controlled automata in (36) and (38), are derived
In the following two theorems, the property of nonblocking of
, where
, and the nonblocking property of
will be proven. Following [
15] (Section 4.9, p. 190), the proof will be accomplished by investigating if the controlled automaton always has an active transition from any non-marked state to a marked state. Finally, a remark, being the second remark of the present section, will cover the nonblocking property of
.
Theorem 3. The synchronous product in (49a), namely the controlled automaton , where , is a nonblocking automaton.
Remark 2. The proof of the nonblocking property of follows the one of Theorem 3, if the events of the loading docks are considered, i.e., if the events and are used instead of the events and in the proof of Theorem 3.
Theorem 4. The synchronous product in (49b), namely the controlled automaton , is a nonblocking automaton.
In the following theorem, the nonblocking property of the overall manufacturing system will be proven.
Theorem 5. The automaton is a nonblocking automaton.
Proof of Theorem 5. Consider the automata
and
, where
. Using Lemma 1, the synchronous product
of the two automata is expressed as follows:
where
denotes the cardinality of the argument set. Using the supervisors
and
twice in the above formula, it is observed that the closed and the marked language of
are equal to the closed and the marked language of the automaton:
Using the remarks before relation (49a,b), it is observed that the closed and the marked behavior of the above automaton are equal to the closed and the marked behavior of the following automaton:
Using (49a,b), it is observed that the closed and the marked behavior of are equal to the closed and the marked behavior of the subautomaton . In Theorems 3 and 4, the nonblocking property of , where , has been proved. Furthermore, in Theorems 1 and 2 it has been shown that all the events from the adjacent control units are considered as uncontrollable events, and they are not restricted by the respective supervisors. Thus, the supervisors of the control unit do not restrict the events of , being common with or . Furthermore, does not have any common event with the rest automata. Thus, the nonblocking property of is not affected by the rest-controlled automata in the synchronous product . Hence, is a nonblocking automaton, and consequently is also a nonblocking automaton. □
In Theorems 1 and 2 and in Remark 1, the physical realizability of the supervisors implemented in with respect to the respective manufacturing devices related to , namely the devices , and where , through the respective synchronous products, has been proved. The events of the adjacent control units have been considered as uncontrollable events and they cannot be restricted by . The latter implies that the events of used in have not been restricted and vice versa. Thus, the PR property of the synchronous product is derived.
From relations (40) and (49), as well as the five theorems and the remarks, presented above, it is concluded that the system performance of the controlled automaton
is satisfactory for every
. Recall that the languages
are prefix-closed languages and
,
, and
, as well as that the languages
are
-closed (see Proposition 1) and
, for every
. Τhe satisfactory performance of the closed and the marked behaviors of the controlled automata, i.e., the satisfactory performance of the languages
and
, for every
, is validated by the following relations:
where for the derivation of the above relations, the relations
and
have been used.
7. Simulation Results
To illustrate the performance of the closed and marked behaviors of the controlled automata of the proposed control scheme, simulation results for the controlled automata of the overall wafer manufacturing system will be presented. Consider the case of the wafer manufacturing process where
and
. In addition, consider the case where the following concatenation of events took place:
The above event concatenation corresponds to a sequence of operation commands appropriately enriched with sensor signals. To interpret the above word, appropriate prefixes of the word will be analyzed. First, consider the prefix . This prefix is analyzed as follows: is commanded to pick a product from the loading dock; is commanded to drop the product to ; then, is commanded to pick the product from . The latter command would lead to malfunction, but the supervisor has disactivated this command. Thus, the supervisor allows the station to manufacture the dropped product and the sensor signal, indicating that finished the manufacturing of the product, to take place. Thus, the prefix has been interpreted. Continuing, the prefix is analyzed as follows: After the sensor signal, indicating that finished the manufacturing of the product, is commanded to pick the product from . After, is commanded to drop the product again to . However, the latter command is disabled by the supervisors and . So, the next command, namely the command to drop the product to , is executed. Continuing with the prefix , the remaining commands of the prefix are analyzed as follows: is commanded to pick another product from the loading dock; is commanded to pick a product from ; is commanded to drop a product to ; is commanded to drop a product to . Since has already finished the manufacturing of the product, is commanded to pick the product from , but the supervisor has disactivated the command till is empty. Thus, the prefix has been interpreted. After finished the manufacturing of the product, the remaining commands of the whole word are interpreted as follows: is commanded to pick a product from , is commanded to pick a product from , is commanded to drop a product to , and is commanded to drop a product to .
In
Table 1, the influence of the previous events concatenation to the automata of the overall controlled wafer manufacturing system are presented. In the first column of
Table 1, the events that take place are presented. In the next six columns of
Table 1, the current states of the automata of the robotic systems
and
, the production stations
and
, and the buffers
and
are presented.
The colored rows in
Table 1 indicate that an event that was restricted by the supervisors took place. According to the third row, the event
has been restricted to take place by the supervisor
. According to the sixth row, the event
has been restricted to take place by the supervisors
and
. Finally, according to the 13th row, the event
has been restricted to take place by the supervisor
. The event
will not provoke a transition in the system until the event
takes place that empties the production machine
. As already mentioned in
Section 3, the supervisor
is not included in the supervisory control scheme proposed in [
7]. However, the decentralized architecture proposed in [
7] guarantees that if there are free slots (buffers and/or production machines), after
and
, then the product will eventually move on; a possible malfunction in the production machine
may cause product blocking in the buffer
.