1-D and 2-D Direction of Arrival Estimation in a Conical Conformal Array: Design and Implementation
Abstract
1. Introduction
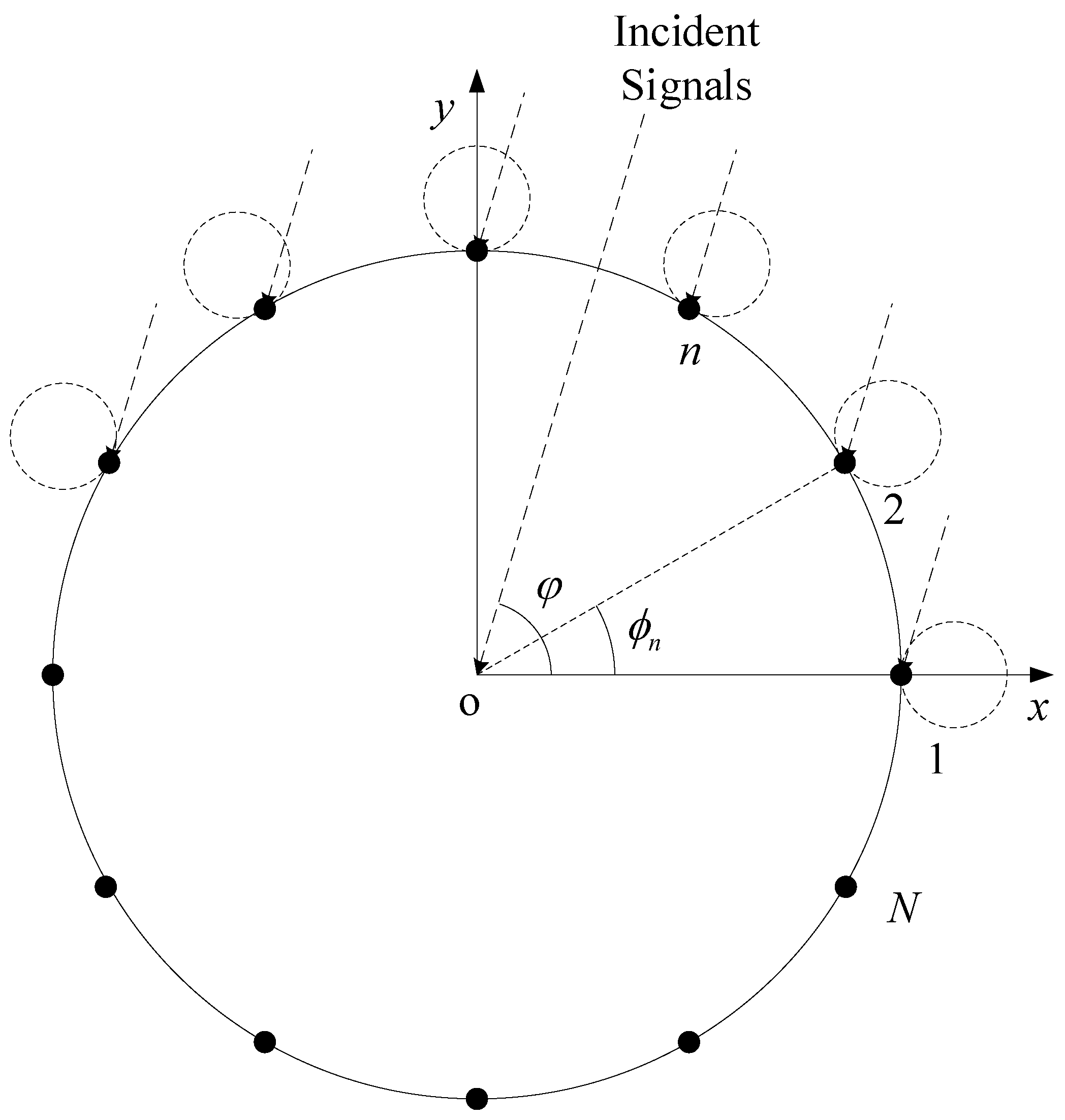
2. CCA Signal Model
3. 1-D Methods
3.1. Manifold Separation on CCA
3.2. The CCA-Coarray Method
3.2.1. The Coarray of CCA
3.2.2. MST Based ESPRIT Algorithm
| Algorithm 1: CCA-Coarray Algorithm. |
|
4. 2-D Methods
4.1. 2-D MUSIC Algorithm
4.2. CCA-PM Algorithm
4.2.1. Phase Mode Transform
4.2.2. An Improved PM Algorithm
| Algorithm 2: The CCA-PM Algorithm. |
5. Simulation Results
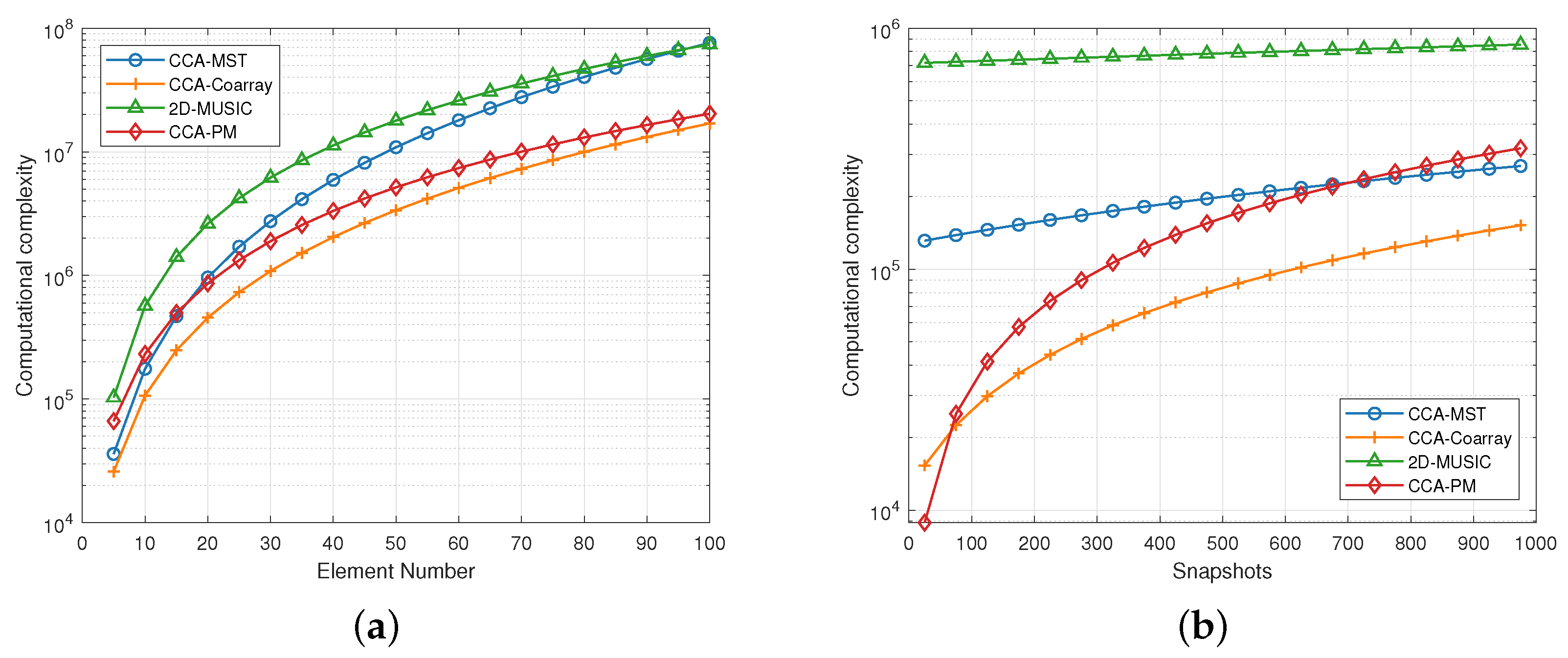
5.1. Computational Complexity
5.2. Performance Analysis on 1-D Methods
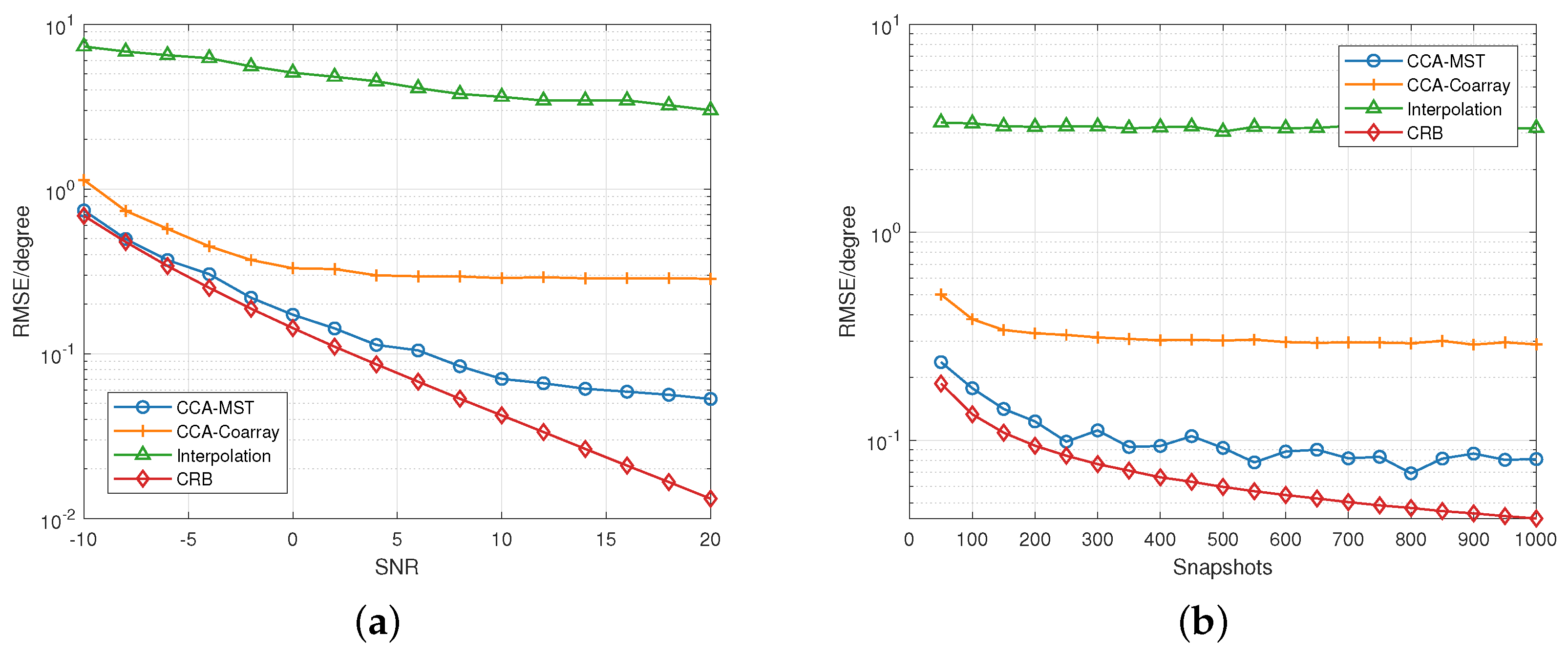
5.2.1. RMSE
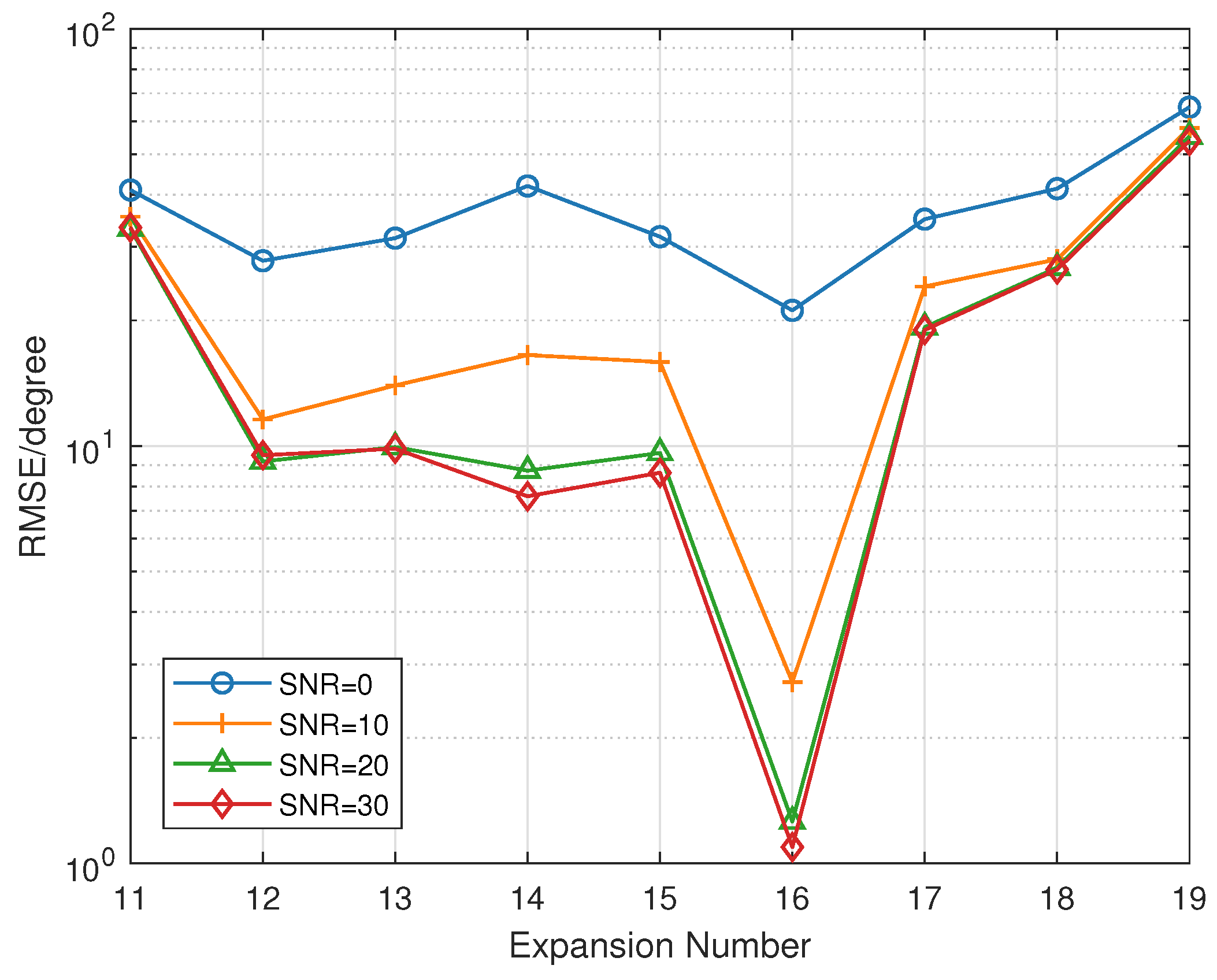
5.2.2. DOF Expansion
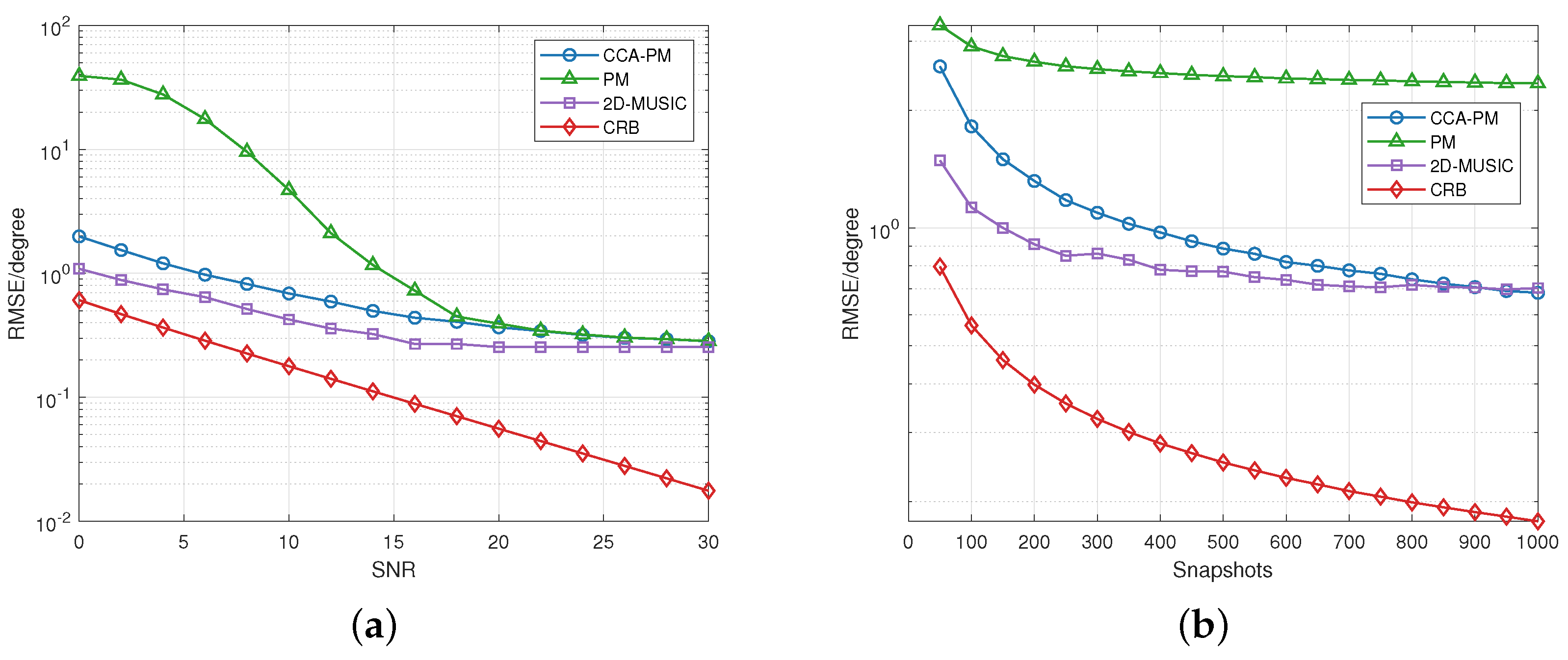
5.3. Performance Analysis on 2-D Methods
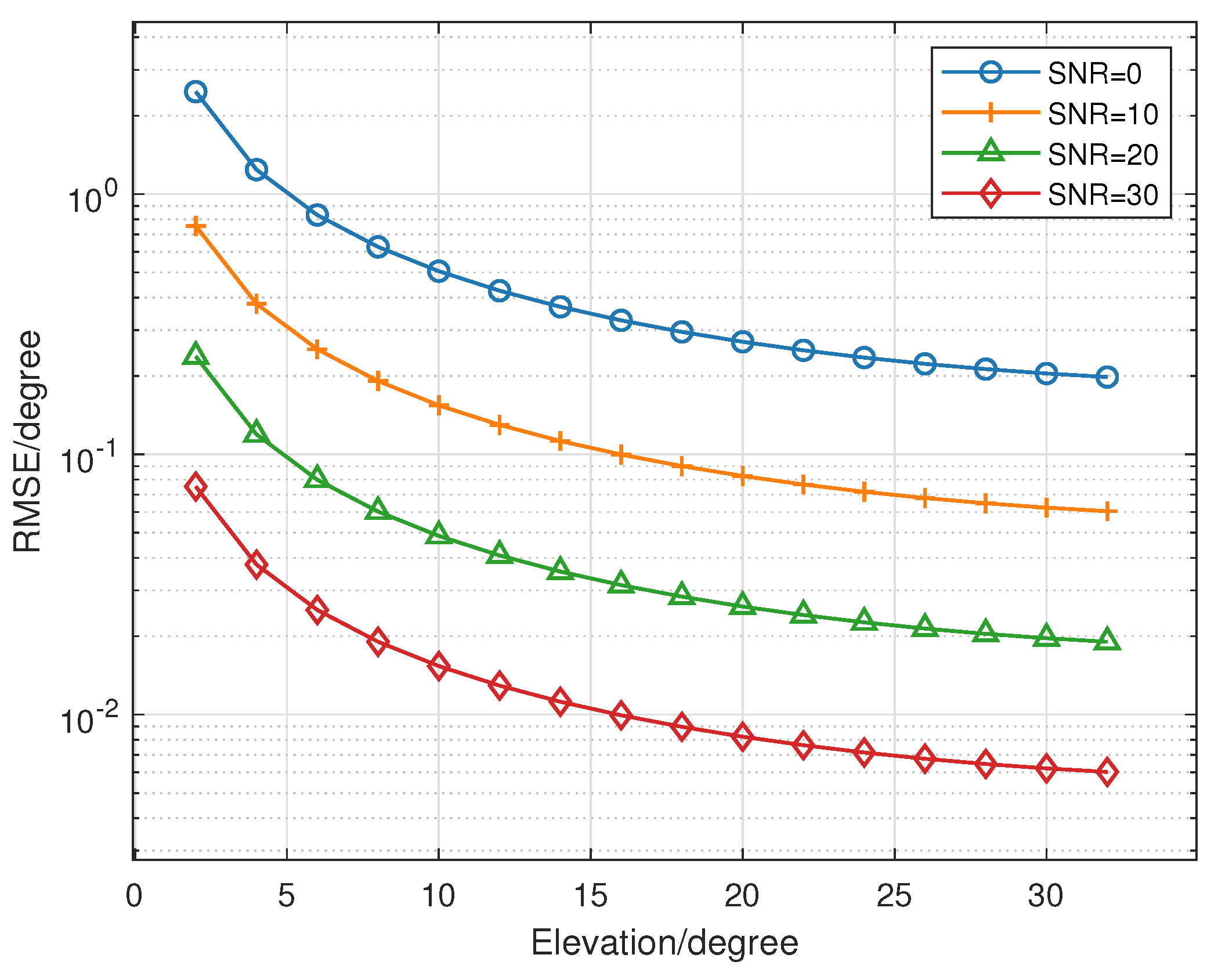
5.3.1. CRB and the Elevation Angle
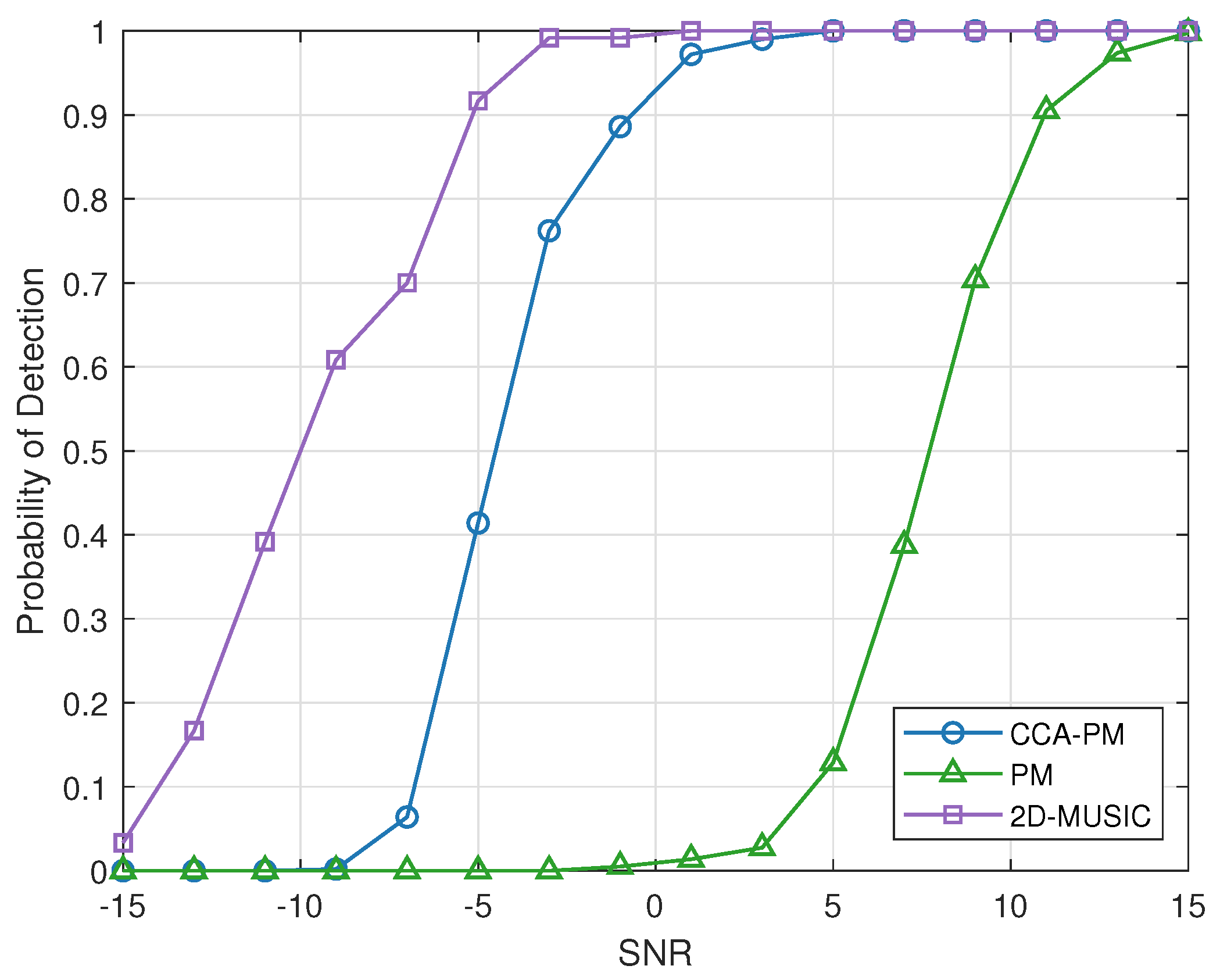
5.3.2. RMSE and Probability of Detection
6. Experimental Results
7. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
Appendix A
Appendix B
References
- Josefsson, L.; Persson, P. Conformal Array Antenna Theory and Design; John Wiley & Sons: New York, NY, USA, 2006; Volume 29. [Google Scholar]
- Yang, P.; Yang, F.; Nie, Z.P. DOA estimation with sub-array divided technique and interporlated esprit algorithm on a cylindrical conformal array antenna. Prog. Electromagn. Res. 2010, 103, 201–216. [Google Scholar] [CrossRef]
- Shahidizandi, S.; Seydnejad, S.R. Blind Beamforming for Conformal Arrays. IEEE Antennas Wirel. Propag. Lett. 2017, 16, 940–943. [Google Scholar] [CrossRef]
- Yao, Q.; Wang, T.; Liu, Y.; Liu, J. Research of Conical Conformal Array Antenna Based on Hybrid Algorithm. In Proceedings of the 2018 International Conference on Microwave and Millimeter Wave Technology (ICMMT), Chengdu, China, 6–9 May 2018; IEEE: New York, NY, USA, 2018; pp. 1–3. [Google Scholar]
- Yang, P.; Yang, F.; Nie, Z.P.; Zhou, H.J.; Li, B.; Tang, X.F. Robust Beamformer Using Manifold Separation Technique for Semispherical Conformal Array. IEEE Antennas Wirel. Propag. Lett. 2011, 10, 1035–1038. [Google Scholar] [CrossRef]
- Liao, B.; Tsui, K.M.; Chan, S.C. Frequency invariant uniform concentric circular arrays with directional elements. IEEE Trans. Aerosp. Electron. Syst. 2013, 49, 871–884. [Google Scholar] [CrossRef]
- Rogier, H.; Bonek, E. Analytical spherical-mode-based compensation of mutual coupling in uniform circular arrays for direction-of-arrival estimation. AEU—Int. J. Electron. Commun. 2006, 60, 179–189. [Google Scholar] [CrossRef]
- Goossens, R.; Rogier, H. A Hybrid UCA-RARE/Root-MUSIC Approach for 2-D Direction of Arrival Estimation in Uniform Circular Arrays in the Presence of Mutual Coupling. IEEE Trans. Antennas Propag. 2007, 55, 841–849. [Google Scholar] [CrossRef]
- Bu Hong, W.; Hui, H.T.; Mook Seng, L. Decoupled 2D Direction of Arrival Estimation Using Compact Uniform Circular Arrays in the Presence of Elevation-Dependent Mutual Coupling. IEEE Trans. Antennas Propag. 2010, 58, 747–755. [Google Scholar] [CrossRef]
- Xie, J.; He, Z.; Li, H.; Li, J. 2D DOA estimation with sparse uniform circular arrays in the presence of mutual coupling. Eurasip J. Adv. Signal Process. 2011, 2011, 127. [Google Scholar] [CrossRef]
- Rahim, T.; Davies, D. Effect of directional elements on the directional response of circular antenna arrays. In IEE Proceedings H (Microwaves, Optics and Antennas); IET: London, UK, 1982; Volume 129, pp. 18–22. [Google Scholar]
- Pesavento, M.; Bohme, J. Direction of arrival estimation in uniform circular arrays composed of directional elements. In Proceedings of the Sensor Array and Multichannel Signal Processing Workshop Proceedings, Trondheim, Norway, 20–23 June 2022; IEEE: New York, NY, USA, 2022; pp. 503–507. [Google Scholar]
- Jackson, B.R.; Rajan, S.; Liao, B.J.; Wang, S. Direction of arrival estimation using directive antennas in uniform circular arrays. IEEE Trans. Antennas Propag. 2014, 63, 736–747. [Google Scholar] [CrossRef]
- Alinezhad, P.; Seydnejad, S.R.; Abbasi-Moghadam, D. DOA estimation in conformal arrays based on the nested array principles. Digit. Signal Process. 2016, 50, 191–202. [Google Scholar] [CrossRef]
- Gao, X.F.; Li, P.; Hao, X.H.; Li, G.L.; Kong, Z.J. A novel DOA estimation algorithm using directional antennas in cylindrical conformal arrays. Defence Technol. 2020, 17, 1042–1051. [Google Scholar] [CrossRef]
- Pal, P.; Vaidyanathan, P.P. Nested arrays: A novel approach to array processing with enhanced degrees of freedom. IEEE Trans. Signal Process. 2010, 58, 4167–4181. [Google Scholar] [CrossRef]
- Mathews, C.P.; Zoltowski, D.M. Eigenstructure techniques for 2-D angle estimation with uniform circular arrays. Signal Process. IEEE Trans. 1994, 42, 2395–2407. [Google Scholar] [CrossRef]
- Belloni, F.; Richter, A.; Koivunen, V. DoA estimation via manifold separation for arbitrary array structures. IEEE Trans. Signal Process. 2007, 55, 4800–4810. [Google Scholar] [CrossRef]
- Doron, M.A.; Doron, E. Wavefield modeling and array processing, Part I—Spatial sampling. IEEE Trans. Signal Process. 1994, 42, 2549–2559. [Google Scholar] [CrossRef]
- Ma, W.K.; Hsieh, T.H.; Chi, C.Y. DOA estimation of quasi-stationary signals with less sensors than sources and unknown spatial noise covariance: A Khatri–Rao subspace approach. IEEE Trans. Signal Process. 2009, 58, 2168–2180. [Google Scholar] [CrossRef]
- Zheng, Z.; Huang, Y.X.; Wang, W.Q.; So, H.C. Augmented Covariance Matrix Reconstruction for DOA Estimation Using Difference Coarray. IEEE Trans. Signal Process. 2021, 69, 5345–5358. [Google Scholar] [CrossRef]
- Cao, M.Y.; Huang, L.; Qian, C.; Xue, J.Y.; So, H.C. Underdetermined DOA estimation of quasi-stationary signals via Khatri–Rao structure for uniform circular array. Signal Process. 2015, 106, 41–48. [Google Scholar] [CrossRef]
- Yadav, S.K.; George, N.V. Underdetermined DOA estimation using arbitrary planar arrays via coarray manifold separation. IEEE Trans. Veh. Technol. 2022, 71, 11959–11971. [Google Scholar] [CrossRef]
- Schmidt, R. Multiple emitter location and signal parameter estimation. IEEE Trans. Antennas Propag. 1986, 34, 276–280. [Google Scholar] [CrossRef]
- Roy, R.; Kailath, T. ESPRIT-estimation of signal parameters via rotational invariance techniques. IEEE Trans. Acoust. Speech Signal Process. 1989, 37, 984–995. [Google Scholar] [CrossRef]
- Marcos, S.; Marsal, A.; Benidir, M. The propagator method for source bearing estimation. Signal Process. 1995, 42, 121–138. [Google Scholar] [CrossRef]
- Li, J.; Zhang, X.; Chen, H. Improved two-dimensional DOA estimation algorithm for two-parallel uniform linear arrays using propagator method. Signal Process. 2012, 92, 3032–3038. [Google Scholar] [CrossRef]
- Liu, C.L.; Vaidyanathan, P. Remarks on the spatial smoothing step in coarray MUSIC. IEEE Signal Process. Lett. 2015, 22, 1438–1442. [Google Scholar] [CrossRef]
- Bowman, F. Introduction to Bessel Functions; Courier Corporation: New York, NY, USA, 2012. [Google Scholar]
- Stoica, P.; Larsson, E.G.; Gershman, A.B. The stochastic CRB for array processing: A textbook derivation. IEEE Signal Process. Lett. 2001, 8, 148–150. [Google Scholar] [CrossRef]
- Nechaev, Y.; Peshkov, I.; Fortunova, N. Evaluation and minimization of Cramer-Rao bound for conformal antenna arrays with directional emitters for DOA-estimation. Prog. Electromagn. Res. C 2019, 90, 139–154. [Google Scholar] [CrossRef]




| Number of UCAs | Elements per UCA | All Difference Sensors | |
|---|---|---|---|
| Even | N | ||
| Odd |
| Method | Computational Complexity | |
|---|---|---|
| 1-D Methods | CCA-MST | |
| CCA-Coarray | ||
| Interpolation | ||
| 2-D Methods | 2-D MUSIC | |
| CCA-PM | ||
| CCA-ESPRIT |
| Parameter | Value |
|---|---|
| Carrier Frequency | 12 GHz |
| Wavelength | 2.5 cm |
| Antenna Gain | 5 dB |
| VSWR | Average 1.24 |
| Radiation Efficiency | 68% |
| Element Number N | 12 |
| Radius of the Array r | 2.26 cm |
| Cone Angle | |
| High h | 3.4 cm |
| Snapshots Q | 1024 |
| (a) CCA-MST | ||
|---|---|---|
| Target 1 | Target 2 | |
| Target Angle | ||
| Estimated Value | ||
| Error | ||
| (b) CCA-Coarray | ||
| Target 1 | Target 2 | |
| Target Angle | ||
| Estimated Value | ||
| Error | ||
| (c) CCA-PM | ||
| Target 1 | Target 2 | |
| Target Angle | ||
| Estimated Value | ||
| Error |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhang, H.; Li, P.; Zhang, G.; Li, G.; Gao, X. 1-D and 2-D Direction of Arrival Estimation in a Conical Conformal Array: Design and Implementation. Sensors 2023, 23, 4536. https://doi.org/10.3390/s23094536
Zhang H, Li P, Zhang G, Li G, Gao X. 1-D and 2-D Direction of Arrival Estimation in a Conical Conformal Array: Design and Implementation. Sensors. 2023; 23(9):4536. https://doi.org/10.3390/s23094536
Chicago/Turabian StyleZhang, Hongyun, Ping Li, Guangwei Zhang, Guolin Li, and Xiaofeng Gao. 2023. "1-D and 2-D Direction of Arrival Estimation in a Conical Conformal Array: Design and Implementation" Sensors 23, no. 9: 4536. https://doi.org/10.3390/s23094536
APA StyleZhang, H., Li, P., Zhang, G., Li, G., & Gao, X. (2023). 1-D and 2-D Direction of Arrival Estimation in a Conical Conformal Array: Design and Implementation. Sensors, 23(9), 4536. https://doi.org/10.3390/s23094536







